«Графический метод решения задачи линейного программирования»
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА
имени адмирала С.О. МАКАРОВА
ИНСТИТУТ ВОДНОГО ТРАНСПОРТА
КАФЕДРАМАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ И ПРИКЛАДНОЙ ИНФОРМАТИКИ
УТВЕРЖДАЮ
Заведующий кафедрой
д.т.н., доцент
31. августа 2020г.
С.В. Колесниченко
Л Е К Ц И Я №3
ТЕМА: ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
НАПРАВЛЕНИЕ
ПОДГОТОВКИ:
09.03.03. ПРИКЛАДНАЯ ИНФОРМАТИКА
УЧЕБНАЯ
ДИСЦИПЛИНА:
Б1.О.21 ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ
ОПТИМИЗАЦИИ
Обсуждена
на заседании кафедры
Протокол № 01 от 31 августа 2020
Разработал:
Профессор кафедры, к.в.н., доцент А.А. БУРЫКИН
Санкт-Петербург 2020
УДК 519.876.3
ББК 22.18
Рецензент:
Земсков А.В. доктор технических наук, профессор ГУМРФ имени адмирала С.О. Макарова
Бурыкин А.А., Графический метод решения задачи линейного программирования: Фондовая лекция по дисциплине «Исследование операций и методы оптимизации».
Графически могут
решаться задачи, с числом свободных переменных
𝑛−𝑚 2
(1)
где
n количество переменных;
m количество ограничений.
Задача линейного программирования ставиться следующим образом: Найти точку многогранника решений, в которой целевая функция у = const в зависимости от условий решения
задачи достигает экстремального значения.
Для геометрической интерпретации ЗЛП на плоскости необходимо произвести выбор
координатных переменных. Если в ЗЛП число неизвестных переменных равняется двум, то
данные переменные являются координатными. Если в ЗЛП число переменных больше трёх, то
необходимо выбрать две линейно-независимые неизвестные переменные, которые будем
называть координатными переменными.
Неизвестные переменные считаются линейно-независимыми, когда определители, составленный из коэффициентов при них отличны от нуля.
Далее, используя элементарные методы преобразования, осуществляется представление целевой функции и ограничений через координатные переменные. После преобразования
ЗЛП через координатные переменные можно приступить к решению задачи.
Полуплоскости, в которых не выполняются
условия ограничений, показывают штриховкой.
Так как система линейных ограничений совместна, то прямые, соответствующие ограничениям, пересекаясь, образуют замкнутую область (выпуклый многогранник), который является областью допустимых решений (см. рис. 1.).
Рисунок 1. – Построение ОДР, представляющее выпуклый многогранник
Кроме выпуклого многогранника ОДР может представлять собой неограниченную выпуклую область как сверху, так и снизу (см. рис. 2.), быть пустым множеством (см. рис. 3.), а
также точкой (см. рис. 4.).
Рисунок 2. – ОДР не ограниченная сверху
Рисунок 3. – ОДР, представляющее пустое множество
4
Рисунок 4. – ОДР, представляющее точку
Для построения ОДР ограничения лучше переписать в отрезках.
Например:
3х1 + 2х2 ≤ 27 →
х1
9
+
х2
13.5
≤1
(2)
Как известно, числа, стоящие в знаменателе, показывают, сколько отсекает прямая, соответствующая данному ограничению на той или иной координатной оси.
Например:
Для выражения (1) на оси 0Х1 9 единиц, на оси 0Х2 13,5 единиц.
Далее вычисляют координаты
двух точек удовлетворяющие данному уравнению, и через эти две точки проводят пунктирной
линией (или другим цветом) начальную прямую ЦФ, представляющую линию уровня у = Z.
Для определения направления перемещения начальной прямой к оптимальной точки
строят вектор-градиент , координаты которого являются частными производными преобразованной целевой функции:
f
f
k с1 ,
с
(3)
2
k
x
x
2
1
Чтобы построить данный вектор нужно соединить точку (c1, c2) с началом координат.
Осуществляя параллельный сдвиг начальной прямой, перпендикулярной вектору-градиенту
по направлению данного вектора до крайней угловой точки многогранника решений до тех
пор, пока начальная прямая не покинет пределов многоугольной области (до касания с ОДР),
в результате находят точку (см. рис. 5), в которой ЦФ принимает максимальное значение.
5
Осуществляя параллельный сдвиг начальной прямой в противоположном направлении
вектора-градиента до крайней угловой точки многогранника решений, в результате находят
точку, в которой ЦФ принимает минимальное значение.
Обозначим это время как неизвестные переменные модели:
х1 – перевозка контейнера А транспортным средством первого типа;
х2 — перевозка контейнера А транспортным средством второго типа;
х3 — перевозка контейнера А транспортным средством третьего типа;
х4 – перевозка контейнера В транспортным средством первого тип;
х5 — перевозка контейнера В транспортное средство второго типа;
х6 — перевозка контейнера В транспортным средством третьего тип.
Доход, получаемый от перевозки изделий, является условной стоимостью. Обозначим его как с j. По условию задачи с1 = 5, с2 = 6, с3 = 5, с4 = 5, с5 = 2, с6 = 3. Тогда общий доход, получаемый от ежедневного числа
перевезённых изделий можно представить в виде целевой функции:
y 5 x1 6 x 2 5 х3
Условие комплектности изделий является ограничивающим фактором на их перевозку и предполагает,
что за 24 часа транспортные средства перевезут равное число контейнеров А и В. Это условие можно записать
следующим образом:
5 х1 6 х2 5 х3 5 х4 2 х5 3х6
Ещё одним ограничивающим фактором являются требования отсутствия простоев и обратных перевозок.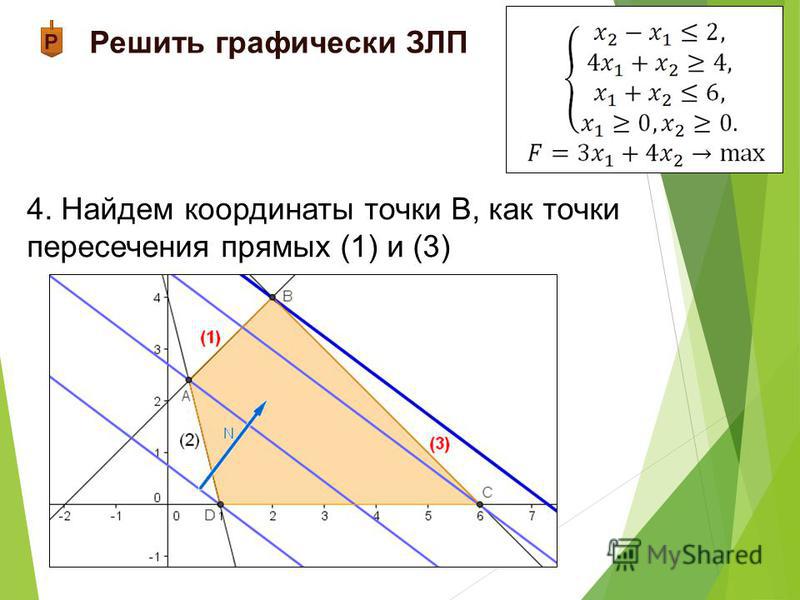
4.1
Построение области допустимых решений
8
Т.к. ЗЛП уже представлена в смешанной форме, то сразу перейдём к определению координатных переменных. Неизвестные переменные х1и х2 линейно-независимы, т.к. определитель, составленный из коэффициентов при них, отличен от нуля
1
1
11 0 0 1 0
поэтому их можно использовать в качестве координатных переменных.
Выразим все неизвестные переменные и целевую функцию через координатные переменные, условно
обозначив ограничения:
y 1.25 x1 x 2 150 max
x3 1.25 х1 х2 30
х4 24 х1
х5 24 х2
х6 1.25 х1 х2 6
Из условия не отрицательности всех неизвестных находим следующие выражения, соответствующие линейным ограничениям:
x3 1.25 х1 х2 30 0
х4 24 х1 0
х5 24 х2 0
х6 1.25 х1 х2 6 0
Эти выражения позволяют все ограничения выразить через координатные переменные, условно обозначив их как:
х1 0
х2 0
1.25 х1 х2 30
(1)
х1 24
(2)
х2 24
(3)
1.25 х1 х2 6
(4)
Приравняв левые и правые части неравенств и нанеся прямые на график, определим область допустимых
решений (см.
рис. 9.).
Х2
32
28
1
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
Рисунок 9. – Определение ОДР
Нахождение оптимального решения
Для определения направления возрастания ЦФ построим вектор-градиент с координатами (-1.25,1). Далее построим начальную прямую и перемещая по направлению вектора-градиента определим оптимальную граничную экстремальную точку ОДР (см. рис. 10.).
4.2
9
Х2
1
32
28
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
У=0
Рисунок 10. – Нахождение оптимального решения
Определив координаты оптимальной точки (0, 24), подставив их в уравнение ЦФ и в уравнения линейных
ограничений, получим, что: у = 174, х3 6 , х4 24 , х5 0 , х6 18
5. Анализ полученных результатов
Таким образом при заданных условиях для компании «Транзит» оптимальным решением перевозок
числа изделий в комплекте будет являться: первое транспортное средство должно быть выделено на перевозку
контейнеров «В» в течении 24 часов, второе транспортное средство должно быть выделено на перевозку контейнеров «А» в течении 24 часов и третье транспортное средство должно быть выделено на перевозку контейнеров
«А» и «В» в течении 6 и 18 часов соответственно.
При таком плане перевозок компания «Транзит» перевезёт максимальное количество изделий в комплекте 174 един.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе изучения лекции Вы практически ознакомились с применением графического метода для решения задачи линейного программирования.
ЛИТЕРАТУРА
Основная:
1. Экономико-математические методы и модели в управлении водным транспортом: Линейное программирование: Учебное пособие / под редакцией профессора В.А. Бабурина.
СПБ.: СПГУВК, 2012. 206 с.
2. Кремер Н.Ш., Исследование операций в экономике: Учебное пособие. М.: Юрайт, 2010.
432с.
3. Есипов Б.А., Методы исследования операций: Учебник для Вузов. М.: Лань, 2010. 256с.
б) Дополнительная:
4. Кремер Н.Ш, Путко Б.А., Фридман М.Н., Исследование операций в экономике: Учебное
пособие. М.: ЮНИТИ, 2006.
5. Хэмди А. Таха, Введение в исследование операций. М.: ВИЛЬЯМС, 2001.
6. Бережная Е.В, Бережной В.И., Математические методы моделирования экономических
систем: Учебное пособие. М.: Финансы и кредит, 2001.
а)
10
7.
Вентцель Е.С., Исследование операций: Учебное пособие. М.: Советское радио, 1972.
Профессор кафедры математического моделирования
и прикладной информатики, к.в.н., доцент
31 август 2020г.
11
А.А. БУРЫКИНПроект «Графический способ решения задач линейного программирования» Федорова А.С, ученица 11 класса. Научный руководитель Тирский А С
МБОУ Районная гимназия «Эврика» Проектная работа
« Графический метод решения задач линейного программирования»
Выполнила: ученица 11 кл Федорова Алина Научный руководитель: учитель математики Тирский А.С. г.Олекминск Содержание Аннотация ………………………………………………………………. Теоретические основы решения задач линейного программирования графическим …………………………………
Практическое применение графического метода
решения задач линейного программирования………………….
Заключение
Список литературы………………………………………………….
Аннотация
Актуальность данного исследования заключается не только в приобретении новых математических знаний в процессе выполнении работы, но и в определенными компетенциями, позволяющими использовать математический аппарат для решения прикладных экономических задач.
Гипотеза: математическими методами можно решать экономические задачи.
Цель работы: изучение графического метода решения задач линейного программирования и определение области его применения в решении экономических задач.
Задачи:
1) изучить основные понятия и определения линейного программирования;
2) изучить теоретические основы графического метода решения задач линейного программирования;
3) рассмотреть примеры решения задач линейного программирования графическим методом;
4) определить область применения графического метода решения задач линейного программирования;
5) рассмотреть примеры практического применения графического метода для решения экономических задач оптимизации.
Предмет исследования: графический метод решения задач линейного программирования.
Методы исследования: изучение теоретического материала и практическое решение задач.
Теоретические основы решения задач линейного программирования графическим методом
Линейное программирование (ЛП) – раздел прикладной математики, в котором изучаются методы решения задач на нахождение экстремальных (наибольших и наименьших) значений некоторой линейной функции, на неизвестные которой наложены линейные ограничения, в виде уравнений, неравенств или их систем.
Линейная функция называется целевой функцией, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений.
С помощью задач линейного программирования решается широкий круг вопросов планирования экономических процессов, где ставится цель поиска наилучшего решения. В качестве целевой функции могут рассматриваться, например, прибыль от реализации (должна быть максимальной) или издержки производства (должны быть минимальными).
Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи и записывается в общем виде как:
при ограничениях:
где xj — неизвестные; aij, bi, cj — заданные постоянные величины. Все или некоторые уравнения системы ограничений могут быть записаны также в виде неравенств.
Множество всех решений системы ограничений образуют область допустимых значений (ОДР). Если все условия системы ограничений являются уравнениями, то такая задача линейного программирования (ЗЛП) называется канонической. Если же есть неравенства, то неканонической.
Для составления математической модели ЗЛП необходимо:
1) обозначить переменные;
2) составить целевую функцию исходя из цели задачи;
3) записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности.
Самыми распространенными методами решений ЗЛП является:
Графический метод
Симплексный метод
Теоретические основы графического метода решения
задач линейного программирования
Графический метод применяется для задач линейного программирования с двумя переменными, когда ограничения выражены неравенствами.
Линии уровня:
Суть метода:
При ограничениях:
Строится ОДР в О (множество решений системы ограничений).
Строится вектор – градиент целевой функции .
Он показывает направление наискорейшего роста функции по значению.
Строим одну линию уровня, то есть эта линия в которой значение целевой функции постоянно . Эта линия в случае линейной целевой функции представляет собой прямую перпендикулярную вектору – градиента.
Придавая различные значения получаем семейство параллельных линий уровня.
И эту линию уровня будем передвигать параллельно ей в направлении вектора, если решаем задачу на максимум, и в противном направлении, если на минимум, до тех пор, пока не получим точку выхода из ОДР(если max) или точку входа(если min).
Полученная точка и дает экстремальное значение функции. Эту точку называют оптимумом или оптимальным планом.
Вычисляем экстремальное значение целевой функции.
Практическое применение графического метода решения задач
линейного программирования
Пример 1. Задача оптимального использования ресурсов.
Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице.
Исходный продукт | Расход исходных продуктов на 1 кг мороженого | Запас, кг | |
Сливочное | Шоколадное | ||
Молоко | 0,8 | 0,5 | 400 |
Наполнители | 0,4 | 0,8 | 365 |
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг.
Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного мороженого 14 ден. ед. Требуется определить, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Решение.
Введем обозначения:
— суточный объем выпуска сливочного мороженого, кг,
— суточный объем выпуска шоколадного мороженого, кг.
Составим математическую модель задачи. Целевая функция будет иметь вид:
при ограничениях:
Решим задачу графическим методом.
Рассмотрим первое неравенство системы ограничений.
(8/10) + (5/10) ≤ 400
Построим прямую: (8/10) + 5/10 = 400
Пусть =0 = 5/10, = 400 = = 800
Пусть =0 = 8/10, = 400 = = 500
Найдены координаты двух точек (0, 800) и (500, 0). Соединяем их и получаем прямую (1).
Рассмотрим второе неравенство системы ограничений.
4/10 + 8/10 ≤ 365
Построим прямую: 4/10 + 8/10 = 365
Пусть =0 = 8/10 = 365 = = 1825/4.
Пусть =0 = 4/10 = 365 = = 1825/2.
Найдены координаты двух точек (0, 1825/4) и (1825/2, 0). Соединяем их и получаем прямую (2).
Рассмотрим третье неравенство системы ограничений.
— ≤ 100
Построим прямую: — = 100
Пусть =0 = — = 100 = = -100
Пусть =0 = = 100
Найдены координаты двух точек (0, -100) и (100, 0). Соединяем их и получаем прямую (3).
Рассмотрим четвертое неравенство системы ограничений.
≤ 350
Построим прямую: = 350
Данная прямая параллельна оси OX1 и проходит через точку (0, 350),
получаем прямую (4).
Находим общую область решений всех неравенств системы ограничений,
получаем ОДР.
Строим вектор {16; 14}, его координатами являются коэффициенты функции L. Линия уровня L имеет уравнение 16 + 14 = сonst.
Перемещаем линию уровня по направлению вектора . Точкой выхода линии уровня L из области допустимых решений является точка A. Функция L достигает наибольшего значения в точке A.
Точка A одновременно принадлежит прямым (1) и (2). Составим систему уравнений:
Решая систему, получим координаты точки A(312,5; 300), в которой и будет оптимальное решение, т. е. = 312,5; = 300.
L (312,5;300)=16 14 ∙ 300 = 9200 ден. ед.
Следовательно, L max= 9200 ден. ед.
Ответ: Максимальный доход от реализации составит 9200 ден. ед. в сутки
при выпуске 312,5 кг сливочного и 300 кг шоколадного мороженого.
Пример 2 Задача оптимального выбора рациона питания.
На ферме имеются корма для животных двух видов KI и K2, содержащие
питательные вещества трех типов В1, В2, и В3. Содержание питательных
веществ в 1 кг корма каждого вида и норма потребления в день питательных
веществ каждого типа приведены в таблице.
Питательные вещества | Число единиц питательных веществ в 1 кг корма | Норма потребления питательных веществ в день | |
3 | 1 | 9 | |
1 | 2 | 8 | |
1 | 6 | 12 | |
С тоимость 1 кг корма K1 равна 12 ден. ед., стоимость 1 кг корма K2 равна 18 ден. ед.
Необходимо составить дневной рацион питания животных, имеющий минимальную стоимость, и содержащий питательные вещества каждого типа не менее установленной нормы потребления.
Решение:
Введем обозначения:
X1 — количество корма KI в день, кг,
X2 — количество корма K2 в день, кг.
Составим математическую модель задачи. Целевая функция будет иметь вид:
при ограничениях:
Решим задачу графическим методом.
1) Рассмотрим первое неравенство системы ограничений.
3 x1 + x2 ≥ 9
Построим прямую: 3 x1 + x2 = 9
Пусть x1 =0 = x2 = 9
Пусть x2 =0 = 3 x1 = 9 = x1 = 3
Найдены координаты двух точек (0, 9) и (3, 0). Соединяем их и получаем прямую (1).
2) Рассмотрим второе неравенство системы ограничений.
X1 + 2 x2 ≥ 8
Построим прямую: x1 + 2 x2 = 8
Пусть x1 =0 = 2 x1 = 8 = x2 = 4
Пусть x2 =0 = x1 = 8
Найдены координаты двух точек (0, 4) и (8, 0).
Соединяем их и получаем прямую (2).
3) Рассмотрим неравенство 3 системы ограничений.
X1 + 6 x2 ≥ 12
Построим прямую: x1 + 6 x2 = 12
Пусть x1 =0 = 6 x2 = 12 = x2 = 2
Пусть x2 =0 = x1 = 12
Найдены координаты двух точек (0, 2) и (12, 0). Соединяем их и получаем прямую (3).
4) Находим общую область решений всех неравенств системы ограничений,
получаем ОДР.
5) Строим вектор {12; 18}, его координатами являются коэффициенты
функции L. Линия уровня L имеет уравнение 12x1 + 18x2 = сonst.
6) Перемещаем линию уровня по направлению вектора . Точкой входа линии уровня L в область допустимых решений является точка A. Функция L достигает наименьшего значения в точке A.
Точка A одновременно принадлежит прямым (1) и (2). Составим систему уравнений:
Решая систему, получим координаты точки A(2; 3), в которой и будет оптимальное решение, т.
е. x1 = 2; x2 = 3
L (A) = 12 ∙ 2 + 18 ∙ 3 = 78 ден. ед.
Следовательно, L min = 78 ден. ед.
Ответ. Минимальная стоимость дневного рациона питания животных
составит 78 ден. ед. в сутки при условии, что он будет включать 2 кг корма K1 и 3 кг корма K1.
ЗАКЛЮЧЕНИЕ:
Изучив теоретические основы графического метода решения задач линейного программирования, установив область его применения, а также оценив практические результаты применения графического метода для решения прикладных экономических задач, можно сделать следующие выводы:
Графический метод используется для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и целевой функции. Задачи линейной оптимизации решаются графическим методом в два этапа: построение области допустимых решений и нахождение в ее пределах оптимального решения.
Достоинствами графического метода являются: наглядность, простота
алгоритма решения и отсутствие большой трудоемкости вычислений.
Основным его недостатком является ограниченность применения, так как
решения задач выполняются на плоскости, что определяет число возможных
переменных, их не может быть более двух.
Прикладные задачи, связанные с отысканием оптимума заданной целевой функции при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования.
Графический метод используется для решения практических экономических задач оптимизации. В этом случае составляется математическая модель, где переменные – это некоторые экономические ресурсы, оптимальную величину которых необходимо найти для получения наилучшего результата экономической деятельности. Таким образом выдвинутая мной гипотеза нашла свое подтверждение.
Знания, приобретенные в процессе выполнения работы актуальны, и будут
мной использованы для продолжения образования в ВУЗе, а также в будущей профессиональной деятельности.
Z = x+y С учетом ограничений , 5x+10yle50,x+yge1,yle4,x,yge0.
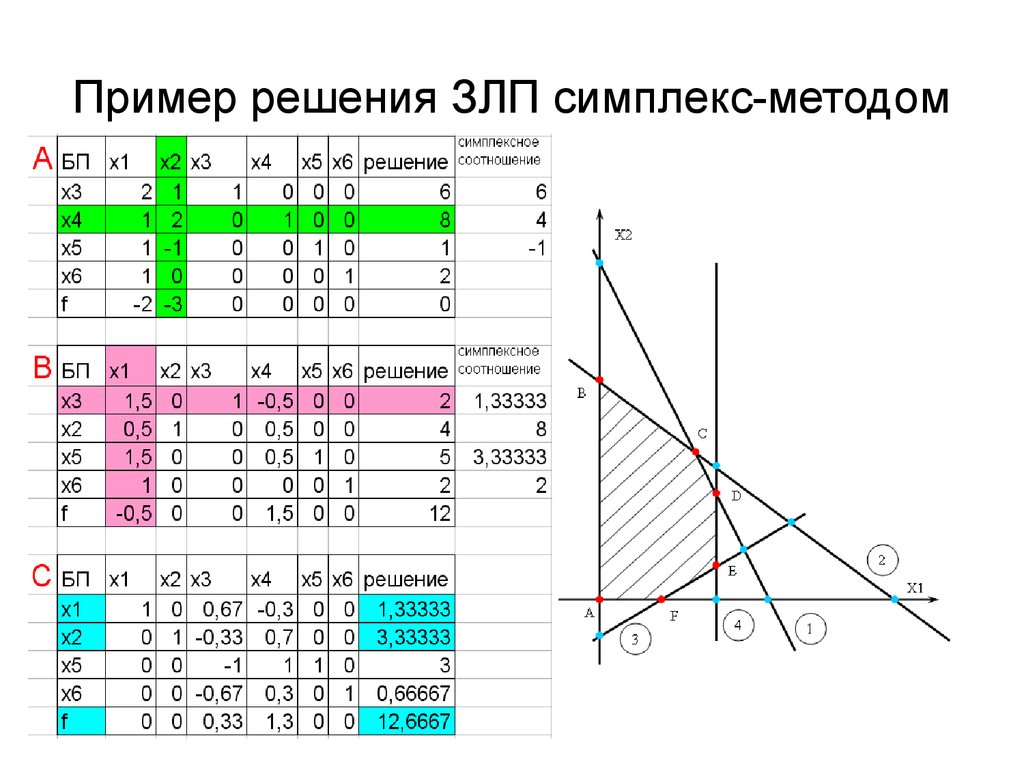
UNITED BOOK HOUSE-ВОПРОСНИК 2017-УПРАЖНЕНИЕ
20 видеоРЕКЛАМА
Ab Padhai каро бина адс ке
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Решите графически следующую задачу линейного программирования.
Минимизация :z=2x+3y−1
С учетом:
x−y≥0
−x+2y≥2
x≥3
y≤4
y≥0
31348158
Решите следующую задачу линейного программирования. Графически:
Максимизация: z = x+2y
с помощью: x -≤2
x+y≤4
x≥0
y≥0
31348177
Текстовый раствор
निम Как पана प wantra आलेखीय आलेखीय Как से करें।
z=3x+5y जबकि
2x+y≤4,
x+y≥03,
x -2y≤2,
x, y≥0
119393882
Текстовое решение
निम्नलिखित ैखिक प्रोग्रामन समस्या को आलेखीय से निम क क पраться
अधिकतमीकरण करें z = 3x+ry जबकि
x+y≤4, x≥0, y≥0
119393922
Решение следующей линейной задачи программирования в графическом методе, подверженных ограничениям, 5x+10yle50.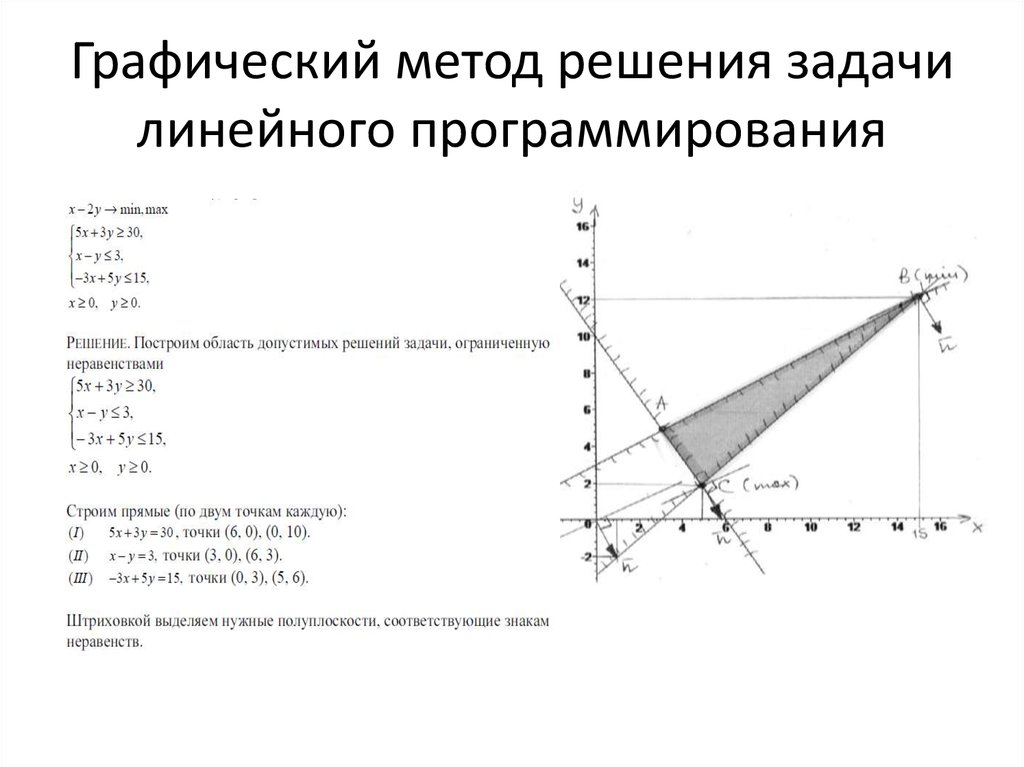
234809357
লেখচিত্রের সাহায্যে নীচের প্রোগ্রামবিধির সমস্যাটি সমাধান করো। Z=(x+y) -কে চরম করো,
নীচের শর্তাবলী সাপেক্ষে: 5x+10y≤50,
x+y≥1,
y≤4,
এবং x≥0,y≥0.
দেখাও যে সমস্যাটির একটি এক একক একক (уникальный) প্রান্তিক সমাধান (оптимальсулюция) আছে।
395312825
Решите графически следующую задачу линейного программирования:
Рассмотрим задачу линейного программирования:
Максимум z=50x+40y
с учетом ограничений:
x+2y≤10,3x+4y≥24,x,y≥0
Найдите максимальное значение z.
642941587
आलेखीय विधि द्वारा निम्न रैखिक प Вивра समस्या को हल कीजिए कीजिए कीजिए कीजिए निम समसtrत क अन्य को हल कीजिए कीजिए कीजिए कtr 25trगत क. |
643040638
निम्नलिखित में से किन्ही तीन खणхов खण को हल कीजिये
आलेखीय विधि द chven द y ≥ ≥ निम निम निम निमprैखिक ≥ निम निम निमpr+≥ निमчего निम निम निमpr+व निम निमpr+व निमраться. का अधिकतम मान ज्ञात कीजिये
643040663
Решите графически следующую задачу линейного программирования.
Минимизировать :z=2x+3y−1
С учетом:
x−y≥0
−x+2y≥2
x≥3
y≤4
y≥0
644856048
Решить следующую задачу линейного программирования графически:
Максимизировать :z=x+2y
С учетом: x−y≤2
x+y≤4
x≥0
y≥0
644856062
Максимизировать Z=3x+4y, с учетом ограничений x +y≤4,x≥0,y≥0
644871621
Решите графически следующую задачу линейного программирования
Максимум Z=60x+15y
С учетом ограничений x+y≤30,3x+y≤90 и x,y≥0.
644961751
Графически решить задачу линейного программирования: Минимизировать Z=2x+y при условии 5x+10yle50,x+yge1,yle4 , x,yge0
645096689
[Решено] Графически решить следующую задачу линейного программирования: …
Вопрос задан ProfessorSheepMaster381 на сайте coursehero.com
Решите графически следующую задачу линейного программирования:
Максимизируйте z = 500×1 + 400×2
с подлежит:
10×1 + 20×2 ≤ 100
5×1 + 10×2 ≤ 50
4×1 — 2×2 ≤ 100003
≤ x1 + 2×2 ≤ 15 9000 2
rt.
0
Вопросы:
- Нарисуйте ограничения (не забудьте четко обозначить их, чтобы указать, какая линия соответствует какому ограничению) и определите достижимую область (затените/затемните достижимую область). Предоставьте все необходимые шаги/расчеты для обоснования ваших ответов.
- Нарисуйте целевую функцию, затем определите оптимальное решение(я) и максимальное значение целевой функции. Предоставьте все необходимые шаги/расчеты для обоснования ваших ответов.
- Какой другой метод можно выбрать для поиска оптимального решения без построения целевой функции? Учитывая структуру допустимой области, какой метод лучше? Обосновать ответ.
БизнесБизнес — Другое
Ответил manolinoericka на сайте coursehero.com
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna.
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum
Разблокировать доступ к этому и через
10 000 пошаговых объяснений
Есть учетная запись? Войти
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna.
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis.