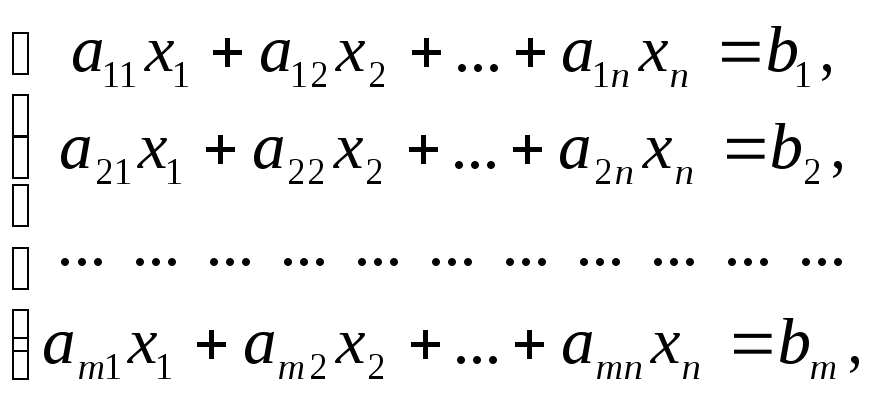Решить однородную систему линейных алгебраических уравнений: Теоретический курс и примеры по курсу линейной алгебры

Свойства решений, эквивалентное преобразование системы.

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называетсятривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Свойства решений систем линейных алгебраических уравнений

Используя свойства линейных операций с матрицыми, нетрудно доказать, справедливость следующих утверждений.

1. Если и— два решения системы, то при любыхи вектор — решение системы.

2. Если и— два решения системы, то вектор— решение приведенной однородной системы.

3. Если решение системы, а— решение системы, то вектор— решение системы.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы

25.

Система совместна – если имеет хотябы одно решение. Несовместна – если не имеет ни одного решениия

Система линейных алгеьраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Если система совместна, найти какой-либо базисный минор порядка r(минор, порядок которого определяет ранг матрицы, называется ранг матриц). Взять r уравнений из коэффицентов которых составлен базисный минор(остальные уравнения отбросить). Неизвестные которые входят в базисный минор называются главными, и оставляются слева, а оставшиеся назыаются свободные, и переносятся вправо

26. Понятие о линейной зависимости решений; существование фундаментальной системы решений

. Пусть дана однородная система линейных уравнений

(*)

Предположим, что набор чисел — какое-то решение этой системы.

И вообще, любая линейная комбинация решений системы (*) является решением этой системы.

Всякий базис в множестве Q состоит из n – r векторов e₁,…,e_n—r. Соответствующая ему в каноническом базисе система вектор-столбцов Е₁,…, Е_n–r наз. фундаментальной системой решений.

К примеру у нас было 4 неизвестных, 2 базисных, 2 свободных.

½ + 3/2c1-1/2c2

C1

C2

Базисные решения Е₁,. .., Е_n–r могут быть получены по правилу Крамера, если свободным неизвестным придавать пооче­редно значение 1, полагая остальные равными 0.

27. Выражение базисных через свободные

Если система совместна, найти какой-либо базисный минор порядка r(минор, порядок которого определяет ранг матрицы, называется ранг матриц). Взять r уравнений из коэффицентов которых составлен базисный минор(остальные уравнения отбросить). Неизвестные которые входят в базисный минор называются главными, и оставляются слева, а оставшиеся назыаются свободные, и переносятся вправо.

После чего выражаем базисные через свободные.

Как пример: Получена система 2×1+x2=2+x3+3×4 ; 4×1 = 3-x3+7×4

у нас было 4 неизвестных, 2 базисных, 2 свободных. X3,x4 заменяем на c1 и с2. Как пример ответ: ( ¾ — 1/4с1+7/4с2)

½ + 3/2c1-1/2c2

C1

C2

28. Понятие обшего решения одногородной системы, теорема об общем решении

Однородная система: АX=0. Неоднородная AX=B

Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т.е. r<n. Если r<n то

Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю

Определяем ранг матрицы. Базисный минор – из него черпаем именно те неизвестные. Остальные неизвестные заменяем на c1…cn. Затем выписываем общее решение, и делаем фундаменталку – т.е. если у нас 3 c1 c2 c3, в каждом решении чередуем 1 и 0 – (x1,x2,1,0,0), (x1,x2,0,1,0)

29.

Решим систему

Преобразуем её к

Тогда переменные иобязательно будут главными, возьмём такжев качестве главной.

Заметим, что является частным решением.

Составим однородную систему:

Тогда, подставив единицу в качестве свободной переменной , получим ФСР однородной системы:

Общее решение системы может быть записано так:

30 МЕТОД ГАУССА

15. Исследование систем линейных алгебраических уравнений методом Гаусса.

Эффективным методом решения и исследования систем линейных уравнений является метод

— метод Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему (имеющей такие же решения) специального вида, которая легко исследуется и решается. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Применим данный метод для решения системы

Пусть в системе (1.7) а₁₁0. Этого можно добиться несколькими способами в числе которых перестановка уравнений местами, элементарные преобразования над строками. Все преобразования в дальнейшем будем проводить с расширенной матрицей. Нужно исключить все коэффициенты при х₁, т.е. обратить все элементы первого столбца, начиная со второй строки в 0. Разделим первую строку на а

Единственное условие, которое должно быть выполнено при выборе, состоит в том, что коэффициент при избранном неизвестном должен быть не равен 0.

x₁++…+=(1.10)

Исключим теперь х₁ из остальных уравнений системы. Будем умножать (1.8) последовательно на а₂₁, а₃₁,…, а_n1 и вычитать соответственно из 2-го, 3-го и последнего уравнений системы. После этого система уравнений (1.7), заменится эквивалентной системой.

(1.11)

Эти уравнения также образуют систему n уравнений с неизвестными х₁,…,х_n. Порядок ее тот же, что и у исходной системы. К ней можно применить такое же преобразование. Выбрать второе уравнение, коэффициент при х₂ привести к 1, исключить х

В результате получаем систему ступенчатого вида:

(1.12)

Возможны 3 случая.

Получаем строку вида: 0+0+0+…+0=d_r.

В этом случае решений нет.

a_nnx_n=b_n

В этом случае единственное решение.

— бесчисленное множество решений.

Пример Решить систему линейных алгебраических уравнений методом Гаусса.

Запишем расширенную матрицу системы:

.

Нужно преобразовать данную матрицу таким образом, чтобы а₁₁=1. Для этого можно разделить первую строку матрицы на 2. А можно переставить местами 1-ю и 2-ю строки, тогда получим а

.

Умножаем первую строку матрицы последовательно на (-2), (-4) и складываем соответственно со второй и третьей строками, получаем:

.

В полученной матрице 2-ю строку нужно разделить на 5, для того чтобы а₂₂=1. В данном примере проще провести следующие эквивалентные преобразования: 3-ю строку разделить на 9, и переставить местами 2-ю и 3-ю строки. Получим:

.

Теперь умножаем 2-ю строку на (-5) и прибавляем к третьей строке:

.

Получили матрицу ступенчатого вида. Третьей строке соответствует уравнение:

-4z=-4. Откуда получаем z=1. Второй строке соответствует уравнение: y—z=-2. Получаем, что у= -1. И, наконец, первой строке соответствует уравнение:

ГЛАВА 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

§ 1. Правило Крамера решения систем линейных уравнений

Определения. Системой линейных уравнений называется система уравнений вида:

(1)

Где

— известные числа, — неизвестные, . РешениемСистемы (1) называется упорядоченный набор чисел , который при подстановке в каждое из уравнений системы обращает его в верное равенство. Система называется Совместной, если она имеет хотя бы одно решение.

Введем следующие обозначения:

— матрица системы, Ã= —

Расширенная матрица,

— столбец неизвестных, — столбец свободных членов.

Матричными уравнениями называются уравнения вида АХ =В, ХА=В, АХВ=С, где A, B, C – известные матрицы, Х – Искомая.

Матрица

называется Решением матричного уравнения, если при подстановке в это уравнение она обращает его в верное равенство.

Лемма. Пусть А – матрица системы (1), а В – столбец ее свободных членов. Тогда система линейных уравнений (1) равносильна матричному уравнению

АХ=В, (2)

В следующем смысле: если

– решение (1), то столбец — решение (2), и наоборот.

►{

– решение (1)}

– решение (2)}.◄

Уравнение (2) называется Матричной формой записи системы (1).

Теорема (правило Крамера). Если в системе линейных уравнений число уравнений равно числу неизвестных и определитель системы

, то эта система имеет единственное решение, которое можно найти по формулам Крамера

, (3)

Где

– определитель, полученный из ∆ заменой J-ого столбца на столбец свободных членов.

►На основании доказанной леммы система (1) равносильна матричному уравнению (2), поэтому теорему доказываем для этого уравнения.

Единственность. Предположим, что (2) имеет два решения

. Тогда

{

и }

— противоречие.

Существование. Покажем, что

— (4)

Решение уравнения (2). Действительно,

Для получения же формул (3) распишем равенство (4) поэлементно. Введем обозначения: .Тогда:

(4)

[теорема замещения] = ◄

§ 2. Ранг матрицы

Определение. Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Ранг нулевой матрицы по определению равен нулю. Ранг матрицы будем обозначать так:

.

Замечание. Если все миноры K-го порядка матрицы А равны нулю, то все ее миноры (K+1)-го порядка тоже равны нулю. Таким образом, если

, это значит, что у матрицы А есть отличный от нуля минор R-го порядка, а все ее миноры (R+1)-го порядка равны нулю.

Определение. Элементарными преобразованиями матрицы называются:

1) умножение строк и столбцов на число, отличное от 0;

2) прибавление к какой либо строке (столбцу) другой строки (столбца), умноженной на число;

3) перестановка строк или столбцов.

Лемма. Последнее элементарное преобразование может быть получено последовательным применением первых двух

►Докажем утверждение для строк матрицы. Будем, как и раньше,

Обозначать сокращенно

I-ю строку матрицы А.

Аналогично утверждение доказывается и для столбцов.◄

Теорема. Элементарные преобразования не меняют ранга матрицы.

►Для первого элементарного преобразования утверждение, очевидно, выполняется, так как ранг матрицы зависит от того, будет ли минор равен нулю или нет. А это свойство минора не изменится при умножении строки или столбца на число, отличное от нуля. Если утверждение справедливо для второго преобразования, то его справедливость для третьего вытекает из доказанной леммы.

Доказательство проведем для строк матрицы А (для столбцов оно будет аналогичным). Обозначим

матрицу, полученную из прибавлением к I — й строке K-й строки, умноженной на число .

Пусть

. Надо доказать, что и . Разобьем доказательство на две части.

1. Покажем, что матрица

имеет отличный от нуля минор R-го порядка.

А) Матрица А имеет отличный от нуля минор R-го порядка, не содержащий I — й строки. Этот же минор является и минором матрицы

.

Б) Все миноры R-го порядка матрицы А, не содержащие I — й строки, равны нулю. Пусть

– отличный от нуля минор R-го порядка матрицы А.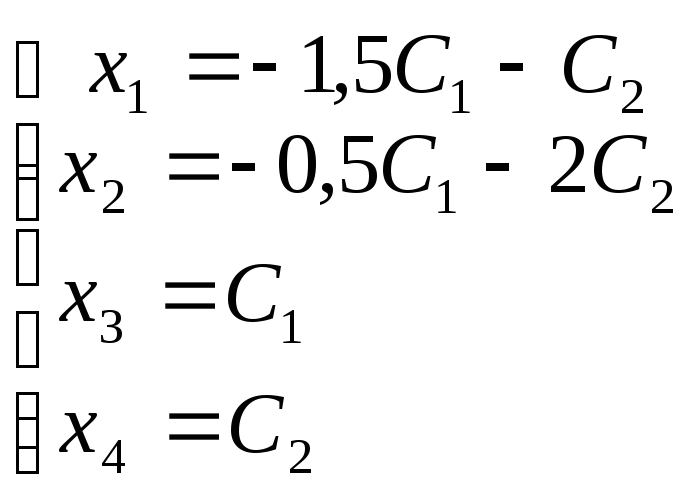 Рассмотрим минор матрицы, расположенный в тех же строках и столбцах.

(1)

(волна указывает, что эти строки короче, они содержат только те элементы, которые принадлежат выделенным столбцам). В равенстве (1) определитель

равен нулю, т. к. при — это минор матрицы А, не содержащий I — й строки, а при — это определитель, имеющий две одинаковые строки. Таким образом, .

2. Покажем, что все миноры (R+1)-го порядка матрицы

равны нулю.

А) Минор (R+1)-го порядка матрицы

не содержит I — й строки. Тогда он является также и минором матрицы А, а значит, равен нулю.

Б) Минор

(R+1)-го порядка матрицы содержит I — ю строку. Тогда

. (2)

В равенстве (2)

— минор (R+1)-го порядка матрицы А и, поэтому, равен нулю.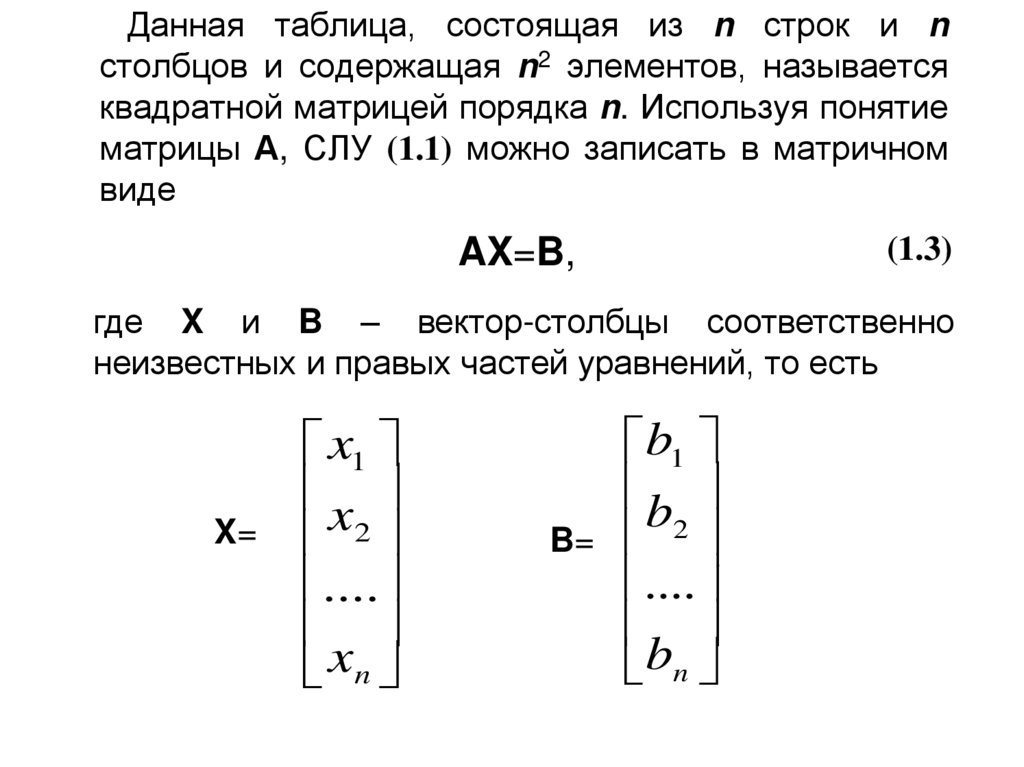 Что касается определителя , то при он содержит две одинаковые строки, а при — это минор (R+1)-го порядка матрицы А, а значит, в обоих случаях =0.◄

Свойства ранга матрицы

1°. Ранг матрицы не превосходит ни количества ее строк, ни количества столбцов.

2°. При транспонировании матрицы ее ранг не меняется.

3°. Если rang A = 0, то A – нулевая матрица.

4°. Если у матрицы вычеркнуть столбец или строку, полностью состоящую из нулей, то ее ранг при этом не изменится.

5°. Если у матрицы вычеркнуть однy из двух пропорциональных строк (столбцов), то её ранг при этом не изменится.

6°. Ранг произведения матриц не превосходит ранга каждого из сомножителей. При этом, если один из сомножителей – невырожденная матрица, то ранг произведения равен рангу второго сомножителя.

Первые четыре свойства очевидны, пятое вытекает из доказанной теоремы, а шестое мы докажем позже, в четвёртой главе.

§ 3. Теорема о базисном миноре

Определение. Строки матрицы А

(1)

Называются Линейно зависимыми, если существуют числа

, не все равные нулю такие, что

. (2)

Строки (1) называются Линейно независимыми, если равенство (2) выполняется Только в том случае, когда

.

Аналогично формулируется определение линейной зависимости и независимости для столбцов матрицы (позднее мы введем понятия линейной зависимости и независимости в более общем случае).

Определение. Базисным минором матрицы называется любой отличный от нуля её минор, порядок которого равен рангу этой матрицы. Строки (столбцы), проходящие через базисный минор, называются Базисными.

Теорема 1 (о базисном миноре). Справедливы следующие утверждения:

1. Базисные строки (столбцы) матрицы линейно независимы.

2. Каждая из небазисных строк (столбцов) может быть представлена в виде линейной комбинации базисных.

►Пусть

. Без ограничения общности можно считать, что базисный минор матрицы расположен в её левом верхнем углу. Если это не так, то с помощью перестановок строк и столбцов, которые не меняют ранга матрицы, его можно переместить в левый верхний угол. Тогда матрица А будет выглядеть так:

.

Обозначим М её базисный минор, М≠0. Приступаем непосредственно к доказательству.

1. Для доказательства линейной независимости строк

(3)

Составляем их линейную комбинацию и приравниваем её нулевой строке:

. (4)

Матрицы равны в том и только в том случае, когда равны их соответствующие элементы. Приравнивая нулю первые R Элементов матрицы-строки из левой части равенства (4), получаем следующую систему:

(5)

Конечно, мы могли бы приравнять нулю и все остальные элементы матрицы, но в этом, как вы увидите, нет никакой необходимости.

Система (5) — система линейных уравнений относительно

, в которой число уравнений равно числу неизвестных и определитель которой совпадает с базисным минором. Поэтому он отличен от нуля. Значит, по правилу Крамера, эта система имеет единственное решение (то, что это решение, проверяется непосредственной подстановкой). Таким образом, система строк (3) – линейно независима.

2. Нужно доказать, что

строка Может быть представлена в виде , что равносильно следующему:

, . (6)

К базисным строкам и столбцам добавим одну из небазисных строк и произвольный столбец и рассмотрим полученный определитель:

.

Определитель

=0 и , т. к. при он содержит два одинаковых столбца, а при — это минор (R+1)-го порядка матрицы А. Разложив по последнему столбцу, получаем:

. (7)

Так как

, то из (7) можно выразить :

. (8)

При вычислении алгебраических дополнений к элементам последнего столбца дописанный J-й столбец вычеркивается, значит, алгебраические дополнения

зависят от K, но никак не могут зависеть от J. Поэтому, полагая , из (8) получаем (6).◄

Теорема 2 (О линейной независимости строк и столбцов). Для того чтобы строки (столбцы) матрицы были линейно независимы необходимо и достаточно, чтобы ее ранг равнялся количеству строк (столбцов).

►Доказательство проводим для строк матрицы (для столбцов оно будет аналогичным).

Необходимость. Дано: строки матрицы линейно независимы. Пусть

. Предположим, что базисный минор матрицы расположен в её левом верхнем углу. Тогда первые R её строк линейно независимы, а каждая из оставшихся строк, в том числе и (R+1)-я, может быть через них выражена, то есть . Положим

. (9)

Среди чисел (9) есть отличные от нуля, и

.

Таким образом, строки матрицы линейно зависимы, и мы пришли к противоречию. Следовательно, предположение неверно и

.

Достаточность. Дано:

. Тогда базисный минор имеет M-й порядок, а значит, все строки являются базисными и поэтому линейно независимы.◄

Следствия.

1. Для того чтобы строки (столбцы) матрицы были линейно зависимы, необходимо и достаточно, чтобы ее ранг был меньше количества строк (столбцов).

2. Для того чтобы строки (столбцы) определителя были линейно независимы необходимо и достаточно, чтобы он был отличен от 0.

►{строки

линейно независимы}◄

3. Для того чтобы строки (столбцы) определителя были линейно зависимы необходимо и достаточно, чтобы он был равен 0.

§ 4. Критерий совместности линейных уравнений

Теорема Кронекера – Капелли (Критерий совместности системы линейных Уравнений). Для того чтобы система линейных уравнений была совместной необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы (

).

►Пусть задана система линейных уравнений

(1)

С матрицей А. Будем обозначать

J-й столбец матрицы А. Система (1) может быть записана следующим образом:

(2)

Необходимость. Дано: система совместна. Следовательно, существует упорядоченный набор чисел

такой, что

Получаем:

[прибавляем к последнему столбцу ]

Достаточность. Дано:

. Предположим, что базисный минор матрицы A Расположен в первых R столбцах. Этот же минор является базисным и для матрицы Ã: он отличен от нуля и его порядок равен R. По теореме о базисном миноре R первых столбцов матрицы Ã линейно независимы, а остальные, в том числе и В, можно через них выразить, т. е. существует такой упорядоченный набор чисел , что . Итак, упорядоченный набор удовлетворяет уравнению (2), значит, является решением системы (1).◄

§ 5. Однородные системы линейных уравнений

Определение. Система линейных уравнений называется Однородной, если во всех ее уравнениях свободные члены равны нулю:

(1)

Часто удобно использовать и матричную запись:

А Х=О. (2)

Однородная система всегда совместна, она имеет, по крайней мере, решение

, которое называется Тривиальным. Исследуем возможность существования других решений. Предположим, что , и что ее базисный минор расположен в левом верхнем углу. Тогда можно отбросить линейно зависимых последних уравнений. Неизвестные, коэффициенты при которых образуют базисный минор, называют Базисными неизвестными, а остальные – Свободными. Преобразуем систему следующим образом: базисные неизвестные оставим в левой части, а свободные перенесем направо. Получим систему уравнений, равносильную исходной:

(3)

Рассмотрим различные случаи.

1. Если

, то в системе (3) число уравнений равно числу неизвестных, а её определитель совпадает с базисным минором и, поэтому, отличен от 0. Значит, по правилу Крамера система (3) имеет единственное решение, которое является тривиальным.

2. Пусть

. Придадим свободным неизвестным какие-либо значения . Подставляя их в (3), получаем систему крамеровского типа:

(4)

Она имеет единственное решение

. Тогда упорядоченный набор

—

Решение системы (3) и исходной системы. Так как свободным неизвестным можно придать значения бесконечным числом способов, то при условии

однородная система линейных уравнений имеет бесконечное множество решений.

Вывод. Для того чтобы однородная система линейных уравнений имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше количества неизвестных. В частности, если в однородной системе число уравнений равно числу неизвестных, то для существования нетривиальных решений необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

.

Свойства решений однородной системы линейных уравнений

1°. Сумма решений однородной системы также является ее решением.

►{X1, X2 – решения (2)}

{A(X1+X2) = AX1+AX2 = О} {X1+X2 – решение (2)}. ◄

2°. Если решение однородной системы умножить на число, то также получим ее решение.

►{Х – решение (2)}

{А(αХ)=α(АХ)=αО=О}{αХ – решение (2)}.◄

3°. При условии

во множестве всех решений однородной системы линейных уравнений существует линейно независимая система, состоящая из решений, которая называется Фундаментальной системой решений Этой однородной системы.

►Построим систему решений следующим образом: для решения

свободным неизвестным придадим значения , для — , и т. д., и найдем базисные неизвестные, решая (4):

, , … , (5)

(звездочками здесь отмечены значения неизвестных, которые для наших рассуждений не так уж и важны). Так как

, то по теореме 2 § 3 система (5) линейно независима.◄

4°. Каждое решение однородной системы может быть представлено в виде линейной комбинации решений её фундаментальной системы

►Обозначим X0 произвольное решение однородной системы,

И построим вспомогательный столбец

. (6)

Из свойств 1° и 2° вытекает, что

и — также решения однородной системы. Но , где — некоторые числа. Подставив в (3), получаем систему крамеровского типа

,

Которая имеет единственное тривиальное решение

. Таким образом, , следовательно .◄

Замечания. 1. При доказательстве свойства 3° мы получили следующее правило: для построения фундаментальной системы решений следует свободным неизвестным придать значения по строкам единичной (или любой невырожденной) матрицы и найти соответствующие значения базисных неизвестных, решая систему (4). На практике сначала решают систему (4) в общем виде, выражая все неизвестные через свободные, а затем придают им необходимые значения.

2. Из доказанных свойств вытекает, что множество всех решений однородной системы линейных уравнений совпадает с множеством всевозможных линейных комбинаций решений её фундаментальной системы (т. е. решений вида (6)).

Определение. Множество всех решений системы линейных уравнений, выраженное через параметры (свободные неизвестные), называется Общим решением системы линейных уравнений. Каждое решение системы называется её Частным решением.

Чтобы получить какое-либо частное решение, следует в общем решении придать свободным неизвестным какие-то конкретные значения

§ 6. Неоднородные системы линейных уравнений

Пусть задана неоднородная система линейных уравнений

АХ=В (1)

В матричной записи. Наряду с (1) рассмотрим однородную систему

АХ=О (2)

С той же матрицей, что и система (1). Однородную систему (2) будем называть союзной для неоднородной системы (1).

Теорема. Справедливы следующие утверждения:

1. Разность решений неоднородной системы линейных уравнений является решением союзной к ней однородной системы.

2. Сумма решения неоднородной системы линейных уравнений и решения союзной к ней однородной является решением неоднородной системы.

3. Если неоднородная система линейных уравнений имеет решение

, то любое ее решение Х может быть представлено в виде

, (3)

Где

— некоторое решение союзной к ней однородной системы.

►1.

— решения (1)} — решение (2)}.

2. {

– решение (1), — решение (2)} Решение (1)}.

3. Пусть система (1) имеет некоторое решение

, и пусть — её произвольное решение. Положим . Тогда — решение (2) и

.◄

Итак, если неоднородная система линейных уравнений имеет решение

, то равенство (3) устанавливает взаимно однозначное соответствие между множеством всех её решений и множеством всех решений союзной к ней однородной системы. Таким образом, если неоднородная система имеет решения, то она имеет их столько, сколько и союзная к ней однородная.

Вывод. Пусть

— число неизвестных системы линейных уравнений (1). Если , то неоднородная система не имеет решений; если , то она имеет единственное решение, если же , то система (1) имеет бесчисленное множество решений. Кроме того, из (3) вытекает, что общее решение неоднородной системы линейных уравнений является суммой некоторого ее частного решения и общего решения союзной к ней однородной системы.

§7. Метод Гаусса решения системы линейных уравнений

Теорема. С помощью элементарных преобразований только над строками и перестановки столбцов любая ненулевая матрица может быть приведена к простейшему виду, т. е. к виду, когда в её левом верхнем углу находится единичная матрица, а последние строки полностью состоят из нулей.

►Пусть задана ненулевая матрица

(верхний индекс будет обозначать номер шага). Предположим, например, что

. Если это не так, выберем какой-либо отличный от нуля элемент, назовем его Опорным (или Разрешающим), и с помощью перестановки строк и столбцов переместим этот элемент в левый верхний угол. Разделив первую строку матрицы А на , получим матрицу

,

Которую, в свою очередь, преобразуем так: к I — й строке прибавим первую, умноженную на

. Тогда матрица перейдет в следующую:

,

Где

— некоторые числа. Если какая-либо из строк матрицы полностью состоит из нулей, мы ее переставим на последнее место.

Выберем теперь среди чисел

, отличное от нуля и переместим его опять же с помощью перестановки строк и столбцов во вторую строку и второй столбец. Теперь , и мы можем разделить на него вторую строку. Получаем новую матрицу

,

Строки которой, в том числе и первую, преобразуем так: к I-й строке прибавляем вторую, умноженную на

. Тогда переходит в следующую матрицу:

Теперь выбираем отличный от нуля элемент в последних (

)-х строках, переставляем его в третью строку и третий столбец и процесс повторяем. Преобразования продолжаем до тех пор, пока не окажется, что все последние строки состоят из одних нулей. Полученная матрица и будет матрицей простейшего вида.◄

Замечание. На самом деле перестановкой столбцов мы заниматься не будем. Базисный минор вовсе не обязательно перемещать в первые столбцы и приводить к виду единичной матрицы, достаточно, чтобы в каждом из его столбцов был единственный отличный от нуля элемент. Кроме того, чтобы избежать дробей, строчки также не будем делить на опорный элемент. При переходе от каждой матрицы к следующей поступаем так:

А) выбираем опорный элемент

в тех строках и столбцах, которые опорными еще не были;

Б) опорную строку оставляем без изменений, опорный столбец дополняем нулями;

В) предыдущие опорные столбцы умножаем на новый опорный элемент;

Г) остальные элементы пересчитываем по правилу прямоугольника:

, т. е. как определитель второго порядка, у которого главной является диагональ, содержащая опорный элемент.

Правило решения системы линейных уравнений

1. Вычисляем одновременно ранг матрицы системы и ранг расширенной матрицы, приводя матрицу А с помощью элементарных преобразований строк матрицы

к простейшему виду. При этом получаем матрицу системы, равносильной исходной. Если , то система решений не имеет.

2. Если

, то система имеет единственное решение, которое получается сразу же, как только мы запишем систему по последней матрице.

3. Если

, то последние уравнений можно отбросить (они имеют вид 0=0), и перейдет в матрицу

.

Её базисный минор расположен в первых

столбцах, поэтому базисными будут первые неизвестных. Выписывая по полученной матрице систему и выражая все неизвестные через свободные, находим общее решение.

Пример. Решим методом Гаусса систему линейных уравнений

▼Составляем расширенную матрицу и приводим её к простейшему виду методом опорного элемента. При этом всякий раз получаем матрицу системы, равносильной исходной. Поэтому между матрицами можно ставить знак равносильности. Опорный элемент будем подчеркивать двойной чертой.

.

Базисный минор можно выбрать, например, в первом, третьем и четвертом столбцах. Тогда базисными будут неизвестные

, а свободным — и . По последней матрице выписываем систему, причем свободные неизвестные переносим направо:

Общее решение выглядит так:

.▲

§ 8. Еще раз об обратной матрице

Если квадратная матрица

имеет второй или третий порядок, то обратную к ней найти очень просто. Это можно сделать практически устно, используя алгебраические дополнения. Если же матрица имеет более высокий порядок, то алгебраические дополнения устно считать уже затруднительно, да и количество их растет. Например, для вычисления обратной к матрице четвертого порядка надо найти один определитель четвертого порядка и 16 определителей третьего. Разберем сейчас ещё один способ вычисления обратной матрицы.

Пусть

— невырожденная квадратная матрица — Го порядка. Обратную к ней можно найти как решение матричного уравнения

. (1)

Обозначим — Столбец матрицы , — — Столбец матрицы ,

. Тогда уравнение (1) можно преобразовать так:

{(1)} {} {} {}.

Таким образом, матричное уравнение (1) равносильно системе

(2)

Состоящей из систем линейных уравнений с одной и той же невырожденной матрицей

. Каждую из этих систем можно решить методом Гаусса, приводя элементарными преобразованиями над строками (или методом опорного элемента) матрицу к единичной (столбец при этом переходит в некоторый столбец ):

{} {} {}.

Тогда .

Так как в (2) все системы имеют одну и туже матрицу, то нет необходимости преобразовывать отдельно расширенную матрицу каждой из этих систем, а можно это сделать вместе, записав матрицу и преобразовывая сразу и матрицу

и все столбцы .

Из вышесказанного вытекает правило нахождения обратной матрицы: записываем расширенную матрицу и, применяя элементарные преобразования только к строкам, приводим матрицу

к единичной. При этом матрица приводится к : .

Пример. С помощью элементарных преобразований найдем обратную для матрицы

.

▼

.

Таким образом,

.▲

Однородные уравнения и линейная алгебра

спросил 3 года 5 месяцев назад

Изменено 3 года, 5 месяцев назад

Просмотрено 569 раз

$\begingroup$

Последние несколько месяцев я изучаю фундаментальные концепции линейной алгебры, чтобы облегчить себе жизнь начинающего разработчика игр. Работая над темой нулевого пространства, я наткнулся на следующее определение:

Нулевое пространство матрицы размером $m × n$ $A$ — это множество всех решений однородного уравнения $Ax = 0$.

Изучив термин «однородное уравнение», я понял, что это понятие мне совершенно незнакомо и, скорее всего, не из тех, которые можно быстро понять.

Глядя в кроличью нору, я вижу:

1). Чтобы понять, что подразумевается под «однородным уравнением», мне, вероятно, придется разбираться в дифференциальном исчислении.

2). Чтобы понять дифференциальное исчисление, мне, вероятно, потребуется хотя бы базовое понимание исчисления.

3). Чтобы иметь базовые знания исчисления, мне, вероятно, придется разбираться в математических функциях.

Я не тратил время на изучение какой-либо из вышеупомянутых тем.

Проблема, с которой я столкнулся сейчас, заключается в том, что для того, чтобы правильно понять определение нулевого пространства, мне, вероятно, придется пройти несколько месяцев в обход тем, которые ведут к однородным уравнениям.

Итак, мой вопрос к читателю: это того стоит? Для тех, кто изучает линейную алгебру для целей программирования игр, стоит ли тратить несколько месяцев на изучение этих тем, и если да, то с чего начать? Или, может быть, мне лучше остановиться на идее «однородных уравнений»?

• линейная алгебра
• однородное уравнение

$\endgroup$

1

$\begingroup$

Все эти темы стоит изучать ради них самих и для развития математической зрелости, но они не нужны, если все, что вас интересует, это линейная алгебра.

Это просто терминология.

Уравнение $Ax = b$, где $A$ — известная матрица, $b$ — известный вектор, а $x$ — неизвестный вектор, называется линейным уравнением. Оно называется однородным, если $b=0$, и неоднородным в противном случае.

$\endgroup$

0

$\begingroup$

Однородное линейное уравнение — это просто уравнение типа $$a_1x_1+a_2x_2+\cdots+a_nx_n=0$$, а система однородных линейных уравнений — это просто система типа $$\left\{\begin{array }{l}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=0\\\vdots\\a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n =0. \end{array}\right.$$Это не имеет ничего общего с дифференциальным исчислением.

$\endgroup$

2

$\begingroup$

Как вы обнаружили, да, вы, безусловно, встретите термин «однородный» в контексте дифференциальных уравнений.

Впрочем, для вашей системы уравнений это не имеет значения. Это то же слово, но в другом контексте. Так что ваша цепочка рассуждений о кроличьей норе не применима.

Обратите внимание, что дифференциальные уравнения часто используются при моделировании физических систем, поэтому в конце концов вы можете их изучить, в зависимости от того, какие игры вы хотите написать, но вам не нужно изучать их, чтобы решить $Ax=0$

Как уже отмечалось, в линейных системах, в контексте линейной алгебры это означает, что правая часть уравнения $Ax=0$ равна нулю. Если оно не равно нулю, оно будет неоднородным.

$\endgroup$

$\begingroup$

Давайте проиллюстрируем это одним уравнением с двумя переменными.

Это однородно, потому что правая часть равна $0$: $$ 3х + 2у = 0. $$

Это не: $$ 3х + 2у = 19. $$

Решения однородного уравнения образуют прямую, проходящую через начало координат $(0,0)$. Всякий раз, когда $(x,y)$ является решением, $(ax, ay)$ является решением для любого значения $a$. Вот почему прилагательное «однородный» уместно. Векторная сумма двух решений снова является решением. В терминах линейной алгебры эта линия является подпространством. Это ядро ​​или нулевое пространство этой системы уравнений. Прилагательное «нулевой» подходит из-за $0$ справа. (В этом случае «система» имеет только одно уравнение.)

Решения второго уравнения тоже образуют линию, но она не проходит через начало координат. Оно параллельно пространству решений однородного уравнения. Это не подпространство.

Если вы помните этот пример, вы сможете прочитать и понять обобщения для большего количества уравнений с большим количеством переменных.

Как отмечали другие, вам действительно понадобится такой материал для разработки игр.

$\endgroup$

$\begingroup$

Система уравнений $Ax=0$ имеет вид

$a_{i1}x_1 + \ldots + a_{in}x_n = 0$

для $i=1,\ldots,m$.

Уравнения однородны, так как многочлены $f_i(x_1,\ldots,x_n)= a_{i1}x_1 + \ldots + a_{in}x_n$ являются однородными полной степени 1. Заметим, что все члены $a_{ij }x_j$ имеют степень 1 (=показатель степени переменной $x_j$).

С другой стороны, уравнение

$a_{i1}x_1 + \ldots + a_{in}x_n = b$

с $b\ne0$ неоднородно, так как многочлен $f_i(x_1,\ldots, x_n) = a_{i1}x_1 + \ldots + a_{in}x_n — b$ неоднородно.

В однородном многочлене все члены имеют одинаковую степень. Например, $x_1x_2 + x_2x_3$ является однородным суммарной степени 2, а $x_1x_2 + x_3$ не является однородным. Надеюсь, поможет.

$\endgroup$

2

$\begingroup$

Это легче понять с точки зрения алгебры. Это понятие, которое используется в исчислении, но не понятие из исчисления. 92 з.$$ Надеюсь это поможет.

$\endgroup$

1

Sage Tutorial, часть 2.2

На этой странице представлены некоторые разделы линейной алгебры, необходимые для построения решений систем линейных алгебраических уравнений и некоторых приложений. Мы используем матрицы и векторы как необходимые элементы для получения и выражения решений.

Матрицы и векторы

Центральной задачей линейной алгебры является решение линейной системы уравнений. Это означает, что неизвестные умножаются только на числа.

Наш первый пример линейной системы имеет два уравнения с двумя неизвестными:

\[ \begin{случаи} х-3у &= -1 , \\ 2х+у &=5 . \end{случаи} \]

Начнем со строк за раз. Первое уравнение \( x-3y=-1 \) дает прямую линию в \(ху-\) плоскость. Второе уравнение \( 2x+y=5 \) определяет другое линия. Построив эти две линии, вы не сможете пропустить точку пересечения, где встречаются две линии. Смысл \( x=2, \ y=1 \) лежит на обеих прямых. Эта точка решает оба уравнения одновременно.

Теперь визуализируем это с помощью рисунка:

 sage: l1=line([(-2,-1/3), (3,4/3)],толщина=2,color="black") 
 sage : l2=line([(1,3), (3,-1)],толщина=2,color="черный") 
 sage: ah = arrow((-2.4,0), (3.4,0)) 
 sage: av = arrow((0,-1), (0,3)) 
 sage: P=circle((2.0,1.0),0.03, rgbcolor=hue(0.75), fill=True) 
 sage: t1 =текст(r"$(2,1)$",(2.25,0.95)) 
 мудрец: t2=текст(r"$x-3y=1$",(1. 0,0.9)) 
 мудрец: t2=текст (r"$x-3y=1$",(1.0,0.9))
мудрец: t3=текст(r"$2x+y=5$",(1.8,2.1)) 
 мудрец: показать(l1+l2+ah+av+t1+t2+t3+P,axes_labels=['$x$','$y$'])
 

Теперь построим другой график:

 мудрец: ah = стрелка((-3.1,0), (2.2,0)) 
 мудрец: av = стрелка((0,-0.2), (0,5.1)) 
 мудрец: a1=стрелка([0 ,0],[-3,1], ширина=2, размер стрелки=3,цвет="черный") 
 sage: a2=стрелка([0,0],[1,2], ширина=2, размер стрелки= 3,color="черный") 
 мудрец: a3=стрелка([0,0],[2,4], ширина=2, размер стрелки=3,цвет="черный") 
 мудрец: a4=стрелка([0 ,0],[-1,5], ширина=2, размер стрелки=3,цвет="черный") 
 sage: l1=line([(-3,1), (-1,5)],color= "синий",linestyle="штрих") 
 sage: l2=line([(2,4), (-1,5)],color="blue",linestyle="dashed") 
 sage: t1=text(r"${\bf v}_1 $",(-3,0.85),color="black") 
 sage: t2=text(r"${\bf v}_2$",(1.1,1.85),color="black") 
 sage: t3=text(r"$2{\bf v}_2$",(2.05,3.75),color="black") 
 sage: t4=text(r"${\bf v}_1 + 2{\bf v }_2$",(-0. 75,4.75),color="black") 
 мудрец: показать(av+ah+a1+a2+a3+a4+l1+l2+t1+t2+t3+t4,axes_labels=[ '$x$','$y$']) 

На изображении строки видно, что две прямые пересекаются в одной точке. Затем обратимся к картинке столбца, переписав систему в векторном виде:

\[ х \begin{bmatrix} 1\\ 2 \end{bmatrix} + у \begin{bmatrix} -3\ 1 \end{bmatrix} = \begin{bmatrix} -1\ 5 \end{bmatrix} = {\bf b} . \]

Два столбца слева. Задача состоит в том, чтобы найти комбинацию этих векторов, которая равна вектору справа. Мы умножаем первый столбец на \(x\), а второй — на \(y,\) и складываем.

На рисунке справа показаны две основные операции с векторами: скалярное умножение и сложение векторов. С помощью этих двух операций мы можем построить линейную комбинацию векторов:

\[ 2 \begin{bmatrix} 1\\ 2 \end{bmatrix} + 1 \begin{bmatrix} -3\ 1 \end{bmatrix} = \begin{bmatrix} -1\ 5 \end{bmatrix} . \]

Матрица коэффициентов в левой части уравнений представляет собой матрицу 2 на 2 A :

\[ {\bf A} = \begin{bmatrix} 1 и -3 \\ 2 и 1 \end{bmatrix} . \]

Это позволяет нам переписать данную систему линейных уравнений в векторной форме (также иногда называемой матричной формой, но мы сохраняем матричную форму для матричных уравнений)

\[ {\bf A} \, {\bf x} = {\bf b} ,\qquad\mbox{что равно}\quad \begin{bmatrix} 1 и -3 \\ 2 и 1 \end{bmatrix} \, \begin{bmatrix} Икс \\ у \end{bmatrix} = \begin{bmatrix} -1\ 5 \end{bmatrix} . \]

Мы используем приведенное выше линейное уравнение, чтобы продемонстрировать отличную технику, называемую исключением. Перед исключением \( x \) и \( y \) появляются в обоих уравнениях. После исключения первое неизвестное \( x \) исчезло из второго уравнения:

\[ {\bf Раньше: }\quad \begin{case} x-3y &= -1 , \\ 2х+у &=5 . \end{cases} \qquad {\bf После: } \quad \begin{cases} x-3y &= -1 , \\ 7\,у &=7 \end{cases} \qquad \begin{array}{l} \mbox{(умножить на 2 и вычесть)} \\ (x \mbox{ был удален).} \конец{массив} \]

Последнее уравнение \( 7\,y =7 \) мгновенно дает \( y=1. \) Подставляя вместо \( y \) в первом уравнении выходит \( x -3 = -1. \) Следовательно, \( x=2 \) и решение \( (x,y) =(2,1) \) завершено.

 sage: l1=line([(-2,-1/3), (3,4/3)],толщина=2,color="black") 
 sage: l2=line([(-2, 1), (3,1)],толщина=2,цвет="черный") 
 мудрец: ah = стрелка((-2.4,0), (3.4,0)) 
 мудрец: av = стрелка((0, -1), (0,1.5)) 
 мудрец: P=circle((2.0,1.0),0.03, rgbcolor=hue(0.75), fill=True) 
 мудрец: t1=текст(r"$(2,1)$",(2.25,0.85)) 
 мудрец: t2=текст(r"$x-3y=1$",(0.6,0.7)) 
 мудрец : t3=text(r"$7y=7$",(1.5,1.1)) 
 sage: show(l1+l2+ah+av+t1+t2+t3+P,axes_labels=['$x$', '$y$'])
 

Система \( m \) уравнений относительно \( n \) неизвестных \( x_1 , \ x_2 , \ \ldots , \ x_n \) представляет собой набор \( m \) уравнения вида

\[ \begin{случаи} a_{11} \,x_1 + a_{12}\, x_2 + \cdots + a_{1n}\, x_n &= b_1 , \\ a_{21} \,x_1 + a_{22}\, x_2 + \cdots + a_{2n}\, x_n &= b_2 , \\ \qquad \vdots & \qquad \vdots \\ a_{m1} \,x_1 + a_{m2}\, x_2 + \cdots + a_{mn}\, x_n &= b_n .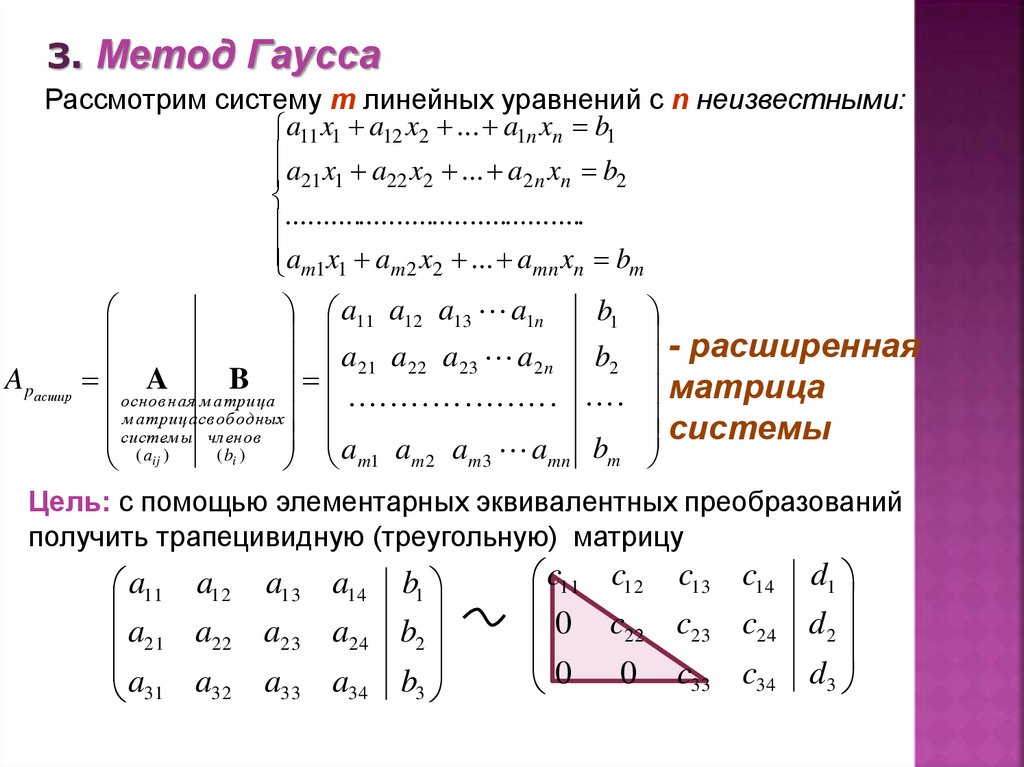 \end{случаи} \]

Числа \( a_{ij} \) известны как коэффициентов системы. Матрица \( {\bf A} = [\,a_{ij}\,] , \) чья запись \( (i,\, j) \) является коэффициент \( a_{ij} \) системы линейных уравнений называется матрицей коэффициентов и обозначается

\[ {\bf A} = \left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ а_{2,1} и а_{2,2} и \cdots и а_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{array} \right] \qquad\mbox{or} \qquad {\bf A} = \left( \ begin{массив}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ а_{2,1} и а_{2,2} и \cdots и а_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{массив} \right) . \] 9T \) — вектор неизвестных. Тогда продукт \( {\bf A}\,{\bf x} \) матрицы коэффициентов \( m \times n \) A и \( n \times 1 \) вектор-столбец x представляет собой \( m \times 1 \) матрицу

\[ \left[ \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ а_{2,1} и а_{2,2} и \cdots и а_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{массив} \right] \, \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \ конец {bmatrix} = \begin{bmatrix} a_{1,1} x_1 + a_{1,2} x_2 + \cdots + a_{1,n} x_n \\ a_{2,1} x_1 + a_{2,2} x_2 + \cdots + a_{2,n} x_n \\ \vdots \\ a_{m,1} x_1 + a_{m,2} x_2 + \cdots + a_{m,n} x_n \end{bmatrix} , \] 9Т\) компоненты которого являются правыми частями \( b_{i} ,\), система эквивалентна векторному уравнению

\[ {\bf A} \, {\bf x} = {\bf b} . \]

Мы говорим, что \( s_1 , \ s_2 , \ \ldots , \ s_n \) является решением системы, если все \( m \) уравнения выполняются, когда

\[ x_1 = s_1 , \ x_2 = s_2 , \\ldots , \ x_n = s_n . \]

Иногда систему линейных уравнений называют набором одновременных уравнений; такая терминология подчеркивает, что решение — это присвоение значений каждому из \( n \) неизвестных, для которых выполняется каждое уравнение с этим заданием. Ее также называют просто линейной системой.

Пример. Линейная система

\[ \begin{случаи} х_1 + х_2 + х_3 + х_4 + х_5 &= 3 , \\ 2\,x_1 + x_2 + x_3 + x_4 + 2\, x_5 &= 4, \\ х_1 — х_2 — х_3 + х_4 + х_5 &= 5, \\ х_1 + х_4 + х_5 &= 4, \end{случаи} \]

является примером системы из четырех уравнений с пятью неизвестными, \( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 . \) Одним из решений этой системы является

\[ х_1 = -1, \ х_2 = -2, \ х_3 = 1, \ х_4 = 3, \ х_5 = 2, \]

в чем легко убедиться, подставив эти значения в уравнения. Каждое уравнение выполняется для этих значений \( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 . \) Однако нет единственного решения этой системы уравнений. Есть много других.

С другой стороны, система линейных уравнений

\[ \begin{случаи} х_1 + х_2 + х_3 + х_4 + х_5 &= 3 , \\ 2\,x_1 + x_2 + x_3 + x_4 + 2\, x_5 &= 4, \\ х_1 — х_2 — х_3 + х_4 + х_5 &= 5, \\ х_1 + х_4 + х_5 &= 6, \end{случаи} \]

не имеет решения. Нет номеров, которые мы можем присвоить неизвестным \( x_1 , \ x_2 , \ x_3 , \ x_4 , \ x_5 \) так, чтобы все четыре уравнения были выполнены. ■

Вообще говоря, мы говорим, что линейная система алгебраических уравнений равна согласованный , если он имеет хотя бы одно решение, и несовместимый , если он не имеет решения. Таким образом, непротиворечивая линейная система имеет либо одно решение, либо бесконечно много решений — других возможностей нет.

Теорема: Пусть A — матрица \( m \× n \) матрица. n . \) 9м\) линейная система \( {\bf A}\,{\bf x} = {\bf b} \) либо несовместна, либо имеет бесконечное множество решений.

Теорема: Если A является матрицей \( m \times n \) с \( м

Теорема: Система линейных уравнений \( {\bf A}\,{\bf x} = {\bf b} \) непротиворечива тогда и только тогда, когда b находится в столбце A .

Теорема: Линейная система алгебраических уравнений \( {\bf A}\,{\bf x} = {\bf b} \) непротиворечива тогда и только тогда, когда вектор 9Т {\bf А} знак равно {\bf 0} . \) ■

Sage использует стандартные команды для решения линейных систем алгебраических уравнений:

\[ {\bf A} \, {\bf x} = {\bf b} . \]

Здесь A представляет собой m — n матрицу, b — заданный вектор размером m , а вектор-столбец x размера n 9024 необходимо определить. Расширенная матрица — это матрица получается путем добавления столбцов двух данных матриц, обычно с целью выполнения одних и тех же элементарных операций над строками на каждой из данных матриц. Сопоставим данной системе линейных уравнений \( {\bf A}\,{\bf x} = {\bf b} \) расширенную матрицу, добавив вектор-столбец b в матрицу A . Такая матрица обозначается \( {\bf M} = \left( {\bf A}\,\vert \,{\bf b} \right) \) или \( {\bf M} = \left[ { \bf A}\,\vert \,{\bf b} \right] : \)

\[ {\bf M} = \left({\bf A}\,\vert \,{\bf b} \right) = \left[{\bf A}\,\vert \,{\bf b} \right «=» \left[ \begin{array}{cccc|c} a_{1,1} & a_{1,2} & \cdots & a_{1,n} & b_1 \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots\\ a_{m,1} & a_{m,2} & \cdots & a_{m,n} & b_m \end{массив} \right] . \]

Теорема: Пусть A — матрица \( m \times n \) матрица. Линейная система уравнений \( {\bf A}\,{\bf x} = {\bf b} \) непротиворечиво тогда и только тогда, когда ранг матрицы коэффициентов A совпадает с рангом расширенной матрицы \( \ left[ {\bf A}\,\vert \, {\bf b} \right] . \) ■

Фактическое использование термина расширенная матрица, по-видимому, было введено американским математиком Максимом Бохером (1867— 1918) в 1907.

Покажем, как это работает на примерах. Система может быть решена с помощью команды решения

 мудрец: решить([eq1==0,eq2==0],x1,x2)
 

Однако это несколько сложно, и мы используем векторный подход:

 мудрец: A = Matrix([[1,2,3],[3,2,1],[1,1,1]]) 
 мудрец: b = вектор([0, -4, -1] )
мудрец: x = A.solve_right(b)
мудрец: х
(-2, 1, 0)
sage: A * x # проверяем наш ответ...
(0, -4, -1)
 

Вместо можно использовать обратную косую черту \ .solve_right ; использовать A \ b вместо A.solve_right(b) .

 шалфей: А\б
(-2, 1, 0)
 9{-1} {\bf б} . \) Мы обсудим этот метод позже в разделе, посвященном обратным матрицам.
  
 Квадратные матрицы 
 Очень важный класс матриц составляют так называемые  квадратных матриц , которые имеют такое же количество строк, как и столбцов. В компьютерной графике для преобразований используются квадратные матрицы.
No related posts.