7 класс. Алгебра. Линейная функция. — Решение линейных уравнений с двумя неизвестными.
Комментарии преподавателяНа данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.Тема: Линейная функция
Урок: Линейное уравнение с двумя переменными и его график
Опредепение
Мы познакомились с понятиями координатной оси и координатной плоскости. Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.
Уравнение вида:
, где a, b, с – числа, причем
Называется линейным уравнением с двумя переменными х и у.
Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.
Пара чисел будет изображаться на координатной плоскости в виде точки.
У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.
Построение графика
Пример 1:
; ; ;
Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:
Пусть , тогда исходное уравнение превращается в уравнение с одной неизвестной:
,
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)
Пусть . Получим исходное уравнение с одной переменной: , отсюда , получили точку В(3; 0)
Занесем пары чисел в таблицу:
|
х |
0 |
3 |
|
у |
3 |
0 |
Построим на графике точки и проведем прямую:
Отметим, что любая точка на данной прямой будет решением заданного уравнения.
Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.
Пример 2 – построить график уравнения:
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:
|
х |
0 |
-2 |
2 |
|
у |
3 |
0 |
6 |
В первой колонке мы взяли удобный , найдем у:
, ,
Во втором столбике мы взяли удобный , найдем х:
, , ,
Возьмем для проверки и найдем у:
, ,
Построим график:
Умножим заданное уравнение на два:
От такого преобразования множество решений не изменится и график останется таким же самым.
Вывод:
мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения
Урок: Линейное уравнение с двумя переменными и его график (более сложные случаи)
Напомним, что линейным уравнением с двумя переменными называется уравнение вида
Мы научились строить графики подобных уравнений и узнали, что они имеют бесчисленное множество решений – пар чиселх и у, которые на графике отображаются в виде точек.
В предыдущих задачах нам было задано уравнение, но как и все другие – линейное уравнение с двумя переменными это математическая модель некоторой реальной ситуации. Теперь рассмотрим такие задачи, в которых нужно для простейшей задачи составить уравнение – математическую модель, а затем его решить.
Пример 1:
Сумма двух чисел равна четырем. Построить математическую модель, то есть соответствующее линейное уравнение, и его график.
Пусть искомые числа это х и у, сумма их равна четырем:
– линейное уравнение с двумя переменными. Построим график, для этого составим таблицу, для контроля возьмем три точки, а не две:
|
х |
0 |
4 |
2 |
|
у |
4 |
0 |
2 |
Решение задачи сведено в таблицу:
|
Словесная модель |
Сумма двух чисел равна четырем |
|
Алгебраическая модель |
, |
|
Геометрическая модель |
Следующая группа задач связана с тем, что в одной задаче могут участвовать два линейных уравнения.
Пример 2:
Графически найти точку пересечения прямых и
Обе прямые являются графиками соответствующих уравнений, построим их. Для этого составим таблицы. Для удобства представим уравнение в следующем виде:
|
х |
0 |
-1 |
|
у |
1 |
0 |
|
х |
0 |
2 |
|
у |
4 |
0 |
Графически найдена точка пересечения А(1; 2)
Чтобы проверить, что точка А(1; 2) удовлетворяет обоим уравнениям, нужно подставить ее координаты в уравнения:
;
точка А удовлетворяет обоим уравнениям, значит, точка пересечения прямых найдена верно.
Уравнение с параметрами
Следующий тип задач – это задачи с параметрами.
Пример 3:
Найдите значение коэффициента в уравнении , если известно, что решением уравнения является пара чисел (3; 2)
Ранее у нас было задано или мы сами составляли линейное уравнение с известными коэффициентами, в данном случае один из коэффициентов неизвестен, но дано одно из решений уравнения, то есть пара значений х и у, удовлетворяющих уравнению. Чтобы найти параметр подставим данные значения в уравнение:
итак, исходное уравнение имеет вид:
Итак, мы рассмотрели линейное уравнение с двумя неизвестными:
Отметим, что в случае, если , мы получаем частный случай данного уравнения – уравнение с одной переменной:
Аналогично если мы получим линейное уравнение с одной переменной:
Вывод: в данном уроке мы рассмотрели более сложные задачи на линейные уравнения с двумя переменными, в частности текстовые задачи, уравнения с параметрами, задачи на два уравнения.
Кроме того мы закрепили знание понятий и терминов.
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-2-lineynaya-funktsiya/lineynoe-uravnenie-s-dvumya-peremennymi-i-ego-grafik?konspekt&chapter_id=8
http://interneturok.ru/ru/school/algebra/7-klass/glava-2-lineynaya-funktsiya/lineynoe-uravnenie-s-dvumya-peremennymi-i-ego-grafik-bolee-slozhnye-sluchai?konspekt&chapter_id=8
Источник видео: https://www.youtube.com/watch?v=8WdpbeZFy_c
Презентация по теме «Системы двух линейных уравнений с двумя неизвестными» | Презентация к уроку по алгебре (7 класс) на тему:
Слайд 1
Системы двух линейных уравнений с двумя неизвестными Бондарева Светлана Владимировна МБОУ «Школа № 5» г. Дзержинск
Слайд 2
Этапы урока Организационный момент – 1 мин Устная работа – 5 мин индивидуальная и фронтальная Изучение нового материала – 15 мин работа с учебником презентация работа у доски и в тетради Закрепление изученного – 15 мин Самостоятельная работа – 5 мин Подведение итогов – 4 мин
Слайд 3
«Математику нельзя изучать, наблюдая как это делает сосед» А.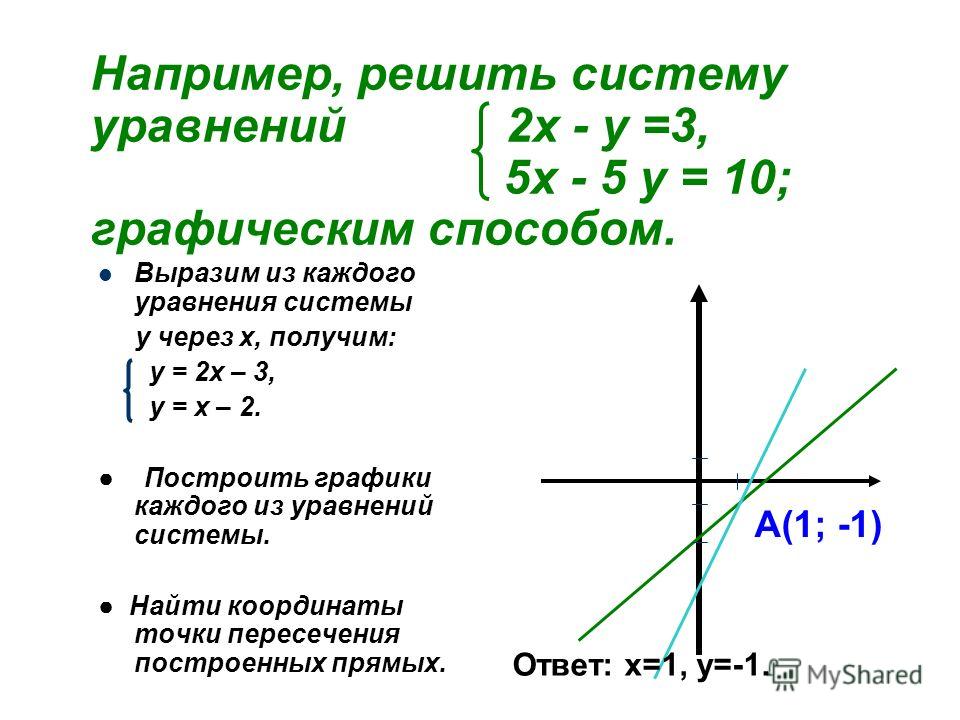
Нивен.
Слайд 4
Тема урока: «Системы уравнений» Цель урока знакомство с понятиями линейного уравнения с двумя неизвестными, системы уравнений, решением систем двух уравнений с двумя неизвестными. Задачи образовательные: познакомить с понятием линейного уравнения с двумя неизвестными; познакомить с понятием системы уравнений; научить решать системы двух уравнений с двумя неизвестными развивающие: развивать культуру устной и письменной речи обучающихся; развивать восприятие, внимание, память; развивать мышление обучающихся через умение анализировать и выделять главное; воспитательные: воспитывать познавательный интерес к предмету; содействовать рациональной организации труда. Тип урока : урок изучения нового материала
Слайд 5
Заполните пропуски так, чтобы получилось верное числовое равенство: 1) 15 – 8 = 4 + 2) 3 * = 47 — 14 2) 3 * = 47 — 14 2. Что такое уравнение ? 3. Что значит решить уравнение? 4. Решите уравнение: 1) 6х=9; 2) 5у – 1=0; 3) 3х – 5=1; 4) 2 + 1=0 5) Корнем каких уравнений является число 2 1/3?
Слайд 6
Задача.
Обозначив за х первое число и за у второе число, составьте соотношение по следующим условиям: а) первое число на 5 больше второго: х – у = 5 б) сумма квадрата первого числа и удвоенного второго числа равна 17: в) утроенное произведение чисел равно 24: 3ху = 24. г) разность куба первого числа и половины второго числа равна 12: Это примеры уравнений с двумя неизвестными
Слайд 7
Примеры уравнений с двумя неизвестными: В чем отличия уравнений первого и второго столбиков? Как в общем виде можно записать примеры второго столбца? ах + b у = с линейные уравнения с двумя неизвестными
Слайд 8
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной, а значит, при их решении можно выполнять аналогичные преобразования. Благодаря этому появляется возможность выражать в таких уравнениях одну переменную через другую. № 615 (1,3), № 616
Слайд 9
Задача . В двух седьмых классах учится 57 школьников. В 7а классе на 5 школьников больше, чем в 7б классе.
Сколько учащихся в каждом классе? Пусть в 7а – х учащихся, в 7б – у учащихся, тогда х + у = 57, х – у = 5 По условию задачи составили два линейных уравнения с двумя переменными (или неизвестными). Необходимо найти такие значения переменных х и у, при которых каждое из уравнений будет верным равенством, т.е.найти общее решение этих уравнений. Пара чисел х=31 и у=26 удовлетворяет каждому уравнению, так как при их подстановке получаем верные числовые равенства.
Слайд 10
х + у = 57 х – у = 5 — система двух линейных уравнений с двумя неизвестными Что будет решением системы двух уравнений с двумя неизвестными? Что значит решить системы уравнений? № 619 . Как, не решая систему уравнений, определить, сколько решений она имеет? — Рассмотрим систему: — Выразим из каждого уравнения у через х: ! Уравнения задаются линейными функциями. Угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит прямые пересекаются и система имеет единственное решение.
Слайд 11
Если к1 ≠ к2 Графики пересекаются Система имеет единственное решение Если к1 = к2, b 1 ≠ b 2 Графики параллельны Система не имеет решений Если к1=к2, b1=b2 Графики совпадают Система имеет бесконечно много решений
Слайд 12
(по рядам) Выяснить, сколько решений имеет система.
1. 2. 3.
Слайд 13
ПРОВЕРКА : к1 к2 Система имеет единственное решение к1 = к2= — 0,5 b 1 ≠ b 2 Система не имеет решений к1=к2, b1=b2 Система имеет бесконечно много решений
Слайд 14
Является ли решением системы уравнений пара (3;1) пара (2;2) верно неверно (3;1) не является решением верно верно (2;2) является решением
Слайд 15
Домашнее задание: п.33, № 621 (2), № 623, № 624.
Слайд 16
Итог урока: линейное уравнение с двумя неизвестными; системы уравнений; решение системы двух линейных уравнений с двумя неизвестными
Всегда ли линейные уравнения $2$ с $2$ неизвестными будут иметь решение?
Возможны три случая для $2$ линейных уравнений с $2$ неизвестными (наклон и точка пересечения):
$\qquad$ $\mathbf{0}$ точки решения $\qquad$ $\qquad$ $\mathbf{1}$ точка решения $\qquad$ $\qquad$ $\mathbf{\infty}$ точек решения
$\qquad \quad$ $\nexists$ не существует $\qquad$ $\qquad$ $\exists !$ уникальность $\qquad$ $\qquad$ $\exists$ нет единственности
Строки имеют вид $y(x) = mx + b$.
Случай 1: параллельные линии
Решение не существует.
Линии параллельны: они имеют одинаковый наклон.
$$ % \начать{выравнивать} % y_{1}(x) &= mx + b_{1} \\ % y_{2}(x) &= mx + b_{2} \\ % \end{выравнивание} % $$
Случай 2: пересекающиеся линии
Имеем существование и уникальность.
Склоны отчетливые.
$$m_{1} \ne m_{2}$$
$$ % \начать{выравнивать} % y_{1}(x) &= m_{1} x + b_{1} \\ % y_{2}(x) &= m_{2} x + b_{2} \\ % \end{выравнивание} % $$
Случай 3: совпадающие строки
Имеем существование , но не уникальность . Существует бесконечное количество решений. Каждая точка решает систему уравнений.
Обе линии совпадают.
$$ % \начать{выравнивать} % y_{1}(x) &= m x + b \\ % y_{2}(x) &= m x + b \\ % \end{выравнивание} % $$
С точки зрения линейной алгебры, посмотрите на проблему с точки зрения пространств $\color{blue}{range}$ и $\color{red}{null}$.
Линейная система для двух уравнений $$ % \начать{выравнивать} % m_{1} x — y &= b_{1} \\ % m_{2} x — y &= b_{1} \\ % \end{выравнивание} $$ который имеет матричную форму $$ % \начать{выравнивать} % \mathbf{A} х &= б \\ % \left[ \begin{массив}{cc} m_{1} и -1 \\ м_{2} и -1 \\ \end{массив} \right] % \left[ \begin{массив}{cc} Икс \\ у \\ \end{массив} \right] % знак равно % \left[ \begin{массив}{cc} б_{1} \\ Би 2} \\ \end{массив} \right] % \end{выравнивание} % $$ 9{*} \правильно)} % \end{выравнивание} $$
Случай 1: Не существует
Матрица $\mathbf{A}$ имеет дефект ранга $(m_{1} = m_{2})$ и $b_{1} \ne b_{2 }$. $$ b = \ цвет {синий} {b _ {\ mathcal {R}}} + \цвет{красный}{b_{\mathcal{N}}} $$ Именно пространственная компонента $\color{red}{null}$ исключает прямое решение. (Интересно, что существует решение методом наименьших квадратов.) $$
Вектор данных $b$ не является комбинацией столбцов $\mathbf{A}$. Пространство столбца $$ \mathbf{С}^{2} = \color{синий}{\mathcal{R} \left( \mathbf{A} \right)} \oplus \color{red} {\mathcal{N} \left(\mathbf{A}^{*} \right)} $$ Разложение $$ \color{синий}{\mathcal{R} \left( \mathbf{A} \right)} = % \text{диапазон} \left\{ \, \цвет синий}{ \левый[ \начать{массив}{с} м\-1 \конец{массив} \правильно] } \, \правильно\} \qquad \color{red}{\mathcal{N} \left( \mathbf{A}^{*} \right)} = % \text{диапазон} \left\{ \, \красный цвет}{ \левый[ \начать{массив}{г} -1\м \конец{массив} \правильно] } \, \правильно\} $$ 9{2} = \color{синий}{\mathcal{R} \left( \mathbf{A} \right)} $$ Разложение $$ \color{синий}{\mathcal{R} \left( \mathbf{A} \right)} = % \text{диапазон} \left\{ \, \цвет синий}{ \левый[ \начать{массив}{с} м_{1} \\ -1 \конец{массив} \правильно] }, \, \цвет синий}{ \левый[ \начать{массив}{с} м_{2} \\ -1 \конец{массив} \правильно] } \правильно\} $$
Случай 3: существование, отсутствие единственности
Матрица $\mathbf{A}$ имеет дефект ранга $(m_{1} = m_{2} = m)$, но $b_{1} = b_{2}$.
{*} \right)} =
%
\text{диапазон} \left\{ \,
\красный цвет}{
\левый[
\начать{массив}{г}
-1\м
\конец{массив}
\правильно] }
\, \правильно\}
$$
Постскриптум: теоретические основы здесь полезны. Путь к пониманию начинается с простых примеров, как в комментарии @Nick.
Одновременные уравнения — Математика GCSE Revision
Одновременные уравнения и линейные уравнения, изучив этот раздел, вы сможете:
- решить одновременные линейные уравнения подстановкой
- решать одновременные линейные уравнения методом исключения
- решать одновременные линейные уравнения с использованием линейных графиков
Если уравнение имеет два неизвестных, например 2y + x = 20, оно не может иметь уникальных решений. Два неизвестных требуют двух уравнений, которые решаются одновременно (одновременно), но даже в этом случае два уравнения с двумя неизвестными не всегда дают уникальные решения.
Видео ниже работает с примерами одновременных уравнений.
В пошаговом примере показано, как сгруппировать одинаковые термины, а затем добавить или вычесть, чтобы удалить одно из неизвестных и оставить одно неизвестное для решения.
Этот метод называется решением путем замены .
Он включает в себя то, что он говорит — подстановка — использование одного из уравнений для получения выражения формы «y = …» или «x = …» и подстановка его в другое уравнение. Это дает уравнение с одним неизвестным, которое можно решить обычным способом. Затем это значение подставляется в то или иное исходное уравнение, что дает уравнение с одним неизвестным.
ПРИМЕЧАНИЕ. При использовании этого метода вам нужно особенно внимательно относиться к алгебре. Если ваши решения представляют собой «странные» дроби, такие как 9/13, скорее всего, вы допустили ошибку — проверьте свою алгебру.
Пример
Решите два одновременных уравнения:
2y + x = 8 [1]
1 + y = 2x [2]
Из [2] y = 2x -1 ← вычесть 1 с каждой стороны
Подстановка этого значения для y в [1] дает:
2(2x – 1) + x = 8
4x – 2 + x = 8 ← раскрыть скобки
5x – 2 = 8 ← убрать
5x = 10 с каждой стороны ← Прибавить 2 10 к каждой стороне
x = 2 ← Разделив обе части на 5, можно найти значение x.
Замените значение x на y = 2x — 1 дает
y = 4 — 1 = 3
Таким образом, x = 2 и y = 3
Примечание:
- Рекомендуется маркировать каждое уравнение. Это поможет вам объяснить, что вы делаете, и может дать вам оценки за метод.
- Это значение x можно подставить в уравнение [1] или [2] или в выражение для y: y = 2x − 1,
- Выберите тот, который проще всего!
- В качестве проверки подставьте значения обратно в каждое из двух исходных уравнений.
Второй метод называется решением методом исключения.
ПРИМЕЧАНИЕ. Этот метод не так сложен, как кажется на первый взгляд, но он помогает, если вы знаете, почему он работает.
Работает благодаря двум свойствам уравнений:
- Умножение (или деление) выражения с каждой стороны на одно и то же число не меняет уравнения.
- Добавление двух уравнений дает еще одно правильное уравнение:
, например. 2х = х + 10 (х = 10) и х — 3 = 7 (х также = 10).
Сложение уравнений дает 2x + x − 3 = x + 10 + 7 (x также = 10).
Цель состоит в том, чтобы манипулировать двумя уравнениями таким образом, чтобы при объединении либо член x, либо член y был устранен (отсюда и название) – полученное уравнение только с одним неизвестным может быть решено:
Здесь мы будем манипулировать одним из уравнений так, чтобы при объединении его с другим уравнением выпадали члены x или y. В этом примере член x выпадет, что даст решение для y.
Затем это подставляется в одно из исходных уравнений.
Подпишите уравнения, чтобы знать, с какими из них вы работаете на каждом этапе.
Уравнение [1] равно 2y + x = 8
Уравнение [2] равно 1 + y = 2x
Перестройте одно уравнение так, чтобы оно было похоже на другое.
[2] y – 2x = -1
также 2 x [1] дает 4y + 2x = 16, которое мы называем [3]
[2] y – 900 0 = -1 [3] 4y + 2x = 16
[2] + [3] дает 5y = 15
, поэтому y = 3
подстановка y = 3 в [1] дает 1 + (3) = 2x
поэтому 2x = 4, что дает x = 2 и y = 3
Решение одновременных линейных уравнений с использованием линейных графиков
Две строки представляют уравнения «4x — 6y = -4» и «2x + 2y = 6».
Есть только одна точка пересечения двух уравнений.
Поскольку графики 4x — 6y = 12 и 2x + 2y = 6 представляют собой прямые линии, их называют линейными уравнениями.