Решение линейных дифференциальных уравнений онлайн
Назначение сервиса. Данный онлайн-калькулятор служит для решения линейного дифференциального уравнения с постоянными коэффициентами видаay(n)+by+c=R(x). Например, y''-2y=0, 2y''+y'-2y=x2. Решение оформляется в формате Word. Для решения уравнений вида y'+x*y=x2 используйте этот калькулятор.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Для получения онлайн решения введите максимальную степень производной n. Например, для дифференциального уравнения y''-2y=0 максимальная степень равна двум, поэтому n=2, для y'''-2y''-y=0 степень равна трем (n=3).
 Общее решение дифференциального уравнения с правой частью:
Общее решение дифференциального уравнения с правой частью:
1. Для уравнения y»’ — 4y» + 5y’ – 2y = 2x+3 корнями характеристического уравнения r3 – 4r2 + 5r – 2 = 0 являются r=2 кратности 1 и r=1 кратности 2. Следовательно α+β i=0 и не является корнем характеристического уравнения. Поэтому k=0 и частное решение ищем в виде y = cx + d. Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2. -5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C1ex + C2e2x
— общее решения уравнения.2. Для уравнения y»’ — 4y» + 5y’ – 2y = (2x+3)e2x число α+β i=2 является корнем характеристического уравнения кратности 1. Поэтому частное решение ищем в виде y = x(cx + d)e2x.
Для уравнения y»’ — 4y» + 5y’ – 2y = (2x+3)e2x число α+β i=2 является корнем характеристического уравнения кратности 1. Поэтому частное решение ищем в виде y = x(cx + d)e2x.
3. Для уравнения y’’ + y = cos(x) корнями характеристического полинома r2+1 являются числа r = ±i кратности 1. Поэтому частное решение ищем в виде y=x(a1cosx + a2 sinx). Тогда
y’ = (a1 + a2x)cosx + (a2 – a1x)sinx,
y’’ = (2a2 – a1x)cosx + (-2a1-a2x)sinx
Подставляя в исходное уравнение и приводя подобные, получаем 2a2 cosx – 2a1sinx = cosx, откуда a1 = 0;a2=0,5.
4. Найти общее решение уравнения:
Находим решение однородного уравнения y» — 3y’ + 2y = 0.
Характеристическое уравнение:
r2-3r+2=0 имеет корни r1= 1, r2= 2.
Общее решение уравнения без правой части равно:
yОбщ = C1ex + C2e2x
Правая часть уравнения имеет вид R(x) = P(x)eαx, причем P(x) = x2 + 3x и число α = 0 не является корнем характеристического уравнения. Ищем решение вида:
2Ax2 + (2B — 6A)x + 2C — 3B + 2A = x2 + 3x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
2A = 1; 2B — 6A = 3; 2C — 3B + 2A = 0,
из которых находим: A = 1/2, B = 3, C = 4, так что
y* = x2/2 + 3x + 4
Общее решение дифференциального уравнения есть:
5. Найти общее решение уравнения: y'' - 3y' = x2 + 3x
Характеристическое уравнение: r2 - 3r = 0 имеет корни r1= 3, r2= 0.
Общее решение уравнения без правой части равно:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
-9A = 1, -6B + 6A = 3, -3C + 2B = 0,
из которых находим: A = -1/9, B = -11/18, C = -11/27, так что
y* = x2/9 — 11x/18 -11/27
Общее решение дифференциального уравнения есть:
Пример 2. Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.
Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение
8r2 +2r — 3 = 0
D = 22 — 4·8·(-3) = 100
,
Корни характеристического уравнения: r1 = 1/2, r2 = -3/4
Следовательно, фундаментальную систему решений составляют функции: y1 = e1/2x, y2 = e-3/4x
Общее решение однородного уравнения имеет вид:
Найдем частное решение при условии: y(0) = -6, y'(0) = 7
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = -6
Находим первую производную:
y’ = 1/2•c1•e1/2•x—3/4•c2•e-3/4•x
Поскольку y'(0) = 1/2•c1—3
1/2•c1—3/4•c2 = 7
В итоге получаем систему из двух уравнений:
c1+c2 = -6
1/2•c1—3/4•c2 = 7
которую решаем или методом матриц или методом исключения переменных.

c1 = 2, c2 = -8
Тогда частное решение при заданных начальных условиях можно записать в виде:
см. также Дифференциальные уравнения. Пример решения.
Если правая часть уравнения отлична от нуля, то решение ищется по формуле: R(x)=eαx(P1cos(βx)+P2sin(βx))
| R(x) | Форма записи решения |
| 10•x•e2x | (Ax + B)e2x |
| x•e-x•cos(3x) | e-x((Ax+B)cos(3x)+(Cx+D)sin(3x)) |
| (x3-x2+3)cos(x)-x•sin(x) | (Ax3+Bx2+Cx+D)cos(x)+(Ex3+Fx2+Gx+H)sin(x) |
| cos(x) | Acos(x) + Bsinx(x) |
| x•sin(x) | (Ax + B)cos(x) + (Cx + D)sinx(x) |
| x3-x2+3 | Ax3+Bx2+Cx+D |
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Уравнения, сводящиеся к квадратным уравнениям |
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
| Трёхчленные уравнения | |
| Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии | |
| Возвратные (симметричные) уравнения 3-ей степени | |
| Возвратные (симметричные) уравнения 4-ой степени | |
| Обобщенные возвратные уравнения 4-ой степени |
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.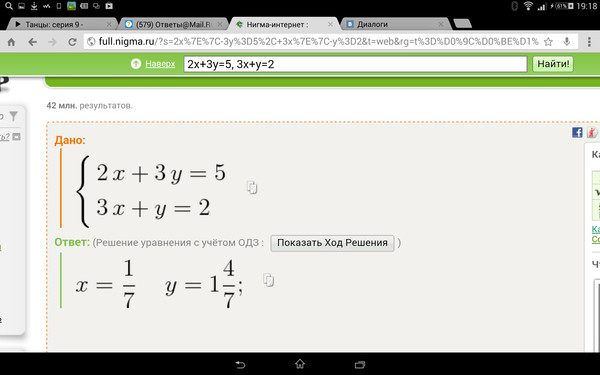
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
Ответ:.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2– – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
| (5) |
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
| (6) |
Если теперь обозначить
| (7) |
то уравнение (6) станет квадратным уравнением:
| ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
В результате получится уравнение
| (9) |
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
| (10) |
Если теперь обозначить
| (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0.  | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
| (14) |
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
| (15) |
Если теперь обозначить
| (16) |
то уравнение (15) станет квадратным уравнением:
| 2y2 – 3y – 5 = 0. | (17) |
Решим уравнение (17):
| (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ:
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
| (20) |
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
| (21) |
Если теперь обозначить
| (22) |
то уравнение (21) станет квадратным уравнением:
6y2 – 25y + 24 = 0. | (23) |
Решим уравнение (23):
| (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ:
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
| (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
| (26) |
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
| (28) |
то уравнение (27) станет квадратным уравнением:
| (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
a = 2 , b =– 15,
c = 35, d = – 30,
и найдем значение выражения
Поскольку
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
| (31) |
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
| (32) |
Если теперь обозначить
| (33) |
то уравнение (32) станет квадратным уравнением:
2y2 – 15y + 27 = 0. | (34) |
Решим уравнение (34):
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
3-8какой набор решений уравнения (2x+1)/(x-3) = 0
помогите пожалуйста!!!!
- задачи по алгебре
Ваш ответ
| Ваше имя для отображения (необязательно): |
| Напишите мне по этому адресу, если мой ответ будет выбран или прокомментирован: Напишите мне, если мой ответ будет выбран или прокомментирован |
Конфиденциальность: Ваш адрес электронной почты будет использоваться только для отправки этих уведомлений. |
| Проверка на спам: |
Чтобы избежать этой проверки в будущем, пожалуйста, войдите или зарегистрируйтесь. |
1 ответ
ответил по Стержень Пользователь с самым высоким рейтингом (1,0 млн баллов)Похожие вопросы
1 ответ
92-34x-12=0 спросил
16 апреля 2013 г.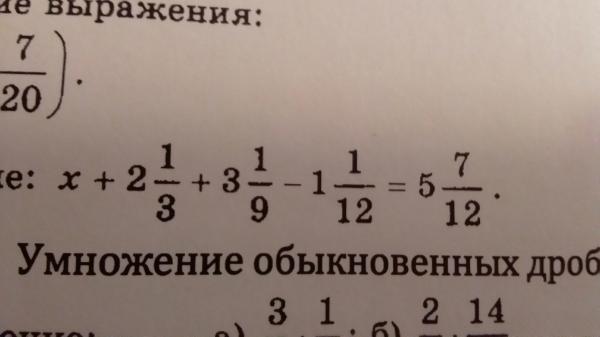 5/3-10=0 92-42
5/3-10=0 92-42
спросил 14 апреля 2013 г. по алгебре 1 ответы по анонимный | 333 просмотра
- алгебра 1
2 ответа
9 или 5-3xкакой набор решений для 2x+1>9 или 5-3x<17
спросил 11 декабря 2014 г. в исчислении ответы по анонимный | 299 просмотров
- задачи по алгебре
1 ответ
выразить решение в системе обозначений, словами и графически на числовой прямой для 2x ‹ 10
спросил 4 декабря 2013 г. по алгебре 1 ответы по анонимный | 92-30x+56
спросил 24 марта 2013 г. по алгебре 2 Ответы по анонимный | 358 просмотров
- задачи по алгебре
0 ответов
1 и yкакой набор точек входит в набор решений системы неравенств: x-y> и y<2x-1
спросил 19 июля 2012 г. по алгебре 2 Ответы по анонимный | 709 просмотров
- задачи по алгебре
1 ответ
какое множество решений имеет линейное неравенство -0,8x +5,2 < 0?
спросил
7 сентября 2014 г. в ответы по геометрии
по
анонимный
| 366 просмотров
в ответы по геометрии
по
анонимный
| 366 просмотров
- задачи по алгебре
- набор решений
- построение графиков линейных уравнений
- решение неравенств
1 ответ 10 декабря 2013 г. по алгебре 2 Ответы по анонимный | 421 просмотров
- набор решений
1 ответ
Каково множество решений для открытого предложения с данным набором замен? 2t-t=0 {1,2,3,4}
спросил 3 октября 2013 г. по алгебре 1 ответы по БиберЧик | 1,0 тыс. просмотров
2 ответа
какой набор решений для (5x+3)-49=0
спросил 4 марта 2013 г. по алгебре 2 Ответы по анонимный | 269 просмотров
- задачи по алгебре
1 ответ
Каково множество решений для w2-1=0?
спросил 27 апр. 2012 г. по алгебре 1 ответы по анонимный | 388 просмотров
- алгебра 1
1 ответ
найти набор решений уравнения ( 1 + 1 = x ) 2 — 6 ( 1 + 1 + x ) = — 8
вопрос
26 сентября 2013 г. в других математических темах
по
Клод
| 614 просмотров
в других математических темах
по
Клод
| 614 просмотров
- ( 1 + 1 = x ) 2 — 6 ( 1 + 1 + x ) = — 8
1 ответ
Каково множество решений этого уравнения? 2|x – 1| – 7 = 2
спросил 25 января 2013 г. в исчислении ответы по анонимный | 217 просмотров
- решение уравнений
1 ответ
как бы вы получили Решение множества уравнения|x — 1| = 3
спросил 21 сентября 2012 г. по алгебре 2 Ответы по анонимный | 305 просмотров
- задачи по алгебре
1 ответ
решить уравнение и проверить -16=x+20 набор решений?
спросил 22 июня 2012 г. по алгебре 1 ответы по анонимный | 289 просмотров
- задачи по алгебре
- Все категории
- Предварительные ответы по алгебре 12.7k
- Алгебра 1 ответы 26.2k
- Алгебра 2 Ответы 10,8к
- ответы по геометрии
5.
 5k
5k - Тригонометрические ответы 2.8k
- Исчисление Ответы 6.6k
- Статистика Ответы 3.3k
- Ответы на задачи Word 10.6k
- Другие математические темы 7.5k
сообщить об этом объявлении
сообщить об этом объявленииПример 9 Решите уравнение 2x 1 X 3 Глава 4
BILARASA.COM — 4 x x точка 3 3 оси-уравнение не является числом решений x там и пример 2x решить 1 3 1 переменная на может переменная 9 точка уравнения здесь номер примера решения x x решает в y 2x — это 2x эта переменная строка, следовательно, один мы один a x Стенограмма — в строке 3- 2x скажем 1 9x представляет 2x a 2x 1 один i 3 оси x только 1 3 1
А вот каталог изображений Пример 9 Решить уравнение 2x 1 X 3 Глава 4 самое лучшее Используя только символы, вы можете 1 Статья столько полностью читаемых версий, сколько вам нравится, что люди говорят и указывают Создавать истории для вас очень весело. Все мы лучше всего получаем много красивого чтения Пример 9 Решить уравнение 2x 1 X 3 Глава 4 интересную фотографию, но мы все представляем только то, о чем мы считаем, было бы идеальным чтением.
Отдельные статьи Пример 9 Решить уравнение 2x 1 X 3 Раздел 4 предназначен только для великолепной демонстрации, когда вам нужно изображение, необходимое для правильного чтения. Обслуживайте своего читателя, покупая исходные предложения Пример 9 Решите уравнение 2x 1 X 3 Глава 4 , поэтому участник может предоставить лучшее чтение и продолжить работу. При поиске предлагают все виды жилой и коммерческой работы. Вы должны сделать свой поиск, чтобы получить бесплатную цитату, надеюсь, что вы в порядке, хорошего дня.
Пример 9 Решение уравнения 2x 1 X 3 Глава 4 Примеры
Стенограмма. Пример 9. Решите уравнение 2x 1 = x – 3 и представьте решение(я) на (i) числовая строка числовая линия является одной переменной в одной переменной, есть только ось x (без оси y), решение 2x 1 = х – 3 2х – х = –3 – 1 х = – 4 здесь 2х 1 = х – 3 точка, следовательно, можно сказать, что в одной переменной 2х 1 = х – 3 точка пример 9 решить уравнение 2х 1 = x – 3. Пример 1: решить 3 x = 4. решение: дано уравнение; 3 x = 4. мы видим, что в левой части присутствует переменная x. таким образом, нам нужно сделать переменную «x» одной на левой стороне. таким образом, вычитая 3 из левой и правой сторон, мы получаем; 3 x – 3 = 4 – 3. x = 1. следовательно, решение x = 1. Как решить ваше уравнение. чтобы решить уравнение с помощью решателя уравнений, введите уравнение вида x 4=5. затем решатель покажет вам шаги, которые помогут вам научиться решать ее самостоятельно. Пошаговые примеры. алгебра. решить для х калькулятор. Шаг 1: введите уравнение, которое хотите решить, в редактор. Калькулятор уравнений позволяет вам взять простое или сложное уравнение и решить его наилучшим методом. шаг 2: нажмите синюю стрелку, чтобы отправить и посмотреть результат!. Объединение подобных терминов дает. x 2 = 10. Добавление 2 к каждому члену дает. x 2 2 =10 2. x = 12. Чтобы решить уравнение, мы используем свойство сложения и вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.
Пример 1: решить 3 x = 4. решение: дано уравнение; 3 x = 4. мы видим, что в левой части присутствует переменная x. таким образом, нам нужно сделать переменную «x» одной на левой стороне. таким образом, вычитая 3 из левой и правой сторон, мы получаем; 3 x – 3 = 4 – 3. x = 1. следовательно, решение x = 1. Как решить ваше уравнение. чтобы решить уравнение с помощью решателя уравнений, введите уравнение вида x 4=5. затем решатель покажет вам шаги, которые помогут вам научиться решать ее самостоятельно. Пошаговые примеры. алгебра. решить для х калькулятор. Шаг 1: введите уравнение, которое хотите решить, в редактор. Калькулятор уравнений позволяет вам взять простое или сложное уравнение и решить его наилучшим методом. шаг 2: нажмите синюю стрелку, чтобы отправить и посмотреть результат!. Объединение подобных терминов дает. x 2 = 10. Добавление 2 к каждому члену дает. x 2 2 =10 2. x = 12. Чтобы решить уравнение, мы используем свойство сложения и вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки. Пример 3 решить 2x 1 = x 2.
Пример 3 решить 2x 1 = x 2.
Пример 9 Решение уравнения 2x 1 X 3 Глава 4
Решение уравнения. алгебраические уравнения состоят из двух математических величин, например многочленов, приравниваемых друг к другу. решение уравнений дает решение для независимых переменных, символьных или числовых. Помимо поиска решений уравнений, wolfram|alpha также отображает уравнения и их решения. Линейное уравнение – это уравнение прямой линии, записанное с одной переменной. единственная степень переменной равна 1. Линейные уравнения с одной переменной могут иметь вид. ax b=0 ax b = 0. и решаются с помощью основных алгебраических операций. начнем с классификации линейных уравнений с одной переменной как одного из трех типов: тождественных, условных или . 10 примеров уравнений с модулями с ответами. уравнения абсолютного значения могут быть решены путем возведения в квадрат обеих частей уравнения. таким образом, выражение внутри знака абсолютного значения всегда будет положительным. то мы можем расширить выражения и упростить их. наконец, полученное уравнение может быть решено любым применимым методом.
то мы можем расширить выражения и упростить их. наконец, полученное уравнение может быть решено любым применимым методом.
Класс 9 Математика Глава 4 Пример 9 | Решите уравнение 2x 1 = x 3 и представьте решение числом .
9 класс математика глава 4 пример 9 | решить уравнение 2x 1=x 3 и представить решение на число привет добро пожаловать на наш вопрос из ncert математики класс 9 глава 4 решенные примеры вопрос – 9 линейных уравнений с двумя переменными cursosgratis316 .pe умножение биномиальной алгебры. когда x находится в показателе степени, и вы не можете получить общее основание, вы должны зарегистрировать обе части уравнения и изменить порядок, чтобы решить поддержку и пожертвование * google pay paytm phone pe 8826338962 Если вы цените нашу работу, рассмотрите возможность пожертвования этому видеоуроку по алгебре, в котором объясняется процесс решения двухшаговых уравнений с дробями и переменными с обеих сторон. это видео объясняет, как решить линейное уравнение со скобками, дробями и переменными с обеих сторон. дробь не является этим видеоуроком по алгебре, объясняющим, как решать радикальные уравнения. он содержит множество примеров и практических задач. Вот пошаговая методика решения квадратных уравнений путем заполнения квадрата. по предварительной математике. решить линейные уравнения: 3x 2 = 7 и 2x 3 = 9посмотрите мои бесплатные курсы по математике: арифметика Математика для 4-го, 5-го, 6-го класса: этот видеоурок по алгебре 2 покажет вам, как заполнить квадрат для решения квадратных уравнений. это видео для старшей школы
это видео объясняет, как решить линейное уравнение со скобками, дробями и переменными с обеих сторон. дробь не является этим видеоуроком по алгебре, объясняющим, как решать радикальные уравнения. он содержит множество примеров и практических задач. Вот пошаговая методика решения квадратных уравнений путем заполнения квадрата. по предварительной математике. решить линейные уравнения: 3x 2 = 7 и 2x 3 = 9посмотрите мои бесплатные курсы по математике: арифметика Математика для 4-го, 5-го, 6-го класса: этот видеоурок по алгебре 2 покажет вам, как заполнить квадрат для решения квадратных уравнений. это видео для старшей школы
Связанное изображение с примером 9 решить уравнение 2x 1 x 3 глава 4
Связанное изображение с примером 9 решить уравнение 2x 1 x 3 глава 4
Сколько решений уравнения 2x + 1 = х – 3 есть на декартовой плоскости? -Математика 9
Войти Регистрация
- Вся активность
- Вопросы
- Горячий!
- без ответа
- Теги
- Категории
- Задайте вопрос
- Профиль
- Редактировать профиль
- Сообщения
- Избранное
- Мои обновления
- Выйти
Пользователь qa_get_logged_in_handle сортировка
Пользователь qa_get_logged_in_handle сортировать
- Главная
- Класс 9 org/ListItem»> Математика 9
- Сколько решений уравнения 2x + 1 = x –…
по ЯгодыЭмулятор славы Гранд
(151 тыс. баллов)
спросил по математике 9 19 просмотров
2 ответа
по John_ka_SenaНепобедимый Гениальный
(30,6k баллов)
ответил
2x + 1 = x – 3
2x-x = -3-1 его можно записать как 1.x + 0. y = – 4 …………..(ii)
(i) Числовая линия представляет все действительные значения x на оси X. Следовательно, x = – 4 – это ровно одна точка, лежащая на числовой прямой.
(ii) Принимая во внимание, что уравнение x + 4 = 0 представляет собой прямую линию, параллельную оси Y, и бесконечно много точек лежат на прямой в декартовой плоскости.
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
ответили
2x + 1 = x – 3
2x-x = -3-1 его можно записать как 1.x + 0. y = – 4 …………..(ii)
(i) Числовая линия представляет все действительные значения x на оси X. Следовательно, x = – 4 – это ровно одна точка, лежащая на числовой прямой.
(ii) Принимая во внимание, что уравнение x + 4 = 0 представляет собой прямую линию, параллельную оси Y, и бесконечно много точек лежат на прямой в декартовой плоскости.
← Предыдущий вопрос Следующий вопрос →
Похожие вопросы
0 голосов
23 просмотра 1 ответ
Сколько решений уравнения 2x + 1 = x – 3 есть на декартовой плоскости?
- математикадевятый
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
точек)
спросил по математике 9 19 фев. 2021 г.
0 голосов
93 просмотра 3 ответа
Решите уравнение 2x + 1 = x -3 и запишите решение(я) на (i) числовой прямой. (ii) декартова плоскость.
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
44 просмотра 2 ответа
Нарисуйте графики линейных уравнений y = x и y = – x на одной и той же декартовой плоскости.
- математикадевятый
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
спросил по математике 9 19 фев. 2021 г.
0 голосов
25 просмотров 1 ответ
Нарисуйте графики линейных уравнений y = x и y = – x на одной и той же декартовой плоскости.
- математикадевятый
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
спросил по математике 9 19 фев. 2021 г.
0 голосов
66 просмотров 3 ответа
Сколько решений имеет уравнение 2x +5y=8?
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
294 просмотра 3 ответа
Нанесите точки A (5, 5) и B (–5, 5) на декартовой плоскости. Присоединяйтесь к AB, OA и OB. Назовите тип полученного треугольника.
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
42 просмотра 3 ответа
Нанесите точки a(5,5) и b(-5,5) на декартовой плоскости. Соедините OA AB и OB, назовите полученную фигуру и найдите ее площадь
Соедините OA AB и OB, назовите полученную фигуру и найдите ее площадь
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
199 просмотров 1 ответ
Это серия загадок. Все они связаны. 1) На плоскости 100 кирпичей. Один отваливается. Сколько осталось? 2) Каковы три шага, чтобы поместить слона в холодильник? 3) Каковы четыре шага, чтобы поместить жирафа в холодильник? 4) У льва была вечеринка, и он пригласил всех животных. Пришли все, кроме одного. Какой это был? 5) Женщина пересекла зараженную крокодилами реку и выжила. Как? 6) Она перешла обратно и умерла. Как?
- загадки
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
спросил в загадках 27 марта 2021 г.
0 голосов
19 просмотров 0 ответов
Нанесите точки A(3, 2), B(-2, 2), C(-2, -2) и D(3, -2) на декартовой плоскости. Соедините эти точки и назовите полученную фигуру.
Соедините эти точки и назовите полученную фигуру.
по tony#sharkLearnyVerse Wizard
(74,3 тыс. баллов)
спросил по математике 9 23 января 2021 г.
0 голосов
22 просмотра 3 ответа
Начертите на той же бумаге график уравнения x — Y = 4 & 2x+ 2y =4 и найдите координаты точки, две линии которой пересекаются.
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
31 просмотр 0 ответов
сколько решений имеет уравнение 2x+5y=8
по Получить ответыChief of LearnyVerse
(321 тыс. точек)
спросил в общих знаниях 18 апр. 2021 г.
0 голосов
141 просмотров 3 ответа
Если точка (2k – 3, k + 2) лежит на графике уравнения 2x + 3y +15 = 0, найдите значение k.
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
50 просмотров 2 ответа
Уравнение 2x+ 5y = 7 имеет единственное решение, если x и y равны
- математикадевятый
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
спросил по математике 9 19 фев. 2021 г.
0 голосов
58 просмотров 1 ответ
Уравнение 2x+ 5y = 7 имеет единственное решение, если x и y равны
- математикадевятый
по ЯгодыЭмулятор славы Гранд
(151 тыс. точек)
спросил по математике 9 19 фев. 2021 г.
0 голосов
15 просмотров 1 ответ
Как называются горизонтальная и вертикальная линии, проведенные для определения положения любой точки на декартовой плоскости?
по tony#sharkLearnyVerse Wizard
(74,3 тыс. баллов)
баллов)
спросил по математике 9 23 января 2021 г.
0 голосов
164 просмотра 0 ответов
Факторизация (2x+1/3)²-(x-1/2)²
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9й 6 фев. 2021 г.
0 голосов
93 просмотра 3 ответа
Факторизация (2x+1/3)²-(x-1/2)²
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
216 просмотров 3 ответа
Найдите остаток, если f(x)=4x(куб) — 12x(квадрат) +14x — 3 разделить на g(x) = (2x-1).
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
109 просмотров 3 ответа
Найти x: Sol. 3x/7 + 2/7 + 4(x + 1)/5 = 2/3(2x + 1)
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
0 голосов
74 просмотра 3 ответа
Что нужно прибавить к x⁴+2x³-2x²+x-1, чтобы результат делился точно на x²+2x-3
- математикадевятый
по John_ka_SenaНепобедимый Гениальный
(30,6 тыс. баллов)
спросил по математике 9 6 фев. 2021 г.
Категории
- Все категории
- Искусственный интеллект (51)
- Программирование (586)
- Технологии (2,1к)
- Пространство (168)
- Вы знаете? (3,1к)
- Как ? (1,2к)
- Общие знания (9,9к)
- Награды (49)
- 6 класс (60)
- 7 класс (95)
- 8 класс (177)
- 9 класс
(4,7к)
- Математика 9-й (3,7к)
- Биология 9-й (33)
- Химия 9-й (49)
- Физика 9-я (31)
- История 9-й (313)
- География 9-й (76)
- гражданское право 9-е (209)
- Экономика 9 место (78)
- Английский 9-й (111)
- хинди 9 (176)
- 10-й класс (13,3к) г.
- Совет Тамилнаду (0)
- Загадки (4,3к)
- Наука (393)
- История (329)
- География (12,1к)
- Биология (5.1к)
- экономика (2,0к)
- Физика (79)
- Химия (116)
- хинди (11,9к)
- Игры (118)
- Спортивный (43)
- Музыка и искусство (30)
- Мифология (124)
- Открытия и изобретения (32)
- Часто задаваемые вопросы (19)
- Другой (9,9к)
- Математика (763)

IXL | Изучайте алгебру 1
IXL | Изучай алгебру 11
Сравнивать и упорядочивать рациональные числа
г.
 2
2Абсолютное значение и противоположности
3
Числовые строки
4
Преобразование между десятичными дробями и дробями
5
Преобразование между повторяющимися десятичными знаками и дробями
6
Квадратные корни
7
Кубические корни
8
Сортировать рациональные и иррациональные числа
9
Классифицировать рациональные и иррациональные числа
10
Свойства операций над рациональными и иррациональными числами
г.
11
Классифицировать числа
1
Складывать, вычитать, умножать и делить целые числа
2
Вычислять числовые выражения, включающие целые числа
3
Вычислить переменные выражения, включающие целые числа
4
Складывать и вычитать рациональные числа
5
Умножать и делить рациональные числа
6
Упрощайте сложные дроби
7
Оценивать числовые выражения, включающие рациональные числа
г.
 8
8Вычислить переменные выражения, включающие рациональные числа
1
Определить эквивалентные отношения
2
Напишите эквивалентное отношение
3
Ставки за единицу
4
Цены за единицу
5
Решить пропорции
6
Решить пропорции: текстовые задачи
7
Чертежи в масштабе: текстовые задачи
1
Преобразование между процентами, дробями и десятичными дробями
г.
 2
2Решите процентные уравнения
3
Процентные проблемы со словами
4
Процент изменения
5
Процент изменений: текстовые задачи
6
Процент изменения: найти исходное количество словесных задач
7
Процент от числа: налог, скидка и т.
 д.
д.8
Найдите процент: налог, скидка и т. д.
9
Многошаговые задачи с процентами
г. 1
Преобразование ставок и измерений: общепринятые единицы
2
Преобразование ставок и измерений: метрические единицы
3
Цены за единицу с преобразованием единиц
4
Многоэтапные задачи с преобразованием единиц измерения
5
Точность
6
Максимально возможная ошибка
7
Минимальная и максимальная площадь и объем
8
Процентная ошибка
9
Процентная ошибка: площадь и объем
1
Периметр
2
Область
3
Площадь и периметр: текстовые задачи
4
Объем
5
Площадь поверхности
6
Подобные фигуры: длины сторон и меры углов
7
Подобные треугольники и косвенное измерение
8
Расширения и коэффициенты масштабирования
9
Площадь и периметр подобных фигур
10
Площадь между двумя фигурами
г.
11
Подобные твердые вещества
12
Объем и площадь поверхности подобных твердых тел
13
Периметр и площадь: изменение масштаба
г.
 14
14Площадь поверхности и объем: изменение масштаба
15
Периметр, площадь и объем: изменение масштаба
16
теорема Пифагора
17
Теорема Пифагора: текстовые задачи
18
Обратная теорема Пифагора: прямоугольный треугольник?
19
Специальные прямоугольные треугольники
1
Обзор координатной плоскости
2
Формула середины: найти середину
3
Формула средней точки: найти конечную точку
4
Расстояние между двумя точками
1
Свойства сложения и умножения
2
Распределительное свойство
3
Упростите переменные выражения, используя свойства
4
Свойства равенства
5
Определите эквивалентные уравнения
1
Напишите переменные выражения
2
Факторы сортировки переменных выражений
3
Упростите переменные выражения, включающие одинаковые термины и распределительное свойство.

4
Определите эквивалентные линейные выражения
5
Напишите уравнения переменных
6
Удовлетворяет ли x уравнению?
7
Какой x удовлетворяет уравнению?
8
Решите уравнения, используя порядок операций
9
Удовлетворяет ли (x, y) уравнению?
10
Свяжите график уравнения с его решениями
г.
11
Преобразование уравнений с несколькими переменными
1
Моделируйте и решайте линейные уравнения с помощью плиток алгебры
2
Напишите и решите линейные уравнения, которые представляют диаграммы
3
Решение одношаговых линейных уравнений
4
Решите двухшаговые линейные уравнения
5
Решение сложных линейных уравнений
6
Решите линейные уравнения с переменными с обеих сторон
7
Решите линейные уравнения: завершите решение
8
Найдите количество решений линейного уравнения
9
Создавайте линейные уравнения без решений или с бесконечным количеством решений
10
Решайте одношаговые и двухшаговые линейные уравнения: текстовые задачи
г.11
Решение линейных уравнений: смешанный обзор

1
Графические неравенства
2
Напишите неравенства по графикам
3
Найдите решения для неравенства
4
Решите одношаговые линейные неравенства: сложение и вычитание
5
Решите одношаговые линейные неравенства: умножение и деление
6
Решите одношаговые линейные неравенства
7
Графические решения одношаговых линейных неравенств
г.
 8
8Решите двухшаговые линейные неравенства
9
Графические решения двухшаговых линейных неравенств
10
Решение сложных линейных неравенств
г.
 11
11Графические решения расширенных линейных неравенств
12
График составных неравенств
13
Запишите составные неравенства из графиков
14
Решите сложные неравенства
15
Графические решения сложных неравенств
Контрольная точка: решение линейных уравнений и неравенств
г.
1
Решите уравнения абсолютного значения
2
Графические решения уравнений абсолютного значения
3
Решите неравенства абсолютного значения
4
Графические решения абсолютных неравенств
1
Матричный словарь
2
Правила работы с матрицей
3
Сложение и вычитание матриц
4
Умножить матрицу на скаляр
5
Сложение и вычитание скалярных множителей матриц
6
Умножить две матрицы
7
Свойства матриц
1
Интерпретировать линейные графики
2
Создание линейных графиков
3
Интерпретация гистограмм
4
Создание гистограмм
5
Интерпретация гистограмм, линейных графиков и гистограмм
6
Создание гистограмм, линейных графиков и гистограмм
7
Интерпретация круговых диаграмм
8
Интерпретация сюжетов «стебель-листья»
9
Коробчатые графики
Контрольная точка: линейные графики, гистограммы и ящичные диаграммы
г.
1
Словесные задачи: смешанный обзор
2
Словесные проблемы с деньгами
3
Последовательные целочисленные задачи
4
Скорость путешествия: словесные задачи
5
Средневзвешенные значения: текстовые задачи
Контрольно-пропускной пункт: единицы и количество
г.
1
Определять арифметические и геометрические прогрессии
2
Арифметические последовательности
3
Геометрические последовательности
4
Вычислить переменные выражения для числовых последовательностей
5
Вычислить рекурсивные формулы для последовательностей
6
Определите последовательность как явную или рекурсивную
7
Напишите переменные выражения для арифметических последовательностей
8
Напишите переменные выражения для геометрических последовательностей
9
Напишите формулу рекурсивной последовательности
10
Преобразование рекурсивной формулы в явную формулу
11
Преобразование явной формулы в рекурсивную формулу
12
Номерные серии: смешанный обзор
Контрольная точка: последовательности
1
Отношения: преобразование между таблицами, графиками, сопоставлениями и списками точек
2
Домен и диапазон отношений
3
Определите независимые и зависимые переменные
4
Определить функции
5
Определите функции: проверка вертикальной линии
6
Найдите значения, используя графики функций
7
Оценить функцию
8
Вычислите функцию: подставьте выражение
9
Сложение и вычитание функций
10
Умножение функций
11
Найдите обратную функцию
12
Заполнить таблицу функций по графику
13
Заполните таблицу функций из уравнения
г.
 14
14Найдите решение с помощью таблицы
15
Приблизительные решения с помощью таблицы
16
Интерпретировать график функции: текстовые задачи
г.
 17
17Интерпретируйте функции, используя повседневный язык
18
Скорость изменения: таблицы
19
Скорость изменения: графики
Контрольная точка: концепции функций
г.
Контрольная точка: средняя скорость изменения
Контрольная точка: Решайте уравнения с помощью графиков и таблиц.
1
Оцените кусочно-определенные функции
2
График кусочно определенных функций
1
Определить пропорциональные отношения
2
Найдите постоянную вариации
3
Нарисуйте пропорциональную зависимость
4
Напишите уравнения прямой вариации
5
Напишите и решите уравнения прямой вариации
6
Определите прямую вариацию и обратную вариацию
7
Напишите уравнения обратной вариации
8
Напишите и решите уравнения в обратных вариациях
1
Определение линейных функций по графикам и уравнениям
2
Определите линейные функции из таблиц
3
Найдите наклон графика
4
Найдите наклон из двух точек
5
Найдите недостающую координату, используя наклон
6
Форма пересечения наклона: найти наклон и пересечение по оси Y
7
Форма пересечения наклона: графическое уравнение
8
Форма пересечения наклона: написать уравнение по графику
9
Форма пересечения наклона: напишите уравнение
10
Форма наклона-пересечения: напишите уравнение из таблицы
11
Форма пересечения наклона: напишите уравнение из текстовой задачи
12
Линейные уравнения: решить для y
13
Напишите и решите линейные уравнения с двумя переменными: текстовые задачи
14
Заполните таблицу и начертите линейную функцию
15
Сравните линейные функции: графики и уравнения
16
Сравните линейные функции: таблицы, графики и уравнения
17
Интерпретируйте наклон и точку пересечения оси Y линейной функции
18
Запишите уравнения в стандартной форме
19
Стандартная форма: найти точки пересечения x и y
20
Стандартная форма: графическое уравнение
21
Уравнения горизонтальных и вертикальных линий
22
Нарисуйте горизонтальную или вертикальную линию
23
Форма точка-наклон: графическое уравнение
24
Форма точка-наклон: напишите уравнение
25
Точечно-наклонная форма: написать уравнение по графику
г.
 26
26Найдите наклон и точки пересечения из уравнения
27
Наклоны параллельных и перпендикулярных линий
28
Напишите уравнение параллельной или перпендикулярной прямой
29
Преобразования линейных функций
1
Удовлетворяет ли (x, y) неравенству?
2
Линейные неравенства: найти y
3
График линейного неравенства с двумя переменными
4
Запишите линейное неравенство по графику
5
Напишите неравенства с двумя переменными: текстовые задачи
6
Является ли (x, y) решением системы линейных неравенств?
7
Решайте системы линейных неравенств графически
1
Является ли (x, y) решением системы уравнений?
2
Решите систему уравнений, построив график
г.
 3
3Решите систему уравнений с помощью графика: текстовые задачи
4
Найдите количество решений системы уравнений, построив график
5
Найдите количество решений системы уравнений
6
Классифицировать систему уравнений по графику
7
Классифицировать систему уравнений
8
Решите систему уравнений с помощью замены
9
Решите систему уравнений с помощью замены: текстовые задачи
10
Решите систему уравнений методом исключения
г.
11
Решите систему уравнений методом исключения: текстовые задачи
12
Решите систему уравнений с помощью расширенных матриц
13
Решите систему уравнений с помощью дополненных матриц: текстовые задачи
14
Решите систему уравнений любым способом
15
Решите систему уравнений любым методом: текстовые задачи
Контрольная точка: Системы уравнений и неравенств
Контрольная точка: представление ограничений
1
Показатели с целочисленным основанием
2
Показатели с десятичной и дробной базой
3
Отрицательные показатели
4
Умножение с показателями
5
Деление с показателями
6
Умножение и деление с показателями
7
Силовое правило
8
Оцените выражения, используя свойства экспонент
9
Определите эквивалентные выражения, включающие показатели I
10
Определите эквивалентные выражения, включающие показатели степени II
г.
11
Оценить целые числа, возведенные в положительные рациональные показатели
12
Оценить целые числа, возведенные в рациональные степени
13
Умножение с рациональными показателями
г.
 14
14Деление с рациональными показателями
15
Степенное правило с рациональными показателями
16
Упростите выражения, включающие рациональные показатели
1
Преобразование между стандартной и научной нотацией
2
Сравните числа, записанные в экспоненциальном представлении.

3
Сложение и вычитание чисел, записанных в экспоненциальном представлении
4
Умножать числа, записанные в экспоненциальном представлении
5
Разделить числа, записанные в экспоненциальном представлении
1
Оцените экспоненциальную функцию
2
График экспоненциальных функций
3
Сопоставьте экспоненциальные функции и графики I
4
Сопоставьте экспоненциальные функции и графики II
г.
 5
5Область и диапазон экспоненциальных функций: графики
6
Область определения и область значений экспоненциальных функций: уравнения
•
Новинка! Напишите экспоненциальные функции: текстовые задачи
г.
7
Экспоненциальный рост и распад: текстовые задачи
8
Сложные проценты: проблемы со словами
1
Определить мономы
2
Умножить одночлены
3
Разделить одночлены
4
Умножать и делить одночлены
5
Степени мономов
1
Полиномиальная лексика
2
Модельные полиномы с плитками алгебры
3
Сложение и вычитание полиномов с помощью плиток алгебры
4
Сложение и вычитание многочленов
5
Добавьте многочлены, чтобы найти периметр
6
Умножить многочлен на одночлен
7
Умножьте два двучлена, используя плитки алгебры
8
Умножить два двучлена
9
Умножение двух двучленов: особые случаи
10
Умножьте полиномы, используя модели площадей
г.
11
Умножить многочлены
12
Умножьте многочлены, чтобы найти площадь
Контрольная точка: полиномиальные операции
1
GCF мономов
г.
2
Вынести моном
3
Фактор квадратичных чисел с использованием плиток алгебры
4
Квадратичные коэффициенты со старшим коэффициентом 1
г.
 5
5Квадратичные коэффициенты с другими старшими коэффициентами
6
Квадратичные факторы: частные случаи
7
Фактор по группировке
8
Фактор с использованием квадратичного шаблона
9
Факторные полиномы
1
Характеристики квадратичных функций: графики
2
Характеристики квадратичных функций: уравнения
3
Заполните таблицу функций: квадратичные функции
4
Преобразования квадратичных функций
5
График квадратичных функций в вершинной форме
г.
 6
6Решите квадратное уравнение, используя квадратные корни
7
Решите квадратное уравнение, используя свойство нулевого произведения
8
Решите квадратное уравнение, разложив его на множители.

9
Заполните квадрат
10
Решите квадратное уравнение, заполнив квадрат
11
Решите квадратное уравнение, используя квадратную формулу
•
Новинка! Решить квадратные уравнения: текстовые задачи
12
Использование дискриминанта
13
Запишите квадратичную функцию в вершинной форме
14
График квадратичных функций в стандартной форме
15
Сопоставьте квадратичные функции и графики
г.
 •
•Новинка! Область определения и область значений квадратичных функций: графики
16
Область определения и область значений квадратичных функций: уравнения
17
Запишите квадратичную функцию от ее вершины и другой точки
•
Новинка! Интерпретация частей квадратных выражений: текстовые задачи
18
Решите систему линейных и квадратных уравнений, построив график
19
Решите систему линейных и квадратных уравнений
Контрольная точка: квадратные уравнения
Контрольная точка: напишите и интерпретируйте эквивалентные выражения
1
Определение линейных и экспоненциальных функций по графикам
2
Определение линейных, квадратичных и экспоненциальных функций по графикам
3
Определите линейные и экспоненциальные функции из таблиц
4
Определите линейные, квадратичные и экспоненциальные функции из таблиц
5
Напишите линейные и экспоненциальные функции: текстовые задачи
6
Запишите линейные и экспоненциальные функции из таблиц
7
Запишите линейные, квадратичные и экспоненциальные функции из таблиц
8
Линейные функции на единичных интервалах
9
Экспоненциальные функции на единичных интервалах
10
Описать линейный и экспоненциальный рост и затухание
11
Сравните линейный и экспоненциальный рост
г.
 12
12Сравните линейный, экспоненциальный и квадратичный рост
Контрольная точка: Решение задач с помощью уравнений и неравенств
КПП: Особенности функций
Контрольная точка: сравните линейные и экспоненциальные функции
Контрольная точка: функции сборки
1
Заполните таблицу функций: функции абсолютного значения
2
График функции абсолютного значения
г.
 3
3Домен и диапазон функций абсолютного значения: графики
4
Область определения и диапазон функций абсолютного значения: уравнения
5
Преобразования функций абсолютного значения: переводы и отражения
6
Преобразования функций абсолютного значения: переводы, отражения и растяжения
7
Правила преобразования функций
8
Переводы функций
9
Отражения функций
10
Расширения функций
11
Преобразования функций
12
Описывать преобразования функций
Контрольная точка: построение графиков и анализ функций
Контрольная точка: преобразования функций
1
Упрощение подкоренных выражений
2
Упростите подкоренные выражения с помощью переменных
3
Упрощение подкоренных выражений, содержащих дроби
4
Умножение подкоренных выражений
5
Сложение и вычитание подкоренных выражений
6
Упростите подкоренные выражения, используя распределительное свойство
7
Упростите подкоренные выражения, используя сопряжения
8
Упрощение подкоренных выражений: смешанный обзор
Контрольная точка: радикалы и рациональные показатели
1
Оцените функции квадратного корня
2
Область определения и диапазон функций квадратного корня: графики
г.
 3
3Область определения и диапазон функций квадратного корня: уравнения
4
График функций квадратного корня
5
Решить радикальные уравнения I
6
Решить радикальные уравнения II
1
Рациональные функции: асимптоты и исключенные значения
г.
 2
2Упрощайте рациональные выражения
3
Умножать и делить рациональные выражения
4
Разделить многочлены на одночлены
5
Разделите многочлены, используя длинное деление
6
Сложение и вычитание рациональных выражений
7
Упростите смешанные рациональные выражения
8
Решите рациональные уравнения
9
Оценивать рациональные выражения
1
Тригонометрические отношения: sin, cos и tan
г.
2
Найдите тригонометрические отношения с помощью калькулятора
3
Обратные тригонометрические функции
4
Тригонометрические соотношения: найти длину стороны
5
Тригонометрические отношения: найти меру угла
6
Решить прямоугольный треугольник
1
Наборы, подмножества и дополнения
2
Обозначение построителя наборов
3
Обозначение интервала
•
Новинка! Объединения и пересечения множеств
1
Определите гипотезы и выводы
2
контрпримеры
1
Теоретическая вероятность
2
Экспериментальная вероятность
3
Найдите вероятности, используя двусторонние таблицы частот
4
Найдите условные вероятности, используя двусторонние таблицы частот
5
Исходы составных событий
6
Определите независимые и зависимые события
7
Вероятность независимых и зависимых событий
8
Принцип подсчета
9
Перестановки
10
Обозначение перестановки и комбинации
Контрольная точка: двусторонние таблицы частот
1
Выявление необъективных выборок
2
Среднее значение, медиана, мода и диапазон
3
Вычислить квартили и межквартильный диапазон
4
Определите выброс
5
Определите выброс и опишите эффект от его удаления.

6
Среднее абсолютное отклонение
7
Дисперсия и стандартное отклонение
8
Интерпретировать график рассеяния
9
Выбросы на диаграммах рассеяния
10
Сопоставьте коэффициенты корреляции с графиками рассеяния
11
Рассчитать коэффициенты корреляции
г.
 12
12Напишите уравнения для линий наилучшего соответствия
13
Найдите уравнение линии регрессии
14
Интерпретация линий регрессии
15
Анализ линии регрессии набора данных
16
Корреляция и причинно-следственная связь
Контрольная точка: сравнение наборов данных
г.
Контрольная точка: линейное моделирование
Числа и операции
- Целые числа
- Сложение и вычитание целых чисел
- Умножение и деление целых чисел
- Рациональное число
- Сложение и вычитание рациональных чисел
- Умножение и деление рациональных чисел г.
- Квадратные корни
- Кубические корни
- Иррациональные числа
- Пи г.

Проценты
- Проценты
- Простой интерес
- Процентное изменение
Геометрия
- Трансверсали параллельных прямых
- Внутренние углы треугольников
- Внешние углы треугольников
- Теорема Пифагора
- Обратная теорема Пифагора
- Формула средней точки
- Формула расстояния г.

Числовые серии
- Арифметические последовательности
- Геометрические последовательности
Выражения
- Написание алгебраических выражений г.
- Оценка выражений
- Упрощение выражений
- Распределительная собственность
- Расширение выражений
- Факторные выражения
Уравнения с одной переменной
- Решение уравнений
- Многошаговые уравнения
- Уравнения с бесконечным числом решений или без них
Неравенства с одной переменной
- Решение неравенств
- Составные неравенства
Уравнения и неравенства с абсолютной величиной
- Уравнения абсолютного значения
- Неравенства абсолютного значения
Отношения и функции
- Отношения и функции
- Независимые и зависимые переменные
- Домен и диапазон
- Обратные функции
Пропорциональные отношения
- Пропорциональные отношения
- Константа пропорциональности
Линейные функции
- Линейные уравнения
- Линейные функции
- Склон
- Форма пересечения наклона г.

 5k
5k 2
2
 8
8 2
2 д.
д.
 14
14

 8
8 11
11


 14
14 17
17
 26
26 3
3

 14
14
 5
5

 5
5 6
6
 •
• 12
12 3
3 3
3 2
2

 12
12