Ряд тейлора для косинуса: Разложение косинуса в ряд Тейлора

Содержание

Ряд Тейлора

Ряд Тейлора — это идея, используемая в информатике, исчислении, химии, физике и других видах математики высшего уровня. Это ряд, который используется для создания оценки (предположения) того, как выглядит функция. Существует также специальный вид ряда Тейлора, называемый рядом Маклорина.

Теория ряда Тейлора заключается в том, что если выбрать точку на координатной плоскости (оси x и y), то можно предположить, как будет выглядеть функция в области вокруг этой точки. Для этого берутся производные функции и складываются вместе. Идея заключается в том, что можно сложить бесконечное число производных и получить одну конечную сумму.

В математике ряд Тейлора представляет функцию в виде суммы бесконечного ряда. Члены суммы берутся из производных функции. Ряды Тейлора происходят от теоремы Тейлора.

Анимация, показывающая, как ряд Тейлора может быть использован для аппроксимации функции. Синяя линия показывает экспоненциальную функцию f ( x ) = e x {\displaystyle f(x)=e^{x}}.

. Красные линии показывают сумму n производных — то есть, n+1 членов ряда Тейлора. По мере увеличения n красная линия приближается к синей.

История

Древнегреческий философ Зенон из Элеи впервые выдвинул идею этой серии. Парадокс, получивший название «пародокс Зенона». Он считал, что невозможно сложить бесконечное число величин и получить в результате одно конечное значение.

Другой греческий философ, Аристотель, дал ответ на этот философский вопрос. Однако именно Архимед нашел математическое решение, используя свой метод исчерпания. Он смог доказать, что если что-то разделить на бесконечное число мелких кусочков, то при повторном сложении они все равно составят единое целое. Древнекитайский математик Лю Хуэй доказал то же самое несколько сотен лет спустя.

Самые ранние известные примеры ряда Тейлора — это работа Мадхавы из Сангамаграмы в Индии в 1300-х годах. Позднее индийские математики писали о его работе с тригонометрическими функциями синуса, косинуса, тангенса и арктангенса. Ни один из трудов или записей Мадхавы не сохранился до наших дней. Другие математики основывали свои работы на открытиях Мадхавы и продолжали работать с этими рядами вплоть до 1500-х годов.

Джеймс Грегори, шотландский математик, работал в этой области в 1600-х годах. Грегори изучил ряд Тейлора и опубликовал несколько рядов Маклаурина. В 1715 году Брук Тейлор открыл общий метод применения ряда ко всем функциям. (Все предыдущие исследования показывали, как применять метод только к конкретным функциям). Колин Маклаурин опубликовал частный случай ряда Тейлора в 1700-х годах. Этот ряд, который базируется вокруг нуля, называется рядом Маклаурина.

Определение

Ряд Тейлора можно использовать для описания любой функции ƒ(x), которая является гладкой функцией (или, в математических терминах, «бесконечно дифференцируемой»). Функция ƒ может быть вещественной или комплексной. Затем ряд Тейлора используется для описания того, как выглядит функция в окрестности некоторого числа a. {5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\! }

Где B n {\displaystyle B_{n}} — n-ое число Бернулли, а ln {\displaystyle \ln } — натуральный логарифм.

Автор

Alegsaonline.com — Ряд Тейлора — Leandro Alegsa — 2022-01-18 21:30:05 — url: https://ru.alegsaonline.com/art/96606

Библиографические ссылки

— www.canisius.edu — «Neither Newton nor Leibniz — The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala»- www.wikidata.org — — d-nb.info — 4184548-1

Формула Тейлора — Математика — Уроки

Формула Тейлора для некоторых элементарных функций

Рассмотрим несколько важнейших элементарных функций и найдём для них многочлены Тейлора при .

1. Рассмотрим функцию . Все её производные совпадают с ней: , так что коэффициенты Тейлора в точке равны

Поэтому формула Тейлора для экспоненты такова:

2. Рассмотрим функцию . Её производные чередуются в таком порядке:

а затем цикл повторяется. Поэтому при подстановке также возникает повторение:

и т. д. Все производные с чётными номерами оказываются равными 0; производные с нечётными номерами равны 1 при , то есть при , и при , то есть при . Таким образом, при всех и коэффициенты Тейлора равны

Получаем формулу Тейлора для синуса:

Заметим, что мы можем записать остаточный член вместо (как можно было бы подумать), поскольку можно считать, что слагаемое порядка , с коэффициентом, равным 0, тоже включено в многочлен Тейлора.

3. Для функции производные также чередуются с циклом длины 4, как и для синуса. Значения в точке имеют то же чередование:

Нетрудно видеть, что при , и при , . Поэтому разложение косинуса по формуле Тейлора имеет вид

Здесь мы также считаем, что последним в многочлене Тейлора выписано слагаемое, содержащее с нулевым коэффициентом.

Упражнение 6.1 Найдите формулу для производной произвольного порядка от функции .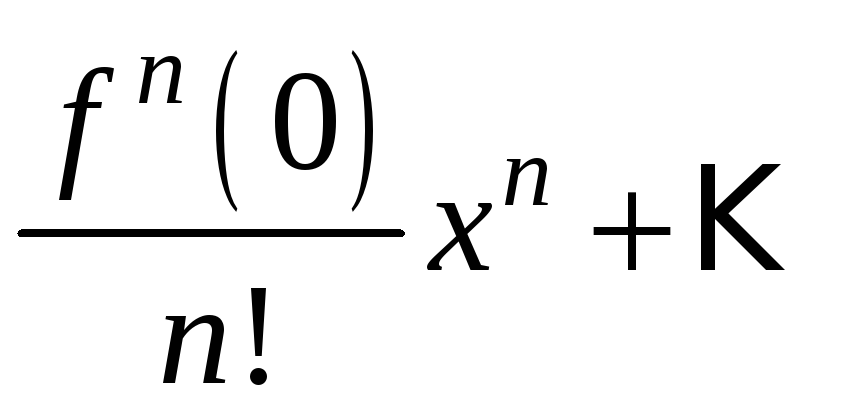 Вычислите значения этих производных при и коэффициенты Тейлора. Покажите, что имеет место разложение

Упражнение 6.2 Найдите формулу для производной произвольного порядка от функции при фиксированном . Вычислите значения этих производных при и коэффициенты Тейлора. Покажите, что имеет место разложение

Упражнение 6.3 Покажите, что разложения по формуле Тейлора для функций и выглядят так:

Сравните найденные разложения с разложениями для , и .

На основе полученных разложений можно получать и разложения многих других функций.

Пример 6.1 Рассмотрим функцию . Найдём её разложение по формуле Тейлора в точке . Начнём с того, что напишем ранее найденное разложение для экспоненты,

и положим в нём :

Теперь умножим левую и правую части этой формулы на :

Заметим, что бесконечно малое при выражение имеет тот же или больший порядок малости, как , и поэтому может рассматриваться как остаточный член в формуле Тейлора для , а предыдущие слагаемые в правой части формулы — как многочлен Тейлора данной функции. Так что её искомое разложение найдено.

Разберём теперь пример того, как полученные разложения элементарных функций можно использовать для раскрытия некоторых неопределённостей.

Пример 6.2 Найдём предел

Для начала найдём разложение по формуле Тейлора в точке 0 для числителя:

где через обозначен остаточный член, имеющий тот же порядок малости, что и . Разложение для знаменателя имеет вид:

где остаточные члены и тоже имеют тот же порядок малости, что и , при . Выполняя приведение подобных членов, получаем, что знаменатель равен

Итак,

Заметим, что этот способ раскрытия неопределённостей типа в некоторых случаях, подобных разобранному в примере, менее трудоёмок, чем применение правила Лопиталя.

тригонометрия — разложение в ряд Тейлора и значение угла косинуса

Это связанный вопрос при получении значений косинуса двумя разными способами сложные углы, такие как 10°, 20° или 1°, 2°, которые не кратны 3.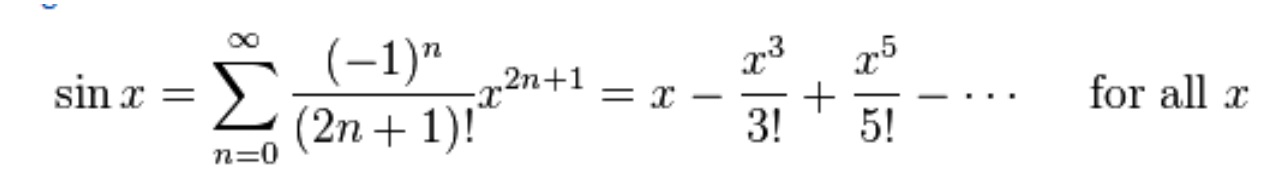

Расширение ряда Тейлора требует преобразования углов в радианы. Поэтому нам нужно значение $\pi$, чтобы получить радианы. Расширение ряда Тейлора происходит с показателями значений внутри функций. показатели радианов (для тригонометрических углов) и возрастающий факториал! 96}{6!}…$

Первый вопрос: какой фактор будет определять точность терминов? Это больше десятичных знаков $\pi$ или больше членов в многочленах Тейлора?

Я пробовал следующим образом с кодированием в python

 #Taylor ряд Значение косинуса для 80 градусов
время импорта
импортировать математику
из десятичного импорта*
получитьконтекст().prec = 30
б = 3,141592653589793238462643383279
print("Значение числа Пи равно", б)
a = 80 # float(input("Введите требуемый угол для вычисления значения cos: \n"))
# Вычислить угол в радианах
Р = б*а/180
print("Угол в радианах: ",Decimal(R))
#r = математические радианы (а)
# печать (г)
# Тейлор расширение
c = int(input("Введите количество членов для расширения cos угла:\n"))
начало = время.
  время()
В = 0
для я в диапазоне (с):
    коэффициент = (-1)**i
    число = десятичное число (R) ** (2 * i)
    denom = math.factorial(2*i)
    V = V + (коэффициент) * ((число) / (номинал))
печать(В)
конец = время.время()
print("Время выполнения \n", конец - начало)
# Печатает с точностью до 16 цифр
# print(math.sqrt(1)/2)
n = int(input("Введите положительное целое число, чтобы получить количество циклов для вычисления cos80\n"))
х = Десятичный (2).sqrt ()
начало = время.время()
для я в диапазоне (n):
    х = десятичный (2 + х).sqrt()
    х = десятичный (2 + х).sqrt()
    х = десятичное число (2 - х).sqrt()
печать (x/2)
конец = время.время()
print("Время выполнения \n", конец - начало)

В приведенном выше коде я принудительно вставил 30 цифр $\pi$ после запятой. Но при запуске программы я получаю только 16 цифр. Это приводит к менее точным последующим цифрам, хотя мы пробуем больше полиномов. (Здесь мне трудно оценить, больше ли терминов или более точное значение $\pi$)

Но с циклическими бесконечными вложенными квадратными корнями ($\sqrt{2-\sqrt{2+\sqrt{2+\) sqrt{2-\sqrt{2+\sqrt{2+.