Считать матрицу онлайн: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Содержание

Калькулятор корреляционной матрицы — MathCracker.com

Решатели Статистика

Инструкции: Этот калькулятор корреляционной матрицы предоставит вам корреляционную матрицу для заданного набора выборок. Введите в поле под двумя или более образцами. Пожалуйста, нажмите «Enter», чтобы начать новый образец.

Введите образцы (через запятую или пробел, нажмите Ввод для нового образца)

Название образцов (через запятую. Необязательно)

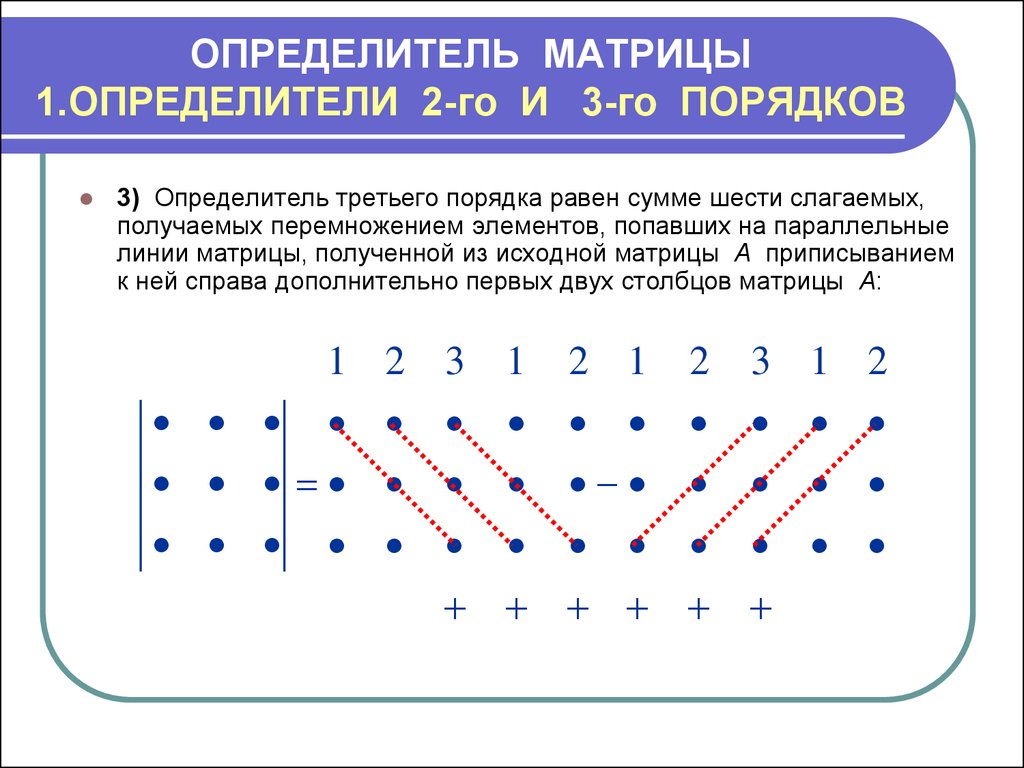
Матрица корреляции — это таблица, в которой попарные корреляции между несколькими переменными удобно организованы в виде матрицы. Значение в i-й строке j-го столбца соответствует корреляции между переменными $X_i$ и $X_j$.

Поскольку $corr(X_i, X_j) = corr(X_j, X_i)$, тогда матрица корреляции является симметричной, и по этой причине, чтобы не быть избыточной, матрица корреляции сообщает только значения от диагонали и выше. Для других операций корреляции вы можете вычислить коэффициент корреляции показывая все шаги, или вы можете использовать это калькулятор критической корреляции .

Как вычислить матрицу корреляции

Чтобы понять, как вычислить корреляционную матрицу, вам нужно сначала узнать, как вычислить корреляцию Пирсона, потому что корреляционная матрица — это просто матрица корреляций между всеми возможными парами переменных.

Базовый пакет статистики Матрица корреляции Статистический решатель

Пример построения и анализа — PowerBranding.

Основы → Лучшие инструменты стратегического анализа → Матрица Бостонской Консалтинговой Группы: подробный обзор → Пример портфельного анализа по модели БКГ

С помощью данного примера матрицы БКГ предприятия Вы сможете без особых усилий оптимизировать ассортиментный портфель компании. Пример содержит подробное описание каждого шага в построении матрицы БКГ, шаблон построения матрицы БКГ в Excel и рекомендации по возможным выводам, которые должны быть сделаны в результате анализа матрицы БКГ.

Рис.1 Матрица БКГ

Теоретическая справка

Перед изучением примера матрицы БКГ рекомендуем прочитать подробную статью «Матрица Бостонской Консалтинговой Группы: подробный обзор» с описанием основных показателей и принципов работы матрицы БКГ, с рекомендациями по составлению идеального портфеля и интерпретации результатов.

Первый шаг: Сбор исходной информации

Соберите данные по продажам и прибыли анализируемых групп в единую таблицу.

Второй шаг: Расчет темпа роста рынка

Рассчитайте средневзвешенный темп роста рынка по каждой товарной группе. Если средневзвешенный темп роста рынка рассчитать не представляется возможным, допускается использование в модели просто доли рынка.

В соответствии с получившимися данными определите по каждому товару в анализе темп роста рынка:

если темп роста меньше 10% — «низкий»
если темп роста рынка более 10% — «высокий»

Третий шаг: Расчет доли рынка товара

Рассчитайте относительную долю рынка каждого товара. В соответствии с получившимися данными определите по каждому товару: является относительная доля рынка «низкой» или «высокой».

если значение относительной доли рынка меньше 1 — «низкая»
если значение относительной доли рынка больше 1 — «высокая»

Если относительную долю рынка рассчитать невозможно из-за отсутствия информации, допускается использовать упрощенный вариант:

если по Вашей экспертной оценке доля Вашего товара меньше доли ключевого конкурента — ставьте «0»
если по Вашей экспертной оценке доля Вашего товара больше доли ключевого конкурента — ставьте «1»

Четвертый шаг: Пример построения матрицы БКГ по объему продаж

Теперь, зная относительную долю рынка товара и темп роста рынка, Вы можете определить для каждого продукта в портфеле компании его место в матрице БКГ.

На основе получившейся информации постройте матрицу БКГ, отразив в каждой ячейке название товара, объем продаж и суммарный объем продаж на группу.

Анализ по объему продаж позволяет судить о том, насколько портфель компании сбалансирован, помогает правильно расставить приоритеты по развитию товаров и выделить ключевые направления бизнеса.

Пятый шаг: Пример построения матрицы БКГ по объему прибыли

Постройте аналогичную матрицу БКГ по прибыли, отразив в каждой ячейки название товара, объем прибыли и суммарную прибыль на группу.

Анализ по объему прибыли позволяет судить о возможности инвестиций и поддержки новых товаров компании, помогает расставить приоритеты в поддержке товарных групп.

Шестой шаг: Проведение анализа, выводы и разработка стратегии

Проанализируйте получившиеся матрицы БКГ по объему продаж и прибыли, напишите выводы и определите стратегию развития портфеля компании.

Ключевые выводы должны описывать: (Подробные стратегии развития групп по матрице БКГ читайте в статье: Матрица БКГ.

Основы)

сбалансирован портфель или есть явные отклонения от идеального портфеля?
какие товарные группы стоит развивать, какие товарные группы следует сокращать?
приоритеты в развитии ассортимента компании?
способна ли прибыль от текущих проектов обеспечить поддержку новых товаров?
достаточно ли у компании товаров, способных обеспечить будущие денежные доходы?
какой стратегии в развитии каждой товарной группы стоит придерживаться для максимизации будущих доходов?
стоит ли ввести какие-то дополнительные товары в ассортимент?

Готовые решения

У нас есть готовый шаблон, с помощью которого вы с легкостью сможете применить теоретические знания данной статьи на практике. Скачать шаблон для построения матрицы БКГ в формате Excel можно в разделе «Полезные шаблоны по маркетингу».

Твитнуть

Please enable JavaScript to view the comments powered by Disqus.comments powered by Disqus

След матричного калькулятора — Tr(A)

Поиск инструмента

Поиск инструмента в dCode по ключевым словам:

Просмотр полного списка инструментов dCode

Трассировка матрицы

Инструмент для вычисления трассировки матрицы. След квадратной матрицы M представляет собой сложение значений ее главной диагонали и обозначается как Tr(M).

Результаты

Трассировка матрицы — dCode

Метки: Матрица

dCode и многое другое решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор трассировки квадратной матрицы NxN

Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)

См. также: Определитель матрицы

Калькулятор трассировки прямоугольной матрицы NxM

Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)

См. также: Транспонирование матрицы

Ответы на вопросы (FAQ)

Что такое трассировка матрицы? (Определение)

Следом квадратной матрицы является сложение значений на ее главной диагонали (начиная с верхнего левого угла и сдвигаясь на одну позицию вправо и вниз).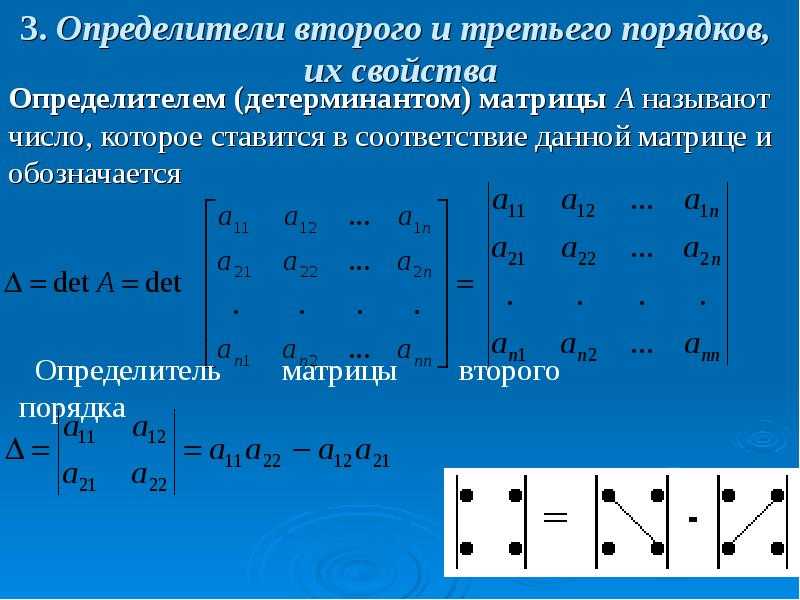 Таким образом, след квадратной матрицы использует следующие значения:

$$ \begin{bmatrix} X & . & . \\ . & ИКС & . \\ . & . & X \end{bmatrix} $$ или, для прямоугольной матрицы: $$ \begin{bmatrix} X & . & . \\ . & ИКС & . \end{bmatrix} $$ или $$ \begin{bmatrix} X & . \\ . & ИКС \\ . & . \end{bmatrix} $$ 9{n} a_{i \, i} $$

— Для матрицы 2×2: $$ M = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \\ \mathrm{Tr}( M) = a+d $$

Пример: $$ M = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \\ \mathrm{Tr}(M) = 1+4 = 5 $$

— Для матрицы 3×3: $$ M = \begin{bmatrix} a & b & c \\d & e & f \\ g & h & i \end{bmatrix} \\ \mathrm{ Tr}(M) = a+e+i $$

— Для прямоугольной матрицы $ M $ размера $ m \times n $ используемая диагональ является диагональю включенной квадратной матрицы (от верхнего левого угла ).

Пример: $$ M = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \Rightarrow \mathrm{Tr}(M) = \mathrm{Tr} \begin {bmatrix} 1 & 2 \\ 4 & 5 \end{bmatrix} $$

Как найти след матрицы по ее собственным значениям?

Что такое математические свойства трассировки?

Трассировка обладает следующими свойствами:

— Трассировка единичной матрицы $I_n$ (размера $n$) равна $n$.

$$ \mathrm{Tr}(I_n) = n $$

— Для A и B одного порядка (можно добавить):

$$ \mathrm{Tr}(A + B) = \mathrm{Tr}(A) + \mathrm{Tr}(B) $$

— След инвариантен для циклической перестановки: для A и B совместимого размера (и, следовательно, A.B является квадратной матрицей путем умножения» > матричного умножения):

$$ \mathrm{Tr}(AB) = \mathrm{Tr}(BA) \\ \mathrm{Tr}(ABC) = \mathrm{Tr}(CAB) = \mathrm{Tr}(BCA) $$

но в общем случае $ \mathrm{Tr }(ABC) \neq \mathrm{Tr}(ACB) \neq \mathrm{Tr}(BAC) $ 9T) = \mathrm{Tr}(A) $$

Исходный код

dCode сохраняет за собой право собственности на исходный код «Trace of a Matrix». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Trace of a Matrix», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Trace Матрицы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Trace of a Matrix» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Trace of a Matrix» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Trace of a Matrix на dCode.fr [онлайн-сайт], получено 27 ноября 2022 г., https://www.dcode.fr/matrix-trace

Сводка

Калькулятор трассировки квадратной матрицы NxN
Калькулятор трассировки прямоугольной матрицы NxM
Что такое матричный след? (Определение)
Как рассчитать матричный след?
Как найти след матрицы по ее собственным значениям?
Что такое математические свойства трассировки?

Similar pages

Determinant of a Matrix
Transpose of a Matrix
Complex Conjugate Matrix
Tensor Product
Matrix Power

Gaussian Elimination
Matrix Product
DCODE’S TOOLS LIST

Поддержка

Paypal
Patreon
Подробнее

Форум/Справка

Калькулятор матриц онлайн — вычисление разницы между двумя матрицами

Разность матриц, расчет онлайн

Резюме :

Калькулятор матриц позволяет вычислить в режиме онлайн разницу между двумя матрицами с пошаговым вычислением.

matrix_difference онлайн

Описание :

Калькулятор может рассчитать онлайн разницу между двумя матрицами . Калькулятор матриц может вычислять разность матриц , коэффициенты которых имеют буквы или цифры, это формальный калькулятор вычисления матрицы.

Вычисление разницы между двумя матрицами

Калькулятор умеет вычислять разность матриц с результатами в точной форме: вычислить разность матриц `((3,3,4),(1,2,0),(-5,1,1))-((3,3,4),(1,4,0) ,(2,1,1))`, введите matrix_difference(`[[3;1;-5];[3;2;1];[4;0;1]];[[3;1;2];[3;4;1];[4; 0;1]]`), после расчета возвращается результат.

Калькулятор допускает символьные вычисления, можно использовать и буквы, чтобы вычислить разность матриц следующим образом: `((a,3),(a/2,4))-((a,1),(a/2,2))`, введите matrix_difference(`[[a;a/2];[3;4]];[[a;a/2];[1;2]]`), после расчета возвращается результат.
Синтаксис:
matrix_difference(matrix;matrix)
Примеры:
matrix_difference(`[[3;1;-5];[3;2;1];[5;2;1]];[ [3;1;2];[3;4;1];[3;0;1]]`) возвращает `[[0;0;-7];[0;-2;0];[2;2;0]]`
Расчет онлайн с matrix_difference (разница между двумя матрицами)
См. также
Список связанных калькуляторов:

Матричный калькулятор : matrix_calculator. Калькулятор матриц позволяет производить расчеты с матрицами онлайн.
Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
Разница между двумя матрицами: matrix_difference. Калькулятор матриц позволяет вычислить в режиме онлайн разницу между двумя матрицами с пошаговым расчетом.
Калькулятор обратной матрицы: inverse_matrix. Функция inverse_matrix позволяет вычислить в режиме онлайн обратную матрицу.
Калькулятор матрицы продуктов: matrix_product. Калькулятор матриц позволяет в режиме онлайн рассчитать произведение двух матриц с шагом вычисления.
Решение системы линейных уравнений :solve_equations. Решатель систем линейных уравнений позволяет решать уравнения с несколькими неизвестными: система уравнений с 2 неизвестными, система уравнений с 3 неизвестными, система с n неизвестными.
Калькулятор матрицы суммы: matrix_sum. Калькулятор матриц позволяет вычислить онлайн сумму двух матриц с шагом расчета.
No related posts.