Теорема синусов. Формулы и доказательства
Железнодорожные рельсы параллельны друг другу, а деревья растут под наклоном к земле. Увы, с соотношением сторон в треугольнике все не так просто: чтобы их определить, нужна теорема синусов.
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, воспользуемся правилом пропорции и получим:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
,где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно:
Для остроугольного треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.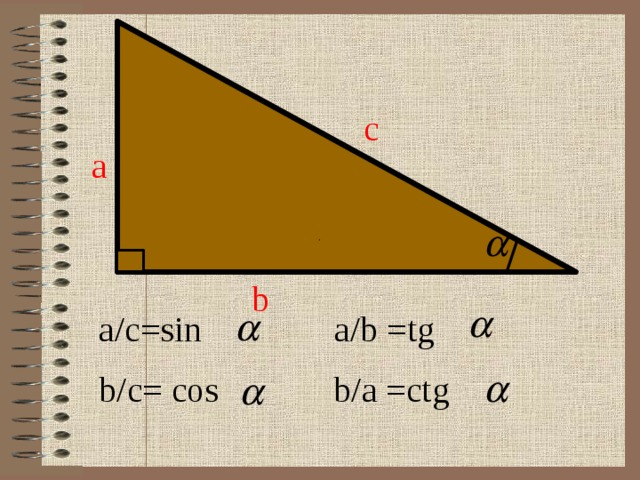
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно:
Для тупоугольного треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3.
Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Следовательно:
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Как решаем:
Согласно теореме о сумме углов треугольника:
∠A + ∠B + ∠C = 180°
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
Ответ: AC = 12.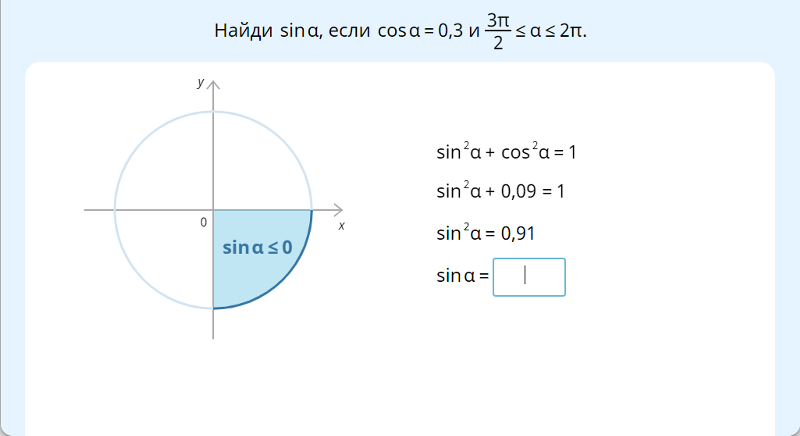
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.
Как решаем:
Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Следовательно:
Значит .
Ответ: угол составляет примерно 53,1°.Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
, где R — радиус описанной вокруг треугольника окружности.
Шпаргалки по математике родителей
Все формулы по математике под рукой
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
09.18
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Точка движется в плоскости XOY.
2)
Как найти синус угла в равнобедренном треугольнике
Равнобедренным треугольником называется выпуклая геометрическая фигура из трех вершин и трех соединяющих их отрезков, два из которых имеют одинаковую длину. А синус — это тригонометрическая функция, которую можно использовать для численного выражения зависимости между соотношением длин сторон и величинами углов во всех треугольниках, включая и равнобедренные.
- Как найти синус угла в равнобедренном треугольнике
- Как найти углы треугольника по трем его сторонам
- Как найти длину основания равнобедренного треугольника
Если из исходных данных известна величина хотя бы одного угла (α) в равнобедренном треугольнике, это позволит найти и два других (β и γ), а значит и синус любого из них. Исходите из теоремы о сумме углов, которая утверждает, что в треугольнике она обязательно должна быть равна 180°. Если угол известной величины лежит между боковыми сторонами, величина каждого из двух других равна половине разности между 180° и известным углом.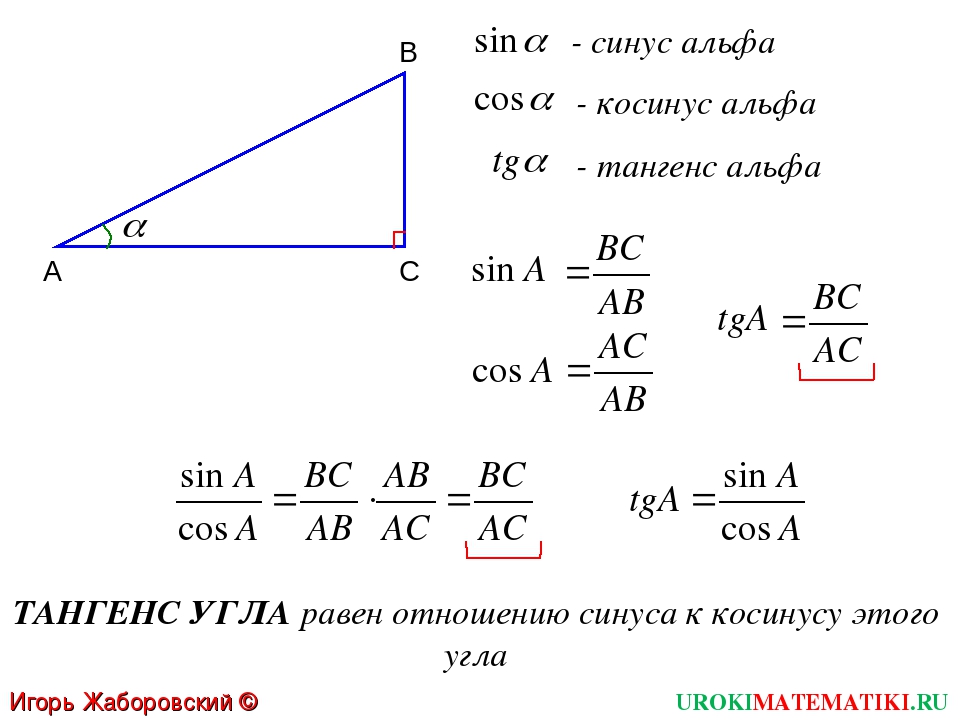
Значит, вы можете использовать в расчетах такое тождество: sin(β) = sin(γ) = sin((180°-α)/2). Если же известный угол примыкает к основанию треугольника, это тождество распадется на два равенства: sin(β) = sin(α) и sin(γ) = sin(180°-2*α).
Зная радиус (R) окружности, описанной около такого треугольника, и длину любой из сторон (например, а) можно не прибегая к вычислению тригонометрических функций рассчитать синус угла (α), лежащего напротив этой стороны. Используйте для этого теорему синусов — из нее вытекает, что нужная вам величина равна половине соотношения между длиной стороны и радиусом: sin(α) = ½*R/a.
Известные площадь (S) и длина боковой стороны (а) равнобедренного треугольника позволят рассчитать синус угла (β), лежащего напротив основания фигуры. Для этого удвойте площадь и поделите результат на возведенную в квадрат длину боковой стороны: sin(β) = 2*S/a². Если кроме длины боковой стороны известна и длина основания (b), квадрат можно заменить произведением длин этих двух сторон: sin(β) = 2*S/(a*b).
Если известны длины боковой стороны (а) и основания (b) равнобедренного треугольника, для вычисления синуса угла при основании (α) можно задействовать даже теорему косинусов. Из нее вытекает, что косинус этого угла равен половине отношения длины основания к длине боковой стороны: cos(α) = ½*b/a. Синус и косинус связаны таким равенством: sin²(α) = 1-cos²(α). Поэтому для вычисления синуса извлеките квадратный корень из разницы между единицей и четвертью соотношения квадратов длин основания и боковой стороны: sin(α) = √(1-cos2(α)) = √(1-¼*b²/а²).
Как найти синус угла по сторонам треугольника
Синус — это одна из базовых тригонометрических функций. Первоначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для более сложных случаев с произвольными треугольниками.
- Как найти синус угла по сторонам треугольника
- Как найти сторону через синус
- Как найти синус, косинус и тангенс
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов.
По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В — по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С). А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С)²).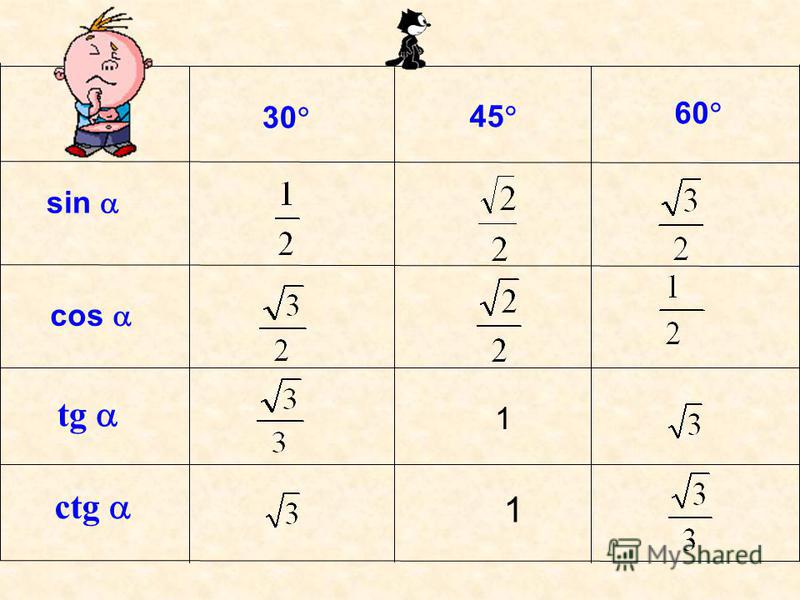
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой — длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)). А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы двух других углов можно найти по аналогичным формулам.
Синус, косинус, тангенс в прямоугольном треугольнике
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь.
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.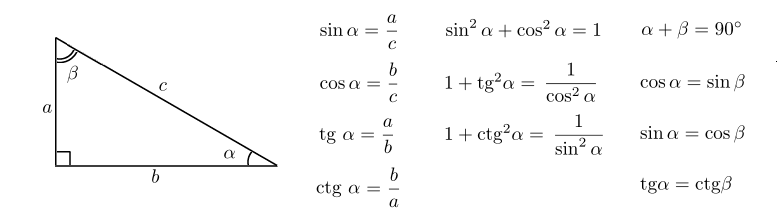
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Читайте также:
- Morrowind как применить яд
- Где бургер шот в гта 5
- Где взять шоковые перчатки batman arkham origins
- Cranium игра настольная как играть
- Когда будет гуань инь genshin impact
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Наклонные треугольники
Наклонные треугольники Наклонный треугольник — это любой треугольник, не являющийся прямоугольным.
Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников. Обозначим углы А, В, и С, , а стороны, противоположные им, обозначим а, b, и с, соответственно.
Решение косоугольных треугольников
Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.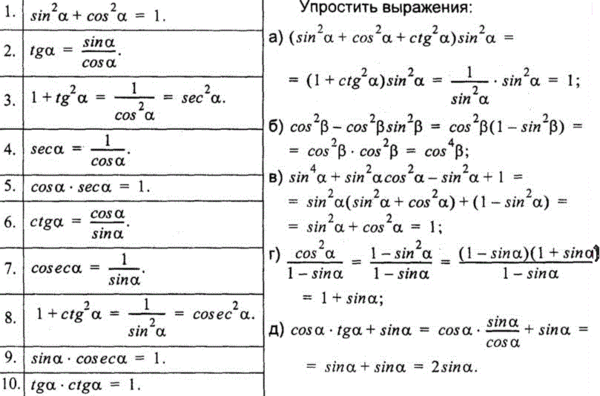
Закон косинусов
Это просто сформулированное уравнение:Это похоже на теорему Пифагора, за исключением последнего члена, и если C — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), так что закон косинусов на самом деле является обобщением закона косинусов. Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, так как вы можете переставлять буквы по своему усмотрению. Затем две другие версии a 2 = b 2 + c 2 – 2 bc cos A, и b 2 = c 2 + a 2 – 2 ca cos B.
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если известен один угол и две смежные стороны, то можно определить и противоположную сторону.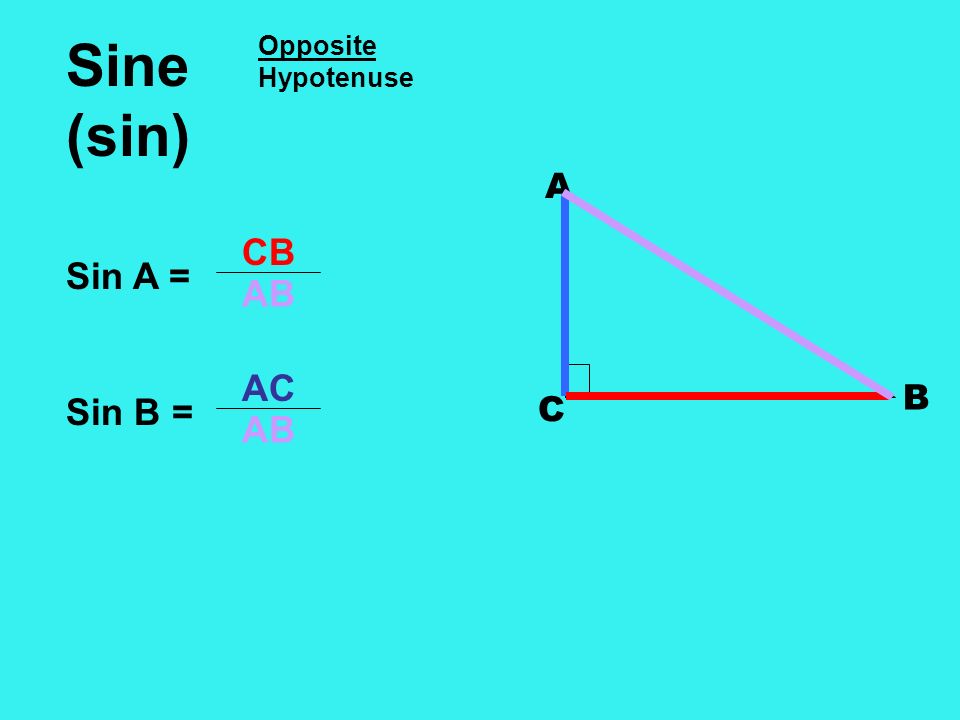
Например, если угол C = 60°, сторона a = 5 и сторона b = 8, то закон косинусов гласит Поскольку косинус угла 60° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7.
Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a = 5, b = 6 и c = 7, то по закону косинусов 49= 25 + 36 – 60 cos C, so cos C = 12/60 = 0,2, а с помощью калькулятора C = 1,3734 радиана = 78,69°
Примечание: Если треугольник тупоугольный, то cos C отрицателен. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов гласит: /60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите C = 2,2556 радиан = 129,237°.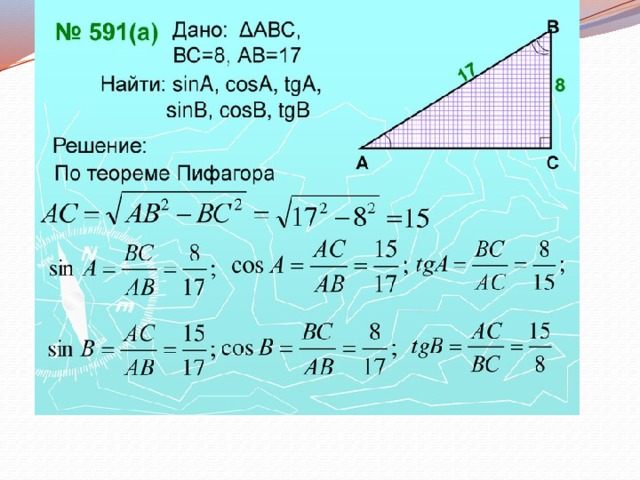
Закон синусов
Закон синусов также представляет собой просто сформулированное уравнениеОбратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них. Например, если угол A = 30°, угол B = 45°, а сторона a = 16, тогда по закону синусов (sin 30°)/16 = (sin 45°)/ b. Решение для b дает b = 16(sin 45°)/(sin 30°) = 22,6274.
Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы почти можете определить угол, противолежащий другой из них. Например, если сторона a = 25, сторона b = 15, а угол A = 40°, то по закону синусов (sin 40°)/25 = (sin В )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0,38567.
Теперь арксинус 0,38567 = 22,686°.
Предупреждение: возможно, у вас нет правильного ответа. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180 – 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
557. В треугольнике ABC, a = 700 футов, B = 73° 48′, и C = 37° 21′. Если M это середина ВС найти длины АМ, и углы БАМ и МАС.
561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B — точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол А = 73° 40′ и С = 52° 38′. Найдите АБ.
570. P и Q две недоступные точки. Чтобы найти расстояние между ними, в произведенном QP берется точка A и измеряется линия AB длиной 1200 футов, образующая угол PAB = 26° 35′. Угол ABP = 48° 12′ и ABQ = 106° 42′. Какова длина PQ ?
579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, затем угол ABC = 110° 48′ 12″, а BAC° 6’3 1 = 1″.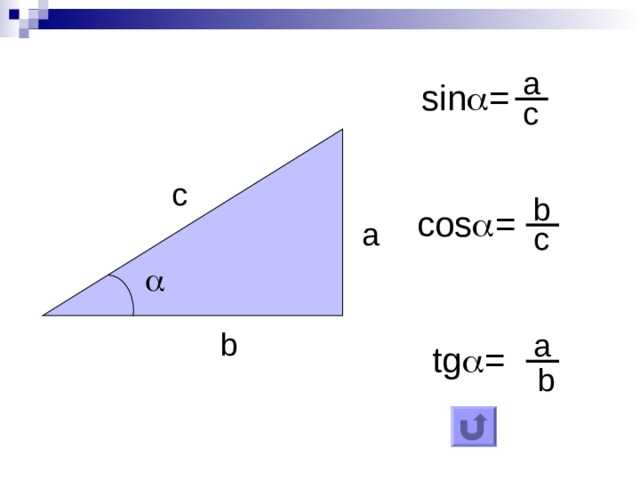
Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.
590. Стороны четырехугольника по порядку равны 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
593. A и B — это две точки на противоположных сторонах водоема, измерения должны производиться по линии AB в точках одна четверть, половина и три четверти расстояния от A до B. На берегу измеряется линия AC длиной 1200 футов и углы BAC = 63° 19′ и ACB = 78° 43′. Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, в соответствующих точках на АВ ?
608. На одной стороне ручья PA = 586,3 фута, PB = 751,6 фута являются мерами, угол APB равен 167° 36′.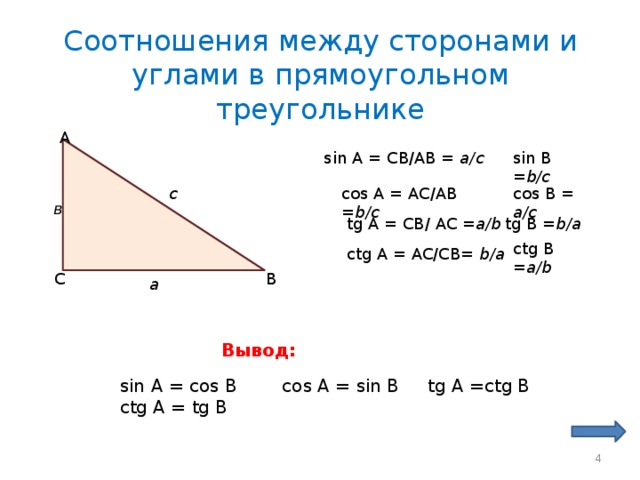
Q — точка на противоположной стороне потока. Угол PAQ = 63° 18′ и PBQ = 49° 24′. Найдите PQ.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, линия AB длиной 763,4 фута откладывается так, что AB пересекает PQ внешне [то есть два отрезка AB и PQ не пересекаются]. Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Советы
553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C — AB. Это означает, что вы опускаете перпендикуляр из C на эту линию и определяете ее длину. Вы можете использовать угол A и прямую AC , чтобы найти его, или вы можете использовать угол B и прямую BC , чтобы найти его.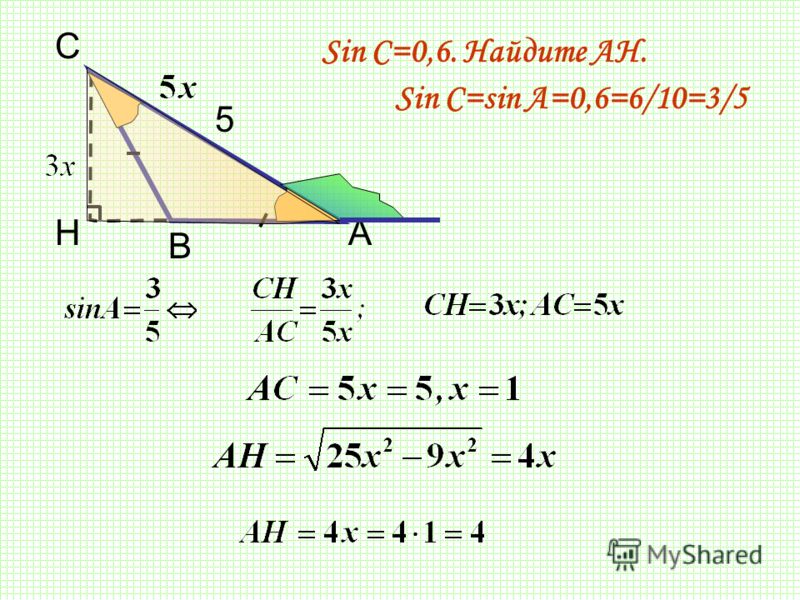
557. Тот же намек, что и 553.
561. Окружности касаются друг друга, поэтому линия из одного центра в другой представляет собой сумму радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9.. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуй фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
579. Вы знаете стороны треугольников ABC и ADC, чтобы можно было определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.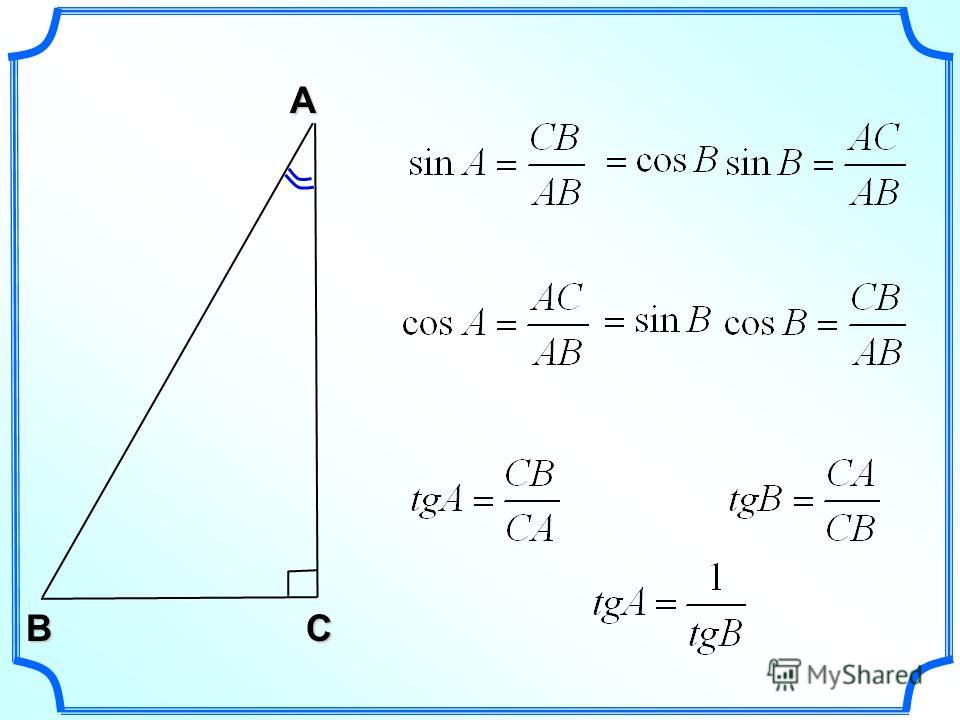
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой прилежащий угол является его дополнением 180° – 70° 12′ 38″. Пусть P — точка пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной. Примените закон косинусов к двум треугольникам с вершинами P и двум вершинам параллелограмма.
590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, , чтобы вы могли найти его углы.
593. Сначала определите расстояние AB по закону синусов. Тогда для каждого из правильных положений лодки P, известны две стороны и угол между ними треугольника PAC, , так что по закону косинусов можно определить нужный угол.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник АКБ.
612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Затем используйте закон косинусов для треугольника PAQ.
Ответы
553. 345,43 фута.
557. 490,83 фута.
561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106° 18′ 46″, 73° 41′ 14″, 452,92.
580. 255,93, 372,11, 369,22.
586. 231,94, 328,93.
590. 125° 6′ 12″, 70° 57′ 54″, 110° 42′ 42″.
593. 23° 27′, 47° 58, 66° 34′.
608. 854,6 фута.
612. 920,76 футов.
MSF – Врачи без границ
Гаити
Медицинский работник MSF следит за состоянием здоровья больных в центре лечения холеры.
Гаити, октябрь 2022 г.© MSF/Александр Марку
Пресс-релиз от 21 октября 2022 г.
Жители Гаити сталкиваются с насилием, отсутствием безопасности, острой нехваткой топлива, новой вспышкой холеры и с трудом получают доступ к медицинской помощи.
Подробнее
Поделись этим
Мы оказываем медицинскую помощь людям, пострадавшим от конфликтов, эпидемий, стихийных бедствий или исключенных из системы здравоохранения. Наши команды состоят из десятков тысяч специалистов в области здравоохранения, логистики и административного персонала, большинство из которых наняты на месте. Наши действия руководствуются медицинской этикой и принципами беспристрастности, независимости и нейтральности .
Узнать больше
12,6 м
12,6 м
амбулаторные консультации
1,6 м
1,6 м
ПРИВИВКИ ПРОТИВ КОРИ В РЕАКЦИИ НА ВСПЫШКУ
1М
1М
госпитализированные пациенты
72
72
страны
Отчет о международной деятельности за 2021 год
Читать отчетИзбранное
Буркина-Фасо
Из-за насилия и острой нехватки снабжения люди в Буркина-Фасо остро нуждаются
17 окт 2022
Средиземноморская миграция
Мальта поручила спасательному кораблю доставить 23 человека в Египет, а не в более близкие порты Европы
Пресс-релиз 19 окт 2022
Пакистан
Семь недель экстренного реагирования в Пакистане
Обновление проекта 14 окт 2022
Сирия
Холера распространяется по Сирии, подвергая уязвимых людей серьезному риску
Обновление проекта 21 окт 2022
grey-mapГде мы работаем
Более чем в 70 странах организация «Врачи без границ» оказывает медицинскую гуманитарную помощь для спасения жизней и облегчения страданий людей в кризисных ситуациях.
Посмотреть все страны
Посмотреть список Просмотр картыНаши программы
Вернуться к нашим программам…
Последние
Южный Судан
Конфликт в Большом Верхнем Ниле препятствует оказанию помощи людям, уже пострадавшим от наводнения
21 окт 2022
Сирия
Холера распространяется по Сирии, подвергая уязвимых людей серьезному риску
21 окт 2022
Гаити
Гаити на грани санитарной катастрофы
21 окт 2022
Украина
Оказание помощи переселенцам в Днепре и Запорожье
20 окт 2022
Средиземноморская миграция
Мальта дает указание спасательному кораблю доставить 23 человека в Египет, а не в более близкие порты Европы
19 окт 2022
Буркина-Фасо
Насилие и острая нехватка снабжения приводят к тому, что люди по всей Буркина-Фасо остро нуждаются
17 окт 2022
Пакистан
Семь недель экстренного реагирования в Пакистане
14 окт 2022
Сомали
Тревожный цикл засухи, недоедания и болезней в Байдабо
12 окт 2022
Йемен
Восстановление жизни людей в Йемене с помощью поддержки психического здоровья
10 окт 2022
Мозамбик
Люди борются за выживание после пяти лет конфликта в Кабо-Дельгадо
5 окт 2022Посмотреть еще
В фокусе
В фокусе
Война на Украине
Российские войска атаковали несколько городов Украины.
Война в Украине вызвала перемещение миллионов людей и высокие неотложные медицинские и гуманитарные потребности. Команды MSF реагируют на конфликт в Украине и соседних странах.В фокусе
Средиземноморская миграция
Каждый год тысячи людей, спасающихся от войны, преследований и нищеты дома, предпринимают предательское путешествие по Средиземному морю. В пути погибает бесчисленное количество жизней.
В фокусе
Нападения на медицинскую помощь
Нападения на медицинские учреждения и медицинских работников, будь то преднамеренные или неизбирательные, являются частью общего насилия и злодеяний, совершаемых против гражданских лиц в ходе вооруженного конфликта. Они лишают население медицинских услуг, зачастую именно тогда, когда оно больше всего в них нуждается.
В фокусе
Пандемия коронавируса COVID-19
Обновленная информация организации «Врачи без границ» (MSF) о пандемии коронавирусной болезни COVID-19.
