| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
01Математика — 10 класс.
 Алгебра — Формулы приведения Skip to main content
Алгебра — Формулы приведения Skip to main content- Классы
- 10 класс. Алгебра
- 04. Тригонометрические выражения
- Теория: 03. Формулы приведения
- 1Пример
- 2Пример
- 3Пример
Задание
Решение
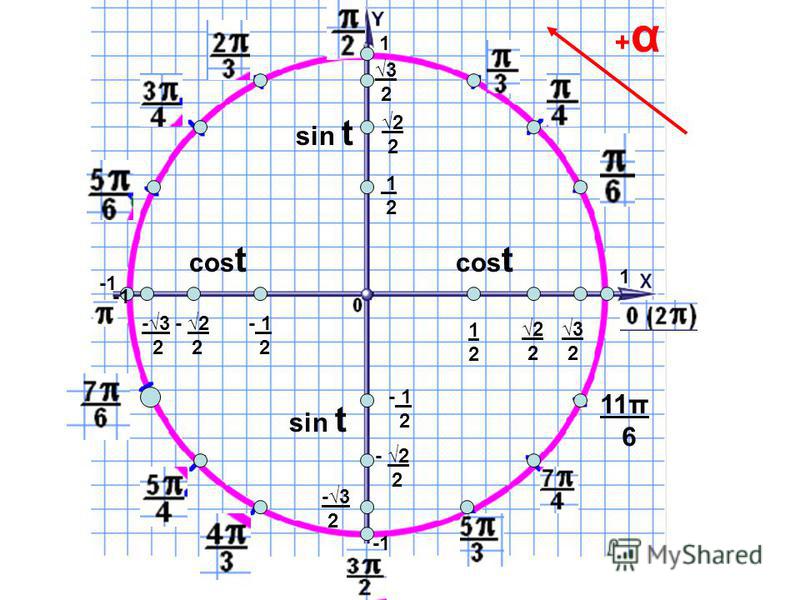
Каждое из выражений
\(\displaystyle \sin\left(\frac{\pi}{2}\pm \alpha\right),\, \cos\left(\frac{\pi}{2}\pm \alpha\right),\, \sin\left(\frac{3\pi}{2}\pm \alpha\right),\, \cos\left(\frac{3\pi}{2}\pm \alpha\right),\, \sin\left(\alpha-\frac{\pi}{2}\right),\, \cos\left(\alpha-\frac{\pi}{2}\right),\)
\(\displaystyle \sin\left(\pi\pm \alpha\right),\, \cos\left(\pi\pm \alpha\right), \, \sin\left(\alpha-\pi \right),\, \cos\left(\alpha-\pi\right)\)
равно либо \(\displaystyle \pm\sin\alpha{ \small ,}\) либо \(\displaystyle \pm\cos\alpha{\small .}\)
- Если в формуле участвует \(\displaystyle \frac{\pi}{2} \) или \(\displaystyle \frac{3\pi}{2} { \small ,}\) то синус меняется на косинус, а косинус меняется на синус, иначе функция не меняется.

- Знак синуса и косинуса определяется по знаку исходного выражения, при условии, что угол \(\displaystyle 0<\alpha<\frac{\pi}{2}{\small .}\)
Так как в выражении \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)\) участвует \(\displaystyle \frac{\pi}{2}{ \small ,}\) то
\(\displaystyle {\bf \cos}\left(\frac{\pi}{2}-\alpha\right)=\,?\,{\bf \sin}\alpha{\small .}\)
Далее определим, какой знак должен стоять перед синусом.
Всегда можно считать, что угол \(\displaystyle \alpha\) – острый (располагается в первой четверти тригонометрического круга):
Тогда угол \(\displaystyle \frac{\pi}{2}-\alpha\) – это угол, полученный вычитанием угла \(\displaystyle \alpha \) из угла \(\displaystyle \frac{\pi}{2}{\small :}\)
Определим знак исходного выражения, то есть знак \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right){\small : }\)
Знак плюс. Значит,
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\color{red}{+}\sin{\alpha}\)
или
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small . }\)
}\)
Ответ: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin{\alpha}{\small .}\)
Формулы приведения и косинус разности
Используем формулу косинуса разности.
Для двух углов \(\displaystyle x\) и \(\displaystyle y\) верно:
\(\displaystyle \cos(x-y)=\cos x\cdot \cos y+\sin x\cdot \sin y{\small .}\)
Тогда
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\cos\frac{\pi}{2}\cdot \cos\alpha+\sin\frac{\pi}{2}\cdot \sin\alpha{\small .}\)
Так как \(\displaystyle \cos\frac{\pi}{2}=0\) и \(\displaystyle \sin\frac{\pi}{2}=1{ \small ,}\) то получаем:
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=0\cdot \cos\alpha+1\cdot \sin\alpha{ \small ,}\)
\(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)
Ответ: \(\displaystyle \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha{\small .}\)
Вход
Войти через
Регистрация
Обратный синус, косинус и тангенс.
 Как SOHCATOA может вычислять углы. Как использовать эти функции…
Как SOHCATOA может вычислять углы. Как использовать эти функции…Рабочий лист обратных триггерных функций
Калькулятор арккосинуса
Калькулятор обратного синуса
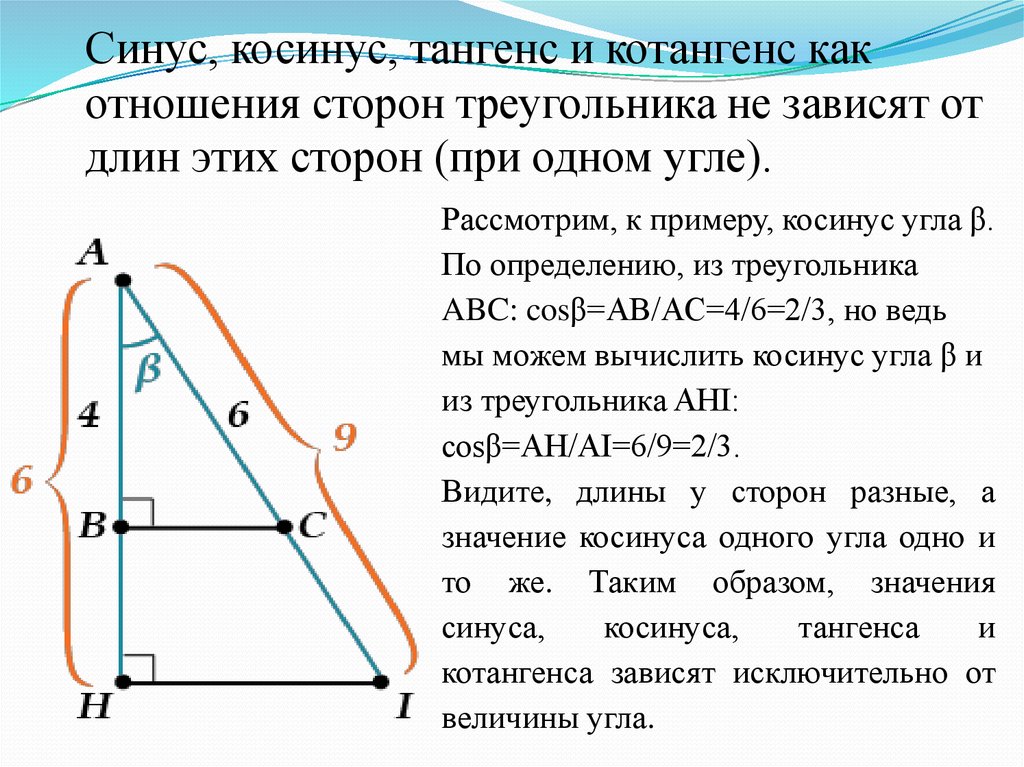
Обратные тригонометрические функции (sin -1 , cos -1 и тангенс -1 ) позволяют найти величину угла в прямоугольном треугольнике. Все, что вам нужно знать, это любые две стороны, а также то, как использовать SOHCATOA.
Обратный путь SOHCATOA против суммы внутренних углов
Сравните этот метод с проверенной теоремой о том, что сумма внутренних углов треугольника равна 180°.
Что является градусной мерой
ЛНМ?
Поскольку сумма внутренних углов треугольника равна 180 градусам, мы можем проверить
ЛНМ:
180° -16° — 90° =74°
В качестве альтернативы вы можете использовать инверсию одной из функций SOHCAHTOA, в данном случае инверсию синуса (sin -1 )! Чтобы найти угол прямоугольного треугольника, нам нужно знать только длину двух сторон! Затем используйте те же отношения SOHCATOA, только по-другому.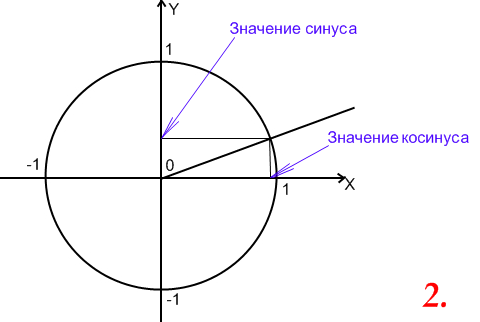
sin -1 (73,24/76,19) = 74°
Видео на YouTube: как рассчитать обратный SOHCATOA
Хорошее видео о том, как использовать калькулятор TI-Graphing для вычисления арксинуса, косинуса или тангенса.
Пример проблемы
Чтобы найти меру $\angle CAB$, заштрихованного угла, рассмотрим известные нам стороны.
Сравнение синуса с обратным синусом.
$ sin(b) $
$$ грех (b) = \frac{ac}{ab} $$ Синус угла выводит отношение 2 сторон треугольника 9{-1} \left( \frac{ac}{ ab} \right) = m\угол ABC $$ Обратный синус двух сторон дает измерение угла
Практика ПроблемыПроблема 1
Используйте арксинус, косинус или тангенс, чтобы вычислить меру заштрихованного угла слева.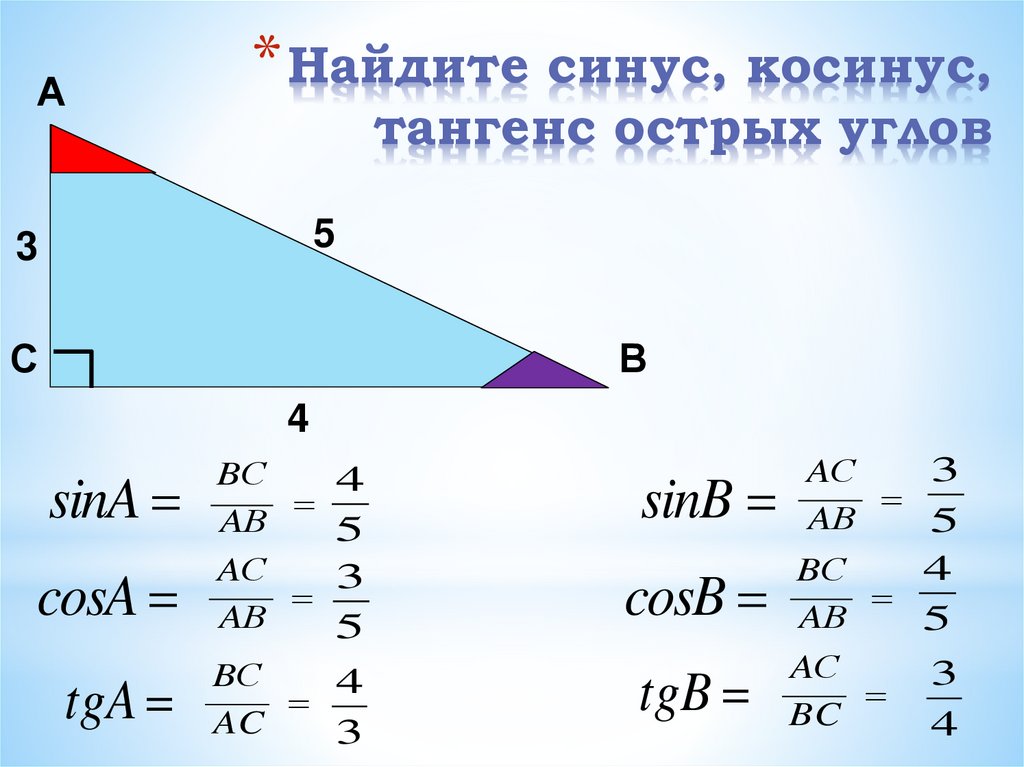
тангенс -1 (24/18) = 53°
Проблема 2
Используйте арксинус, косинус или тангенс, чтобы вычислить меру заштрихованного угла слева.
загар -1
Проблема 3
Какова мера заштрихованного угла слева?
sin -1 (36/39) = 67°
Проблема 4
Какова мера
в треугольнике ниже? Округлите ответ до десятых долей градуса.
Поскольку вы знаете все 3 стороны, вы можете использовать любой из следующих вариантов:
= sin -1 (7/25) = 16,3°
= потому что -1 (6/15) = 16,3°
= тангенс -1 (7/24) = 16,3°
Проблема 5
Используйте обратную sohcahtoa, чтобы вычислить меру
в треугольнике ниже. Округлите ответ до сотых долей градуса.
Округлите ответ до сотых долей градуса.
Поскольку вы знаете все 3 стороны, вы можете использовать любой из следующих вариантов:
= sin -1 (8/10) = 53,13°
= потому что -1 (6/10) = 53,13°
= тангенс -1 (8/6) = 53,13°
Обратные тригонометрические тождества — GeeksforGeeks
В математике обратные тригонометрические функции также известны как аркус-функции или антитригонометрические функции. Обратные тригонометрические функции — это обратные функции основных тригонометрических функций, т. е. синуса, косинуса, тангенса, косеканса, секанса и котангенса. Он используется для нахождения углов с любым тригонометрическим соотношением. Обратные тригонометрические функции обычно используются в таких областях, как геометрия, инженерия и т. д. Представление обратных тригонометрических функций:
е. синуса, косинуса, тангенса, косеканса, секанса и котангенса. Он используется для нахождения углов с любым тригонометрическим соотношением. Обратные тригонометрические функции обычно используются в таких областях, как геометрия, инженерия и т. д. Представление обратных тригонометрических функций:
Если a = f(b), то обратной функцией будет x, tan -1 x и т. д.
В следующей таблице показаны некоторые тригонометрические функции с их областью определения и диапазоном значений.
| Функция | Домен | Диапазон |
| y = sin -1 x | [-1, 1] | [-π/2, π/2] |
| y = cos -1 x | [-1, 1] | 0 [9 π] |
| y = cosec -1 x | R – (-1,1 ) | [-π/2, π/2] – {0} | 0y = |
| R – (-1, 1) | [0 , π] – {π/2} | |
| y = tan -1 x | R | (- п/2, п/2) |
| Y = COT -1 x | R | (0, π) |
.
 1:
1: - sin -1 (1/x) = cosec -1 x, для x ≥ 1 или x ≤ -1
- cos -1 (1/x) = sec -1 x, для x ≥ 1 или x ≤ -1
- tan -1 (1/x) = cot -1 x, для x > 0
Свойство 2:
- sin -1 (-x) = -sin -1 x, для x ∈ [-1 , 1]
- tan -1 (-x) = -tan -1 x, для x ∈ R
- cosec -1 (-x) = -cosec -1 x, для |х| ≥ 1
Свойство 3
- cos -1 (-x) = π – cos -1 x, для x ∈ [-1 , 1]
- cot -1 (-x) = π – cot -1 x, for x ∈ R
- sin -1 x + cos -1 x = π/2, для x ∈ [-1,1]
- tan -1 x + cot -1 x = π/2, для x ∈ R
- cosec -1 x + sec — 1 x = π/2 , для |x| ≥ 1
- тангенс -1 x + тангенс -1 y = tan -1 ( x + y )/(1 – xy), для xy < 1
- tan -1 x – tan -1 y = tan -1 (x – y)/(1 + xy), при xy > -1
- tan -1 x + tan -1 y = π + tan -1 (x + y)/(1 – xy), для ху >1; x, y >0
- 2tan -1 x = sin -1 (2x)/(1 + x 2 ), для |x| ≤ 1
- 2tan -1 x = cos -1 (1 – x 2 )/(1 + x 2 ), для x ≥ 0
- 2tan -1 x = tan -1 (2x)/(1 – x 2 ), для -1 < x <1
- sin -1 (sin x) = x при условии –π/2 ≤ x ≤ π/2
- cos -1 (cos x) = x при условии 0 ≤ x ≤ π
- tan -1 (tan x) = x при условии –π/2 < x < π/2
- sin(sin -1 x) = x при условии -1 ≤ x ≤ 1
- cos(cos -1 x) = x при условии -1 ≤ x ≤ 1
- tan(tan -1 x ) = x при условии x ∈ R
- cosec(cosec -1 x) = x при условии -1 ≤ x ≤ ∞ или -∞ < x ≤ 1
- sec(sec -1 x) = x при условии 1 ≤ x ≤ ∞ или -∞ < x ≤ 1
- кроватка(кроватка -1 x) = x при условии -∞ < x < ∞
- 2cos 9 x
-3 90 cos0012 -1 (2x 2 – 1)
- 2sin -1 x = sin -1 2x√(1 – x 2 )
- 3sin -1 x = sin -1 (3x – 4x 3 )
- 3cos -1 x = cos -1 (4x 3 – 3x)
- 3tan -1 x = tan -1 ((3x – x 3 /1 – 3x 2 ))
- sin -1 x + sin -1 y = sin -1 { x√(1 – y 2 ) + y√(1 – x 2 )}
- sin -1 x – sin -1 y = sin -1 { x√(1 – y 2 ) – y√(1 – x 2 )3
- cos -1 x + cos -1 y = cos -1 [xy — √{(1 — x 2 )(1 — y 2 )}] — 3
- 1 cos 1 x – cos -1 y = cos -1 [xy + √{(1 – x 2 )(1 – y 2 )}
- тангенс -1 x + тангенс 12 -3 у = тангенс -1 (х + у/1 — ху)
- tan -1 x – tan -1 y = tan -1 (x – y/1 + xy)
- tan -1 x + tan -1 y2 +tan 9
z = tan -1 (x + y + z — xyz)/(1 — xy — yz — zx) - cos -1 x + cos -1 y = cos -1 [xy — √{(1 — x 2 )(1 — y 2 )}] — 3
Property 4
Свойство 5
Свойство 6
Тождества обратной тригонометрической функции
Ниже приведены тождества обратных тригонометрических функций:
Примеры задач
Вопрос 1: Докажите sin -1 x = sec -1 1/√(1-x 2 )
Решение:
.
= √(1-перпендикуляр 2 )/гипотенуза )
⇒ cos y = √(1 – x 2 ), здесь гипотенуза = 1
⇒ sec y = 1/cos y
⇒ sec y( 1 – x √ 2 )
⇒ y = сек -1 1/√(1 – х 2 )
⇒ sin -1 х = сек -2 х 900 0(1 ⚪ 900 0 3 х 901 1/√ )
Значит, доказано.
Вопрос 2: Докажите tan -1 x = cosec -1 √(1 + x 2 )/x
Решение:
Пусть tan -1 x = y
⇒ tan y = x , перпендикуляр = x и основание = 1
⇒ sin y = x/√(x 2 + 1) , (поскольку гипотенуза √ (перпендикулярный 2 + База 2 ))
⇒ cosec y = 1/sin y
⇒ cosec y = √ (x 2 + 1)/x
⇒ y = cosec -1 √(x 2 + 1)/x
⇒ tg -1 x = cosec -1 √(x 2 + 1)/x
Следовательно, доказано.
Вопрос 3: Оцените TAN (COS -1 X)
Решение:
Let COS -1 X = Y
⇒ COS Y = X, базовая = x и гипотенерация = = Y
1, следовательно, sin y = √(1 – x 2 )/1
⇒ tan y = sin y/ cos y
⇒ tan y = √(1 – x 2 )/x
⇒ y -1 √(1 – x 2 )/x
⇒ cos -1 x = tan -1 √(1 – x 2 )/x
Следовательно, tan(cos -1 x) = tan(tan -1 √(1 – x 2 )/x ) = √(1 – x 2 )/x.
Вопрос 4: tan -1 √(sin x) + cot -1 √(sin x) = y. Найдите cos у.
Решение:
Мы знаем, что tan -1 x + cot -1 x = /2, поэтому, сравнивая это тождество с уравнением, данным в вопросе, мы получаем y = π/2
Таким образом, , cos y = cos π/2 = 0,
Вопрос 5: tan -1 (1 – x)/(1 + x) = (1/2)tan -1 x, x > 0. Найдите x.
Найдите x.
Решение:
тангенс -1 (1 – х)/(1 + х) = (1/2)тангенс -1 х
⇒ 2тангенс
⇒ 2тангенс
-1 )/(1 + x) = tan -1 x …(1)
Мы знаем, что 2tan -1 x = tan -1 2x/(1 – x 2 ).
Таким образом, LHS уравнения (1) можно записать как
тангенс -1 [ { 2(1 – x)/(1 + x)}/{ 1 – [(1 – x)(1 + x)] 2 }]
= тангенс -1 [ {2(1 – x)(1 + x)} / { (1 + x) 2 – (1 – x) 2 }]
= тангенс -1 [ 2(1 – x) 2 )/(4x)]
= tan -1 (1 – x 2 )/(2x)
Так как LHS = RHS, следовательно,
tan -1 (1 – x )/(2x) = тангенс -1 x
⇒ (1 – x 2 )/2x = x
⇒ 1 – x 2 = 2x 2
⇒ 3x 2 = 1
⇒ x = ± 1/√1/3
⇒ x = ± 1/√1/3
, следовательно, x = ± 1/√1/3
.
является приемлемым ответом.
Вопрос 6. Докажите tan -1 √x = (1/2)cos -1 (1 – x)/(1 + x)
Решение: 9002 100308 4 8 -1 √x = y
⇒ тангенс y = √x
⇒ tan 2 y = x
Следовательно,
RHS = (1/2)cos -1 ( 1- тангенс 2 y)/(1 + tan 2 y)
= (1/2)cos -1 (cos 2 y – sin 2 y)/(cos 2 y + sin 2 y)
= (1/2)cos -1 (cos 2 y – sin 2
)
= (1/2)cos -1 (cos 2y)
= (1/2)(2y)
= y
= tan -1 √x
= LHS
2, следовательно, доказано .
Вопрос 7: загар -1 (2x)/(1 – x 2 ) + кроватка -1 (1 – x 2 )/(2x) = π /2,0068 1 < x < 1. Найдите x.
Решения:
tan -1 (2x)/(1 – x 2 ) + кроватка -1 (1 – x x 2) 9002
⇒ тангенс -1 (2x)/(1 – x 2 ) + тангенс -1 (2x)/(1 – x 2 ) = π/2
⇒ 2tan -1 (2x)/(1 – x 2 ) = ∏/2
⇒ tan -1 (2x)/(1 – x 2 ) = ∏/4
⇒ (2x)/(1 – х 2 ) = тангенс ∏/4
⇒ (2х)/(1 – х 2 ) = 1
⇒ 2х = 1 – х 2
⇒ 3 9012 012 х 9 = 0
⇒ х = [-2 ± √(2 2 – 4(1)(-1))] / 2
⇒ х = [-2 ± √8] / 2
⇒ х = — 1 ± √2
⇒ x = -1 + √2 или x = -1 – √2
Но согласно вопросу x ∈ (-1, 1), следовательно, для данного уравнения множество решений есть x ∈ ∅.
Вопрос 8: тангенс -1 1/(1 + 1,2) + тангенс -1 1/(1 + 2,3) + … + тангенс -1 1/(1 + n(n) + 1)) = тангенс -1 х. Решите для х.
Решение:
тангенс -1 1/(1 + 1,2) + тангенс -1 1/(1 + 2,3) + … + тангенс + n(1/ n + 1)) = тангенс -1 x
⇒ тангенс -1 (2 – 1)/(1 + 1,2) + тангенс -1 (3 – 2)/(1 + 2,3) + … + загар -1 (n + 1 – n)/(1 + n(n + 1)) = тангенс -1 x
⇒ (тангенс -1 2 – тангенс -1 1) + (тангенс -1 3 – тангенс -1 2) + … + (тангенс -1 (n + 1) – тангенс -1 n) = тангенс -1 x
⇒ тангенс
-1 (n + 1) – тангенс -1 1 = тангенс -1 x
⇒ тангенс -1 n/(1 + (n + 1).1) = тангенс -1 x
⇒ тангенс -1 n/(n + 2) = тангенс -1 x
⇒ x = n/(n + 2)
Вопрос 9: Если 2tan -1 (sin x) = tan -1 (2sec x), то найдите x.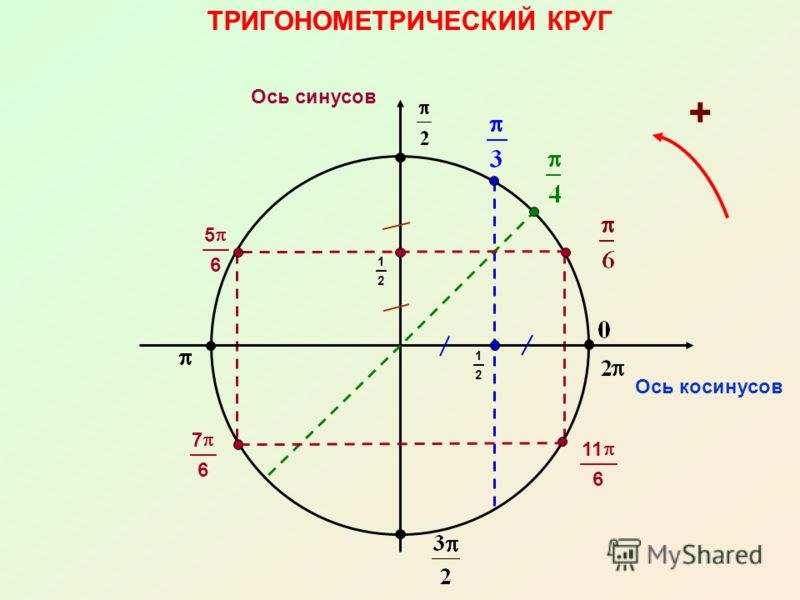


 = √(1-перпендикуляр 2 )/гипотенуза )
= √(1-перпендикуляр 2 )/гипотенуза )
 является приемлемым ответом.
является приемлемым ответом.