Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105)
Как найти значения тригонометрических функций для угла 105 градусов
Найдем значения синуса, косинуса и тангенса для угла 105 градусов аналитическим способом.На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 105 градусов — задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.
Поэтому, для начала, представим себе угол в 105 градусов как (90 + 15)
Тогда
sin ( 90 + α ) = cos α
sin 105 = sin( 90 + 15 ) = cos 15
cos ( 90 + α ) = — sin α
cos 105 = cos( 90 + 15 ) = -sin 15
tg ( 90 + α ) = -ctg α
tg 105 = tg( 90 + 15 ) = -ctg 15
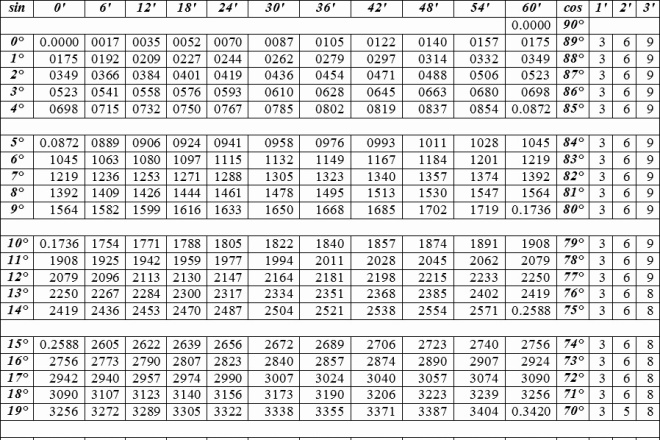
Примечание. Уже на данном этапе можно посмотреть значения в таблицах синуса, косинуса и тангенса 105 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 15 градусов.
Поэтому, на данном этапе нам на помощь придут формулы преобразования двойного угла тригонометрических функций.
Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).
Тогда, отталкиваясь от тождества:
cos 2α = 1 — 2sin2α
Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 — 2sin215
sin215 = ( 1 — cos 30 ) / 2
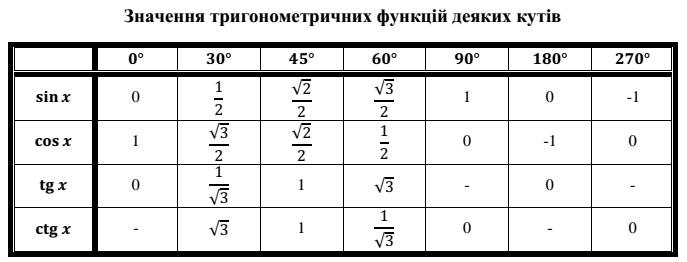
Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin215 = ( 1 — √3/2 ) / 2
sin 15 = √ (( 1 — √3/2 ) / 2 )
cos 105 = — sin 15
cos 105 = — √ (( 1 — √3/2 ) / 2 )
путем несложных агебраических преобразований получаем:
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 105 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.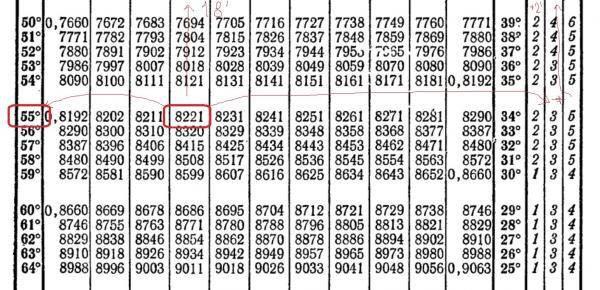
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 105 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
5π/12 |
синус 105 sin 105 |
косинус 105 cos 105 |
тангенс 105 |
котангенс 105 ctg 105 |
|
Значение |
0,9659 |
-0,2588 |
-3,7321 |
-0,2679 |
0
Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60) | Описание курса | Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)
Sin 210 как найти
Обновлено: 25.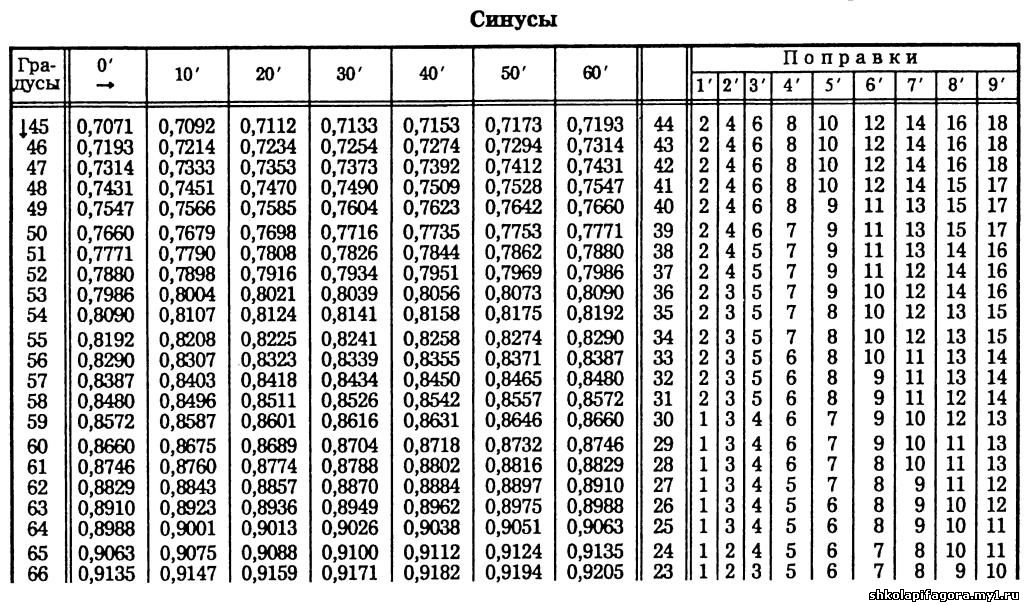
12.2022
Доброй ночи
Я хочу попросить Вас помочь мне разобраться с темой синусов. А точнее с одним из примеров, который у меня вызвал трудность. Этот пример выглядит так: sin 210 найти. А что с ним делать и самое главное — как, для меня непонятно! Помогите пожалуйста разобраться с этим!
Доброй ночи!
Очень интересный вопрос, надеюсь, мы сможем Вам помочь. Нам с вами нужно sin 210 найти.
Чаще всего для решения таких задач нужно определить показатели косинуса либо же синуса. Для углов от 0 до 360 градусов практически любое значение cos или sin можно с лёгкостью найти в соответствующих табличках, которые существуют и распространены. Но что же нам делать, когда в задании просят найти другие величины, которые никак не отражаются в известных таблицах? Далее мы рассмотрим с Вами пример, как найти синус 210 градусов.
Давайте первым делом теперь подумаем, как мы можем разложить наш синус 105 градусов, да и таким образом, чтоб получившиеся значения мы легко могли найти в таблице.
sin суммы, как мы вспомним, раскладывается по формуле: произведение cos второго угла на sin первого угла плюс произведение sin второго угла на cos первого в сумме:
Теперь давайте попробуем разложить наш sin 210 по этой формуле:
Надеюсь, данная информация будет для Вас полезна и в дальнейшем, так как благодаря такой схеме можно вычислять значения любых углов.
Ответ:
Таблица синусов для 181°-360°
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Чему равен синус 210° градусов — sin(210°)?
Что такое тригонометрия? Дословно можно перевести, как «треугольник+измерять», в математике это раздел, отвечающий за применение в решении задач различных тригонометрических функций, возможность с помощью известных величин в треугольнике поиска неизвестных.
Синус – такая величина, которая изменяется вместе с изменением угла, переводится, как «кривизна» или «изгиб».
Для более простого вычисления значений углов больше 180 градусов, необходимо помнить о том, что всегда можно представить выражение в виде суммы 180 градусов и остатка.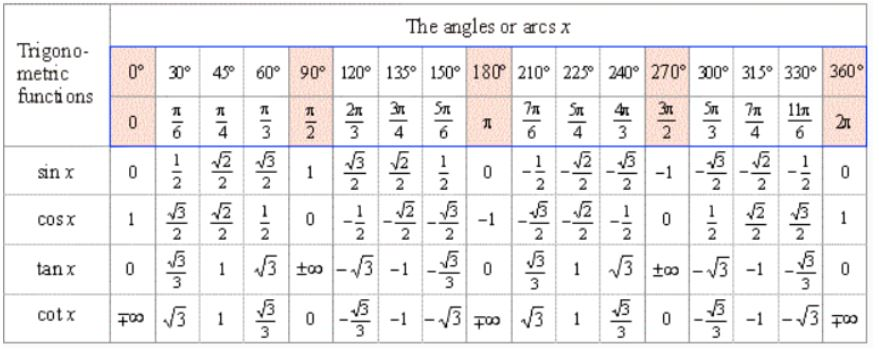
Оставшееся значение – этот самый хвостик и необходимо вычислить.
Естественно нам понадобится единичная окружность для того, чтобы правильно определить знак полученного выражения. В третьей четверти окружности знак является отрицательным, следовательно берем значение синуса тридцати градусов с отрицательным знаком.
Таблица синусов для 0°-180°
Таблица синусов углов (градусы, значения)
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
Читайте также:
- Как узнать репутацию в деревне майнкрафт
- Как создать персонажа с историей в симс 4
- Как ловить кроликов в hay day
- Кто такой вольный сталкер
- Где найти кусок аметиста геншин
Sin 105 градусов — Найдите значение Sin 105 градусов
LearnPracticeDownload Значение sin 105 градусов равно 0,9659258.
. . . Sin 105 градусов в радианах записывается как sin (105° × π/180°), т. е. sin (7π/12) или sin (1,832595…). В этой статье мы обсудим способы нахождения значения sin 105 градусов на примерах.
- Sin 105°: 0,9659258. . .
- Sin 105° в дробях: (√6 + √2)/4
- Sin (-105 градусов): -0,9659258. . .
- Sin 105° в радианах: sin (7π/12) или sin (1,8325957 . . .)
Сколько стоит грех 105 градусов?
Значение sin 105 градусов в десятичной системе равно 0,965925826. . .. Sin 105 градусов также можно выразить с помощью эквивалента заданного угла (105 градусов) в радианах (1,83259 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 105 градусов = 105° × (π/180°) рад = 7π/12 или 1,8325. . .
∴ sin 105° = sin(1,8325) = (√6 + √2)/4 или 0,9659258. . .
Объяснение:
Для sin 105 градусов угол 105° лежит между 90° и 180° (второй квадрант).
Поскольку функция синуса положительна во втором квадранте, значение sin 105° = (√6 + √2)/4 или 0,9659258. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 105° как sin 105 градусов = sin(105° + n × 360°), n ∈ Z.
⇒ sin 105° = sin 465° = sin 825° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-105°) = -sin(105°).
Методы определения значения Sin 105 градусов
Функция синуса положительна во 2-м квадранте. Значение sin 105° равно 0,96592. . .. Мы можем найти значение sin 105 градусов по:
- Используя Unit Circle
- Использование тригонометрических функций
Sin 105 градусов с использованием единичного круга
Чтобы найти значение sin 105 градусов, используя единичную окружность:
- Поверните «r» против часовой стрелки, чтобы образовать угол 105° с положительной осью x.
- Грех в 105 градусов равен координате y (0,9659) точки пересечения (-0,2588, 0,9659) единичной окружности и r.
Следовательно, значение sin 105° = y = 0,9659 (приблизительно)
Sin 105° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 105 градусов как:
- ± √(1-cos²(105°))
- ± тангенс 105°/√(1 + тангенс²(105°))
- ± 1/√(1 + раскладушка²(105°))
- ± √(сек²(105°) — 1)/сек 105°
- 1/косек 105°
Примечание. Поскольку 105° лежит во 2-м квадранте, конечное значение sin 105° будет положительным.
Мы можем использовать тригонометрические тождества для представления sin 105° как
- sin(180° — 105°) = sin 75°
- -sin(180° + 105°) = -sin 285°
- cos(90° — 105°) = cos(-15°)
- -cos(90° + 105°) = -cos 195°
☛ Также проверьте:
- sin 90 градусов
- грех 104 градуса
- грех 60 градусов
- грех 12 градусов
- грех 89 градусов
- грех 356 градусов
Примеры использования Sin 105 градусов
Пример 1: Используя значение sin 105°, решите: (1-cos²(105°)).
Решение:
Мы знаем, (1-cos²(105°)) = (sin²(105°)) = 0,933
⇒ (1-cos²(105°)) = 0,933Пример 2: Найдите значение 2 × (sin 52,5° cos 52,5°). [Подсказка: используйте sin 105° = 0,9659]
Решение:
Используя формулу sin 2a,
2 sin 52,5° cos 52,5° = sin(2 × 52,5°) = sin 105°
∵ sin 105° = 0,9659
⇒ 2 × (sin 52,5° cos 52,5°) = 0,9659Пример 3: Упростить: 2 (sin 105°/sin 465°)
Решение:
Мы знаем sin 105° = sin 465°
⇒ 2 sin 105°/sin 465° = 2(sin 105°/sin 105°)
= 2(1) = 2
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 105 Degrees
Что такое Sin 105 Degrees?
Sin 105 градусов — значение тригонометрической функции синуса для угла, равного 105 градусам. Значение sin 105° равно (√6 + √2)/4 или 0,9659 (приблизительно).
Каково значение Sin 105 градусов в пересчете на Cot 105°?
Мы можем представить функцию синуса в терминах функции котангенса, используя тригонометрические тождества, sin 105° можно записать как 1/√(1 + cot²(105°)). Здесь значение cot 105° равно -0,2679.4.
Как найти Sin 105° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 105° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(105°))
- ± тангенс 105°/√(1 + тангенс²(105°))
- ± 1/√(1 + раскладушка²(105°))
- ± √(сек²(105°) — 1)/сек 105°
- 1/косек 105°
☛ Также проверьте: тригонометрическую таблицу
Как найти значение Sin 105 градусов?
Значение sin 105 градусов можно рассчитать, построив угол 105° с осью x и затем найдя координаты соответствующей точки (-0,2588, 0,9659) на единичной окружности.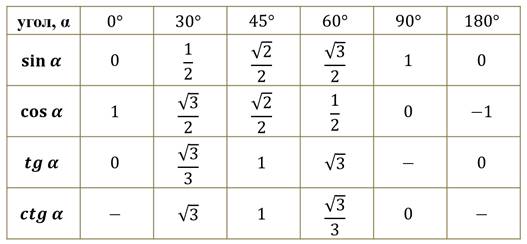
Значение sin 105° равно координате y (0,9659). ∴ sin 105° = 0,9659.
Каково точное значение sin 105 градусов?
Точное значение sin 105 градусов может быть задано с точностью до 8 знаков после запятой как 0,96592582 и (√6 + √2)/4 в дробях.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc (45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек (30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | кос(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение | кос(45) | |
| 34 | Упростить | 92||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |