2_30°…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
ГеографияУкраїнська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
тригонометрия — Общее решение $\sin\alpha +\sin\beta$ и $\cos\alpha+\cos\beta$?
Задавать вопрос
спросил
Изменено 3 года, 8 месяцев назад
Просмотрено 753 раза
$\begingroup$
Для некоторых углов $\alpha,\beta$, что такое $\sin\alpha+\sin\beta$? А как насчет $\cos\alpha + \cos\beta$?
Я думал обозначить $\theta=\alpha+\beta$ для $0\le\alpha\le 2\pi$.
Путем долгих экспериментов и почесывания головы, когда я увидел, что $\sin$ нужен член горизонтального сдвига, который зависит от $\theta$, а $\cos$ нет, я в конце концов наткнулся на:
$$\sin\ альфа + \sin\beta = \sin\alpha + \sin\left(\theta-\alpha\right) = \\ 2\sin\left(\frac{\theta}2\right)\sin\left(\ alpha+\frac{\pi-\theta}2\right) = \\ 2\sin\left(\frac{\theta}2\right)\cos\left(\alpha-\frac{\theta}2\right )$$
и
$$\cos\alpha + \cos\beta = \cos\alpha + \cos\left(\theta-\alpha\right) = \\ 2\cos\left(\frac{\theta} 2\right)\cos\left(\alpha-\frac{\theta}2\right)$$
Тем не менее, я не могу доказать что-либо из этого. Это было после полудня, когда мы набрасывали кучу тестовых углов для $\theta$, строили кривую $\sin x + \sin(\theta-x)$ и манипулировали другой функцией, пока она не совпадала с первой. Есть ли способ продемонстрировать численно что приведенные выше эквивалентности на самом деле верны?
- тригонометрия
$\endgroup$
3
$\begingroup$
Используя тождества суммы/разности функции синуса, мы находим, что
$$\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta)+\sin(\beta)\cos(\alpha)$$
$$\sin(\alpha — \beta) = \sin(\alpha)\cos(\beta)-\sin(\beta)\cos(\alpha)$$
Складывая их вместе, мы находим, что
$$\sin(\alpha + \beta) + \sin(\alpha — \beta) = 2\sin(\alpha)\cos(\beta)$$ Теперь предположим, что мы хотим найти $\sin(x) + \sin(y)$, где $x
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Advanced Trig Formulas — Magoosh SAT
Теперь мы можем поговорить о некоторых продвинутых формулах триггеров. В этом видео я расскажу о нескольких продвинутых формулах из тригонометрии. Как правило, вам не нужно ничего запоминать в этом видео. Я покажу вам несколько сложных формул. Вам просто нужно уметь работать с формулами, если и когда тест представит их вам.
Если вы заранее ознакомитесь с этими формулами, вам будет намного проще. Во-первых, то, что я назову правилами знаков. В этой первой категории есть правила изменения положительного и отрицательного знаков x. Синус(-х) = -синус(х), а косинус(-х) = просто косинус(х).
В единичной окружности, начиная с нуля, если мы переместимся на некоторый угол по часовой стрелке, а затем на тот же угол против часовой стрелки, мы придем к точкам, имеющим противоположные координаты y и одинаковые координаты x. Другими словами, мы собираемся двигаться туда и сюда.
Вот почему синусы, синус(х) являются отрицательными друг другу, а косинусы(х) идентичны. Эти формулы влияют на форму графика. Стандартный график косинуса является отражением самого себя по оси Y. Синусоидальный график представляет собой изображение самого себя при 180-градусной вращательной симметрии вокруг начала координат.
Теперь, если вы знакомы с понятиями четной функции и нечетной функции, косинус — это четная функция, а синус — нечетная функция. Это удобно знать, если вы понимаете это, но ACT не спрашивает о таких видах симметрии. Далее мы поговорим о правилах сложения и вычитания углов. Мы можем получить точные значения синуса и косинуса для трех острых углов: пи больше 6, пи больше 4 и пи больше 3.
Это наши углы в специальных треугольниках. Если сложить и вычесть эти углы в различных комбинациях, то можно получить еще несколько углов. И математики вывели формулы синуса или косинуса суммы или разности двух известных углов.
Предположим, что альфа и бета — это углы, для которых известны значения синуса и косинуса.
Эти четыре формулы представляют собой синус (альфа + бета), синус (альфа-бета), косинус (альфа + бета) и косинус (альфа-бета). Итак, опять же, вам не нужно запоминать эти четыре сложные формулы. Тест даст вам один из них, если вы должны его знать. Но с ними полезно потренироваться, так что если вам дали один в задаче, он вам знаком.
Вот практическая задачка. Поставьте видео на паузу, а потом мы поговорим об этом. Хорошо, для углов QI, углов альфа и бета квадранта I синус (альфа) равен трем пятым, а косинус (бета) равен двенадцати тринадцатым. Учитывая это, найдите косинус (альфа + бета).
Итак, первое, что нам нужно сделать, это осознать, что мы имеем дело с некоторыми очень важными пифагорейскими триплетами. А если идея пифагорейских троек вам не знакома, предлагаю вернуться и посмотреть видео Прямоугольный треугольник, в разделе по геометрии. Мы имеем дело с этими пифагорейскими тройками, 3, 4, 5 и 5, 12, 13.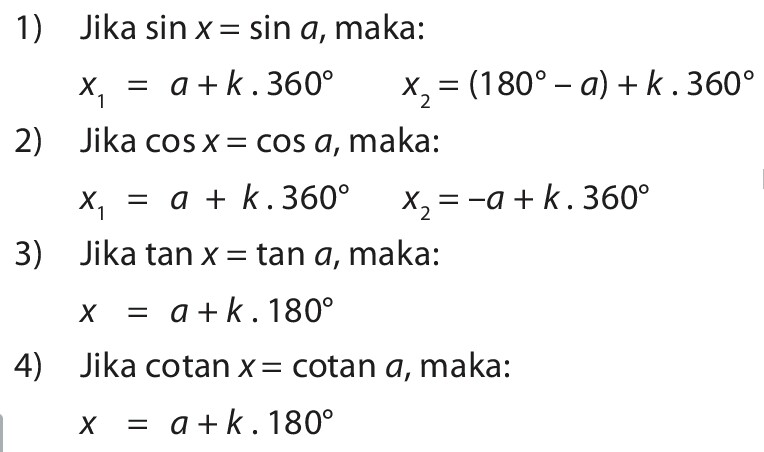
Итак, обратите внимание, что альфа имеет синус три пятых, поэтому мы видим, что соседний катет равен 4.
Бета имеет косинус двенадцать тринадцатых, так что противоположный катет равен 5. А это значит, что мы можем найти косинус (альфа), это четыре пятых, и синус (бета), это пять тринадцатых. Итак, теперь, когда у нас есть эти четыре значения, мы можем подставить их в формулу. Они дают нам формулу косинус (альфа + бета) = косинус альфа косинус бета-синус альфа синус бета.
Подставляем все эти значения, умножаем. Получаем сорок восемь шестьдесят пятых — пятнадцать шестьдесят пятых, что составляет тридцать три шестьдесят пятых. И вариант ответа А является ответом. Далее мы поговорим о формулах для непрямоугольных треугольников. Отношения SOHCATOA прекрасно подходят для нахождения сторон прямоугольных треугольников, но большинство треугольников в геометрии и многие треугольники в реальной жизни не являются прямоугольными.
Для этого мы будем следовать соглашениям о том, что вершины обозначаются заглавными буквами, которые также служат именами углов.
И каждая сторона является строчной буквой той же буквы, что и ее противоположная вершина. Так, например, здесь мы видим, что у нас есть три вершины, A B и C, а напротив угла находится сторона, обозначенная строчной буквой той же буквы. Таким образом, для любого треугольника ABC есть два важных правила для этих непрямоугольных треугольников.
Одним из них является закон косинусов, который является своего рода обобщенной версией теоремы Пифагора, а затем закон синусов. Итак, учитывая числовые значения в комбинации SAS, то есть сторона, сторона и прилежащий угол, или ASA, угол, угол и прилежащая сторона. Или ААС, два угла и невключенная сторона, или только все три стороны, ССС. Теперь обратите внимание, что это четыре комбинации, которые определяют треугольник.
Они достаточно хороши для сравнения треугольников. Итак, если нам даны числовые значения в любой из этих комбинаций, мы могли бы найти все остальные углы и стороны треугольника. Вот проблема с практикой. Поставьте видео на паузу, а потом мы поговорим об этом.