Синус косинус тангенс тангенс котангенс функции роялти бесплатно вектор
Синус косинус тангенс тангенс котангенс функции роялти бесплатно векторы- лицензионные векторы
- Функциональные векторы
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный/редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменить | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по требованию |
Владение Узнать больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка 9 долларов0082 0,69Оплатить стандартные лицензии можно тремя способами. Цены составляют $ $.
| Оплата с помощью | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий.
| Оплата с помощью | Стоимость изображения |
|---|---|
| Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США). | |
Оплата
Плата за изображение $ 399Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение 9 долларов0082 85,00Нравится изображение, но нужно всего лишь несколько модификаций? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменить размер до новых размеров
- Включить логотип или символ
- Добавьте название своей компании или компании
Включенные файлы
Подробности загрузки. ..
..
- Идентификатор изображения
- 4763626
- Цветовой режим
- RGB
- Художник
- логотипы2012
Синус, косинус, тангенс, формулы и примеры
ЧТО ТАКОЕ СОХКАТОА?
Синус, косинус и тангенс — три основные тригонометрические функции в тригонометрии. Чтобы найти значение этих тригонометрических функций, мы просто получаем отношение двух сторон прямоугольного треугольника. SOHCAHTOA — это мнемоника, используемая для легкого запоминания формулы этих трех тригонометрических функций.
В таблице ниже показано значение мнемоники SOHCATOA и соответствующей формулы.
| Значение | Формула | |
| SOH | SOH означает, что $\sin\theta$ равно обратному делению на гипотенузу. | $\sin \theta =\frac{opposite}{hypotenuse}$ или $\sin \theta =\frac{o}{h}$ |
| CAH | CAH означает, что $\cos \theta$ равно к соседнему, деленному на гипотенузу. | $\cos \theta=\frac{adjacent}{гипотенуза}$ или $\cos \theta=\frac{a}{h}$ |
| TOA | TOA означает, что $\tan \theta$ равно противоположному деленному на прилежащее. | $\tan \theta =\frac{opposite}{adjacent}$ или $\tan \theta =\frac{o}{a}$ |
Существуют и другие способы запомнить три фундаментальные тригонометрические функции. от мнемоники СОХКАТОА. В приведенном ниже списке показаны некоторые другие мнемоники, которые можно использовать для ознакомления с тригонометрическими функциями.
| Мнемоники для синуса, косинуса и тангенса |
| У некоторых из ее детей проблемы с алгеброй |
| Она предложила своей кошке полную чайную ложку кислоты |
| Седлайте наших лошадей, галопом, и отправляйтесь в другие приключения. |
| Школа! О, как у кого-то могут быть проблемы с академиками? |
Какая-то старая лошадь поймала другую лошадь, уносившую овес. |
| Два старых ангела перепрыгнули через небеса, неся древние арфы |
| У простых армейских офицеров кудрявые каштановые волосы |
КАКИЕ ЧАСТИ ПРЯМОТРЕУГОЛЬНИКА?
SOHCATOA может помочь нам определить неизвестные углы измерения и неизвестные длины сторон прямоугольного треугольника. Чтобы эффективно использовать концепцию SOHCAHTOA, нужно знать части прямоугольного треугольника. На рисунке ниже показан прямоугольный треугольник и его части.
Гипотенуза — самая длинная сторона прямоугольного треугольника. Это сторона, противоположная прямому углу.
Сторона , противоположная , является стороной, противоположной заданному углу.
Смежная сторона — это сторона, не являющаяся гипотенузой, которая находится рядом с заданным углом.
Всегда помните, что смежная сторона всегда находится рядом с заданным углом.
Скажем, например, у нас есть ∆ABC, как показано на рисунке ниже:
Данным углом является ∠B. Следовательно,
Следовательно,
$\bar{AB}$ – гипотенуза;
$\bar{BC}$ – прилежащая сторона; а
$\bar{AC}$ – противоположная сторона.
Идентификация частей прямоугольного треугольника является одним из основных принципов использования SOHCAHTOA.
ПРИМЕР
Определите стороны прямоугольного треугольника по рисунку ниже.
РЕШЕНИЕ
Учитывая, что прямой угол равен ∠D, мы можем легко сказать, что $\bar{FE}$ является гипотенузой ΔDEF. Так как данный острый угол представлен ∠E, то $\bar{DF}$ является противоположной стороной ∠E, а $\bar{DE}$ является прилежащей стороной к ∠E
КОГДА ИСПОЛЬЗОВАТЬ СОХКАТОА?
Прежде чем использовать формулу SOHCATOA, убедитесь, что данный треугольник является прямоугольным. Более того, при наличии прямоугольного треугольника можно использовать SOHCATOA только в том случае, если они удовлетворяют следующим условиям:
- даны две стороны прямоугольного треугольника; или
- дана одна сторона прямоугольного треугольника и один острый угол.

Давайте посмотрим на различные примеры прямоугольных треугольников ниже.
КАК ПОЛЬЗОВАТЬСЯ СОХКАТОА?
SOHCATOA используется для нахождения неизвестных мер прямоугольного треугольника, независимо от того, есть ли недостающий угол или недостающая длина прямоугольного треугольника.
РЕШЕНИЕ НЕИЗВЕСТНЫХ УГЛОВ
Чтобы решить неизвестные углы прямоугольного треугольника, убедитесь, что длины двух сторон прямоугольного треугольника заданы. Затем уже можно переходить к следующим шагам:
- Определите гипотенузу, прилежащую сторону и противоположную сторону.
- Используйте соответствующую формулу, предоставленную SOHCATOA. 9{-1}$).
- Не забудьте округлить до двух знаков после запятой.
ПРИМЕР #1
Какова мера ∠C?
РЕШЕНИЕ
Шаг 1: Поскольку угол ∠C неизвестен, мы отложим примыкающую и противоположную сторону от угла ∠C.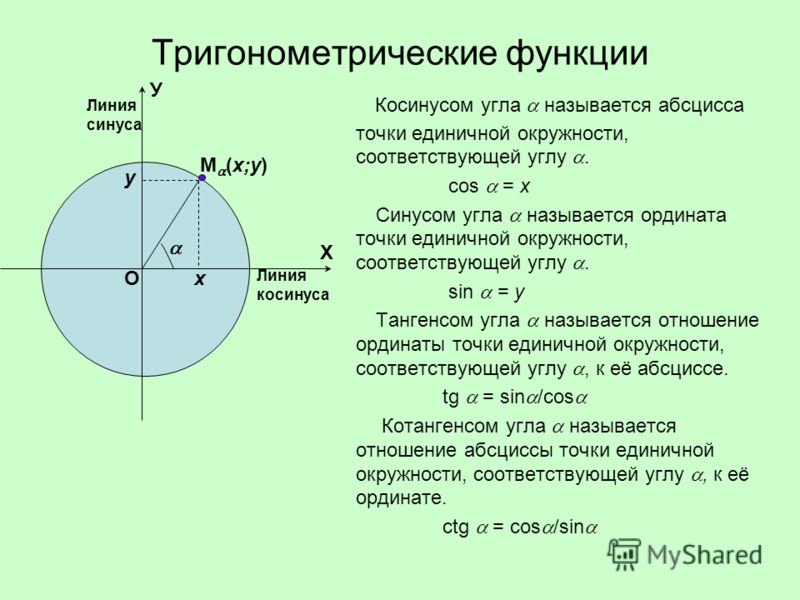 Таким образом, прилежащая сторона ∠C равна $\bar{BC}$, противолежащая сторона равна $\bar{BA}$, а гипотенуза равна $\bar{AC}$.
Таким образом, прилежащая сторона ∠C равна $\bar{BC}$, противолежащая сторона равна $\bar{BA}$, а гипотенуза равна $\bar{AC}$.
Шаг 2: Как показано на рисунке, $\bar{BA}=10$ и $\bar{AC}=14$. Следовательно, у нас есть противолежащая сторона и гипотенуза для ввода в формулу. 9{-1}(\frac{10}{14})$
$\theta =45,58$
Следовательно, мера $∠C$ равна 45,58.
ПРИМЕР #2
Какова мера $∠L$?
РЕШЕНИЕ
Шаг 1: Поскольку угол $∠L$ неизвестен, мы возьмем смежную и противоположную сторону от $∠L$. Следовательно, прилежащая сторона $∠L$ равна $\bar{JL}$, противолежащая сторона равна $\bar{JK}$, а гипотенуза равна $\bar{KL}$.
Шаг 2. На рисунке $\bar{JL}=8$ и $\bar{KL}=21$. Таким образом, мы имеем известное значение прилежащего катета и гипотенузы. 9{-1}(\frac{8}{21})$
$\theta=67,61$
Следовательно, ∠L = 67,61.
ПРИМЕР #3
Найдите меру $∠U$.
РЕШЕНИЕ
Шаг 1: Так как ∠U – неизвестный угол, мы будем основывать противоположную и прилежащую стороны от ∠U. Таким образом, прилежащая сторона равна $\bar{UT}$, противолежащая сторона равна $\bar{TV}$, а гипотенуза равна $\bar{UV}$.
Таким образом, прилежащая сторона равна $\bar{UT}$, противолежащая сторона равна $\bar{TV}$, а гипотенуза равна $\bar{UV}$.
Шаг 2: В ∆TUV уже заданы меры для $\bar{UT}$ и $\bar{TV}$ , где $\bar{UT}=3$ и $\bar{TV}=5$ . 9{-1}(\frac{5}{3})$
$\theta =59,04$
Следовательно, мера ∠U равна 59,04.
РЕШЕНИЕ НЕИЗВЕСТНОЙ МЕРЫ СТОРОНЫ
Чтобы найти неизвестную меру стороны прямоугольного треугольника, проверьте, задана ли мера другой стороны прямоугольного треугольника и одного острого угла. Затем выведите различные формулы из SOHCATOA, чтобы найти значение недостающей стороны.
В таблице ниже показаны различные формулы, полученные из SOHCATOA.
| Отсутствует противоположная сторона | Отсутствует смежная сторона | Отсутствует гипотенуза | |
| SOH | {о}{\ sin \theta}$ | ||
| CAH | $a=(\cos \theta)(h)$ | $h=\frac{o}{\cos \theta}$ | |
| $o=(\tan \theta)(a)$ | $a=\frac{o}{\tan \theta}$ |
Чтобы найти неизвестную меру стороны прямоугольного треугольника,
- Определите часть треугольника относительно заданного угла.

- Используйте соответствующую формулу, полученную из SOHCATOA.
- Найдите неизвестный угол с помощью инженерного калькулятора.
- Не забудьте округлить до двух знаков после запятой.
ПРИМЕР #1
Определите меру $\bar{EN}$.
РЕШЕНИЕ
Шаг 1. Используйте ∠B в качестве опорного угла для определения смежной и противоположной сторон. Таким образом, $\bar{BN}$ – прилежащая сторона ∠B, $\bar{EN}$ – противолежащая сторона ∠B, а $\bar{BE}$ – гипотенуза. 9{\circ })(15)$
$o=12,29$
Следовательно, $\bar{EN}=12,29$
ПРИМЕР #2
Найдите длину $\bar{CT}$ .
РЕШЕНИЕ
Шаг 1. Используйте ∠C в качестве исходного угла для определения смежной и противоположной сторон. Следовательно, $\bar{CA}$ прилегает к ∠C, $\bar{AT}$ противоположна ∠C, а $\bar{BC}$ является гипотенузой.
Шаг 2: Учитывая $\bar{AC}$ и ∠C=32°, используйте производную формулу для недостающей длины гипотенузы.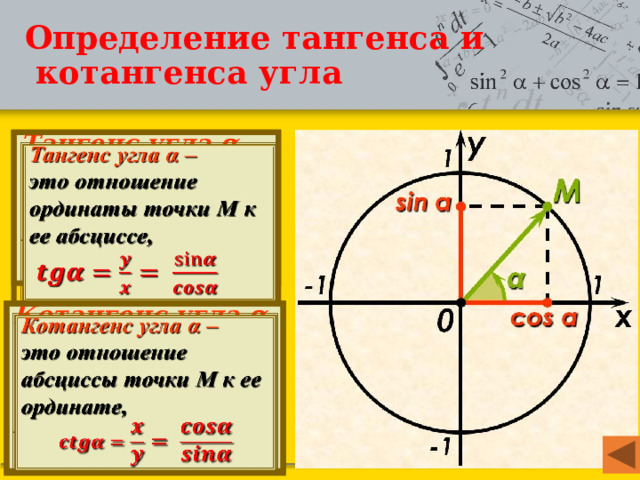 Таким образом, 9{\circ })}$
Таким образом, 9{\circ })}$
$h=22,04$
Следовательно, размер $\bar{CT}$ равен 22,04.
ПРИМЕР #3
Найдите неизвестные величины сторон и углов ∆DOR.
РЕШЕНИЕ
Шаг 1: Используйте ∠R , чтобы определить соседнюю и противоположную стороны. Следовательно, $\bar{RO}$ – это смежная сторона ∠R, $\bar{OD}$ – противолежащая сторона ∠R, а $\bar{RD}$ – гипотенуза ∆DOR.
Шаг 2: Как показано на рисунке, данные значения равны ∠R=20° и $\bar{OD}$ , что является противоположной стороной ∠R. По SOHCATOA мы будем использовать производную формулу TOA для определения длины $\bar{RO}$. Таким образом, 9{2}}$
$\bar{RD}=\sqrt{4718,32+625}$
$\bar{RD}=\sqrt{5343,32}$
$\bar{RD}=73,10$
Шаг 4: Найдите градусную меру углов ∠O и ∠D. Учитывая ∆DOR, мы уже можем заметить, что ∠O — прямой угол. Следовательно, ∠O=90°. Чтобы найти ∠D, используйте теорему о сумме углов треугольника, которая утверждает, что сумма трех внутренних углов треугольника всегда равна 180°. Таким образом,
Таким образом,
∠D+∠O+∠R=180°
∠D+90°+20°=180°
∠D+110°=180°
∠D=180°-110°
1
1 =70°
Следовательно, меры неизвестных сторон и углов равны $\bar{RO}=68,69$, $\bar{RD}=73,10$, $∠O=90°$ и $∠D=70°$.
РЕШЕНИЕ СЛОВНЫХ ЗАДАЧ С SOHCATOAКогда дело доходит до решения словесных задач, не существует точного пошагового правила, которому нужно следовать, так как каждая задача имеет свой подход к решению. Однако вот некоторые из стратегий, которые могут помочь вам решить текстовые задачи с использованием тригонометрических функций:
- Прочтите и внимательно проанализируйте проблему. Убедитесь, что вы понимаете всю идею или концепцию проблемы.
- Запишите всю предоставленную информацию. Таким образом, вы можете быстро определить неизвестное.
- Если возможно, сделайте набросок ситуации, так как это также поможет вам полностью понять ситуацию или проблему.
- Не округляйте десятичные числа в середине вашего решения, так как иногда это может сильно повлиять на окончательный ответ.

ПРИМЕР #1
Гвинет планирует построить грот для своей маленькой лодки. Эскиз ее грота показан на рисунке ниже. Какой будет размер ее грота?
РЕШЕНИЕ
Шаг 1: Обозначьте точки треугольника, образованного на рисунке, назначив случайные буквы. Таким образом, маркировка
облегчает определение недостающих частей треугольника и процесс, который необходимо с ним выполнить.
Шаг 2. Из треугольника, полученного на шаге 1, теперь мы можем назвать части прямоугольного треугольника, где ∠T=45° – исходный угол. Таким образом, $\bar{TA}$ – сторона, примыкающая к ∠T, $\bar{AS}$ – сторона, противоположная ∠T, а $\bar{TS}$ – гипотенуза. 9{2}}$
$\bar{AS}=\sqrt{128-64}$
$\bar{AS}=\sqrt{64}$
$\bar{AS}=8$
Обратите внимание, что на шаге 3 мы не использовали значение $8\sqrt{2}=11,31$ , так как использование 11,31 на шаге 4 существенно повлияет на показатель $\bar{AS}$.
Таким образом, размер грота, который Гвинет хочет создать, составляет 8 футов x 8 футов x 11,31 фута.