Синус косинус тангенс значения: Синус, косинус, тангенс и котангенс

Формула значений Sin Cos Tan, таблица, применение с примерами

0

Сохранить

Скачать публикацию в формате PDF

Значения Sin Cos Tan являются основными тригонометрическими отношениями, которые помогают в изучении отношений между углами и сторонами треугольника, предпочтительно для прямоугольного треугольника. Пифагор установил отношения между сторонами прямоугольного треугольника, а Гиппарк работал над установлением отношений между сторонами и углами треугольника с помощью тригонометрии. Мы можем найти недостающие стороны и углы прямоугольного треугольника, используя значения sin cos и tan и формулы.

Что такое значения Sin Cos Tan?

Sin cos tan — это основные соотношения, используемые в тригонометрии. Это сжатые версии синуса, косинуса и тангенса соответственно. Каждое из этих соотношений определяет отношение между сторонами и углами прямоугольного треугольника в фиксированной схеме.

Важные термины треугольников:

Гипотенуза : Это самая длинная сторона прямоугольного треугольника.

Противоположная сторона: Сторона треугольника, лежащая против угла. Это также можно назвать перпендикулярной стороной треугольника.

Смежная сторона : Сторона треугольника, которая примыкает к углу или касается угла. Его также можно назвать основанием треугольника.

Формула Sin Cos Tan

Чтобы определить формулу для sin cos и tan, мы используем две из трех сторон прямоугольного треугольника.

Рассмотрим приведенную выше диаграмму и обозначения, определяющие гипотенузу, противоположную сторону и примыкающую сторону.

Формулы sin cos tan:

\(\sin\theta\)= Противоположная сторона/Гипотенуза

\(\cos\theta\)= Прилежащая сторона/Гипотенуза

\(\tan\theta\)= Противоположная сторона/прилежащая сторона

Помимо этих тригонометрических соотношений, некоторые другие соотношения, полученные из обратных величин этих соотношений, представляют собой косеканс, секанс и котангенс, которые являются обратными значениями sin, cos и tan соответственно.

Таблица значений Sin Cos Tan

Значение sin cos и tan полностью зависит не только от длин сторон, но и от угла между двумя сторонами. Таблица значений sin cos tan помогает нам найти значения этих тригонометрических отношений для стандартных углов.

При выполнении вычислений, связанных со значениями sin cos и tan, мы можем легко взять эти значения из таблицы тригонометрии, чтобы упростить вывод.

Давайте проверим значения sin cos и tan для разных углов в таблице ниже:

a

Angles (In Degrees)	0	30	45	60	90	120	150	180	210	270	300	330	360
Angles (In Radians)	0	π/6	π/4	π/3	π/2	2π/3	5π/6	π	7π/6	3π/2	5π/3	11π/6	2π
SIN	0	1/2	1/√2	√3/2	1	-1/2	-1	-A 2	0	-1/2	-√3/2	-1	-√3/2	0	1/2	√3/2	1
tan	0	1/√3	1	√3	∞	-√3	-1/√3	0	√1/3	∞	-,3	-1/√3	0

Важные советы, чтобы изучить значения sin cos tan

аббревиатуры «СОХКАТОА».

SOH = \(sin\theta\) = напротив/ гипотенуза

CAH = \(cos\theta\) = Смежный/ Гипотенуза

TOA = \(tan\theta\) = Противоположный/ Смежный

Также, чтобы узнать значения sin cos tan для интервала от 0 до 90 -степень, нам нужно просто выполнить следующие шаги:

• Первую строку, имеющую синусоидальное значение, нужно запомнить как \(\frac{0}{2},\ \frac{\sqrt{1}}{2} , \ гидроразрыва {\ sqrt {2}} {2}, \ гидроразрыва {\ sqrt {3}} {2} \).
• Вторая строка, предназначенная для значений cos, является полной инверсией значений sin между интервалом от 0 до 9.0-градус.
• И затем третью строку, которая предназначена для значений тангенса, можно найти, просто разделив значения sin и cos.

Sin Cos Tan на единичной окружности

Для любого заданного угла значение sin cos и tan может быть рассчитано на единичной окружности. Под единичным кругом на координатной плоскости мы подразумеваем, что радиус круга равен 1 с центром в точке (0,0) на декартовой плоскости.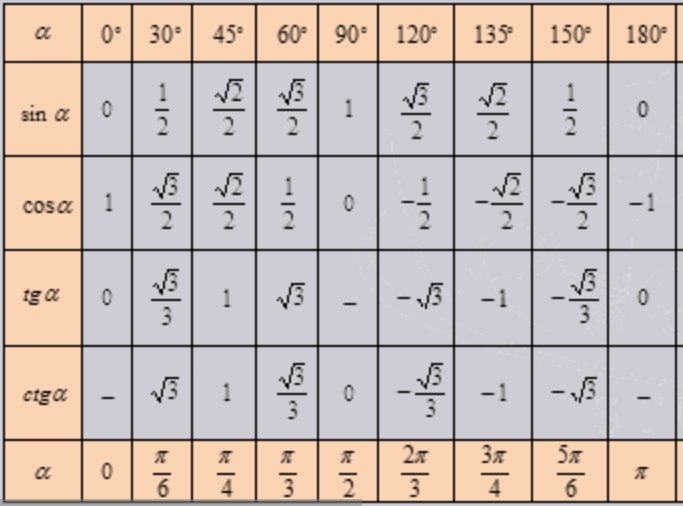

Для любой точки единицы измерения, скажем, кружком (x,y), отношения для значений sin cos и tan могут быть указаны как:

\(sin\theta\) = y/1

\(cos\theta\) = x/1

\(tan\theta\) = y/x

Здесь \(\theta\) равно угол между линией, соединяющей начало координат с точкой, и положительной осью x.

Применение значений sin costan

Тригонометрия, особенно значения sin costan, имеют широкий спектр применений в реальной жизни. Давайте рассмотрим некоторые из них ниже:

• Эти значения можно использовать для измерения высоты зданий и гор.
• Значения sin cos и tan необходимы для конструкций, чтобы вычислять параллели и перпендикуляры, наклоны, высоты и т. д.
• Бортинженеры используют тригонометрию, чтобы найти взаимосвязь между скоростью, расстоянием и направлением для эффективного полета.
• Используется в качестве моделей механики волн и для нахождения компонентов векторов.
• Используется в морской технике для постройки морских судов и управления ими.

Решенные примеры значений Sin Cos Tan 92\) = 3.

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о значениях Sin Cos Tan

В.1 Что такое значения sin cos tan?

Ans.1 Sin co tan – это основные соотношения, используемые в тригонометрии. Каждое из этих соотношений определяет отношение между сторонами и углами прямоугольного треугольника.

Q.2 Как найти sin Cos Tan угла?

Ответ 2 \(\sin\theta\)= Противоположная сторона/Гипотенуза

\(\cos\theta\)= Прилегающая сторона/Гипотенуза
\(\tan\theta\)= Противоположная сторона/ смежная сторона

Q.

No related posts.