Произведение косинусов, синусов и синуса на косинус
Формулы произведений косинусов cos(α)×cos(β), синусов sin(α)×sin(β) и синуса на косинус sin(α)×cos(β) можно выразить из четырех базовых формул — косинуса разности cos(α−β), косинуса суммы cos(α+β), синуса разности sin(α−β) и синуса суммы sin(α+β):
cos(α−β) = cos(α)×cos(β) + sin(α)×sin(β) (I) cos(α+β) = cos(α)×cos(β) − sin(α)×sin(β) (II) sin(α−β) = sin(α)×cos(β) − cos(α)×sin(β) (III) sin(α+β) = sin(α)×cos(β) + cos(α)×sin(β) (IV)
Эти четыре формулы вывести трудно, поэтому их проще запомнить. Но с их помощью можно вывести искомые тригонометрические тождества.
Произведение косинусов
Сложим базовые равенства I и II — косинус разности и косинус суммы:
cos(α−β) + cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) + cos(α)×cos(β) − sin(α)×sin(β) = {одинаковые произведения синусов сокращаются} = cos(α)×cos(β) + cos(α)×cos(β) = 2×cos(α)×cos(β)
Получаем равенство:
cos(α−β) + cos(α+β) = 2×cos(α)×cos(β)
В этом равенстве можно и левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения косинусов:
cos(α)×cos(β) = [cos(α−β) + cos(α+β)] / 2,
т.
е. произведение косинусов равно полусумме косинуса разности и косинуса суммы.
Произведение синусов
Воспользуемся базовыми формулами I и II — косинус разности и косинус суммы. Из равенства I вычтем равенство II:
cos(α−β) — cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) — cos(α)×cos(β) + sin(α)×sin(β) = {одинаковые произведения косинусов сокращаются} = sin(α)×sin(β) + sin(α)×sin(β) = 2×sin(α)×sin(β)
Получаем равенство:
cos(α−β) — cos(α+β) = 2×sin(α)×sin(β)
В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синусов:
sin(α)×sin(β) = [cos(α−β) — cos(α+β)] / 2,
т.е. произведение синусов равно полуразности косинуса разности и косинуса суммы.
Произведение синуса на косинус
Сложим базовые равенства III и IV — синус суммы и синус разности:
sin(α−β) + sin(α+β) = = sin(α)×cos(β) − cos(α)×sin(β) + sin(α)×cos(β) + cos(α)×sin(β) = {одинаковые cos(α)×sin(β) сокращаются} = sin(α)×cos(β) + sin(α)×cos(β) = = 2×sin(α)×cos(β)Получаем равенство:
sin(α−β) + sin(α+β) = 2×sin(α)×cos(β)
В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синуса на косинус:
sin(α)×cos(β) = [sin(α−β) + sin(α+β)] / 2,
т.
е. произведение синуса на косинус равно полусумме синуса разности и синуса суммы.
Итоговые формулы произведения косинусов, синусов и синуса на косинус
cos(α)×cos(β) = [cos(α−β) + cos(α+β)] / 2 sin(α)×sin(β) = [cos(α−β) — cos(α+β)] / 2 sin(α)×cos(β) = [sin(α−β) + sin(α+β)] / 2
Эти формулы мы получили из четырех базовых формул: косинуса разности cos(α−β), косинуса суммы cos(α+β), синуса суммы sin(α−β) и синуса разности sin(α+β). И эти четыре равенства мы между собой складывали и вычитали.
Оглавление
Следующий урок →
Синус и косинус. Запомнить навсегда!
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-01
Синус косинус, определение. Друзья! В прошлой статье, где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий).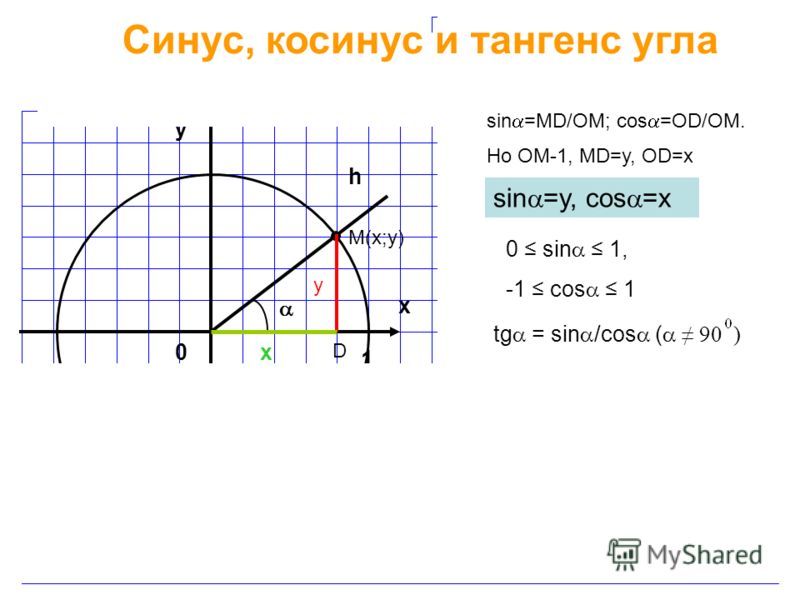
Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
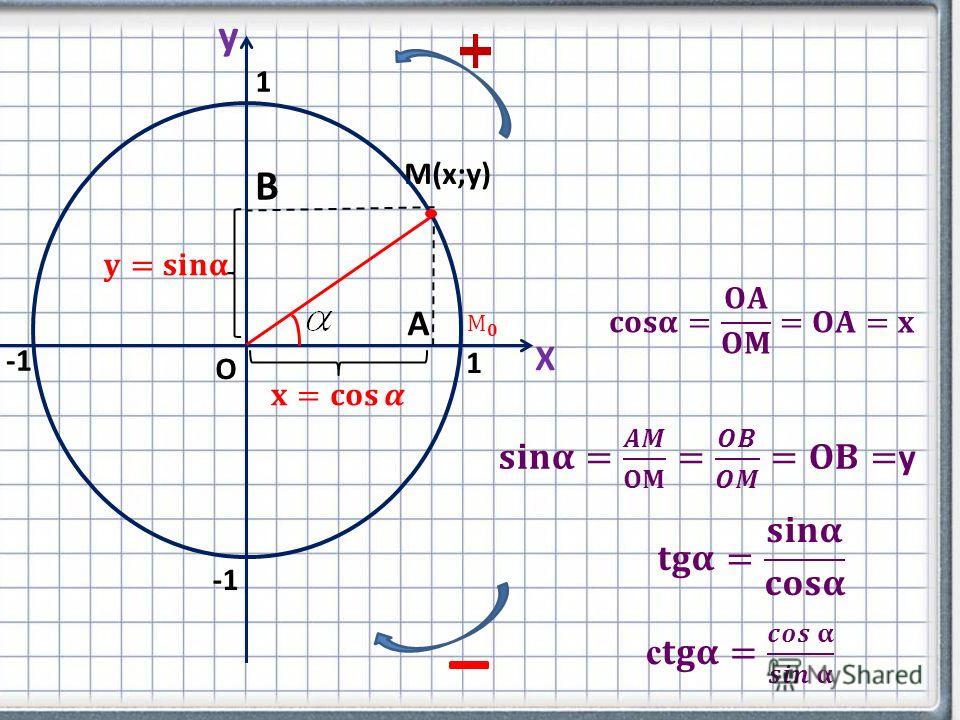
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте «Математический тандем», посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Приёмы | Как запомнитьФормулы
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Функции синуса и косинуса
Синус и косинус: свойства
Функция синуса имеет ряд свойств, которые
в результате получается периодических и нечетных .
Функция косинуса имеет ряд свойств, которые
результат того, что периодические и даже .
Читателю не следует запоминать большинство следующих уравнений; пока что,
читатель должен быть в состоянии мгновенно получить их
от понимания характеристик функции.
Функции синуса и косинуса периодические с периодом 2р. Отсюда следует, что
sin(q) = sin(q + 2p)
cos(q) = cos(q + 2p)
или, в более общем случае,
sin(q) = sin(q + 2pk)
cos(q) = cos(q + 2pk),
где k — целые числа.
Функция синуса нечетное ; следовательно,
sin(-q) = -sin(q)
Функция косинуса равна даже ; следовательно,
cos(-q) = cos(q)
Формула:
sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
Тогда легко вывести из , что
sin(x — y) = sin(x)cos(y) — cos(x)sin(y)
Или, в более общем смысле,
sin(x y) = sin(x)cos(y) cos(x)sin(y)
cos(x + y) = cos(x)cos(y) — sin(x)sin (у)
Тогда легко вывести из , что
cos(x — y) = cos(x)cos(y) + sin(x)sin(y)
Или, в более общем случае,
cos(x y) = cos(x)cos(y) (-/+) sin(x)sin(y)
Из приведенного выше уравнения синусов мы можем вывести, что
sin(2x) = 2sin(x)cos(x)
Из приведенного выше уравнения косинуса мы можем вывести, что
cos(2x) = cos 2 (x) — sin 2 (x)
(Обозначение sin 2 (x) эквивалентно (sin(x)) 2 .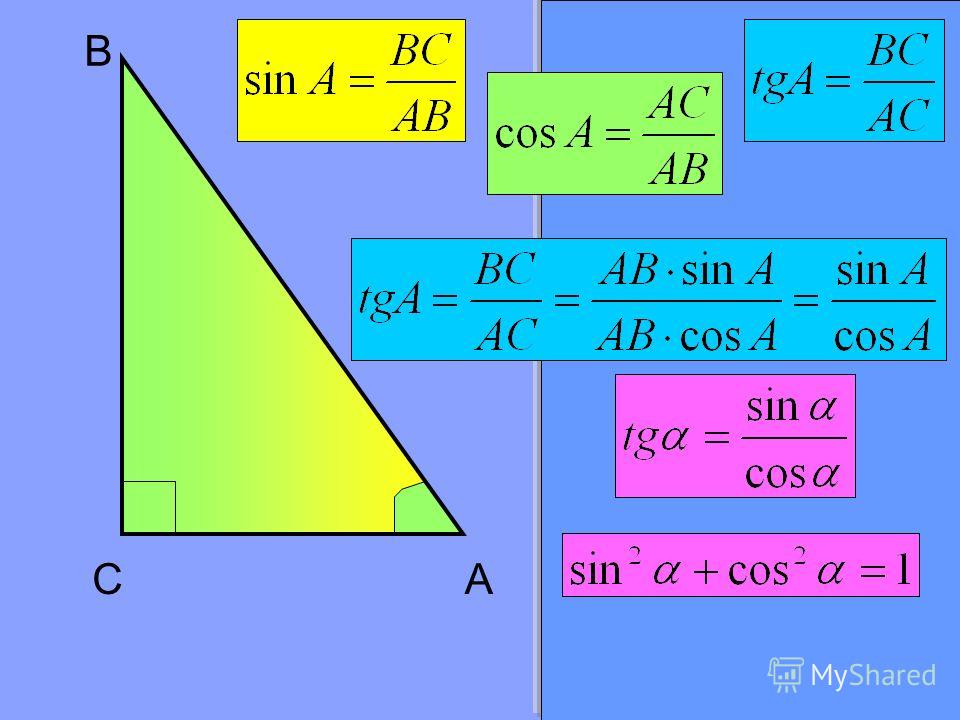
Предупреждение: sin -1 (x) означает arcsin(x), а не обратный мультипликатив.
греха (х).)
Наблюдая графики синуса и косинуса, мы можем выразить
функция синуса через косинус и наоборот:
sin(x) = cos(90° — x)
и функция косинуса через синус:
cos(x) = sin(90° — x)
Такая триггерная функция (f), обладающая свойством
f(q) = g(дополнение(q))
называется кофункцией функции g, отсюда и названия «синус» и « co синус».
Пифагорейское тождество, sin 2 (х) + cos 2 (х) = 1, дает альтернативное выражение для синуса через косинус и наоборот Закон синусов связывает различные стороны и углы произвольного (не обязательно прямоугольного) треугольника:
sin(A)/a = sin(B)/b = sin(C)/c = 2r.
где А, В и С — углы, противоположные сторонам а, b и
с соответственно.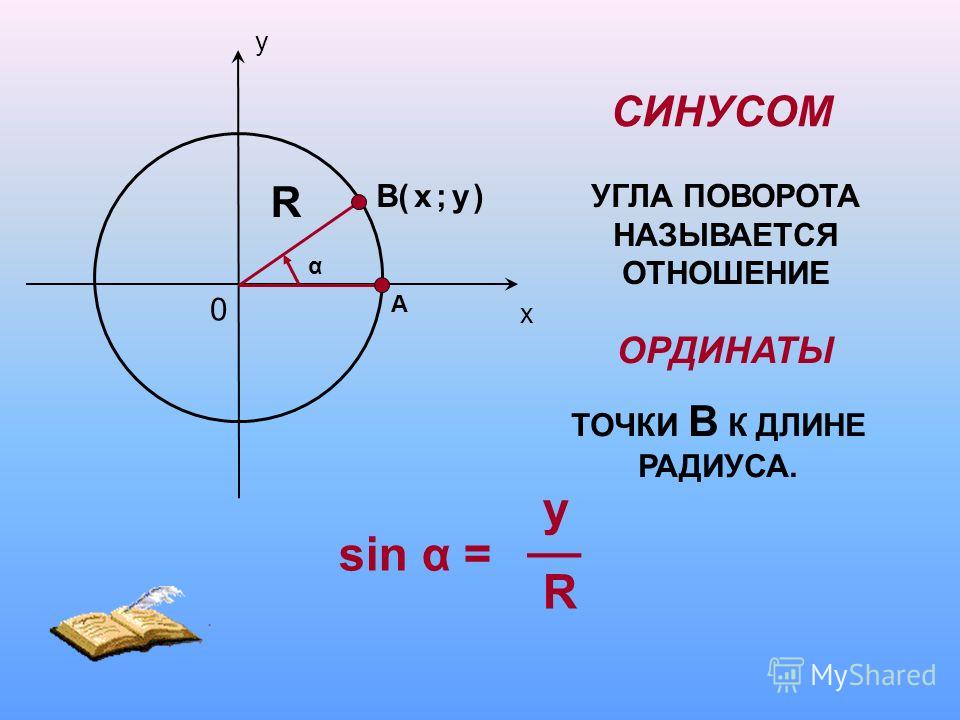
Кроме того, r — это радиус
окружность, описанная в этом треугольнике.
Закон косинусов связывает все три стороны и один из углов произвольного (не обязательно прямоугольного) треугольника:
c 2 = a 2 + b 2 — 2ab cos(C).
где А, В и С — углы, противоположные сторонам а, b и
с соответственно. Его можно рассматривать как обобщенную форму
по теореме Пифагора. Предупреждение : Вы должны быть осторожны
при решении для одной из сторон, примыкающих к интересующему углу,
поскольку часто будут два треугольника, которые удовлетворяют заданным условиям.
Это можно понять из геометрии. Треугольник, определяемый
SAS (сторона-угол-сторона) уникален, и, следовательно, любой треугольник с
ему должны соответствовать те же параметры SAS. Треугольник, определенный
по SSA, однако, не всегда уникален, и два треугольника с
одни и те же параметры SSA могут совпадать, а могут и не совпадать.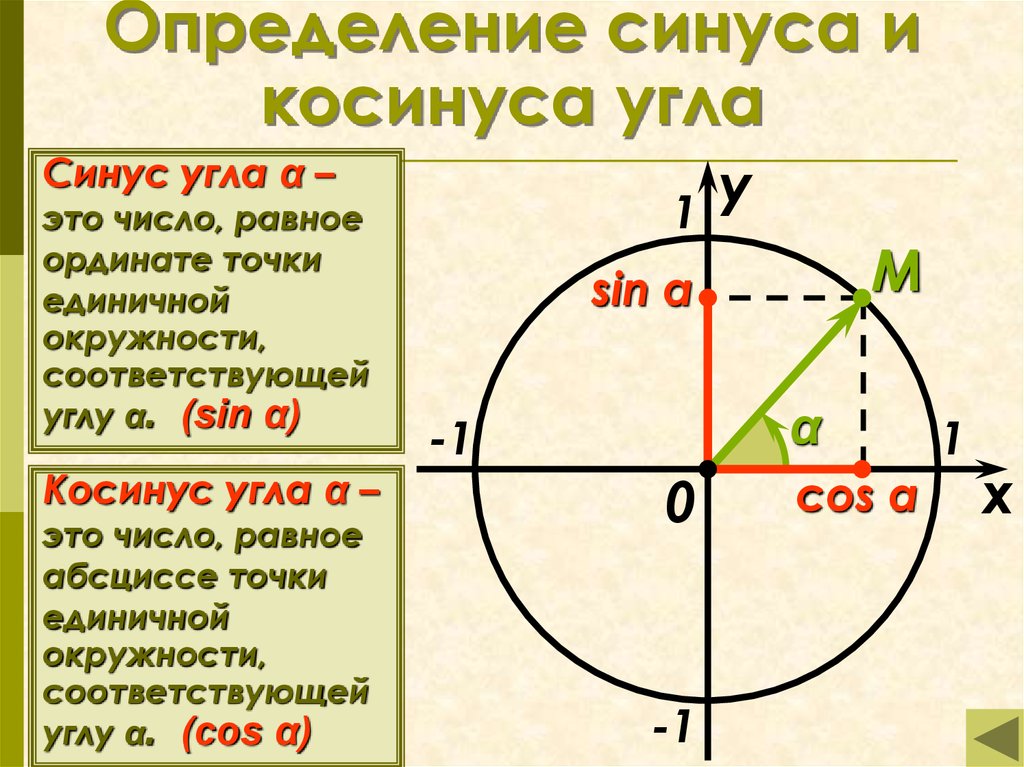
Сравнение функций косинуса и синуса на графике
BY: Мэри Джейн Стерлинг и
Обновлено: 12-21-2021
Из книги: Тригонометрия для Dummomies
7 Dummometry Dummometry
37 Купить книгу на Amazon
Связь между графиками косинуса и синуса заключается в том, что косинус такой же, как и синус, только он сдвинут влево на 90 градусов, или π/2. Уравнение тригонометрии, которое представляет эту связь, равно 9.0004 Посмотрите на графики функций синуса и косинуса на одних и тех же осях координат, как показано на следующем рисунке. График косинуса — более темная кривая; обратите внимание, как он смещен влево от синусоиды.Графики y = sin x и y = cos x на одних и тех же осях
Графики функций синуса и косинуса иллюстрируют свойство, которое существует для нескольких пар различных триггерных функций.
Представленное здесь свойство основано на прямоугольном треугольнике и двух острых или дополнительных углах в прямоугольном треугольнике. Тождества, возникающие из треугольника, называются кофункция тождества .Тождества кофункций следующие:
Эти тождества показывают, как связаны значения функций дополнительных углов в прямоугольном треугольнике. Например, cosθ = sin (90° – θ) означает, что если θ равно 25 градусам, то cos 25° = sin (90° – 25°) = sin 65°. Это уравнение — окольный способ объяснить, почему графики синуса и косинуса отличаются всего лишь одним слайдом.
Вы, наверное, заметили, что все эти тождества кофункций используют разность углов, но сдвиг синусоидальной функции влево представляет собой сумму. График сдвинутого синуса и график косинуса действительно эквивалентны — они становятся графиками одного и того же набора точек. Вот как доказать это утверждение.
Вы хотите показать, что функция синуса, сдвинутая на 90 градусов влево, равна функции косинуса:
Замените cos x на его кофункцию.
