свойства и значения функции косинус
Оглавление
Время чтения:: 4 минуты
755
Определения
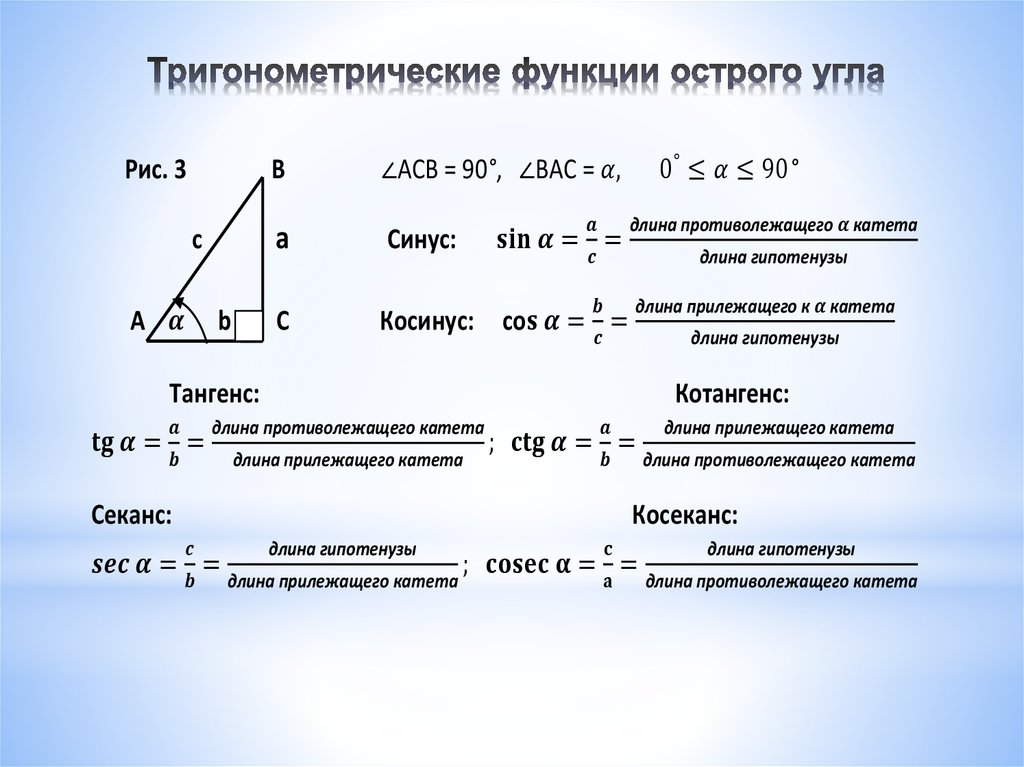
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Косинус угла А обозначается cos A.
Наглядно это видно на следующем рисунке:
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.

- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
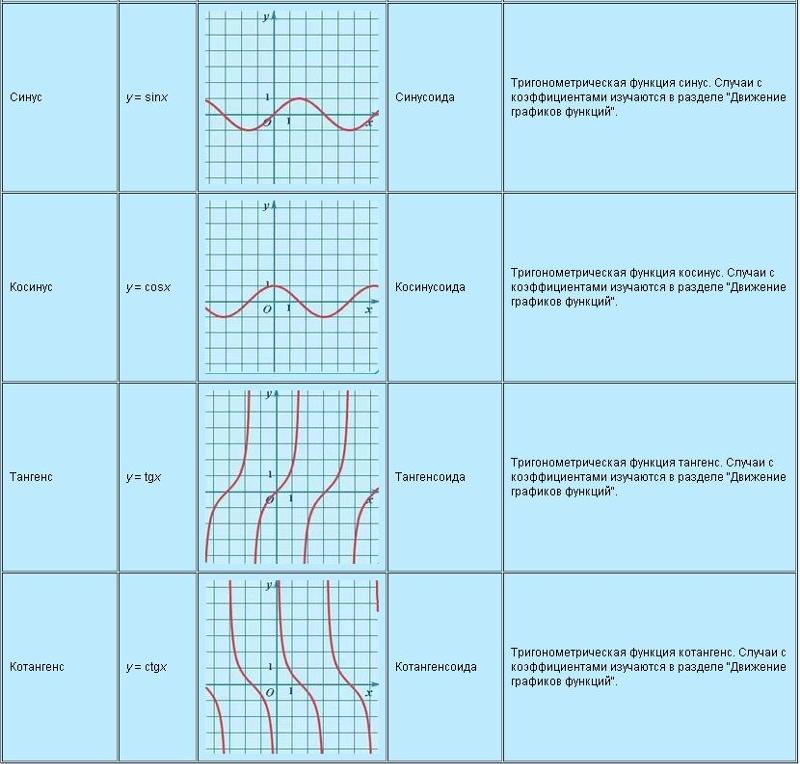
График функции косинус
Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние \[\frac{\pi}{2}\] влево. Он выглядит следующим образом:
Как построить график функции косинус икс
График функции косинуса можно построить следующим образом:
Используем данные единичной окружности, приведённой на рисунке выше.
Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.
Соединим их плавной линией
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как найти значение функции косинуса при x равном 45 градусам
Построим прямоугольный треугольник с катетами, равняющимися единице. {2}}=\sqrt{1+1}=\sqrt{2}\]
{2}}=\sqrt{1+1}=\sqrt{2}\]
Из определения косинуса находим \[\cos (a)=1 / \sqrt{2}\]
После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.
Оценить статью (0 оценок):
Поделиться
Федор Разовский — Кандидат математических наук
Популярные статьи
Выполнение любых работ по математике
Тригонометрические функции y = sin x и y = cos x . Их свойства и графики презентация, доклад
ТЕМА: ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
y =sin x и y = cos X ИХ СВОЙСТВА
И ГРАФИКИ.
III
II
I
IY
III
IY
I
II
π — шесть клеток
О
с
ь
С
и
н
у
с
о
в
Построение графика функции y = sinx с применением тригонометрического круга
Аналогично строится график функции y=cosx, он симметричен относительно оси OY.
III
IY
I
II
III
IY
Свойства функции y = cos x
Область определения: D(f): х ∈ R;
Множество значений: у ∈ [-1;1];
Периодичность: Т = 2π;
Четность: четная, т.к. cos(-x) = cos x, график симметричен относительно оси ординат;
Функция возрастает при: π+2πn ≤ x ≤ 2π(n+1), n∈Z;
Функция убывает при: πn ≤ x ≤ π + 2πn, n ∈ Z.
Свойства функции y = cos x (продолжение)
Функция принимает значения:
Равные нулю при х=π/2+πn, n∈Z;
Положительные при -π/2+2πn Отрицательные при π/2+2πn Наибольшее, равное 1, при x = 2πn, n ∈ Z;
Наименьшее, равное –1, при x = π + 2πn, n ∈ Z.
Свойства функции y = sin x
Область определения: D(f): х ∈ R;
Множество значений: у ∈ [-1;1];
Периодичность: Т = 2π;
Четность: НЕчетная, т. к. sin(-x) = — sinx, график симметричен относительно начала координат;
к. sin(-x) = — sinx, график симметричен относительно начала координат;
Функция возрастает при: -π/2+2πk ≤ x ≤ π/2+2πk, k∈Z;
Функция убывает при: π/2+2πk ≤ x ≤ 3π /2 + 2π k, k ∈ Z.
Свойства функции y = sin x (продолжение)
Функция принимает значения:
Равные нулю при х=πk, k∈Z;
Положительные при 2πk Отрицательные при π+2πk Наибольшее, равное 1, при x = π /2+2πk, k ∈ Z;
Наименьшее, равное –1, при x = 3π /2+ 2πk, k ∈ Z.
ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
у = sinx + m
y= sin(x+t)
y=f(kx)
y=kf(x)
График функции y=f(x)+m получается параллельным переносом графика функции y=f(x) вдоль оси ОУ,
вверх на m единиц, если m>0,
или вниз, если m
График функции y = f(x + t) получается параллельным переносом графика функции y=f(x) вдоль оси ОХ на |t| единиц масштаба
влево, если t > 0
и вправо, если t
Если известен график функции y=f(x), то график функции y=kf(x) строится посредством растяжения вдоль оси Оy исходного графика, пропорционально коэффициенту в k раз, а именно:
— если m>0, то растяжение в k раз
— если 0
Если известен график функции y=f(x), то график функции y=f(kx) строится посредством
сжатия по оси Оx исходного графика пропорционально коэффициенту k при аргументе, а именно:
— если k>1, то сжатие в k раз
— если 0
y
x
1
-1
3
-3
I I I I I I I
O
x
y
-1
1
3cos x
=
y
–
Какие свойства еще изменились?
y
x
1
-1
-1
Какие свойства еще изменились?
I I I I I I I
O
x
y
-1
1
Как найти период функции?
y
x
1
-1
2
Скачать презентацию
Базисные свойства p, q-синусоидальных функций
. 2015 8 февраля; 471(2174):20140642.
2015 8 февраля; 471(2174):20140642.
doi: 10.1098/rspa.2014.0642.
Лайонелл Бултон 1 , Габриэль Дж. Лорд 1
принадлежность
- 1 Факультет математики и Институт математических наук им. Максвелла, Университет Хериот-Ватт, Эдинбург Eh24 4AS, Великобритания.
- PMID: 25663809
- PMCID: PMC4309129
- DOI: 10.1098/rspa.2014.0642
Бесплатная статья ЧВК
Лайонелл Боултон и др. Proc Math Phys Eng Sci. .
Proc Math Phys Eng Sci. .
Бесплатная статья ЧВК
. 2015 8 февраля; 471(2174):20140642.
doi: 10.1098/rspa.2014.0642.
Авторы
Лайонелл Боултон
принадлежность
- 1 Факультет математики и Институт математических наук им. Максвелла, Университет Хериот-Ватт, Эдинбург Eh24 4AS, Великобритания.
- PMID: 25663809
- PMCID: PMC4309129
- DOI:
10.
 1098/rspa.2014.0642
1098/rspa.2014.0642
Абстрактный
Мы улучшаем известные к настоящему времени пороги базисности семейства периодически расширяющихся
p , q — функции синуса. Наши результаты основаны на разложении Берлинга соответствующей замены координат в терминах операторов сдвига бесконечной кратности. Мы также определяем уточненные оценки константы Рисса, связанной с этим семейством. Эти результаты заполняют математические пробелы в существующей литературе по этому вопросу.Ключевые слова: основа Рисса; базис Шаудера; обобщенные тригонометрические функции.
Цифры
Рисунок 1.
Оптимальная область обратимости в…
Рисунок 1.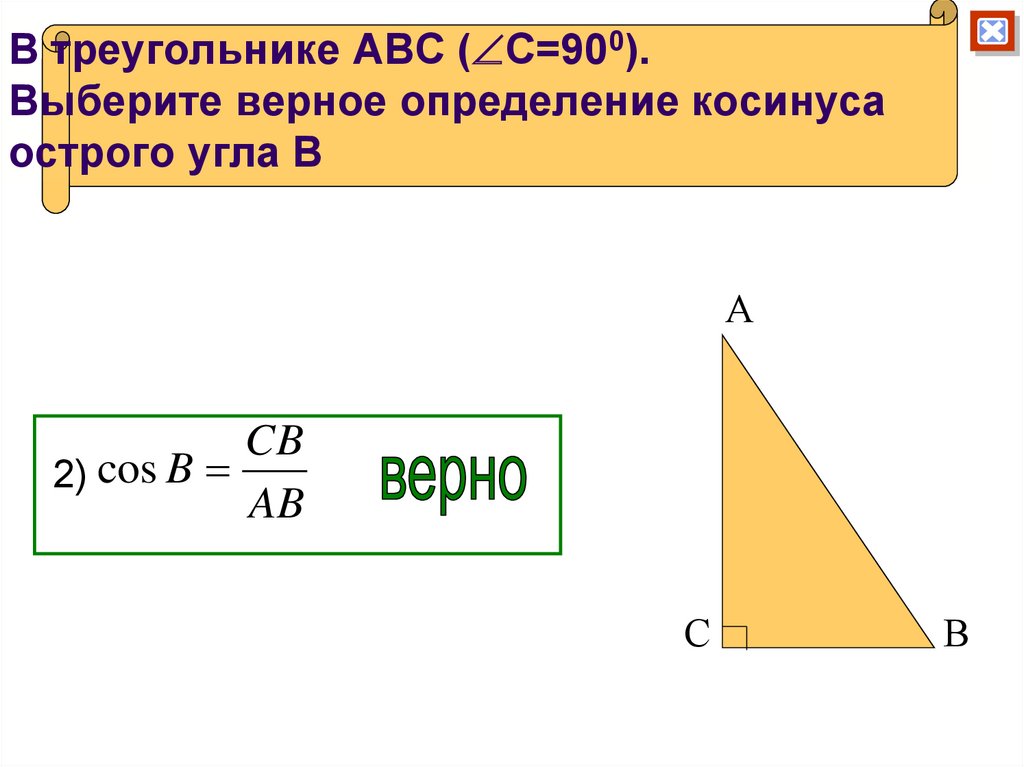
Оптимальная область обратимости в лемме 4.1. Горизонтальная ось α и…
Фигура 1.Оптимальная область обратимости в лемме 4.1. Горизонтальная ось равна α и вертикальная ось β .
Рисунок 2.
Аппроксимации ℓ j ( x…
Рисунок 2.
Аппроксимации ℓ j ( x ) используются для демонстрации границы (a) в лемме…
Фигура 2. аппроксимаций ℓ j ( x ), использованных для демонстрации границы (a) в лемме 6.1. Для справки мы также показываем sinp6,p6(πp6,p6x), sin(3πx), sin4/3,4/3(π4/3,4/3x) и sin2,2(πx)=sin (пх).
Рисунок 3.
Связь между различными утверждениями…
Рисунок 3.
Связь между различными утверждениями этой статьи и ссылками [4,5],…
Рисунок 3. Связь между различными утверждениями этой статьи и ссылками [4,5], для случая p = q . Позиции p 1 , p~2 и значение ε установлены только для иллюстрации, так как мы уверены только в том, что p2
Рис. 4.
( а – е )…
Рисунок 4.
( a – e ) Различные отношения и границы между регионами…
Рисунок 4.
( a – e ) Различные отношения и границы между областями ( p , q )-плоскости, где теорема 5.2(a) и (b), а также предложение 7.1 (при разных значениях k ). На всех графиках p соответствует горизонтальной оси, а q — вертикальной оси, а пунктирная линия показывает p = q . (Онлайн-версия в цвете.)
Рисунок 5.
Регион (
р…
Рисунок 5.
Регион ( стр , q )-плоскости, где применима теорема 5.2(c). Даже…
Рисунок 5. Область ( p , q )-плоскости, где применяется теорема 5.2(c). Даже когда мы знаем, что A обратимо в этой области вследствие теоремы 5.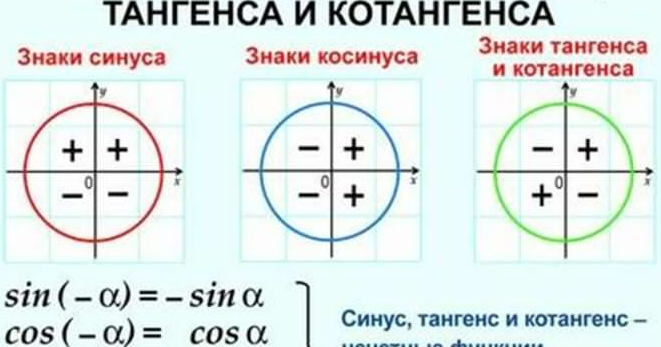 2(a), верхняя граница константы Рисса, обеспечиваемая (4.2), улучшает оценку, обеспечиваемую (1.2) (случай r =2) . На этом графике p соответствует горизонтальной оси и q относительно вертикальной оси, а пунктирная линия показывает p = q . (Онлайн-версия в цвете.)
2(a), верхняя граница константы Рисса, обеспечиваемая (4.2), улучшает оценку, обеспечиваемую (1.2) (случай r =2) . На этом графике p соответствует горизонтальной оси и q относительно вертикальной оси, а пунктирная линия показывает p = q . (Онлайн-версия в цвете.)
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Распад ( p , q )-коэффициентов Фурье.
Эдмундс Д.Э., Гурка П., Ланг Дж. Эдмундс Д.Э. и соавт. Proc Math Phys Eng Sci. 2014 8 октября;470(2170):20140221. дои: 10.1098/rspa.2014.0221. Proc Math Phys Eng Sci. 2014. PMID: 25294961 Бесплатная статья ЧВК.
О различных двойственных по Риссу последовательностях для реперов Шаудера.

Нейси АР, Асгари МС. Неиси А.Р. и соавт. Гелион. 21 сентября 2020 г.; 6(9):e04963. doi: 10.1016/j.heliyon.2020.e04963. электронная коллекция 2020 сен. Гелион. 2020. PMID: 33005789 Бесплатная статья ЧВК.
Сохраняющие форму свойства нового семейства обобщенных операторов Бернштейна.
Цай QB, Сюй XW. Cai QB и др. J Неравное применение 2018;2018(1):241. doi: 10.1186/s13660-018-1821-9. Epub 2018 14 сентября. J Неравное применение 2018. PMID: 30839680 Бесплатная статья ЧВК.
Управляемость вейвлета и преобразование Рисса высшего порядка.
Унсер М., Ван Де Виль Д. Унсер М. и соавт. Процесс преобразования изображений IEEE. 2010 март; 19(3): 636-52. doi: 10.1109/TIP.2009.
 2038832. Epub 2009 22 декабря.
Процесс преобразования изображений IEEE. 2010.
PMID: 20031498
2038832. Epub 2009 22 декабря.
Процесс преобразования изображений IEEE. 2010.
PMID: 20031498[Обзор математических дескрипторов асферичности роговицы].
Гатинель Д., Хауат М., Хоанг-Суан Т. Гатинель Д. и соавт. J Fr Офтальмол. 2002 янв; 25 (1): 81-90. J Fr Офтальмол. 2002. PMID: 11965125 Рассмотрение. Французский.
Посмотреть все похожие статьи
использованная литература
- Линдквист П. 1995. Некоторые замечательные функции синуса и косинуса. Ricerche di Matematics 44, 290–296.
- Эдмундс Д., Ланг Дж. 2011. Вложения собственных значений и обобщенные тригонометрические функции.
 Берлин, Германия: Springer.
Берлин, Германия: Springer.
- Эдмундс Д., Ланг Дж. 2011. Вложения собственных значений и обобщенные тригонометрические функции.
- Эдмундс Д., Гурка П., Ланг Дж. 2012. Свойства обобщенных тригонометрических функций. Дж. Прибл. Теория 164, 47–56 (doi: 10.1016 / j.jat.2011.09.004) — DOI
- Бушелл П.Дж., Эдмундс Д. 2012. Обобщенные тригонометрические функции. Скалистая гора Дж. Математика. 42, 25–57 (doi:10.1216/RMJ-2012-42-1-25) — DOI
- Binding P, Boulton L, Cepicka J, Drábek P, Girg P.
 2006. Базисные свойства собственных функций $p$-лапласиана. проц. Являюсь. Мат. соц. 134, 3487–3494 (doi:10.1090/S0002-9939-06-08001-4)
—
DOI
2006. Базисные свойства собственных функций $p$-лапласиана. проц. Являюсь. Мат. соц. 134, 3487–3494 (doi:10.1090/S0002-9939-06-08001-4)
—
DOI
- Binding P, Boulton L, Cepicka J, Drábek P, Girg P.
свойств синуса · PyPI
чтение/запись файла .properties в простом линейном формате
Описание проекта
чтение/запись файла .properties в построчном формате
ключ=значение на строку через функцию .
код ссылается на java.util.Properties в Java 1.6.
файловый ввод/вывод:
# ввод свойства = загрузить (файл) # или обновить существующий словарь загрузить (файл, свойства) # вывод хранить (файл, свойства)
- Пользовательский ввод
:
класс LineReaderсчитывает данные в одном ключе-значении. Он пропускает все строки комментариев,
Он пропускает все строки комментариев,
пустых строк, ведущие пробелы и обрабатывает многострочные данные.
loadSingle(string)прочитать каждую часть данных, указанных выше, в ключ-значение.для строки в LineReader(file): # каждая строка ключ-значение не имеет разделителя строк ключ, значение = loadSingle (строка) # сделай что-нибудь пользовательский вывод:
storeComments(доступно для записи, комментарии, linesep=os.linesep))
написать комментарий (допускается многострочный), можно указать признак конца строки.
storeSingle(доступно для записи, ключ, значение, sep='=', linesep=os.linesep)
записать один ключ-значение, можно указать разделитель и признак конца строки.storeComments(файл, 'это комментарий') storeSingle (файл, 'ключ', 'значение')
Обычно каждая строка является строкой комментария или парой ключ-значение.
основные характеристики:
- отдельный ключ и значение одним из
=,:,\ т - игнорировать пробелы в начале строки или около
=или: Строка комментария - начинается с
#или! - escape unicode by
\uxxxx - избежать специальных символов, добавив
\
другие:
- строка данных заканчивается на
\отбросить разрыв строки
отличия от Java:
- метод хранения не будет записывать комментарий даты и времени
v0.1.1, 2019-2-9
- изменение для работы с python3
v0.1.0, 7 июня 2018 г.
- настроен.
Детали проекта
Эта версия
0.1.1
0.1.0
Загрузить файлы
Загрузить файл для вашей платформы. Если вы не уверены, что выбрать, узнайте больше об установке пакетов.
Исходный дистрибутив
sine.properties-0.1.1.tar.gz (13,1 КБ посмотреть хеши)
Загружено источник
Закрывать
Хэши для sine.



 1098/rspa.2014.0642
1098/rspa.2014.0642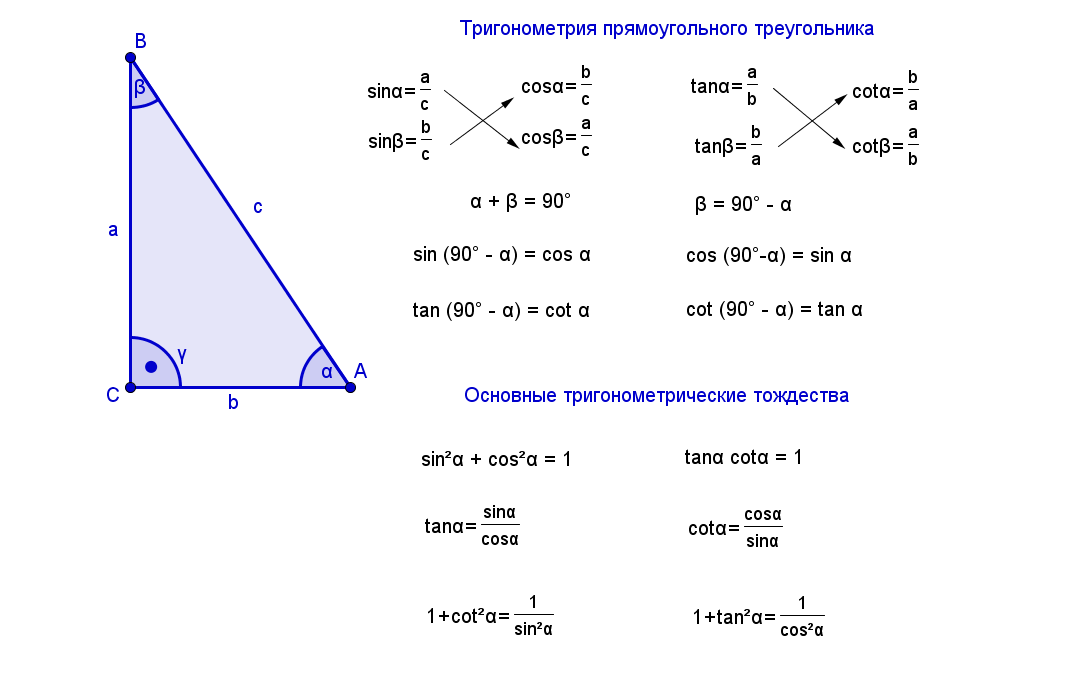
 2038832. Epub 2009 22 декабря.
Процесс преобразования изображений IEEE. 2010.
PMID: 20031498
2038832. Epub 2009 22 декабря.
Процесс преобразования изображений IEEE. 2010.
PMID: 20031498 Берлин, Германия: Springer.
Берлин, Германия: Springer. 2006. Базисные свойства собственных функций $p$-лапласиана. проц. Являюсь. Мат. соц. 134, 3487–3494 (doi:10.1090/S0002-9939-06-08001-4)
—
DOI
2006. Базисные свойства собственных функций $p$-лапласиана. проц. Являюсь. Мат. соц. 134, 3487–3494 (doi:10.1090/S0002-9939-06-08001-4)
—
DOI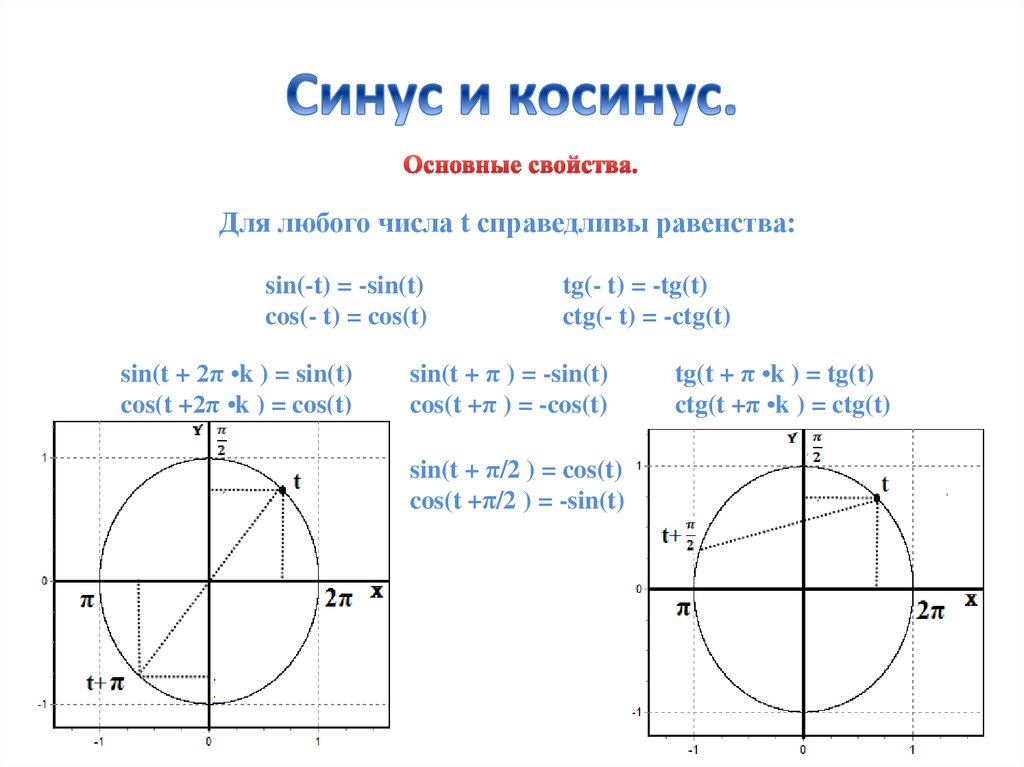 Он пропускает все строки комментариев,
Он пропускает все строки комментариев,