Синус, косинус и тангенс острого угла прямоугольного треугольника 8 класс онлайн-подготовка на Ростелеком Лицей |
Повторение основных понятий, связанных с прямоугольным треугольником
На этом уроке мы познакомимся с синусом, косинусом и тангенсом – тригонометрическими функциями, связывающими острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Это очень важные понятия, которые будут встречаться не только в геометрии, но и в алгебре, физике и во многих других науках.
Напомним основные сведения о прямоугольном треугольнике (см. Рис. 1).
Рис. 1
;
– катеты; AB=c – гипотенуза.
Также в прямоугольном треугольнике сумма острых углов равна : .
Для прямоугольного треугольника также верна теорема Пифагора: .
Введём теперь понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Определение
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе.
, .
Определение
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
, .
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему катету.
, .
Связь катетов и гипотенузы, двух катетов через тригонометрические функции угла
С помощью введённых понятий можно находить катеты или гипотенузу.
Например, из формулы: . Аналогично: .
Также можно получить формулу для связи длин двух катетов: .
Связь синуса и косинуса двух острых углов прямоугольного треугольника
При решении задач очень важно знать соотношения между синусом, косинусом и тангенсом острого угла прямоугольного треугольника.
Рассмотрим следующие две формулы: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Аналогично получаем: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Формула, связывающая тангенс с синусом и косинусом
Докажем теперь важную формулу, связывающую тангенс с синусом и косинусом:
Доказательство независимости значения тригонометрических функций от размеров треугольника
Доказательство
Запишем определение синуса и косинуса острого угла прямоугольного треугольника: , . Тогда: . Доказано.
Аналогично: .
Рассмотрим следующую важную задачу.
Задача
Даны прямоугольные треугольники . Кроме того, .
Доказать:.
Доказательство
(так как оба треугольника прямоугольные с равными острыми углами). Значит, выполняется следующее соотношение: .
Отсюда получаем: .
.
.
Доказано.
Вывод: синус, косинус и тангенс не зависят от треугольника, а зависят только от угла.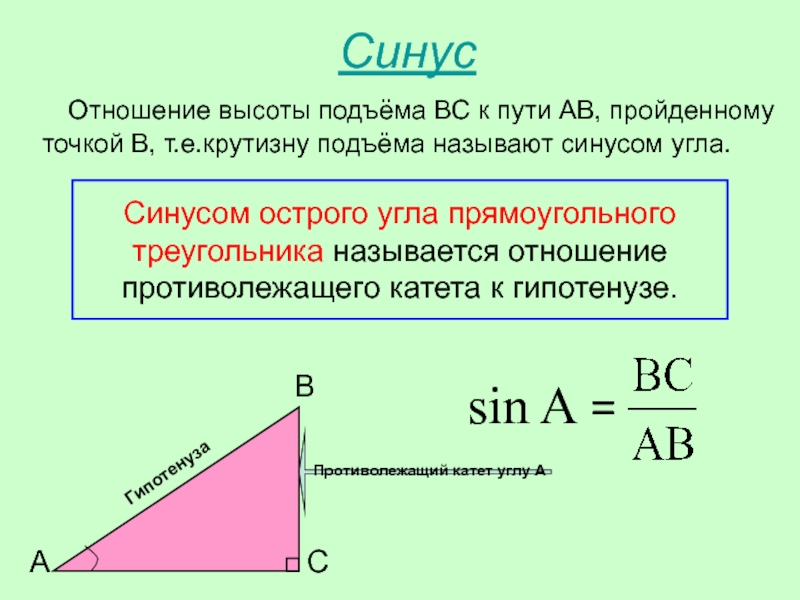
Основное тригонометрическое тождество
Сформулируем и докажем одну из важнейших теорем, связывающих синус и косинус острого угла прямоугольного треугольника, – основное тригонометрическое тождество.
Основное тригонометрическое тождество: .
Примечание:
Доказательство
, тогда: (при доказательстве мы пользовались теоремой Пифагора: ).
Доказано.
Рассмотрим пример, иллюстрирующий связь тригонометрических функций.
Решение примера
Дано: – прямоугольный (), .
Найти:
Решение
Воспользуемся основным тригонометрическим тождеством: . Подставим в него известное нам значение синуса: . Отсюда: . Так как косинус, по определению, – это отношение катета к гипотенузе, то он может быть только положительным, поэтому: .
Найдём теперь тангенс угла, пользуясь формулой: .
Ответ: .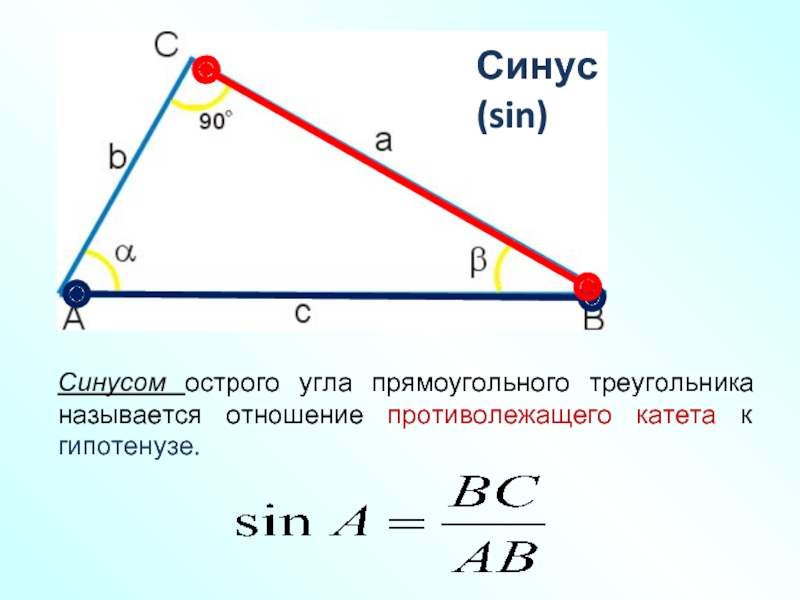
На этом уроке мы рассмотрели понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника, вывели некоторые их свойства и формулы связи между этими величинами. На следующем уроке мы познакомимся со значениями синуса, косинуса и тангенса для некоторых конкретных значений углов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Xvatit.com (Источник).
- Egesdam.ru (Источник).
Домашнее задание
- № 133(а-г), 134(а-г), Бутузов В.Ф., Кадомцев С.
 Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011. - Найдите синус, косинус и тангенс наименьшего угла египетского треугольника.
- Найдите косинус и тангенс острого угла прямоугольного треугольника, синус которого равен .
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
30 июня, 2022
1 минМтмт 📈
🖇 Понятия синуса (sin), косинуса (cos), тангенса (tg), котангенса (ctgc) неразрывно связаны с понятием угла.
⚜️ Угол в тригонометрии может измеряться в ГРАДУСАХ и РАДИАНАХ.
✏️ Углом в 1∘ называют центральный угол в окружности, опирающийся на круговую дугу, равную 1/360 части окружности.
✏️ Углом в 1 радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
✏️ 180°≈3,14 радиан =>180°=π радиан
=> 1 радиан≈57°.
📌 Например :
30°=π/6
60°=π/4
360°=2π и тд.
А что же все-таки такое синус, косинус, тангенс, котангенс угла? 🤔
🔺 Синус угла – это отношение противолежащего катета к гипотенузе.
🔺Косинус угла – это отношение прилежащего катета к гипотенузе.
🔺Тангенс угла – это отношение противолежащего катета к прилежащему.
🔺Котангенс угла – это отношение прилежащего катета к противолежащему.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
45 подписчиков
+ Подписаться
Редакция Без Сменки13 июня, 2022
1 мин
Био 🦠
Конкуренция в живой природе
Вот наша первая пара: щука и окунь в реке, решившие, что этот водоём слишком мал для них двоих.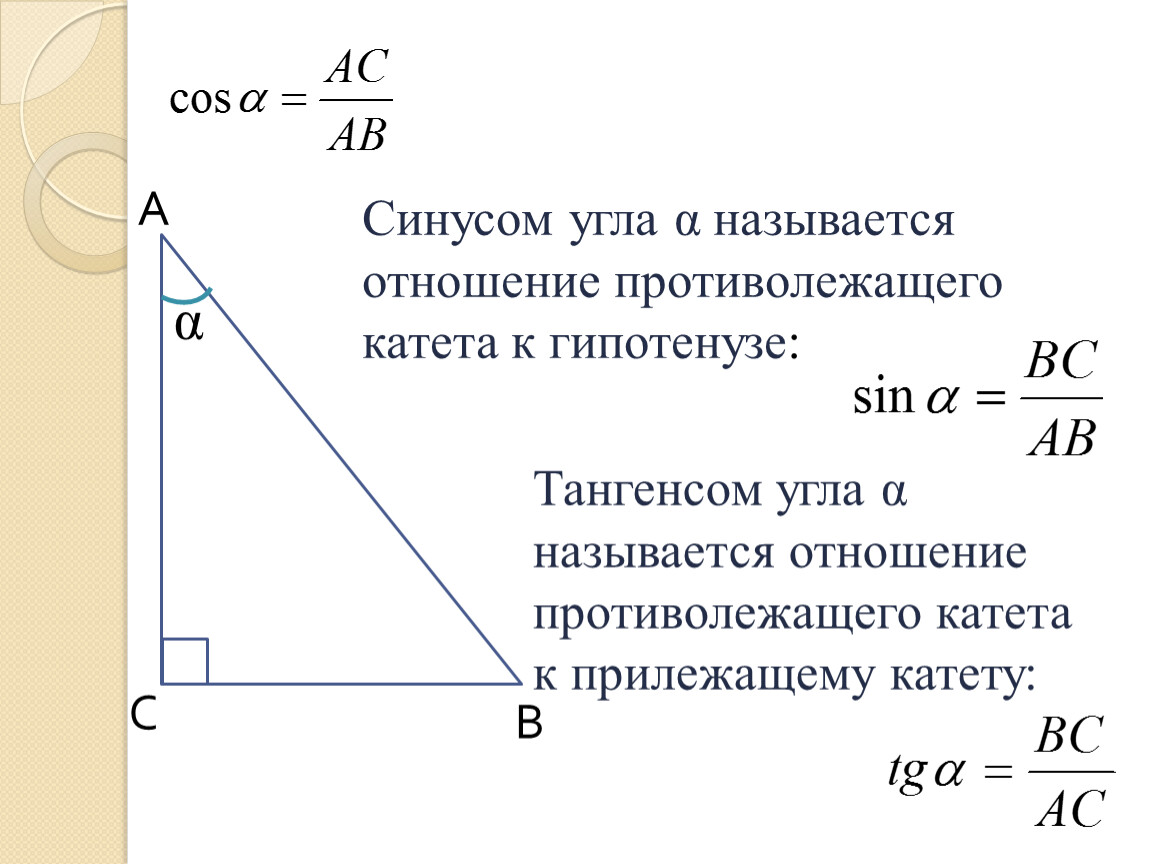 …
…
Редакция Без Сменки
29 июня, 2022
1 мин
Физ 🔬
Удельная теплота плавления
Такая же величина выделяется и при кристаллизации 1 кг вещества. Обозначается удельная теплота…
Редакция Без Сменки
01 июля, 2022
1 мин
Хим 🧪
ОКСИДЫ АЗОТА
Нам в ЕГЭ могут встретится и несолеобразующие оксиды (NO, N₂O), и солеобразующие (N₂O₃, NO₂, N₂O₅) …
Редакция Без Сменки
15 июня, 2022
1 мин
Инф 💻
Бинарный поиск
Такой алгоритм применяется для задач поиска, например: мы ищем значение слова на букву К в словаре.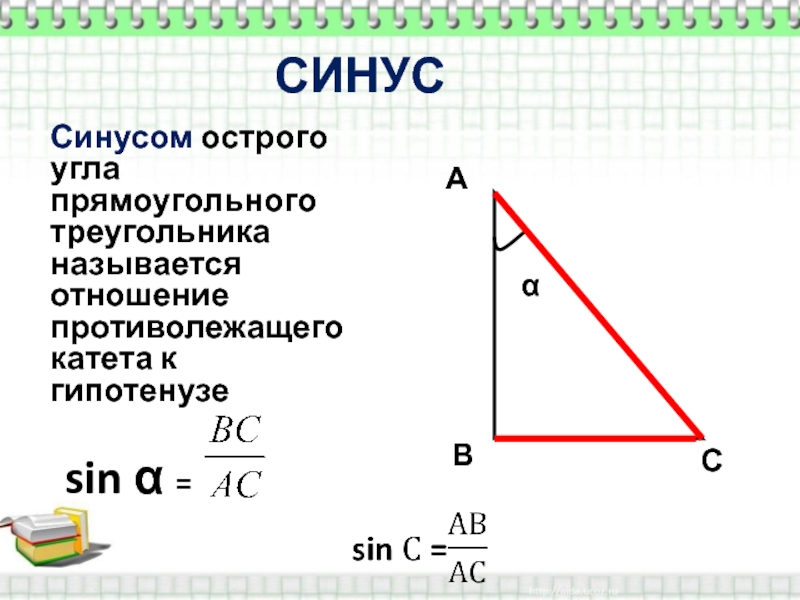
Геометрия: коэффициент синуса
Функция тангенса исследовала значения отношения двух катетов прямоугольного треугольника. Также можно взять отношение длины одного катета к длине гипотенузы. У тебя две ноги, так какую использовать?
В прямоугольном треугольнике у каждого угла есть противоположный сторона и соседняя сторона. И всегда есть гипотенуза. Не забывайте про гипотенузу. Если вы работаете с противоположной стороной и гипотенуза вы имеете дело с синусом соотношение. синус угла есть отношение длина противоположной стороны, деленная на длина гипотенузы.
Твердые факты
В прямоугольном треугольнике синус угла равен отношению длины противоположной стороны к длине гипотенузы.
Давайте воспользуемся теоремой Пифагора, чтобы исследовать некоторые свойства соотношения синусов. Дан прямоугольный треугольник (подобный показанному на рис.
Рис. 20.4 Прямоугольный треугольник с длинами сторон a и b и длиной гипотенузы c.
Если вам дан прямоугольный треугольник и вы знаете тангенс угла, вы можете найти синус угла, применив теорему Пифагора.
- Пример 2 : Предположим, что прямоугольный треугольник имеет угол с отношением тангенса 5 / 12 .
 Найдите отношение синусов этого угла.
Найдите отношение синусов этого угла. - Решение : Рисунок 20.5 поможет вам визуализировать происходящее.
- Вам дано, что tan A = 5 / 12 , поэтому a = 5 и b = 12. Вы можете использовать теорему Пифагора, чтобы найти длину гипотенузы:
- в 2 = а 2 + б 2
- с 2 = 5 2 + 12 2 = 25 + 144 = 169
- с = 13
Касательная
Давайте изучим отношение синусов для прямого угла. Определение отношения синуса — это отношение длины противоположной стороны к длине гипотенузы. Итак, длина стороны, противоположной C , равна
Рисунок 20.5 Прямоугольный треугольник с загаром A = 5 / 12 .
Теперь, когда вы знаете длину гипотенузы, нужно просто найти отношение синусов этого угла (это отношение длины стороны, противоположной углу, деленное на длину гипотенузы):
- sin A = 5 / 13
Этот расчет работает в обе стороны. Зная отношение синусов угла треугольника, можно найти отношение тангенсов угла.
- Пример 3 : Если прямоугольный треугольник имеет угол с отношением синусов 4 / 5 , найдите отношение тангенсов этого угла.
- Решение . Давайте посмотрим на рисунок 20.6. Для того, чтобы найти отношение тангенсов угла, нужно знать длину стороны, противолежащей углу, и длину стороны, примыкающей к углу. Потому что отношение синусов равно 3 / 5 , длина стороны, противоположной углу, равна 3, а длина гипотенузы равна 5. Используя теорему Пифагора, вы можете найти длину стороны, прилегающей к углу:
- а 2 + б 2 = в 2
- 3 2 + б 2 = 5 2
- 9 + б 2 = 25
- б 2 = 16
- b = 4
Таким образом, отношение тангенса равно 3 / 4 .
Рисунок 20.6 Прямоугольный треугольник, угол которого имеет отношение синусов
Теорема Пифагора будет использоваться в этом разделе так часто, что вы будете знать ее как свои пять пальцев к тому времени, когда закончите с этим разделом!
Выдержки из «Полное руководство идиота по геометрии» © 2004 Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , член Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
- Геометрия: соотношение косинусов
Население штата США по рангу (обновление на 2023 г.!)
Королевские биографии: король Карл III
Текущие события на этой неделе: Май 2023
Книги Библии: книги Нового Завета по порядку
Медсестра
Мост Золотые Ворота: факты, история и профиль
Коэффициент синуса
Чтобы помочь вам понять, что такое коэффициент синуса, мы выполним действие, аналогичное тому, которое мы выполняли для отношения тангенса.
В уроке о соотношении тангенсов мы использовали эти треугольники, чтобы найти отношение тангенсов.
Вместо того, чтобы вычислять отношения противоположностей к смежным, что, если бы мы вычисляли отношения противоположностей к гипотенузе? Давайте попробуем это. Чтобы получить значение гипотенузы, у вас есть два варианта.
Можно воспользоваться теоремой Пифагора или измерить длину линейкой.
Я измерил линейкой и нашел следующие длины. Имейте в виду, что эти измерения не идеальны, и это не главное.
Треугольник слева: 2,24 см
Треугольник посередине: 3,8 см
Треугольник справа: 5,3 см
Вычислите соотношение:
опора противоположная 45 градусов / гипотенуза
1,6 см / 2,24 см
= 0,714
2,7 см / 3,8 см
= 0,71
3,8 см / 5,3 см
= 0,716
Обратите внимание, что отношение почти равно 0,71 см независимо от размера треугольников.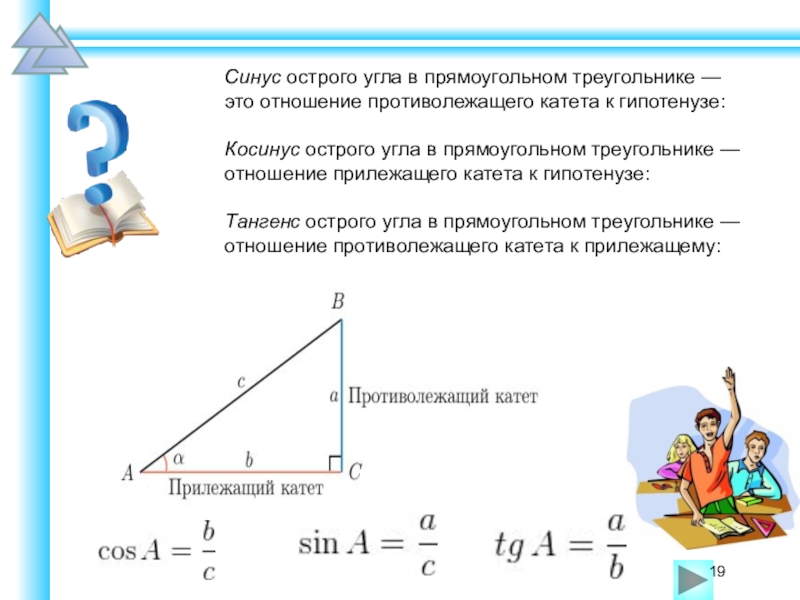
Более простой способ найти отношение синусов.
Существует способ найти более точное значение коэффициента синуса. Поскольку размер треугольника не имеет значения, вы можете использовать значение 1 для противоположной и смежной стороны.
Обратите внимание, что на этот раз я не использую никаких устройств. Опять же, потому что размер не имеет значения.
На этот раз воспользуемся теоремой Пифагора, чтобы найти длину гипотенузы
гипотенуза 2 = 1 2 + 1 2
гипотенуза 2 = 1 + 1
гипотенуза 2 = 2 900 03
гипотенуза = √ 2
отношение противоположного к гипотенузе =
1 / √ 2
= 0,707
Как видите, то, что мы получили здесь, близко к значениям, которые мы нашли ранее.
Это тригонометрическое отношение называется отношением синуса
Всякий раз, когда отношение находится с помощью противолежащего катета и гипотенузы, мы называем его отношением синуса, а не отношением тангенса.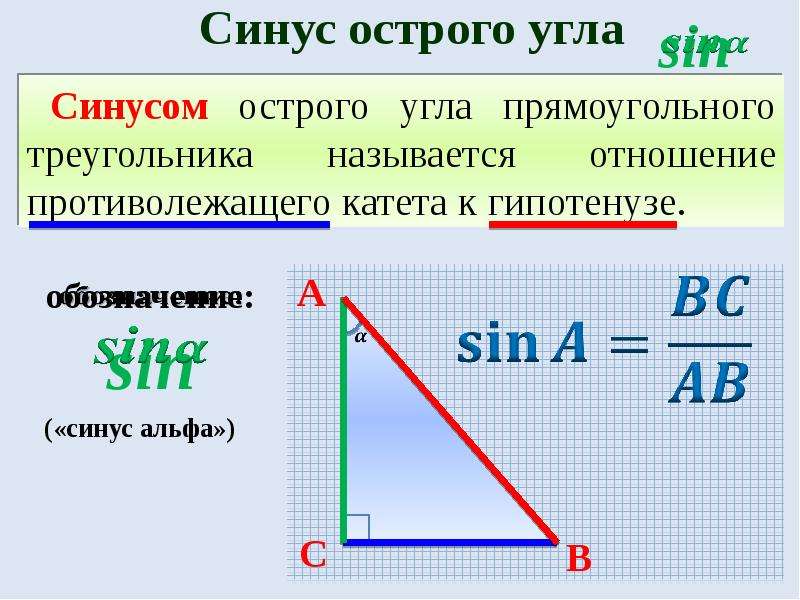
Тогда мы говорим, что синус 45 градусов равен 0,707. Короче говоря, мы можем использовать символ sin вместо синуса и написать sin (45 градусов) = 0,707
В общем случае синус угла A =
длина стороны, противоположной углу А / гипотенуза
грех (А) =
напротив / гипотенуза
Отношение косинуса
Когда вы делаете отношение смежных с гипотенузой, это отношение называется отношением косинуса.
Взгляните еще раз на треугольники. Вы увидите, что соседняя сторона имеет то же значение, что и противоположная сторона.
Это означает, что косинус 45 градусов равен синусу 45 градусов.
Вместо косинуса можно использовать символ cos и написать cos (45 градусов) = 0,707
В общем случае косинус угла A =
длина стороны, прилегающей к углу А / гипотенуза
потому что (А) =
смежный / гипотенуза
Треугольник 45-45-90
01, 23 мая 07:00
Что такое треугольник 45-45-90? Определение, доказательство, площадь и простые примеры из реальной жизни.


 Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.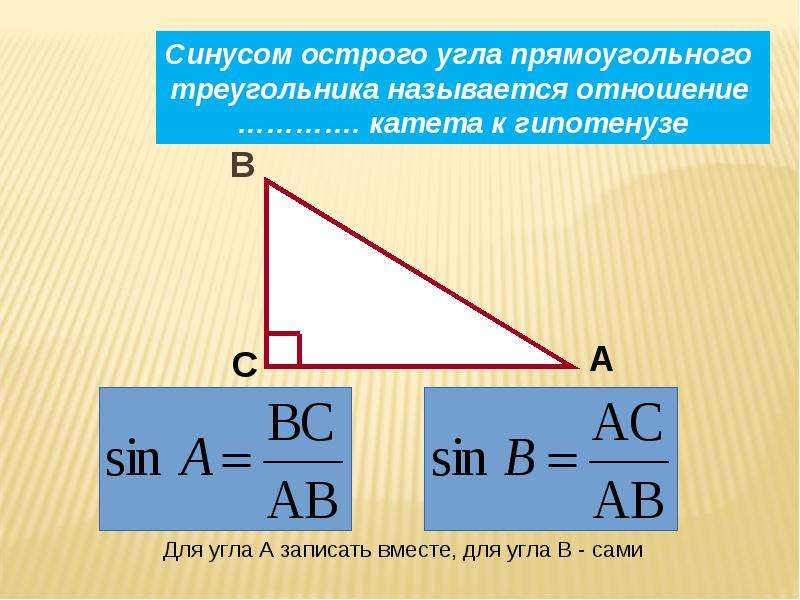 Найдите отношение синусов этого угла.
Найдите отношение синусов этого угла.