Синус умножить на косинус одного угла: Синус умножить на косинус, формула и примеры

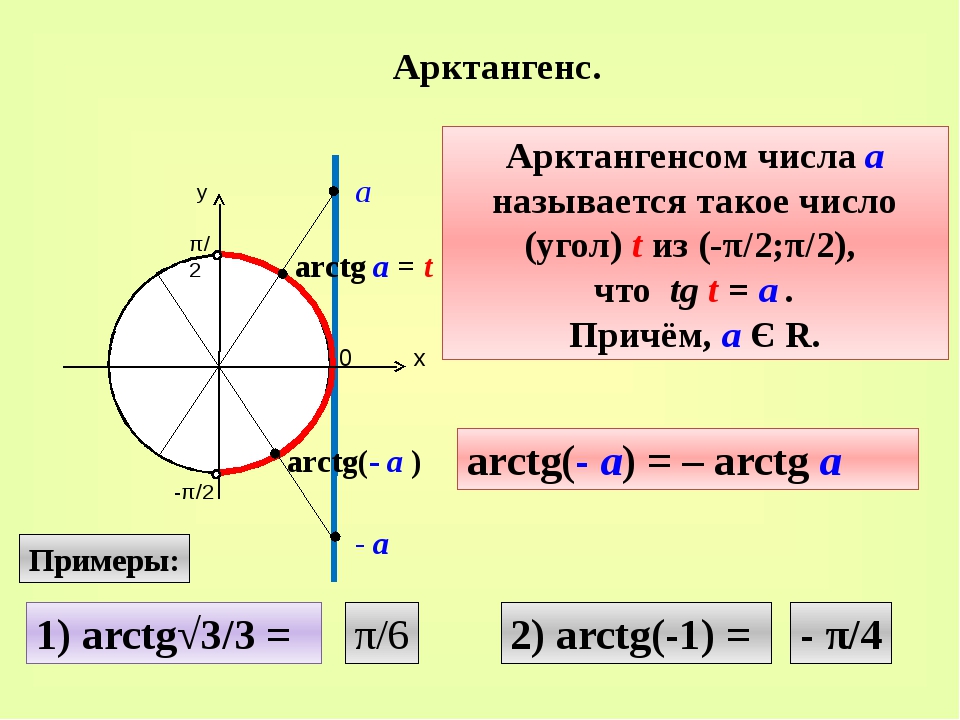
Что будет если sin умножить на sin

Обновлено: 24.11.2022

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$\sin \sin = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_ = 0$$
$$x_ = \pi$$
Численное решение
$$x_ = 53.4070756765$$
$$x_ = 37.6991120192$$
$$x_ = -28.2743337166$$
$$x_ = -106.814150358$$
$$x_ = 72.2566310277$$
$$x_ = 69.1150385886$$
$$x_ = 91.1061867314$$
$$x_ = -47.1238901511$$
$$x_ = 6.28318528425$$
$$x_ = 59.6902605977$$
$$x_ = -15.7079632965$$
$$x_ = -84.8230014101$$
$$x_ = 47.1238895894$$
$$x_ = 97.3893725149$$
$$x_ = 43.9822971694$$
$$x_ = -50.2654822953$$
$$x_ = 3.14159287686$$
$$x_ = -62.8318528379$$
$$x_ = -81.681409038$$
$$x_ = -100.530964673$$
$$x_ = 75.3982239389$$
$$x_ = -87.9645943588$$
$$x_ = 34.5575190305$$
$$x_ = -40.840704266$$
$$x_ = 31.4159267865$$
$$x_ = 91.

1061871584$$
$$x_ = -25.1327414731$$
$$x_ = 97.3893727097$$
$$x_ = -25.1327416321$$
$$x_ = 87.9645943358$$
$$x_ = 69.1150381602$$
$$x_ = 9.42477821024$$
$$x_ = -69.1150386737$$
$$x_ = 12.5663704519$$
$$x_ = -3.14159311568$$
$$x_ = 18.8495554002$$
$$x_ = -69.1150386253$$
$$x_ = 3.14159244884$$
$$x_ = -31.415926796$$
$$x_ = -72.2566308741$$
$$x_ = 62.8318524523$$
$$x_ = -94.247779453$$
$$x_ = 0$$
$$x_ = -40.8407046898$$
$$x_ = 31.4159271479$$
$$x_ = -47.1238900493$$
$$x_ = -1734.15914476$$
$$x_ = 25.1327410189$$
$$x_ = -18.8495561207$$
$$x_ = 75.3982241945$$
$$x_ = 25.1327414478$$
$$x_ = 62.8318528327$$
$$x_ = -12.5663703661$$
$$x_ = -31.4159267052$$
$$x_ = 53.4070753627$$
$$x_ = 15.7079634407$$
$$x_ = -34.5575189426$$
$$x_ = -21.9911485865$$
$$x_ = 84.8230014093$$
$$x_ = 100.530964767$$
$$x_ = -78.5398160958$$
$$x_ = 65.9734457529$$
$$x_ = 56. 5486676091$$
$$x_ = -6.28318513794$$
$$x_ = 40.8407039199$$
$$x_ = -12.5663700417$$
$$x_ = -75.398223862$$
$$x_ = 40.8407042561$$
$$x_ = 84.8230010167$$
$$x_ = 94.2477796094$$
$$x_ = 9.4247785908$$
$$x_ = -43.9822971746$$
$$x_ = 50.2654824463$$
$$x_ = -65.973445765$$
$$x_ = 18.8495556796$$
$$x_ = -3.14159289677$$
$$x_ = -91.1061872003$$
$$x_ = -97.3893724404$$
$$x_ = -59.6902604576$$
$$x_ = -91.1061872013$$
$$x_ = -37.6991118772$$
$$x_ = 78.5398161878$$
$$x_ = 47.1238900184$$
$$x_ = 21.9911485852$$
$$x_ = -56.5486675192$$
$$x_ = -84.8230018263$$
$$x_ = -53.4070752836$$
$$x_ = -9.42477812668$$
$$x_ = -62.8318532584$$
$$x_ = -34.5575189701$$
$$x_ = -18.8495556944$$
$$x_ = 28.2743338652$$
$$x_ = 81.6814091761$$

График пересекает ось Y, когда x равняется 0:

подставляем x = 0 в sin(x)*sin(x).
$$\sin \sin$$
Результат:
$$f = 0$$
Точка:

Для того, чтобы найти экстремумы, нужно решить уравнение
$$\frac f = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac f = $$
Первая производная
$$2 \sin \cos = 0$$
Решаем это уравнение
Корни этого ур-ния
$$x_ = 0$$
$$x_ = \frac$$
$$x_ = \pi$$
$$x_ = \frac$$
Зн. экстремумы в точках:

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_ = 0$$
$$x_ = \pi$$
Максимумы функции в точках:
$$x_ = \frac$$
$$x_ = \frac$$
Убывает на промежутках

Возрастает на промежутках

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках

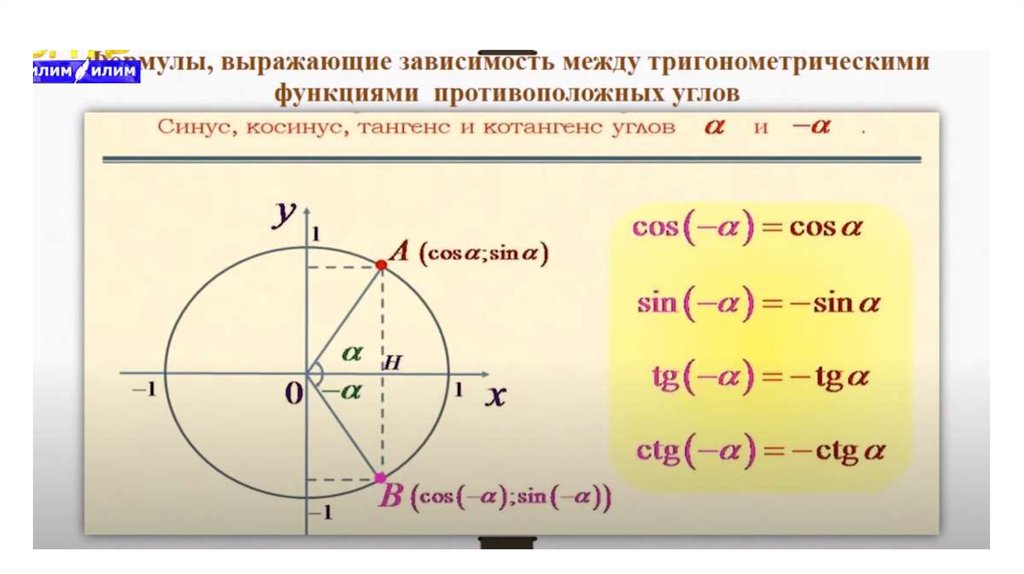
Тангенс и котангенс через синус и косинус

• Синус угла — это ордината y.
• Косинус угла — это абсцисса x.
• Тангенс угла — это отношение ординаты к абсциссе.
• Котангенс угла — это отношение абсциссы к ординате.

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. 2, если 1<x<2 (во втором примере вся дробь под корнем) ​

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.

1. Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
   
2. В результате деления получаем формулу tg 2 α + 1 =
   
3. Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
   1 + ctg 2 α = .
   
4. Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
   
5. А тригонометрическое тождество 1 + ctg 2 α = применимо для любого угла, не равного π * z, где z — это любое целое число.

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.

Основные тригонометрические тождества

sin 2 α + cos 2 α = 1

tg 2 α + 1 =

1 + ctg 2 α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Теорема синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.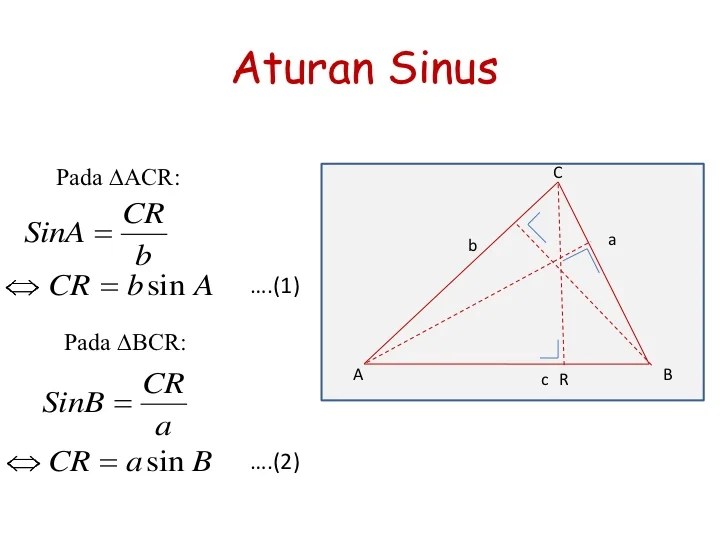

• Тождество записывается в следующем виде:
  tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Взаимно обратные числа — это два числа, произведение которых равно 1.

Основное тригонометрическое тождество

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin 2 α + cos 2 α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.

sin 2 α + cos 2 α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin 2 α + cos 2 α = 1

• Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
• Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.

Образовался прямоугольный треугольник OA₁B.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть.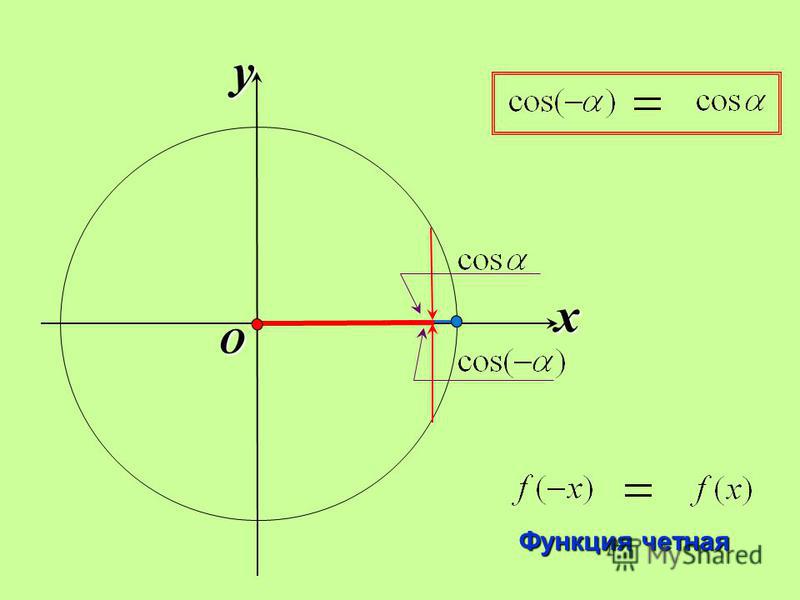 Таким образом без труда можно определить, какой знак нам требуется.

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Чтобы решить задачу, необходимы следующие тригонометрические тождества:

Задачка 2. Найдите значение cos α,
если:

Чтобы решить задачу, необходимы следующие тригонометрические тождества:

Подставляем значения sin α:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Пример 2.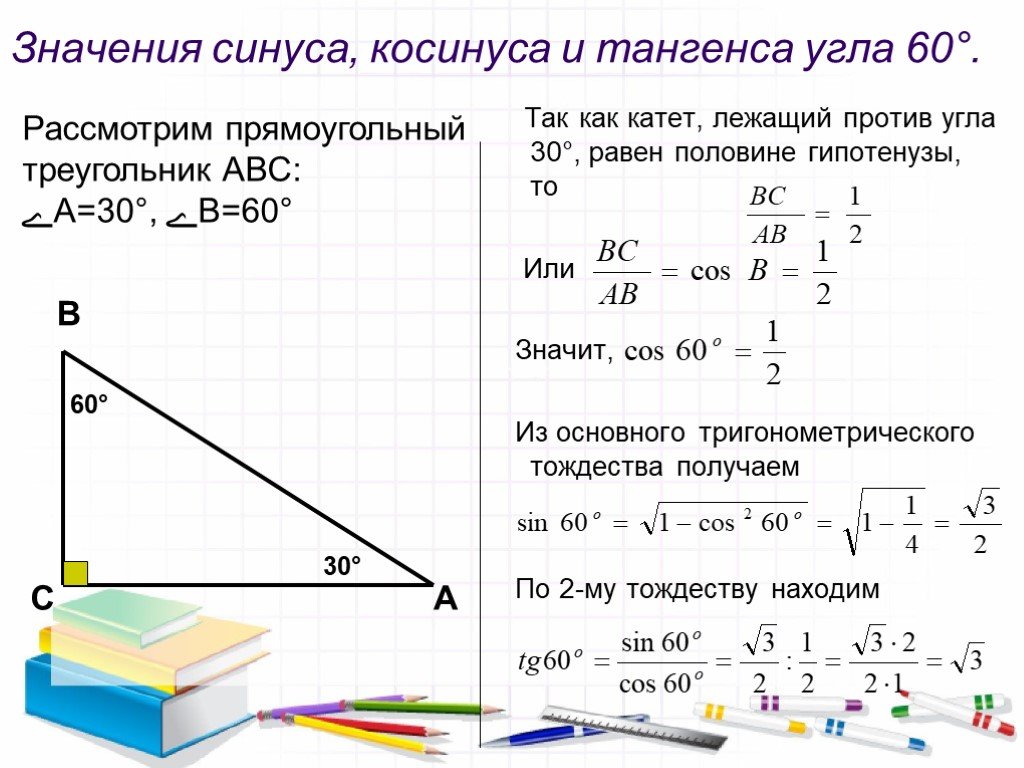 Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.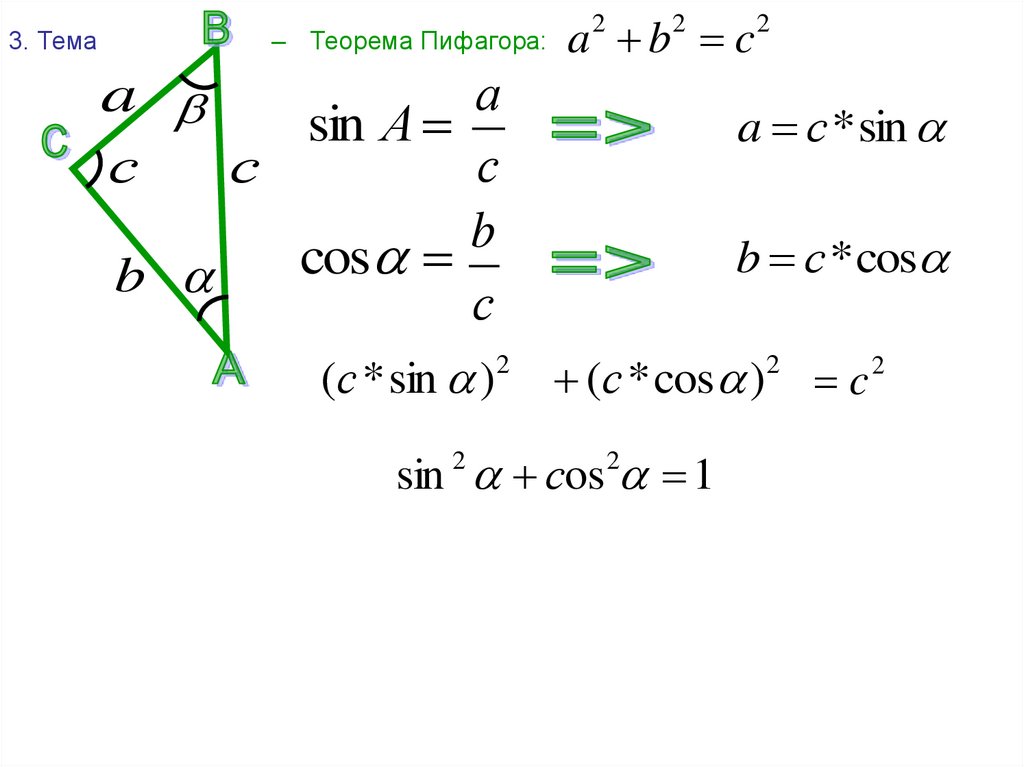

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Читайте также:

  
• Как выбраться из золота в овервотч
  
• Как в игре ассасин
  
• Готика соты шершня где найти
  
• Где в гта 5 найти declasse stallion
  
• Как убить тролля готика 2

Что такое синус, косинус и тангенс?

Основополагающие принципы объясняются на 3 листах с решениями

Это лист 1

Есть две чрезвычайно важные вещи, которые следует помнить о тригонометрических фактах, которые вам показали.

#color(blue)(«Точка 1»)color(brown)(«Это отношения длин сторон треугольника.»)#

#color(blue)(«Point 2»)color(brown )(«Треугольник, используемый для них, является прямоугольным треугольником»)#
#» «#У него угол #9о#. Треугольник имеет 3 угла
#» «#и правильное имя угла в этом контексте — Вершина.#» «#Итак, треугольник имеет 3 Вершины.

‘~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Вокруг этой попытки ходят разные поговорки. чтобы помочь вам вспомнить порядок и отношения. Я использую SohCahToa. Я объясню это очень скоро.

Давайте посмотрим на некоторые числа. Рассмотрим #1/2#

Если вы умножите на 1, вы не измените его значение. Итак, #1/2xx1# по-прежнему #1/2#

Но предположим, что я пишу 1 как, скажем, #3/3#. Это по-прежнему 1

Теперь я умножаю #1/2# на 1, но в виде:#» «1/2xx3/3#. Это все еще стоит #1/2#

Итак:#» 1/2xx3 /3=(1xx3)/(2xx3)=3/6# Выглядит иначе, но все равно стоит #1/2#
‘~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~
Предположим, у нас есть #(«Противоположность»)/(«Гипотенуза») # с использованием сокращений # o/h#

Предположим, мы сделали противоположность равной 3, а гипотенузе равной 4.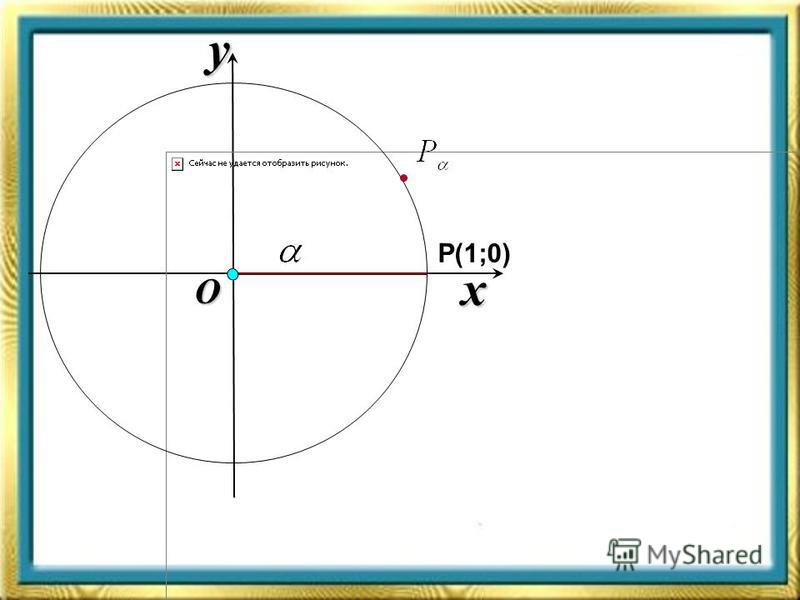 Тогда мы получили бы:

#o/h=3/4# Давайте изменим числа, но сохраним то же соотношение

#o/h=3/4 = (3xx2)/(4xx2) =6/8″ «#Все они имеют одинаковое соотношение. Давайте
#» «#пойдем другим путем!

#o/h=3/4=(3-:4)/(4-:4) = (0,75)/1″ «#Все они имеют одинаковое соотношение.

Что на самом деле говорит #(0.75)/1#?

Он говорит, что; если у вас есть треугольник, в котором длина противоположной стороны равна 1, то длина наклона будет 0,75

Если в треугольнике 1 #o/h = 3/4#, а в треугольнике 2 #o/h = 0,75/1#

Тогда они имеют одинаковую форму, так как соотношение такое же, но треугольник 2 меньше. Противоположность для треугольника 1 имеет длину 3, в то время как противоположность для треугольника 2 имеет длину всего 0,74
‘~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~

Дело в том, что вместо #0.75/1# они пишут просто #» » 0.75#.

Ссылка для ответа

Основополагающие принципы объясняются на 3 листах решений

Это лист 2

Эти отношения имеют специальные названия

#»Полное наименование» «Сокращенное наименование» «Части треугольника»#
#»Синус» » «sin» «(«Противоположность»)/(«Гипотенуза») = o/h#

#»Косинус» » cos»» «(«Смежный»)/(«Гипотенуза») =a/h#

#» Касательная» » tan»» «(«Противоположный»)/(«Смежный»)» «= o/a#

На примере

Пусть ангел #/_ABC» будет «theta» «# (значение неизвестно)

Тогда:
#sin(theta)=(«противоположное»)/(«гипотенуза») = 4/5 =(4-:5)/(5-:5)= 0,8/1=0,8#

#cos (тета)(«прилегающая»)/(«гипотенуза»)=3/5=(3-:5)/(5-:5)=0,6/1=0,6#

#tan(тета)(«противоположная» )/(«прилегающий»)=4/3=(4-:3)/(3-:3) =(1. o» ?»)# 9o#

Итак, мы получаем

#tan(theta)= x/2.5#

Мы ищем значение tan(30) и находим, что оно составляет 0,5774 с точностью до 4 знаков после запятой. Мы заменяем это на #tan(theta)# в уравнении, дающем

#color(brown)(tan(theta)=x/2.5) color(blue)(->0.5774=x/2.5)#

so #color (зеленый)(0,5774/1=x/2,5)# Это снова наше отношение!

Чтобы получить #x# отдельно, умножьте обе части на #color(blue)(2.5)#

#color(green)(0.5774/1color(blue)(xx2.5)=x/2.5color(blue)( хх2.5))#

#1.4435=цвет(зеленый)(x xx цвет(синий)(2.5)/2.5)#

Но #2.5/2.5# совпадает с 1

#1.4435=x xx 1#

#x= 1.4435 # до 4 знаков после запятой

#color(blue)(«Высота треугольника 1,4435 до 4 знаков после запятой»)#

Ссылка на ответ

В базовой тригонометрии мы работаем с прямоугольными треугольниками.

Trig — это СРАВНЕНИЕ длин сторон треугольников.
Одним из способов сравнения является деление. Это скажет нам, является ли одна сторона «половиной» длины другой или в полтора раза длиннее и т. д.

Известный треугольник имеет стороны 3см, 4см и 5см.

Мы можем записать 6 различных сравнений/делений/дробей, используя эти 3 значения:

#3/5, 3/4, 4/3, 4/5, 5/3, 5/4#

Каждое из этих сравнения имеют другое название.
Три имени — синус, косинус и тангенс, в зависимости от того, какие стороны вы разделили.

Синус — это ответ, который получается при делении длины стороны, противоположной углу, на гипотенузу. Он всегда дает один и тот же ответ для определенного угла, независимо от размера треугольника.

Например, синус 30° = #1/2 =0,5 = 50%#

Это говорит нам о том, что для угла 30° в треугольнике сторона, противоположная 30°, всегда будет вдвое длиннее (50% ) как гипотенуза.

Это действительно полезно знать.

Эти «сравнения» также известны как коэффициенты триггера.

Ссылка для ответа

Влияние этого вопроса

5267 просмотров по всему миру

Вы можете повторно использовать этот ответ
Лицензия Creative Commons

Что такое синус, косинус и тангенс?

21 декабря 2020 г. от Abdullah Sam

Синус, косинус и тангенс — элементы, составляющие геометрические знания. Знание того, для чего оно нужно, как его использовать и вычислять, необходимо для получения всесторонних знаний в тригонометрии . Следующий текст посвящен этой теме, я надеюсь, что он будет способствовать вашему обучению.

Индекс

• Что такое синус, косинус и тангенс?
• Формулы синуса, косинуса и тангенса
• Как определить противоположную и соседнюю ногу?
• Синус, косинус и тангенс известных углов
• Песня замечательных ракурсов
• Получение значений заметных углов путем математических расчетов
• Как узнать, когда использовать синус, косинус и тангенс

Что такое синус, косинус и тангенс?

Синус, косинус и тангенс — это  тригонометрические соотношения, полученные посредством отношений между сторонами прямоугольного треугольника. Помните, что этот тип треугольника имеет:

• Угол, равный 90°.
• Два катета и гипотенуза.

Глядя на рисунок, можно заметить, что гипотенуза всегда находится напротив угла 90°, а отрезки, образующие угол 90°, являются сторонами.

Формулы синуса, косинуса и тангенса

Общие формулы синуса, косинуса и тангенса описаны ниже:

• СИНУС

Описание:  Синус — это тригонометрическое отношение, установленное в прямоугольном треугольнике между противолежащей стороной и гипотенузой.

• Косинус

Описание:  Косинус — это тригонометрическое отношение, установленное в прямоугольном треугольнике между прилежащим катетом и гипотенузой.

• ТАНГЕНТ

Описание:  Тангенс — это тригонометрическое отношение, установленное в прямоугольном треугольнике между прилежащим катетом и гипотенузой.

Обс . α может принимать любое значение в градусах тригонометрического цикла, а также может принимать значения в π рад, то есть пи радианах.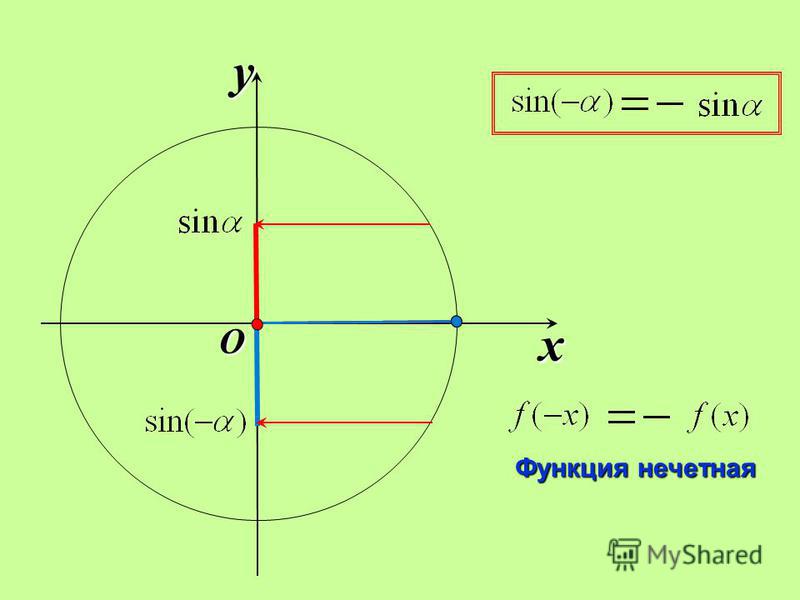

Как отличить противоположную и соседнюю ногу?

Чтобы ответить на этот вопрос, мы должны обратить свой взор на острые внутренние углы прямоугольного треугольника.

Обратите внимание, что каждый угол назван греческой буквой. Противоположный и прилежащий катет для каждого угла являются разными отрезками прямой, но гипотенуза всегда будет одним и тем же отрезком прямой.

Чтобы понять, как идентифицировать противоположную и смежную стороны, обратите внимание на отрезки, которые используются в каждом тригонометрическом соотношении.

• Угол α
• Угол β

Синус, косинус и тангенс известных углов

Замечательными считаются углы: 30°, 45° и 60°. Это связано с тем, что эти углы встречаются чаще  в тригонометрических расчетах.

Проверьте в таблице ниже числовые значения, которые принимают эти известные углы при вычислении синуса, косинуса и тангенса.

При частом использовании этой таблицы вы запомните значения. Если у вас есть трудности с запоминанием, вы можете разучить песню ниже или в соседней теме узнать, как найти значения замечательных углов с помощью математических вычислений.

Сонг Замечательные углы

Получение значений заметных углов с помощью математических вычислений

Чтобы продемонстрировать, как получить значения синуса, косинуса и тангенса для заметных углов, сначала нарисуйте равносторонний треугольник. Помните, что у равностороннего треугольника все стороны одинаковой величины и все углы равны 60°.

Далее определим высоту этого треугольника, для этого построим биссектрису угла (А). Эта биссектриса пересекает прямую (СВ). Биссектриса будет медианой, а медиана будет определять середину отрезка (CB).

Затем мы должны:

Обс. Равносторонний треугольник обладает всеми специфическими свойствами и характеристиками, которые позволяют высоте, биссектрисе и медиане быть одним и тем же отрезком. Важно отметить, что в геометрии есть много других случаев, когда этого не происходит.

Теперь мы определим высоту этого треугольника, применив Теорему Пифагора к треугольнику ACD, выполните следующие действия:

Чтобы получить значения заметных углов, рассмотрим только одну сторону треугольника, представленного выше.

Теперь применим формулы синуса, косинуса и тангенса, уже представленные выше.

После обнаружения числовых значений синуса, косинуса и тангенса для знатных углов 30° и 60° нам еще нужно узнать для 45°. Чтобы получить значения синуса, косинуса и тангенса этого угла, нам нужно начертить квадрат и провести его диагональ, см.:

Квадрат имеет все четыре внутренних угла размером 90°. Когда мы проводим диагональ (d) квадрата, мы делим угол 90° пополам, то есть новые углы становятся 45°.

Применим теорему Пифагора, чтобы найти значение диагонали треугольника ABC через (a).

Со значением диагонали/гипотенузы и коллекторов в единицах (а) мы смогли вычислить синус, косинус и тангенс 45°, следуйте:

Если вы не можете запомнить соответствующие значения к замечательным углам, теперь вы хотя бы умеете их вычислять.

Как узнать, когда использовать синус, косинус и тангенс

Изображение иллюстрирует использование треугольника на одном из самых известных мостов в мире, Золотых Воротах, в США (Фото: Depositphotos)

Мы будем использовать синус, косинус и тангенс, когда нам нужно найти мера для любой стороны прямоугольного треугольника или когда нам нужно знать меру острых внутренних углов.

Структура треугольников широко используется в строительстве объектов и сооружений , и может быть легко найдена в гражданском строительстве. Это связано с тем, что треугольник считается жесткой геометрической фигурой, то есть он не деформируется легко. Таким образом, любая конструкция, имеющая в своей структуре треугольники, является более устойчивой конструкцией.

Помните, что с помощью геометрических понятий можно получить прямоугольные треугольники в любом другом треугольнике.

Знание того, как использовать синус, косинус и тангенс, может помочь вам, если вам когда-нибудь понадобится что-то построить или смоделировать и выбрать геометрическую модель треугольника .