| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как доказать \\[\\dfrac{{\\sin x — \\sin 3x + \\sin 5x — \\sin 7x}}{{\\cos x — \\cos 3x
Подсказка: Сначала нам нужно вспомнить основные правила тригонометрии, в основном формулу суммы тождеств произведения.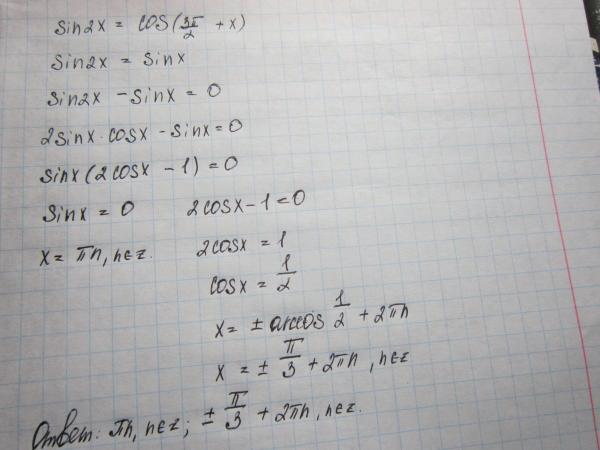
К ним относятся формулы для \[\sin x + \sin y\], \[\sin x — \sin y\], \[\cos x + \cos y\], \[\cos x — \cos y\ ]. Применяя эти формулы, мы можем легко решить этот вопрос.
Полное пошаговое решение:
Чтобы доказать: \[\dfrac{{\sin x — \sin 3x + \sin 5x — \sin 7x}}{{\cos x — \cos 3x — \ cos 5x + \cos 7x}} = \cot 2x\]
Доказательство:
Во-первых, нам нужно взять здесь LHS и RHS:
LHS\[ = \dfrac{{\sin x — \sin 3x + \sin 5x — \sin 7x}}{{\cos x — \cos 3x — \cos 5x + \cos 7x}}\]
RHS\[ = \cot 2x\]
Сначала попробуем решить LHS. В LHS мы также попытаемся сначала решить числитель. Числитель:
\[\Стрелка вправо \sin x — \sin 3x + \sin 5x — \sin 7x\]
Сначала попробуем составить группы. Сгруппируем два первых и два последних члена, и получим:
\[ \Rightarrow (\sin x — \sin 3x) + (\sin 5x — \sin 7x)\]
Теперь воспользуемся тригонометрической формулой:
\[\sin a — \sin b = 2\cos \dfrac{{a + b}}{2}\sin \dfrac{{a — b}}{2} \]
Теперь подставим значения по формуле и получим:
\[ \Стрелка вправо (\sin x — \sin 3x) + (\sin 5x — \sin 7x) = \left( {2\ cos \dfrac{{x + 3x}}{2}\sin \dfrac{{x — 3x}}{2}} \right) + \left( {2\cos \dfrac{{5x + 7x}}{2 }\sin \dfrac{{5x — 7x}}{2}} \right)\]
Теперь упростим и получим:
\[ \Rightarrow \left( {2\cos \dfrac{{4x }}{2}\sin \dfrac{{ — 2x}}{2}} \right) + \left( {2\cos \dfrac{{12x}}{2}\sin \dfrac{{ — 2x}} {2}} \справа)\]
Теперь сократим сходные и делимые члены, и получим:
\[ \Стрелка вправо \left( {2\cos (2x)\sin ( — x)} \right) + \left( { 2\cos (6x)\sin ( — x)} \right)\]
Раскрывая скобки, получаем:
\[\Стрелка вправо 2\cos (2x)\sin ( — x) + 2\cos ( 6x)\sin ( — x)\]
Теперь попробуем убрать знак минус и получим:
\[ \Стрелка вправо — 2\cos (2x)\sin (x) — 2\cos (6x) \sin (x)\]
Теперь мы удалим общий термин \[ — 2\sin x\], и мы получим:
\[\Стрелка вправо — 2\sin x(\cos (2x) + \cos (6x))\]
Аналогично решим и знаменатель.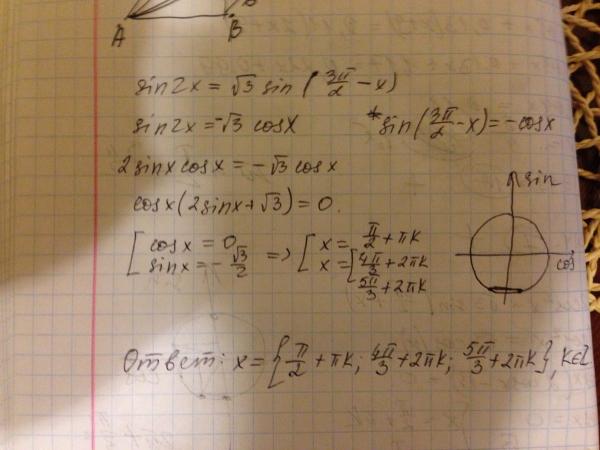
Знаменатель:
\[ \Стрелка вправо \cos x — \cos 3x — \cos 5x + \cos 7x\]
Сначала попробуем составить группы. Сгруппируем два первых и два последних члена, и получим:
\[\Стрелка вправо (\cos x — \cos 3x) — (\cos 5x — \cos 7x)\]
Теперь воспользуемся тригонометрическим формула:
\[\Стрелка вправо \cos x — \cos y = — 2\sin \dfrac{{x + y}}{2}\sin \dfrac{{x — y}}{2}\]
Теперь подставим значения по формуле и получим:
\[ \Стрелка вправо (\cos x — \cos 3x) — (\cos 5x — \cos 7x) = \left( { — 2\sin \dfrac{{x + 3x}}{2}\sin \dfrac{{x — 3x}}{2}} \right) + \left( { — 2\sin \dfrac{{5x + 7x}}{2 }\sin \dfrac{{5x — 7x}}{2}} \right)\]
Теперь упростим и получим:
\[\Rightarrow \left( { — 2\sin \dfrac{{ 4x}}{2}\sin \dfrac{{ — 2x}}{2}} \right) + \left( { — 2\sin \dfrac{{12x}}{2}\sin \dfrac{{ — 2x }}{2}} \right)\]
Теперь сократим сходные и делимые члены, и получим:
\[ \стрелка вправо \влево( { — 2\sin (2x)\sin ( — x)} \right) + \left( { — 2\sin (6x)\sin ( — x)} \right)\]
Когда мы раскрываем скобки, мы получаем:
\[\Стрелка вправо — 2\sin (2x)\sin ( — x) — 2\sin (6x)\sin ( — x)\]
Теперь попробуем убираем знак минус и получаем:
\[ \Стрелка вправо 2\sin (2x)\sin (x) + 2\sin (6x)\sin (x)\]
Теперь уберем общий термин \ [2\sin x\], и мы получаем:
\[\Rightarrow 2\sin x(\sin (2x) + \sin (6x))\]
Теперь, когда мы перепишем нашу LHS, мы получим:
LHS\[ \Rightarrow \dfrac{{\sin x — \sin 3x + \sin 5x — \sin 7x}}{{\cos x — \cos 3x — \cos 5x + \cos 7x}} = \dfrac{ { — 2\sin x(\cos (2x) + \cos (6x))}}{{2\sin x(\sin (2x) + \sin (6x))}}}\]
Теперь мы можем отменить аналогичные члены, и мы получаем:
\[ \Rightarrow \dfrac{{\sin x — \sin 3x + \sin 5x — \sin 7x}}{{\cos x — \cos 3x — \cos 5x + \cos 7x}} = \dfrac{{ — (\cos (2x) + \cos (6x))}}{{(\sin (2x) + \sin (6x))}}\]
Теперь воспользуемся тригонометрические формулы:
\[\cos a + \cos b = 2\cos \dfrac{{x + y}}{2}\cos \dfrac{{x — y}}{2}\]
\[\sin a — \sin b = 2\cos \dfrac{{x + y}}{2}\sin \dfrac{{x — y}}{2}\]
Теперь подставим значения по формуле, и получаем:
\[\Rightarrow \dfrac{{ — (\cos (2x) + \cos (6x))}}{{(\sin (2x) + \sin (6x))} } = \dfrac{{ — \left( {2\cos \dfrac{{2x + 6x}}{2}\cos \dfrac{{2x — 6x}}{2}} \right)}}{{\left ( {2\cos \dfrac{{2x + 6x}}{2}\sin \dfrac{{2x — 6x}}{2}} \right)}}\]
\[\Стрелка вправо \dfrac{{ — \ влево( {2\cos (4x)\cos ( — 2x)} \right)}}{{\left( {2\cos (4x)\sin ( — 2x)} \right)}}\]
Теперь аналогичные члены сокращаются, и мы получаем:
\[\Rightarrow \dfrac{{ — \left( {2\cos ( — 2x)} \right)}}{{\left( {2\sin ( — 2x)} \right)}}\]
\[\Rightarrow \dfrac{{ — \left( {\cos ( — 2x)} \right)}}{{\left( {\sin ( — 2x) } \right)}}\]
Мы знаем, что \[\cos ( — \theta ) = \cos \theta \].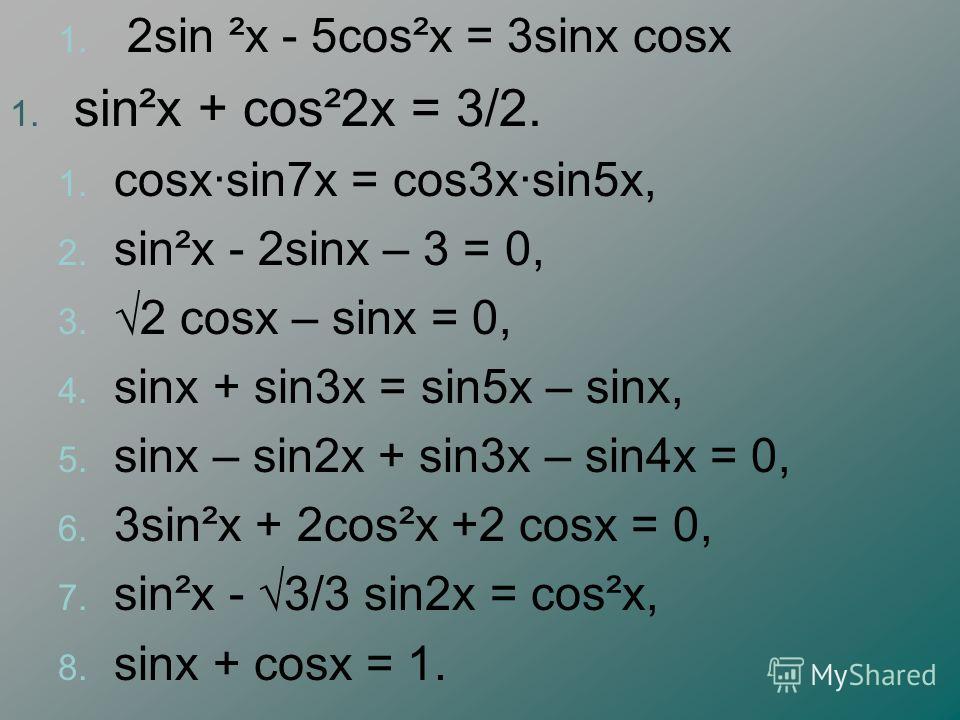
Итак, получаем:
\[ \Rightarrow \dfrac{{ — \cos 2x}}{{ — \sin 2x}}\]
\[ \Rightarrow \cot 2x\]
LHS\[ = \cot 2x\]
Следовательно, LHS=RHS (следовательно, доказано). Следовательно, \[\dfrac{{\sin x — \sin 3x + \sin 5x — \sin 7x}}{{\cos x — \cos 3x — \cos 5x + \cos 7x}} = \cot 2x\] доказано.
Примечание: При решении нам нужно проверять как левую, так и правую стороны. В этом вопросе, когда мы решали наш LHS, мы должны были проверить, в каких терминах присутствует наша RHS, а затем в соответствии с этим нам нужно изменить наш LHS, чтобы доказать вопрос. Здесь, в вопросе, который мы использовали, у нас есть несколько тригонометрических формул для решения задачи, например \[\sin a — \sin b = 2\cos \dfrac{{a + b}}{2}\sin \dfrac{{a — b}}{2}\] , \[\Стрелка вправо \cos x — \cos y = — 2\sin \dfrac{{x + y}}{2}\sin \dfrac{{x — y}}{2 }\].
Найти lim x → 0 sin5x-sin3x/x с помощью тригонометрических тождеств
- Математические сомнения
- Проблемы
- Пределы
- Тригонометрические функции
Сначала проверим процесс нахождения предела отношения синуса пятикратного $x$ минус синус трехкратного $x$ на $x$ при стремлении значения $x$ к нулю прямой подстановкой метод.
$\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{5x}-\sin{3x}}{x}}$ $\,=\,$ $ \dfrac{0}{0}$
В соответствии с методом прямой подстановки вычислено, что предел является неопределенным для синуса пятикратного $x$ минус синус угла трехкратного $x$, деленного на $x$, поскольку значение $x$ ближе к нуль.
Он показывает, что вычисление предела для данной тригонометрической функции в рациональной функции не рекомендуется, и указывает нам на альтернативный метод.
Преобразование разности в форму произведения
Различие функций синуса в числителе и выражения в знаменателе является основной причиной получения предела данной тригонометрической рациональной функции как неопределенной.
Разность синусоидальных функций может быть преобразована в форму произведения тригонометрических функций в соответствии с разницей в произведение тригонометрической идентичности синусоидальных функций.
$ = \, \, \, $ $ \ displaystyle \ large \ lim_ {x \, \ to \, 0} {\ normalsize \ dfrac {2 \ cos {\ bigg (\ dfrac {5x + 3x} {2 }\bigg)}\sin{\bigg(\dfrac{5x-3x}{2}\bigg)}}{x}}$
Выражение в знаменателе является переменной.
Так что никаких действий по этому поводу предпринимать не нужно.
Упрощение тригонометрической функции
Пришло время упростить математическое выражение, и это поможет нам математически найти предел.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{2\cos{\bigg(\dfrac{8x}{2}\ bigg)}\sin{\bigg(\dfrac{2x}{2}\bigg)}}{x}}$
$=\,\,\,$ $\displaystyle \large \lim_{x\,\ to\,0}{\normalsize \dfrac{2\cos{\bigg(\dfrac{\cancel{8}x}{\cancel{2}}\bigg)}\sin{\bigg(\dfrac{\cancel {2}x}{\cancel{2}}\bigg)}}{x}}$
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0} {\ normalsize \ dfrac {2 \ cos {(4x)} \ sin {(x)}} {x}} $
Найдите пределы функций
В числителе есть синусоидальная функция, а в знаменателе есть угол внутри синусоидальной функции. Они указывают нам отделить их от рациональной функции. Разделение играет жизненно важную роль в нахождении предела данной тригонометрической рациональной функции.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{2\cos{(4x)} \times \sin{(x) }}{x}}$
Теперь рациональную функцию можно разделить как произведение двух функций по правилу умножения дробей.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \bigg(2\cos{(4x)} \times \dfrac{\sin{ (x)}}{x}\bigg)}$
Используйте правило произведения пределов, чтобы найти предел произведения двух функций на произведение их пределов.
$=\,\,\,$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize 2\cos{(4x)}}$ $\times$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{(x)}}{x}}$
$=\,\,\,$ $\displaystyle \large \lim_{ х\,\к\,0}{\normalsize 2\cos{(4x)}}$ $\times$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\ sin{x}}{x}}$
Математическое выражение состоит из двух факторов. Каждый фактор выражает предел функции. Итак, давайте найдем предел каждой функции по очереди. Во-первых, найдем предел функции на месте первого множителя, а это можно сделать прямой подстановкой.
$=\,\,\,$ $2\cos{\big(4(0)\big)}$ $\times$ $\displaystyle \large \lim_{x\,\to\,0}{\ normalsize \dfrac{\sin{x}}{x}}$
$=\,\,\,$ $2\cos{(4 \times 0)}$ $\times$ $\displaystyle \large \lim_{ х\,\к\,0}{\normalsize \dfrac{\sin{x}}{x}}$
$=\,\,\,$ $2\cos{(0)}$ $\times$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{ x}}{x}}$
$=\,\,\,$ $2\cos{0}$ $\times$ $\displaystyle \large \lim_{x\,\to\,0}{\normalsize \dfrac{\sin{x}}{x}}$
$=\,\,\,$ $2 \times \cos{0}$ $\times$ $\displaystyle \large \lim_{x\,\ to\,0}{\normalsize \dfrac{\sin{x}}{x}}$
Согласно тригонометрии косинус нуля равен единице.