3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
Пусть 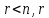 переменных
переменных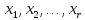 называются основными (или базисными),
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальные
называются основными (или базисными),
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальные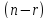 переменных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний
переменных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний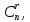 то
и базисных решений имеется не более
то
и базисных решений имеется не более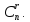
Совместная
система  линейных уравнений с
линейных уравнений с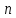 переменными
переменными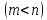 имеет
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее
имеет
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее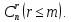
Достоинства метода Гаусса по сравнению с другими:
— менее трудоемкий метод;
— позволяет однозначно установить, совместна система или нет и в случае совместности найти ее решение;
— дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
Составим расширенную матрицу по данной системе
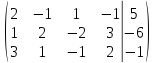
поменяем местами первую и вторую строку
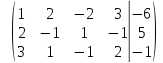
умножим
первую строку на 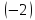 и сложим со второй строкой; умножим
первую строку на
и сложим со второй строкой; умножим
первую строку на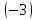 и сложим с третьей строкой
и сложим с третьей строкой
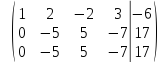
умножим
вторую строку на 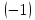 и сложим с третьей строкой
и сложим с третьей строкой
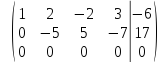
последняя строка вычеркивается, так как все ее элементы равны нулю
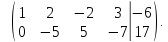
Ранг
основной матрицы 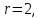 ранг
расширенной матрицы
ранг
расширенной матрицы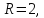 следовательно, система совместна. Число
строк в основной матрице
следовательно, система совместна. Число
строк в основной матрице число
столбцов в основной матрице
число
столбцов в основной матрице следовательно, система имеет множество
решений.
следовательно, система имеет множество
решений.
Выявим базисные переменные
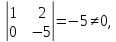
следовательно, 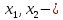 базисные
переменные, тогда
базисные
переменные, тогда
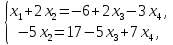
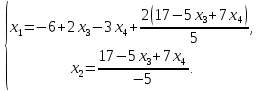
3.4. Однородные системы линейных алгебраических уравнений
Система 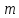 линейных уравнений с
линейных уравнений с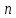 переменными называетсясистемой
линейных однородных уравнений,
если все их свободные члены равны нулю.
переменными называетсясистемой
линейных однородных уравнений,
если все их свободные члены равны нулю.
Системы линейных однородных уравнений:
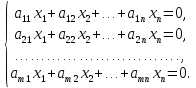
Система
линейных однородных уравнений всегда
совместна, так как имеет, по крайней
мере, нулевое решение 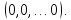
Если
в однородной системе 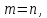 а
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.
а
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.
Система
линейных однородных уравнений имеет
ненулевое решение тогда и только тогда,
когда ранг ее матрицы коэффициентов
при переменных меньше числа переменных,
т.е. при 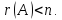
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
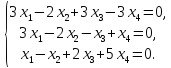
Составим по данной системе расширенную матрицу
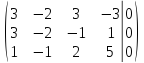
поменяем местами первую и третью строки
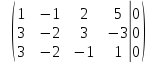
умножим
первую строку на  и сложим со второй строкой, а затем с
третьей строкой, получим
и сложим со второй строкой, а затем с
третьей строкой, получим
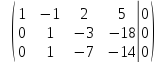
умножим
вторую строку на 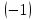 и сложим с третьей строкой
и сложим с третьей строкой
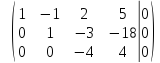
разделим
последнюю строку на 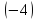
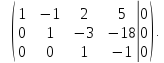
Таким
образом, ранг расширенной матрицы и
ранг основной матрицы равны 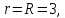 следовательно,
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные
следовательно,
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные
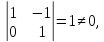
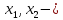 базисные
переменные.
базисные
переменные.
Перейдем
от матрицы к системе, выразим переменные 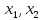 через другие переменные
через другие переменные
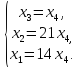
Контрольные вопросы
Сформулировать теорему Кронекера – Капелли.
Сформулировать Метод Гаусса решения систем m линейных уравнений с n неизвестными.
Дать определение базисному решению систем линейных алгебраических уравнений.
Какие системы линейных алгебраических уравнений называют однородными?
Лекция №4. Векторы
4.1. Векторы в науке и технике. Понятие вектора. Координаты вектора.
4.2. Линейные операции над векторами.
4.3. Декартова система координат. Базис векторного пространства.
4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме.
4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме.
4.6. Применение векторного произведения векторов к решению задач.
4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме.
4.8. Применение смешанного произведения векторов к решению задач.
Векторы в науке и технике. Понятие вектора. Координаты вектора
В физике и математике вектор – это величина, которая характеризуется численным значением и направлением. В физике встречается немало важных величин, которые характеризуются направлением. Например, сила, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким как масса, объем, давление, температура, плотность, которые можно описать обычным числом и называются они скалярными величинами.
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, необходимо описать положение предмета, но полностью определить местоположение предмета невозможно, пока не будет известно направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.При изучении и расчете цепей переменного тока удобно пользоваться векторными диаграммами, на которых синусоидальные напряжения и токи условно изображают с помощью векторов. Применение этих диаграмм упрощает изучение и расчет цепей и вносит наглядность в рассматриваемые соотношения.
Вектором
на плоскости называется
направленный отрезок 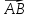 с начальной точкой
с начальной точкой 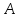
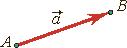

Рис. 1
Вектор на плоскости
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос. При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и тоже расстояние.
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Абсолютной величиной или модулем вектора называется длина отрезка, изображающего вектор. Другими словами длина вектора есть расстояние между началом и концом вектора
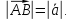
Векторы
называются коллинеарными, если они
расположены на одной или на параллельных
прямых. Нулевой вектор коллинеарен
любому вектору. Если векторы 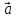 и
и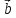 коллинеарны и их лучи сонаправлены, то
векторы
коллинеарны и их лучи сонаправлены, то
векторы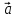 и
и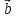 называютсонаправленными.
Обозначают
называютсонаправленными.
Обозначают 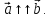 Если векторы
Если векторы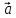 и
и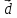 коллинеарны,
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают
коллинеарны,
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают 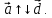 Нулевой вектор условились считать
сонаправленным с любым вектором.
Нулевой вектор условились считать
сонаправленным с любым вектором.

Рис.2
Коллинеарные вектора
Свойство коллинеарных векторов.
Если
векторы 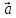 и
и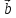 коллинеарны и
коллинеарны и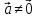 ,
то существует число
,
то существует число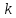 такое,
что
такое,
что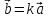 .
Причем, если
.
Причем, если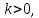 то векторы
то векторы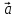 и
и сонаправленные, если
сонаправленные, если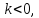 то
противоположно направленные.
то
противоположно направленные.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Признак компланарности трех векторов.
Если
вектор 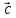 можно разложить по векторам
можно разложить по векторам и
и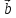 ,
т.е. представить в виде
,
т.е. представить в виде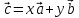 ,
где
,
где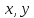 -некоторые
числа, то векторы
-некоторые
числа, то векторы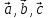 -компланарны.
-компланарны.
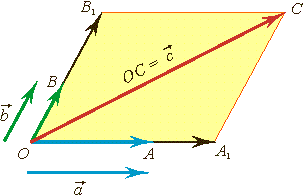
Рис.3
Компланарные вектора
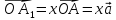 ,
где
,
где 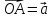 ;
;
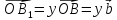 ,
где
,
где 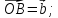
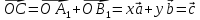 ,
где
,
где 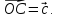
Произвольные системы m линейных уравнений с n неизвестными. Понятие общего, частного и базисного решений системы уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
,
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение. Для системы линейных уравнений матрица
А = называется матрицей системы, а матрица
А*= называется расширенной матрицей системы
Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.
Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:
Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.
Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.
- Базисное решение (вектор) называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
- Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.
32.Метод Жордана-Гаусса.
Переход от одного базисного решения к другому. ( не нашел, к сожалению)
Понятия опорного и допустимого решений систем линейных уравнений.
Решение системы m-линейных уравнений с n-неизвестными, в которых значения всех переменных неотрицательны называются допустимыми решениями, а совокупность всех допустимых значений областью допустимых решений. Базисные допустимые решения называются опорными решениями, число которых решений меньше числа базисных.
35.Симплексные преобразования. Теорема о симплексных преобразованиях.
Переход от одного опорного решения к другому.
Общая задача оптимизации.
Типы задач математического программирования: линейное программирование, нелинейное программирование, динамическое программирование.
Оптимизационные задачи, в которых приходится учитывать последовательность действий или фактор времени, рассматриваются в разделе динамического программирования. В отличие от предыдущих задач математического программирования задачи динамического программирования являются многоэтапными или многошаговыми.
§2.3. Системы линейных уравнений.
Общий вид СЛУ задается системой:
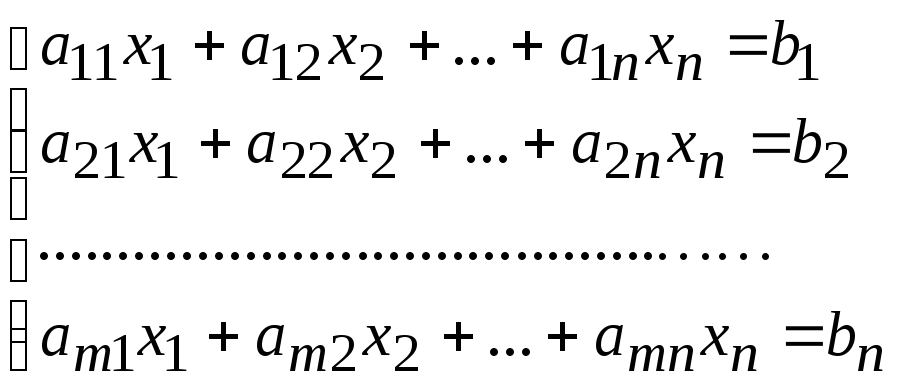 (*)
(*)
Набор чисел  такой, который при подстановке вместо
такой, который при подстановке вместо ,
каждое из уравнений системы обращает
в тождество, называется еечастным
решением.
Найти общее
решение СЛУ, значит указать метод, позволяющий
получить все частные ее решения. СЛУ
называется совместной,
если она имеет хотя бы одно частное
решение, и несовместной–
иначе.
,
каждое из уравнений системы обращает
в тождество, называется еечастным
решением.
Найти общее
решение СЛУ, значит указать метод, позволяющий
получить все частные ее решения. СЛУ
называется совместной,
если она имеет хотя бы одно частное
решение, и несовместной–
иначе.
Классической является следующая
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ. Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной.
ДОКАЗАТЕЛЬСТВО.
Пусть СЛУ (*) имеет частное решение 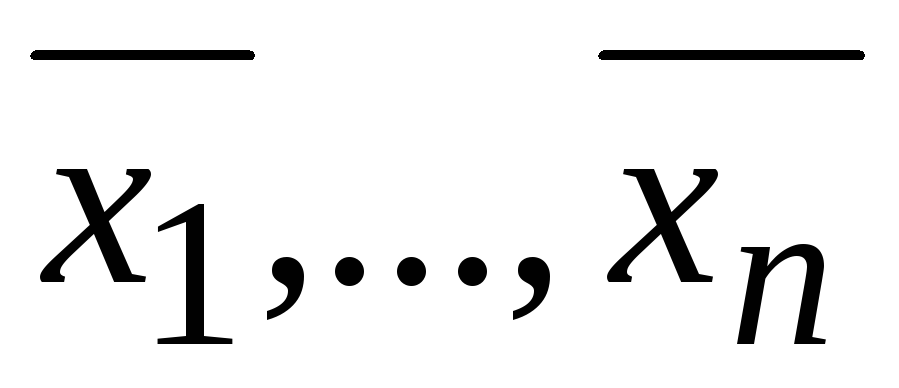 .
Видно, что столбец из свободных членов
СЛУ является линейной комбинацией
столбцов ее основной матрицы. Поэтому
ранг основной матрицы равен рангу
расширенной.
.
Видно, что столбец из свободных членов
СЛУ является линейной комбинацией
столбцов ее основной матрицы. Поэтому
ранг основной матрицы равен рангу
расширенной.
Обратно, пусть
ранг основной матрицы СЛУ равен рангу
расширенной. С точностью до перестановки
уравнений и переименования неизвестных
можно считать, что минор наивысшего
порядка r находится на пересечении первых r строк и
столбцов основной матрицы. Следовательно,
существуют такие числа 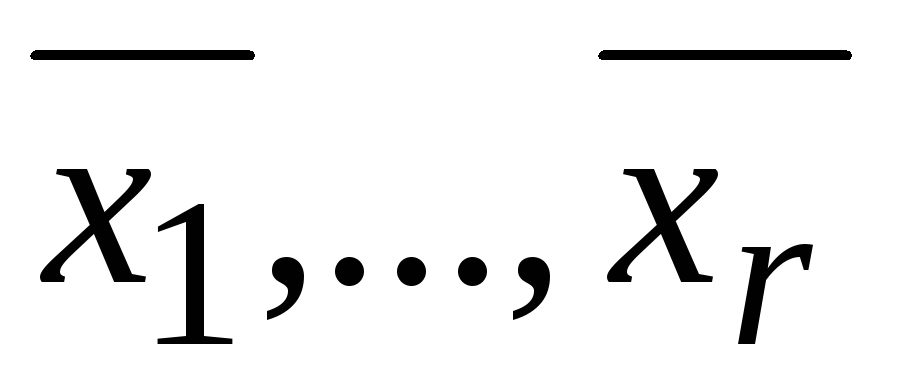 ,
что столбец из свободных членов равен
линейной комбинации первых
,
что столбец из свободных членов равен
линейной комбинации первых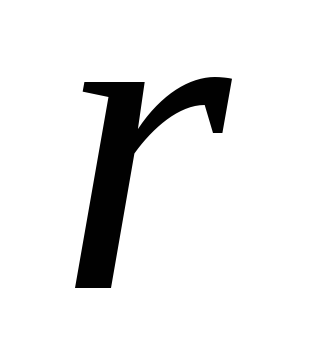 столбцов основной матрицы. Полагая
столбцов основной матрицы. Полагая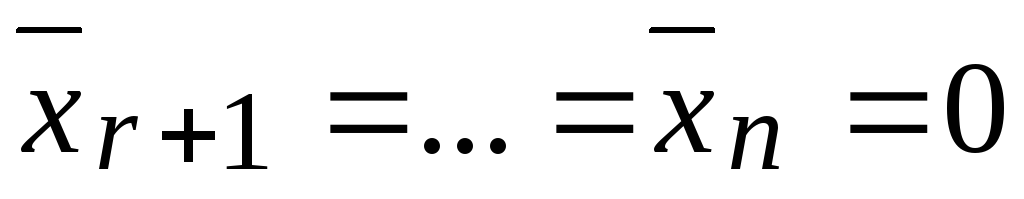 ,
видно, что
,
видно, что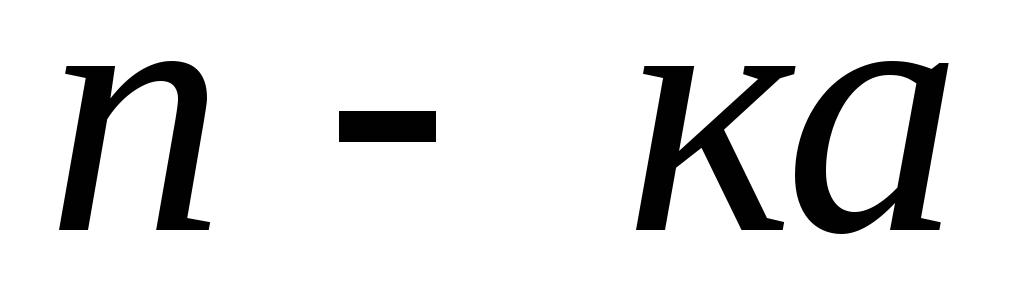 (
(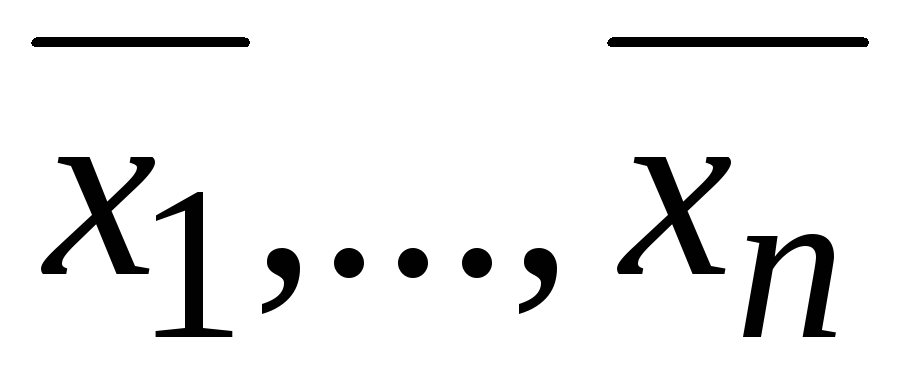 )
является решением
СЛУ
(*). □
)
является решением
СЛУ
(*). □
Две СЛУ от одного и того же числа неизвестных называются равносильными, если они обе не совместны, либо множества их частных решений равны. Нетрудно показать, что полученная СЛУ равносильна исходной, если
из СЛУ вычеркнуть уравнение вида
 ;
;обе части какого-то уравнения СЛУ умножить на число, отличное от нуля;
прибавить к одному из уравнений другое, умноженное на некоторое число.
Изложим один метод
решения СЛУ (*), называемый методом
последовательного исключения переменных
(или методом Гаусса). Будем считать, что 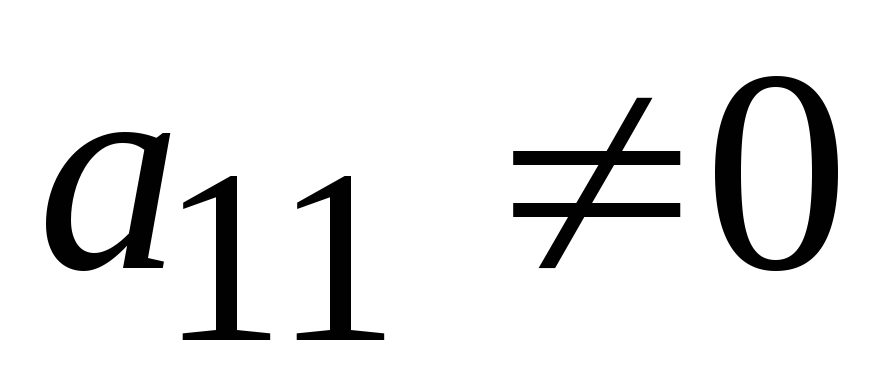 (этого можно всегда добиться с помощью
перестановок строк). Попытаемся теперь,
умножая первое уравнение на подходящие
числа и прибавляя его к последующим,
уничтожить в них слагаемые, содержащие
(этого можно всегда добиться с помощью
перестановок строк). Попытаемся теперь,
умножая первое уравнение на подходящие
числа и прибавляя его к последующим,
уничтожить в них слагаемые, содержащие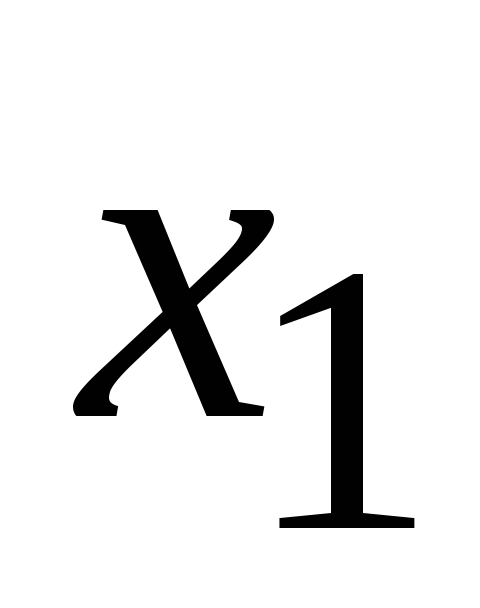 .
Для этого, умножаем первое уравнение
на
.
Для этого, умножаем первое уравнение
на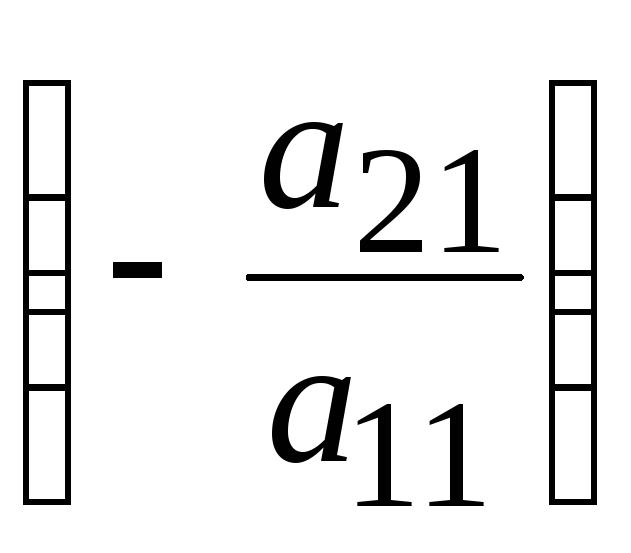 и прибавляем ко второму, и так далее,
пока не умножим первое уравнение на
и прибавляем ко второму, и так далее,
пока не умножим первое уравнение на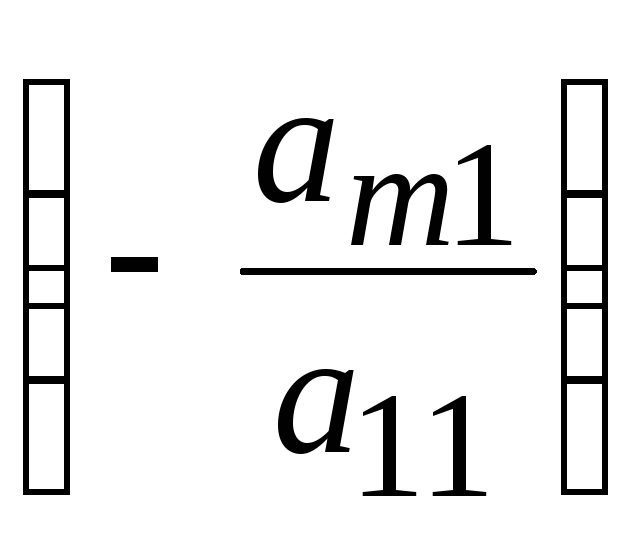 и не прибавим к последнему. Получим
равносильную СЛУ вида
и не прибавим к последнему. Получим
равносильную СЛУ вида

Полагаем, что  (этого
можно добиться, переставляя строки или
переименовывая переменные). Затем
временно «забываем» про первое уравнение
и продолжаем такую процедуру с
оставшимися. Если в результате этой
процедуры возникнет уравнение вида
(этого
можно добиться, переставляя строки или
переименовывая переменные). Затем
временно «забываем» про первое уравнение
и продолжаем такую процедуру с
оставшимися. Если в результате этой
процедуры возникнет уравнение вида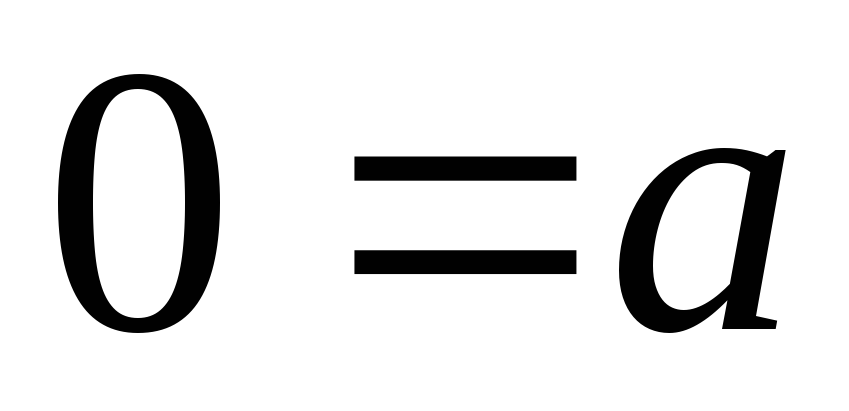 и
и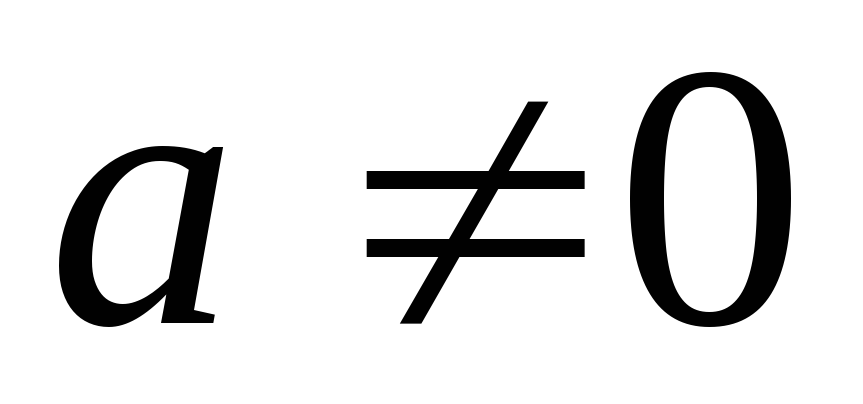 ,
то система несовместна, если же одно
из уравнений окажется вида
,
то система несовместна, если же одно
из уравнений окажется вида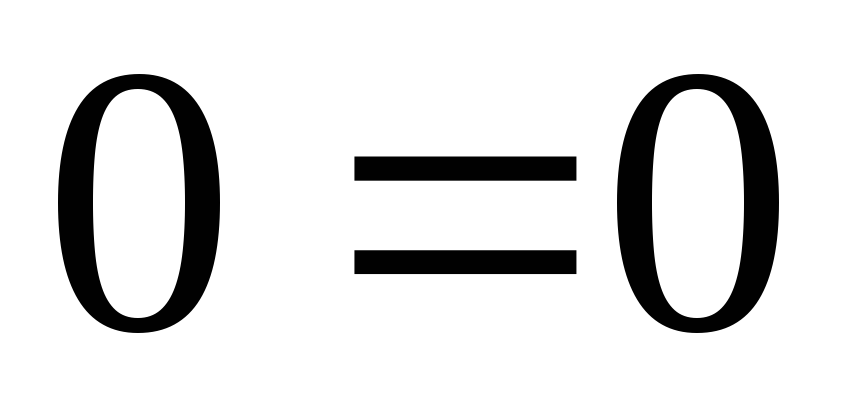 ,
то это уравнение можно опустить. В
результата придем к ступенчатой СЛУ,
которая имеет вид
,
то это уравнение можно опустить. В
результата придем к ступенчатой СЛУ,
которая имеет вид

Эта часть метода
Гаусса часто носит название «прямого
хода». Заметим, что число 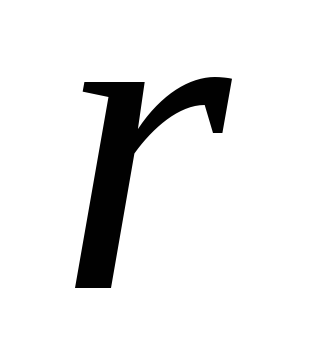 является рангом основной матрицы СЛУ
и он равен рангу расширенной. Теперь
для нахождения общего решения СЛУ (*)
воспользуемся «обратным ходом». Для
этого из последнего уравнения системы
выразим
является рангом основной матрицы СЛУ
и он равен рангу расширенной. Теперь
для нахождения общего решения СЛУ (*)
воспользуемся «обратным ходом». Для
этого из последнего уравнения системы
выразим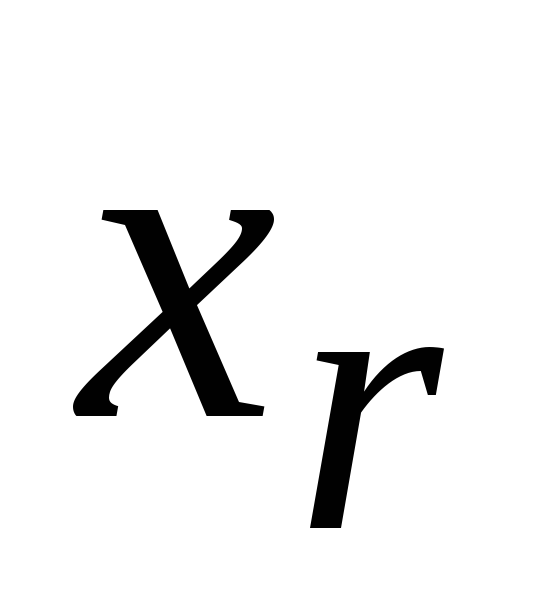 через
через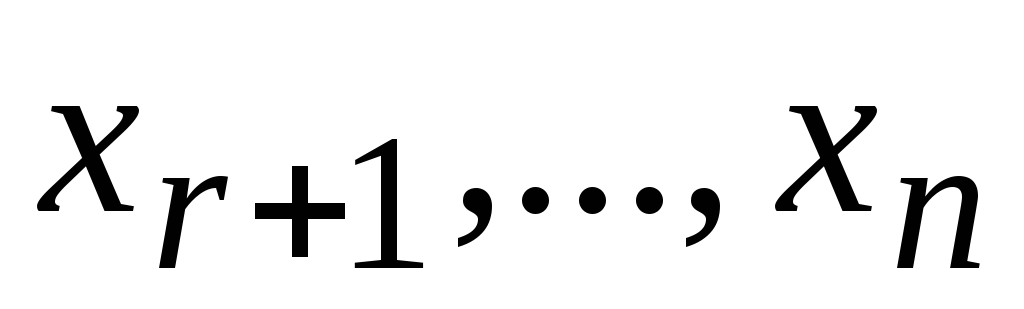 .
Зная это выражение из предпоследнего
уравнения можно выразить
.
Зная это выражение из предпоследнего
уравнения можно выразить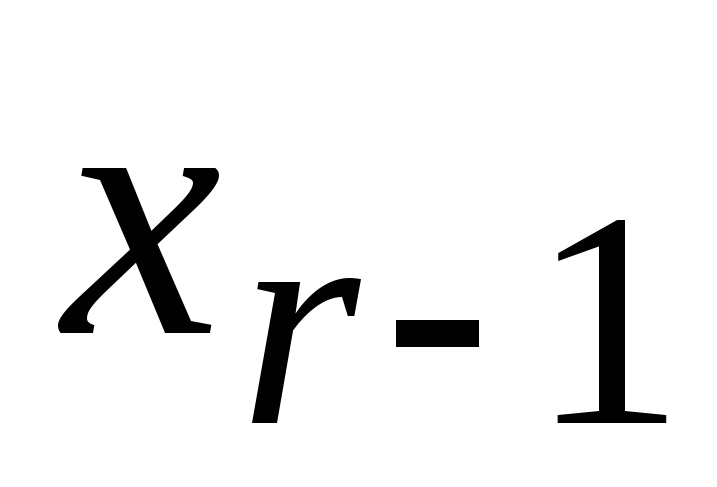 также через
также через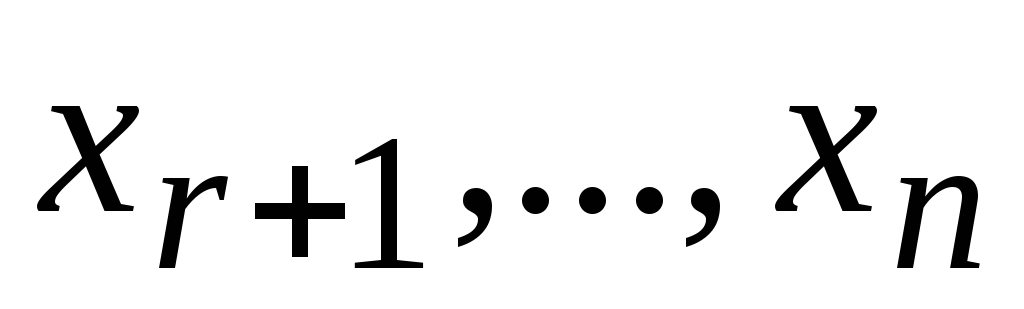 ,
и так далее. Наконец получим систему
,
и так далее. Наконец получим систему
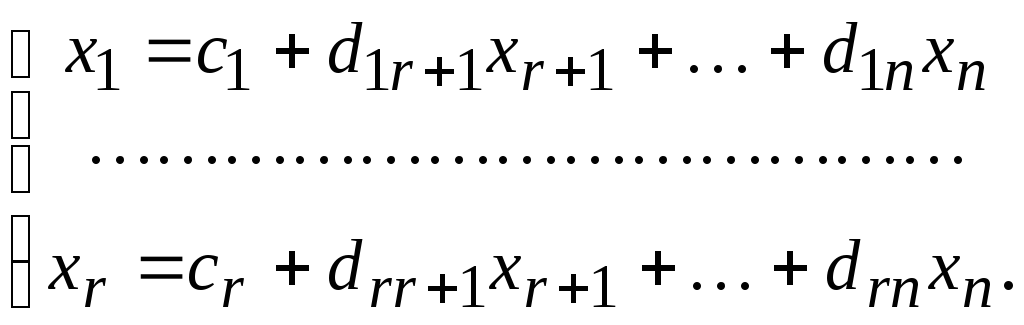
Она равносильна
исходной и называется общим
решением СЛУ (*). Теперь подставляя вместо
неизвестных произвольные значения 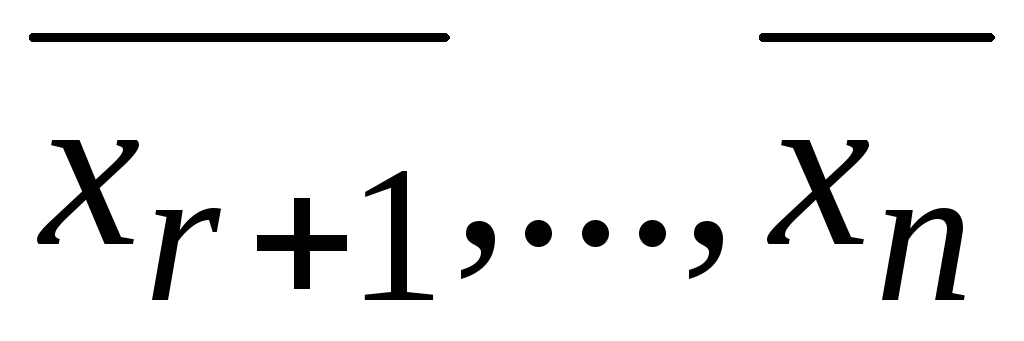 и вычисляя
и вычисляя можно получить все частные решения (
можно получить все частные решения (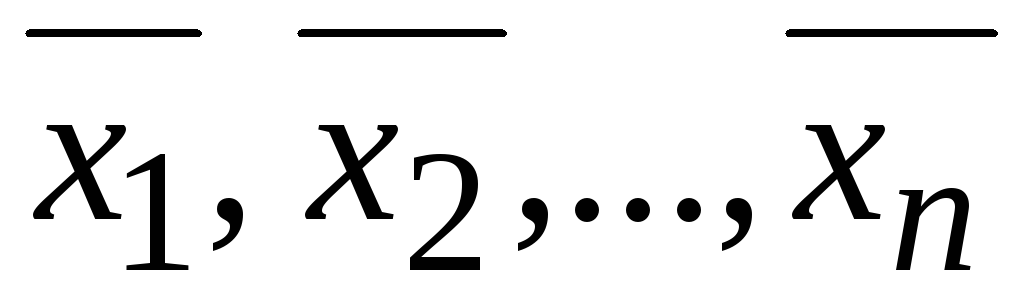 )
СЛУ (*).
)
СЛУ (*).
Пример 3. Решить систему уравнений
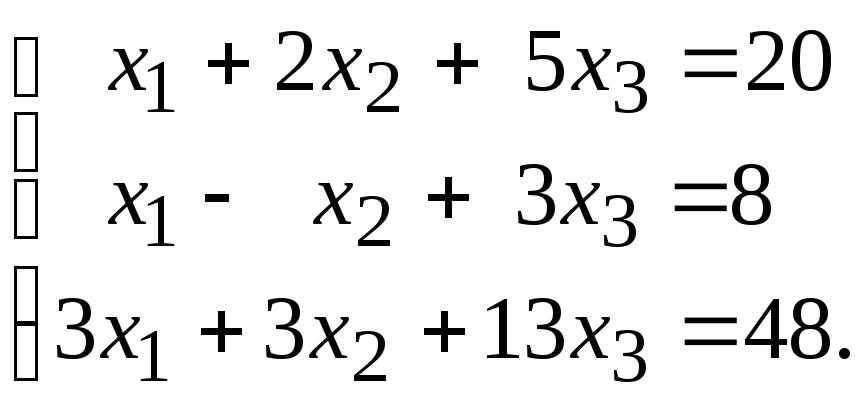
Решение. Подвергнем преобразованиям расширенную матрицу этой системы:
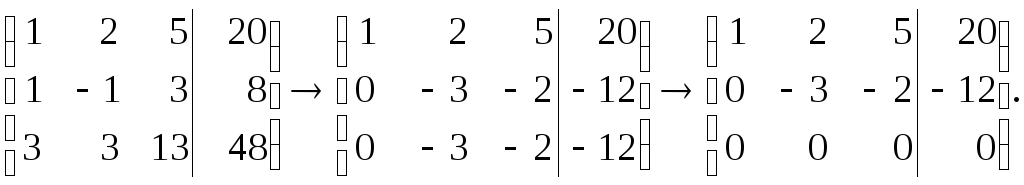
Ранг основной матрицы системы равен рангу расширенной матрицы и равен двум. Приходим, следовательно, к системе уравнений, равносильной исходной
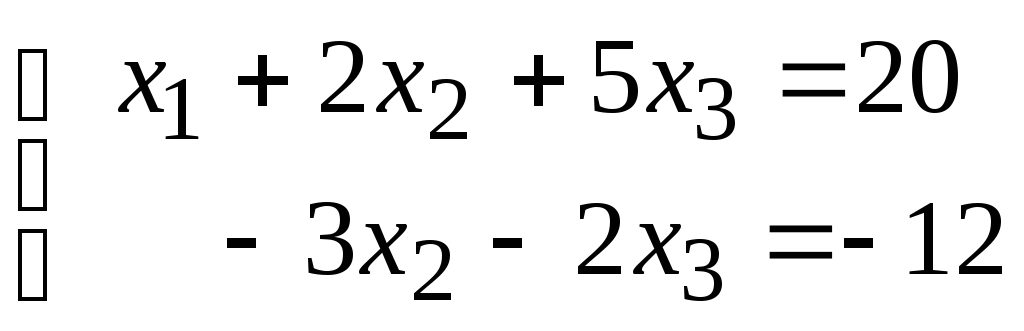 ,
,
в которой одна
переменная является независимой. В
качестве независимой переменной возьмём  ,
и выразим через неё остальные, получим:
,
и выразим через неё остальные, получим:
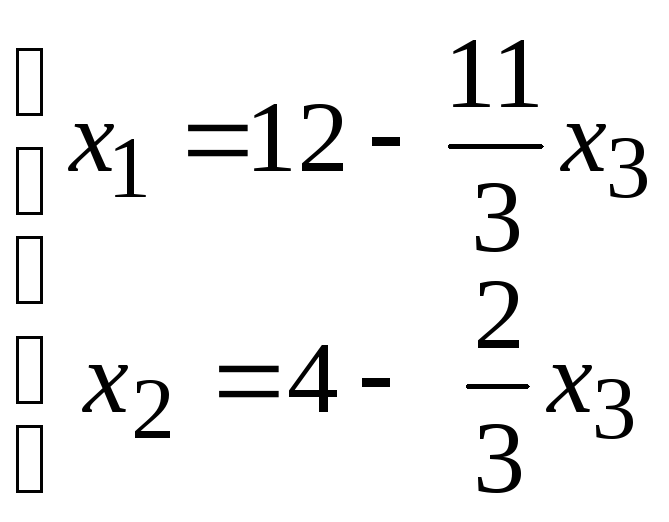 .
.
Полагая, например, 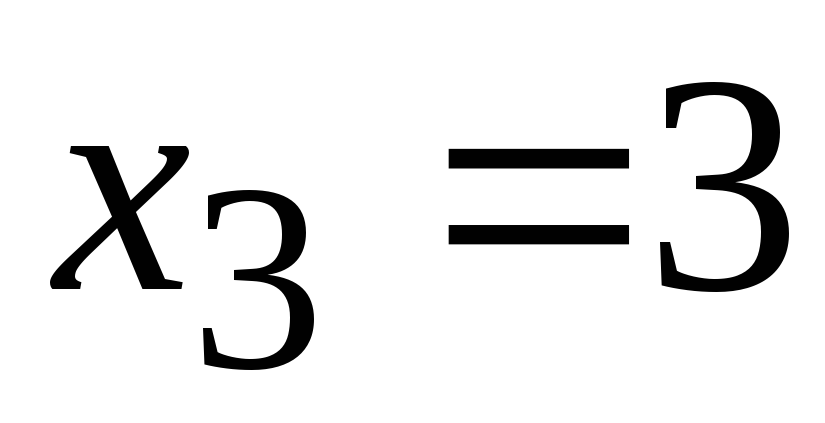 ,
получим одно из частных решений системы:
,
получим одно из частных решений системы:
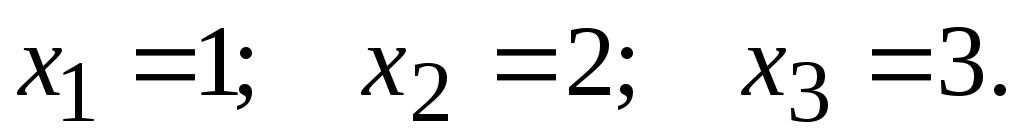
Если все свободные
члены СЛУ 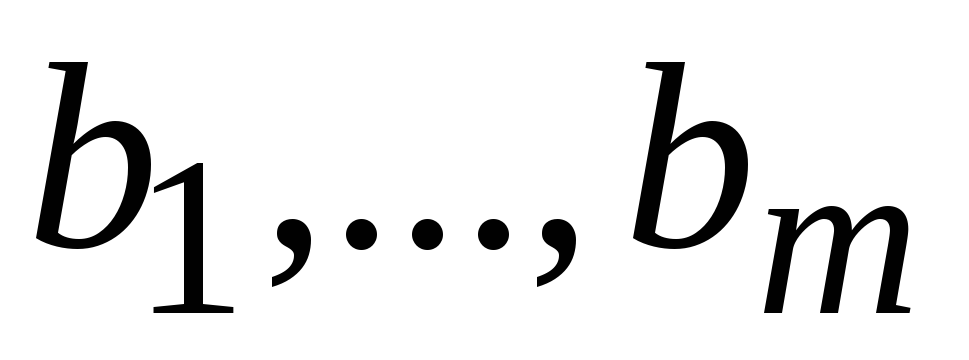 равны
равны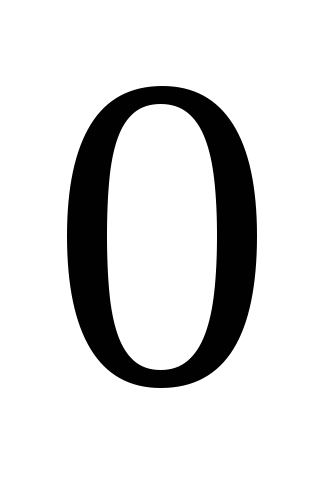 ,
то СЛУ называется системой линейных однородных уравнений (СЛОУ). СЛОУ
всегда имеет тривиальное (нулевое)
решение
,
то СЛУ называется системой линейных однородных уравнений (СЛОУ). СЛОУ
всегда имеет тривиальное (нулевое)
решение 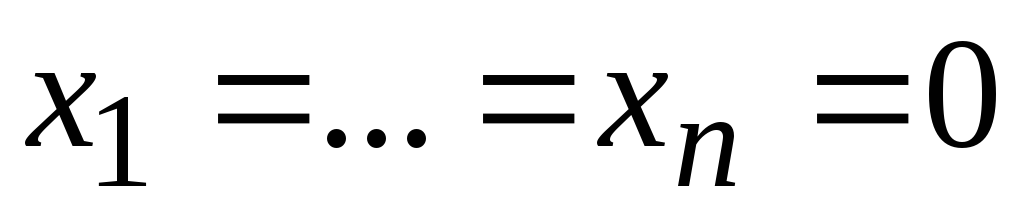 .
Несложно проверить истинность следующих
утверждений:
.
Несложно проверить истинность следующих
утверждений:
сумма двух частных решений СЛОУ также является ее частным решением;
если число умножить на частное решение СЛОУ, то получится также ее частное решение.
В частности, если
СЛОУ зависит от n неизвестных, то множество всех частных
решений ее образует подпространство
в пространстве 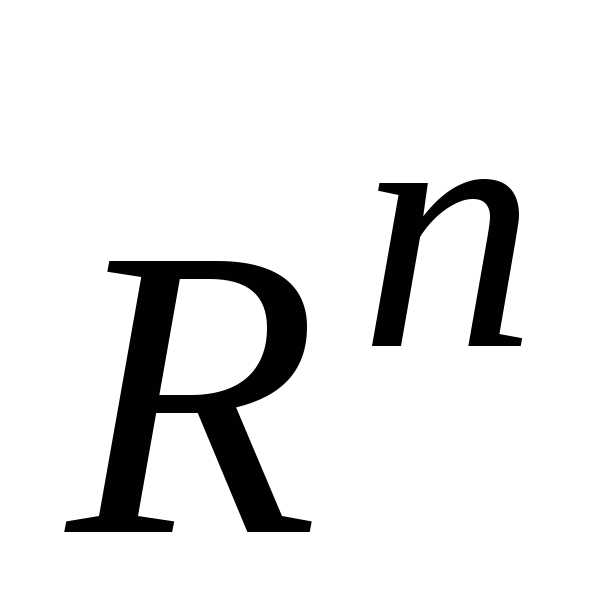 .
Базис этого подпространства называетсяфундаментальной
системой решений СЛОУ.
.
Базис этого подпространства называетсяфундаментальной
системой решений СЛОУ.
ТЕОРЕМА (о СЛОУ). Фундаментальная
система решений СЛОУ состоит из  некоторых ее частных решений, где
некоторых ее частных решений, где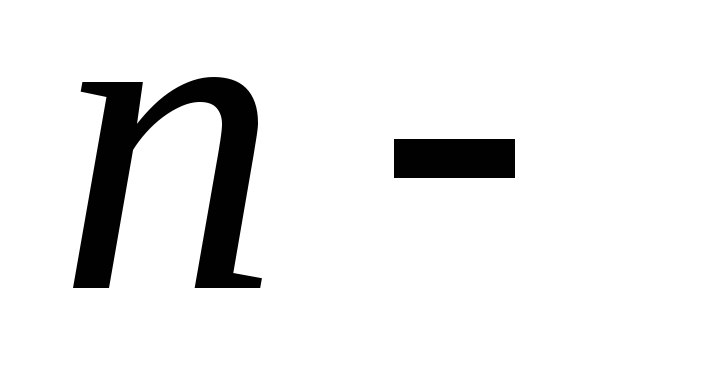 число неизвестных СЛОУ, а
число неизвестных СЛОУ, а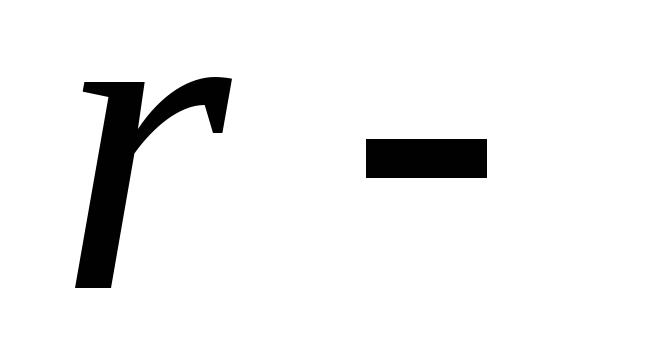 ранг ее основной матрицы.
ранг ее основной матрицы.
ДОКАЗАТЕЛЬСТВО. Рассмотрим
СЛОУ (*), считая, что  .
Найдем ее общее решение, которое будет
иметь вид
.
Найдем ее общее решение, которое будет
иметь вид


Далее свободным
неизвестным 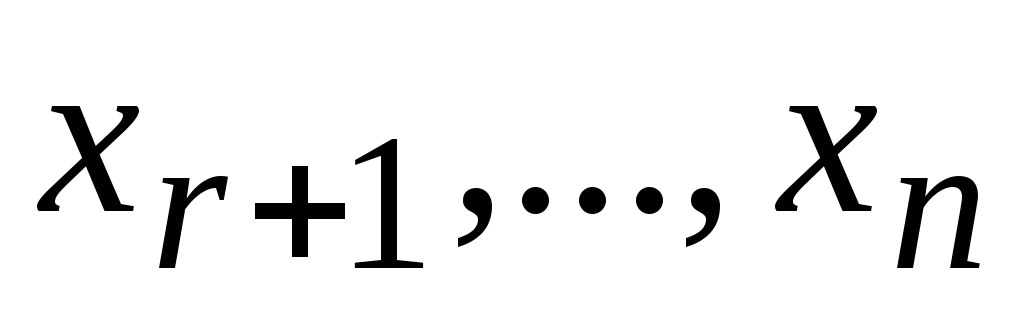 будем приписывать последовательно,
а всем остальным
будем приписывать последовательно,
а всем остальным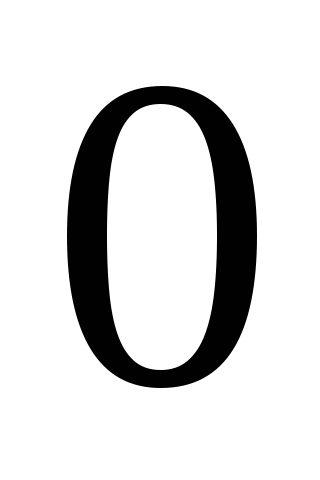 .
Получим
.
Получим  частных решений, которые сведем в
следующую таблицу
частных решений, которые сведем в
следующую таблицу
Покажем, что
векторы 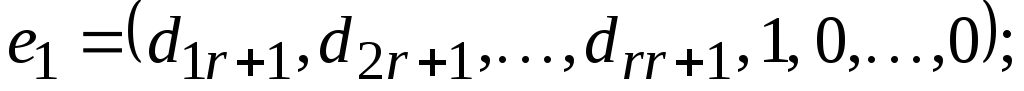


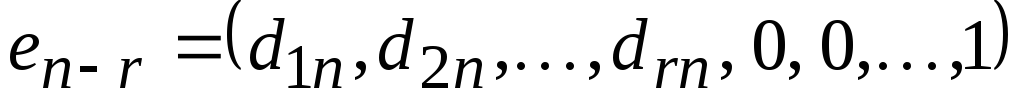
образуют фундаментальную систему СЛОУ (*).
Минор, стоящий на
пересечении всех ее решений и последних
их  столбцов не равен
столбцов не равен 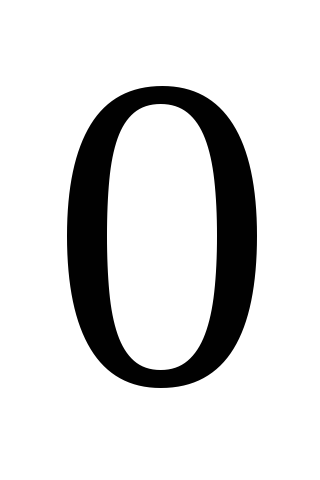 .
Значит, решения линейно независимы.
Пусть теперь
.
Значит, решения линейно независимы.
Пусть теперь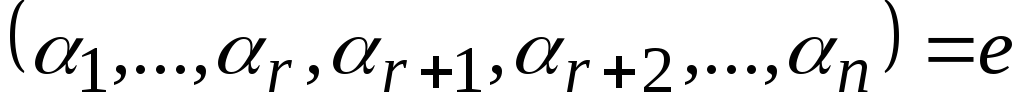 какое-то ее частное решение. Докажем,
что вектор
какое-то ее частное решение. Докажем,
что вектор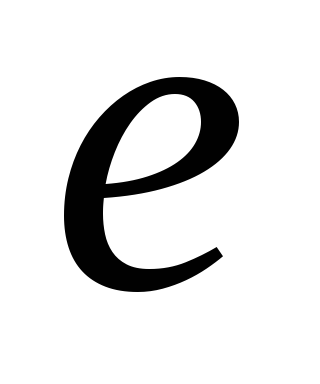 линейно выражается через векторы
линейно выражается через векторы .
Рассмотрим линейную комбинацию
.
Рассмотрим линейную комбинацию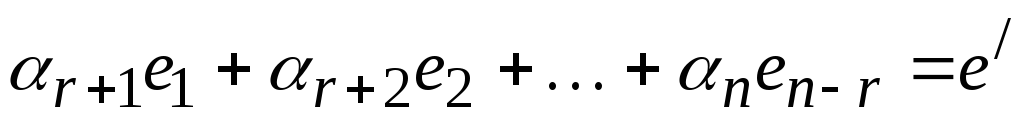 ,
вектор
,
вектор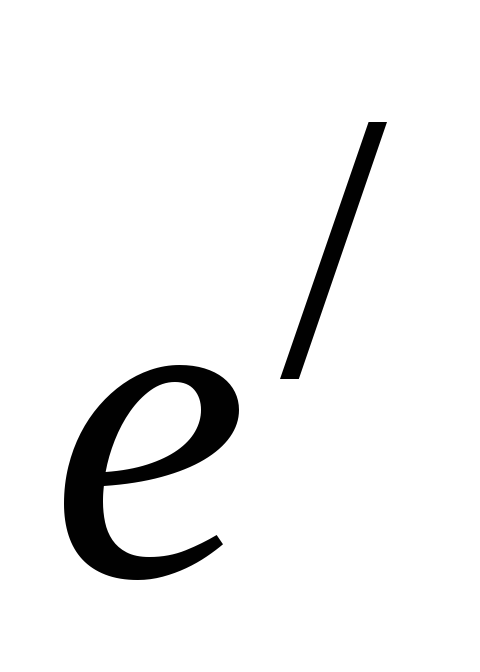 тоже является решением СЛОУ. Имеем,
тоже является решением СЛОУ. Имеем,
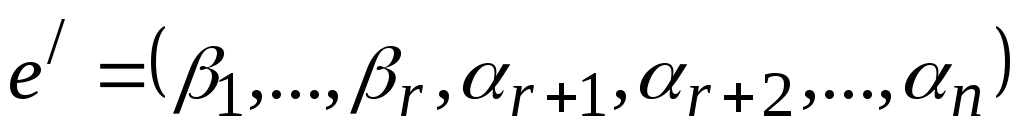 .
Но
.
Но и
и однозначно определяются в общем решении
через значения
однозначно определяются в общем решении
через значения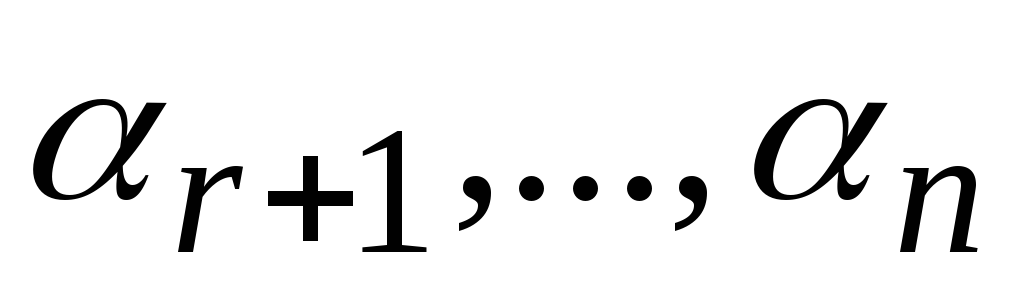 ,
придаваемых свободным неизвестным.
Поэтому
,
придаваемых свободным неизвестным.
Поэтому .
Таким образом, векторы
.
Таким образом, векторы являются и системой порождающих
подпространства решений СЛОУ, т.е. ее
базисом. □
являются и системой порождающих
подпространства решений СЛОУ, т.е. ее
базисом. □
СЛЕДСТВИЕ. СЛОУ имеет тривиальное решение в том и только в том случае, когда ранг ее основной матрицы равен числу неизвестных. □
Таблица, приведенная выше, позволяет практически находить фундаментальную систему решений СЛОУ, чем должно заканчиваться ее решение.
Пример 4. Решить систему
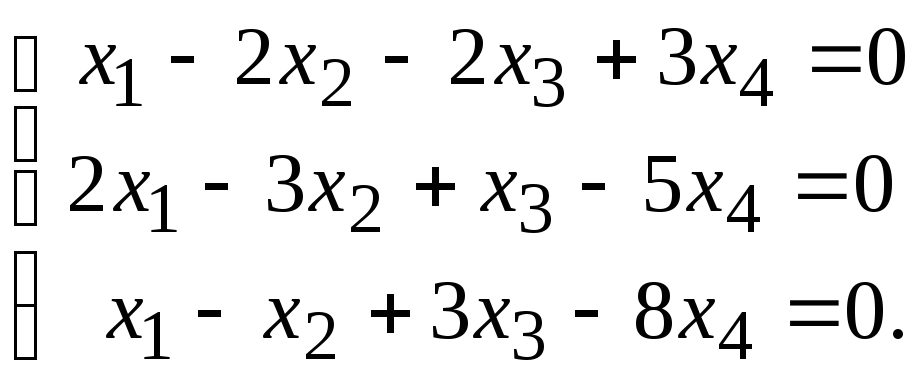
Решение. Это система однородных уравнений, причём число уравнений меньше числа неизвестных; она будет иметь множество решений. Так как все свободные члены равны нулю, то будем подвергать преобразованиям лишь матрицу из коэффициентов системы:

Мы пришли к системе уравнений
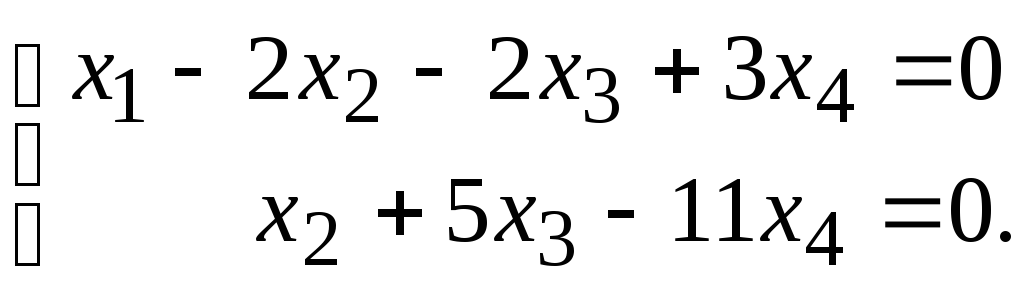
В качестве
независимых выберем две переменные,
например 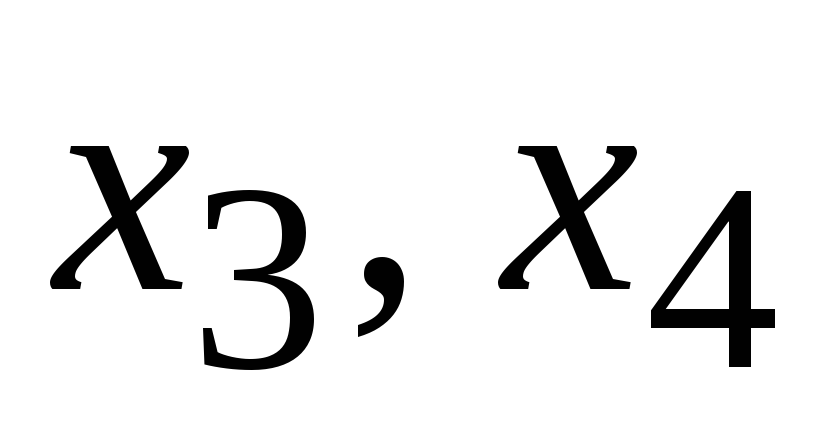 .
Выразим остальные переменные через
независимые. Получим
.
Выразим остальные переменные через
независимые. Получим
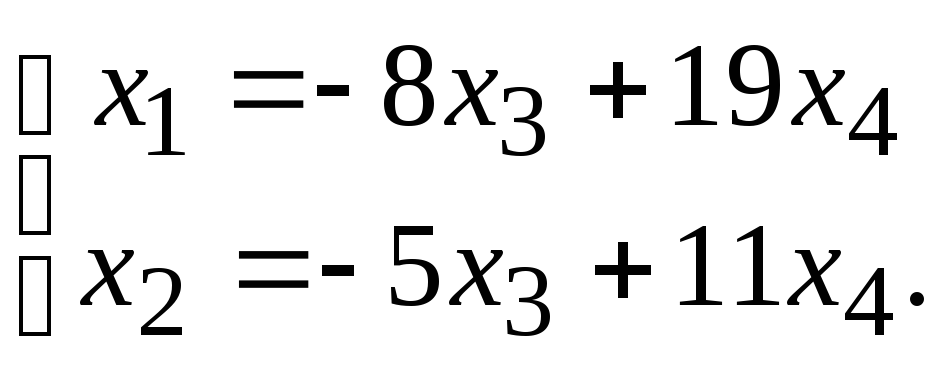
Тогда фундаментальная система будет иметь следующий вид:
Любое частное решение системы может быть представлено в виде линейной комбинации фундаментальных решений, т. е. общее решение системы
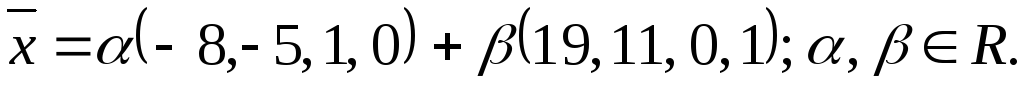
ЗАДАЧИ К ГЛАВЕ II.
Найти ранг следующих матриц методом окаймления миноров:
78. 
79. 
80. 
Вычислить ранг следующих матриц при помощи элементарных преобразований:
81. 
82. 
83. 
84. 
85. 
86. 
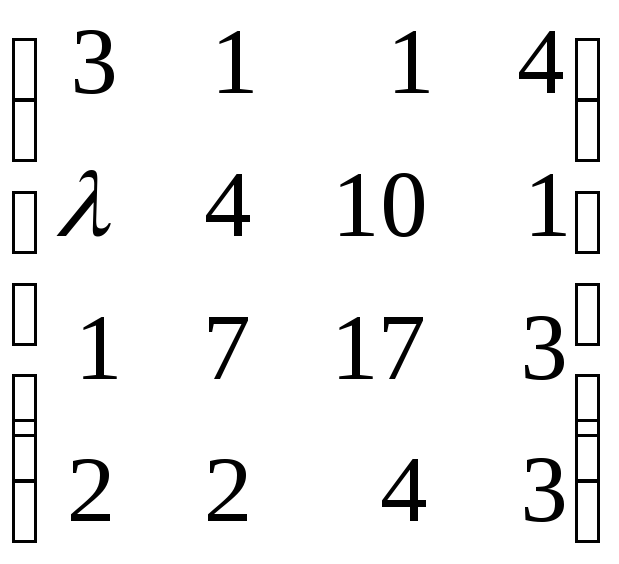
Определить ранг
матриц при различных значениях  :
:
87. 
88. 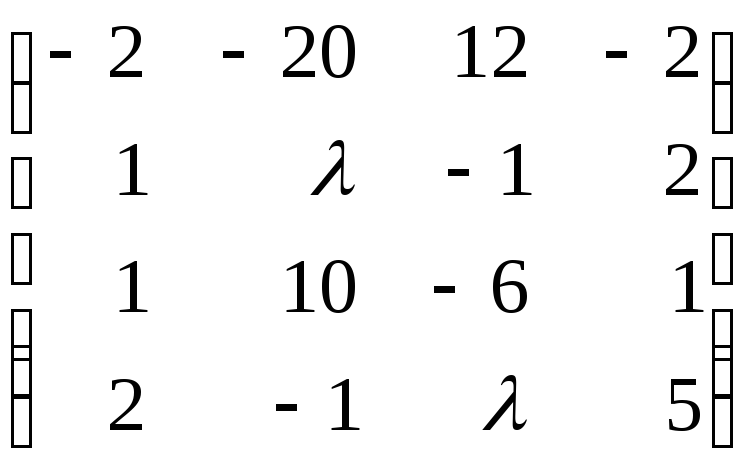
Исследовать совместность и найти общее и одно частное решение системы уравнений:
89. 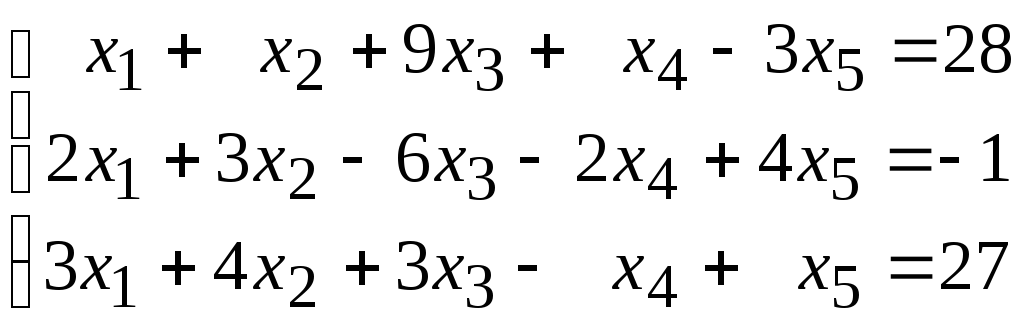
90. 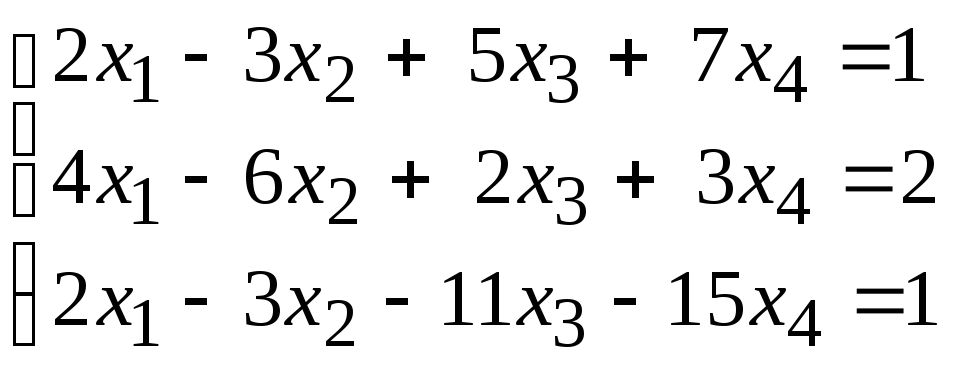
91. 
92. 
93. 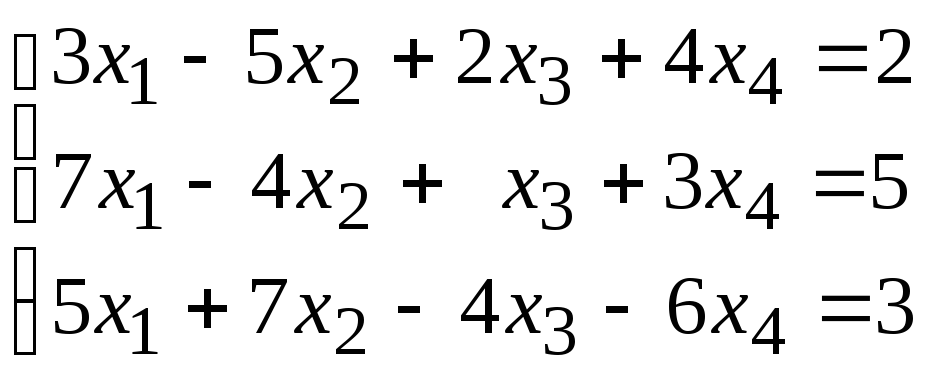
94. 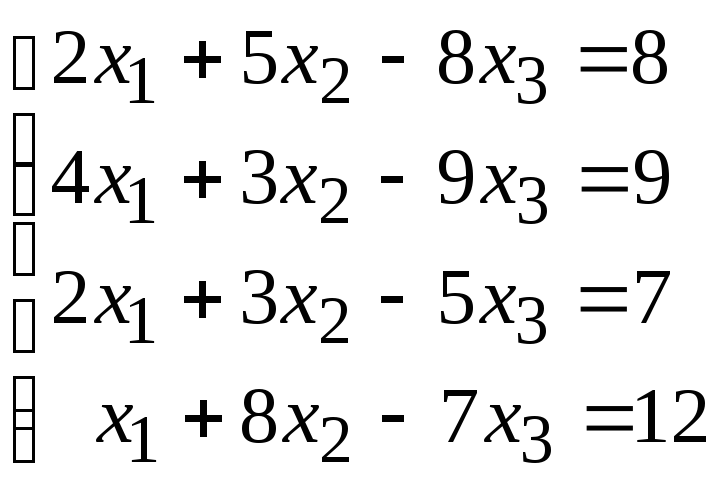
95. 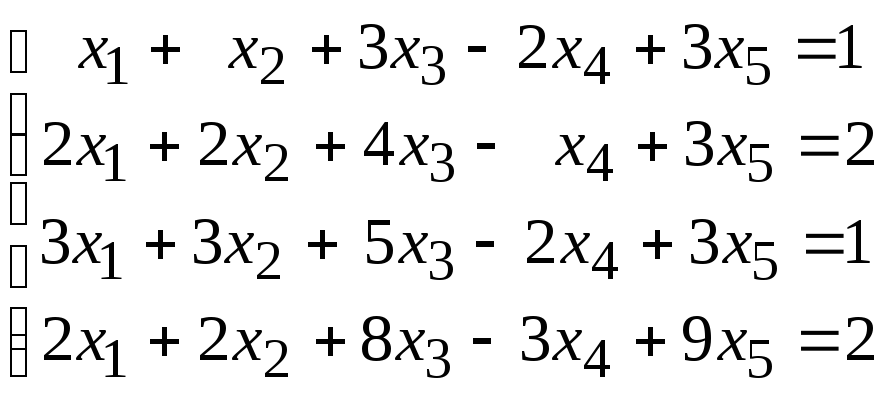
96. 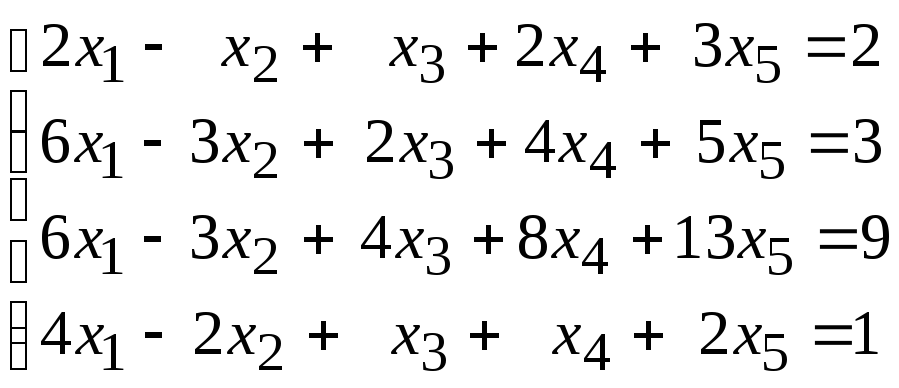
97. 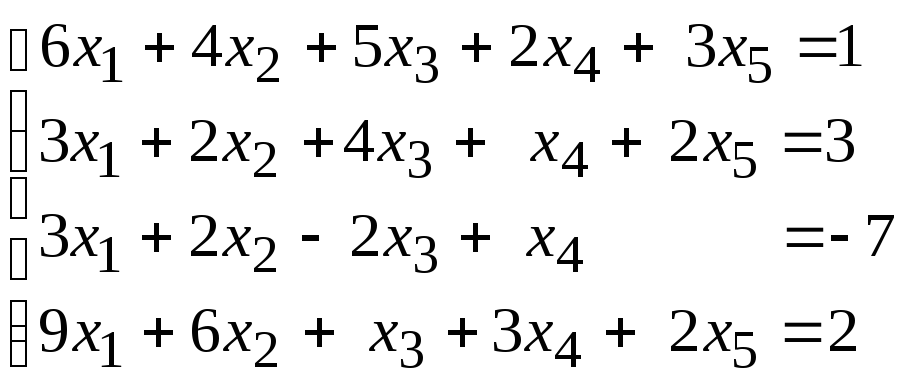
98. 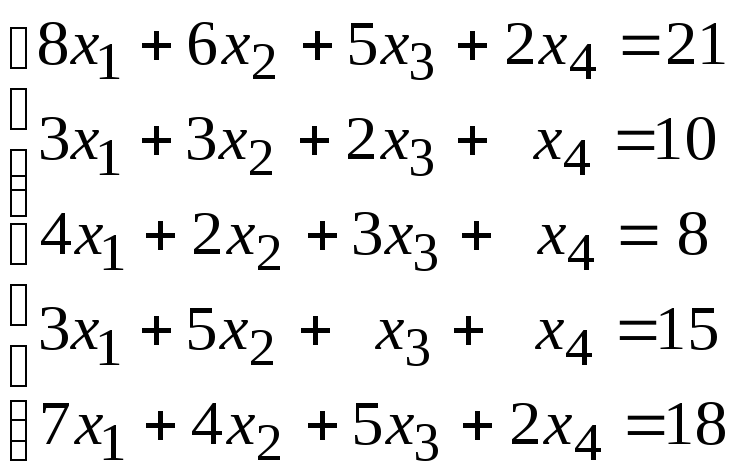
99. 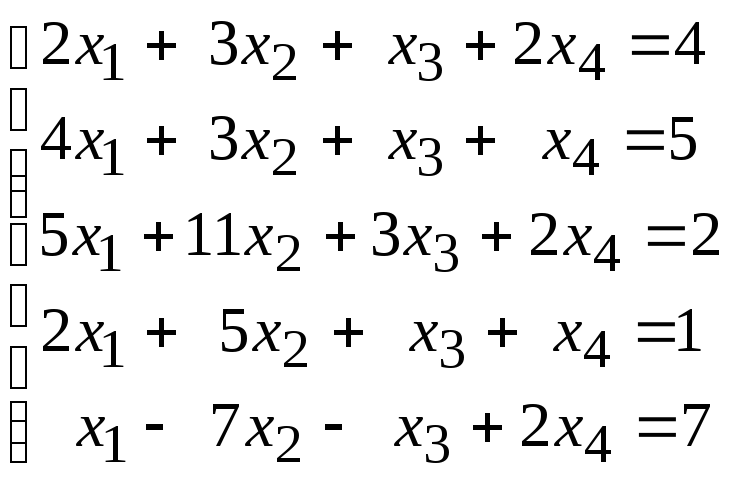
Исследовать
систему и найти общее решение в
зависимости от значений параметра  :
:
100. 
101. 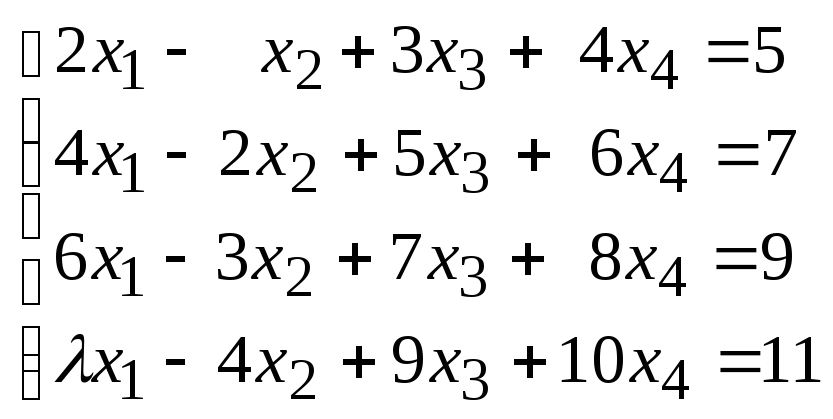
Найти общее решение и фундаментальную систему решений для систем уравнений:
102. 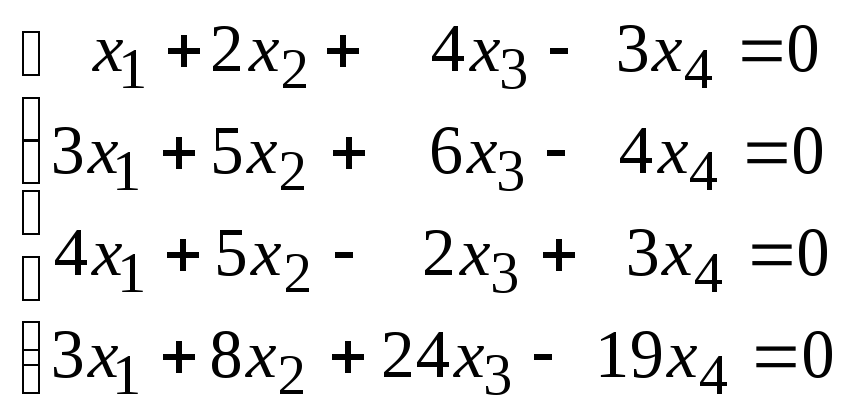
103. 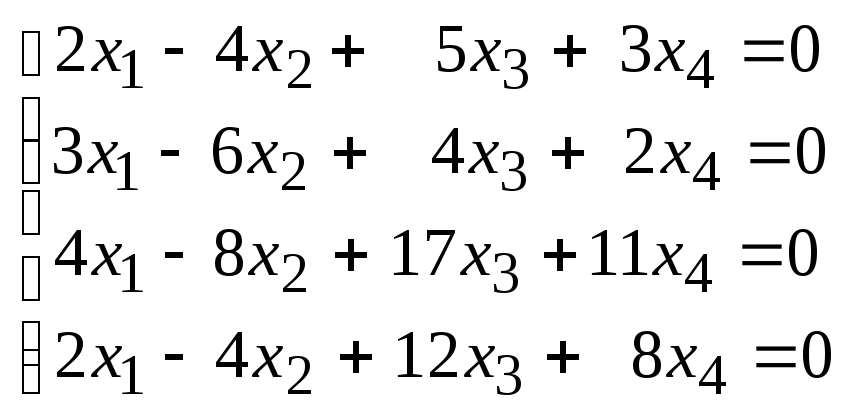
104. 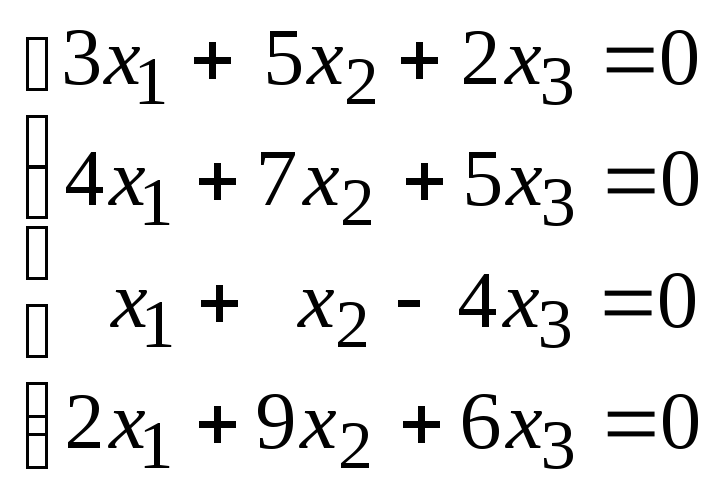
105. 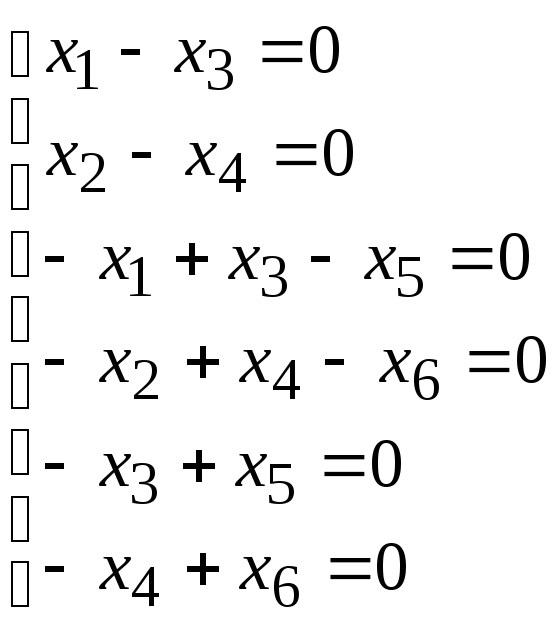
106. 
107. 
108. 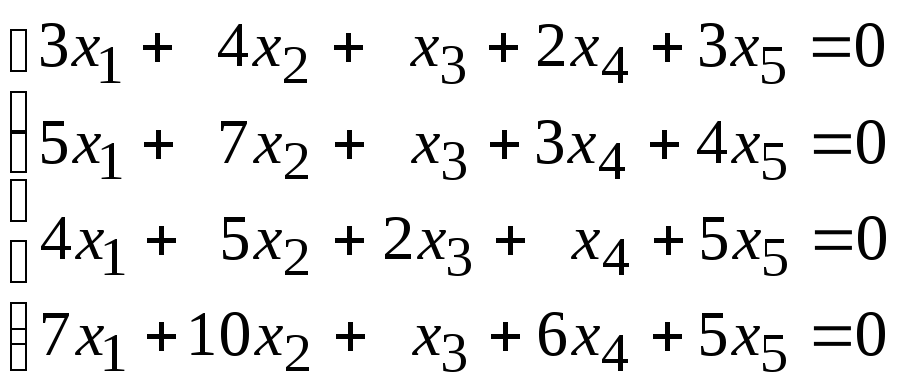
109. Какие из строк матрицы

образуют фундаментальную систему решений для системы уравнений
Общее решение неоднородной системы — Студопедия
2.4.1. Определение. Пусть дана неоднородная система линейных уравнений
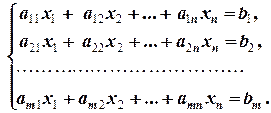 (2.4.1)
(2.4.1)
Рассмотрим однородную систему
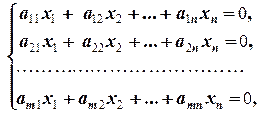 (2.4.2)
(2.4.2)
у которой матрица коэффициентов совпадает с матрицей коэффициентов системы (2.4.1). Тогда система (2.4.2) называется приведённой однородной системы (2.4.1).
2.4.2. Теорема. Общее решение неоднородной системы равно сумме некоторого частного решения неоднородной системы и общего решения приведённой однородной.
Таким образом, для нахождения общего решения неоднородной системы (2.4.1) достаточно:
1) Исследовать её на совместность. В случае совместности:
2) Найти общее решение приведённой однородной этой системы.
3) Найти какое-либо частное решение исходной (неоднородной).
4) Сложив найденные частное решение и общее решения приведённой, найти общее решение исходной системы.
2.4.3. Упражнение. Исследовать систему на совместность и в случае совместности найти её общее решение в виде суммы частного и общего приведённого.
а) 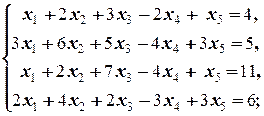 б)
б) 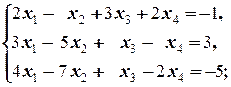
в) 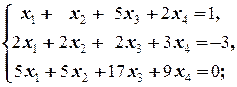 г)
г) 
д) 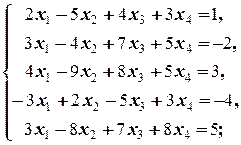 е)
е) 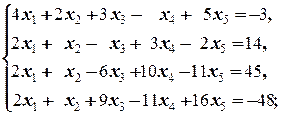
ж) 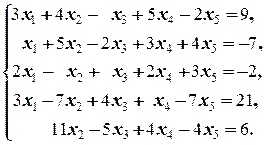
Решение. а) Для решения задачи применяем вышеуказанную схему:
1) Исследуем систему на совместность (методом окаймления миноров): Ранг основной матрицы равен 3 (см. решение упр. 2.2.5, а), причём ненулевой минор максимального порядка 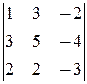 составлен из элементов 1-й, 2-й, 4-й строк и 1-го, 3-го, 4-го столбцов. Для нахождения ранга расширенной матрицы окаймляем его 3-ей строкой и 6-м столбцом расширенной матрицы:
составлен из элементов 1-й, 2-й, 4-й строк и 1-го, 3-го, 4-го столбцов. Для нахождения ранга расширенной матрицы окаймляем его 3-ей строкой и 6-м столбцом расширенной матрицы: 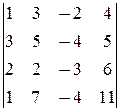 =0. Значит, rgA=rg
=0. Значит, rgA=rg  =3, и система совместна. В частности, она равносильна системе
=3, и система совместна. В частности, она равносильна системе
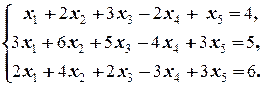 (2.4.3)
(2.4.3)
2) Найдём общее решение X0 приведённой однородной этой системы
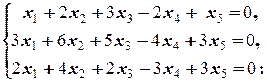 .
.
X0={(-2a—  b; a;
b; a;  b; b; b) | a, bÎR}
b; b; b) | a, bÎR}
(см. решение упр. 2.2.5, а)).
3) Найдём какое-либо частное решение xч исходной системы. Для этого в системе (2.4.3), равносильной исходной, свободные неизвестные x2 и x5 полагаем равными, например, нулю (это наиболее удобные данные):
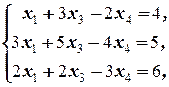
и решаем полученную систему: x1=- 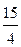 , x3=-
, x3=- 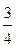 , x4=-5. Таким образом, (-
, x4=-5. Таким образом, (- 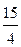 ; 0; —
; 0; — 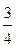 ; -5; 0) ¾ частное решение системы.
; -5; 0) ¾ частное решение системы.
4) Находим общее решение Xн исходной системы:
Xн={xч}+X0 ={(- 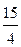 ; 0; —
; 0; — 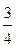 ; -5; 0)} + {(-2a—
; -5; 0)} + {(-2a—  b; a;
b; a;  b; b; b)}=
b; b; b)}=
={(- 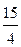 -2a—
-2a—  b; a; —
b; a; — 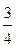 +
+  b; -5+b; b)}.
b; -5+b; b)}.
Замечание. Сравните полученный ответ со вторым ответом в примере 1.2.1 в). Для получения ответа в первом виде для 1.2.1 в) в качестве базисных неизвестных берутся x1, x3, x5 (минор при которых тоже не равен нулю), а в качестве свободных ¾ x2 и x4.
§3. Некоторые приложения.
3.1. К вопросу о матричных уравнениях. Напоминаем, что матричным уравнением над полем F называется уравнение, в котором в качестве неизвестной выступает некоторая матрица над полем F.
Простейшими матричными уравнениями являются уравнения вида
AX=B, XA=B (2.5.1)
где A, B ¾ данные (известные) матрицы над полем F, а X ¾ такие матрицы, при подстановке которых уравнения (2.5.1) обращаются в верные матричные равенства. В частности, матричный метод определённых систем сводится к решению матричного уравнения.
В случае, когда матрицы A в уравнениях (2.5.1) невырожденны, они имеют решения соответственно X=A 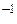 B и X=BA
B и X=BA 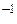 .
.
В случае, когда хотя бы одна из матриц в левой части уравнений (2.5.1) является вырожденной, данный метод уже не годится, так как соответствующая обратная матрица A 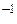 не существует. В этом случае нахождение решений уравнений (2.5.1) сводится к решению систем.
не существует. В этом случае нахождение решений уравнений (2.5.1) сводится к решению систем.
Но прежде введём некоторые понятия.
Множество всех решений системы назовём общим решением. Отдельно взятое решение неопределённой системы назовём её частным решением.
3.1.1. Пример.Решитьматричное уравнение над полем R.
а) X 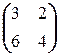 =
= 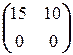 ; б)
; б) 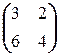 X=
X= 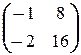 ; в)
; в) 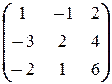 X =
X =  .
.
Решение. а) Так как 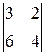 =0, то формула X=A
=0, то формула X=A 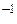 B для решения этого уравнения не годится. Если в произведении XA=B матрица A имеет 2 строки, то матрица X имеет 2 столбца. Число строк X должно совпасть с числом строк B. Поэтому X имеет 2 строки. Таким образом, X ¾ некоторая квадратная матрица второго порядка: X=
B для решения этого уравнения не годится. Если в произведении XA=B матрица A имеет 2 строки, то матрица X имеет 2 столбца. Число строк X должно совпасть с числом строк B. Поэтому X имеет 2 строки. Таким образом, X ¾ некоторая квадратная матрица второго порядка: X= 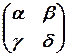 . Подставим X в исходное уравнение:
. Подставим X в исходное уравнение:
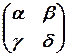
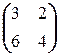 =
= 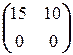 . (2.5.2)
. (2.5.2)
Перемножая матрицы в левой части (2.5.2), приходим к равенству
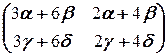 =
= 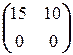 . (2.5.3)
. (2.5.3)
Две матрицы равны тогда и только тогда, когда они одинаковых размерностей и равны их соответствующие элементы. Поэтому (2.5.3) равносильно системе
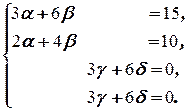
Эта система равносильна системе
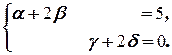
Решая её, например, методом Гаусса, приходим к множеству решений (5-2b, b, -2d, d), где b, d независимо друг от друга пробегают R. Таким образом, X= 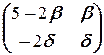 .
.
б) Аналогично а) имеем X= 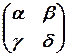 и .
и .
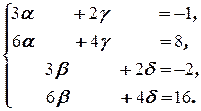
Эта система несовместна (убедитесь в этом!). Поэтому данное матричное уравнение решений не имеет.
в) Обозначим это уравнение через AX=B. Так как A имеет 3 столбца, а B имеет 2 столбца, то X ¾ некоторая матрица размерности 3´2: X= 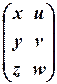 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
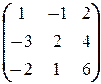
 =
=  Û
Û 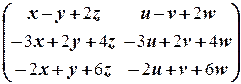 =
=  Û
Û
Û 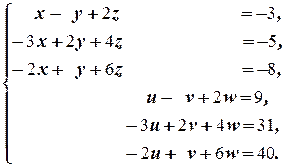
Решаем последнюю систему методом Гаусса (комментарии опускаем)
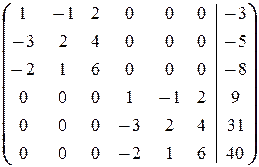 ®
® 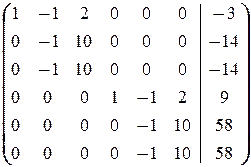 ®
®
® 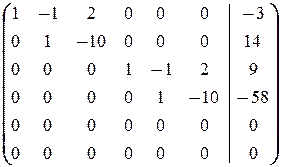 .
.
Таким образом, приходим к системе

решением которой является (11+8z, 14+10z, z, -49+8w, -58+10w, w) где z, w пробегают независимо друг от друга R.
Ответ: а) X= 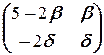 , b, d ÎR.
, b, d ÎR.
б) Решений нет.
в) X= 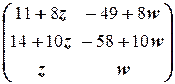 z, w ÎR.
z, w ÎR.
3.2. К вопросу о перестановочности матриц.В общем случае произведение матриц неперестановочно, то есть если A и B такие, что AB и BA определены, то, вообще говоря, AB¹BA. Но пример единичной матрицы E показывает, что возможна и перестановочность AE=EA для любой матрицы A, лишь бы AE и EA были определены.
В этом пункте мы рассмотрим задачи на нахождение множества всех матриц, перестановочных с данной.
3.2.1. Пример. Найти все матрицы, перестановочные с матрицей A (над полем R):
а) 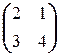 ; б)
; б) 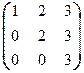 .
.
Решение. а) Допустим, X ¾ перестановочна с A: AX=XA. Легко видеть, что X ¾ квадратная матрица второго порядка: X= 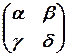 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
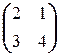
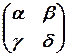 =
= 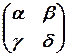
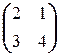 Û
Û 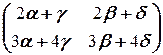 =
= 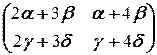 Û
Û
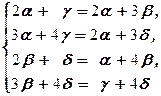 Û
Û 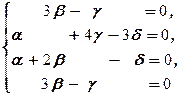 Û
Û 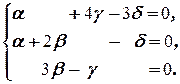
Решая полученную однородную систему, получаем 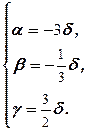 Таким образом, X=
Таким образом, X= 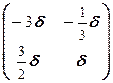 ¾ матрицы, перестановочные с
¾ матрицы, перестановочные с 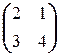 , d ¾ любое число.
, d ¾ любое число.
б) Аналогично предыдущему, матрица X, перестановочная с A=  , имеет вид
, имеет вид 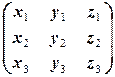 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
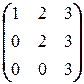
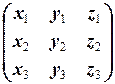 =
= 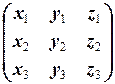
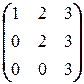 Û
Û
Û 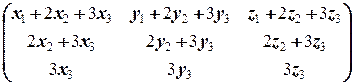 =
= 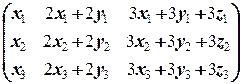
Û 
В последней системе из 3-го, 1-го и 6-го уравнений последовательно получаем x3=x2 = y3 =0. Учитывая это, из системы получаем систему
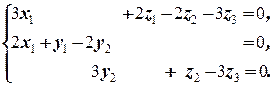
Неизвестные x1, y2 и z3 могут принимать любые значения: x1=a, y2=b, z3=g. Тогда 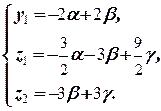
Таким образом, X= 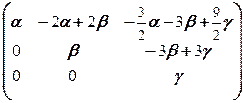 .
.
Ответ. а) X ¾ множество матриц вида 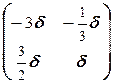 , где d ¾ любое число.
, где d ¾ любое число.
б) X ¾ множество матриц вида 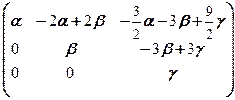 , где a, b и g ¾ любые числа.
, где a, b и g ¾ любые числа.
Решение однородных систем линейных уравнений
Однородная
система 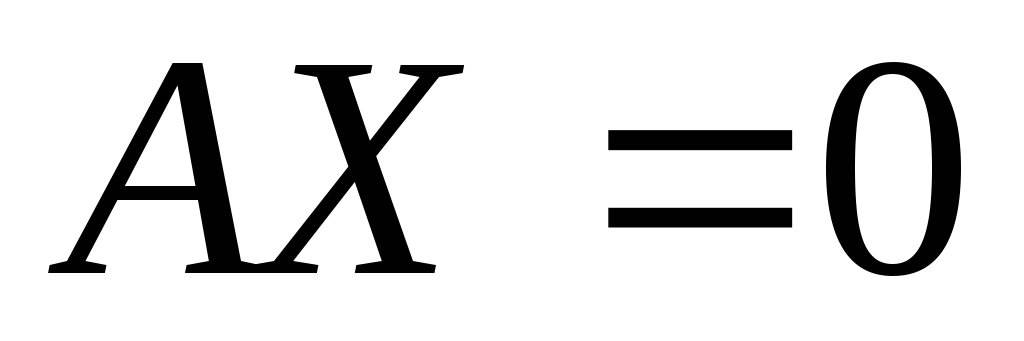 всегда совместна и имеет тривиальное
решение
всегда совместна и имеет тривиальное
решение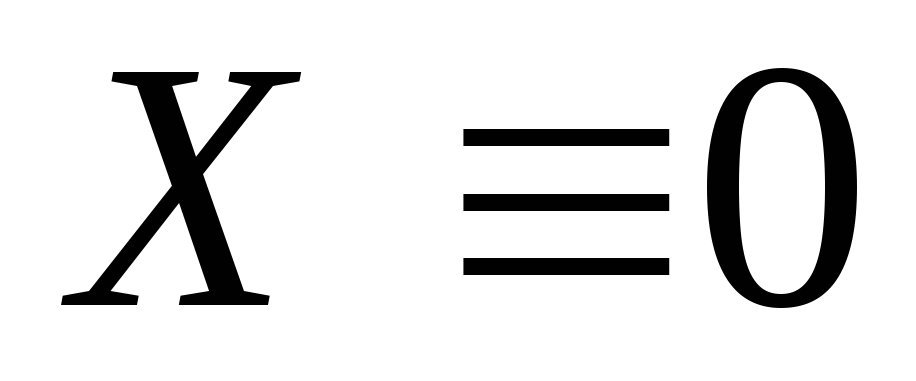 .
Для существования нетривиального
решения необходимо, чтобы ранг матрицы
.
Для существования нетривиального
решения необходимо, чтобы ранг матрицы был меньше числа неизвестных:
был меньше числа неизвестных:
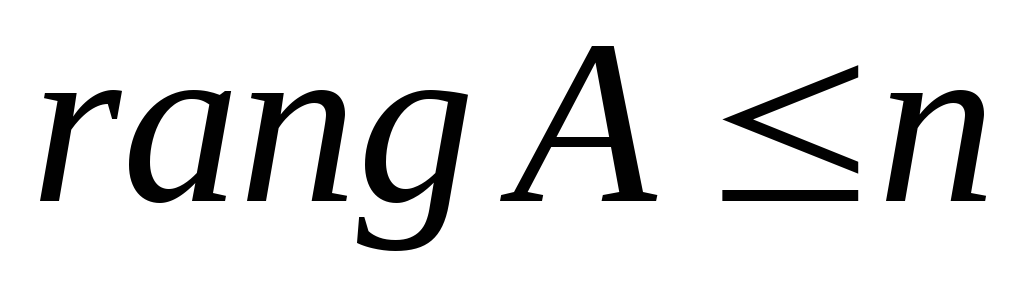 .
.
Фундаментальной
системой решений однородной системы 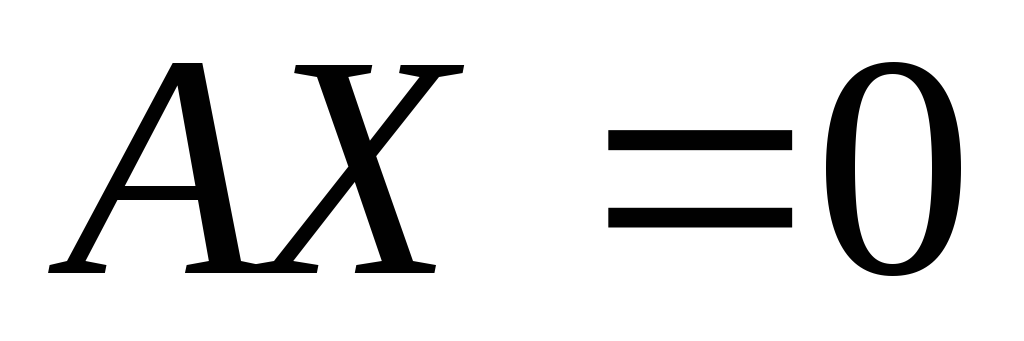 называют систему решений в виде
векторов-столбцов
называют систему решений в виде
векторов-столбцов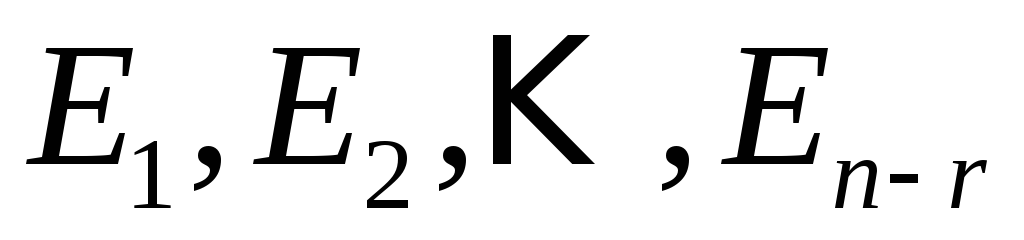 ,
которые соответствуют каноническому
базису, т.е. базису, в котором произвольные
постоянные
,
которые соответствуют каноническому
базису, т.е. базису, в котором произвольные
постоянные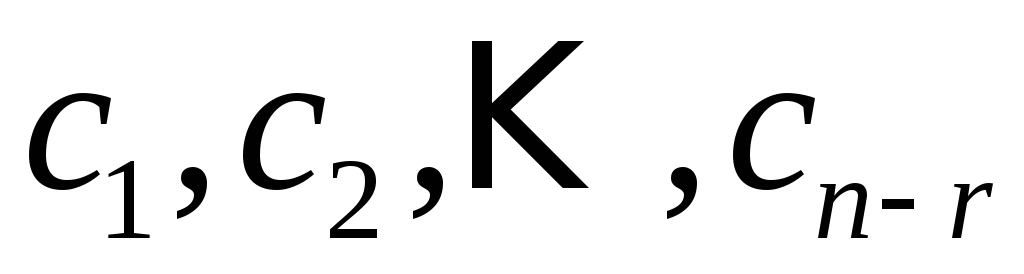 поочередно полагаются равными единице,
тогда как остальные приравниваются
нулю.
поочередно полагаются равными единице,
тогда как остальные приравниваются
нулю.
Тогда общее решение однородной системы имеет вид:
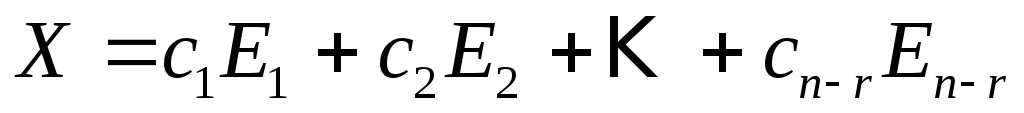 ,
,
где 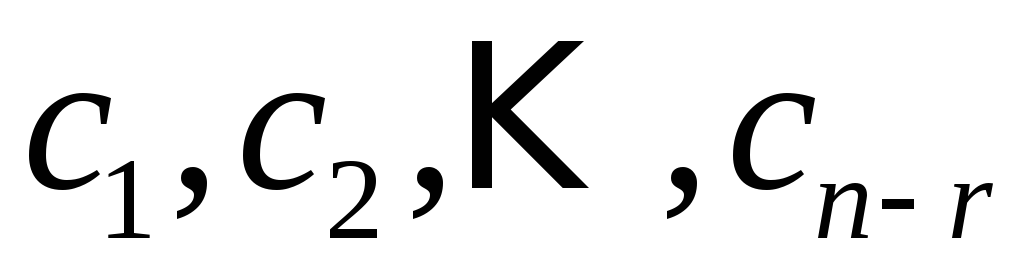 — произвольные постоянные. Другими
словами, общее решение есть линейная
комбинация фундаментальной системы
решений.
— произвольные постоянные. Другими
словами, общее решение есть линейная
комбинация фундаментальной системы
решений.
Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.
Пример. Найдем решение системы
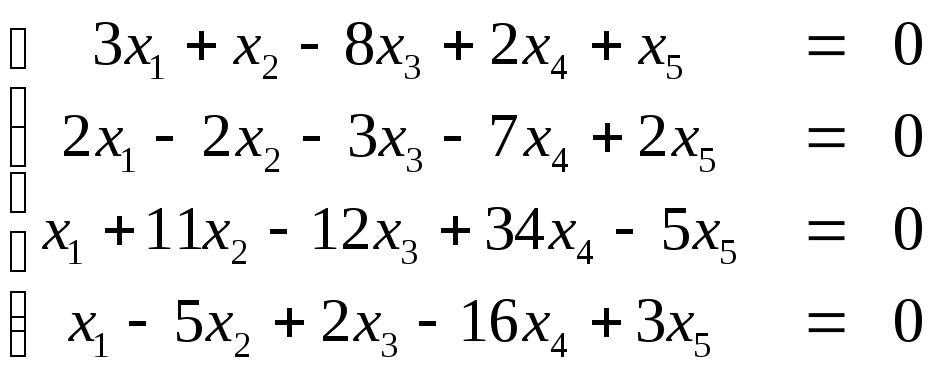
Примем 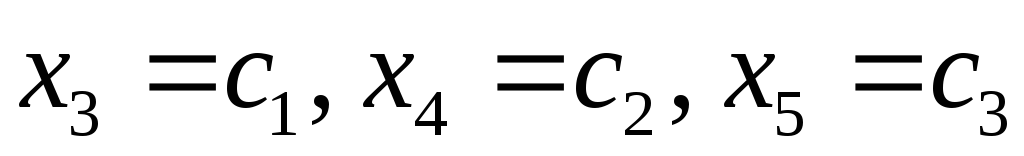 ,
тогда получим решение в виде:
,
тогда получим решение в виде:
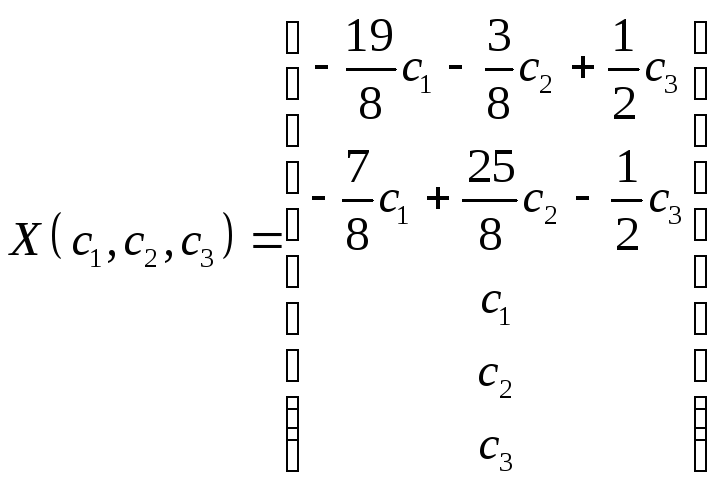
Построим теперь фундаментальную систему решений:
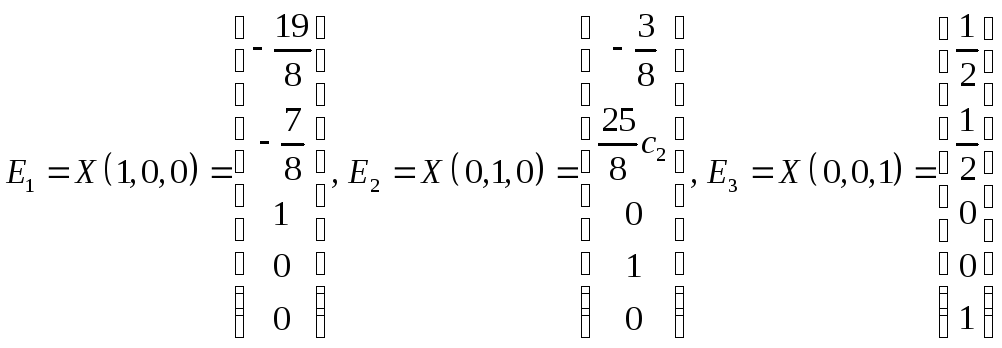 .
.
Общее решение запишется в виде:
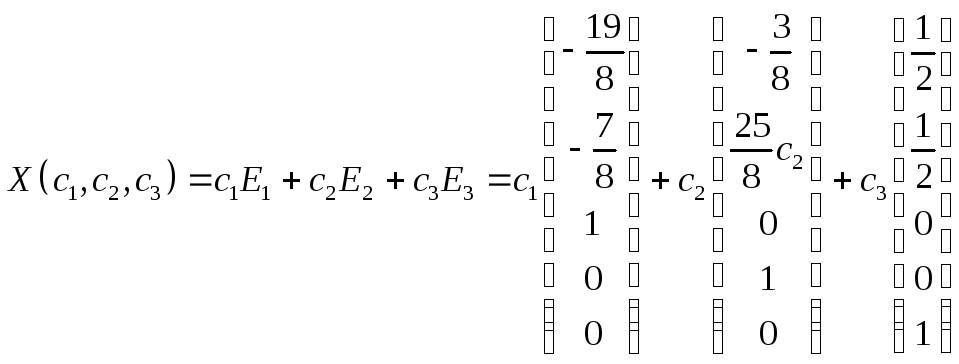
Решения системы однородных линейных уравнений имеют свойства:
Если
 — решение системы, то и
— решение системы, то и — также решение.
— также решение.Если
 и
и — решения системы, то и
— решения системы, то и — также решение.
— также решение.
Другими словами, любая линейная комбинация решений однородной системы есть опять решение.
Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.
Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Такие системы позволяют последовательно находить все неизвестные в определенном порядке.
Предположим,
что в системе (1) 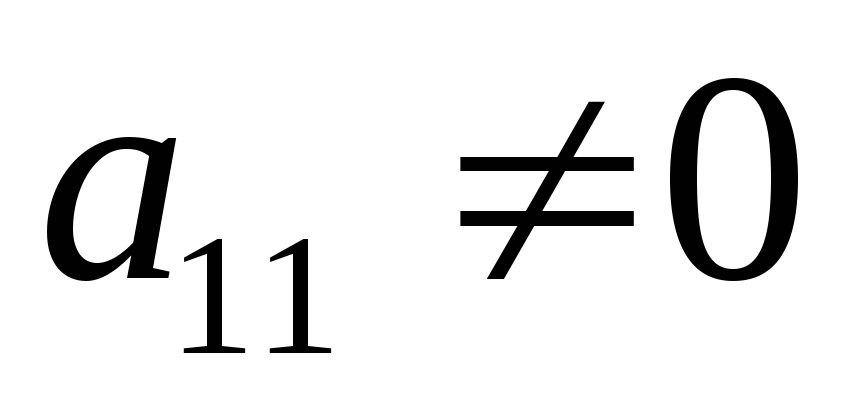 (что всегда возможно).
(что всегда возможно).
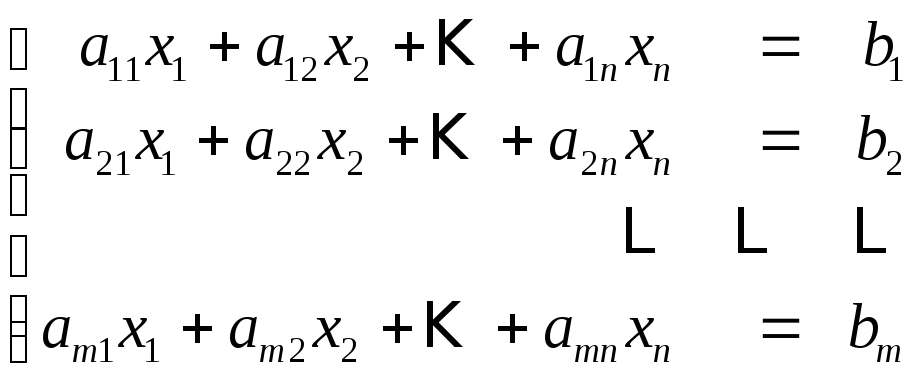 (1)
(1)
Умножая поочередно первое уравнение на так называемые подходящие числа
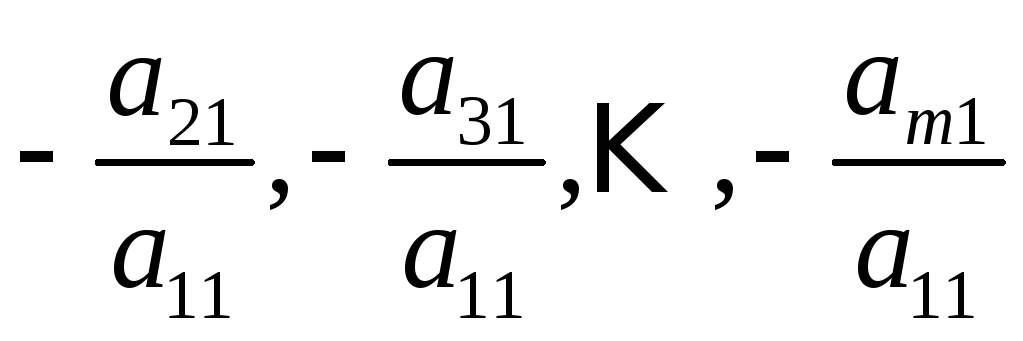
и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная х1
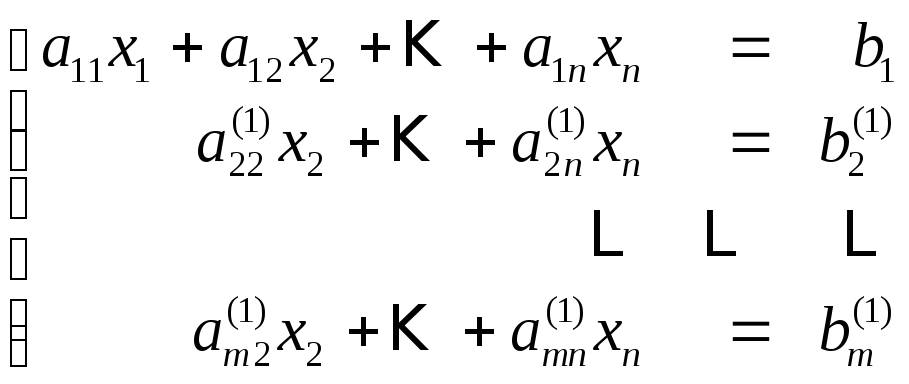 (2)
(2)
Умножим
теперь второе уравнение системы (2) на
подходящие числа, полагая, что 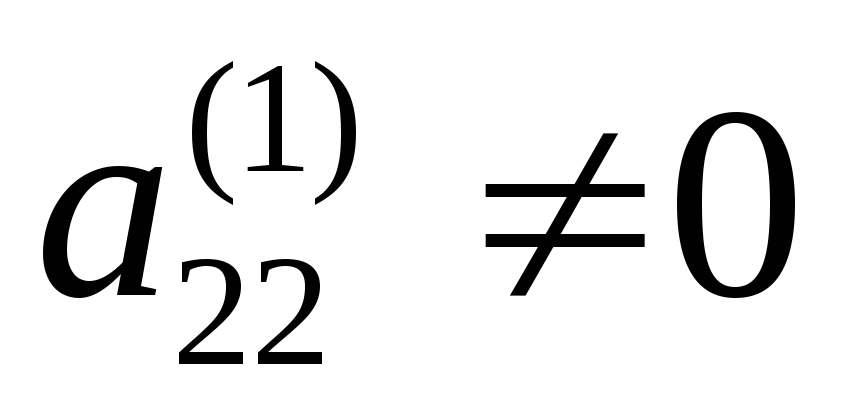
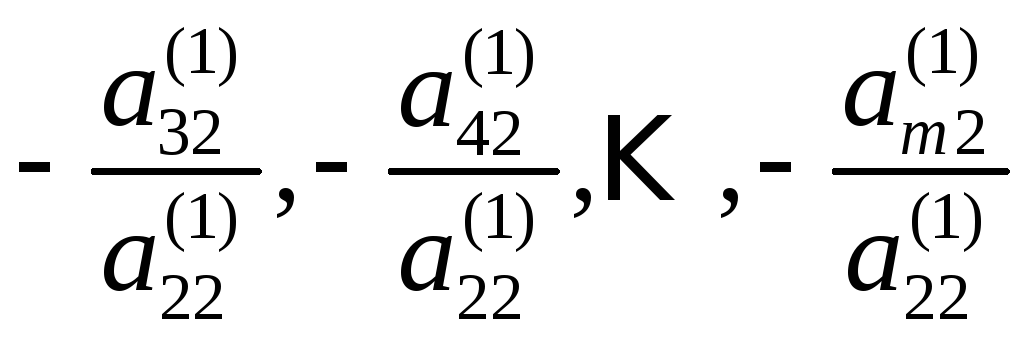 ,
,
и
складывая его с нижестоящими, исключим
переменную 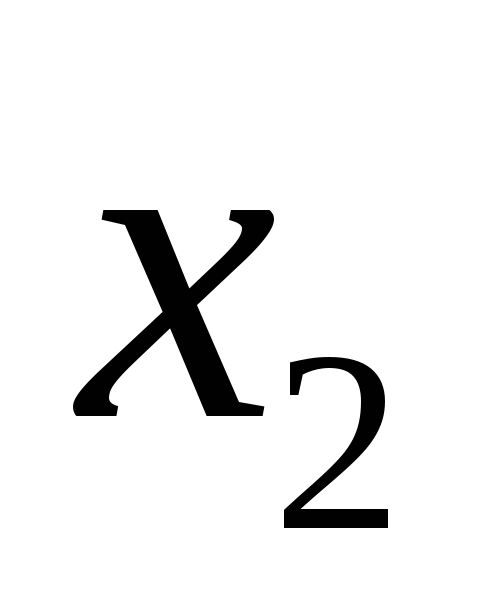 из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая
этот процесс, после  шага мы получим:
шага мы получим:
(3)
Если
хотя бы одно из чисел 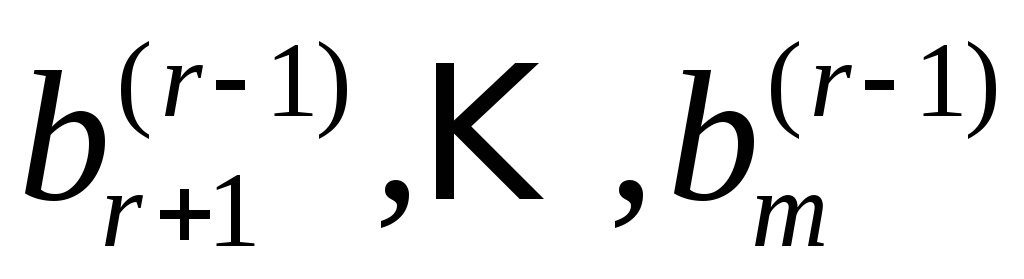 не равно нулю, то соответствующее
равенство противоречиво и система (1)
несовместна. Обратно, для любой совместной
системы числа
не равно нулю, то соответствующее
равенство противоречиво и система (1)
несовместна. Обратно, для любой совместной
системы числа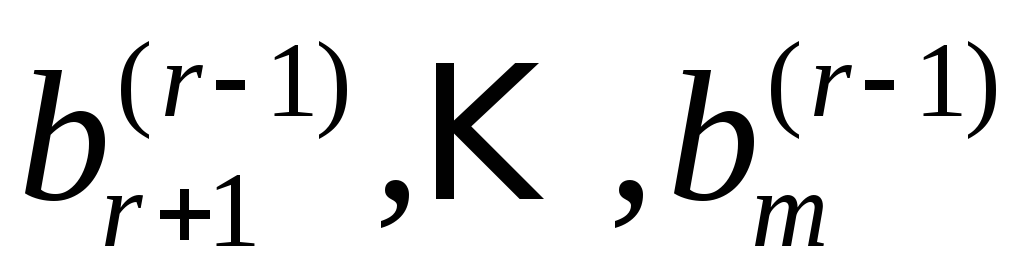 равны нулю. Число
равны нулю. Число — это ни что иное, как ранг матрицы системы
(1).
— это ни что иное, как ранг матрицы системы
(1).
Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) – обратным ходом.
Замечание: Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).
Пример. Найдем решение системы
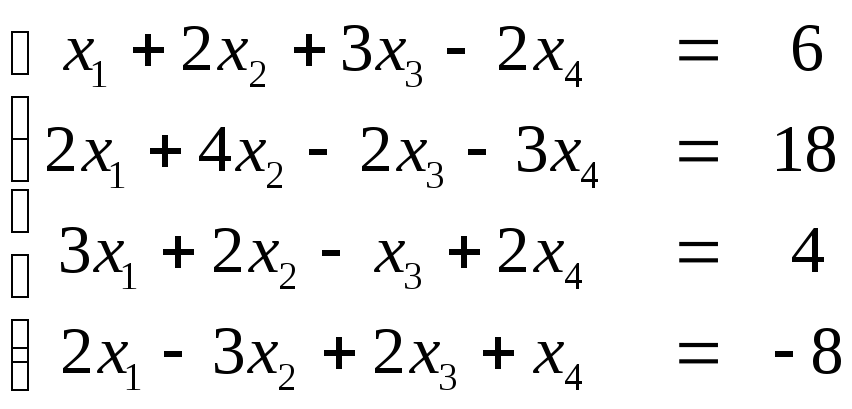 .
.
Запишем расширенную матрицу системы:
 .
.
Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:
 .
.
Поменяем
строки 2 и 3 местами, затем в получившейся
матрице добавим к строке 4 строку 2,
умноженную на  :
:
 .
.
Прибавим
к строке 4 строку 3, умноженную на 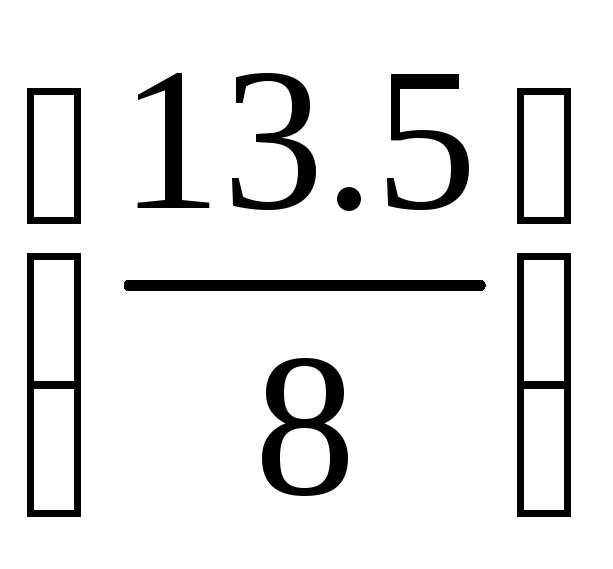 :
:
 .
.
Очевидно,
что 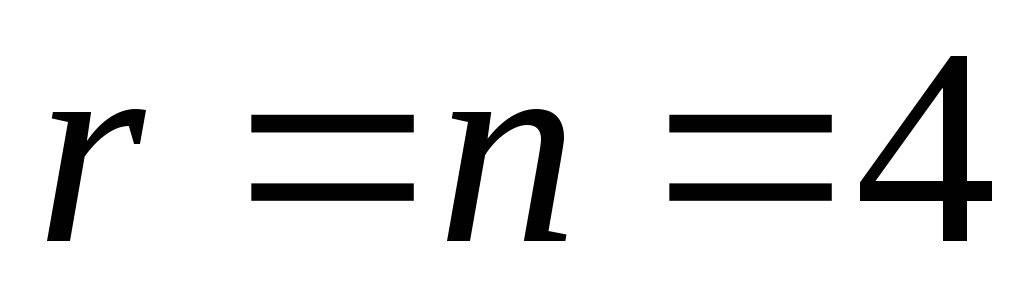 ,
следовательно, система совместна. Из
полученной системы уравнений
,
следовательно, система совместна. Из
полученной системы уравнений
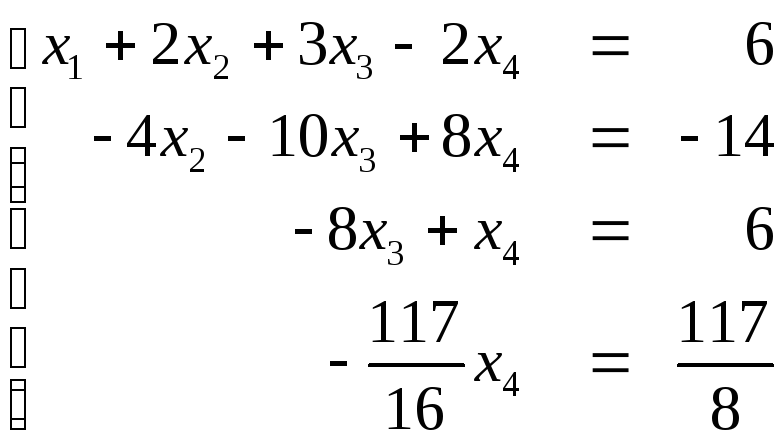
находим решение обратной подстановкой:
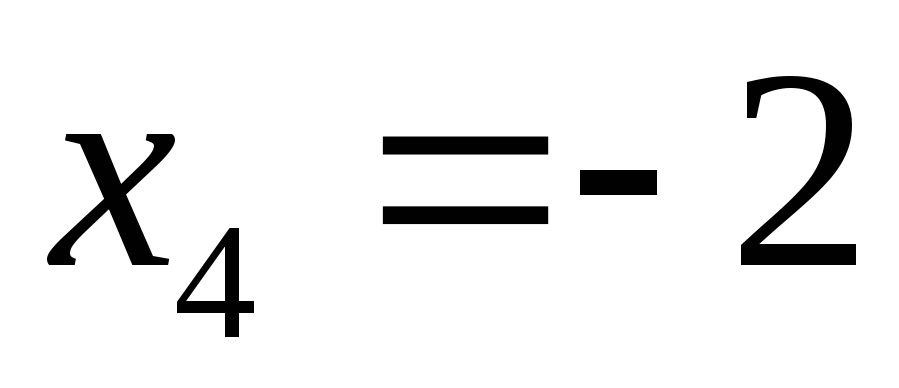 ,
,  ,
,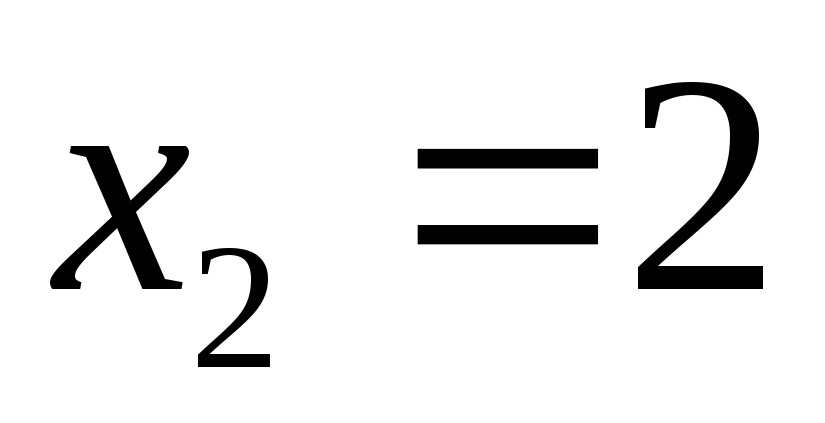 ,
,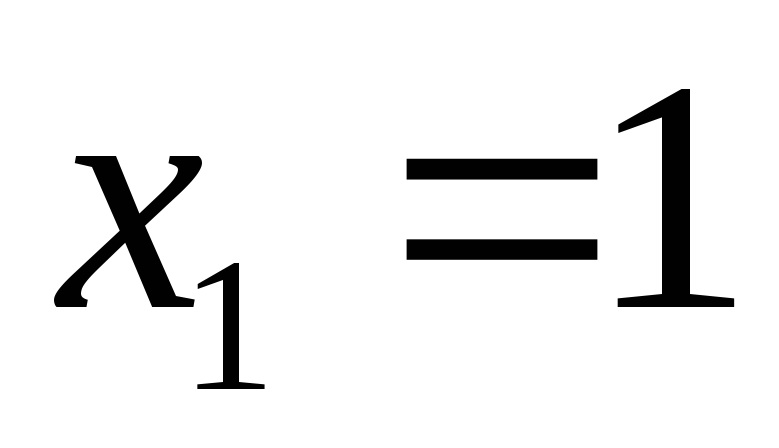 .
.
Пример 2. Найти решение системы:
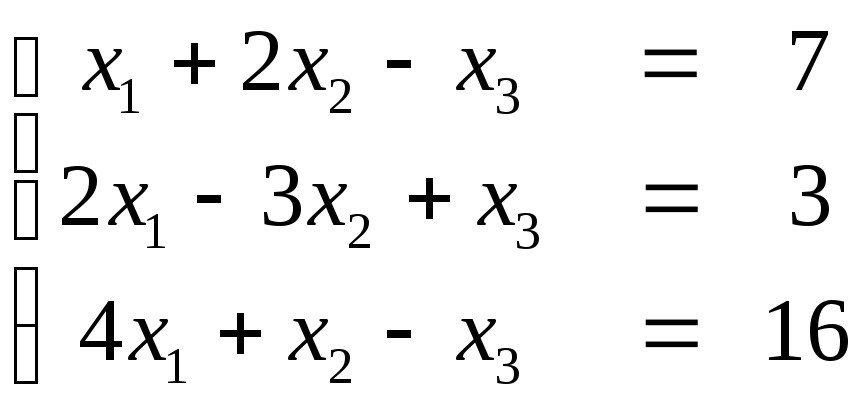 .
.
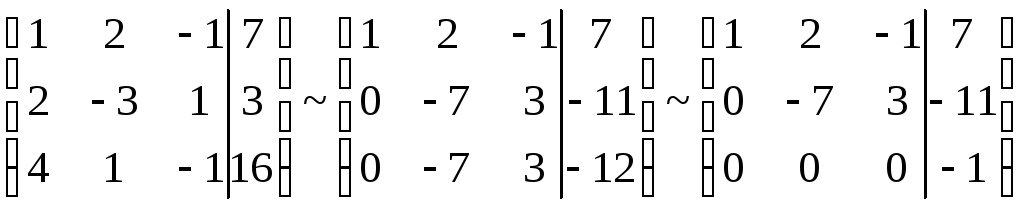
Очевидно,
что система несовместна, т.к.  ,
а
,
а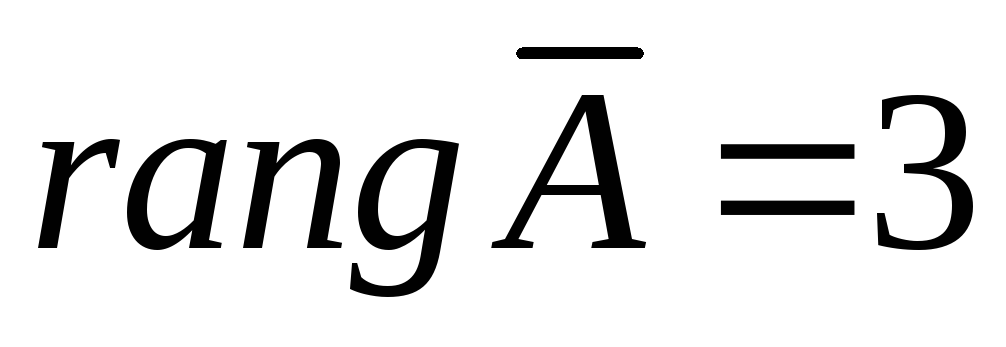 .
.
Достоинства метода Гаусса:
Менее трудоемкий, чем метод Крамера.
Однозначно устанавливает совместность системы и позволяет найти решение.
Дает возможность определить ранг любых матриц.
Системы линейных уравнений
Линейное уравнение — это уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 — 0,5x ,
Также может быть как y = 0,5 (7 — x)
Или как y + 0,5x = 3,5
Или как y + 0,5x — 3,5 = 0 и более.
(Примечание: все это одно и то же линейное уравнение!)
Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
Вместе они представляют собой систему линейных уравнений.
Можете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Попробуем построить и решить реальный пример:
Пример: вы против лошади
Это гонка!
Можно бегать 0,2 км каждую минуту.
Лошадь может бегать 0.5 км каждую минуту. Но оседлать лошадь нужно за 6 минут.
Как далеко вы можете уйти, прежде чем лошадь вас поймает?
Мы можем составить из двух уравнений ( d = расстояние в км, t = время в минутах)
- Вы бежите со скоростью 0,2 км каждую минуту, поэтому d = 0,2 т
- Лошадь бежит со скоростью 0,5 км в минуту, но мы берем на ее время 6: d = 0,5 (t − 6)
Итак, у нас есть система уравнений ( линейных ):
Решаем на графике:
Вы видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут… тебе всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Существует множество способов решения линейных уравнений!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим это с помощью алгебры!
Хммм … как это решить? Способов может быть много! В этом случае оба уравнения имеют «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y — (−3x + y) = 6 — 2
Теперь упростим:
х + у + 3х — у = 6-2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x = 1 .
И мы можем найти совпадающее значение y , используя любое из двух исходных уравнений (поскольку мы знаем, что они имеют одинаковое значение при x = 1). Воспользуемся первым (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
x = 1 и y = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. Нет x 2 , y 3 , √x и т. Д. :
Линейное против нелинейного
Размеры
| Линейное уравнение может быть в 2 измерениях … (например, x и y ) | ||
| … или в 3-х измерениях … (делает самолет) | ||
| … или 4 размера … | ||
| … или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они разделяют одну или несколько переменных:
Система уравнений состоит из двух или более уравнений в одной или нескольких переменных
Множество переменных
Таким образом, Система уравнений может иметь многих уравнений и многих переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | года | – | 2z | = | 3 |
| х | – | года | – | z | = | 0 |
| х | + | года | + | 3z | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений в 4 переменных,
- 9000 уравнений в 567 переменных,
- и др.
Решения
Когда количество уравнений равно , то же , что и количество переменных, , вероятно, будет решением. Не гарантировано, но вероятно.
На самом деле есть только три возможных случая:
- Нет раствор
- Одно решение
- Бесконечно много решений
Когда нет решения , уравнения называются «несовместимыми» .
Одно или бесконечно много решений называются «согласованными»
Вот диаграмма для 2 уравнения с 2 переменными :
Независимая
«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае это «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
Эти уравнения — «Зависимые» , потому что они на самом деле такое же уравнение , только умноженное на 2.
Итак, второе уравнение не дало новой информации .
Истинные уравнения
Уловка состоит в том, чтобы найти, где , все уравнений являются истинными одновременно .
Верно? Что это значит?
Пример: вы против лошади
Линия «ты» истинна по всей ее длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t = 5 и d = 1 уравнение истинно (d = 0,2t? Да, поскольку 1 = 0,2 × 5 верно)
- при t = 5 и d = 3 уравнение не соответствует действительности (верно ли d = 0,2t? Нет, поскольку 3 = 0,2 × 5 неверно )
Точно так же «конская» линия также верна на всем протяжении (но больше нигде).
Но только в точке, где они пересекают (при t = 10, d = 2), оба являются истинными .
Значит, они должны быть правдой одновременно …
… поэтому некоторые люди называют их «Одновременные линейные уравнения»
Решить с помощью алгебры
Для их решения принято использовать алгебру.
Вот пример «Лошади», решенный с помощью алгебры:
Пример: вы против лошади
Система уравнений:
В данном случае кажется самым простым приравнять их друг другу:
d = 0.2т = 0,5 (т − 6)
Начать с : 0,2t = 0,5 (t — 6)
Расширить 0,5 (t − 6) : 0,2t = 0,5t — 3
Вычтем 0,5t с обеих сторон: −0,3t = −3
Разделим обе части на −0,3 : t = −3 / −0,3 = 10 минут
Теперь мы знаем , когда тебя поймают!
Зная t , можно вычислить d : d = 0,2t = 0,2 × 10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра против графиков
Зачем использовать алгебру, если графики настолько просты? Потому что:
Более двух переменных невозможно решить с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение заменой
- Решение путем исключения
Мы увидим каждый с примерами по 2 переменным и 3 переменным. Вот и …
Решение заменой
Это шаги:
- Напишите одно из уравнений в стиле «переменная = …»
- Заменить (т.е. заменить) эту переменную в другое уравнение (а).
- Решите другое уравнение (а)
- (при необходимости повторить)
Вот пример с 2 уравнения с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Воспользуемся вторым уравнением и переменной «y» (это выглядит как простейшее уравнение).
Напишите одно из уравнений в стиле «переменная =»… «:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 — x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 — x» в другом уравнении:
- 3x + 2 (8 — x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Развернуть 2 (8 − x) :
- 3x + 16 — 2x = 19
- у = 8 — х
Тогда 3x − 2x = x :
И на последок 19−16 = 3
Теперь мы знаем, что такое x , мы можем поместить его в уравнение y = 8 — x :
И ответ:
х = 3
у = 5
Примечание: поскольку — это решение, уравнения «непротиворечивы»
Проверка: почему бы вам не проверить, работают ли x = 3 и y = 5 в обоих уравнениях?
Решение подстановкой: 3 уравнения с 3 переменными
ОК! Давайте перейдем к длинному примеру : 3 уравнения с 3 переменными .
Это несложно, сделать … просто нужно много времени !
Пример:
- х + г = 6
- z — 3y = 7
- 2x + y + 3z = 15
Мы должны аккуратно выровнять переменные, иначе мы потеряем из виду то, что делаем:
| х | + | z | = | 6 | |||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | года | + | 3z | = | 15 |
WeI может начать с любого уравнения и любой переменной.Воспользуемся первым уравнением и переменной «x».
Напишите одно из уравнений в стиле «переменная = …»:
| x | = | 6 — z | |||||||
| – | 3 года | + | z | = | 7 | ||||
| 2x | + | года | + | 3z | = | 15 | |||
Теперь представим
.Система линейных уравнений — Simple English Wikipedia, бесплатная энциклопедия
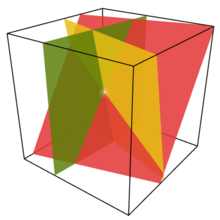 Линейная система с тремя переменными определяет набор плоскостей (по одной плоскости для каждого уравнения). Точка пересечения — это решение.
Линейная система с тремя переменными определяет набор плоскостей (по одной плоскости для каждого уравнения). Точка пересечения — это решение.В математике система линейных уравнений (или линейная система ) представляет собой набор линейных уравнений с одним и тем же набором переменных.
Математики показывают взаимосвязь между различными факторами в форме уравнений.«Линейные уравнения» означают, что переменная появляется только один раз в каждом уравнении без возведения в степень. «Система» линейных уравнений означает, что все уравнения верны одновременно. Итак, человек, решающий систему уравнений, ищет значения каждой переменной, которые сделают все уравнения истинными одновременно. Если никакие такие значения не могут удовлетворять всем уравнениям в системе, то уравнения называются «несовместимыми».
Например,
- 3 Икс + 2 y — z знак равно 1 2 Икс — 2 y + 4 z знак равно — 2 — Икс + 1 2 y — z знак равно 0 {\ displaystyle {\ begin {alignat} {7} 3x && \; + \; && 2y && \; — \; && z && \; = \; && 1 & \\ 2x && \; — \; && 2y && \; + \; && 4z && \; = \ ; && — 2 & \\ — x && \; + \; && {\ tfrac {1} {2}} y && \; — \; && z && \; = \; && 0 & \ end {alignat}}}
— это система трех уравнений от трех переменных Икс {\ displaystyle x} , y {\ displaystyle y} , z {\ displaystyle z} .«Решение» линейной системы — это присвоение чисел переменным таким образом, чтобы все уравнения выполнялись одновременно. Решение указанной выше системы дается формулой
- Икс знак равно 1 y знак равно — 2 z знак равно — 2 {\ displaystyle {\ begin {alignat} {2} x & = & 1 \\ y & = & — 2 \\ z & = & — 2 \ end {alignat}}}
, поскольку он делает все три уравнения действительными: [1]
- 3 ( 1 ) + 2 ( — 2 ) — ( — 2 ) знак равно 1 2 ( 1 ) — 2 ( — 2 ) + 4 ( — 2 ) знак равно — 2 — ( 1 ) + 1 2 ( — 2 ) — ( — 2 ) знак равно 0 {\ displaystyle {\ begin {alignat} {7} 3 (1) && \; + \; && 2 (-2) && \; — \; && (- 2) && \; = \; && 1 & \\ 2 (1 ) && \; — \; && 2 (-2) && \; + \; && 4 (-2) && \; = \; && — 2 & \\ — (1) && \; + \; && {\ tfrac {1 } {2}} (- 2) && \; — \; && (- 2) && \; = \; && 0 & \ end {alignat}}}
В математике теория линейных систем — это раздел линейной алгебры, предмет, который является фундаментальным для современной математики.Компьютерные алгоритмы поиска решений являются важной частью численной линейной алгебры, и такие методы играют важную роль в инженерии, физике, химии, информатике и экономике. Система нелинейных уравнений часто может быть аппроксимирована линейной системой (см. Линеаризация), что является полезным методом при создании математической модели, компьютерной модели или компьютерного моделирования относительно сложной системы. Для сложных систем существует множество уравнений и много переменных, а не только две или три.Во многих случаях количество уравнений и переменных в системе одинаково. В некоторых случаях переменных больше, чем уравнений, и решение будет представлять собой диапазон различных значений, а не одно точное решение.
Простейшая линейная система включает два уравнения и две переменные:
- 2 Икс + 3 y знак равно 6 4 Икс + 9 y знак равно 15 .{\ displaystyle {\ begin {alignat} {5} 2x && \; + \; && 3y && \; = \; && 6 & \\ 4x && \; + \; && 9y && \; = \; && 15 &. \ end {alignat}}}
Один из методов решения такой системы заключается в следующем. Сначала решите верхнее уравнение для Икс {\ displaystyle x} с точки зрения y {\ displaystyle y} :
- Икс знак равно 3 — 3 2 y .{\ displaystyle x = 3 — {\ frac {3} {2}} y.}
Теперь подставьте это выражение для x в нижнее уравнение:
- 4 ( 3 — 3 2 y ) + 9 y знак равно 15. {\ displaystyle 4 \ left (3 — {\ frac {3} {2}} y \ right) + 9y = 15.}
Это приводит к единственному уравнению, включающему только переменную y {\ displaystyle y} . Решение дает y знак равно 1 {\ displaystyle y = 1} , и подставив это обратно в уравнение для Икс {\ displaystyle x} дает Икс знак равно 3 / 2 {\ displaystyle x = 3/2} :
- 2 ( 3 2 ) + 3 ( 1 ) знак равно 6 4 ( 3 2 ) + 9 ( 1 ) знак равно 15 .{\ displaystyle {\ begin {alignat} {5} 2 \ left ({\ frac {3} {2}} \ right) && \; + \; && 3 (1) && \; = \; && 6 & \\ 4 \ left ({\ frac {3} {2}} \ right) && \; + \; && 9 (1) && \; = \; && 15 &. \ end {alignat}}}
Этот метод обобщается на системы с дополнительными переменными.
Очень часто все коэффициенты записываются в виде матрицы A, которая называется матрицей коэффициентов.
- А знак равно [ а 11 а 12 ⋯ а 1 п а 21 год а 22 ⋯ а 2 п ⋮ ⋮ ⋱ ⋮ а м 1 а м 2 ⋯ а м п ] {\ displaystyle A = {\ begin {bmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22} & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \ end {bmatrix}}}
Примерно так же переменные можно записать в виде вектора:
- Икс знак равно [ Икс 1 Икс 2 ⋮ Икс п ] ; б знак равно [ б 1 б 2 ⋮ б м ] {\ displaystyle x = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix}}; \ qquad b = {\ begin {bmatrix} b_ { 1} \\ b_ {2} \\\ vdots \\ b_ {m} \ end {bmatrix}}} .
Это позволяет писать
- А ⋅ Икс знак равно б {\ displaystyle A \ cdot x = b} .
Математически вектор, определенный выше, представляет собой матрицу размером 1 на n. Затем система уравнений может быть решена с помощью операции умножения, определенной для матриц. A, x и b — все части одного алгебраического поля.
Решение системы линейных уравнений [изменить | изменить источник]
Возможны три случая поиска решения системы линейных уравнений:
- Нет решения
- Есть ровно одно решение
- Есть много решений; точное количество зависит от свойств поля.Во многих случаях решений будет бесконечное количество.
Есть две категории методов решения системы линейных уравнений. Итерационные методы используют много шагов для получения решения, прямые методы требуют только одного шага:
- Примером прямого метода является решение системы для одной переменной; эту переменную можно исключить и заменить выражением, в котором используются только другие переменные, или числом. Выполнение этого для всех переменных уравнения приведет к решению системы, если оно существует.
- Другой метод — преобразовать два уравнения так, чтобы одна из сторон уравнений была одинаковой в обоих случаях; тогда можно написать другое уравнение, которое заменяет два уравнения и сокращает количество уравнений на одно.
- Исключение по Гауссу
- QR-разложение
- Разложение Холецкого
- Правило Крамера
Примеры итерационных методов:
Есть такие примеры, как геодезия, где измерений намного больше, чем неизвестных.Такая система почти всегда переопределена и не имеет точного решения. Каждое измерение обычно неточно и включает некоторую погрешность. Поскольку измерения неточны, невозможно получить точное решение системы линейных уравнений; такие методы, как наименьшие квадраты, могут использоваться для вычисления решения, которое наилучшим образом соответствует переопределенной системе. Это решение методом наименьших квадратов часто может использоваться в качестве замены для точного решения.
Решение системы линейных уравнений имеет сложность не более O (n 3 ).Для решения общей системы из n линейных уравнений требуется не менее n 2 операций. Лучший алгоритм, известный на сегодняшний день, был разработан Доном Копперсмитом и Шмуэлем Виноградом и датируется 1990 годом. Он имеет сложность n 2.376 [2] К сожалению, практического применения он не имеет.
Использование компьютеров для решения систем линейных уравнений используется каждый день. Например, он используется в моделях прогнозирования погоды. Фабрики хот-догов используют его, чтобы внести небольшие изменения в рецепт при изменении цен на пищевые ингредиенты.Кафетерии колледжей используют его, чтобы выяснить, сколько еды нужно приготовить, исходя из прошлого опыта, когда в кафетерии студентам предоставляется выбор между несколькими блюдами.
- ↑ Линейная алгебра, обсуждаемая в этой статье, — это очень хорошо сложившаяся математическая дисциплина, для которой существует множество источников. Почти весь материал в этой статье можно найти в Lay 2005, Meyer 2001 и Strang 2005.
- ↑ Джин Голуб, Чарльз Ван Лоан: Matrix Computations , Johns Hopkins University Press, 3-е издание, 1996; ISBN 978-0-8018-5414-9
Учебники [изменить | изменить источник]
- Axler, Sheldon Jay (1997), Linear Algebra Done Right (2-е изд.), Springer-Verlag, ISBN 0387982590
- Лэй, Дэвид К. (22 августа 2005 г.), Линейная алгебра и ее приложения (3-е изд.), Эддисон Уэсли, ISBN 978-0321287137
- Мейер, Карл Д. (15 февраля 2001 г.), Матричный анализ и прикладная линейная алгебра , Общество промышленной и прикладной математики (SIAM), ISBN 978-0898714548
- Пул, Дэвид (2006), Линейная алгебра: современное введение (2-е изд.), Брукс / Коул, ISBN 0-534-99845-3
- Антон, Ховард (2005), Элементарная линейная алгебра (прикладная версия) (9-е изд.), Wiley International
- Леон, Стивен Дж. (2006), Линейная алгебра с приложениями (7-е изд.), Pearson Prentice Hall
- Стрэнг, Гилберт (2005), Линейная алгебра и ее приложения
Системы линейных уравнений: определения (стр. 1 из 7) Разделы: определения, решения путем построения графиков, подстановки, исключения / добавления, исключения Гаусса. А «система» уравнения — это набор или набор уравнений, с которыми вы работаете вместе однажды.Линейные уравнения (те, которые отображаются в виде прямых линий) проще чем нелинейные уравнения, и простейшая линейная система — это система с два уравнения и две переменные. Вспомните линейные уравнения. Например, рассмотрим линейное уравнение y = 3 x — 5. «Решение» к этому уравнению была любая точка x , y , которая «работала» в уравнении. Итак (2, 1) было решением, потому что подключение 2 для x : С другой стороны, (1, 2) не было решением, потому что, подключение 1 для x : … что не равно и (что было 2, для этого пункта). Конечно, в практическом плане решений вы не нашли в уравнение, выбирая случайные точки, вставляя их и проверяя чтобы увидеть, «работают» ли они в уравнении. Вместо этого вы выбрали значения x а затем вычислили соответствующие значения и . И вы использовали ту же процедуру для построения графика уравнение. это указывает на важный факт: каждая точка на графике была решением к уравнению, и любое решение уравнения отмечалось точкой на графике. Теперь рассмотрим следующее система линейных уравнений с двумя переменными:
В частности, этот фиолетовый точка отмечает пересечение двух линий.Поскольку эта точка находится на обе линии, таким образом, он решает оба уравнения, поэтому он решает всю систему уравнения. И это соотношение всегда верно: для систем уравнений «решения» — это «пересечения». Вы можете подтвердить решение, подставив его в систему уравнений и подтвердив, что решение работает в каждом уравнении. Проверить данные возможные решения, я просто подключаю x — и y — координаты в уравнения и проверьте, работают ли они. авторское право © Элизабет Стапель 2003-2011 Все права защищены Поскольку данная точка работает в каждом уравнении, это решение системы. Теперь проверю другой пункт (который мы уже знаем, глядя на график, это не решение): Итак, решение работает в одном из уравнений. Но чтобы решить систему, она должна работать в обоих уравнениях.Продолжая чек: Но –2 не равно –6, так что это «решение» не проверяет. Тогда ответ: только точка (–1, –5) — это решение системы Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Возвращение к указателю Вперед >>
|
подпрограмм LAPACK: линейные уравнения
Подпрограммы LAPACK: линейные уравненияПримеры LAPACK для библиотеки Intel® Math
Подпрограммы LAPACK: линейные уравнения
Библиотека ядра Intel® Math включает процедуры LAPACK для решения систем линейных уравнений, факторизации и обращения матриц, и оценка числа условий.
Для решения той или иной задачи можно вызвать два или более вычислительных подпрограмм или вызовите соответствующую подпрограмму драйвера , которая объединяет несколько задач за один вызов, например ? gesv для факторинг и решение.Например, чтобы решить систему линейных уравнений с общей матрицей звоните ? getrf ( LU факторизация), а затем ? getrs (вычисление решение). Позвоните по номеру ? Gerfs , чтобы уточнить решение. и получите границы ошибок. В качестве альтернативы можно использовать программу драйвера ? Gesvx , которая выполняет все эти задачи за один вызов.
Вы также можете найти подходящую программу, используя характеристики вашего данные и операции , необходимые с помощью Intel® MKL Советник по поиску функций LAPACK, который поможет вам найти подходящую процедуру ваши потребности лучше всего.
Осторожно
Стандартные функции LAPACK не проверьте входные данные (матрицы) на предмет INF с плавающей запятой IEEE 754 или NANS. INF и NAN будут распространяться через вычисления и могут вызвать неожиданные результаты или нестабильность. Это ответственность пользователя чтобы гарантировать, что входные данные не содержат INF или NaN.
Функции LAPACKE (интерфейс C для LAPACK) проверьте наличие NaN во входных данных (матрицах) и код ошибки возвращается, если найдена NAN.
Подпрограммы драйвера для решения систем линейных уравнений:
Обычный | Описание | Примеры |
|---|---|---|
? Gesv | Вычисляет решение системы линейные уравнения с квадратной матрицей A и множественные правые части. | cgesv dgesv гесв zgesv |
? Posv | Вычисляет решение системы линейные уравнения с симметричным или эрмитовым положительно определенным матрица A и несколько правых частей. | cposv dposv спосв zposv |
? Sysv | Вычисляет решение системы линейные уравнения с вещественной или комплексной симметричной матрицей A и кратными правыми частями. | csysv dsysv ssysv zsysv |
? Hesv | Вычисляет решение системы линейные уравнения с эрмитовой матрицей A и множественные правые части. | чешв жесв |

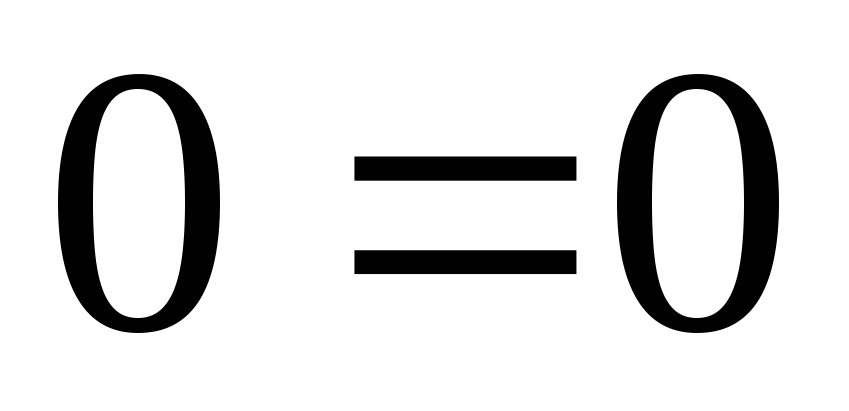 ;
;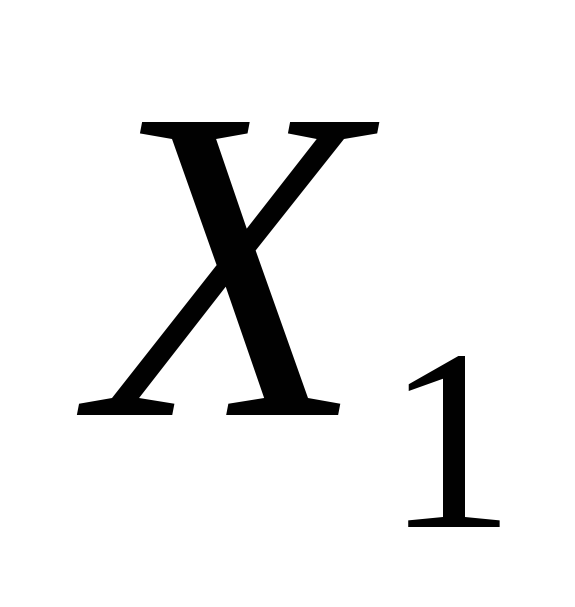 — решение системы, то и
— решение системы, то и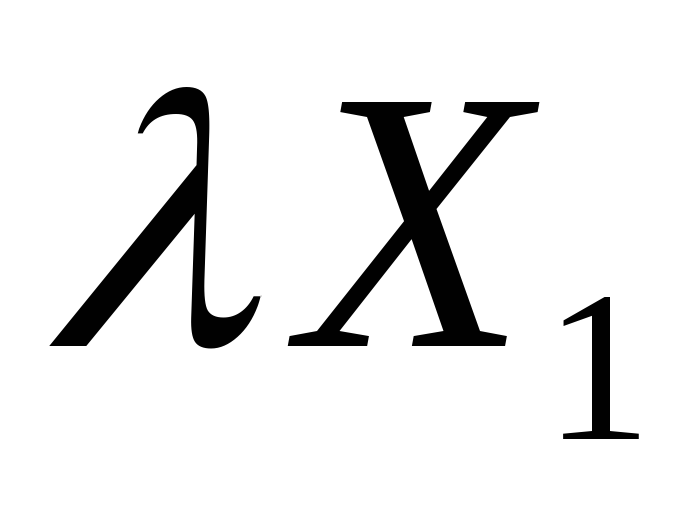 — также решение.
— также решение.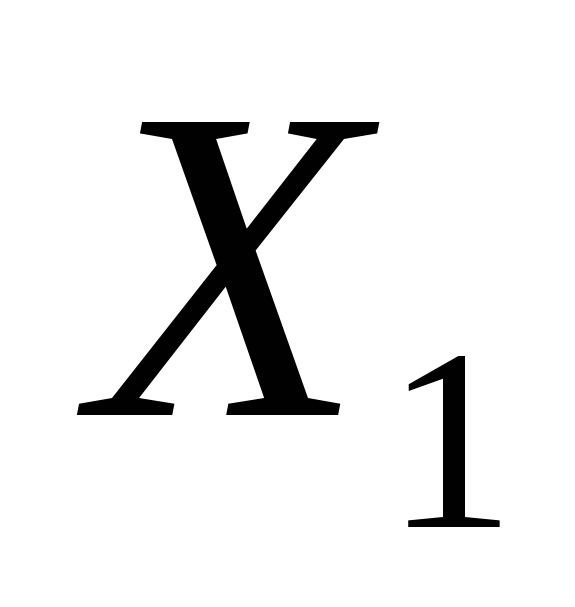 и
и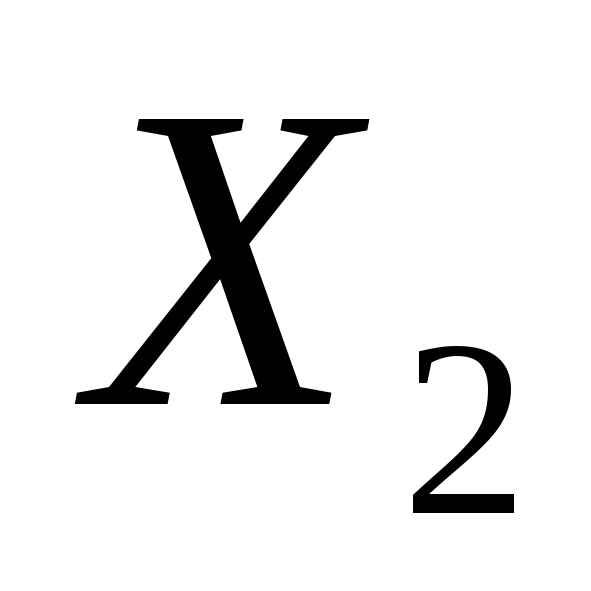 — решения системы, то и
— решения системы, то и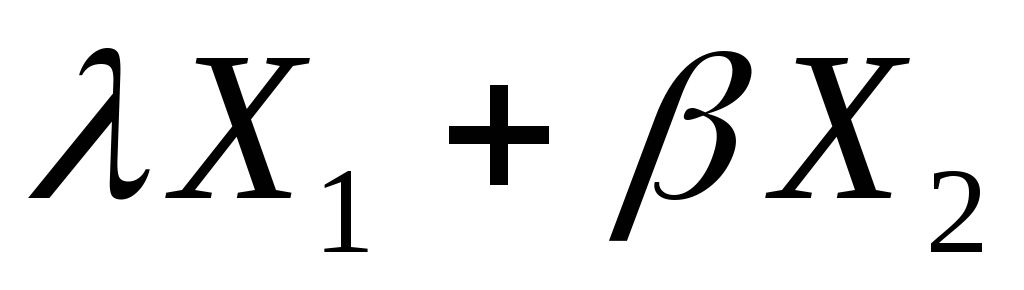 — также решение.
— также решение.