Системы неравенств с одним неизвестным: Системы неравенств с одним неизвестным

Системы неравенств с одним неизвестным

Система, которая содержит неравенства с одним неизвестным, еще называется системой линейных неравенств.

Определение 1

Система неравенств с одним неизвестным — это совокупность двух или большего числа неравенств, которые содержат одну и ту же неизвестную величину.

Например, $\left\{ \begin{array}{c} {x-1 >2,} \\ {3+x\le 7;} \end{array} \right.$

решения системы неравенств

С этой целью необходимо отдельно найти все возможные решения каждого из неравенств системы, а после отыскать общее решение, которое состоит из общей части всех найденных решений, т. е. все значения, входящие в каждое из этих решений.

При решении любого вида системы из двух неравенств с одним неизвестным каждое неравенство сводится к виду $xc$ (переменная переносится в левую часть неравенства, а свободный член — в правую). Результатом такого преобразования является получение простейших систем.

Рассмотрим возможные варианты таких систем:

Пусть $a

1. $\left\{ \begin{array}{c} {x

   Решение системы: $x

2. $\left\{ \begin{array}{c} {x >a,} \\ {x >b,} \end{array} \right.$

   Решение системы: $x >b$.

3. $\left\{ \begin{array}{c} {x >a,} \\ {x

   Решение системы: $a

4. $\left\{ \begin{array}{c} {xb,} \end{array} \right.$

Решение системы: система решения не имеет, т.к. не существует таких чисел, которые одновременно меньше меньшего числа и больше большего числа.

Все четыре случая описывают все возможные варианты систем из двух неравенств с одним неизвестным и интуитивно понятны.

Часто для решения систем как двух, так и большего числа неравенства, используют числовую прямую, на которую наносят все решения каждого из неравенств системы, а затем ищут те значения, которые принадлежат каждому из решений. Найденные значения и являются решением заданной системы неравенств.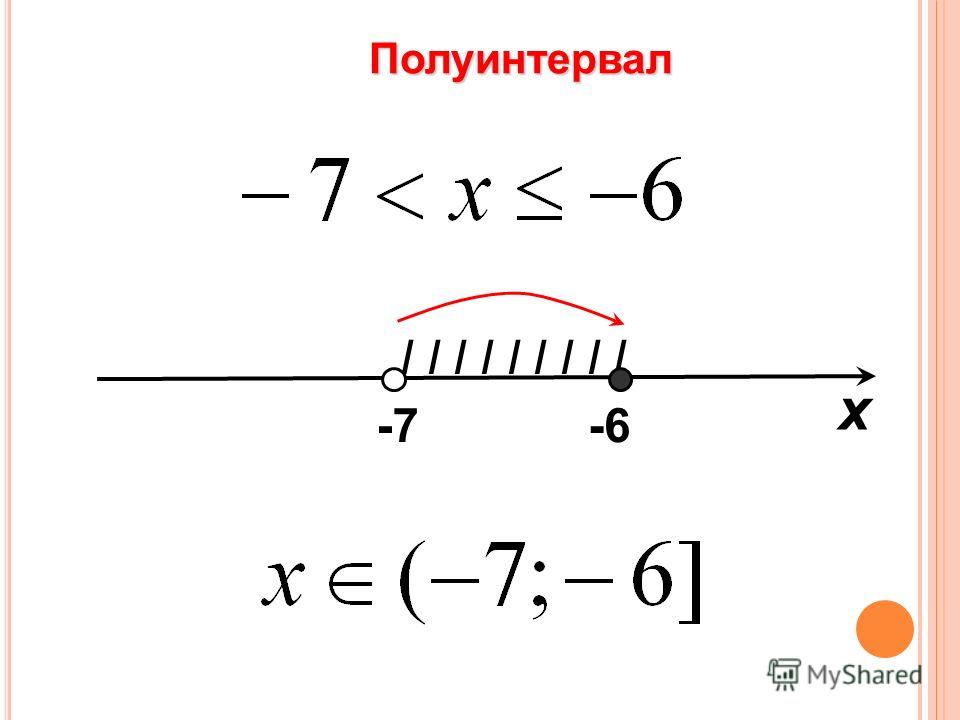

Пример 1

Найти решение системы:

\[\left\{ \begin{array}{c} {7x+19Решение.

Преобразуем оба неравенства системы к виду $xc$):

\[\left\{ \begin{array}{c} {7x+19Мы получили 2-й вариант системы неравенств, при котором решением системы будет $x

Ответ: $x

Легко получить или проверить данное решение, если нанести решение каждого неравенства на числовую прямую. Сразу станет очевидным общее решение системы.

Пример 2

Найти решение системы:

\[\left\{ \begin{array}{c} {4x-28.} \end{array} \right.\]

Решение.

Преобразуем оба неравенства системы к виду $xc$:

\[\left\{ \begin{array}{c} {4x-28.} \end{array} \right.\] \[\left\{ \begin{array}{c} {2×14;} \end{array} \right.\] \[\left\{ \begin{array}{c} {x7.} \end{array} \right.\]

Мы получили 4-й вариант системы неравенств, при котором система решений не имеет.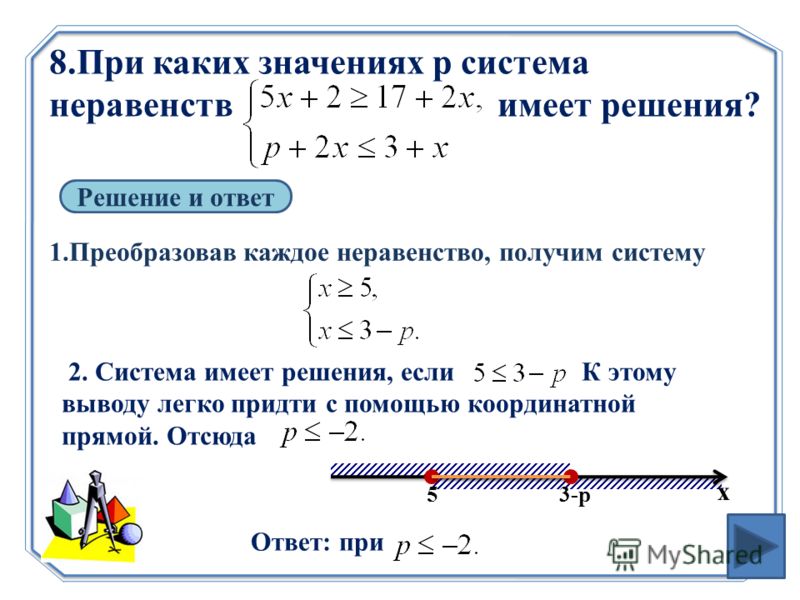

Ответ: система решений не имеет.

Пример 3

Найти значения, при которых дробь $\frac{3x+3}{8x-20}$ будет принимать отрицательные значения.

Решение.

Дробь будет отрицательной, если ее числитель и знаменатель будут иметь разные знаки. Составим два возможных варианта системы:

1. $\left\{ \begin{array}{c} {3x+3 >0,} \\ {8x-20

2. $\left\{ \begin{array}{c} {3x+30.} \end{array} \right.$

Решим первую систему:

\[\left\{ \begin{array}{c} {3x+3 >0,} \\ {8x-20-1,} \\ {8x-1,} \\ {x

Решением первой системы будут значения переменной, удовлетворяющие условию $-1

Решим вторую систему:

\[\left\{ \begin{array}{c} {3x+30;} \end{array} \right.\] \[\left\{ \begin{array}{c} {3x >-3,} \\ {8×2,5;}; \end{array} \right.\]

Данная система решений не имеет.

Ответ: дробь $\frac{3x+3}{8x-20}$ будет принимать отрицательные значения при $-1

При решении подобных примеров ошибочно составляют третью систему, которая состоит из решений первой и второй системы. Такой подход является грубой ошибкой, т.к. каждая из систем является самостоятельной и не зависит от другой.

Системы также могут состоять из нестрогих неравенств, которые содержат знаки $\le $ и $\ge $. Решение таких систем ничем не отличается от выше рассмотренных с той лишь разницей, что в случае нестрогого неравенства в решение включается значение конца или начала промежутка.

Пример 4

Найти решение системы:

\[\left\{ \begin{array}{c} {x+7\ge 3,} \\ {2x\le -6.} \end{array} \right.\]

Решение.

Преобразуем оба неравенства системы к виду $x\le c$ или $x\ge c$:

\[\left\{ \begin{array}{c} {x+7\ge 3,} \\ {2x\le -6.} \end{array} \right.\] \[\left\{ \begin{array}{c} {x\ge -4,} \\ {x\le -3.} \end{array} \right.\]

Найдем решение с помощью числовой прямой:

Решением системы будут значения переменной, удовлетворяющие условию $-4\le x\le -3$.

Ответ: $-4\le x\le -3$.

Презентация «Системы неравенств с одним неизвестным.

Числовые промежутки.» 8 класс | Презентация к уроку по математике (8 класс) по теме:

Опубликовано 16.10.2017 — 19:12 — Харитонова Дарья Александровна

Несколько неравенств с одной переменной образуют систему, если задача ставится  найти все общие решения заданных неравенств.

Систему неравенств символически обозначают фигурной скобкой, которая была введена  в начале 17 века. Предложил фигурные скобки Ф. Виет. 

Числовые промежутки

Отметим на координатной прямой точки с координатами  -4 и 3

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Слайд 1

Системы неравенств с одним неизвестным. Числовые промежутки.

Слайд 2

Несколько неравенств с одной переменной образуют систему, если задача ставится найти все общие решения заданных неравенств. Систему неравенств символически обозначают фигурной скобкой, которая была введена в начале 17 века. Предложил фигурные скобки Ф. Виет.

Слайд 3

Числовой промежуток -4 3 х -4 3

Слайд 4

Обозначение числовых промежутков -4 3 -4

Слайд 5

Обозначение числовых промежутков 8 х > 8 Промежуток: Промежуток: 8 х

Слайд 6

Обозначение числовых промежутков 8 х ≥ 8 Промежуток: Промежуток: 8 х ≤ 8 х – любое число Промежуток :

Слайд 7

I I I I I I I I I I I I I I I I х 2

Слайд 8

I I I I I I I I I I I I I I I х -2,3

Слайд 9

I I I I I I I I I I I I I I I х -2,31

Слайд 10

I I I I I I I I I х 2 2,5 Интервал

Слайд 11

I I I I I I I I I х -7 -6 Полуинтервал

Слайд 12

I I I I I I I I I х -11 11 Полуинтервал

Слайд 13

I I I I I I I I I х -11 -10 Отрезок

Слайд 14

Решите неравенство и укажите два его решения Вариант I Вариант II Самостоятельная работа

По теме: методические разработки, презентации и конспекты

Методическая разработка урока «Система неравенств с одним неизвестным.

Числовые промежутки»

Методическая разработка урока для 8 класса….

План – конспект урока по алгебре «Неравенства с одним неизвестным. Системы неравенств»

План – конспект урока по алгебре «Неравенства с одним неизвестным. Системы неравенств». Алгебра 8 класс. Учебник для общеобразовательных учреждений. Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др.Цель…

Линейные неравенства с одним неизвестным

решение неравенств…

9 класс. Тест 1. «Линейные неравенства с одним неизвестным»

9 класс. Тест 1. «Линейные неравенства с одним неизвестным», 4 варианта. Тематические тесты П.В. Чулкова к учебнику С.М. Никольского, 9 класс…

9 класс. Самостоятельная работа по теме: «Системы линейных неравенств с одним неизвестным»

9 класс. Самостоятельная работа по теме: «Системы линейных неравенств с одним неизвестным&quot…

Алгоритм решения линейных неравенств с одним неизвестным (8 класс)

Алгоритм решения линейных неравенств с одним неизвестным с примерами решения (8 класс). …

Конспект урока по теме «Решение линейных неравенств с одной переменной. Числовые промежутки»

Конспект урока…

Поделиться:

 

Система линейных неравенств с одной переменной

Что такое линейные неравенства

Линейные функции включают линейные уравнения и неравенства. Линейные неравенства — это алгебраические выражения, которые содержат знак неравенства, например больше «>», меньше «<», больше равно «» или меньше равно «». Линейные неравенства с одной переменной содержат только одну переменную. В отличие от множества решений линейного уравнения с двумя переменными, которое задается упорядоченной парой, удовлетворяющей обоим неравенствам, линейное неравенство с одной переменной задается в интервальной записи. Мы знаем, что график линейного неравенства с двумя переменными представляет собой прямую линию. Область, представляющая набор решений, заштрихована. С другой стороны, решения линейных неравенств с одной переменной изображаются на числовой прямой. При подстановке в каждое неравенство значений из множества решений системы неравенств с одной переменной множество решений является истинным для каждого неравенства.

Лучшие репетиторы по математике

Поехали

Система линейных неравенств

Мы пишем системы линейных неравенств так же, как системы уравнений, используя фигурную скобку «{«. Общая стратегия решения неравенств такая же, как и решение уравнений, однако набор решений системы неравенств представляется иначе, чем система линейных уравнений. Каждое линейное неравенство решается отдельно, а их наборы решений объединяются для получения окончательного решения всей системы. Набор решений записывается либо в скобках, либо в квадратных скобках. В этой статье мы увидим, как решить систему линейных неравенств, записать их решения в интервальной записи и представить решения на числовой прямой.

Найдите лучших репетиторов по математике рядом со мной.

Пример 1

Решите следующую систему линейных неравенств с одной переменной. Запишите набор решений в интервальной записи и представите систему на числовой прямой.

Решение

Чтобы найти набор решений, мы решим приведенное выше неравенство в несколько шагов.

Шаг 1-Решение неравенств в системе отдельно

Первое неравенство . Решите его алгебраически, как вы решаете линейное уравнение.

Вычитание 3 из обеих частей неравенства даст следующее выражение:

Чтобы выделить левую часть неравенства, обе части неравенства будут разделены на 2.

На словах мы можем выразить это неравенство как больше или равно -1. Теперь решим второе неравенство системы.

Вычтем -2 из обеих частей неравенства, чтобы получить следующее выражение:

Теперь вы помните правило неравенства, которое гласит, что если обе части неравенства умножить на отрицательные числа, знак неравенства меняется на противоположный. Поскольку с переменной связан отрицательный знак, умножение обеих сторон неравенства на -1 даст следующий результат:

Мы можем видеть, что умножение обеих сторон на минус 1 изменило знак неравенства на меньшее чем или равно.

Шаг 2 — Запись набора решений обоих неравенств в интервальной записи по отдельности

Прежде чем записывать систему линейных неравенств в интервальной записи, сначала запишите каждое неравенство в интервальной записи отдельно. После упрощения первого неравенства получили . В интервальной записи это будет записано как:

Упрощенная форма второго неравенства была . В интервальной записи это будет записано так:

Шаг 3- Объединение множества решений в интервальной записи обоих неравенств

Теперь мы объединим множество решений обоих неравенств. Множествами решений обоих неравенств являются и . Мы объединим их следующим образом:

U

Теперь мы возьмем наименьшую начальную точку и наибольшую конечную точку из обоих интервалов. Наименьшая начальная точка равна -1, а наибольшая конечная точка равна 3, поэтому в записи интервала окончательное решение будет записано как:

Как видите, мы использовали квадратные скобки с обеих сторон от начальной и конечной точки, потому что -1 и 3 были частью набора решений. Это также показывает, что это закрытый интервал.

Шаг 4. Представление набора решений на числовой прямой

Теперь последний шаг — представление набора решений на числовой прямой. Вы можете либо напрямую представить набор решений на числовой прямой, либо сначала представить оба неравенства по отдельности, как показано ниже. Вы можете видеть, что мы использовали закрытые кружки для -1 и 3, потому что эти два числа были частью набора решений.

 

Пример 2

Решите следующую систему линейных неравенств с одной переменной. Запишите набор решений в интервальной записи и представите систему на числовой прямой.

Решение

Как и в примере 1, мы будем решать вышеуказанное неравенство в несколько шагов.

Шаг 1-Решение неравенств в системе по отдельности

Сначала решите первое неравенство в системе следующим образом:

Вычитая 3 из обеих частей неравенства, получим следующее выражение:

Чтобы выделить переменную в левой части неравенства, разделим обе части на 2:

Теперь, решить вторую часть неравенства

Из обеих частей неравенства вычесть 6:

Так как переменная в полученном неравенстве отрицательна, то обе части умножим на -1. Это также перевернет знак неравенства и изменит знак -3 в правой части.

Шаг 2 — Запись набора решений обоих неравенств в интервальной записи по отдельности

После упрощения первого неравенства мы получили . В интервальных обозначениях это будет записано как:

Вы можете видеть, что мы использовали круглые скобки с обеих сторон неравенства, потому что -1 не является частью решения.

Упрощенная форма второго неравенства была . В интервальной записи это будет записано как:

Мы снова не использовали квадратные скобки до или после начальной и конечной точек, потому что 3 не включено в набор решений.

Шаг 3. Объединение набора решений в интервальной записи обоих неравенств

Теперь мы объединим набор решений в интервальной записи обоих неравенств. Интервальное обозначение первого неравенства есть, а решение, заданное в интервальном обозначении второго неравенства, есть .

Объединение этих неравенств вообще не дает решения.

Шаг 4. Представление множества решений на числовой прямой

Поскольку система неравенств вообще не имеет решения, то на числовой прямой не будут представлены общие значения, которые являются частью обоих неравенств.

Найдите репетитора по математике на Superprof.

Пример 3

Решите следующую систему линейных неравенств с одной переменной. Запишите набор решений в интервальной записи и представите систему на числовой прямой.

Решение

Чтобы найти набор решений, мы решим приведенное выше неравенство в несколько шагов.

Шаг 1-Решение неравенств в системе отдельно

Сначала решите первое неравенство в системе следующим образом:

Примените основные операции сложения и вычитания, чтобы упростить приведенное выше неравенство:

Прибавив 4 к обе стороны неравенства дадут:

Вычтите из обеих частей неравенства, чтобы выделить переменную в левой части:

Теперь, для решения второй части неравенства, объедините одинаковые члены, как вы делаете при решении линейных уравнений:

Разделите обе части на 4, чтобы получить результирующее неравенство в упрощенной форме:

Шаг 2. Запись набора решений обоих неравенств в интервальной записи по отдельности

Упрощение первого неравенства дало нам . Интервальную запись первого неравенства запишем так:

Аналогично, упростив второе неравенство, получили . Интервальное обозначение второго неравенства будет записано так:

Шаг 3. Объединение набора решений в интервальной записи обоих неравенств

Теперь мы объединим набор решений в интервальной записи обоих неравенств. Интервальное обозначение первого неравенства есть, а решение, заданное в интервальном обозначении второго неравенства, есть . Объедините эти два неравенства следующим образом:

U

Окончательное решение, заданное в интервальной записи, будет записано путем взятия меньшей начальной точки и больших конечных точек из интервалов обоих неравенств. Так как меньшая начальная точка равна 1, а большая конечная точка , то запись интервала системы будет:

Окончательное решение — открытый интервал.

Шаг 4-Представление набора решений на числовой прямой

Интервальное обозначение системы неравенств . Он показывает, что интервал имеет бесконечно много решений. В числовой строке это будет выглядеть так:

Как видите, поскольку 1 не входит в интервал, мы использовали незакрашенный кружок для его представления на числовой прямой.

Пример 4

Решите следующую систему линейных неравенств с одной переменной. Запишите набор решений в интервальной записи и представите систему на числовой прямой.

Решение

Выполните следующие шаги, чтобы решить вышеуказанное неравенство.

Шаг 1-Решение неравенств в системе отдельно

Возьмите первое неравенство из системы и объедините одинаковые члены, взяв коэффициенты в левой части и константы в правой части неравенства:

Теперь решите второе неравенство следующим образом:

Вычтите и прибавьте 2 к обеим частям неравенства:

Шаг 2 — Запись набора решений обоих неравенств в интервальной записи по отдельности

Упрощая первое неравенство, получаем . Интервальную запись первого неравенства запишем так:

Аналогично, упростив второе неравенство, получили . Интервальное обозначение второго неравенства будет записано так:

 

Шаг 3. Объединение набора решений в интервальной записи обоих неравенств

Теперь мы объединим набор решений в интервальной записи обоих неравенств неравенства. Интервальное обозначение первого неравенства равно  , а решение, заданное в интервальном обозначении второго неравенства, равно . Объедините эти два неравенства следующим образом:

U

Окончательное решение, заданное в интервальной записи, будет записано путем взятия наименьшей начальной точки и наибольшей конечной точки из интервалов обоих неравенств. Поскольку наименьшая начальная точка равна 1, а большая конечная точка также равна 1, интервальная запись системы будет следующей:

Следовательно, система имеет только одно решение. Мы заключили единственное решение в квадратных скобках, потому что интервал замкнут.

Шаг 4. Представление набора решений в числовой строке

Интервальная запись системы неравенств . Это показывает, что интервал имеет только одно решение. На числовой строке это будет выглядеть так:

Вы можете видеть, что, поскольку 1 включена в интервал, мы использовали замкнутый кружок, чтобы представить его на числовой строке.

Найдите лучших репетиторов по математике на Superprof.

Проверьте, нет ли рядом со мной выдающегося репетитора по математике.

Решение систем неравенств — SAT Математика

Все математические ресурсы SAT

137 Практические тесты Вопрос дня Карточки Learn by Concept

SAT Mathematics Help » Неравенства и абсолютное значение » Решение систем неравенств

Если  и , что из следующего должно быть верным?

Возможные ответы:

Правильный ответ:

Объяснение:

Системы неравенств можно решать так же, как системы уравнений, но с тремя важными оговорками:

1) Вы можете использовать только метод исключения, но не метод замены. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) При объединении неравенств всегда нужно складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Имея все это в виду, здесь вы можете сложить эти два неравенства и сложить их вместе:

Обратите внимание, что условия сокращаются, и что с  сверху и снизу у вас остается только одна переменная, . Новое неравенство дает вам ответ, .

Обратите внимание, что если бы это появилось в разделе разрешенных калькулятором, вы могли бы просто изобразить неравенства графически и найти их перекрытие, чтобы использовать процесс исключения для вариантов ответа.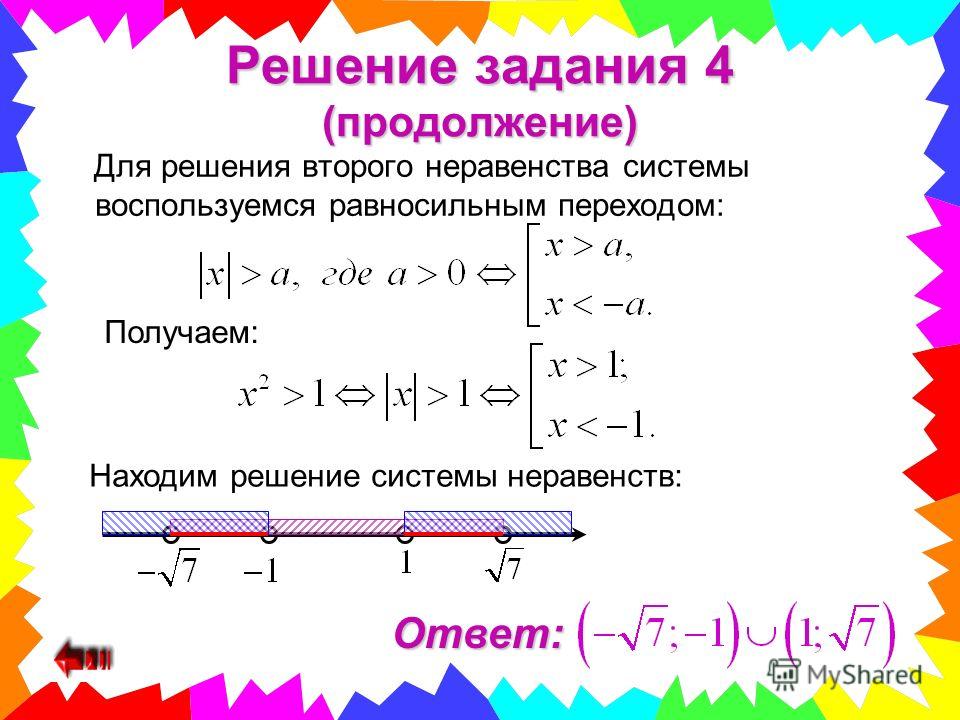 Эти два неравенства пересекаются в точке (15, 39).

 

Сообщить об ошибке

На основании приведенной выше системы неравенств, какое из следующих утверждений должно быть верным?

Возможные ответы:

Правильный ответ:

Объяснение:

Системы неравенств можно решать так же, как и системы уравнений, но с тремя важными оговорками:

1) Вы можете использовать только метод исключения, а не метод подстановки. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) При объединении неравенств всегда нужно складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Имея все это в виду, вы можете сложить эти два неравенства, чтобы получить:

Итак. Это соответствует варианту ответа, так что все готово. Обратите внимание, что процесс исключения здесь сложен, учитывая, что  это всегда положительная переменная на стороне «больше чем» неравенства, что означает, что она может быть настолько большой, насколько вы хотите. И пока  больше чем ,  может быть очень большим или очень маленьким. Вот почему проблемы с системами неравенств лучше всего решать с помощью алгебры; возможности могут быть бесконечными, пытаясь визуализировать числа, но алгебра поможет вам найти прямые, известные пределы.

 

Сообщить об ошибке

Если x > r и y < s, какое из следующих утверждений также должно быть верным?

Possible Answers:

x — y > r — s

x — s > r — y 

x + y > r + s

xs>ry

Правильный ответ:

x — y > r — s

Объяснение:

Из-за всех перечисленных здесь переменных многие студенты испытывают искушение выбрать свои собственные числа, чтобы попытаться доказать или опровергнуть каждый вариант ответа. Но важная техника работы с системами неравенств заключается в том, чтобы обращаться с ними почти так же, как с системами уравнений, только с тремя важными оговорками:0005

1) Вы можете использовать только метод исключения, но не метод замены. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) При объединении неравенств всегда нужно складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Здесь первый шаг — сделать так, чтобы знаки указывали в одном направлении. У вас уже есть x > r , поэтому переверните другое неравенство, чтобы получить s > y (что то же самое — на самом деле вы не манипулируете им; если y меньше s, то, конечно, s больше, чем г). Теперь у вас есть:

x > r

s > y

И вы можете добавить неравенства:

x + s > r + y

900 , а теперь посмотрите на другие варианты ответов. Два из них включают член x и y с одной стороны и член s и r с другой, поэтому вы можете вычесть одни и те же переменные (y и s) с каждой стороны, чтобы получить:

x — y > r — s

Сообщить об ошибке

Если  и , что из следующего должно быть правдой?

Возможные ответы:

Правильный ответ:

Объяснение:

Системы неравенств можно решать так же, как и системы уравнений, но с тремя важными оговорками:

1) Вы можете использовать только метод исключения, а не метод подстановки. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) При объединении неравенств всегда нужно складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Так что это значит для вас здесь? У вас есть два неравенства, одно касается  , а другое – . Но все ваши варианты ответов представляют собой одно равенство как с , так и  в сравнении. Поскольку оба заданных вами неравенства «больше», то есть знаки указывают в одном направлении, вы можете сложить эти два неравенства вместе:

Суммирует:

А теперь вы можете просто разделить обе части на 3, и вы получите:

Какое число

соответствует варианту ответа и, следовательно, является вашим правильным ответом.

Сообщить об ошибке

Что из следующего состоит из -координат всех точек, которые удовлетворяют приведенной выше системе неравенств?

Возможные ответы:

Правильный ответ:

Объяснение:

Системы неравенств можно решать так же, как и системы уравнений, но с тремя важными оговорками:

1) Вы можете использовать только метод исключения, а не метод подстановки. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) Когда вы комбинируете неравенства, вы всегда должны складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Здесь у вас есть знаки, указывающие в одном направлении, но у вас нет одинаковых коэффициентов для  , чтобы исключить его, чтобы остались только  члены (что и является вашей целью, поскольку вас просят решить для диапазон для ). Итак, вы захотите умножить второе неравенство на 3, чтобы коэффициенты совпали. Это дает:

Когда вы затем складываете два неравенства и суммируете их, у вас есть:

+

:

Вы можете разделить обе стороны на 4, чтобы получить свой ответ:

. Сообщить об ошибке

Что из следующего состоит из -координат всех точек, которые удовлетворяют приведенной выше системе неравенств?

Возможные ответы:

Правильный ответ:

Пояснение:

Эта задача о системах неравенств вознаграждает вас за творческую алгебру, учитывающую свойство транзитивности. Вы это знаете, и, поскольку вас спрашивают о чем-то, вы хотите извлечь из этого заявления как можно больше пользы. И хотя вы точно не знаете, что такое, второе неравенство говорит вам об этом. Обратите внимание, что алгебра позволяет прибавлять (или вычитать) одно и то же к обеим сторонам неравенства, поэтому, если вы хотите узнать больше, вы можете просто прибавить к обеим частям этого второго неравенства. При этом  вы обнаружите, что  становится , или .

Теперь у вас есть два неравенства, каждое из которых включает .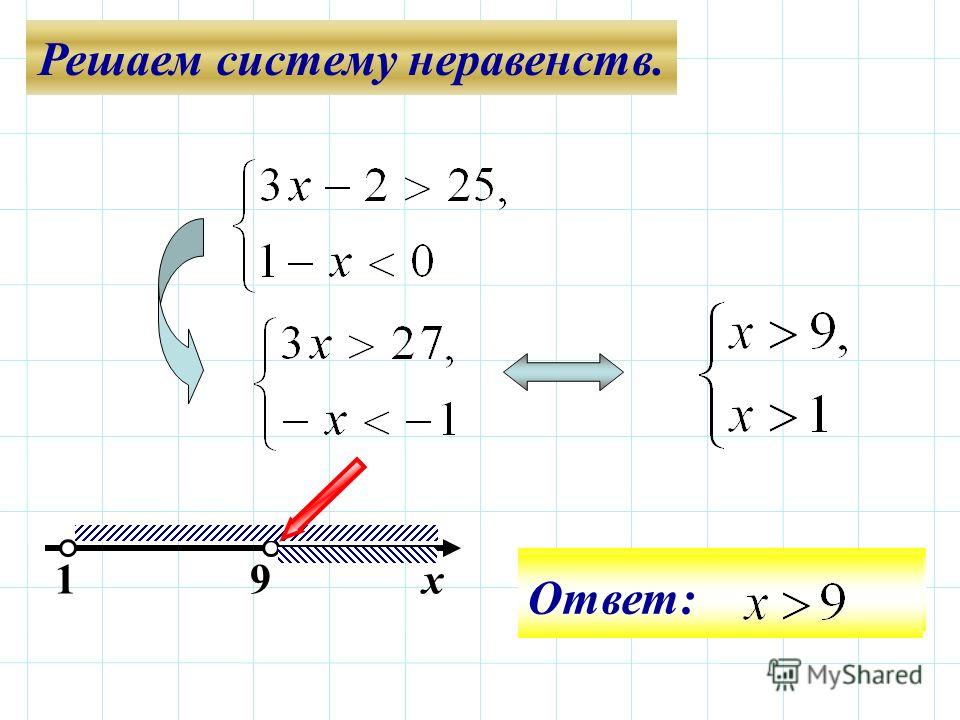 Если  и , то по транзитивному свойству, .

 

Сообщить об ошибке

Какое из следующих значений представляет полный набор значений для , которые удовлетворяют приведенной выше системе неравенств?

Возможные ответы:

Правильный ответ:

Объяснение:

Системы неравенств можно решать так же, как системы уравнений, но с тремя важными оговорками:

1) Вы можете использовать только метод исключения, но не метод замены. Поскольку вы решаете только диапазоны в неравенствах (например, a < 5), а не точные числа (например, a = 5), вы не можете сделать прямую замену числа для переменной.

2) Для объединения неравенств знаки неравенств должны быть направлены в одну сторону.

3) При объединении неравенств всегда нужно складывать и никогда не вычитать. Поскольку вычитание неравенств сродни умножению на -1 и сложению, это приводит к ошибкам с перевернутыми знаками и отрицательными членами. Всегда старайтесь добавлять неравенства, когда пытаетесь их комбинировать.

Здесь вы должны увидеть, что члены имеют одинаковый коэффициент (2), а это означает, что если вы можете переместить их в одну и ту же сторону соответствующих им неравенств, вы сможете объединить неравенства и исключить переменную. Для этого вычтите из обеих частей второго неравенства, получив систему:

 (первое, неизменное неравенство)

 (новое второе неравенство)

Когда вы просуммируете эти неравенства, у вас останется:

Здесь вам нужно запомнить важное правило о неравенствах: если вы умножаете или делите на минус, вы должны перевернуть знак. Таким образом, чтобы разделить на -2, чтобы изолировать , вам придется перевернуть знак:

 

 

Сообщить об ошибке

Если   и , что из следующего должно быть правдой?

Возможные ответы:

Правильный ответ:

Объяснение:

Когда учащиеся сталкиваются с абстрактными проблемами неравенства, они часто выбирают числа для проверки результатов. Но это может занять много времени и сбить с толку — обратите внимание, что с таким количеством переменных и каждым заданным неравенством, включая вычитание, вам придется учитывать возможности положительных и отрицательных чисел для каждого, чисел, которые расположены близко друг к другу, а не далеко друг от друга. Есть много вариантов.

Более прямой способ решения функций с помощью алгебры. Обратите внимание, что за два шага алгебры вы можете получить оба неравенства в одних и тех же терминах: Если вы прибавите к обеим частям, вы получите:

А если вы прибавите к обеим частям, вы получите:

Если вы затем объедините неравенства, вы знаете, что и, поэтому должно быть верно то, что.

Сообщить об ошибке

Какое из следующих значений является возможным значением x с учетом приведенной ниже системы неравенств?

3x+4y> 54

-4x+2y <10

Возможные ответы:

5

4

-5

-3

Правильный ответ: 5 9000 5

. Правильный ответ: 5 9000 5

. Объяснение:

Чтобы объединить эту систему неравенств, мы хотим, чтобы наши знаки указывали в одном направлении, чтобы мы могли складывать неравенства. Мы также пытаемся найти диапазон x в неравенстве, поэтому нам нужно исключить другое неизвестное, y. Чтобы выполнить обе эти задачи за один шаг, мы можем умножить оба знака второго неравенства на -2, что даст нам

3x+4y > 54 (наше исходное первое неравенство)

8x-4y > -10 (наше новое, измененное второе неравенство)

 

Теперь мы можем сложить неравенства, поскольку наши знаки имеют одинаковое направление (и когда Я начинаю с чего-то большего и добавляю к нему что-то большее, конечный результат всегда будет больше), чтобы получить

3x+4y > 54

+8x-4y > -10

11x > 44

5

Таким образом, разделив на 11, мы получим 9. 0005

x > 4. Этому упрощенному неравенству соответствует только положительное число 5 .

Сообщить об ошибке

Какой из следующих наборов координат находится в графическом наборе решений для системы неравенств ниже?

x+2y > 16

-3x+y < 1

Возможные ответы:

(3, 8)

(1, 1)

(-7, 05) 1900 )

Правильный ответ:

(3, 8)

Объяснение:

Чтобы объединить эту систему неравенств, мы хотим, чтобы наши знаки указывали в одном направлении, чтобы мы могли складывать неравенства. Мы также хотим иметь возможность исключить одну из наших переменных. Для этого мы можем умножить обе части нашего второго уравнения на -2, получив

x+2y > 16 (наше исходное первое неравенство)

6x- 2y > -2 (наше новое второе неравенство, измененное)

 

Добавление этих неравенств дает нам

x +2y> 16

+6x- 2y> -2

7x> 14

Разделив это неравенство на 7 до

x> 2.