Глава I Системы двух линейных уравнений с двумя неизвестными
Муниципальное общеобразовательное учреждение
гимназия №64
II научно – практическая конференция
исследовательских работ
секция «Математика»
РЕШЕНИЕ СИСТЕМ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ДВУМЯ НЕИЗВЕСТНЫМИ
С ПОМОЩЬЮ МЕТОДА ПОДСТАНОВКИ, МЕТОДА СЛОЖЕНИЯ И ВЫЧИТАНИЯ, ГРАФИЧЕСКОГО МЕТОДА И ПРАВИЛА КРАМЕРА
Подготовили: учащиеся 7 классов
МБОУ гимназия №10
Руководитель: учитель математики
МБОУ гимназия №164,
Педагог Пономарёва Ю.Г.
2012 год
Оглавление
Введение 3
1.1 Основные методы решения: подстановка, сложение или вычитание
1.
2
Графический метод решения системы
двух линейных уравнений с двумя
неизвестными
Глава II Формулы Крамера – один из способов
решения систем линейных уравнений 4
Историческая справка 4
Определитель второго порядка 5
2.3 Решение систем двух линейных уравнений с
двумя неизвестными с помощью правила Крамера 6
Глава III Применение правила Крамера к решению систем
двух линейных уравнений с двумя неизвестными 9
3.1. Вычисление определителей второго порядка 9
3.2. Решение систем двух линейных уравнений с двумя
переменными с помощью формул Крамера 9
Заключение 13
Список литературы 14
Введение
С
решением систем уравнений мы познакомились
в 7 класса, изучив понятие системы
уравнений и основные методы решения
систем: метод подстановки, метод сложения,
графический метод.
Системы уравнений – одна из важнейших тем курса алгебры, которая традиционно входит в материалы итоговой аттестации по алгебре в 9 классе, в материалы единого государственного экзамена в 11 классе.
Цель исследования: познакомиться и научиться применять на практике метод подстановки, метод сложения и вычитания, графический метод и новый способ решения систем двух линейных уравнений с двумя неизвестными – правило Крамера.
Задачи исследования:
— изучить математическую литературу, периодические издания по математике;
— рассмотреть историю развития вопроса в математике;
— научиться вычислять определители второго порядка;
— научиться решать системы уравнений новым способом.
Глава I Системы двух линейных уравнений с двумя неизвестными
1.1 Основные методы решения: подстановка, сложение или вычитание
Системы двух линейных уравнений с двумя неизвестными имеют вид:
где
a,
b, c, d, e, f –
заданные числа; x,
y
– неизвестные.
Метод подстановки.
1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:
x = ( c – by ) / a . (2)
2) Подставляем во второе уравнение вместо x :
d ( c – by ) / a + ey = f .
3) Решая последнее уравнение, находим y :
y = ( af – cd ) / ( ae – bd ).
4) Подставляем это значение вместо y в выражение (2) :
x = ( ce – bf ) / ( ae – bd ) .
П р и м е р . Решить систему уравнений:
Из первого уравнения выразим х через коэффициенты и y :
x = ( 2y + 4 ) / 3 .
Подставляем это выражение во второе уравнение и находим y :
( 2y + 4 ) / 3 + 3y = 5 , откуда y = 1 .
Теперь находим х, подставляя найденное значение вместо y в
выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .
Сложение
или вычитание.
Этот
метод состоит в следующем.
1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их:
Отсюда получаем: y = ( af – cd ) / ( ae – bd ).
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b( af – cd ) / ( ae – bd ) = c.
3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ).
П р и м е р . Решить систему уравнений:
методом сложения или вычитания.
Умножаем первое уравнение на –1, второе – на 3 и складываем их:
отсюда y = 1. Подставляем это значение во второе уравнение
(а в первое можно?): 3x + 9 = 15, отсюда x = 2.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т. | ||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Системы уравнений. Понятие системы уравнений. Свойства систем уравнений. Линейные системы уравнений. Основные методы решения систем уравненийПоделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | |||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||
д.
Разновидности СЛАУ — совместная, несовместная, определенная, неопределенная, однородная, неоднородная… Обратная матрица и ее нахождение.
Системы уравнений: Системы уравнений
Системы уравнений
Мы работали с двумя типами уравнений — уравнениями с одной переменной и уравнениями с двумя переменными. В общем, мы могли бы найти ограниченное количество решений одного уравнения с одной переменной, в то время как мы могли бы найти бесконечное количество решений одного уравнения с двумя переменными.
Это связано с тем, что одно уравнение с двумя переменными недоопределено — переменных больше, чем уравнений. Но что, если мы добавим еще одно уравнение?
Система уравнений — это набор из двух или более уравнений с одинаковыми переменными. Решением системы уравнений является набор значений переменной, удовлетворяющих одновременно всем уравнениям. Чтобы решить систему уравнений, нужно найти все наборы значений переменных, которые составляют решения системы.
Пример : Какая из упорядоченных пар в наборе {(5, 4), (3, 8), (6, 4), (4, 6), (7, 2)} является решением следующей системы уравнений:
| у + 2 x | = | 14 | |
| ху | = | 24 |
(5, 4) является решением первого уравнения, но не второго.
(3, 8) является решением обоих уравнений.
(6, 4) является решением второго уравнения, но не первого.
(4, 6) является решением обоих уравнений.
(7, 2) не является решением ни одного уравнения.
Таким образом, множество решений системы равно {(3, 8),(4, 6)}.
Решение систем линейных уравнений с помощью графика
Когда мы изображаем линейное уравнение с двумя переменными в виде линии на плоскости, все точки на этой линии соответствуют упорядоченным парам, удовлетворяющим уравнению. Таким образом, когда мы рисуем два уравнения, все точки пересечения — точки, лежащие на обеих линиях, — это точки, удовлетворяющие обоим уравнениям.
Чтобы решить систему уравнений с помощью графика, нарисуйте все уравнения в системе. Точки, в которых пересекаются все прямые, являются решениями системы.
Пример : Решите следующую систему графически:
| y — 3 | — ( x + 2) | ||
| у | = | 3 х — 2 |
График системы
Поскольку две прямые пересекаются в точке (1, 1), эта точка является решением системы.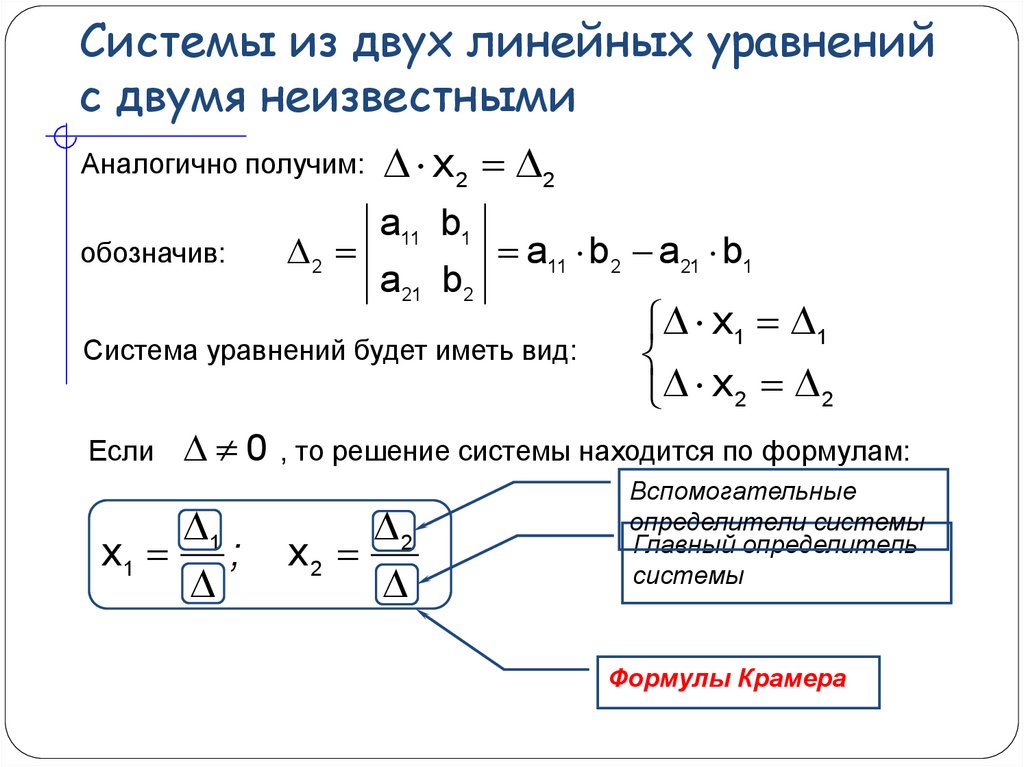
Таким образом, решением системы уравнений является {(1, 1)}.
Для проверки подставьте (1, 1) в оба уравнения:
1 — 3 = — (1 + 2) ? Да.
1 = 3(1) — 2 ? Да.
Написание систем уравнений: объяснение, обзор и примеры
Точно так же, как английский язык можно перевести на другие языки, мы также можем перевести его на язык математики. Многие слова, которые мы используем каждый день, могут подразумевать различные математические операции. Например, «всего» может означать знак равенства, а «увеличить на» может означать символ сложения. Умение переводить с английского на математику позволяет нам превращать слова в уравнения. Продолжайте читать, чтобы увидеть, как это работает для письма системы уравнений .
Что такое система уравнений?
Прежде чем мы начнем писать системы уравнений, давайте убедимся, что знаем, что такое система уравнений. Система уравнений — это просто два или более уравнений с одними и теми же переменными.
В Алгебре 1 вы в основном сосредоточитесь на системах с двумя уравнениями и двумя переменными.
Две переменные, которые вы, вероятно, знаете лучше всего, это x и y. Вам может быть интересно, почему x и y? Осями координатной плоскости являются оси x и y. Таким образом, x и y в уравнениях представляют собой координаты x и y на графике. Когда вы решаете систему уравнений с двумя переменными, ваша цель — найти точку — (x, y) — где пересекаются два графика. Эта точка пересечения является решением системы уравнений.
На этом графике показана система уравнений и ее решение.Вы могли также заметить, что большинство систем уравнений, которые вы решаете в Алгебре 1, являются системами двух линейных уравнений. Чтобы ознакомиться с линейными уравнениями и их многочисленными формами, ознакомьтесь с записью в блоге Альберта Forms of Linear Equations.
Забегая вперед: что, если у вас есть три уравнения и три переменные, составляющие систему уравнений с тремя переменными? Вам понадобится третья ось, ось Z.
Знаете ли вы, что существует несколько способов представления системы уравнений? Четыре основных способа представления системы уравнений: уравнения (алгебра), таблица (числа), график (визуальное) и словесное описание (слова). Давайте посмотрим, как выглядит каждая форма, используя систему двух линейных уравнений:
Форма уравнения (алгебра):
у=3х+1
у=х+3
Table (numbers) form:
| x_1 | -2 | -1 | 0 | 1 | 2 |
| y_1 | -5 | -2 | 1 | 4 | 7 |
| y_2 | 1 | 2 | 3 | 4 | 5 |
Graph (визуальная) форма:
Вербальное описание (слова) форма:
Вы с другом находитесь в читательском клубе.До начала клуба вы прочитали 1 книгу, а ваш друг прочитал 3 книги. Вы ставите цель читать 3 книги в месяц, а ваш друг ставит цель читать 1 книгу в месяц. Из этого описания вы могли бы написать систему уравнений и решить, чтобы ответить на вопрос: через сколько месяцев вы и ваш друг прочитаете одинаковое количество книг?
До начала клуба вы прочитали 1 книгу, а ваш друг прочитал 3 книги. Вы ставите цель читать 3 книги в месяц, а ваш друг ставит цель читать 1 книгу в месяц. Из этого описания вы могли бы написать систему уравнений и решить, чтобы ответить на вопрос: через сколько месяцев вы и ваш друг прочитаете одинаковое количество книг? Теперь, когда мы изучили различные способы представления системы линейных уравнений, мы увидим, как написать систему линейных уравнений. В следующих разделах этого поста будет рассмотрено, как написать форму уравнения системы уравнений из таблицы, графика и словесного описания или того, что ваш учитель, вероятно, называет словесными задачами.
Заинтересованы в лицензии школы Альберта?
Как составить систему уравнений Написать систему уравнений из таблицы Запись системы линейных уравнений из таблицы аналогична записи линейного уравнения из таблицы. Однако на этот раз мы будем писать двумя уравнениями .
Давайте вспомним две вещи, которые вам нужно вычислить из таблицы, чтобы написать линейное уравнение: 1) наклон и 2) точку пересечения по оси Y. Если вам повезет, y-перехват окажется в таблице. Если нет, то есть еще немного работы, но вы все еще можете это сделать!
Давайте посмотрим на таблицу ниже, чтобы попрактиковаться в написании системы линейных уравнений из таблицы:
| x | -5 | -2 | 1 | 4 |
| y_1 | -2 | 0 | 2 | 4 |
| y_2 | -2 | -5 | -8 | -11 |
Обратите внимание, что имеется только одна строка x, а строк y две, потому что наша таблица показывает систему из ДВУХ уравнений. Мы можем разделить эту таблицу на две таблицы, по одной для каждого уравнения:
| x | -5 | -2 | 1 | 4 |
| y_1 | -2 | 0 | 2 | 4 |
| x | -5 | -2 | 1 | 4 |
| y_2 | -2 | -5 | -8 | -11 |
Now we need to apply наши навыки написания линейных уравнений и вычисление наклона и y-перехвата из каждой таблицы.
Помните, что форма уравнения с пересечением наклона имеет вид y=mx +b , где m представляет собой наклон, а b представляет собой пересечение с осью y.
Вы можете найти наклон первой таблицы, рассчитав отношение изменения значений y к изменению значений x, используя две точки из таблицы, например (-2, 0) и (1, 2):
м=\dfrac{y_2-y_1}{x_2-x_1}
м=\dfrac{2-0}{1-(-2)}
м=\dfrac{2}{3}
Потренируйтесь находить уклон на Альберте прямо сейчас!
Теперь нам нужно использовать точку в таблице для вычисления точки пересечения по оси Y. Используем точку (-2, 0). Подставьте -2 вместо x, 0 вместо y и \frac{2}{3} вместо m в уравнении и найдите b.
у=\dfrac{2}{3} х +b
0=\dfrac{2}{3}(-2) +b
0=-\dfrac{4}{3}+b
\dfrac{4}{3}=b
Теперь, когда мы знаем наклон и точку пересечения с осью y, мы можем написать наше первое уравнение:
y_1=\dfrac{2}{3}x+\dfrac{4}{3}
Мы можем использовать этот же процесс для записи второго уравнения в нашей системе.
Сначала вычислите наклон как отношение изменения значений y к изменению значений x между двумя точками, такими как (1, -8) и (4, -11):
м=\dfrac{y_2-y_1}{x_2-x_1}
м=\dfrac{-11-(-8)}{4-1}
м=\dfrac{-3}{3}
м=-1
И еще раз, мы можем вычислить точку пересечения с осью y, подставив точку — например, (1, -8) — в наше уравнение и найдя b.
у=- х +б
-8=- (1) +б
-8=-1+б
-7=б
Итак, наше второе уравнение y_2= -x-7. Теперь мы можем написать нашу систему уравнений для данной таблицы:
y_1=\dfrac{2}{3}x+\dfrac{4}{3}
у_2=-х-7
Заинтересованы в лицензии школы Альберта?
Если у вас возникли проблемы с написанием линейных уравнений с использованием таблицы или двух точек, ознакомьтесь с этими блогами Альберта, чтобы помочь: Как найти наклон и форму пересечения наклона.
Запись системы линейных уравнений из графика похожа на запись системы из таблицы.
Нам нужно определить наклон и точку пересечения по оси Y каждой линии на графике, чтобы написать нашу систему уравнений.
Попрактикуйтесь в написании линейных уравнений на Альберте прямо сейчас!
Давайте посмотрим на приведенный ниже график, чтобы попрактиковаться в написании системы линейных уравнений из графика:
На этом графике показана система двух линейных уравнений.Начав с линии А, рассчитаем уклон. Мы можем использовать формулу наклона и точки (0, -4) и (4, -2), чтобы найти наклон:
м=\dfrac{y_2-y_1}{x_2-x_1}
м=\dfrac{-2-(-4)}{4-0}
м=\dfrac{2}{4}
м=\dfrac{1}{2}
Повторим этот процесс с двумя точками из линии B, такими как (0, 1) и (4, -2):
m=\dfrac{-2-1}{4-0}
м=\dfrac{-3}{4}
м=-\dfrac{3}{4}
Далее мы можем определить точки пересечения по оси Y каждой линии на графике. Помните, точка пересечения оси y всегда находится там, где линия пересекает ось y, а координата {x} равна {0}:
Две точки на изображении являются точками пересечения линий y.Итак, точка пересечения по оси y линии A равна -4, а точка пересечения по оси y линии B равна 1. Теперь мы можем подставить наклоны и точки пересечения по оси y двух наших линий в уравнения вида y=mx+b, чтобы получить наша система:
у=\dfrac{1}{2}х — 4
y=-\dfrac{3}{4}x+1
Если у вас возникли проблемы с написанием линейных уравнений с использованием графика или двух точек, ознакомьтесь с этими блогами Альберта, чтобы помочь: Как найти наклон и форму пересечения наклона.
Заинтересованы в лицензии школы Альберта?
Написание систем уравнений из текстовых задачПри написании систем уравнений из текстовых задач важно создать список общих переводов слов в эквивалентные им математические операции. Если вы еще не делали этого в классе, вот таблица для начала:
| Математическая операция | Слова/Фразы | |
| = | , общая, общая, Sum | |
| + 01201201201201201412014201420142014201420141414141414141414141414141414141414149201414141414149. | — | вычитание, разность, минус, меньше |
| \times | умножение, умножение, удвоение, на | |
| \div | деление, отношение 9 012 9012 |
Потренируйтесь писать на Альберте прямо сейчас!
Чтобы попрактиковаться в написании систем уравнений из текстовых задач, давайте рассмотрим следующие два примера:
Пример 1: В конце баскетбольного матча ваша команда набрала 53 очка. Вы знаете, что команда забросила всего 23 мяча. Одни корзины приносили 2 очка, а другие — 3 очка. Удивительно, но никто не добрался до линии штрафных бросков. Напишите систему уравнений, описывающую эту ситуацию.
Шаг 1: Запишите, что вы знаете из задачи .- команда набрала 53 очка
- всего было забито 23 мяча
- количество 2-х очковых корзин
- количество 3-х очковых корзин
Это важный шаг, который может показаться непосильным. Однако, если вы идентифицировали слова в словесной задаче, которые говорят вам о том, что неизвестно, теперь у вас есть определения переменных. Помните, переменная представляет неизвестное.
- x: количество 2-очковых бросков
- y: количество 3-очковых бросков
Обратите внимание, что указанная важная информация представляет собой итоги или окончательный результат. Эти значения будут идти после знака равенства. Вам нужно выяснить, как ваши переменные (неизвестные) связаны с окончательным счетом и общим количеством корзин. Давайте посмотрим:
- Количество 2-очковых и 3-очковых бросков составляет в общей сложности 23 забитых мяча.
- 2-кратное количество 2-х очковых корзин и 3-кратное количество 3-х очковых корзин равняется итоговому счету 53 очка.
Не забудьте использовать приведенную выше таблицу и найти слова, которые можно перевести в математическую операцию.
- х+у= 23
- 2х + 3у = 53
х + у = 23
2х + 3у = 53
Пример 2: Два числа имеют разность 7, а их сумма в сумме равна 33. Напишите систему уравнений, чтобы представить эту ситуацию.
Шаг 1: Запишите, что вы знаете из задачи .- разница двух чисел 7
- сумма двух одинаковых чисел 33
Поскольку два числа имеют разность, одно число должно быть больше, а другое меньше.
- значение меньшего числа
- значение большего числа
- x: меньшее число
- y: большее число
Обратите внимание, что в исходной задаче есть несколько слов, которые можно перевести как математические операции: слово разность означает вычитание (минус), а слова сумма и объединение означают сложение. Давайте посмотрим:
- Большее число минус меньшее число составляет разность 7.
- Большее число в сочетании с меньшим числом составляет сумму 33.
- у — х = 7
- y + x = 33
у – х = 7
у + х = 33
Чтобы больше попрактиковаться в написании систем уравнений из текстовых задач, посмотрите этот видео-пример.
Написание систем уравнений: ключи к запоминанию- Система уравнений — это когда у вас есть два или более уравнений, которые используют одни и те же переменные.
- Четыре способа представить систему уравнений: ее уравнения (алгебра), таблица (числа), график (визуальный) и словесное описание (слова).
