Сложение и вычитание векторов правило треугольника: Правило треугольника — урок. Геометрия, 9 класс.

Сложение и вычитание векторов. Умножение вектора на число 10 класс онлайн-подготовка на Ростелеком Лицей

 

 

Отметим, что сложение векторов производится аналогично планиметрии, только все действия выполняются в пространстве.

 

Итак, пусть заданы два произвольных вектора в пространстве (рис. 1):

Рис. 1. Произвольные векторы в пространстве

Определим, что же называется суммой двух этих векторов.

Точно так же, как в планиметрии, из любой удобной точки, назовем ее точкой А, можно единственным образом отложить вектор, равный вектору . Напомним, что заданные векторы, как и любые другие, свободны, важно лишь направление и длина, сам вектор можно параллельно переносить в любое место как на плоскости, так и в пространстве. Так, мы получили вектор  – в результате действия вектора  точка А переместилась в точку В. Теперь из точки В откладываем единственно возможным образом вектор , получаем вектор  – так, в результате действия вектора  точка В переместилась в точку С. В результате точка А переместилась в точку С, получен вектор , который и называется суммой векторов  и  (рис. 2).

Рис. 2. Сумма двух векторов в пространстве

Так, получено правило треугольника для сложения векторов в пространстве.

Правило треугольника

Из любой точки пространства (точка А) откладываем первый вектор, из конца первого вектора (точка В) откладываем второй вектор и получаем точку С. Вектор, соединяющий начало первого вектора (точка А) и конец второго (точка С), и будет результирующим.

Отметим, что результат сложения векторов не зависит от выбора начальной точки, существует соответствующая теорема, которая это доказывает на основании того, что из точки можно отложить вектор, равный заданному, единственным образом.

Определение

Разностью двух векторов называется такой третий вектор, который, будучи сложенным со вторым вектором, даст первый вектор.

Введем разность векторов  и , для этого сложим вектор  с противоположным вектором :

Итак, из произвольной точки А откладываем вектор , получаем точку В.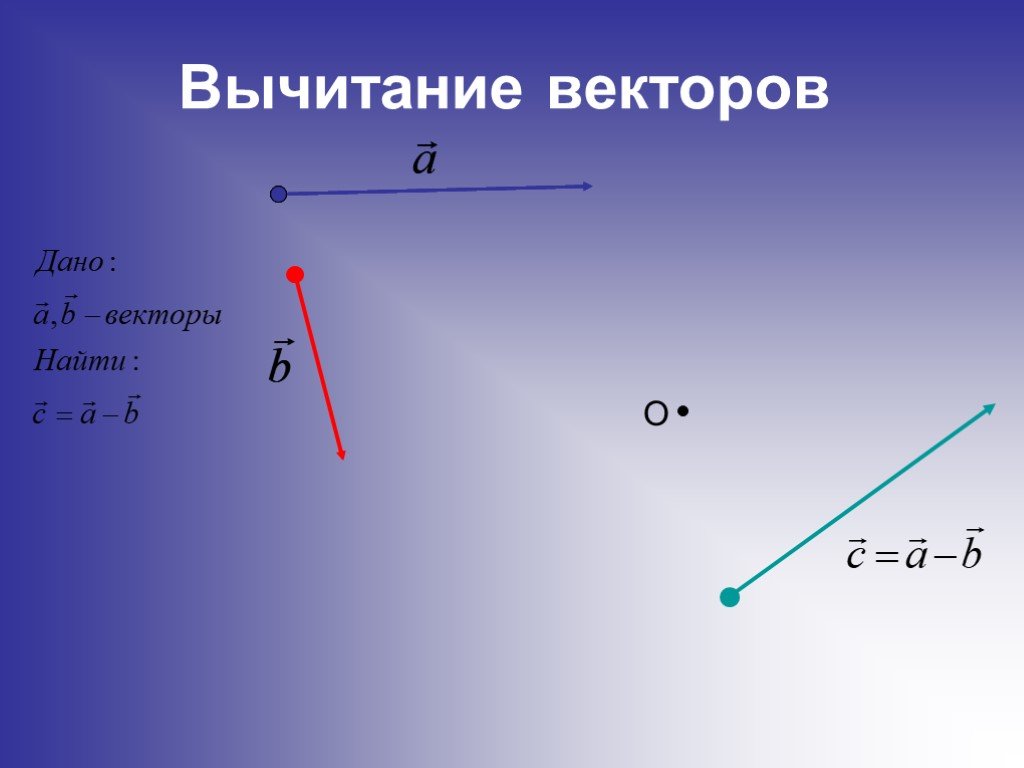 Чтобы получить вектор  мы строим вектор, равный вектору  по длине, но противонаправленный. Полученный вектор откладываем из точки В – получаем точку D. Вектор  и будет искомым вектором разности.

Проиллюстрируем (рис. 3):

Рис. 3. Вычитание двух векторов в пространстве

Построим на заданных векторах  и  параллелограмм (рис. 4):

Рис. 4. Параллелограмм на двух заданных векторах

Т. к. вектор ; аналогично .

По правилу треугольника:

Так, одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов.

Рассмотрим разность векторов. По правилу треугольника:

.

Так, вторая диагональ параллелограмма, построенного на двух векторах, соответствует разности этих векторов.

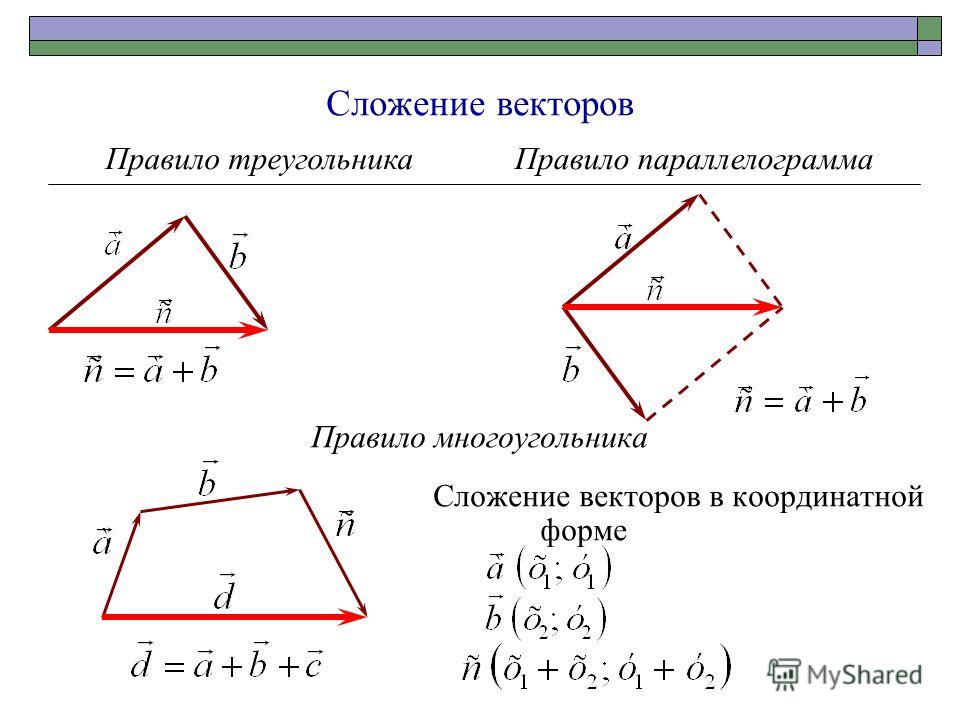
Для сложения и вычитания нескольких векторов применяется правило многоугольника. Пусть заданы векторы  и :

Рис. 5. Три вектора в пространстве

Необходимо построить вектор .

Видим, что перед некоторыми векторами стоят численные множители. Напомним, что при умножении вектора на число получаем сонаправленный вектор, длина которого – это длина исходного вектора, умноженная на заданное число. Получим векторы  и . Вектор  сонаправлен с вектором , длина его в три раза больше. Вектор  противонаправлен вектору , длина его в два раза больше. Проиллюстрируем (рис. 6):

Рис. 6. Умножение вектора на число

Приступаем к сложению. Из произвольной точки А откладываем полученный вектор  – получаем точку В. Из точки В откладываем вектор  – получаем точку С. Из точки С откладываем вектор  – получаем точку D. Согласно правилу многоугольника, вектор  соответствует искомому вектору :

Рис. 7. Сложение векторов по правилу многоугольника

Задача 1:

Задан тетраэдр ABCD (рисунок 8). Доказать:

 

Рис. 8. Тетраэдр, задача 1

Решение:

По правилу треугольника:

Аналогично:

, ч. т. д.

По правилу треугольника:

Аналогично: , ч. т. д.

Задача 2

Упростить выражение:

Рассмотрим отдельно сумму двух векторов: , ее значение очевидно:

Проиллюстрируем (рис. 9):

Рис. 9. Сумма двух векторов

Теперь сократим противоположные векторы:

Можно было сразу заметить:

.

В результате упрощения получено:

.

Итак, мы ввели операции сложения и вычитания векторов, умножения вектора на число в стереометрии, отметили, что операции аналогичны таким же для планиметрии. Кроме того, решили несколько задач, базирующихся на описанных операциях.

 

Список литературы

1. Геометрия. 10–11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил.
2. Геометрия. 10–11 класс: учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Геометрия. 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Ru.onlinemschool.com (Иточник).
2. Emomi.com (Источник).
3. Cleverstudents.ru (Источник).

 

Домашнее задание

Задача 1: задан параллелепипед (рисунок 10). Доказать:

1.

2.

3.

Рис. 10. Параллелепипед

Задача 2: упростить выражение:

Задача 3: построить вектор , если векторы  и  заданы на рисунке 11:

Рис. 11. Векторы, задача 3

 

Сложение и вычитание векторов | Презентация к уроку по геометрии (9 класс) по теме:

Слайд 1

Сложение и вычитание векторов Л.С. Атанасян «Геометрия 7-9»

Слайд 2

А В С Какая запись является верной? 45 0 A В > BC ; A В > BC AC = BC ; AC = BC

Слайд 3

Назовите коллинеарные сонаправленные векторы Назовите коллинеарные противоположнонаправленные векторы A B C D N M R E S F H J K L Z I O P X G Q V T Y U Назовите равные векторы

Слайд 4

Сложение векторов. Правило треугольника. a a b b a + b А В С АВ + ВС = АС a + 0 = a ! ! Для любого нулевого вектора справедливо равенство

Слайд 5

В 1 Докажем, что если при сложении векторов точку А заменить другой точкой А 1 , то полученный вектор А 1 С 1 будет равен АС. Рассмотрим случай. a b В b a b a b a + А С b a + С 1 А 1 АВВ 1 А 1 – параллелограмм ВСС 1 В 1 – параллелограмм АСС 1 А 1 – параллелограмм

Слайд 6

= OK АВ + ВС = Правило треугольника. АС АО + ОР = АР MN + NR = MR MK + KM = MM = 0 MK + OM = OM + MK = KE А S + S С = АС NM + ML = NL RP + PR = RR = 0 ZK + KZ = ZZ = 0 DE + KD = KD + DE =

Слайд 7

Правило треугольника. АС = АВ + ВС OB + В N ON = AR + RS AS = XK + KH XH = MA + AD MD = OF + FP OP = ON + N В OB = RS + SA RA = KH + HX KX = AM + MD AD = FP + PO FO =

Слайд 8

По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получается a b a + b a b a + b

Слайд 9

a b a + b c f c + f

Слайд 10

Законы сложения векторов Для любых векторов справедливы равенства: a , b, c 1 2 a + b = b + a переместительный закон сочетательный закон ( a + b ) + c = a + (b + c) ! ! Теорема

Слайд 11

a a b b a + b А В D C АС = АВ + ВС a = b + АС = А D + D С b = a + Докажем свойство Рассмотрим случай, когда векторы и не коллинеарны.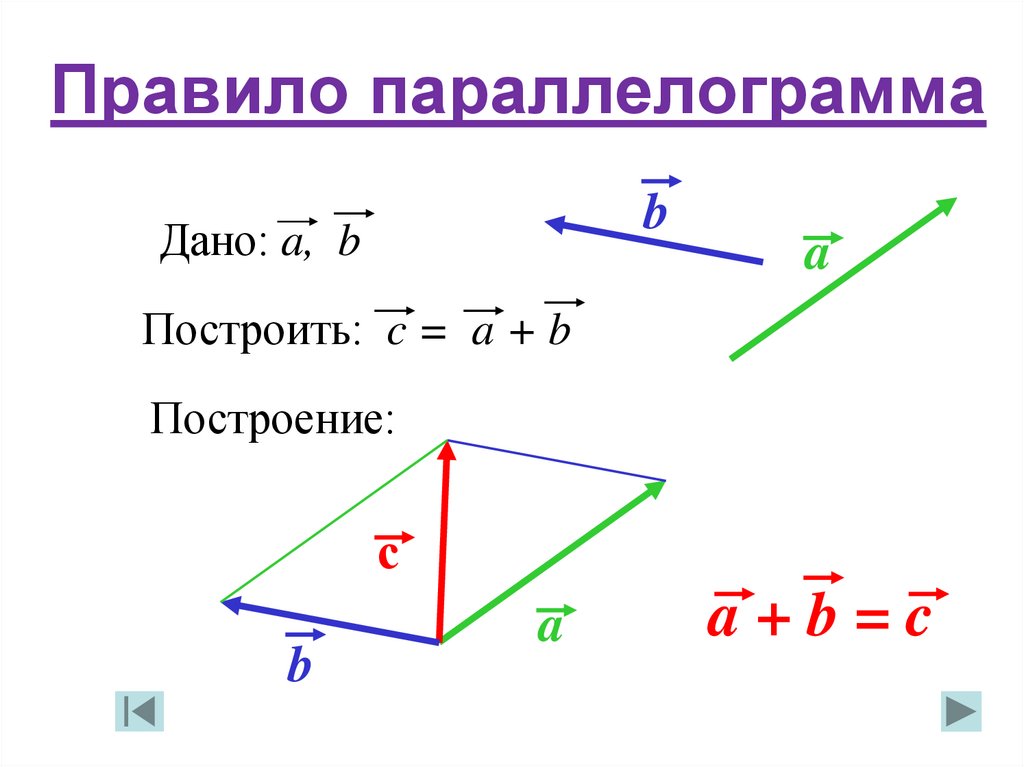 b a 1

Слайд 12

1 2 9 6 12 11 10 8 7 4 5 3 При доказательстве свойства 1 0 мы обосновали правило параллелограмма сложения неколлинеарных векторов. Чтобы применить правило параллелограмма, надо отложить векторы от одной точки, как стрелки часов.

Слайд 13

Сложение векторов. Правило параллелограмма. 1 2 9 6 12 11 10 8 7 4 5 3 a b a+b a b

Слайд 14

a a b b В D C (a + b)+c Докажем свойство 2 c c = ( АВ + ВС ) + CD А = АС + CD = А D А C a + (b+c) = АВ + ( ВС + CD) = А B + BD = А D BD

Слайд 15

Сложение векторов. Правило многоугольника. = А O АВ + ВС + С D + DO a c n m c m n a+c+m+n a

Слайд 16

Правило многоугольника можно сформулировать также следующим образом: если А 1 , А 2 , …, А n – произвольные точки плоскости, то = А 1 A n А 1 А 2 + А 2 А 3 + … + А n-1 A n А 2 А 3 А 4 А 5 А 6 А 7 А 1

Слайд 17

! Если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору. a 1 +a 2 +a 3 +a 4 +a 5 = 0 a 1 a 1 a 2 a 2 a 3 a 4 a 5 a 3 a 4 a 5

Слайд 18

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены. a 1 b — b a a a 1 — b b Вектор , противоположный вектору А В А В Вектор ВА , противоположный вектору АВ a + (-a) = 0 ВА = – АВ a a 1 a = a 1 ; a a 1

Слайд 19

a b № 766 На рисунке изображены векторы ХУ . Представьте вектор ХУ в виде суммы остальных или им противоположных векторов. a, b, c, d c d У Х – a – b + c + d = ХУ – –

Слайд 20

Вычитание векторов. a a — b b a — b b a – = a +(– b ) — b

Слайд 21

Вычитание векторов. MF — SF = MF + FS = MS RO — RM = RO + MR = MR + RO MD — SD = MD + DS = MS — OS — ST = SO + TS = TS + SO RO — AO = RO + OA = RA RO — RO = RO + OR = RR = 0 = TO = MO

Слайд 22

№ 768 Точки М и N – середины сторон АВ и АС треугольника АВС. Выразите векторы ВМ, NC, MN, BN через векторы = АМ и = А N a b С ВМ = a — NC = MN = b MA + AN — = a + b BN = BA + AN = — a + b — a В А М N a b

Слайд 23

( ) Найдите АВ + AD – DC – OD ABCD — прямоугольник А B C D АВ + AD – DC – OD = АС – DC – OD = АС + CD + DO = АО О 3 4 5

Слайд 24

АВ + ВС = АО + ОР = MN + NR = MK + KM = MK + OM = А S + S С = NM + ML = RP + PR = ZK + KZ = DE + KD = ON = AS = XH = MD = OP = OB = RA = KX = AD = FO =

электромагнетизм — Подчиняется ли электрическое поле треугольному закону сложения и вычитания векторов?

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 448 раз

$\begingroup$

Я знаю, что напряженность электрического поля — это сила на единицу заряда, но я еще не совсем понял, как электрическое поле может подчиняться законам сложения и вычитания векторов, исключая линейную ситуацию?

Полностью ли электрическое поле подчиняется треугольному закону векторов? Производит ли он равнодействующую, как и другие векторы, когда два электрических поля встречаются под углом?

Если да, то используется ли он практически везде в нашем мире.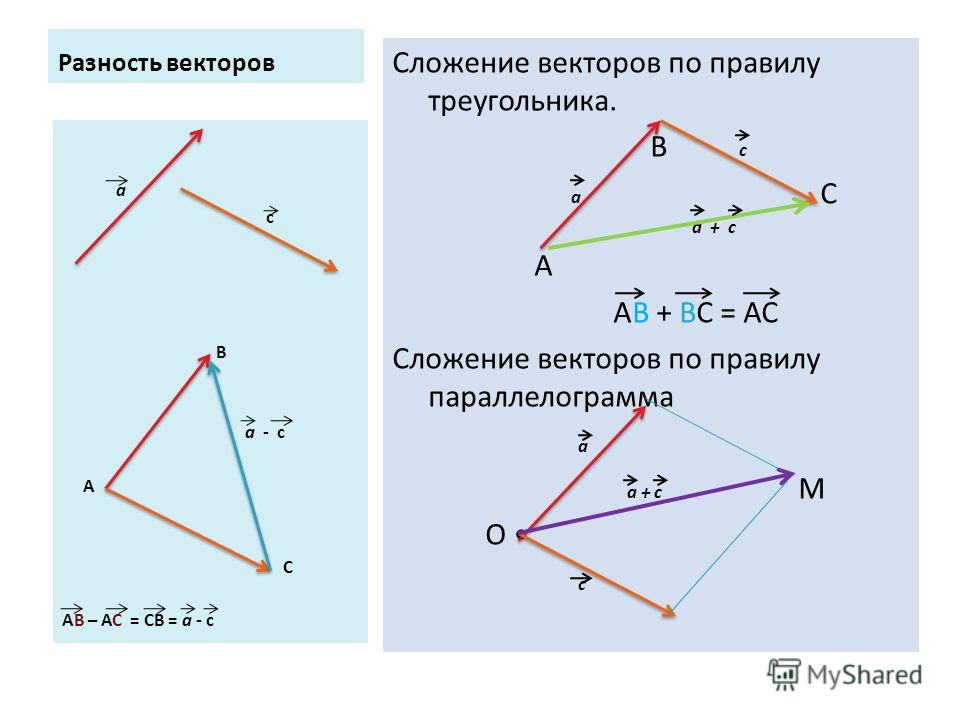

• электромагнетизм
• электрические поля
• векторы
• векторные поля
• линейные системы

$\endgroup$

$\begingroup$

Электрическое поле — сила на единицу заряда. Поскольку сила является вектором, вектор, деленный на скаляр, также дает вектор. Просто подумайте таким образом; в точке результирующая сила получается по законам сложения векторов, поэтому электрическое поле также эффективно получается таким же образом. Это имеет смысл

$\endgroup$

3

$\begingroup$

Электрическое поле, как вы говорите, есть сила на единицу заряда.
В классической механике мы постулируем, что силы ведут себя как векторы. Заряд — скалярная величина, и отношение между вектором и скаляром — тоже вектор; это последнее утверждение имеет мало общего с физикой, это просто то, как векторы работают математически, или, что еще лучше, это просто то, как мы определяем работу векторов.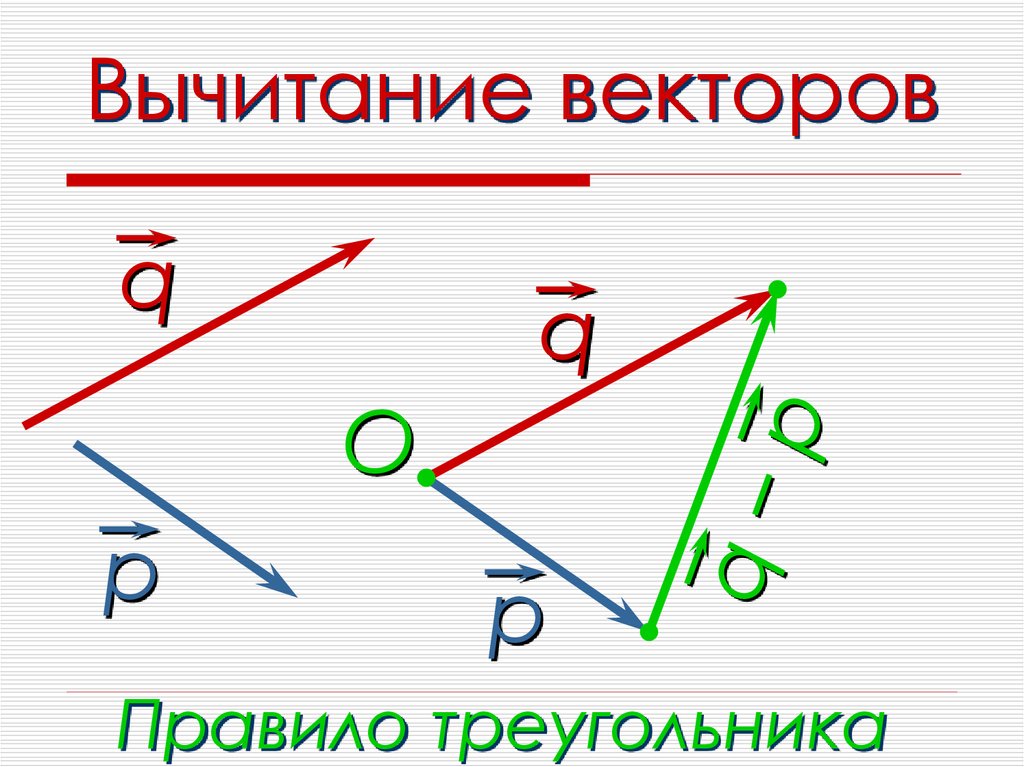 Отсюда следует, что электрическое поле также является вектором, поэтому оно ведет себя как вектор, это поведение включает правило суммирования между векторами.
Так что да, два разных электрических поля суммируются в каждой точке по правилу суммирования векторов. Всегда. Потому что они векторы.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

3.

3 Сложение и вычитание векторов: аналитические методы

Сложение векторов с использованием аналитических методов

Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рис. 3.30, на котором векторы размера AA 12{A} {} и размера BB 12{B} {} складываются для получения результирующего размера RR 12{R} {} .

Рис. 3.30 Векторы размера AA 12{A} {} и размера BB 12{B} {} представляют собой два участка пути, а размер RR 12{R} {} представляет собой результирующее или полное перемещение. Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.

Если AA и BB представляют собой два этапа ходьбы (два перемещения), то RR представляет собой общее перемещение. Человек, совершающий прогулку, оказывается на вершине RR. Есть много способов попасть в одну и ту же точку. В частности, человек мог пройти сначала в направлении x , а затем в направлении

y . Этими путями являются x — и y -компоненты результирующего, RxRx и RyRy size 12{R rSub { size 8{y} } } {}. Если мы знаем RxRx и RyRy size 12{R rSub { size 8{y} } } {} мы можем найти РР и θθ с помощью уравнений A=Ax2+Ay2A=Ax2+Ay2 и θ=tan–1(Ay/Ax)θ=tan–1(Ay/Ax) размер 12{θ=»tan» rSup { размер 8{–1}} \( A rSub { размер 8{y}} /A rSub { размер 8 {x} } \) } {}. Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.

Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей . Используйте уравнения Ax=AcosθAx=Acosθ размер 12{A rSub {размер 8{x}} =A»cos»θ} {} и Ay=AsinθAy=Asinθ size 12{A rSub { size 8{y} } =A»sin»θ} {}, чтобы найти компоненты. На рис.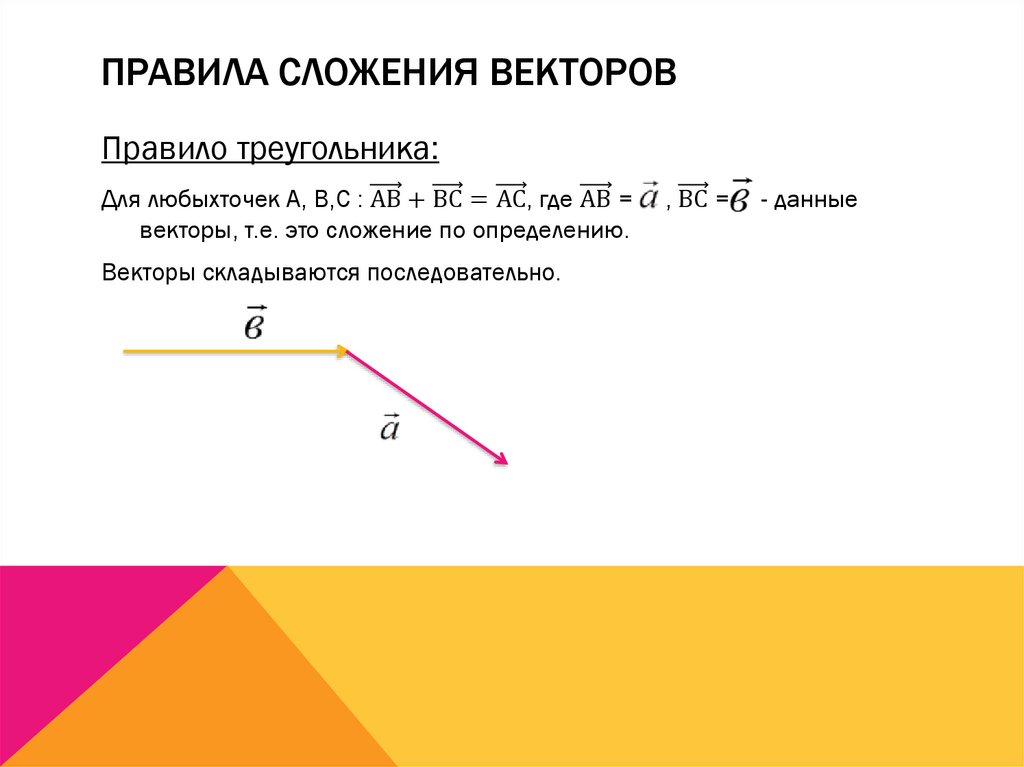 3.31 эти компоненты Размер AxAx 12 {A rSub { размер 8 {x} } } {}, AyAy размер 12 {A rSub { размер 8 {y} } } {}, BxBx размер 12{B rSub { размер 8{x} } } {}, и ByBy size 12{B rSub { size 8{y} } } {}. Углы, которые составляют векторы размера AA 12{A} {} и размера BB 12{B} {} с x -ось θAθA размера 12{θ rSub {размер 8{A} } } {} и θBθB размера 12{θ rSub {размер 8{B} } } {} соответственно.

Рисунок 3.31. Чтобы добавить векторы размера AA 12{A} {} и размера BB 12{B} {}, сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы AxAx size 12{A rSub { size 8{x} } } {}, AyAy size 12{A rSub { size 8{y} } } {}, BxBx size 12{B rSub { size 8{x } } } {} и ByBy size 12{B rSub { size 8{y} } } {} показаны на изображении.

Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси .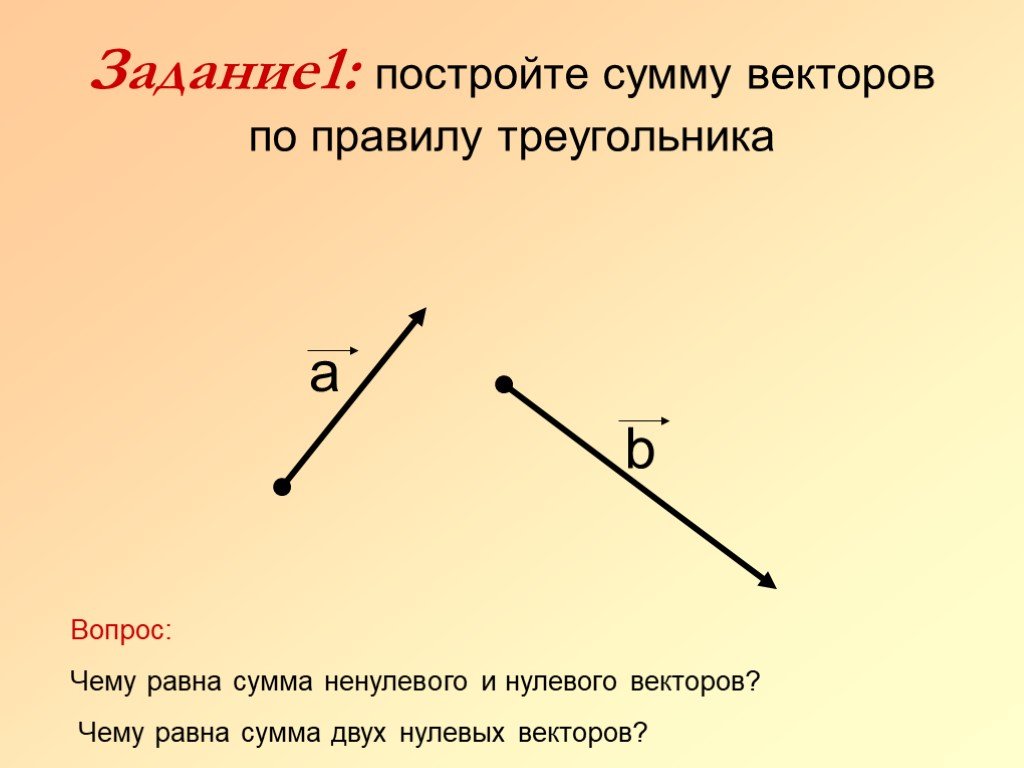 То есть, как показано на рисунке 3.32,

3.12 Rx=Ax+BxRx=Ax+Bx размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8 {x} } } {}

и

3.13 Ry=Ay+By.Ry=Ay+By. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y} } } {}

Рисунок 3.32. Величина векторов AxAx size 12{A rSub { size 8{x} } } {} и BxBx size 12{B rSub { size 8{x} } } {} в сумме дает величину RxRx size 12{ R rSub { size 8{x} } } {} результирующего вектора в горизонтальном направлении. Аналогично, величины векторов AyAy size 12{A rSub { size 8{y} } } {} и ByBy size 12{B rSub { size 8{y} } } {} в сумме дают величину RyRy size 12{R rSub { size 8{y} } } {} результирующего вектора в вертикальном направлении.

Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси и .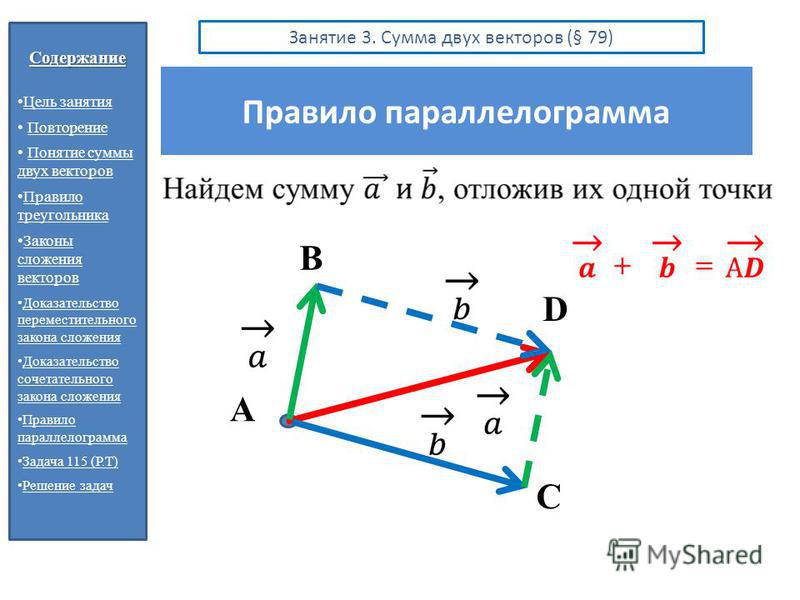 Например, пройти 9 кварталов на восток можно двумя этапами: первые три квартала на восток и вторые шесть кварталов на восток, всего девять, потому что они идут в одном направлении. Таким образом, разложение векторов на компоненты вдоль общих осей облегчает их добавление. Теперь, когда компоненты размера RR 12{R} {} известны, можно найти его величину и направление.

Шаг 3. Чтобы получить величину RR size 12{R } {} результирующей, используйте теорему Пифагора.

3.14 R=Rx2+Ry2.R=Rx2+Ry2. размер 12{R= sqrt {R rSub { размер 8{x} } rSup { размер 8{2} } +R rSub { размер 8{y} } rSup { размер 8{2} } } «.»} {}

Шаг 4. Чтобы получить направление равнодействующей

3,15 θ=tan-1(Ry/Rx).θ=tan-1(Ry/Rx). size 12{θ=»tan» rSup { size 8{- 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «. «} {}

В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.

Пример 3.3 Добавление векторов с использованием аналитических методов

Добавьте вектор размера AA 12{A} {} к вектору размера BB 12{B} {}, показанному на рисунке 3.33, используя перпендикулярные компоненты вдоль x — и и -оси. Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор AA размера 12{A} {} представляет первый этап ходьбы, в котором человек проходит 53,0 м53,0 м размера 12{«53» «.» «0 м»} {} в направлении 20,0º20,0º размер 12{«20» «.» 0º } {} к северу от востока. Вектор BB размером 12{B} {} представляет собой вторую ветвь водоизмещением 34,0 м34,0 м размером 12{«34» «. » «0 м»} {} в направлении 63,0º63,0º размер 12{«63» «.» 0º } {} к северу от востока.

Рис. 3.33 Вектор AA размера 12{A} {} имеет величину 53,0 м53,0 м размера 12{«53» «.» «0 м»} {} и направление 20,0º20,0º размер 12{«20» «.» 0 { size 12{ circ } } } {} к северу от оси x . Вектор BB размера 12{B} {} имеет звездную величину 34,0 м34,0 м размера 12{«34» «.» «0 м»} {} и направление 63,0º63,0º размер 12{«63» «.» 0° } {} к северу от оси x . Можно использовать аналитические методы для определения величины и направления RR размера 12{R} {}.

Стратегия

Компоненты размера AA 12{A} {} и BB размера 12{B} {} вдоль x — и y -осей представляют собой ходьбу строго на восток и строго на север, чтобы добраться до одного и того же конечная точка. После обнаружения они объединяются для получения результирующего.

Решение

Следуя описанному выше методу, мы сначала находим компоненты Размер AA 12{A} {} и BB размер 12{B} {} вдоль x — и y -оси. Обратите внимание, что A=53,0 мА=53,0 м размер 12{«A» «=» «53,0 м»} {}, θA=20,0ºθA=20,0º размер 12{«θ» «subA» «=» «20,0°» } {}, B=34,0 mB=34,0 м размер 12{«B» «=» «34,0» «м»} {} и θB=63,0ºθB=63,0º размер 12{θ rSub {размер 8{B} } } {}. Мы находим x -компоненты, используя Ax=AcosθAx=Acosθ size 12{A rSub { size 8{x} } =A»cos»θ} {}, что дает

3,16 Ax=AcosθA=(53,0 m)(cos 20,0º)=(53,0 м)(0,940)=49,8 мAx=AcosθA=(53,0 м)(cos 20,0º)=(53,0 м)(0,940)=49,8 malignl { stack { size 12{A rSub { size 8{x} } =A»cos»θ rSub {size 8{A}} = \(«53» «. 0″ m» \) \( «cos»»20″ » .» 0 { размер 12 { круг } } \) } {} # » «= \( «53» «.» 0″ м» \) \( 0 «.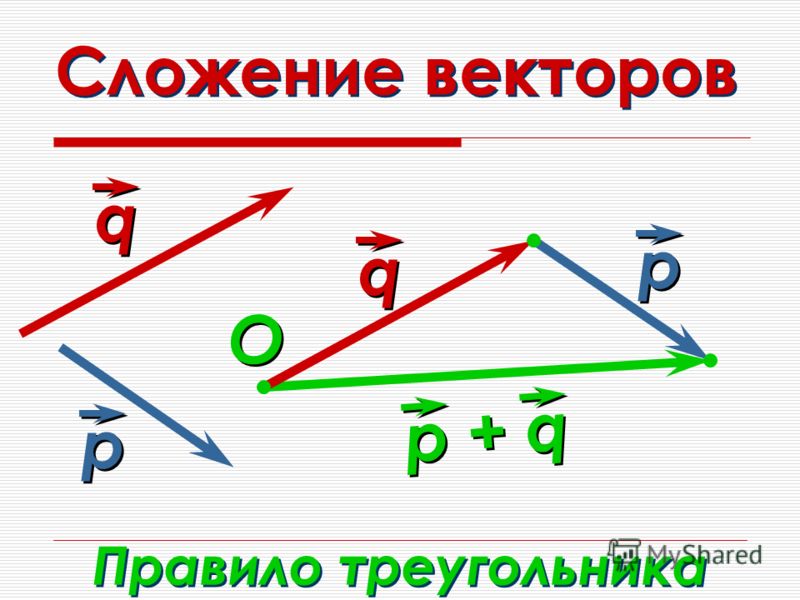 » «940» \) = «49» «.» 8″ м» {} } } {}

и

3,17 Bx=BcosθB=(34,0 м)(cos 63,0°)=(34,0 м)(0,454)=15,4 м.Bx=BcosθB=(34,0 м)(cos 63,0°)=( 34,0 м)(0,454)=15,4 м.alignl { stack { размер 12{B rSub { размер 8{x} } =B»cos»θ rSub { размер 8{B}} = \(«34» «. 0″ m» \) \( «cos»»63″ » .» 0 { размер 12 { круг } } \) } {} # » «= \( «34» «. 0″ м» \) \( 0 «.» «454» \) =»15″ «.» 4 «м» {} } } {}

Аналогично, y -компоненты находятся с помощью Ay=AsinθAAy=AsinθA size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A} } } { }.

3,18 Ay=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 мAy=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 malignl { куча { size 12{A rSub { size 8{y} } =A»sin»θ rSub { size 8{A}} = \(«53» «.» 0″ m» \) \( «sin»»20″ » .» 0 { размер 12 { круг } } \) } {} # » «= \(«53» «. 0″ м» \) \( 0 «.» «342» \) =»18″ «.» 1 «м» {} } } {}

и

3.19 By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891)=30,3 м.By=BsinθB=(34,0 м)(sin 63,0º)=( 34,0 м)(0,891)=30,3 м. alignl {стек { size 12{B rSub { size 8{y} } =B»sin»θ rSub { size 8{B}} = \(«34» «. 0″ m» \) \( «sin»»63″ » .» 0 { размер 12 { круг } } \) } {} # » «= \( «34» «.» 0″ м» \) \( 0 «.» «891» \)=»30″ «.» 3″ м» «.» {} } } {}

Таким образом, x — и y -компоненты равнодействующей равны

3,20 Rx=Ax+Bx=49,8 m+15,4 m=Ax=64,2 mRx= +15,4 м=65,2 м размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +B rSub { размер 8{x} } =»49″ «.» 8″ м»+»15″ «.» 4″ м»=»65″ «.» 2″ м»} {}

и

3,21 Ry=Ay+By=18,1 м+30,3 м=48,4 м. Ry=Ay+By=18,1 м+30,3 м=48,4 м. размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +B rSub { размер 8{y}} =»18″ «.» 1″ м»+»30″ «.» 3″ м»=»48″ «.» 4″ м.»} {}

Теперь мы можем найти величину равнодействующей по теореме Пифагора

3,22 R=Rx2+Ry2=(65,2)2+(48,4)2 mR=Rx2+Ry2=(65,2)2+(48,4)2 m размер 12 {R = sqrt {R rSub { размер 8 {x} } rSup { размер 8 {2} } +R rSub { размер 8 {y} } rSup { размер 8 {2} } } = sqrt { \ («65 » «.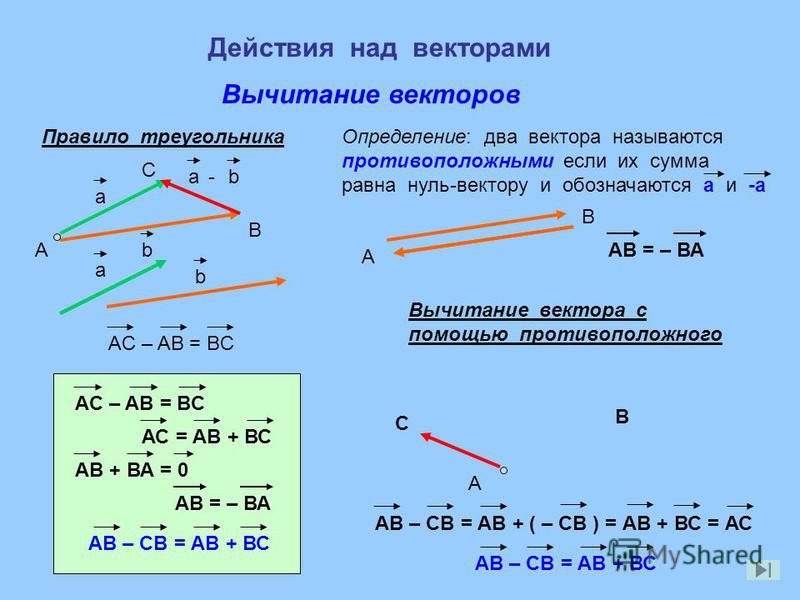 » 2 \) rSup { size 8{2} } + \( «48» «.» 4 \) rSup { size 8{2} } } «m»} {}

так что

3.23 R =81,2 м.R=81,2 м. size 12{R =»81.2″ «m.»} {}

Наконец, мы находим направление равнодействующей

3,24 θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2).θ=tan-1(Ry/Rx)=+tan-1(48,4/65,2). size 12{θ=»tan» rSup { size 8{ — 1} } \( R rSub { size 8{y} } /R rSub { size 8{x} } \) «=+»»tan» rSup { size 8{ — 1} } \(«48» «.» 4/»65″ «.» 2 \) «.»} {}

Таким образом,

3,25 θ=tan−1(0,742)=36,6º. θ=тангенс-1(0,742)=36,6º. size 12{θ=»tan» rSup { size 8{ — 1} } \( 0 «.» «742» \) =»36″ «.» 6 {размер 12{круг}} «.»} {}

Рисунок 3.34 Используя аналитические методы, мы видим, что величина RR размера 12{R} {} составляет 81,2 м81,2 м размера 12{«81» «.» «2 м»} {} и его направление 36,6º36,6º размер 12{«36» «.» 6°} {} к северу от востока.

Обсуждение

В этом примере показано сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.

Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A−B≡A+(–B)A−B≡A+(–B) размер 12{A – B эквивалент A+ \(- B \)} {}. Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты –B–B – минусы компонентов BB размер 12 {B} {}. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R size 12{A- полужирный «B = R»} {} равны

3,26 Rx=Ax+(–Bx )Rx=Ax+(–Bx) размер 12{R rSub { размер 8{x} } =A rSub { размер 8{x} } +-B rSub { размер 8{x} } } {}

и

3,27 Ry=Ay+(–By)Ry=Ay+(–By) размер 12{R rSub { размер 8{y} } =A rSub { размер 8{y} } +-B rSub { размер 8{y} } } {}

, а в остальном описанный выше метод идентичен методу сложения (см.