Сложение векторов по правилу треугольника примеры: Правило треугольника — урок. Геометрия, 9 класс.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

как производится в пространстве, законы, формулы с примерами

Содержание:

• Основные законы сложения векторов в геометрии
• Как происходит сложение по правилу треугольника
• Сложение по правилу параллелограмма
• Как и когда применяется правило многоугольника
• Задачи с примерами решения

Содержание

• Основные законы сложения векторов в геометрии
• Как происходит сложение по правилу треугольника
• Сложение по правилу параллелограмма
• Как и когда применяется правило многоугольника
• Задачи с примерами решения

Основные законы сложения векторов в геометрии

Суммой двух векторов \(\vec a+\vec b\) называют третий вектор \(\vec c\), который проведен из начала \(\vec a\) и упирается в конец \(\vec b\) при условии, что конец \(\vec a\) совпадает с началом \(\vec b\).

 

На плоскости найти сумму векторов можно, воспользовавшись формулой:

\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Если ситуация переходит в пространственное измерение, то достаточно всего лишь а тот же пример добавить новую координату:

\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y;a_z+b_z\right\}\)

Основные законы:

1. Переместительный закон (или коммутативный). Суть его свойства заключается в формуле: \(\vec a+\vec b=\vec b+\vec a\).

2. Сочетательный закон. Выглядит, как \(\left(\vec a+\vec b\right)+\vec c=\vec a+\left(\vec b+\vec c\right)\).

Примечание

Помимо покоординатного сложения направленных отрезков, существуют геометрические нормы, которые позволяют узнать их сумму. Наиболее широко используемых методов в системе три: правило треугольника, параллелограмма и многоугольника.

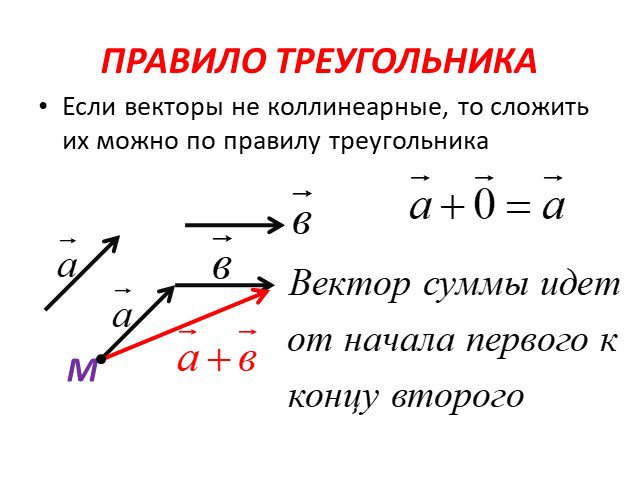
Как происходит сложение по правилу треугольника

Чтобы узнать сумму векторов x и y, необходимо из произвольной точки отложить первый из них, а затем из его конца уже отложить второй. Следующий шаг — построить направленный отрезок, который соединит начало \vec x с концом \vec y. Образовавшаяся сторона треугольника и будет результатом сложения двух векторов. Теорема считается доказанной.

 

Сложение по правилу параллелограмма

Найти сумму векторов можно без построения треугольника. Для этого от начала первого вектора нужно отложить второй вектор. Дополним получившийся чертеж до параллелограмма. Две его стороны у нас уже имеются. Выстроить оставшиеся поможет способ параллельного переноса. Диагональ готовой фигуры, которая исходит из начальной точки векторов, считается их суммой. Теорема доказана.

 

Как и когда применяется правило многоугольника

Данный способ потребуется для того, чтобы сложить более двух векторов.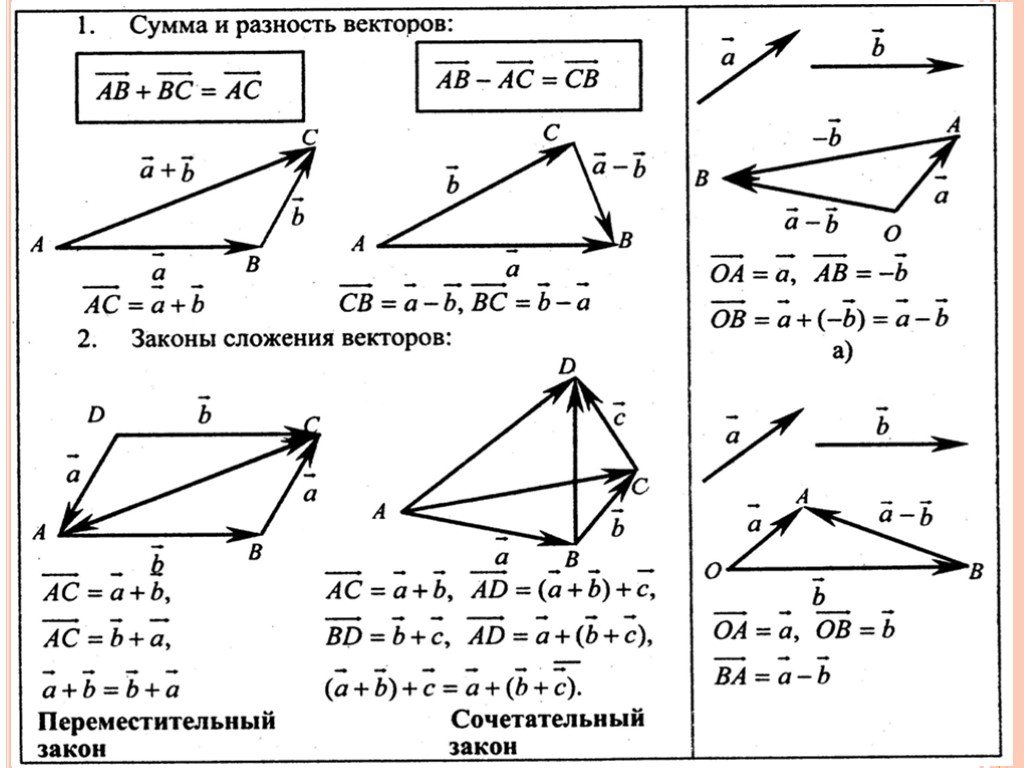

Принцип действий в данном случае похож на последовательность шагов, как в случае с треугольником. Из произвольной точки провести первый вектор. Из его конца — второй, из второго — третий и так далее. Затем окончание последнего вектора соединить с началом первого — это будет результат сложения всех векторов. Доказательство теоремы выполнено.

 

Задачи с примерами решения

Задача 1

Дано

 \(\vec a=\left\{2; 3\right\}, \vec b=\left\{5; 7\right\}\).

Найти \(\vec a+\vec b\).

Решение

\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}=\left\{2+5; 3+7\right\}=\left\{7; 10\right\}\)

Задача 2

С помощью правила треугольника постройте сумму заданных векторов a и b.

Решение 1

Параллельным переносом совмещаем конец вектора a с началом b. Далее соединяем исходную точку вектора a с конечной вектора b. Выходит \(\vec c\). Длина отрезка, изображающего этот направленный отрезок, и будет общим значением \(\vec a\) и \(\vec b\).

Решение 2

С помощью параллельного переноса устанавливаем конец \(\vec b\) таким образом, чтобы он совпадал с началом \(\vec a\). Затем конечную точку первого совмещаем с началом второго. Получилось \(\vec c=\vec b+\vec a\).

Одна цель достигнута разными способами, что наглядно демонстрирует действие переместительного закона.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Треугольный закон сложения векторов

Треугольный закон сложения векторов — это математическое понятие, которое используется для нахождения суммы двух векторов. Этот закон используется для сложения двух векторов, когда голова первого вектора соединяется с хвостом второго вектора, а затем присоединяется хвост первого вектора к началу второго вектора, чтобы сформировать треугольник, и, следовательно, получить результирующий вектор суммы . Вот почему треугольный закон сложения векторов также называют прямым методом сложения векторов.

Изучим треугольный закон сложения векторов, его формулировку, формулу и доказательство. Этот закон используется для определения чистого смещения, скорости, ускорения и т. д. Мы также будем решать вопросы и примеры, основанные на законе сложения векторов треугольника, чтобы понять его применение и концепцию.

1.	Что такое треугольный закон сложения векторов?
2.	Треугольный закон формулы сложения векторов
3.	Треугольный закон векторного сложения Доказательство
4.	Часто задаваемые вопросы о законе сложения векторов треугольника

Что такое треугольный закон сложения векторов?

Закон треугольника сложения векторов — это закон, который используется в векторной алгебре для определения результирующего вектора суммы при сложении двух или более векторов. Предположим, у нас есть автомобиль, который движется из точки А в точку Б, как показано на рисунке ниже. Как только он достигает точки B, он снова начинает двигаться до точки C. Теперь, чтобы определить чистое перемещение автомобиля, мы используем концепцию сложения векторов. Чистое перемещение автомобиля задается вектором AC, который можно рассчитать, используя треугольный закон сложения векторов, как:

\(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}\)

Аналогично, если у нас есть два вектора P и Q, как указано ниже, и нам нужно найти их сумму, то мы можем двигаться вектор Q таким образом, не меняя своей величины и направления, что его хвост соединяется с головой вектора P. Тогда сумма векторов P и Q с использованием треугольного закона сложения векторов определяется выражением

\( \overrightarrow{R} = \overrightarrow{P} + \overrightarrow{Q}\)

Закон треугольника формулы сложения векторов

Рассмотрим два вектора P и Q, угол между которыми равен θ, а их результирующий вектор суммы с использованием треугольного закона сложения векторов определяется вектором R.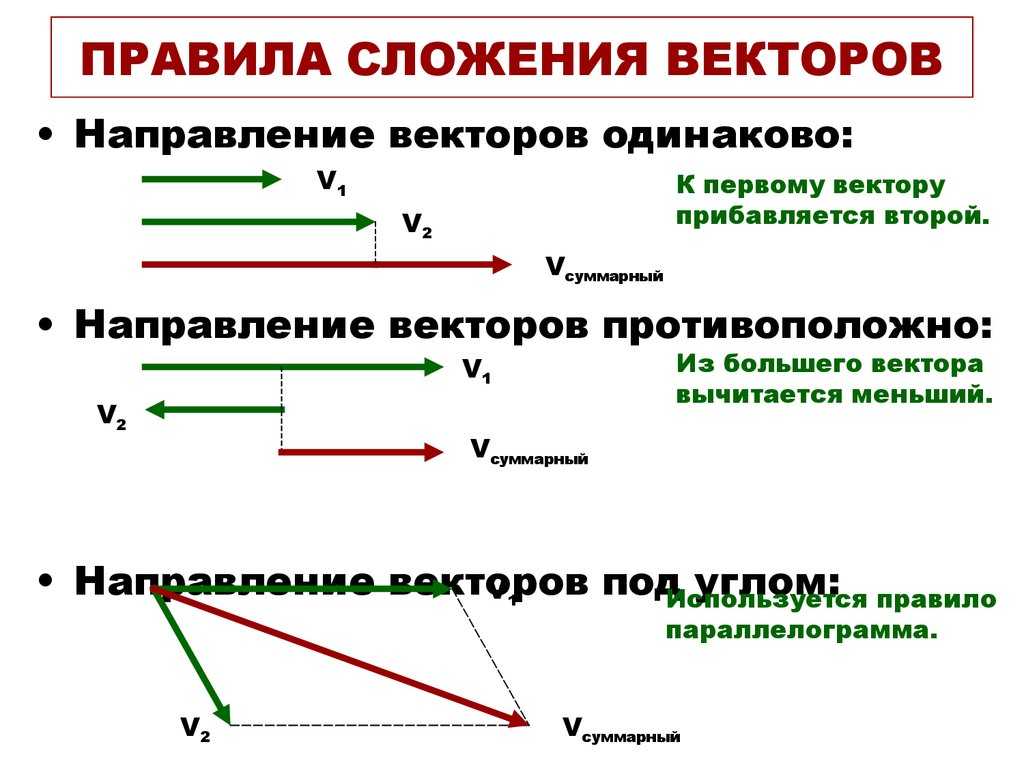 Формула для величины |R| и направление ϕ результирующего вектора R с использованием закона треугольника для сложения векторов определяется как

|R| = √(P ² + Q ² + 2PQ cos θ)

ϕ = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

Треугольный закон векторного сложения Доказательство

Прежде чем перейти к доказательству закона треугольника, давайте сначала посмотрим на формулировку закона треугольника сложения векторов:

Утверждение: Если два вектора, действующие одновременно на тело, представлены как по величине, так и по направлению двумя сторон треугольника, взятых в порядке, то результирующий вектор суммы (как величина, так и направление) этих двух векторов определяется третьей стороной этого треугольника, взятой в обратном порядке.

На приведенном ниже рисунке рассмотрим два вектора P и Q, величины которых заданы сторонами OA и AB соответственно. Теперь сумма этих векторов с использованием треугольного закона сложения векторов определяется результирующим вектором R (сторона OB треугольника), величина и направление которого равны

• |R| = √(P ² + Q ² + 2PQ cos θ)
• ϕ = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

Теперь продолжим сторону OA до точки C так, чтобы BC была перпендикулярна к OC, а угол между векторами P и Q был равен θ.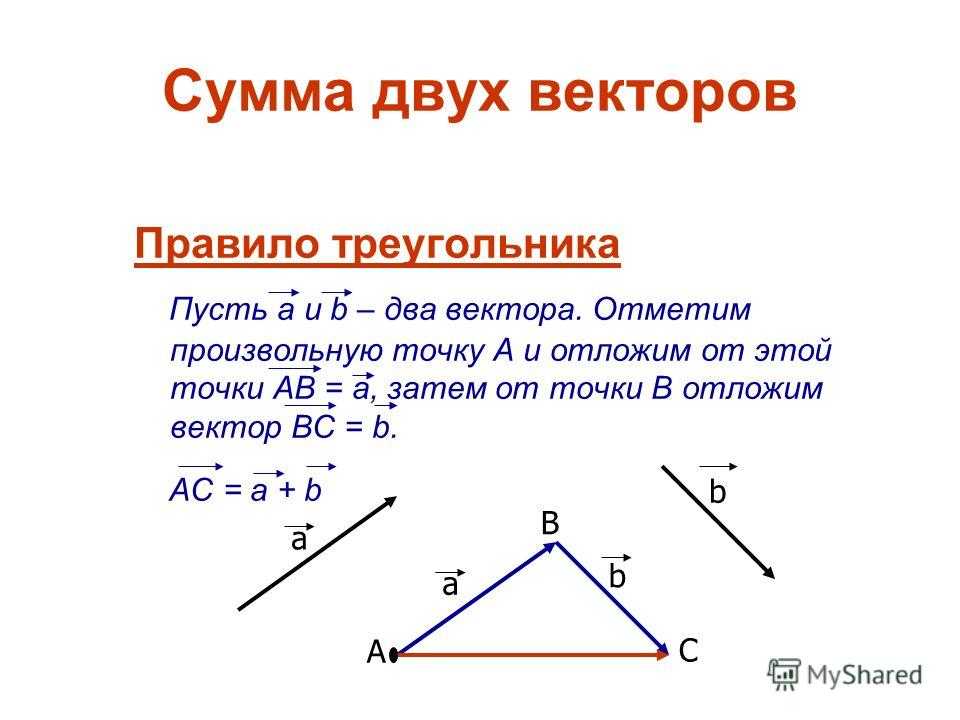 Кроме того, направление результирующего вектора R задается углом ϕ. В прямоугольном треугольнике OBC имеем

ОБ ² = ОС ² + ВС ²

⇒ ОБ ² = (ОА + АС) ² + ВС ^{9-0 2 0 0002 В прямоугольном треугольнике ABC имеем}

cos θ = AC/AB и sin θ = BC/AB

⇒ AC = AB cos θ и BC = AB sin θ

⇒ AC = Q cos θ и BC = Q sin θ — ( 2)

Подставляя значения из (2) в (1), имеем

R ² = (P + Q cos θ) ² + (Q sin θ) ²

⇒ R ² = P ² + Q ² cos ² θ + 2PQ cos θ + Q ² sin ² θ 90

5 = P ² + 2PQ cos θ + Q ² (cos ² θ + sin ² θ)

⇒ R ² = P ² + 2PQ cos θ 9 9 0 + Q

0 [cos 990 0

0 θ + sin ² θ = 1]

⇒ R = √(P ² + 2PQ cos θ + Q ² ) → Величина результирующего вектора R

Теперь, чтобы найти направление R, мы имеем в прямом треугольнике OBC,

tan ϕ = BC/OC

⇒ tan ϕ = Q sin θ/(OA + AC) [Из (2)]

⇒ tan ϕ = Q sin θ/(P + Q cos θ) [Из (2)]

⇒ ϕ = tan ^-1 [(Q sin θ)/(P + Q cos θ)] → Направление результирующего вектора R

Итак, мы доказали формулы треугольного закона сложения векторов.

Важные замечания о треугольном законе сложения векторов

• Треугольный закон сложения векторов используется для нахождения суммы двух векторов, когда вершина первого вектора соединяется с хвостом второго вектора.
• Величина результирующего вектора суммы R: R = √(P ² + 2PQ cos θ + Q ² )
• Направление результирующего вектора R: ϕ = tan ^-1 [(Q sin θ)/(P + Q cos θ)]

Темы, связанные с важными замечаниями по закону треугольника сложения векторов

• Векторные величины
• Нулевой вектор
• Типы векторов

Часто задаваемые вопросы о законе треугольника сложения векторов

Что такое треугольный закон сложения векторов в математике?

Треугольный закон сложения векторов — это математическая концепция, используемая для нахождения суммы двух векторов. Этот закон используется для сложения двух векторов, когда голова первого вектора соединяется с хвостом второго вектора, а затем присоединяется хвост первого вектора к началу второго вектора, чтобы сформировать треугольник, и, следовательно, получить результирующий вектор суммы .

Что такое формула треугольного закона сложения векторов?

Сумма двух векторов P и Q с использованием треугольного закона сложения векторов определяется результирующим вектором R, величина и направление которого равны:

• |R| = √(P ² + Q ² + 2PQ cos θ)
• ϕ = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

Как сложить векторы, используя закон треугольника для сложения векторов?

При сложении двух векторов P и Q мы складываем векторы и определяем результирующий вектор R по формулам:

• |Р| = √(P ² + Q ² + 2PQ cos θ)
• ϕ = тангенс ^-1 [(Q sin θ)/(P + Q cos θ)]

В чем разница между законом параллелограмма и законом треугольника сложения векторов?

Результирующий вектор суммы определяется диагональю параллелограмма по закону параллелограмма и третьей стороной треугольника по закону сложения векторов треугольника.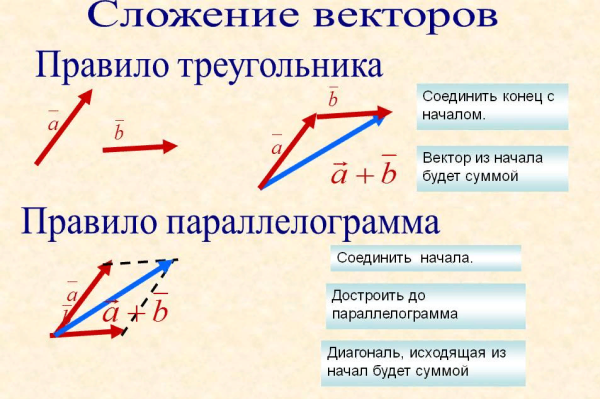

Закон параллелограмма и закон треугольника сложения векторов — одно и то же?

Закон параллелограмма и закон треугольника сложения векторов являются эквивалентными методами сложения векторов. Оба закона дают одинаковую величину и направление результирующего вектора суммы.

Как доказать формулу сложения векторов по закону треугольника?

Закон треугольника сложения векторов можно доказать, увеличив длину стороны первого вектора и применив формулы прямоугольного треугольника.

Треугольный закон сложения векторов

Состояние Треугольный закон сложения векторов или Укажите и объясните треугольный закон сложения векторов:

Закон сложения векторов треугольника гласит, что когда два вектора представляются как две стороны треугольника с одинаковым порядком величины и направлением, то величина и направление результирующего вектора представляются третьей стороной треугольника, взятой в обратный порядок.

Закон сложения векторов полигонов

Закон сложения векторов полигонов штата

Закон сложения векторов полигонов гласит, что если стороны многоугольника взяты в одном порядке для представления ряда векторов по величине и направлению, тогда результирующий вектор можно представить по величине и направлению замыкающей стороной многоугольника, взятой в обратном порядке.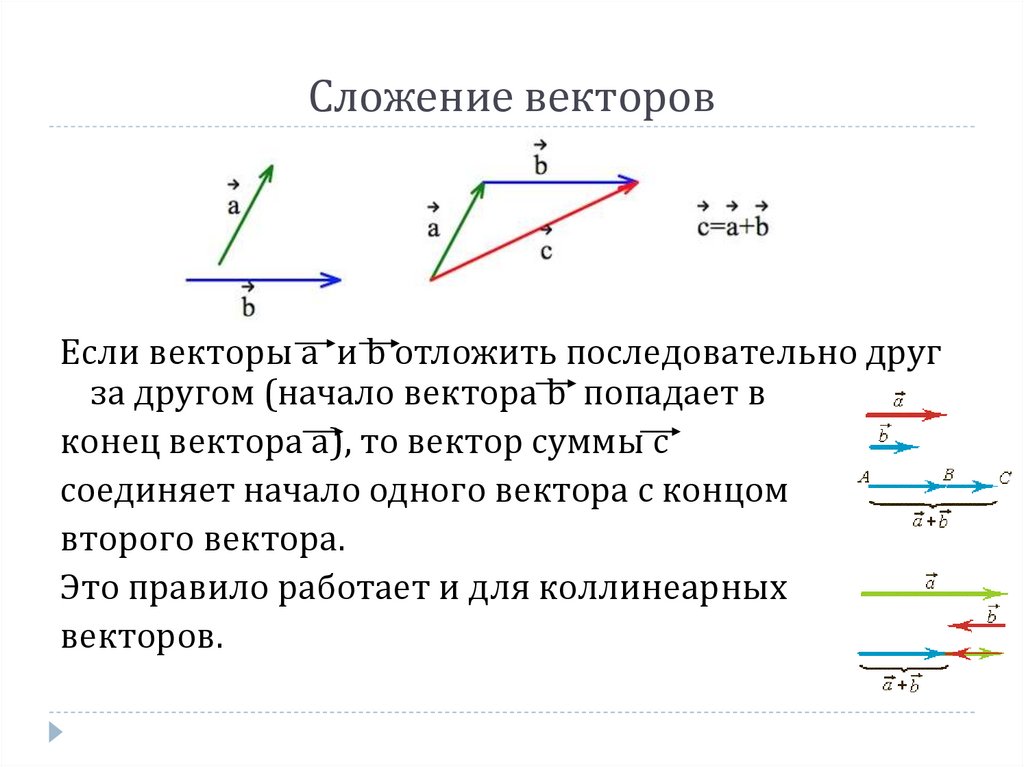

(Источник: Использование Paint)

Законы сложения векторов

Векторы записываются/представляются с помощью алфавита и стрелки над ними и представляются как комбинация направления и величины. Добавление двух или более векторов называется добавлением векторов. Когда мы добавляем векторы, мы используем операцию сложения, чтобы сложить два или более векторов, чтобы получить новый вектор, равный сумме двух или более векторов. Сложение векторов можно использовать для объединения двух векторов, a и b , и, таким образом, результирующий вектор может быть выражен как:

R = a + b здесь жирным шрифтом показано, что R, a и b являются векторами

Существуют разные законы сложения векторов, а именно:

Закон сил треугольника

Закон сил треугольника применим, когда на тело, находящееся в равновесии, действуют три силы. Затем две силы представляются как две стороны треугольника в том же порядке, с масштабированием их величины до подходящего масштаба, а результирующая в противоположном порядке является третьей стороной или замыкающей стороной треугольника.

Закон Треугольника Сил также можно использовать для вычисления равнодействующей двух сил, действующих в точке.

Читайте также —

• Решения NCERT для 11 класса по физике
• Решения NCERT для 12 класса по физике
• Решения NCERT для всех предметов

Треугольный закон сложения векторов 1 9003 класс 18 03 Что такое закон Треугольника силы сложения векторов треугольника?

Треугольный закон сложения векторов гласит, что если два вектора представлены сторонами треугольника, взятыми в порядке величины и направления, то результирующая сумма векторов определяется третьей стороной треугольника в обратном порядке величины и направление.

(Источник: Using Paint)

Сформулируйте и докажите закон сложения векторов треугольника или вывод из закона сложения векторов треугольника

Рассмотрим два вектора P и Q , представленные как по величине, так и по направлению сторонами OA и AB треугольника ОАВ соответственно. Пусть R будет произведением/результатом треугольного закона сложения векторов. Следовательно, результирующая P и Q представлена ​​стороной OB в соответствии с треугольным законом сложения или треугольным законом сложения векторов.

(Источник: использование инструментов ms)

У нас есть,

R=P+Q

Разверните A в C и проведите перпендикуляр BC.

Из треугольника OCB имеем

OB ² =OC ² +BC ²

OB ² =(OA+OC) 9 0 6 2 9 0 59 2 9 0 6 0 ….(i)

В треугольнике ACB,

cosθ=AC/AB

AC=ABcosθ=Qcosθ

Также

Sinθ=BC/AB

BC=ABsinθ=Qsinθ

902 величина:0005

Подставьте значения AC и BC в (i),

R ² =(P+Qcosθ) ² +(Qsinθ) ²

R ² 9P Qcosθ+ Q ²

R2=√(P ² +2PQcosθ+Q ² )

Приведенное выше уравнение дает нам величину равнодействующей.

Найти модуль и направление результирующего вектора

Направление модуля результирующего вектора определяется выражением;

Из треугольника OBC,

tan∅=BC/OC

Так как, OC=OA+AC.

tan∅=BC/(OA+AC)

tan∅=Qsinθ/(P+Qcosθ)

Приведенное выше уравнение дает нам направление результирующего вектора.

Читайте также:

• Решения NCERT для Класса 11 Физика Глава 3 Движение по прямой прямая

Примеры треугольного закона сложения векторов

Пример: Два вектора A и B величиной 5 единиц и 7 единиц соответственно составляют угол 60 ^o . Определите величину результирующего вектора.

Решение: Следуя треугольному закону сложения векторов, результирующий вектор определяется как:

R=A+B

Величина R равна:

R=|R|=√7 ² +5 ² +2*5*7cos60 ^o

R=√25+49+70/2

R=√109 единиц

Важные замечания о сложении векторов

Ниже приведен список некоторых моментов, которые следует учитывать при изучении сложения векторов:

1. направление и величина.

   No related posts.