Мерзляк 5 класс — § 1. Ряд натуральных чисел
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
- Как называют числа, используемые при счёте предметов? — натуральные числа
- Есть ли среди натуральных чисел наименьшее число? Наибольшее число? В случае утвердительного ответа назовите это число. Наименьшее число натурального ряда — 1. В натуральном ряду нет наибольшего числа — этот ряд бесконечен.
- Опишите ряд натуральных чисел. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …
- Каждое ли число в ряду натуральных чисел имеет:
- последующее число — да, каждое натуральное число имеет последующие, которое на 1 больше предыдущего. Например, для числа 5 последующим будет 6 (5 + 1 = 6)
- предыдущее число? — предыдущее число имет все натуральные числа кроме 1.
Решаем устно
1. Сложите:
- 48 + 7 = 55
- 16 + 9 = 25
- 25 + 34 = 59
- 52 + 49 = 101
2. Вычтите:
- 14 — 6 = 8
- 23 — 7 = 16
- 32 — 8 = 24
- 45 — 19 = 26
3. Умножьте:
- 12 • 4 = 48
- 5 • 20 = 100
- 13 • 6 = 78
- 10 • 100 = 1000
4. Разделите:
- 36 : 12 = 3
- 55 : 11 = 5
- 96 : 8 = 12
- 160 : 20 = 8
5. Около школы растут каштаны и тополя. Каштанов растёт семь, а тополей — в 3 раза больше. Сколько деревьев растёт около школы?
7 + 7 • 3 = 7 + 21 = 28 (деревьев) — растёт около школы.
Ответ: 28 деревьев.
6. В школе учатся 370 учеников. Найдутся ли среди них хотя бы два ученика, которые отмечают день рождения в один и тот же день?
Да, так как в году максимально может быть 366 дней (в високосный год).
370 > 366, значит у нескольких учеников дни рождения будут отмечаться в один и тот же день.
Упражнения
1. Назовите 14 первых натуральных чисел.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
2. Какого числа не хватает в записи натурального ряда чисел: 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, … ?
В записи натурального ряда не хватает числа 8.
3. Из чисел 5, , 8, 129, 0, , 4 128, — выберите натуральные.
5, 8, 129, 4 128
4. Запишите число, которое в натуральном ряду следует за числом: 1) 34; 2) 246; 3) 8 297.
- за числом 34 следует число 35
- за числом 246 следует число 247
- за числом 8 297 следует число 8 298
5. Запишите число, которое в натуральном ряду следует за числом: 1) 72; 2) 121; 3) 6 459.
- за числом 72 следует число 73
- за числом 121 следует число 122
- за числом 6 459 следует число 6 460
6.
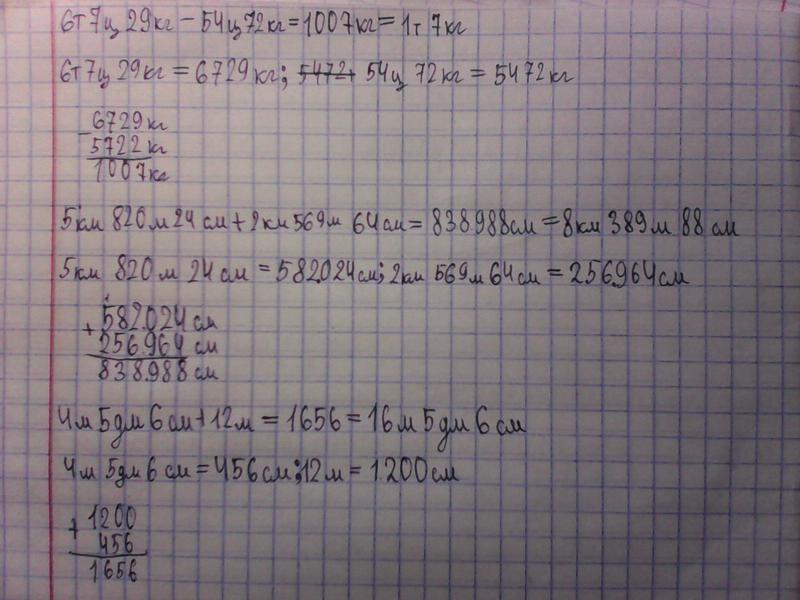Запишите число, которое в натуральном ряду является предыдущим числу: 1) 58; 2) 631; 3) 4 500.
- предыдущим к числу 58 является число 57
- предыдущим к числу 631 является число 630
- предыдущим к числу 4 500 является число 4 499
7. Запишите число, которое в натуральном ряду является предыдущим числу: 1) 42; 2) 215; 3) 3 240.
- предыдущим к числу 42 является число 41
- предыдущим к числу 215 является число 214
- предыдущим к числу 3 240 является число 3 239
8. Сколько чисел стоит в натуральном ряду между числами: 1) 6 и 24;
2) 18 и 81?- между числами 6 и 24 стоит 17 натуральных чисел: 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23.
- между числами 18 и 81 стоит 62 натуральных числа: 19, 20, 21, …, 78, 79, 80.
9. Сколько чисел стоит в натуральном ряду между числами: 1) 13 и 28; 2)29 и 111?
- между числами 13 и 28 стоит 14 натуральных чисел: 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27.
- между числами 29 и 111 стоит 81 натуральное число: 30, 31, 32, …, 108, 109, 110.
10. Некоторое натуральное число, большее 3, обозначили буквой а. Запишите для числа а два предыдущих и три последующих натуральных числа.
Если а — данное натуральное число, большее трёх, то первое предыдущее число для него будет (а — 1), а второе предыдущее — (а — 2). Три последующих числа будут записаны так: (а + 1), (а + 2) и (а + 3).
Проверка: Пусть а = 15. Тогда:
- 15 — 1 = 14 — первое предыдущее число
- 15 — 2 = 13 — второе предыдущее число
- 15 + 1 = 16 — первое последующее число
- 15 + 2 = 17 — второе последующее число
- 15 + 3 = 18 — третье последующее число.
Упражнения для повторения
11. Вычислите:
12. Первое летописное упоминание о Москве встречается в Ипатьевской летописи в 1147 г. Сколько лет прошло от первого летописного упоминания Москвы?
Ответ: От первого летописного упоминания Москвы прошло 873 года.
13. Выполните действия:
14. Собираясь в гости к своей бабушке, Карлсон решил подкрепиться. Для этого на завтрак он съел 26 банок варенья, а на обед — на 16 банок больше. Сколько банок варенья съел Карлсон?
1) 26 + 16 = 42 (банки) — Карлсон съел на обед.
2) 26 + 42 = 68 (банок) — съел Карлсон
Ответ: Карлсон съел 68 банок варенья.
15. На одном участке растут 34 куста смородины, а на другом — на 18 кустов меньше. Сколько всего кустов смородины растёт на двух участках?
1) 34 — 18 = 16 (кустов) — растёт на втором участке.
2) 34 + 16 = 50 (кустов) — растёт на двух участках.
Ответ: На двух участках растёт 50 кустов.
Задача от мудрой совы
16. В квадрате (рис. 1) суммы чисел в каждом столбце, в каждой строке и диагоналях должны быть одинаковыми. Найдите число, которое должно быть записано вместо звёздочки.
1) Посчитаем сумму чисел в одном столбце.
Все цифры у нас известны в первом столбце:
10 + 9 + 14 = 33
Это значит, что в кадом столбце, строке или диагонали сумма чисел должна равняться 33.
2) Рассмотрим вторую строку. У нас известно два числа и общая сумма. Найдём неизвестное число:
33 — (9 + 13) = 33 — 12 = 11 — число в середине второй строки.
3) Рассмотрим диагональ от нижнего левого угла до верхнего правого угла:
33 — (14 + 11) = 33 — 25 = 8 — число в верхнем правом углу.
4) Рассмотрим третий столбец:
33 — (8 + 13) = 33 — 21 = 12 — число в нижнем правом углу
5) Рассмотрим нижнюю строку:
33 — (14 + 12) = 33 — 26 = 7 — число в середине нижней строки.
6) Рассмотрим средний столбец:
33 — (11 + 7) = 33 — 18 = 15 — искомое число на месте звёздочки.
Ответ: На месте звёздочки надо написать число 15.
Комментарий: На самом деле для поиска искомого числа достаточно было выполнить первые три действия, а затем вычислить искомое рассмотрев верхнюю строчку.
Остальные неизвестные, согласно заданию, искать было не обязательно.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Решить (28+24.5+x/48+50+48+52)*0.1+8/10*0.15+15/30*0.75>0.5 | Microsoft Math Solver
\frac{52.5+x}{48+50+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Чтобы вычислить 52.5, сложите 28 и 24.5.
\frac{52.5+x}{98+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Чтобы вычислить 98, сложите 48 и 50.
\frac{52.5+x}{146+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Чтобы вычислить 146, сложите 98 и 48.
\frac{52.5+x}{198}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Чтобы вычислить 198, сложите 146 и 52.
\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times 0.15+\frac{15}{30}\times 0.75>0.5
Привести дробь \frac{8}{10} к несократимому виду, разделив числитель и знаменатель на 2.
\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times \left(\frac{3}{20}\right)+\frac{15}{30}\times 0.75>0.5
Преобразовать десятичное число 0.15 в дробь \frac{15}{100}. Привести дробь \frac{15}{100} к несократимому виду, разделив числитель и знаменатель на 5.
\frac{52.5+x}{198}\times 0.1+\frac{4\times 3}{5\times 20}+\frac{15}{30}\times 0.75>0.5
Умножить \frac{4}{5} на \frac{3}{20}, перемножив числители и знаменатели.
\frac{52.5+x}{198}\times 0.1+\frac{12}{100}+\frac{15}{30}\times 0.75>0.5
Выполнить умножение в дроби \frac{4\times 3}{5\times 20}.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{15}{30}\times 0.75>0.5
Привести дробь \frac{12}{100} к несократимому виду, разделив числитель и знаменатель на 4.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times 0.75>0.5
Привести дробь \frac{15}{30} к несократимому виду, разделив числитель и знаменатель на 15.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times \left(\frac{3}{4}\right)>0.
5
Преобразовать десятичное число 0.75 в дробь \frac{75}{100}. Привести дробь \frac{75}{100} к несократимому виду, разделив числитель и знаменатель на 25.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1\times 3}{2\times 4}>0.5
Умножить \frac{1}{2} на \frac{3}{4}, перемножив числители и знаменатели.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{3}{8}>0.5
Выполнить умножение в дроби \frac{1\times 3}{2\times 4}.
\frac{52.5+x}{198}\times 0.1+\frac{24}{200}+\frac{75}{200}>0.5
Наименьшим общим кратным чисел 25 и 8 является число 200. Преобразуйте числа \frac{3}{25} и \frac{3}{8} в дроби с знаменателем 200.
\frac{52.5+x}{198}\times 0.1+\frac{24+75}{200}>0.5
Поскольку числа \frac{24}{200} и \frac{75}{200} имеют одинаковый знаменатель, выполните операцию сложения с помощью числителей.
\frac{52.5+x}{198}\times 0.1+\frac{99}{200}>0.5
Чтобы вычислить 99, сложите 24 и 75.
\left(\frac{35}{132}+\frac{1}{198}x\right)\times 0.
1+\frac{99}{200}>0.5
Разделите каждый член 52.5+x на 198, чтобы получить \frac{35}{132}+\frac{1}{198}x.
\frac{7}{264}+\frac{1}{198}x\times 0.1+\frac{99}{200}>0.5
Чтобы умножить \frac{35}{132}+\frac{1}{198}x на 0.1, используйте свойство дистрибутивности.
\frac{7}{264}+\frac{1}{198}x\times \left(\frac{1}{10}\right)+\frac{99}{200}>0.5
Преобразовать десятичное число 0.1 в дробь \frac{1}{10}.
\frac{7}{264}+\frac{1\times 1}{198\times 10}x+\frac{99}{200}>0.5
Умножить \frac{1}{198} на \frac{1}{10}, перемножив числители и знаменатели.
\frac{7}{264}+\frac{1}{1980}x+\frac{99}{200}>0.5
Выполнить умножение в дроби \frac{1\times 1}{198\times 10}.
\frac{175}{6600}+\frac{1}{1980}x+\frac{3267}{6600}>0.5
Наименьшим общим кратным чисел 264 и 200 является число 6600. Преобразуйте числа \frac{7}{264} и \frac{99}{200} в дроби с знаменателем 6600.
\frac{175+3267}{6600}+\frac{1}{1980}x>0.5
Поскольку числа \frac{175}{6600} и \frac{3267}{6600} имеют одинаковый знаменатель, выполните операцию сложения с помощью числителей.
\frac{3442}{6600}+\frac{1}{1980}x>0.5
Чтобы вычислить 3442, сложите 175 и 3267.
\frac{1721}{3300}+\frac{1}{1980}x>0.5
Привести дробь \frac{3442}{6600} к несократимому виду, разделив числитель и знаменатель на 2.
\frac{1}{1980}x>0.5-\frac{1721}{3300}
Вычтите \frac{1721}{3300} из обеих частей уравнения.
\frac{1}{1980}x>\frac{1}{2}-\frac{1721}{3300}
Преобразовать десятичное число 0.5 в дробь \frac{5}{10}. Привести дробь \frac{5}{10} к несократимому виду, разделив числитель и знаменатель на 5.
\frac{1}{1980}x>\frac{1650}{3300}-\frac{1721}{3300}
Наименьшим общим кратным чисел 2 и 3300 является число 3300. Преобразуйте числа \frac{1}{2} и \frac{1721}{3300} в дроби с знаменателем 3300.
\frac{1}{1980}x>\frac{1650-1721}{3300}
Поскольку числа \frac{1650}{3300} и \frac{1721}{3300} имеют одинаковый знаменатель, выполните операцию вычитания с помощью числителей.
\frac{1}{1980}x>-\frac{71}{3300}
Вычтите 1721 из 1650, чтобы получить -71.
x>-\frac{71}{3300}\times 1980
Умножьте обе части на 1980 — число, обратное \frac{1}{1980}. Так как \frac{1}{1980} >0, знак неравенства сохраняется.
x>\frac{-71\times 1980}{3300}
Отобразить -\frac{71}{3300}\times 1980 как одну дробь.
x>\frac{-140580}{3300}
Перемножьте -71 и 1980, чтобы получить -140580.
x>-\frac{213}{5}
Привести дробь \frac{-140580}{3300} к несократимому виду, разделив числитель и знаменатель на 660.
Что такое совместимые номера? Определение, примеры и факты
Что такое совместимые числа?
Совместимые числа в математике — это числа, которые легко складывать, вычитать, умножать или делить в уме. Они близки по значению к реальным числам, что облегчает оценку ответа и вычисление задач. Давайте посмотрим, как они облегчают расчеты на примере.
Кейт хочет купить ховерборд и защитный шлем. Цена ховерборда $\$244$, а цена защитного шлема $\$38$. У Кейт всего $\$275$ на руках. Она хочет знать, достаточно ли у нее денег, чтобы купить оба предмета.
Используя совместимые числа, Кейт может мысленно оценить общую стоимость, фактически не добавляя 244 и 38.
$244 + 38 =$ ?
240 $ + 40 = 280 $
Теперь она знает, что ей нужно больше денег, чтобы купить ховерборд и шлем.
Родственные игры
Где мы используем совместимые числа в математике?
Если мы хотим получить оценку или приблизить расчет, мы можем заменить фактические числа совместимыми числами. Они обычно используются для решения задач, где допустима некоторая неточность или допускается приближение. Ответ будет не точным, а разумной оценкой.
Давайте посмотрим, как мы можем легко выполнять сложение, вычитание, умножение и деление, используя совместимые числа.
Связанные рабочие листы
Совместимые числа в сложении
При вычислении суммы двух или более чисел числа, оканчивающиеся на 5 или 0, всегда удобны для работы. Примеры: $65 + 15 = 80$
Кроме того, пары чисел, сумма которых кратна 10 (или число, оканчивающееся на 0), также облегчают сложение.
Пара чисел, оканчивающихся на 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5 совместимы.
Примеры: $18 + 22 = 40, 13 + 7 = 20, 11 + 19 = 30$
Мы можем округлить числа до ближайших десяти, сотен, тысяч или десяти тысяч. Давайте посмотрим пример.
Пример 1: Числа округлены до ближайших десятков, сотен или тысяч.
Например, если нам нужно сложить 493 и 549, мы можем сделать числа совместимыми, округлив их до ближайших десятков или сотен.
493 и 549при округлении до ближайших десятков получается 490 и 550 соответственно.
493 и 549 округляя до ближайших сотен, получаем 500 и 500 соответственно.
Пример 2: Оценка сложения десятичных чисел.
Пример 3: Сложите 58 и 13.
Совместимые числа при вычитании
Как и при сложении, числа, оканчивающиеся нулями, также совместимы при вычитании. Кроме того, числа с одинаковой последней цифрой помогают найти разницу.
Пример 1. Вычтите 376 из 612.
Пример 2: Вычитание десятичных дробей.
Пример 3: Числа, оканчивающиеся на одну и ту же цифру.
Совместимые числа при умножении
Всегда легко умножать числа, оканчивающиеся одним или несколькими нулями. Мы можем игнорировать их в начале и сначала умножать ненулевые числа. После завершения умножения можно добавить необходимое количество нулей.
Пример 1: Умножение 62 на 13.
Пример 2: Умножение десятичных дробей
Пример 3: Числа, таблица умножения которых нам известна, поэтому мы можем легко умножать.
Фактическое произведение 34$ и 9$ = 34 \times 9 = 306$
Используя совместимые числа, мы получаем: 34$ \rightarrow 34$ и $9 \rightarrow 10$
Произведение с использованием совместимых чисел: $34 \times 10 = 340 $
Совместимые числа в делении
Числа, оканчивающиеся на 1 или более нулей, также совместимы в делении.
Пример 1: Числа округлены до ближайших десятков, сотен или тысяч.
Пример 2: Деление десятичных дробей с помощью совместимых чисел.
Пример 3: Числа, таблица умножения которых нам известна, так что мы можем легко делить.
Фактическое частное от деления 70$ и 4$: 70\дел 4 = 17,5$
Используя совместимые числа, мы получаем: 70$\rightarrow 68$ и 68$\дел 4 = 17$
Важное примечание: При оценке с деление, если вы уменьшаете значение одного числа, вы также должны уменьшить значение другого. Если вы увеличиваете значение одного числа, вы должны увеличить значение другого. Это помогает максимально приблизить оценку к точному ответу.
9Мы можем видеть, что мы получаем более точную оценку, когда мы уменьшаем значение обоих чисел, чем когда мы уменьшаем значение одного и увеличиваем значение другого.
Совместимые числа и оценка
Совместимые числа часто используются для оценки значений путем преобразования фактических значений в числа, которые легко вычислить в уме.
Пример: Дин сэкономил $\$37$, а Том сэкономил $\$52$. Оцените общую сумму, сэкономленную братьями.
Сначала замените числа на совместимые числа:
$\$37$ заменено на $\$40$
$\$52$ заменено на $\$50$
$\$40 + \$50 = \$90$
Дин и Том сэкономили около $\$90$ вместе .
Если есть более сложные значения, мы пытаемся сбалансировать их оценку.
Например, если в одном случае мы оцениваем $\$37$ как $\$40$, мы должны попытаться округлить другое число до такой же суммы, если это возможно. Так наша оценка будет более точной.
Совместимые номера против округления
Совместимые числа и округление довольно похожи, но между ними есть небольшая разница. Мы выбираем более близкие числа, чтобы упростить решение задачи в совместимых числах.
Пример: Радж хочет разделить свое учебное время в 166 минут поровну между 4 предметами.
Фактическое деление: 166 разделить на 4 равно 41,5 минут на предмет.
Используя совместимые числа, мы можем решить это как: $166$ -\gt 160$
160 разделить на 4 дает 40 минут на предмет.
Округление 166 до ближайших десятков дает 170. Деление 170 на 4 дает 42,5 минут на предмет.
Заключение
Мы узнали о совместимых числах, которые упрощают сложные вычисления, включающие сложение, вычитание, умножение или деление. В следующий раз, когда вы будете стоять в очереди, чтобы получить счет за продукты, используйте совместимые числа, чтобы быстро найти общую сумму до того, как это сделает человек за прилавком для выставления счетов.
Решенные примеры
Оцените следующее, используя совместимые числа.
- 83$ + 18$
- 134$ − 67$
- 319$\умножить на 89$
- $7810 \дел 37$
Решение: Совместимые числа — это числа, которые легко складывать, вычитать, умножать или делить в уме.
- 83$ + 18$
Замените числа совместимыми числами сложения.
83$ \rightarrow 80$
18$ \rightarrow 20$
Теперь найдите сумму.
80$ + 20 = 100$
- 134$ − 67$
Здесь мы можем использовать совместимые числа двумя разными способами.
(c) $319 \times 89$
Замените числа совместимыми числами умножения.
319$ \rightarrow 300$
89$ \rightarrow 90$
Теперь найдите произведение.
300$ х 90 = 27000$
(d) 7810$ \div 37$
Замените числа соответствующими числами деления.
$7810 \rightarrow 8000$
$37 \rightarrow 40$
Теперь найдите частное.
8000$ \дел 40 = 200$
2. Лиза пошла за покупками и провела картой на $\$487$ в первом магазине и на $\$192$ во втором магазине. Прикиньте, сколько она потратила в обоих магазинах вместе?
Решение:
Сумма, которую Лиза провела в первом магазине $= \$487$
Сумма, которую Лиза провела во втором магазине $= \$192$
Сумма, потраченная Лизой в обоих магазинах $= \$487 + \$192$.
Чтобы найти оценку, мы заменяем числа совместимыми числами.
$\$487 \rightarrow \$500$
$\$192 \rightarrow \$200$
$\$500 + \$200 = \$700$
Лиза потратила около $\$700$ в обоих магазинах вместе.
3. В кондитерскую поступил заказ на 3897 пончиков. Если в каждой коробке может поместиться 4 пончика, сколько примерно коробок понадобится магазину?
Решение:
Количество пончиков в упаковке $= 3897$
Количество пончиков в коробке $= 4$
Количество коробок, необходимых для упаковки всех пончиков $= 3897 \div 4$
Найти в оценке мы заменяем числа совместимыми числами.
$3897 \rightarrow 4000$ и $4\rightarrow4$
$4000 \div 4 = 1000$
Магазину нужно около 1000 коробок, чтобы упаковать 4132 пончика.
4. Баланс на банковском счете Джона составлял $\$693$ . Если он вывел $\$129$ , каков его примерный новый баланс?
Решение:
Баланс счета Джона $= \$693$
Сумма, которую Джон снял $= \$129$
Новый баланс счета Джона $= \$693 − \$129$
числа с совместимыми числами.
$693\rightarrow693$
$129\rightarrow123$
$\$693 − \$123 = \$570$
Новый баланс Джона составляет приблизительно $\$570$.
5. Эльза готовится к конкурсу правописания. Если она выучит 81 слово в день, то сколько примерно слов она выучит за 19 дней?
Решение:
Количество слов, которые Эльза выучит за $1$ день $= 81$
Количество слов, которое Эльза выучит за $19$ дней $= 81 \times 19$
Чтобы найти оценку, заменим числа с совместимыми номерами.
81$ \rightarrow 80$ и 19$ \rightarrow 20$
80$ \умножить на 20 = 1600$
Эльза может выучить около 1600 слов за 19 дней.
Практические задачи
1
Найдите оценку 167 + 35, используя совместимые числа.
250
200
180
230
Правильный ответ: 200
Оценка суммы с использованием совместимых чисел: 167 долларов + 33 = 200 долларов.
2
На благотворительном шоу $\$1289$ было собрано в первый день и $\$899$ во второй день. Какой из следующих способов является правильным способом оценки сбора в оба дня?
$\$1200 + \$800$
$\$1000 + \$100$
$\$1300 + \$900$
$\$1588 + \$599$
Правильный ответ: $\$9000 + \$9000 Правильный способ оценки сбора в оба дня: $\$1300 + \$900$.
3
Ежемесячная плата в институте $\$408$. Оцените сумму взноса студента за 4 года.
$\$22,000$
$\$2000$
$\$20,000$
$\$15,000$
Правильный ответ: $\$20,000$
4 года $= 4 х 12 = 48$ месяцев.
Ориентировочный взнос, внесенный студентом за 4 года, составляет $\$400 \х50 = \$20,000$.
4
Продуктовый магазин имеет в наличии 45 239 фунтов цельной пшеницы. Если они продали 39 782 фунта, сколько приблизительно цельной пшеницы осталось на складе?
10000 фунтов
7000 фунтов
5000 фунтов
2000 фунтов
Правильный ответ: 5000 фунтов
5
Оценка Оценка Оценка, когда 20 891 делится на 687.
3
30
300
3000
Правильный ответ: 30
Оценка кожура с использованием совместимых чисел как 21 доллар, \ div 700 = 30313. $.
Часто задаваемые вопросы
Дружественные номера также называются совместимыми?
Дружественные номера также называются совместимыми номерами. Это числа, которые легко складывать, обычно их сумма кратна десяти. Например, 3 и 7 — это дружественные числа, которые также называются совместимыми числами.
Всегда ли совместимые числа заканчиваются нулями?
Совместимые числа — это числа, облегчающие вычисления. Они не должны всегда заканчиваться нулями. 45 и 5 также являются совместимыми числами, поскольку складывать их в уме несложно.
Какой метод оценки лучше? Совместимые числа или округление чисел?
Оба часто используемых метода оценки. Выбор метода зависит от степени точности требуемой оценки.
Можем ли мы использовать совместимые числа для вычисления дробей?
Да, мы можем оценить дроби, заменив их эталонными дробями , которые являются обычными дробями, которые мы можем измерить или на основании которых можно судить при измерении, сравнении или заказе других дробей. Эталонные дроби легко визуализировать и идентифицировать, и, таким образом, они помогают в оценке частей.
Например,
$\frac{5}{6} + \frac{1}{2}$
$\frac{5}{6}$ близко к 1, поэтому его можно заменить на 1.
$1 + \frac{1}{2} = 1\frac{1}{2}$
Title
Блок переключения содержимого для Gutenberg упрощает создание переключаемого содержимого. Этот блок-переключатель поставляется с хорошо продуманными параметрами настройки.
Упростить: 7/8=n/48 Tiger Algebra Solver
Переставить:
Преобразовать уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения:
7/8-(n/ 48)=0
Пошаговое решение:
Шаг 1 :
нет
Упростить ——
48
Уравнение в конце шага 1 :
7 n — — —— = 0 8 48
Шаг 2 :
7
Упростить —
8
Уравнение в конце шага 2 :
7 n — — —— = 0 8 48
Шаг 3 :
Вычисление наименьшего общего кратного:
3. 1 Найдите наименьшее общее кратное
Левый знаменатель: 8
Правый знаменатель: 48
| Prime Фактор | Деновис | Дено | 2 | 2 | 2 | . ,Right} | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 4 | ||||||||
| 3 | 0 | 1 | 1 | ||||||||
| Производство всех Прайс | 8 | 48 | 48 |
Наименее множество:
48
Множественные:
48
. Обычный кратный через L.C.M
Обозначьте левый множитель через Left_M
Обозначьте правый множитель через Right_M
Обозначьте левый знаменатель через L_Deno
Обозначите правый множитель с помощью R_DENO
LEATE_M = L. C.M/L_DONO = 6
Right_M = L.C.M/R_DENO = 1
Создание эквивалентных фракций:
3.3 Перепишите два фракции в эквивалентные фракции
имеют одинаковое числовое значение.
Например: 1/2 и 2/4 эквивалентны, y/(y+1) 2 и (y 2 +y)/(y+1) 3 также эквивалентны.
Чтобы рассчитать эквивалентную дробь, умножьте числитель каждой дроби на соответствующий множитель.
Л. Мульт. • L. Num. 7 • 6
"="
ЛКМ 48
Р. Мульт. • R.Число. н
"="
ЛКМ 48
Сложение дробей, имеющих общий знаменатель:
3.4 Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, имеющих общий знаменатель
Соедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:
7 • 6 - (n) 42 - n
"="
48 48
Уравнение в конце шага 3 :
42 - n
—————— = 0
48
Шаг 4 :
Когда дробь равна нулю :
4.