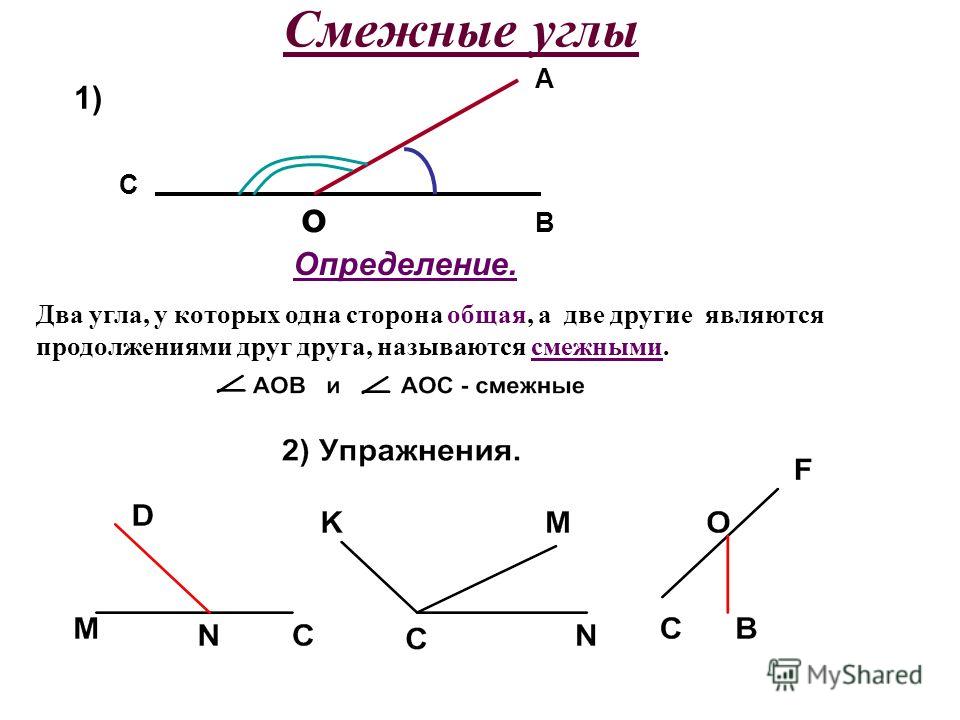
Решение задач по теме «Смежные и вертикальные углы»
- Графуткина Галина Ивановна, заместитель директора по УВР,учитель математики
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (9 МБ)
Тип урока: урок закрепления нового материала
Цели урока:
- Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
- Развивающие: развивать умение анализировать условие задачи;
- Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).

Структура урока:
- I этап. Организационный момент
- II этап. Актуализация опорных знаний
- III этап. Закрепление изученного материала
- IV этап. Зарядка для глаз
- V этап. Самостоятельная работа
- VI этап. Домашнее задание
- VII этап. Итог урока
(Слайд 1-2)
Приветствие, сообщение темы, целей и задач.
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.
(Слайд 3)
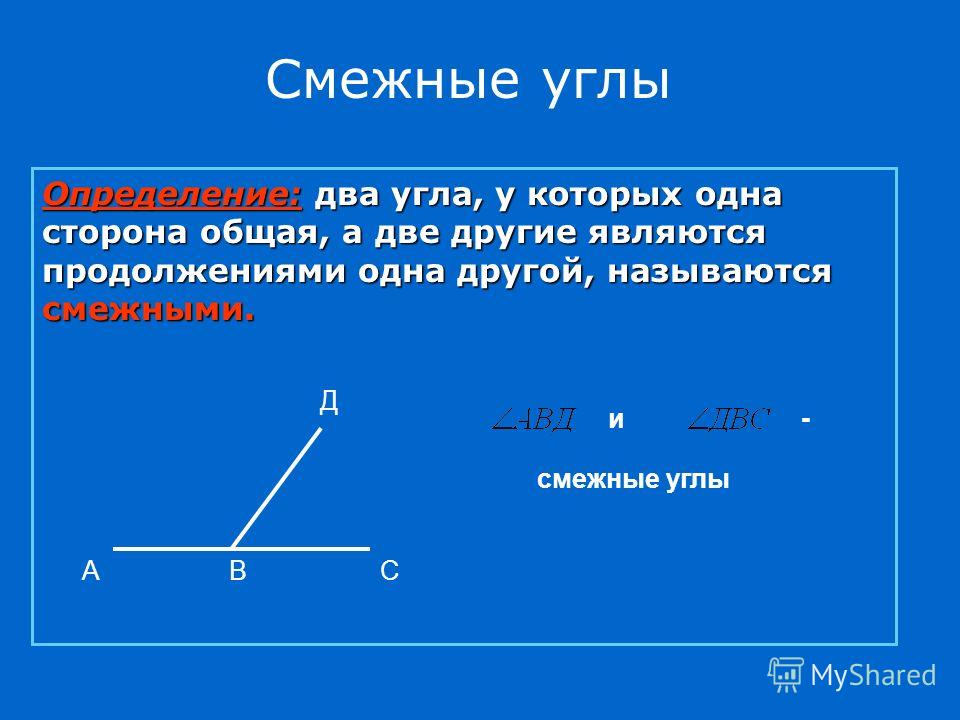
Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)
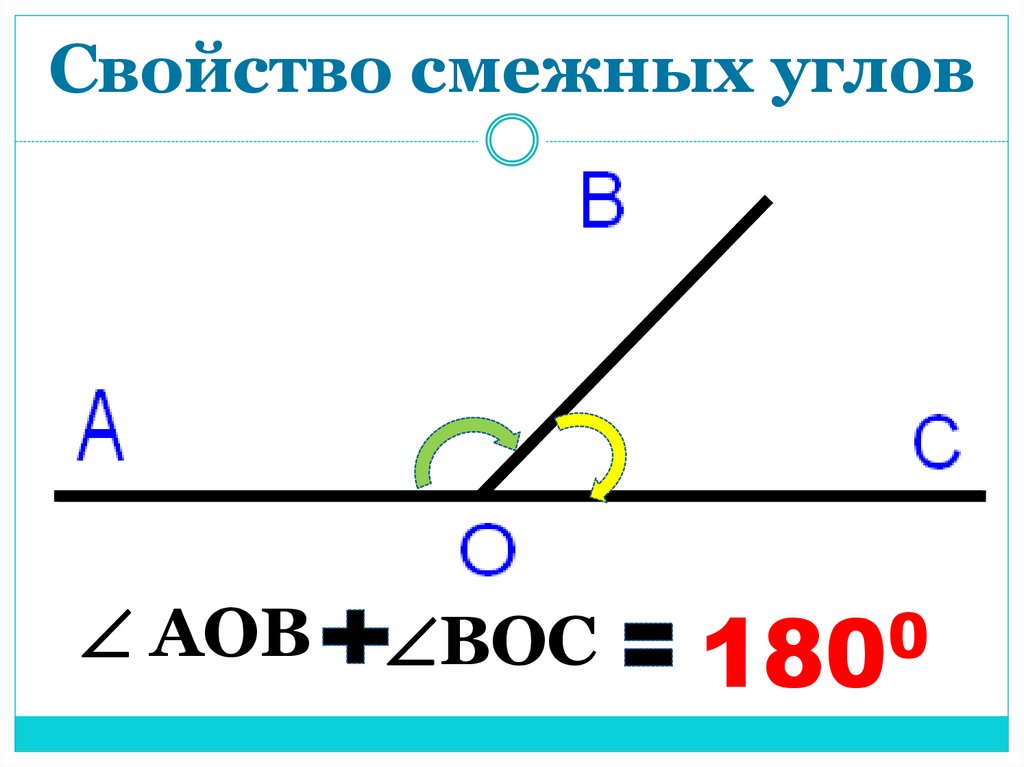
Вопрос. Из рисунка назвать смежные углы.
Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)
Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)
(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?
Ответ.
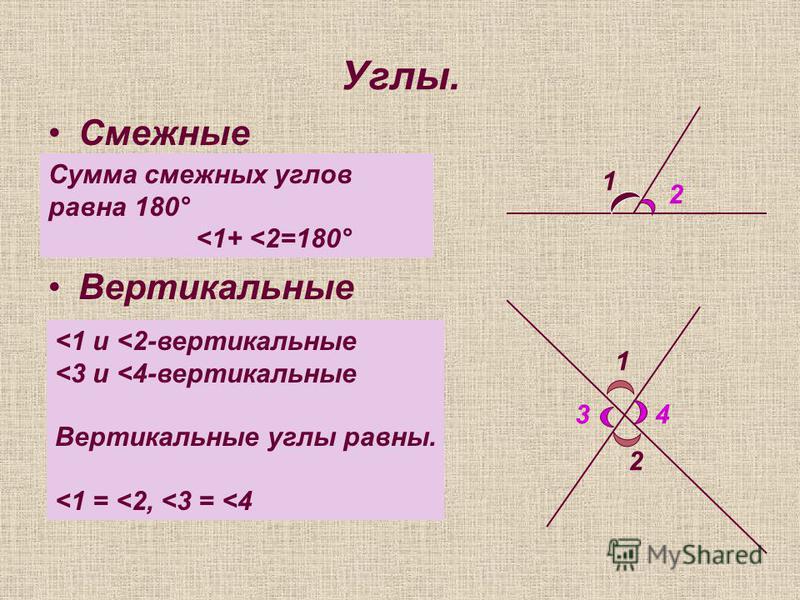
- Сумма смежных углов равна 180° (теорема)
∠1 + ∠2 = 180°
- Если два угла равны, то и смежные с ними углы равны.
- Если угол не развернутый, то его градусная мера меньше 180°.
- Угол, смежный с прямым, есть прямой угол.
(Слайд 5)
Вопросы. Могут ли два смежных угла быть равными:
а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ:(да, т. к. 83° + 97°= 180°)
(Слайд 6)
Устно.
| Дано:
∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4 |
Доказательство.
1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, |
Доказать ∠1 = ∠2 |
(Слайд 7)
Вопрос. Какие углы называются вертикальными?
(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).
∠ 1 и ∠ 3 – вертикальные углы
∠ 2 и ∠ 4 – вертикальные углы
(Слайд 8)
Вопрос. Каким свойством обладают смежные углы?
Каким свойством обладают смежные углы?
Ответ. Вертикальные углы равны. (теорема)
∠ 1 = ∠ 3
∠ 2 = ∠ 4
III этап. Закрепление изученного материала. Решение задач.(Слайд 9)
№3 (учебник)
Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза |
Решение. 1. Пусть ∠2 = х, тогда ∠1=2х х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60°, |
| Найти ∠1 и ∠2 |
(Слайд 10)
№6(2)
Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7 |
Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. |
| Найти ∠1 и ∠2 |
(Слайд 11)
Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1 |
Решение 1. Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию). 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° |
| Найти ∠1 и ∠2 |
(Слайд 12)
Дано: а ∩ b ∠2 меньше ∠1 в 4 раза |
Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), 3. ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), Ответ: 144°, 36°, 144°, 36°. |
| Найти ∠1, ∠2, ∠3 и ∠4 |
(Слайд 13)
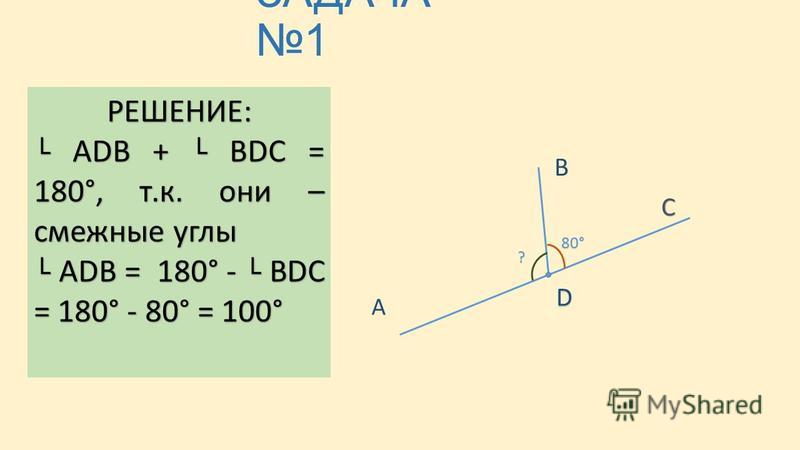
Дано: AС ∩ ВD = O ∠ВОС = 23° |
Решение 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, 3. ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). Ответ: 157°, 157°, 23°. |
Найти: ∠СОD, ∠АОВ, ∠АОD. |
(Слайд 14)
Устно. Вопрос. Назовите смежные и вертикальные углы.
Ответ.
Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .
Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠ NОМ.
IV этап. Зарядка для глаз(Слайд 15)
V этап.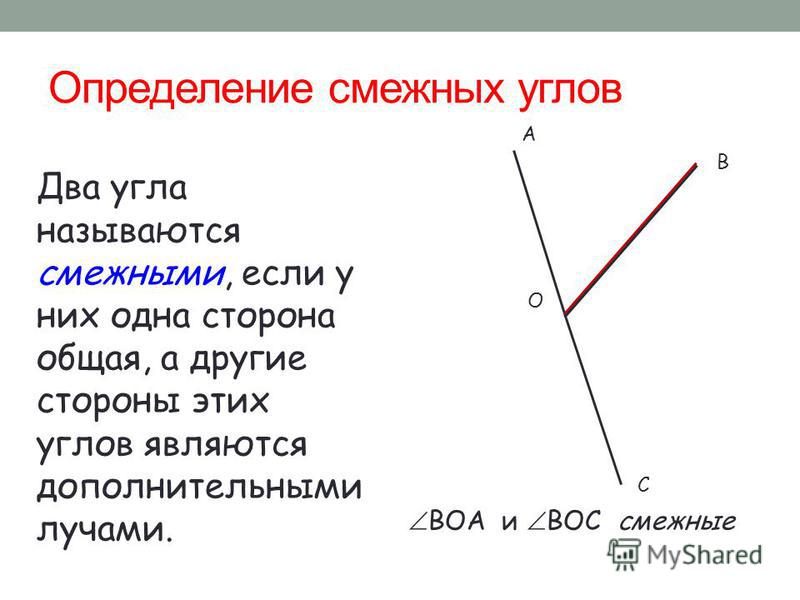 Самостоятельная работа (на листочках).
Самостоятельная работа (на листочках).| Вариант 1 | Вариант 2 |
| №1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы. | №1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы. |
| №2. Разность смежных углов равна 50°. Найдите меньший угол. | №2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол. |
Ответы
| Вариант 2 | |
№1.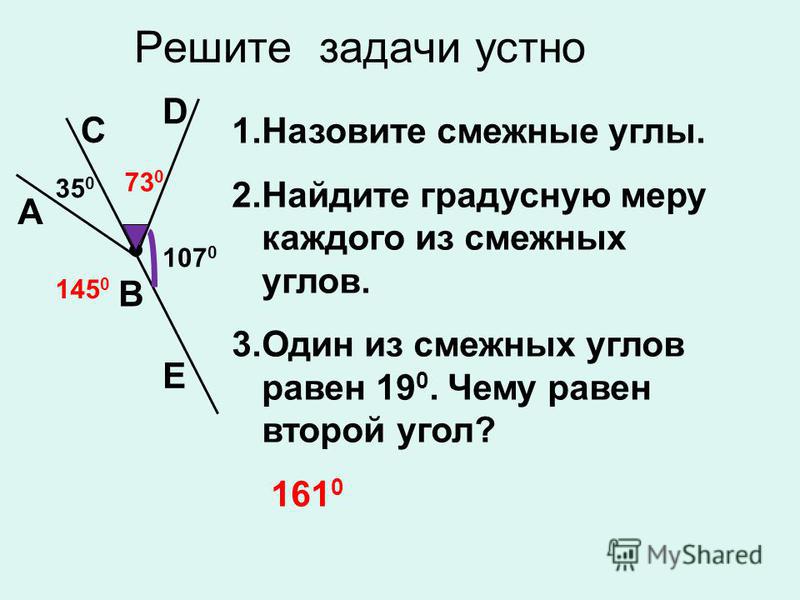 93°, 87°, 93°. 93°, 87°, 93°. |
№1. 62°, 118°, 62° |
| №2. 75°. | №2. 36°. |
- §2. Пункты 14-15.
- Задачи на стр. 26. № 6(4), № 12.
- Повторили понятия смежных и вертикальных углов
- Научились решать задачи, используя знания о смежных и вертикальных углах.
- Стали еще на одну ступеньку выше в изучении геометрии.
Смежные углы и их свойства
УРОК 5
ТЕМА: Смежные углы и их свойства.
ЦЕЛИ:
1)образовательная: научить учащихся распознавать смежные углы, строить угол, смежный с данным углом, решать задачи, используя свойство смежных углов.
2) развивающая: развивать логическое мышление и навыки исследовательской работы, тренировать память и математическую речь, научить анализировать данный материал и делать выводы.
3) развивать самостоятельность, прививать аккуратность и трудолюбие.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
Предметные : знать понятие смежных углов; уметь применять свойство смежных углов при решении простейших задач.
Метапредметные: научить ставить учебные задачи, самостоятельно делать выводы;
планировать пути достижения целей; учитывать разные мнения, аргументировать свою точку зрения.
Личностные: осознание ценности изученной теоремы;
умение сотрудничать, работать в паре; оценивание своей работы и полученного результата.
Оборудование: учебник, электронное приложение к учебнику «Геометрия 7-9».
Тип урока: урок изучения нового материала
ПЛАН УРОКА:
1.Смежные углы.
2. Свойства смежных углов.
Свойства смежных углов.
ХОД УРОКА:
I. Организационный момент.
II. Проверка домашнего задания: № 47(а) – по образцу
С В Дано:
Найдем
Решение. Пусть
По условию задачи
х + х + 15 = 155, 2х = 140, х = 70.
А О Итак,
№ 49(проверить наличие, ответить на вопросы)
III. Актуализация опорных знаний обучающихся:
Прием « Интеллектуальная разминка»
1. Геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки (угол)
2.Точка, из которой исходят эти лучи называется (вершина).
3.Лучи, исходящие из точки называются (стороны).
4. Угол, градусная мера которого меньше 900(острый).
5. Угол, градусная мера которого больше 90°,но меньше1800(тупой).
6. Угол, градусная мера которого равна 900(прямой).
7. Угол, градусная мера которого равна 1800(развернутый).
8.1/180 часть развёрнутого угла (градус).
9. 1/60 часть градуса (минута).
10. 1/60 часть минуты (секунда).
11. Инструмент для измерения углов (транспортир)
12.Прибор для измерения углов на местности (астролябия)
IV. Мотивация и целеполагание
Прием «Отсроченная догадка»
О чем шла речь в интеллектуальной разминке? (об углах).
Об углах мы уже много знаем, хорошо все запомнили. Сегодня на уроке мы продолжим наше знакомство с геометрическими углами.
V. Изучение нового материала.
1.Смежные углы.
Работа с учебником рис.40 «Смежные углы» стр.22.
Рассмотрите и обсудите, какие углы называются смежными?
2.Свойства смежных углов.
ПРИЕМ « Мини- исследование»
Для этого выполним лабораторную работу (работа в парах по рядам).
Ребята выполняют построение смежных углов.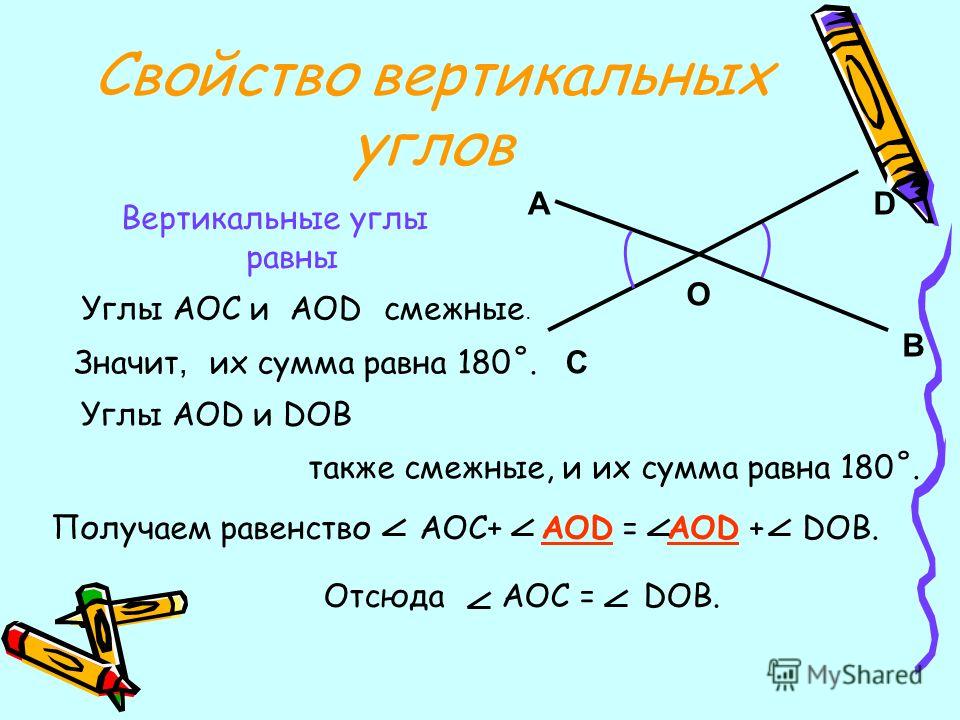 С помощью транспортира строят углы 45°, 150°, 90°. Измеряют транспортиром смежный угол.
С помощью транспортира строят углы 45°, 150°, 90°. Измеряют транспортиром смежный угол.
Угол,градусная мера угла | Смежный угол, градусная мера | Сумма углов |
Острый, 450 | ||
Тупой, 150 0 | ||
Прямой, 900 |
Вывод: Сумма смежных углов равна 180 О
VI. Первичная проверка понимания учащимися нового учебного материала.
Прием «Закончите предложения»
Угол, смежный с острым углом всегда (тупой).
Угол, смежный с тупым углом всегда (острый).
Угол, смежный с прямым углом всегда (прямой).
Два смежных угла могут быть оба острыми? (нет).
Два смежных угла могут быть оба прямыми? (да).
Два смежных угла могут быть оба тупыми? (нет).
Если смежные углы равны, то они (прямые).
Сумма смежных углов всегда равна (180°).
VII. Закрепление новых знаний и умений.
1.Устно. Найдите угол, смежный с углом АВС, если 1) AВС = 1300; 2) AВС = 450; 3) AВС = 900 .
2.Всем классом решить письменно задачу № 62.
3. Устно. В С
F О 32° Е
А D
Найти
VIII. Подведение итогов урока. Что больше всего понравилось на уроке? Что вас удивило? Что показалось трудным?
Что нового вы узнали на уроке? Сделайте вывод.
IX.Оценивание работы обучающихся на уроке.
X. Домашнее задание.
читать п.11, решить (дифферинцированно) «3» №58, «4»№58,59, «5» №58,64
Использованные информационные материалы:
Геометрия.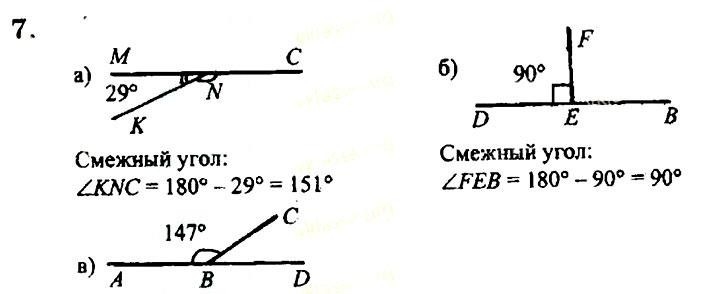 7 – 9 классы. Электронное приложение к учебнику Л.С. Атанасян, С.Б. Кадомцев и др (СD).
7 – 9 классы. Электронное приложение к учебнику Л.С. Атанасян, С.Б. Кадомцев и др (СD).
Использованные печатные источники:
Учебник «Геометрия. 7-9 класс», Л.С. Атанасян, С.Б. Кадомцев и др. Москва,
« Просвещение»,2014
Смежные углы
Урок по теме: «Смежные углы»
Класс: 7
Подготовила: Чурина Елена Вениаминовна, учитель первой квалификационной категории МБОУСОШ № 1 г. Южи Ивановской области
Предмет | Геометрия |
Тип урока | усвоение новых знаний |
Учебник: | ГЕОМЕТРИЯ. 7-9. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, |
Цель урока | ввести понятие смежных углов и рассмотреть их свойство; научить применять свойство смежных углов при решении задач. |
Задачи урока | Образовательные: определить понятие смежных углов и узнать их свойство, решать задачи, применяя определение и свойство смежных углов, строить угол, смежный данному. Воспитательные: воспитывать уважительное отношение к мнению других, умение слушать и слышать окружающих; способствовать формированию и развитию культуры учащихся, повышению уровня познавательного интереса к предмету; формировать позитивную психологическую атмосферу в группе. Развивающие: формировать умения устанавливать причинно-следственные связи, строить логические цепочки, делать выводы, развивать внимание, математическую речь. |
Образовательные ресурсы | Компьютер, проектор, презентация, раздаточный материал; классная доска; чертежные приборы. |
План урока | 1) Организационный этап. 2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся. 3) Актуализация знаний. 4) Первичное усвоение новых знаний. 5) Первичная проверка понимания 6) Первичное закрепление. 7) Информация о домашнем задании, инструктаж по его выполнению 8) Рефлексия (подведение итогов занятия) |
Педагогические технологии: | ИКТ-технологии, здоровьесберегающие технологии, технологии критического мышления. |
Планируемые результаты | ||
Предметные | Метапредметные УУД | Личностные УУД |
Научиться строить угол, смежный с данным, находить смежные углы на чертеже, решать задачи с использованием свойств смежных углов. | Коммуникативные: представлять конкретное содержание и обобщать его в письменной и устной форме; уметь с помощью вопросов добывать недостающую информацию. Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно; самостоятельно формулировать познавательную цель и строить действия в соответствии с ней. Познавательные: проводить анализ способов решения задач | Формирование устойчивой мотивации к изучению нового |
Ход урока:
1) Организационный этап и мотивация учебной деятельности учащихся.
Добрый день, Ребята.
Нанём урок! Прочтем!
«Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать».
Р. Декарт -французский философ, математик, механик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.
Почему на ваш взгляд так сказал Р. Декарт?
Декарт?
2. Актуализация знаний и постановка темы, целей и задач урока.
2.1 Графический диктант с самопроверкой.
(Если утверждение верное, то «+», если утверждение неверное, то «-«)
1) Луч — это часть прямой, ограниченной двумя точками.
2) Лучи, на которые прямая разбивается своей точкой, называются дополнительными.
3) Угол — это геометрическая фигура, состоящая из точки и луча, исходящего из этой точки.
4) Градус- единица измерения угла.
5) Угол называется прямым, если его градусная мера равна 90о.
6) Угол называется острым, если его градусная мера меньше 90о.
7) Угол называется тупым, если его градусная мера больше 90о.
8) Развернутый угол — это угол, стороны которого образуют прямую.
9) Градусная мера развернутого угла 180о.
10) Углы называются равными, если равны их градусные меры.
Ключ: -+-+++++++
Критерии: верно выполнены 10 заданий -«5», верно выполнены 8-9 заданий -«4», верно выполнены 5-7 заданий -«3», верно выполнены менее 5 заданий — «2»
2.2. Задание классу, фронтальная работа (1 учащийся у доски):
Постройте два дополнительных луча ОА и ОВ.
Какой угол образуют эти лучи?
Какова его величина?
Постройте луч ОС, проходящий между сторонами развернутого угла
Какой луч называется проходящим между сторонами угла? (любой луч, выходящий из вершины угла, отличный от сторон угла)
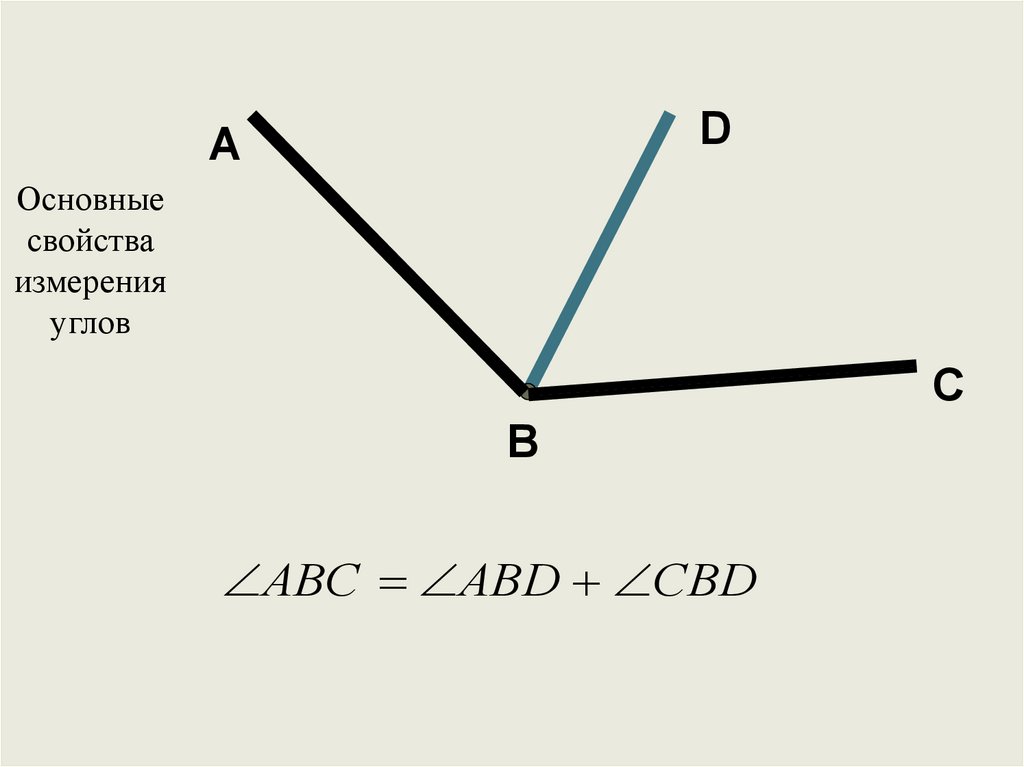
Сформулируйте основное свойство измерения углов.
2.3 Работа в парах:
1.Запишите данное основное свойство для чертежа:
∠ АОС+∠ ВОС=∠AOB
2. Постройте два угла, у которых одна сторона общая.
3.Постройте два угла, у которых одна сторона
первого из углов является дополнительным лучом стороны второго угла.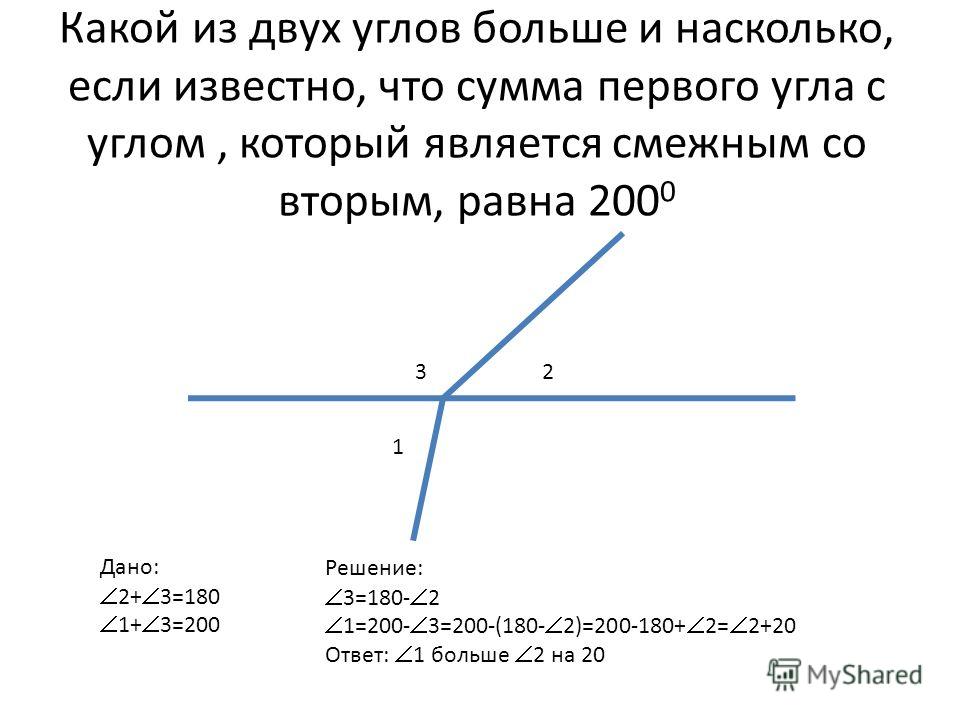
4.Постройте два угла, у которых одна сторона общая, а две другие – дополнительные лучи.
5.Чтобы определить тему урока, разгадайте ребус:
Как вы поняли, тема нашего сегодняшнего урока – Смежные углы.
Как вы думаете, какая цель нашего урока? Какие задачи мы перед собой поставим? (учащиеся формулируют цель и задачи урока)
3. Первичное усвоение новых знаний.
3.1. Учитывая последний чертеж в тетради, формулируем (дети предлагают разные варианты) и запишем определение:
Смежные углы – это два угла, у которых одна сторона общая, а две другие – дополнительные лучи.
3.2. Подумаем над таким вопросом:
Ответ: 4
3.3. Постройте угол ХУЕ. Построим угол смежный ему. Сколько таких углов можно построить?
3.4.Внимательно рассмотрите чертеж и найдите значение выражения:
<АВС+<ВСD=?
Почему?
Вариант рассуждений: ∠AВD развернутый, следовательно, его градусная мера равна 180о .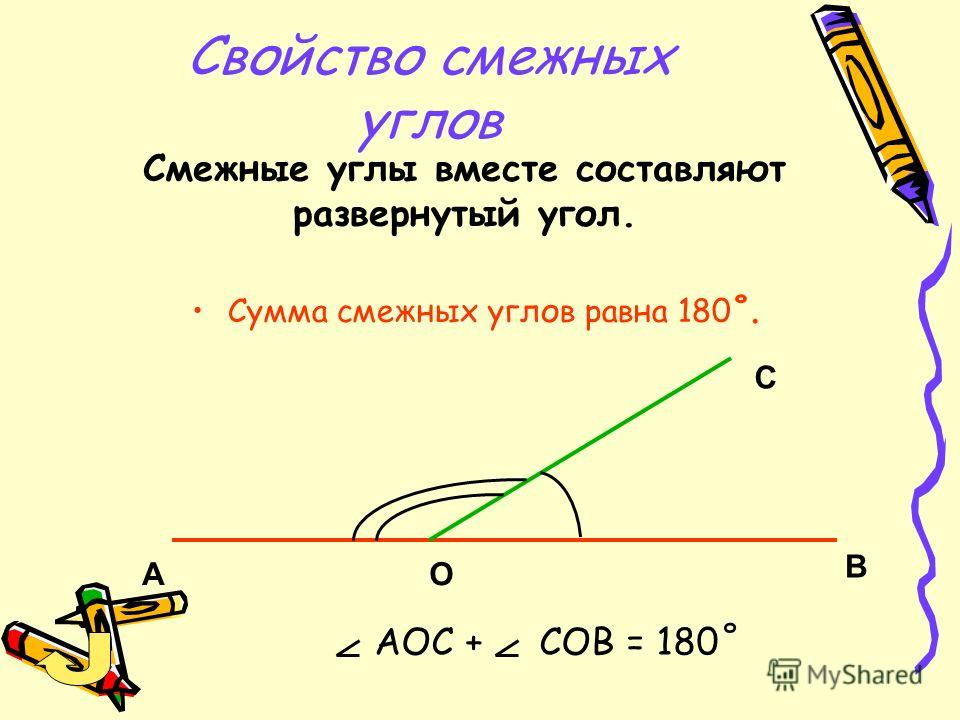 Луч ВС проходит между сторонами этого угла, поскольку он выходит из его вершины и отличен от его сторон. На основании основного свойства <АВС+<ВСD =∠AВD, т.е. ∠ACD+∠BCD=180о .
Луч ВС проходит между сторонами этого угла, поскольку он выходит из его вершины и отличен от его сторон. На основании основного свойства <АВС+<ВСD =∠AВD, т.е. ∠ACD+∠BCD=180о .
Вывод: Сумма смежных углов равна 180о
3.5. Доказательство теоремы. Фронтальная работа (1 учащийся у доски):
Физкультминутка: https://www.youtube.com/watch ?v=abd1NWTWfEs
4. Первичная проверка понимания. Фронтальная работа:
1. Является ли верным утверждение: если сумма двух углов равна 180, то они смежные? (Нет, уместно привести контрпример)
2.Может ли разность двух смежных углов быть равной прямому углу (Да, )
3.Один из смежных углов 400. Найди другой угол.
Смежные углы относятся как 2:7. Найди эти углы.
5. Первичное закрепление:
Работа в группах с последующим отчетом каждой:
1 группа. Один из смежных углов на больше, чем второй. Найдите эти углы.
2 группа.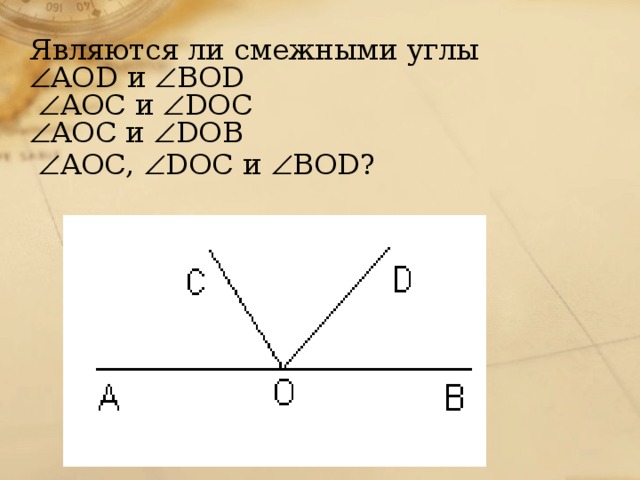 Найди смежные углы, если один из них в 5 раз меньше другого.
Найди смежные углы, если один из них в 5 раз меньше другого.
3 группа. Разность двух смежных углов равна 50⁰. Найдите эти углы.
6. Домашнее задание. П.11( Выучить определение смежных углов, уметь доказывать теорему о смежных углах и следствия из нее), №58
7. Подведение итогов урока. Рефлексия
«Комплимент» — учащиеся оценивают вклад друг друга в урок и благодарят друг друга и учителя за проведенный урок.
Источники:
https://ru.wikipedia.org/wiki /Декарт,_Рене
https://multiurok.ru/files/smiezhnyie-ughly-zadachi-na-ghotovykh-chiertiezhak.html
http://kvestodel.ru/generator-rebusov
Какому алгоритму вы бы научили кого-нибудь для PLL в соседнем углу на 2×2?
Добро пожаловать на Speedsolving.
 com, дом крупнейшего в сети сообщества головоломок!
com, дом крупнейшего в сети сообщества головоломок!
В настоящее время вы просматриваете наш форум в качестве гостя, что дает вам ограниченный доступ к обсуждениям и другим функциям.Регистрация быстрая, простая и абсолютно бесплатная. Пожалуйста, присоединяйтесь к нашему сообществу из более чем 40 000 человек со всего мира сегодня !
Если вы уже являетесь участником, просто войдите, чтобы скрыть это сообщение, и начните участвовать в жизни сообщества!
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы Мэтт11111
- Дата начала
А Пермь
Т Пермь
Результаты доступны для просмотра только после голосования.
Матовый11111
Участник
Из того, что я могу сказать, два наиболее распространенных алгоритма, которые люди изучают для перестановки соседних углов для PLL на 2×2, — это перманенты Aa и T. Алгоритм, которому я обучал людей для этого случая, на самом деле представляет собой пермь Ja/L (R’ U L’ U2 R U’ R’ U2 RL, хотя последние два движения выполняются больше как R2 на 2×2). Это 9 ходов, если вы называете последний ход R2 и не включаете AUF, что делает его самым коротким алгоритмом, который вы можете использовать для этого случая, если я не ошибаюсь (он был бы связан с пермами A, но они сложно выполнить на 2×2). Это также алгоритм, который я лично использую из-за его малого количества ходов? Я все делаю не так? Кто знает, но я научил этому своего друга около 4 лет назад, и он говорит, что куберы в его школе были удивлены, что он использовал этот алгоритм.
Полагаю, еще один вопрос будет заключаться в том, рассмотрите ли вы возможность обучения L-перманенту вместо T или A-перманента, если вы учите кого-то, как решать 2×2.
Кубиккубер
Участник
Jb пермь
Филипе Тейшейра
Участник
Это зависит от человека, которого вы обучаете.
Для меня это либо:
Пермь: смехотворно легко запомнить
F2 (R2 U’ L2 U)2 F2
или
J допуск: быстрый
R’ F R F’ R U2 R’ U R U2 R’
рип-замки
0 000
Последнее редактирование:
Бен Кристман1
Участник
Либо:
T perm: (R U R’ U’) R’ F (R2 U’ R’ U’) (RU R’) F’
ИЛИ
Jb perm: (R U R’) F’ (R U R’ U’ ) Р’Ф (Р2 У’Р’)
Шимпанзе_Кубер608
Участник
Т Пермь
Кошмар Паритета
Участник
T perm или jb perm
Большинство людей знают букву T, но не букву Jb, поэтому я бы назвал букву t.
Я лично использую Jb, потому что он быстрее для меня.
T: в лучшем случае 0,98 секунды
Jb: в лучшем случае 0,91 секунды
Петр Гроховский
Участник
Jb-пермь спереди (U’ R U R’ F’) (R U R’ U’ R’ F) (R2 U’ R)
ПапаСмурф
Участник
Филипе Тейшейра сказал:
J доп.
: быстрый
R’ F R F’ R U2 R’ U R U2 R’
Нажмите, чтобы развернуть…
Определенно 100% этот. Я могу подставить 0,9, что относительно последовательно.
Сольвадор Куби
Участник
другой вариант: R U’ R F2 R’ U R F2 R2
Это может быть полезно и в некоторых сценариях 3×3, так как сохраняет L и R блоки
Кубинвитдапицца
Гость
пфф, кто бы использовал что-нибудь кроме химической завивки JB?
Последнее редактирование модератором:
Простар
Участник
Т-Пермь для меня
ГАН 356 Х
Участник
ЖБ Пермь
КодингКубер
Участник
R’ F R’ B2 R F’ R’ B2 R2
Я знаю, что это плохо, но мне это помогает
Простар
Участник
CodingCuber сказал:
R’ F R’ B2 R F’ R’ B2 R2
Я знаю, что это плохо, но мне это помогает
Нажмите, чтобы развернуть.
..
Раньше я использовал этот LOL
Вы должны войти или зарегистрироваться, чтобы ответить здесь.
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
| BLDDB, база данных алгоритмов 3BLD | Обсуждение решения вслепую | 8 | ||
| Big Cubes Parity Big Cubes без использования алгоритмов OLL — PLL 4×4 5×5 6×6 7×7 Расчет с помощью интуитивно понятного метода без использования алгоритма | Общее обсуждение спидкубинга | 0 | ||
| Что на самом деле делает этот алгоритм? | Область программного обеспечения | 26 | ||
| Пакетный решатель — автоматически генерируйте большие наборы алгоритмов! | Область программного обеспечения | 58 | ||
| Обучение новичков без алгоритмов | Теория головоломок | 14 |
| BLDDB, база данных алгоритмов 3BLD |
| Большие кубы четности без использования алгоритмов OLL — PLL 4×4 5×5 6×6 7×7 Расчет с использованием интуитивно понятного метода без использования алгоритмов |
| Что на самом деле делает этот алгоритм? |
| Пакетный решатель — автоматически генерируйте большие наборы алгоритмов! |
| Обучение новичков без алгоритмов |
Верх
Кубик Рубика — Решение для начинающих
Решение для начинающих
Эта страница поможет новичкам и чайникам в сборке кубика Рубика… но сначала вам нужно выучить нотацию ходов… Затем можно приступать к обучению…
РЕШЕНИЕ
Первый слой Первый слой решается в два этапа:
1. Формируем крест
2. Вставляем 4 уголка первого слоя
Я считаю, что первый слой надо делать интуитивно. Вам нужно понять ее и решить без изучения алгоритмов. Пока вы не сможете сделать это, я бы не стал пробовать остальную часть куба! Итак, проведите некоторое время, играя с кубом и знакомясь с тем, как перемещать фигуры по кубу.
Вам нужно понять ее и решить без изучения алгоритмов. Пока вы не сможете сделать это, я бы не стал пробовать остальную часть куба! Итак, проведите некоторое время, играя с кубом и знакомясь с тем, как перемещать фигуры по кубу.
Вот несколько советов, которые помогут вам начать работу.
Крест
Я предпочитаю начинать с белого креста, потому что белый легче определить на полностью перемешанном кубике, однако вы можете использовать любой цвет.
Есть 4 кромки белого цвета (т.е. 4 стороны креста), которые имеют определенные позиции. Вы не можете поместить какую-либо белую крайнюю часть в плечо креста, потому что другой цвет на краю куба должен совпадать с его центром на среднем слое.
Вот изображение правильно сформированного креста.
Углы первого слоя
После того, как вы завершили крест, для завершения первого слоя необходимо вставить каждый из 4 углов отдельно. Первое, что нужно сделать, это изучить свой куб и найти все ребра верхнего слоя — они будут находиться либо в первом, либо в последнем слое.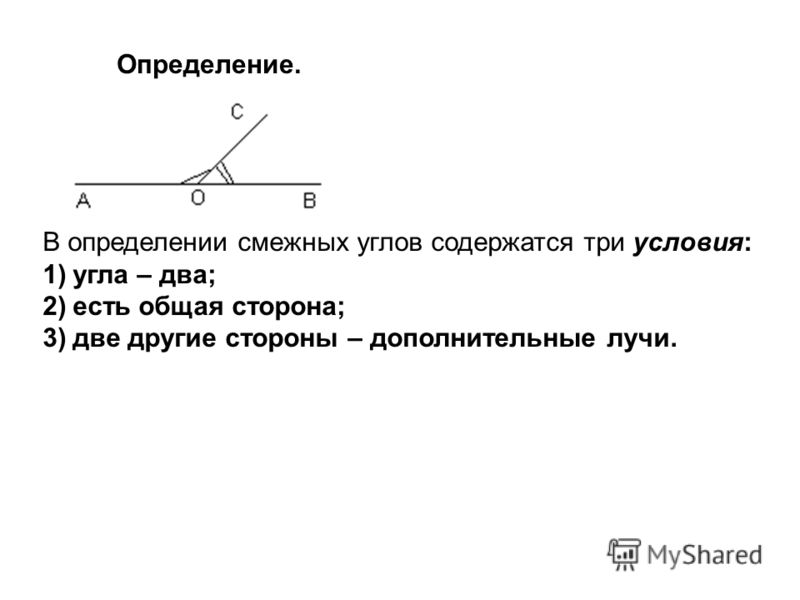 Вставка углов первого слоя должна выполняться интуитивно, а не путем обучения алгоритмам. Ниже приведены пошаговые алгоритмы… R’ D’ R D.
Вставка углов первого слоя должна выполняться интуитивно, а не путем обучения алгоритмам. Ниже приведены пошаговые алгоритмы… R’ D’ R D.
Вот несколько советов по вставке углов верхнего слоя:
Начните с угла первого слоя, который находится в последнем слое.
Если в последнем слое есть несколько углов первого слоя (обычно они есть), начните с того, у которого нет белой части угла на грани, противоположной белой грани. Или, если вы использовали другой цвет для креста («цвет X»), начните с угла, у которого нет части угла «цвета X» на грани, противоположной грани «цвета X».
При работе с угловым элементом первого слоя, который находится в первом слое (но в неправильном угловом положении первого слоя), вам нужно будет вывести его из первого слоя в последний слой, а затем вставить в правильное первое положение. угловое положение слоя. Тот же принцип применяется, если угловой элемент первого слоя находится в правильном угловом положении первого слоя, но его необходимо перевернуть.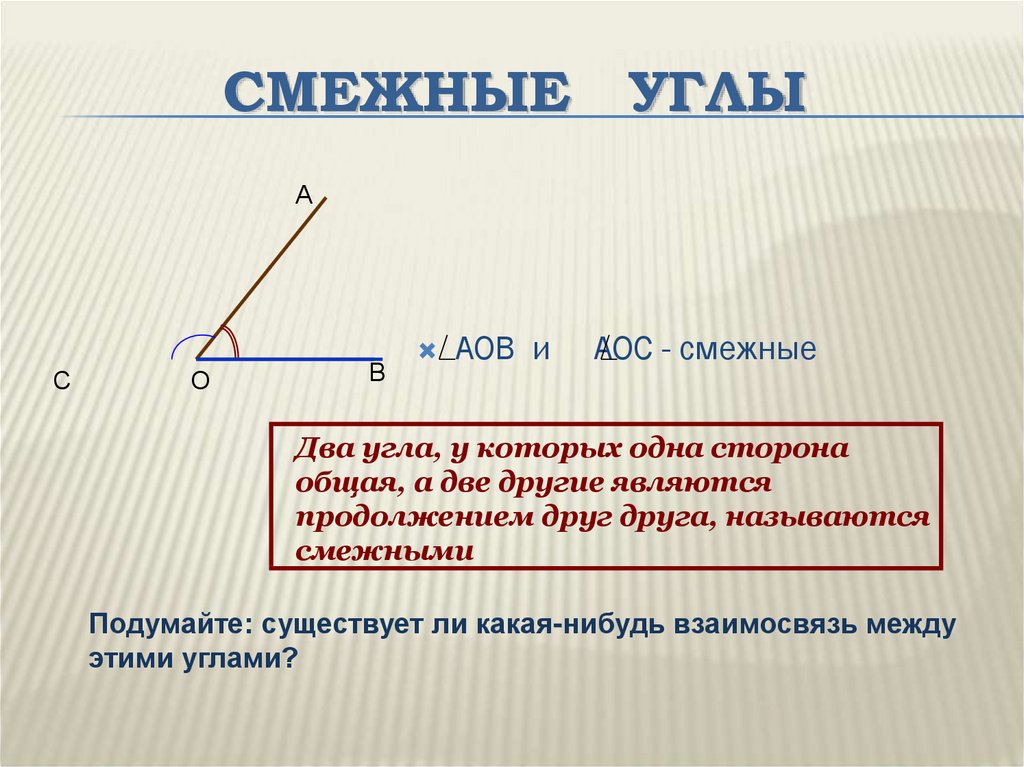 Вам нужно извлечь его из первого слоя (т.е. в последний слой), а затем снова вставить его в первый слой правильным образом.
Вам нужно извлечь его из первого слоя (т.е. в последний слой), а затем снова вставить его в первый слой правильным образом.
Вот как должен выглядеть первый слой после завершения.
Все четыре угла расположены правильно
Средний слой/Второй слой
Средний слой состоит из одного этапа:
1. Вставьте 4 края среднего слоя (каждое ребро вставляется отдельно).
Вам нужно выучить только один алгоритм (плюс алгоритм зеркала) для второго слоя. Есть еще много алгоритмов, но давайте сначала изучим основной.
Сначала поверните куб так, чтобы финишная грань оказалась внизу, затем найдите край среднего слоя, который в данный момент находится в последнем слое. Я собираюсь использовать край красный / зеленый для этого примера.
Вставка ребра справа
Алгоритм для этого случая: U R U’ R’ U’ F’ U F
Вставка ребра слева
Перед выполнением этого алгоритма выберите левую грань (в этот рисунок зеленый в центре), так что лицо будет спереди. Тогда алгоритм таков: U’ L’ U L U F U’ F’.
Тогда алгоритм таков: U’ L’ U L U F U’ F’.
Переворот одного ребра в правильное положение
В этом случае это можно сделать двумя способами:
1. Ребро должно быть повернуто наружу, затем начните с одного из алгоритмов, как показано выше.
2. Выполнение этого алгоритма: R2 U2 F R2 F’ U2 R’ U R’
Последний слой
Последний слой («LL») выполняется в 4 этапа:
1. Ориентируем края ( 2 algs) — т.е. образуют крест на грани U.
2. Переставьте углы (1 вариант) – т. е. установите углы в правильное положение в 3D-пространстве (не беспокойтесь, если их все еще нужно повернуть).
3. Ориентировать углы (1 алг + зеркальный алг) — т.е. перевернуть углы.
4. Переставить ребра (1 alg) — т. е. поменять ребра местами. Теперь куб должен быть решен! 🙂
Все алгоритмы последнего слоя выполняются с крестом (т.е. первый слой — белая сторона в этом примере) внизу.
Ориентация краев LL
Когда вы закончите первые два слоя («F2L»), держите куб белой стороной вниз.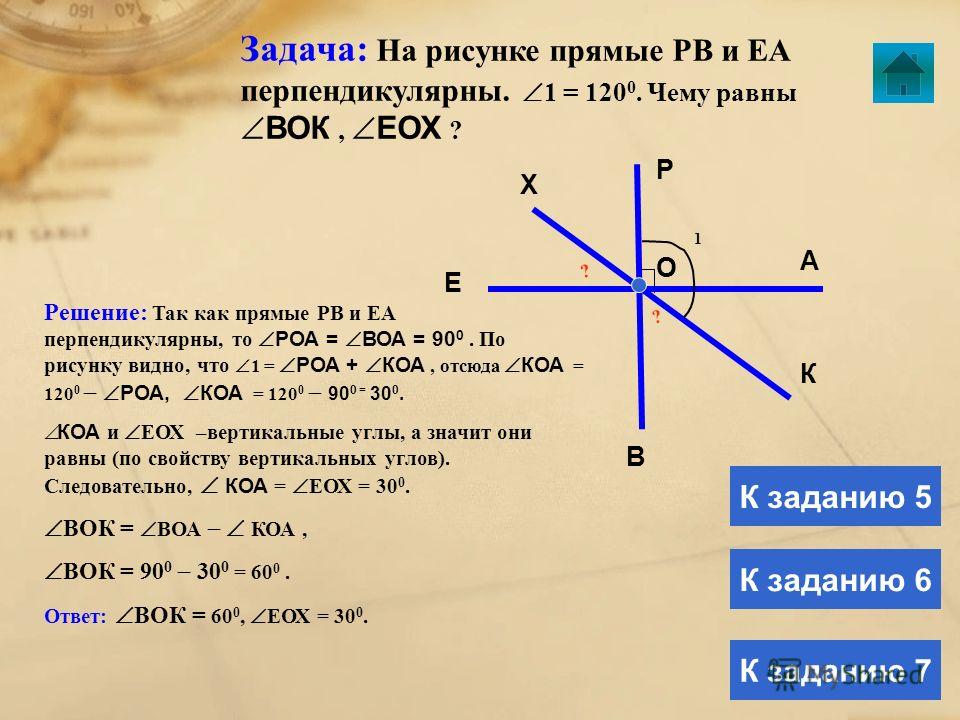 Белая сторона будет внизу для остатка раствора. Это означает, что белая сторона является стороной D для всех алгоритмов последнего слоя.
Белая сторона будет внизу для остатка раствора. Это означает, что белая сторона является стороной D для всех алгоритмов последнего слоя.
В моем кубе белый цвет противоположен желтому, поэтому желтый — это U-образная грань для всех алгоритмов последнего слоя в моем кубе. Обратите внимание, что ваш куб может иметь другой цвет напротив белого (например, синий). Теперь взгляните на свой последний слой, и, в частности, посмотрите на лицо последнего слоя — есть 4 возможных шаблона краев LL, которые вы можете увидеть.
Состояние 1
Все края уже ориентированы правильно. Переходим к перестановке углов.
Государство 2
Мы собираемся переориентировать наши лица для этого алгоритма. Грань, на которую вы смотрите прямо на этом изображении, теперь является гранью U (это была грань D, когда вы делали края второго слоя). Выполните следующий алгоритм: F U R U’ R’ F’
Состояние 3
Как и в случае состояния 2, лицо, на которое вы смотрите прямо на этом изображении, теперь является лицом U. Выполнить следующий алгоритм: Ф Р У Р’ У’ Ф’
Выполнить следующий алгоритм: Ф Р У Р’ У’ Ф’
Состояние 4
Состояние 4 на самом деле является комбинацией состояний 2 и 3, поэтому все, что вам нужно сделать, это выполнить алгоритм для состояния 2 или состояния 3. Сделав это, вы увидите, что ребра LL теперь выглядят как Состояние 2 или Состояние 3, поэтому просто выполните соответствующий алгоритм, и у вас будет крест на LL.
Перестановка углов LL
Два возможных состояния:
1. необходимо поменять местами два соседних угла LL; или
2. необходимо поменять местами два диагональных угла LL.
Это единственные два возможных состояния. Если вы не можете идентифицировать одно из этих двух состояний с вашими углами LL, тогда должно быть верно одно или несколько из следующих утверждений:
1. Вы не закончили F2L.
2.Кто-то оторвал угол вашего куба и поставил его неправильно.
3.Кто-то сорвал несколько ваших наклеек и приклеил их обратно не на то место.
4. Вы плохо ищете. 😉
Перестановка соседних углов
Держите куб белой стороной вниз, а два угла, которые нужно поменять местами, находятся в переднем правом верхнем и заднем правом верхнем положениях. Выполните следующий алгоритм: L U’ R’ U L’ U’ R U2 .
Замена диагональных углов
Замена диагональных углов может быть выполнена путем двукратного выполнения алгоритма замены соседних углов. Выполните это один раз, чтобы поменять местами любые два угла LL. Пересмотрите свой куб, и вы увидите, что теперь есть только два угла LL, которые нужно поменять местами. Расположите его правильно для окончательной замены смежных углов LL и выполните алгоритм замены смежных углов LL.
Ориентация углов LL
Существует 8 возможных состояний ориентации углов LL. В одном случае все 4 угла ориентированы правильно. Остальные 7 выглядят так.
State 1- Orienting 3 corners anti clockwise
R’ U’ R U’ R’ U2 R U2
State 2- Orienting 3 corners clockwise
R U R’ U R U2 R’ U2
Состояние 3 — Состояние 7
Зная алгоритмы для состояний 1 и 2, вы сможете решить любое состояние LL-ориентации. Остальные состояния можно ориентировать, используя максимум 2 алгоритма. Вам нужно будет выполнить одно из следующих действий: (i) алгоритм состояния 1 дважды, (ii) алгоритм состояния 2 дважды, (iii) алгоритм состояния 1, затем алгоритм состояния 2 или (iv) алгоритм состояния 2, затем алгоритм состояния 1.
Остальные состояния можно ориентировать, используя максимум 2 алгоритма. Вам нужно будет выполнить одно из следующих действий: (i) алгоритм состояния 1 дважды, (ii) алгоритм состояния 2 дважды, (iii) алгоритм состояния 1, затем алгоритм состояния 2 или (iv) алгоритм состояния 2, затем алгоритм состояния 1.
В предыдущем издании этого решения я сказал, что не буду рассказывать вам, как именно комбинировать алгоритмы состояний 1 и 2 для решения состояний 3-7. Моя причина этого заключалась в том, что важно, чтобы вы попытались понять, как работают алгоритмы Состояния 1 и Состояния 2, и что, как только вы их поймете, вы сможете понять, как использовать их для решения всех состояний. Я все еще верю в это, однако я получил электронные письма от нескольких человек, у которых были проблемы с состояниями 3-7, поэтому я решил написать несколько дополнительных советов. Я все же предлагаю вам попробовать самостоятельно проработать состояния 3-7
Перестановка ребер LL и РЕШЕНО..
Существует 5 возможных состояний перестановки ребер LL. В одном случае все 4 ребра переставлены правильно. Остальные 4 выглядят так.
В одном случае все 4 ребра переставлены правильно. Остальные 4 выглядят так.
Состояние 1
R2 U F B ‘R2 F’ B U R2
Состояние 2
R2 U ‘F B’ R2 F ‘B U’ R2
6666666666 это 1. Разница только в том, что 2-й ход и 2-й последний ход.
Состояние 3
Примените алгоритм для Состояния 1 или Состояния 2. Повторно изучите куб, и теперь он будет выглядеть как Состояние 1 или Состояние 2.
Состояние 4
Примените алгоритм для любого Состояния 1 или Состояние 2. Пересмотрите свой кубик, и теперь он будет выглядеть как Состояние 1 или Состояние 2.
И это все, что вам действительно нужно знать, чтобы собрать кубик Рубика! С практикой вы сможете достигать 60 секунд (или быстрее) с помощью этого метода. Когда вы освоитесь с этим методом и захотите узнать больше, взгляните на следующий раздел.
Следующие шаги
Если этот метод для начинающих кажется вам слишком простым и скучным, рассмотрите следующее.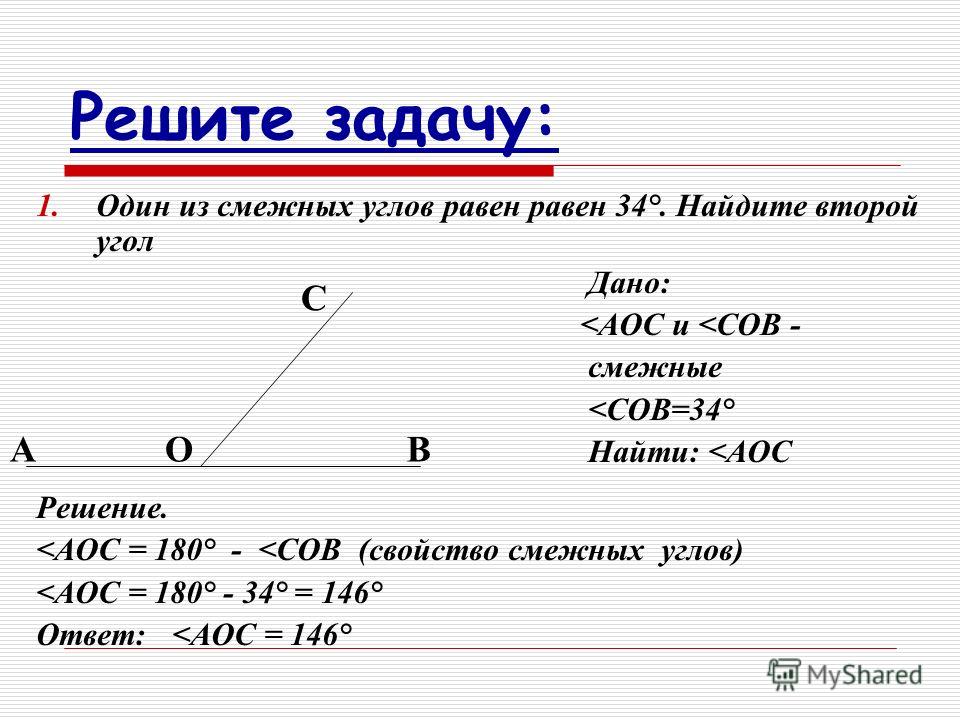
Промежуточный метод
Решите каждый угол первого слоя + соответствующее ребро среднего слоя за один шаг. Это означает, что после пересечения у вас есть только 4 шага (4 пары углов/ребер) для завершения F2L. Этот метод для начинающих состоит из 8 шагов: решите каждый из 4 углов первого слоя, затем решите каждый из 4 краев среднего слоя. Я бы предложил просто поиграть с вашим кубом и выяснить пары угол/край F2L самостоятельно. Чтобы получить некоторые советы по интуитивному решению F2L, взгляните на Интуитивное руководство Дуга Рида по F2L . Если вы все еще застряли и вам просто нужны алгоритмы, ознакомьтесь с Дэном Харрисом на странице F2L и Джессикой Фридрих на странице F2L .
Изучите 4 конкретных алгоритма (точнее, 3 алгоритма плюс один зеркальный алгоритм) для каждого из 4 различных состояний перестановки ребер LL. Мое решение для начинающих уже показывает вам 2 из 4 алгоритмов перестановки краев последнего слоя, два других алгоритма перестановки краев последнего слоя — это случай № 5 и случай № 17 на Страница PLL Дэна Харриса .
Усовершенствованный метод
Узнайте все из промежуточного метода.
Изучите 3-взгляд LL. Это требует изучения 7 конкретных алгоритмов для 7 различных состояний ориентации углов LL и изучения 21 алгоритма PLL (перестановка алгоритмов последнего слоя), чтобы вы могли одновременно переставлять края LL и углы LL. Полный 3-look LL использует 30 алгоритмов.
Для получения более подробной информации о расширенном методе см. т Rubiks Galaxia 3-look LL , Сайт Дэна Харриса и Страница PLL Ларса Ванденберга .
Экспертный метод
Выполните F2L в 5 шагов (первая точка промежуточного метода).
Выучить полный 2-look LL. Это требует запоминания 21 алгоритма PLL плюс 57 алгоритмов OLL (ориентирующие алгоритмы последнего слоя).
Для получения более подробной информации об экспертном методе посетите сайт Дэна Харриса, сайт Джоэля ван Ноорта и Сайт Ларса Ванденберга .
алгоритмов для сборки кубика рубика
алгоритмов для сборки кубика рубика
Я набрал это, чтобы показать как пример АЛГОРИТМА. Все, что ниже, основано на Видео Дэна Брауна на YouTube.
Обозначение: -------- F = Передняя сторона куба (лицом к вам) U = Верхняя сторона Л = левая сторона R = правая сторона D = Нижняя сторона зеленая сторона = сторона с зеленым в центре белая сторона = сторона с белым в центре так далее... центральная часть = часть в центре стороны угловая деталь = детали по углам краевая часть = не центральная или угловая часть
Обозначение алгоритма:
------------------
F = повернуть лицевую сторону по часовой стрелке на 90 градусов
F' = повернуть переднюю сторону против часовой стрелки на 90 градусов
U = повернуть верхнюю сторону по часовой стрелке на 90 градусов
U' = повернуть верхнюю сторону против часовой стрелки на 90 градусов
2U = повернуть верхнюю сторону на 180 градусов
(по часовой стрелке или против часовой.. . не важно)
R = повернуть правую сторону по часовой стрелке на 90 градусов
(по часовой стрелке, как будто вы стоите перед ней)
R' = повернуть правую сторону против часовой стрелки на 90 градусов
так далее...
. не важно)
R = повернуть правую сторону по часовой стрелке на 90 градусов
(по часовой стрелке, как будто вы стоите перед ней)
R' = повернуть правую сторону против часовой стрелки на 90 градусов
так далее...
1. Сначала решите зеленую сторону
> начать с зеленой стороны вверх
> найти зеленую кромку и переместить ее на нижнюю сторону
> повернуть вниз до другого цвета на кромке
соответствует центральной части
> теперь поверните сторону на 180 градусов, чтобы получить зеленый край на зеленой стороне
> если все в порядке, переходим к следующему краю
> если ребро находится в правильном месте, но перевернуто, выполните Ф'У Л'У'
в этот момент, после установки всех 4 зеленых краев, у вас должен быть зеленый крест сверху и все краевые части должно быть правильно
> исправить зеленые боковые углы:
> найди зеленый угол и вставь его прямо под то место, где он должен быть
идти (сопоставьте два других цвета на угловой части с
два других боковых цвета)
> с фрагментом, над которым вы работаете, в правом нижнем углу,
сделать R' D' RD от 1 до 6 раз (все время держать одно и то же лицо вперед)
> как только этот угол будет готов, решите остальные 3
на этом этапе вы должны сделать зеленую сторону и все первый слой готов (и все краевые части соответствуют своим правильным стороны)
2.Решите второй слой... > повернуть зеленой стороной вниз, синей стороной вверх > найдите крайнюю часть без синего цвета (см. **, если не можете этого сделать) > поверните верхнюю синюю сторону так, чтобы кромка совпадала по цвету с боковой стороной > с этой частью спереди и в центре, посмотрите, с какой стороны (слева или справа) соответствует верхнему цвету и выполните одно из следующих действий: верхние совпадения справа: У Р У' Р' У' Ф' У Ф верхние совпадения слева: U'L' U L U F U' F'
> повторить для всех краев второго слоя.... ** если вы не можете найти верхний край без синего цвета, найдите тот, который является краевой частью в среднем слое, и сделайте его передний правый-средний, затем сделайте так: U R U' R' U' F' U F на данный момент у вас должно быть два слоя!
3. Решите СИНИЙ КРЕСТ....
> посмотрите на верхний синий слой для одного из этих случаев:
не маленький L: сделать F R U R' U' F' , чтобы получить маленький L
маленький L: сделайте это вверху сзади слева, сделайте F R U R' U' F'
буква «L», которую вы ищете, состоит из трех синих частей,
центральная и две боковые части
теперь у вас должно быть три подряд. заставить 3 в ряд идти слева направо через верх
заставить 3 в ряд идти слева направо через верх
и снова сделайте F R U R' U' F' , чтобы получить синий крест
> попробуй скрутить верхнюю синюю сторону так, чтобы две крайние части выровнялись
своими правильными сторонами
если вы не можете поставить два в ряд, сделайте Р У Р' У Р 2У Р'
если вы выстроились в два ряда, и они
друг напротив друга, сделайте выровненные края
лицевая и изнаночная стороны и сделать R U R' U R 2U R'
(это должно сделать две выстроенные стороны смежными)
если два выстроенных рядом, сделайте
их правая и задняя стороны и сделать R U R' U R 2U R'
теперь должен быть синий крест сверху и иметь возможность крутить
сверху, чтобы выровнять все краевые части
4. решить последние 4 угла!!! > проверьте углы, чтобы увидеть, правильно ли они местоположения (даже если они могут быть перевернуты). Вам следует либо 0, 1, либо все 4 на своих местах.


 к. 83° + 97°= 180°)
к. 83° + 97°= 180°)



 com, дом крупнейшего в сети сообщества головоломок!
com, дом крупнейшего в сети сообщества головоломок!  : быстрый
: быстрый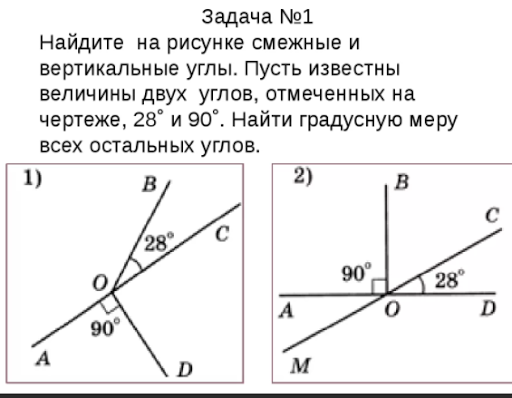 ..
.. . не важно)
R = повернуть правую сторону по часовой стрелке на 90 градусов
(по часовой стрелке, как будто вы стоите перед ней)
R' = повернуть правую сторону против часовой стрелки на 90 градусов
так далее...
. не важно)
R = повернуть правую сторону по часовой стрелке на 90 градусов
(по часовой стрелке, как будто вы стоите перед ней)
R' = повернуть правую сторону против часовой стрелки на 90 градусов
так далее...
 Решите второй слой...
> повернуть зеленой стороной вниз, синей стороной вверх
> найдите крайнюю часть без синего цвета (см. **, если не можете этого сделать)
> поверните верхнюю синюю сторону так, чтобы кромка совпадала по цвету с боковой стороной
> с этой частью спереди и в центре, посмотрите, с какой стороны (слева
или справа) соответствует верхнему цвету и выполните одно из следующих действий:
верхние совпадения справа: У Р У' Р' У' Ф' У Ф
верхние совпадения слева: U'L' U L U F U' F'
Решите второй слой...
> повернуть зеленой стороной вниз, синей стороной вверх
> найдите крайнюю часть без синего цвета (см. **, если не можете этого сделать)
> поверните верхнюю синюю сторону так, чтобы кромка совпадала по цвету с боковой стороной
> с этой частью спереди и в центре, посмотрите, с какой стороны (слева
или справа) соответствует верхнему цвету и выполните одно из следующих действий:
верхние совпадения справа: У Р У' Р' У' Ф' У Ф
верхние совпадения слева: U'L' U L U F U' F'
 заставить 3 в ряд идти слева направо через верх
заставить 3 в ряд идти слева направо через верх