Теория вероятности. Готовимся к егэ по математике
Продолжение статьи «Теория вероятности. Классическое определение».
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Итак, теория.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет  , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
, потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом: 
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности –  . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
. Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: 

Подборку задач на отработку темы смотрите здесь.
Зависимые и независимые события — Студопедия
Классическое определение вероятности.
Вероятность события –это количественная мера, которая вводится для сравнения событий по степени возможности их появления.
Событие, представимое в виде совокупности (суммы) нескольких элементарных событий, называется составным.
Событие, которое нельзя разбить на более простые, называется элементарным.
Событие называется невозможным, если оно не происходит никогда в условиях данного эксперимента (испытания).
Достоверные и невозможные события не являются случайными.
Совместные события– несколько событий называют совместными, если в результате эксперимента наступление одного из них не исключает появления других.
Несовместные события – несколько событий называют несовместными в данном эксперименте, если появление одного из них исключает появление других. Два события называются противоположными, если одно из них происходит тогда и только тогда, когда не происходит другое.
Вероятностью события А – Р(А) –называется отношение числа m элементарных событий (исходов), благоприятствующих появлению события А, к числу n всех элементарных событий в условиях данного вероятностного эксперимента.
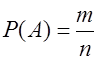 (1)
(1)
Из определения вытекают следующие свойства вероятности:
1.Вероятность случайного события есть положительное число, заключенное между 0 и 1:
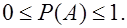 (2)
(2)
2. Вероятность достоверного события 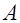 равна 1:
равна 1: 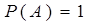 (3)
(3)
3. Если событие невозможное, то его вероятность равна
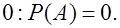 (4)
(4)
4. Если события 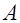 и
и 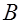 несовместны, то
несовместны, то
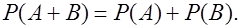 (5)
(5)
5. Если события А и В совместны, то вероятность их суммы равна сумме вероятностей этих событий без вероятности их совместного наступления:
Р(А+В) = Р(А) +Р(В) — Р(АВ) (6)
6. Если 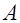 и
и 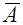 — противоположные события, то
— противоположные события, то 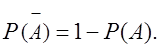 (7)
(7)
7. Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна 1:
Р(А1) + Р(А2) + …+ Р(Аn) = 1. (8)
В экономических исследованиях значения 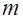 и
и 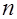 в формуле могут интерпретироваться по-другому. При
в формуле могут интерпретироваться по-другому. При 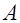 под
под 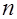 понимается количество наблюдений результатов эксперимента, в которых событие
понимается количество наблюдений результатов эксперимента, в которых событие 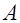 встречалось ровно
встречалось ровно 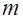 раз. В этом случае отношение
раз. В этом случае отношение 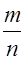 называется относительной частотой (частостью) события
называется относительной частотой (частостью) события 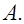
События А, В называются независимыми, если вероятности каждого из них не зависит от того, произошло или нет другое событие. Вероятности независимых событий называются безусловными.
События А, В называются зависимыми, если вероятность каждого из них зависит от того, произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью.
Если два события А и В – независимые, то справедливы равенства:
Р(В) = Р(В/А), Р(А) = Р(А/В) или Р(В/А) – Р(В) = 0 (9)
Вероятность произведения двух зависимых событий А, В равна произведению вероятности одного из них на условную вероятность другого:
Р(АВ) = Р(В) ∙ Р(А/В) или Р(АВ) = Р(А) ∙ Р(В/А) (10)
Вероятность события В при условии появления события А:
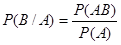 (11)
(11)
Вероятность произведения двух независимых событий А, В равна произведению их вероятностей:
Р(АВ) = Р(А) ∙ Р(В)
Если несколько событий попарно независимы, то отсюда еще не следует их независимость в совокупности.
События А1, А2, …, Аn (n>2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Р(А1∙А2∙А3∙…∙Аn) = Р(А1)∙Р(А2)∙Р(А3)∙…∙Р(Аn). (13)
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Теория вероятностей и статистика

Вероятность суммы двух событий
Пусть A и B – два произвольных события в случайном эксперименте с множеством элементарных исходов Ω .
Справедливо следующее утверждение.
Утверждение 1. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.
Другими словами, верна формула:
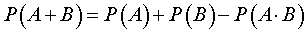 | (1) |
Доказательство. Рассмотрим диаграммы Эйлера – Венна для суммы двух событий и произведения двух событий, разместив их на одном рисунке (рис.1).
Рис.1
Проведем доказательство утверждения 1 на примере геометрического определения вероятности.
Если площадь произвольной фигуры F обозначить символом S (F) , то из рисунка 1 легко установить справедливость равенства:
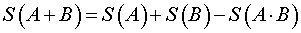 , , | (2) |
которое словами можно выразить так: «Площадь фигуры A + B равна сумме площадей фигур A и B минус площадь фигуры 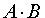 ».
».
Если обе части равенства (2) разделить на число S (Ω) , то мы получим равенство
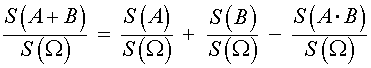 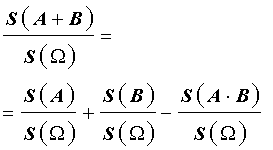 | (3) |
В силу геометрического определения вероятности справедливы формулы
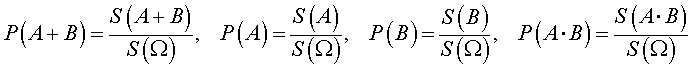
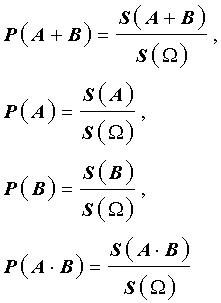
с помощью которых равенство (3) преобразуется к виду (1), что и завершает доказательство утверждения 1.
Доказательство утверждения 1 для классического определения вероятности проводится аналогичным образом, и мы оставляем его читателю в качестве полезного упражнения.
Несовместные события
Определение. Два события A и B называют несовместными, если они не пересекаются.
Другими словами, события A и B несовместны, если
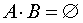
Замечание 1. События A и B несовместны в том, и только в том случае, если событие B является подмножеством события 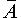 , то есть
, то есть 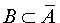 .
.
Замечание 2. События A и B несовместны в том, и только в том случае, если событие A является подмножеством события 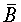 , то есть
, то есть 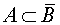 .
.
Замечание 3. Если события A и B несовместны, то вероятность их произведения равна нулю.
Другими словами, для несовместных событий A и B верна формула
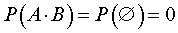
Замечание 4. Если события A и B несовместны, то вероятность суммы событий A + B равна сумме вероятностей событий A и B .
Другими словами, для несовместных событий A и B верна формула
P (A + B) = P (A) + P (B)
Независимость двух событий. Вероятность произведения двух независимых событий
Два события A и B называют независимыми, если появление одного из этих событий никак не влияет на вероятность появления второго события.
Замечание 5. Несовместные события и независимые события – это совершенно разные понятия, и их не следует путать.
Справедливо следующее утверждение.
Утверждение 2. Вероятность произведения двух независимых событий равна произведению их вероятностей.
Другими словами, для двух независимых событий A и B верна формула
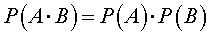 | (4) |
Проиллюстрируем справедливость формулы (4) на примере.
Пример 1. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 .
Решение. Сформируем следующую таблицу, в которой записаны все 36 возможных вариантов пар чисел, выпадающих при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании синей кости, а первый столбец таблицы – это числа, выпавшие при бросании красной кости. На пересечении строки и столбца указана пара чисел, выпавших на двух костях.
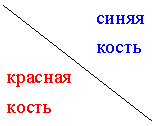 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1, 1 | 1, 2 | 1, 3 | 1, 4 | 1, 5 | 1, 6 |
| 2 | 2, 1 | 2, 2 | 2, 3 | 2, 4 | 2, 5 | 2, 6 |
| 3 | 3, 1 | 3, 2 | 3, 3 | 3, 4 | 3, 5 | 3, 6 |
| 4 | 4, 1 | 4, 2 | 4, 3 | 4, 4 | 4, 5 | 4, 6 |
| 5 | 5, 1 | 5, 2 | 5, 3 | 5, 4 | 5, 5 | 5, 6 |
| 6 | 6, 1 | 6, 2 | 6, 3 | 6, 4 | 6, 5 | 6, 6 |
Благоприятным является только один исход, а именно, клетка с результатом 4, 3 , окрашенная в таблице желтым цветом. Следовательно, вероятность события, состоящего в том, что на синей игральной кости выпадает число 3 , а на красной игральной кости выпадает число 4 , равна 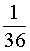 .
.
Теперь рассмотрим случайный эксперимент, описанный в примере 1, с другой стороны. Для этого обозначим буквой A случайное событие, состоящее в том, что на синей игральной кости выпадает число 3 , а буквой B — случайное событие, состоящее в том, что на красной игральной кости выпадает число 4 . События A и B являются независимыми событиями, а их вероятности равны:
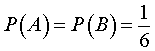
Событие 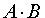 состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
состоит в том, что на синей игральной кости выпадет число 3 , а на красной игральной кости выпадет число 4 . Поскольку,
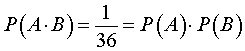
то в рассматриваемом случайном эксперименте по подбрасыванию двух игральных костей формула (4) верна.
В заключение приведем ещё одну иллюстрацию применимости формулы для вероятности суммы двух событий и формулы для вероятности произведения двух независимых событий.
Пример 2. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью 0,9 . Второй стрелок поражает мишень с вероятностью 0,8 . Найти вероятность того, что мишень будет поражена.
Решение. Обозначим буквой A случайное событие, состоящее в том, что в мишень попадает первый стрелок, а буквой B обозначим случайное событие, состоящее в том, что в мишень попадает второй стрелок. Тогда событие A + B означает, что мишень поражена, а событие 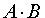 означает, что в мишень попали оба стрелка. По условию
означает, что в мишень попали оба стрелка. По условию
P (A) = 0,9 и P (B) = 0,8
а поскольку события A и B независимы, то в силу формулы (4)
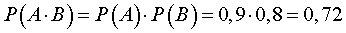
Воспользовавшись формулой (1), находим
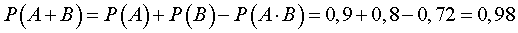
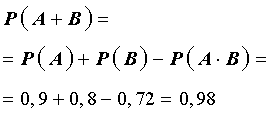
Ответ: 0,98

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Вероятность несовместных событий
Факт 1.
Случайное событие – это событие, которое при данных условиях может произойти, а может не произойти.
Например, событие “при бросании игральной кости выпало 3 или 4 очка”. Напомним, что игральная кость – это кубик с шестью гранями, на которых написаны числа от 1 до 6.
Предположим, что мы проводим некоторое испытание (эксперимент), например, бросаем игральную кость. Результатом нашего испытания может быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событиями (то есть это “простейшие” события, которые в совокупности образуют все множество исходов нашего эксперимента).
Например, событие “при бросании игральной кости выпало 3 или 4 очка” не является элементарным, оно состоит из двух элементарных событий “при бросании игральной кости выпало 3 очка” и “при бросании игральной кости выпало 4 очка”.
Если сложить вероятности всех возможных элементарных событий у некоторого эксперимента, то получится \(1\).
Два события мы будем называть равновероятными (равновозможными), если вероятности наступления любого из них одинаковы. Например, при бросании игральной кости вероятности любого из событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, одинаковы. Или, например, при подбрасывании монеты вероятности событий “выпадет орел” и “выпадет решка” также одинаковы.
Примером неравновероятных событий могут послужить два события: “при бросании игральной кости выпадет 1 очко” и “при бросании игральной кости выпадет нечетное количество очков”. Почему? В первом случае нам удовлетворяет только исход, когда кубик упадет кверху гранью, на которой написано 1; во втором случае нам подходит целых три исхода: он может выпасть кверху гранью с 1, с 3 или с 5.
Факт 2.
Если при проведении некоторого эксперимента возможны \(N\) равновероятных элементарных событий, то вероятность события \(A\) : \[P(A)=\dfrac mN,\] где \(m\) – количество “подходящих” элементарных событий.
Вероятность обозначается буквой \(P\).
На рисунке схематично изображено множество всех возможных равновероятных (одинаковые по размеру круги) исходов у некоторого эксперимента, которые не пересекаются: 
Таким образом, под такой вероятностью можно понимать часть, которую составляют “подходящие” исходы от всех возможных исходов.
Давайте рассмотрим несколько примеров, в которых используется данная формула.
Пример 1.
Найдите вероятность того, что при бросании игральной кости выпадет 3 очка.
Решение. Всего при бросании игральной кости возможны шесть исходов (в данном случае, элементарные события), которые мы описывали ранее. Как мы уже говорили, вероятности наступления каждого из этих исходов одинаковы. Следовательно, \(N=6\). Подходит нам только один исход: когда выпадет 3 очка. Следовательно, \(m=1\).
Таким образом, вероятность нашего события равна \(\dfrac16\).
Вообще говоря, вероятность любого из исходов: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, равна \(\frac16\).
Пример 2.
Найдите вероятность того, что при бросании двух игральных костей в сумме выпадет 4 очка.
Решение. Для начала нужно найти количество всех возможных исходов у нашего эксперимента. Предположим, на первом кубике выпало 1. Тогда на втором кубике может выпасть 1, 2, 3, 4, 5 или 6. То есть уже есть шесть возможных исходов.
Если на первом кубике выпало 2, то на втором также может выпасть 1, 2, 3, 4, 5 или 6. То есть еще шесть исходов.
Рассуждая аналогично, мы получим шесть “блоков” по шесть исходов. То есть всего у нашего события 36 возможных исходов (в данном случае, они будут элементарными событиями).
На самом деле, если мы бросаем \(k\) игральных костей, то всего у такого эксперимента будет \(6^k\) элементарных исходов.
Теперь давайте подумаем, сколько из них нам подходит. Чтобы в сумме на обоих кубиках было 4 очка, нужно, чтобы:
– на первом кубике выпало 1, на втором 3 очка;
– на первом кубике выпало 2, а на втором 2 очка;
– на первом кубике выпало 3, а на втором 1 очко.
Таким образом, нам подходит только три исхода.
Следовательно, вероятность равна \(\dfrac3{36}=\dfrac1{12}\).
Пример 3.
Торт разделен на 9 кусков, которые условно пронумерованы числами от 1 до 9. Найдите вероятность того, что Маша возьмет кусок с номером 6.
Решение. Маша может взять любой из девяти кусков, следовательно, у нашего эксперимента всего девять исходов. Подходящий нам исход только один – Маша должна взять кусок с номером 6. Следовательно, вероятность равна \(\dfrac19\).
Пример 4.
В соревнованиях по толканию ядра участвуют 8 спортсменов из Аргентины, 6 спортсменов из Бразилии, 5 спортсменов из Парагвая и 6 — из Уругвая. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Аргентины.
Решение. Заметим, что вероятность того, что спортсмен, выступающий последним, окажется из Аргентины, такая же, как вероятность, что он будет выступать первым, вторым, третьим и т.п. Всего претендентов на последнее место \(8+6+5+6=25\) спортсменов. Нам удовлетворяют лишь \(8\) из Аргентины.
Следовательно, вероятность равна отношению количества удовлетворяющих
исходов к количеству всех: \(\dfrac8{25}\).
События, виды событий —
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События А1, А2, … , Аn называются попарно несовместными, если любые два из них являются несовместными.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба {Г} и выпадение цифры {Ц} при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Определение. События ω1, ω2, … , ωn, образующие полную группу попарно несовместных и равновозможных событий, называются элементарными событиями.
Элементарными событиями являются выпадение цифр «1», … ,«6» при бросании кости. Эти события несовместны, равновозможны и образуют полную группу (предполагается, что кость является однородной и центрированной).
Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = {1, 2, 3, 4, 5, 6}.
Элементарные события, составляющие пространство Ω, обозначаются ω1, ω2, …, ω6.
Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.
Зависимые и независимые, совместные и несовместные события. — КиберПедия
Событие А называется зависимым от события В, если вероятность события А зависит от того, произошло событие В или нет.
Событие A называют независимым от события B, если появление события B не изменяет вероятности появления события A.
Если появление одного события исключает появление другого, то они называются несовместными; в противном случае два события называются совместными.
Формула сложения вероятностей для любых двух событий.
Теорема 1: Если события несовместны, то вероятность суммы событий равна сумме вероятностей этих событий.
Р(А + В) = Р(А) + Р(В). (2.7)
Доказательство:
N – число всех исходов испытаний.
m1 – число исходов испытаний, благоприятствующих наступлению события А.
m2 – число испытаний, благоприятствующих наступлению события В.
Р(А + В) = = + = Р(А) + Р(В). Что и требовалось доказать.
Следствие из теоремы:
Вероятность суммы нескольких несовместных событий равна сумме вероятности этих событий.
Р(А1 + А2 + … + Аn) = Р(А1) + Р(А2) + … + Р(Аn)
Теорема 2: Сумма вероятностей событий, образующих полную группу, равна единице.
Доказательство:
Пусть А1,А2, …, Аn – полная группа событий. Тогда наступление одного из этих событий – событие достоверное, т.е. Р(А1 + А2 + … +Аn) = 1. Но по теореме сложения несовместных событий можно записать:
Р(А1) + Р(А2) + … Р(А) = 1.
Следствие из теоремы:
Сумма вероятностей противоположных событий равна 1. Р(А) + Р(Ā) = 1.
Теорема 3: Если события совместны, то вероятность их суммы вычисляется по формуле:
Р(А + В) = Р(А) + Р(В) – Р(А×В)
Доказательство:
m1 – число исходов испытаний, благоприятствующих наступлению события А.
m2 – число исходов испытаний, благоприятствующих наступлению события В.
m3 – число исходов испытаний, благоприятствующих наступлению совместных событий А×В.
N – число всех исходов испытаний.
Р(А + В) = = = Р(А) + Р(В) – Р(А×В).Что и требовалось доказать.
Формулы умножения вероятностей для любых событий.
Теорема умножения: Вероятность произведения событий равна вероятности одного из этих событий, умноженной на условную вероятность другого при условии, что первое событие уже произошло.
Р(А × В) = Р(А) × РA(В).
Доказательство:
N – число всех исходов испытания.
M – число исходов, благоприятствующих наступлению события А.
К – число исходов, благоприятствующих наступлению события В, при условии, что А имело место, т.е. к – число исходов, когда А и В наступили вместе.
Поэтому Р(А × В) = = = = P(A) × PA(B).
Теорема умножения вероятностей обобщается на случай произвольного числа событий:
Р(АВСD) = Р(А)· РA(В) ·РAB(С) · РABC(D), т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Следствия.
Если события независимы, то вероятность события В, при условии, что А наступило.
РA(В) = Р(В).
РA(А) = P(A).
Зависимые и независимые события — Студопедия
Зависимость событий понимается в вероятностном смысле, а не в функциональном. Это значит, что по появлению одного из зависимых событий нельзя однозначно судить о появлении другого. Вероятностная зависимость означает, что появление одного из зависимых событий только изменяет вероятность появления другого. Если вероятность при этом не изменяется, то события считаются независимыми.
Определение: Пусть 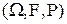 — произвольное вероятностное пространство,
— произвольное вероятностное пространство, 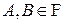 — некоторые случайные события. Говорят, что событие А не зависит от события В, если его условная вероятность
— некоторые случайные события. Говорят, что событие А не зависит от события В, если его условная вероятность 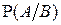 совпадает с безусловной вероятностью
совпадает с безусловной вероятностью 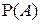 :
:
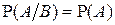 .
.
Если 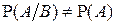 , то говорят, что событие А зависит от события В.
, то говорят, что событие А зависит от события В.
Понятие независимости симметрично, то есть, если событие А не зависит от события В,то и событие В не зависит от события А. Действительно, пусть 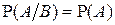 . Тогда
. Тогда 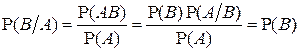 . Поэтому говорят просто, что события А и В независимы.
. Поэтому говорят просто, что события А и В независимы.
Из правила умножения вероятностей вытекает следующее симметричное определение независимости событий.
Определение: События А и В, определенные на одном и том же вероятностном пространстве 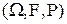 , называются независимыми, если
, называются независимыми, если
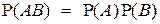 .
.
Если 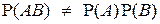 , то события А и В называются зависимыми.
, то события А и В называются зависимыми.
Отметим, что данное определение справедливо и в случае, когда 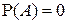 или
или 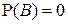 .
.
Свойства независимых событий.
1. Если события А и В являются независимыми, то независимыми являются также следующие пары событий: 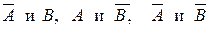 .
.
▲ Докажем, например, независимость событий 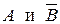 . Представим событие А в виде:
. Представим событие А в виде: 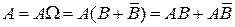 . Поскольку события
. Поскольку события 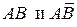 являются несовместными, то
являются несовместными, то 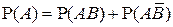 , а в силу независимости событий А и В получаем, что
, а в силу независимости событий А и В получаем, что 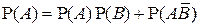 . Отсюда
. Отсюда 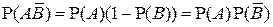 , что и означает независимость
, что и означает независимость 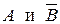 . ■
. ■
2. Если событие А не зависит от событий В1 и В2, которые являются несовместными ( 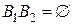 ), то событие А не зависит и от суммы
), то событие А не зависит и от суммы 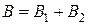 .
.
▲ Действительно, используя аксиому аддитивности вероятности и независимость события А от событий В1 и В2, имеем:
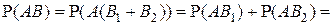
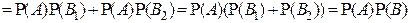 . ■
. ■
Связь между понятиями независимости и несовместности.
Пусть А и В — любые события, имеющие ненулевую вероятность: 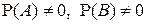 , так что
, так что 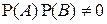 . Если при этом события А и В являются несовместными (
. Если при этом события А и В являются несовместными ( 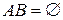 ), то
), то 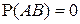 и поэтому равенство
и поэтому равенство 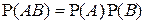 не может иметь место никогда. Таким образом, несовместные события являются зависимыми.
не может иметь место никогда. Таким образом, несовместные события являются зависимыми.
Когда рассматривают более двух событий одновременно, то попарная их независимость недостаточно характеризует связь между событиями всей группы. В этом случае вводится понятие независимости в совокупности.
Определение: События 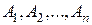 , определенные на одном и том же вероятностном пространстве
, определенные на одном и том же вероятностном пространстве 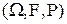 , называются независимыми в совокупности, если для любого 2 £ m £ n и любой комбинации индексов
, называются независимыми в совокупности, если для любого 2 £ m £ n и любой комбинации индексов 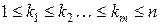 справедливо равенство:
справедливо равенство:
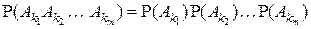 .
.
При m = 2 из независимости в совокупности следует попарная независимость событий. Обратное неверно.
Пример. (Бернштейн С.Н.)
Случайный эксперимент заключается в подбрасывании правильного четырехгранника (тетраэдра). Наблюдается грань, выпавшая книзу. Грани тетраэдра окрашены следующим образом: 1 грань — белая, 2 грань — чёрная,
3 грань — красная, 4 грань — содержит все цвета.
Рассмотрим события:
А = {Выпадение белого цвета}; B = {Выпадение черного цвета};
C = {Выпадение красного цвета}.
Тогда 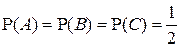 ;
;
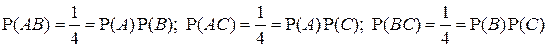 .
.
Следовательно, события А, В и С являются попарно независимыми.
Однако, 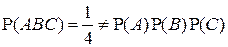 .
.
Поэтому события А, В и С независимыми в совокупности не являются.
На практике, как правило, независимость событий не устанавливают, проверяя ее по определению, а наоборот: считают события независимыми из каких-либо внешних соображений или с учетом обстоятельств случайного эксперимента, и используют независимость для нахождения вероятностей произведения событий.
Теорема (умножения вероятностей для независимых событий).
Если события 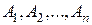 ,определенные на одном и том же вероятностном пространстве
,определенные на одном и том же вероятностном пространстве 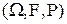 , являются независимыми в совокупности, то вероятность их произведения равна произведению вероятностей:
, являются независимыми в совокупности, то вероятность их произведения равна произведению вероятностей:
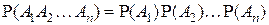 .
.
▲ Доказательство теоремы следует из определения независимости событий в совокупности или из общей теоремы умножения вероятностей с учетом того, что при этом
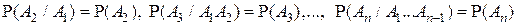 .■
.■
Пример 1(типовой пример на нахождение условных вероятностей, понятие независимости, теорему сложения вероятностей).
Электрическая схема состоит из трех независимо работающих элементов. Вероятности отказов каждого из элементов соответственно равны 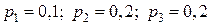 .
.
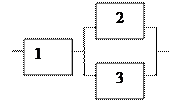 1) Найти вероятность отказа схемы.
1) Найти вероятность отказа схемы.
2) Известно, что схема отказала.
Какова вероятность того, что при этом отказал:
а) 1-й элемент; б) 3-й элемент?
Решение. Рассмотрим события 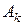 = {Отказал k-й элемент},
= {Отказал k-й элемент}, 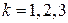 и событие А = {Отказала схема}. Тогда событие А представляется в виде:
и событие А = {Отказала схема}. Тогда событие А представляется в виде:
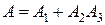 .
.
1) Поскольку события 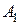 и
и 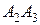 несовместными не являются, то аксиома аддитивности вероятности Р3) неприменима и для нахождения вероятности
несовместными не являются, то аксиома аддитивности вероятности Р3) неприменима и для нахождения вероятности 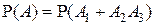 следует использовать общую теорему сложения вероятностей, в соответствии с которой
следует использовать общую теорему сложения вероятностей, в соответствии с которой
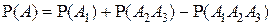 .
.
Используя далее независимость событий 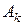 ,
, 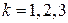 , имеем
, имеем
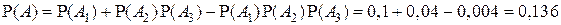 .
.
2) Если уже известно, что схема отказала, то для нахождения вероятности отказа при этом 1-го элемента необходимо определить условную вероятность 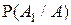 . По определению условной вероятности и с учетом того, что
. По определению условной вероятности и с учетом того, что 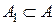 , получаем:
, получаем:
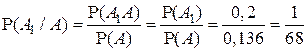 .
.
Поскольку 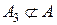 , то условная вероятность
, то условная вероятность 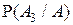 находится несколько иначе:
находится несколько иначе:
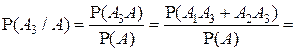
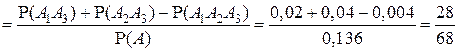 .
.
Пример 2.
Вероятность попадания в цель при каждом выстреле 0,9. Сколько надо сделать независимых выстрелов, чтобы поразить цель с вероятностью не менее, чем 0,9999?
Решение. Пусть n – число сделанных выстрелов, событие 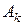 = {Попадание в цель при k-м выстреле},
= {Попадание в цель при k-м выстреле}, 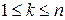 , событие А = {Поражение цели}. Очевидно, что
, событие А = {Поражение цели}. Очевидно, что 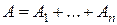 , но поскольку события
, но поскольку события 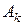 ,
, 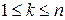 не являются попарно несовместными, то для нахождения вероятности
не являются попарно несовместными, то для нахождения вероятности 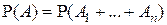 следует использовать теорему сложения вероятностей в общем виде.
следует использовать теорему сложения вероятностей в общем виде.
Удобнее перейти к противоположному событию и использовать свойство 1 независимых событий:
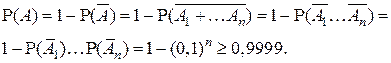
Разрешая полученное неравенство 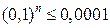 относительно n, получаем, что
относительно n, получаем, что 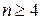 .
.
Разработка транзакционных микросервисов с использованием агрегатов, источников событий и CQRS
Ключевые выводы
- Event Sourcing — это метод надежного обновления состояния и публикации событий, который преодолевает ограничения других решений.
- Концепции проектирования управляемой событиями архитектуры с использованием источников событий хорошо согласуются с шаблонами архитектуры микросервисов. Моментальные снимки
- могут повысить производительность при запросе агрегатов за счет объединения всех событий до определенного момента времени.
- Источники событий могут создавать проблемы для запросов, но их можно решить, следуя рекомендациям CQRS и материализованным представлениям.
- Event sourcing и CQRS не требуют каких-либо специальных инструментов или программного обеспечения, и существует множество структур, которые могут заполнить некоторые низкоуровневые функции.
Часть 1 описывает, как ключевым препятствием при использовании микросервисной архитектуры является то, что модели предметной области, транзакции и запросы на удивление устойчивы к функциональной декомпозиции.Он показал, что решение состоит в реализации бизнес-логики для каждой службы в виде набора агрегатов DDD. Каждая транзакция обновляет или создает единый агрегат. События используются для поддержания согласованности данных между агрегатами (и службами).
В части 2 мы описываем, как ключевой проблемой при использовании событий является атомарное обновление агрегата и публикация события. Мы покажем, как решить эту проблему с помощью источника событий, который представляет собой ориентированный на события подход к проектированию и сохранению бизнес-логики.После этого мы опишем, как микросервисная архитектура затрудняет реализацию запросов. Мы покажем, как подход, называемый разделением ответственности за запросы команд (CQRS), может реализовать масштабируемые и высокопроизводительные запросы.
Надежное обновление состояния и публикация событий
На первый взгляд, использование событий для поддержания согласованности между агрегатами кажется довольно простым. Когда сервис создает или обновляет агрегат в базе данных, он просто публикует событие. Но есть проблема: обновление базы данных и публикация события должны выполняться атомарно.В противном случае, если, например, произошел сбой службы после обновления базы данных, но до публикации события, система останется в несогласованном состоянии. Традиционное решение — это распределенная транзакция с участием базы данных и брокера сообщений. Но по причинам, описанным ранее в части 1, 2PC не является жизнеспособным вариантом.
Есть несколько способов решить эту проблему без использования 2PC. Одно из решений, показанное на рисунке 1, заключается в том, что приложение выполняет обновление путем публикации события в брокере сообщений, таком как Apache Kafka.Потребитель сообщений, который подписывается на брокера сообщений, в конечном итоге обновляет базу данных. Такой подход гарантирует, что база данных обновлена, а событие опубликовано. Недостатком является то, что он реализует гораздо более сложную модель согласованности. Приложение не может сразу читать свои собственные записи.
Рисунок 1. Обновление базы данных путем публикации в брокере сообщений
Другой вариант, показанный на рисунке 2, заключается в том, чтобы приложение отслеживало журнал транзакций базы данных (файл.k.a. журнал фиксации), преобразовать каждое записанное изменение в событие и опубликовать
.c # — Источники событий: воспроизведение событий во вложенных сущностях в совокупности
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
— как правильно обрабатывать отношения агрегатов в Event Sourcing?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Обеспечить соблюдение инвариантов, охватывающих несколько агрегатов (проверка набора) в доменно-ориентированном дизайне
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
