Сокращ умнож: Формулы сокращ умнож. Формулы сокращенного умножения

3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Yandex.RTB R-A-339285-1

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.

Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.

Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.

7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа

a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .

10x — Викисловарь

Текущая версия (не проверялась)

Содержание

• 1 Английский
  • 1.1 10x I
    • 1.1.1 Морфологические и синтаксические свойства
    • 1.1.2 Произношение
    • 1.1.3 Семантические свойства
      • 1.1.3.1 Значение
      • 1.1.3.2 Синонимы
      • 1.1.3.3 Антонимы
      • 1.1.3.4 Гиперонимы
      • 1.1.3.5 Гипонимы
    • 1. 1.4 Родственные слова
    • 1.1.5 Этимология
    • 1.1.6 Фразеологизмы и устойчивые сочетания
    • 1.1.7 Библиография
  • 1.2 10x II

Морфологические и синтаксические свойства[править]

10x

Прилагательное. Условное обозначение для ten times «(в) десять раз». Альтернативные написания: 10X, 10×.

Корень: —.

Произношение[править]

• МФА: [ˈtʰɛn ˈɛks]

Семантические свойства[править]

Значение[править]

Общее прототипическое значение — в 10 раз.

1. десятикратный (сокращ. форма: 10-кратный), увеличивающий в 10 раз ◆ For forest work, where light is limited and birds are often close to the observer, 7—8x magnification serves well. It works well, also, for older and smaller people who have problems steadying the heavier 10x binoculars. — Для работы в лесу, где света недостаточно и птицы часто находятся недалеко от наблюдателя, подойдет увеличение в 7—8 раз. Оно удобно также для пожилых или некрупных людей, которым трудно удерживать более тяжелые 10-кратные бинокли. Peter Ryan, «Birdwatching in Southern Africa», 2006 г.
2. десятикратный (сокращ. форма: 10-кратный), увеличенный в 10 раз, удесятерённый, десятерной ◆ Older computers can import only at slower speeds such as 10x or even as little as 5x. — Более старые компьютеры могут импортировать [звукозапись с CD-дисков] только на низких скоростях: удесятерённой или даже всего лишь упятерённой. Brian Tiemann, «IPod + ITunes for Windows and Mac in a Snap», 2005 г. ◆ A 10x dose of the vaccine was found to be safe for 2-weeks-old broiler chicks of commercial origin. — Было установлено, что 10-кратная доза вакцины безопасна для 2-недельных цыплят фабричного разведения. M. W. Jackwood et al., «Rapid heat-treatment attenuation of infectious bronchitis virus», 2010 г. // «Avian pathology», vol. 39, no. 3
3. субстантивир. 10-кратное увеличение ◆ For clarity grading purposes, if an inclusion can’t be seen at 10x, it doesn’t exist.  — Для целей оценки чистоты [драгоценного камня] принято считать, что если вкрапление нельзя увидеть при 10-кратном увеличении, то его нет. A. L. Matlins, ‎A. C. Bonanno, «Jewelry & Gems: the Buying Guide», 2009 г.

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Ближайшее родство

Этимология[править]

Происходит от математической записи умножения, наподобие 10 × 5 (ten times five, букв. «десять раз пять»), в которой знак умножения был заменен похожей по начертанию буквой.

Фразеологизмы и устойчивые сочетания[править]

Библиография[править]

Статья нуждается в доработке.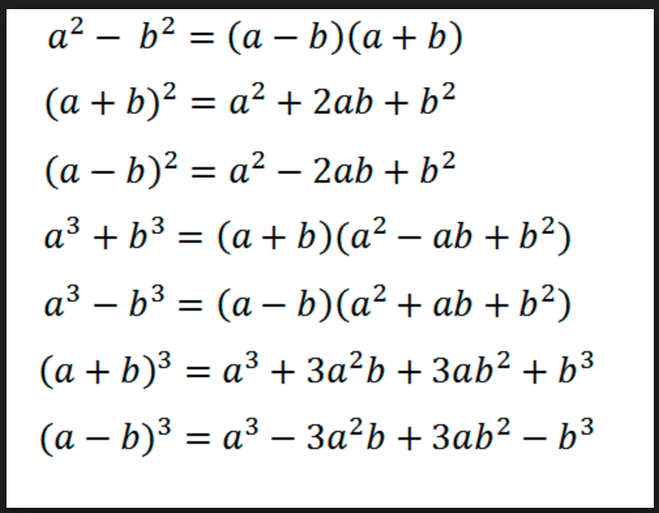 Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её. В частности, следует уточнить сведения о: морфологии произношении семантике этимологии (См. Общепринятые правила).

10x

• Сокращение-ребус от thanks «спасибо, благодарю» (написание из околокомпьютерного жаргона, по созвучию thanks [θæŋks] c ten x [tʰɛn ks]). Альтернативные написания: 10X, thx, thanx.

Список

— умножение парных элементов в python с использованием сокращения

спросил 5 лет, 1 месяц назад

Изменено 5 лет, 1 месяц назад

Просмотрено 338 раз

Для списка вида:

 a = [1,2,3,4,5,6]
 

Я хочу использовать приведенный ниже код для умножения парных элементов следующим образом:

 (а[0] + а[1]) * (а[2] + а[3]) * (а[4] + а[5])
 

Я пытался использовать что-то вроде:

 уменьшить ((лямбда x, y: (x + y)), числа)
 

и:

 уменьшить((лямбда x, y: (x+y)*(x+y)), числа)
 

Но я не знаю, как заставить его работать над всем списком. Любая помощь будет принята с благодарностью.

Все решение должно соответствовать уменьшению, и я не могу импортировать другие модули.

• питон
• список
• уменьшить
• Python-itertools

1

Вы можете уменьшить свой собственный генератор, который дает сумму пар в вашей итерации:

 defpairwise_sum(seq):
    нечетная_длина = длина (последовательность) % 2
    это = итер (последовательность)
    для item1, item2 в zip(it, it):
        выход элемент1 + элемент2
    если нечетная_длина:
        выход последовательности [-1]
>>> уменьшить (лямбда х, у: х * у, попарная_сумма ([1,2,3,4,5,6]))
231
 

Или, если вы хотите более общий, вы можете использовать grouper рецепт, чтобы сложить все пары, а затем использовать , уменьшить , чтобы умножить все суммы:

 из itertools import zip_longest
из functools импортировать уменьшить
от оператора import mul
def grouper (итерируемый, n, fillvalue = None):
    args = [iter(итерируемый)] * n
    вернуть zip_longest(*args, fillvalue=fillvalue)
>>> уменьшить (mul, map (sum, grouper ([1,2,3,4,5,6], 2, fillvalue=0)))
231
 

4

Это можно сделать в два этапа:

1. сумма последовательных элементов в списке: [сумма (a[i:i+2]) для i в диапазоне (0, len(a), 2)]
2. применить сокращение: уменьшить (лямбда x, y: x * y, новый_список)

---

Соединить их вместе:

 уменьшить(лямбда x, y: x * y, [сумма(a[i:i+2]) для i в диапазоне (0, len(a), 2)])
 

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Сокращение уравнений умножением

176. Неизвестная величина, вместо того чтобы быть соединенной с известной величиной знаком + или -, может быть разделена на на , как в уравнении х/а = Ь.

Здесь редукция не может быть произведена, как в предыдущих случаях, путем перестановки. Но если оба члена будут умножить на а, (статья 167), уравнение станет
         х = аб.

Дробь умножается на знаменатель путем удаления знаменателя. Это доказано свойствами дробей. (Ст. 156.) Это видно и из шестой аксиомы.

Таким образом, x = ax/a = 3x/3 = [(a + b)x]/(a + b) = (dx + 5x)/(d + 5). Ибо в каждом из этих случаев х умножается и делится на одно и то же количество; и это не меняет ценности. Следовательно,

177. Когда неизвестная величина равна , разделенной на известной величиной, уравнение сокращается на , умножая с каждой стороны на эту известную величину.

В этом случае нужно сделать те же перестановки, что и в предыдущих примерах. Следует также заметить, что каждые члена уравнения должны быть умножены. Ибо несколько членов в каждом члене составляют составное множимое, которое должно быть умножено в соответствии со ст. 96.

Бывший. 1. Сократим уравнение      x/c + a = b + d
Умножение обеих частей на      c
Произведение равно        x + ac = bc + cd
И         x = bc + cd — ac.

2. Сократим уравнение      x/(a + b) + d = h
Умножение на a + b      x + ad + bd = ah + bh.
И         x = ag + bh — ad — bd.

178. Когда неизвестная величина стоит в знаменателе дроби, сокращение производится аналогичным образом, путем умножения уравнения на этот знаменатель.

Бывший. 3. Сократите уравнение      6/(10 — x) + 7 = 8
Умножение на 10 — x       6 + 70 — 7x = 80 — 8x
И          x = 4.

179. Хотя обычно не является необходимым , тем не менее часто бывает удобно удалить знаменатель из дроби, состоящей только из известных величин. Это можно сделать так же, как у дроби, содержащей неизвестную величину, удаляют знаменатель.