Признаки параллельных прямых – определение параллельности
4.1
Средняя оценка: 4.1
Всего получено оценок: 221.
4.1
Средняя оценка: 4.1
Всего получено оценок: 221.
Параллельность – очень полезное свойство в геометрии. В реальной жизни параллельные стороны позволяют создавать красивые, симметричные вещи, приятные любому глазу, поэтому геометрия всегда нуждалась в способах эту параллельность проверить. О признаках параллельности прямых мы и поговорим в этой статье.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение для параллельности
Выделим определения, которые необходимо знать для доказательства признаков параллельности двух прямых.
Прямые называют параллельными, если они не имеют точек пересечения и лежат в одной плоскости. Кроме того, в решениях обычно параллельные прямые идут в связке с секущей прямой.
При правильном оформлении пишется: «Накрест лежащие углы при двух параллельных прямых а и b и секущей с», потому что для двух параллельных прямых может существовать бесконечное множество секущих, поэтому необходимо указывать, какую именно секущую, вы имеете в виду.
Также для доказательства понадобится теорема о внешнем угле треугольника, которая гласит, что внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
Признаки
Все признаки параллельности прямых завязаны на знание свойств углов и теоремы о внешнем угле треугольника.
Признак 1
Две прямые параллельны, если накрест лежащие углы равны.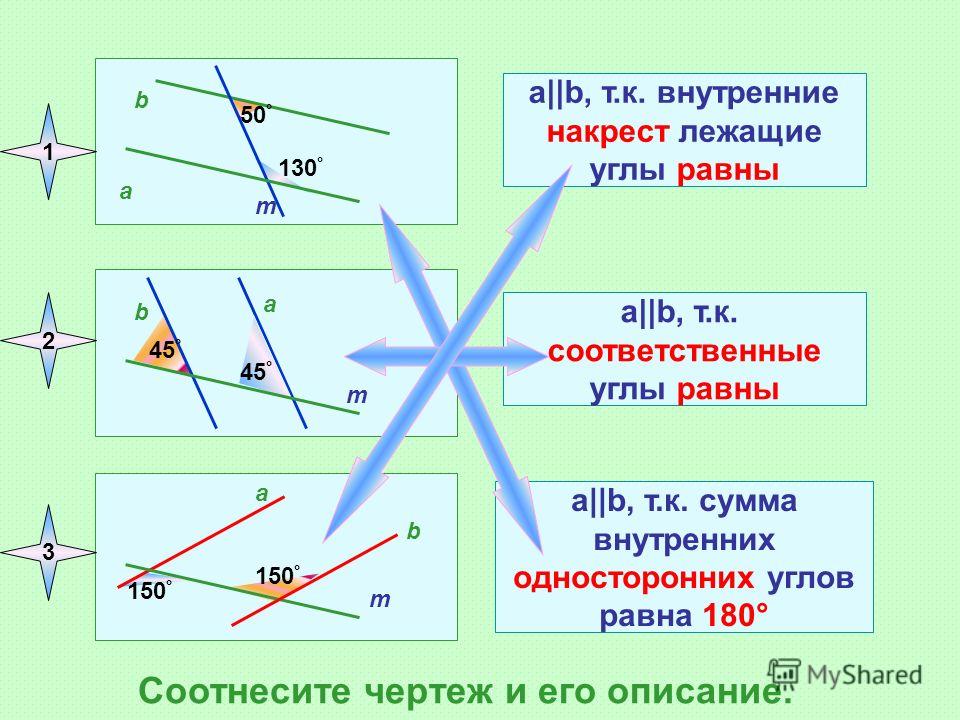
Рассмотрим две прямые а и b с секущей с. Накрест лежащие углы 1 и 4 равны. Предположим, что прямые не параллельны. Значит прямые пересекаются и должна быть точка пересечения М. Тогда образуется треугольник АВМ с внешним углом 1. Внешний угол при вершине В должен быть равен сумме углов 4 и АМВ, как несмежных с ним, по теореме о внешнем угле в треугольнике. Но тогда получится, что угол 1 больше угла 4, а это противоречит условию задачи, значит, точки М не существует, прямые не пересекаются, то есть параллельны.
Рис. 2. Рисунок к доказательству.Признак 2
Две прямые параллельны, если соответственные углы при секущей равны.
Рассмотрим две прямые а и b с секущей с. Соответственные углы 7 и 2 равны. Обратим внимание на угол 3. Он является вертикальным для угла 7. Значит, углы 7 и 3 равны. Значит, углы 3 и 2 также равны, так как <7=<2 и <7=<3. А угол 3 и угол 2 являются накрест лежащими. Следовательно, прямые параллельны, что и требовалось доказать.
Признак 3
Две прямые параллельны, если сумма односторонних углов равна 180 градусам.
Рис. 4. Рисунок к доказательству.Рассмотрим две прямые а и b с секущей с. Сумма односторонних углов 1 и 2 равна 180 градусов. Обратим внимание на углы 1 и 7. Они являются смежными. То есть:
$$<1+<7=180$$
$$<1+<2=180$$
Вычтем из первого выражения второе:
$$(<1+<7)-(<1+<2)=180-180$$
$$(<1+<7)-(<1+<2)=0$$
$$<1+<7-<1-<2=0$$
$$<7-<2=0$$
$<7=<2$ – а они являются соответственными. Значит, прямые параллельны.
Что мы узнали?
Мы в подробностях разобрали, какие углы получаются при пересечении параллельных прямых третьей прямой, выделили и подробно расписали доказательство трех признаков параллельности прямых.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Мария Граблина
5/5
Нина Зухова
5/5
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 221.
А какая ваша оценка?
Углы при пересечении двух прямых третьей прямой (секущей). Виды углов урок 5. Геометрия 7 класс
12+
3 месяца назад
Математика от Баканчиковой171 подписчик
Геометрия 7 класс. Сколько углов получается при пересечении 2-х прямых третьей (секущей)? Как называются эти углы, как их запомнить находить на разных рисунках? Сегодня на 5 уроке про виды углов мы ответим на эти вопросы. А чтобы Вы лучше и быстрее запомнили новый материал, сначала мы поясним Вам, что такое секущая, и как она расположена. Затем напомним Вам об углах, которые получаются при пересечении двух прямых или углов «в паре»: вертикальных и смежных. Подробно мы остановимся на 5 видах углов: внутренние односторонние, внешние односторонние, внутренние накрест лежащие, внешние накрест лежащие и соответственные.
Свойство углов при основании равнобедренного треугольника. Геометрия 7 класс. https://rutube.ru/video/2a2b7dfc5b44830f209dc9cc4e28d2f7/
Геометрия 7 класс. Треугольники. Признаки равенства треугольников. Урок 3. https://rutube.ru/video/0339e0588490b1b5ca732547aac3ec06/
Геометрия 7 класс. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач на свойства медианы и биссектрисы. Урок 5.
https://rutube.ru/video/3c88c497ce7a312249ea9e2b770fb8b1/
Геометрия 7 класс. Треугольники. Высота треугольника. Определение, свойства, точки пересечения высот. Примеры построения. Урок 6. https://rutube.ru/video/575bead43e6717ec773788d15e7380c1/
Геометрия 7 класс. Вертикальные углы. Определение. Доказательство теоремы о свойстве вертикальных углов. Виды углов урок 3. https://rutube.ru/video/10ca7111475a4f1a6dbe6b67fd71588c/
Геометрия 7 класс. Смежные углы. Определение. Свойства. Примеры задач на свойство смежных углов. Виды углов урок 2. https://rutube.ru/video/f12d3379fb0751e037c1f1bede88805f/
Что такое обратная и прямая теоремы.
типов угловых отношений — соответствующий, альтернативный интерьер, и больше
, написанные
Малкольм МакКинси
Проверка по фактам
Пол Маццола
Типы Angles
in Geometry, Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Thate Than Thate Than Ther Есть много типов углов, таких как конгруэнтные, смежные, вертикальные, соответствующие, знакопеременные, внешние и внутренние углы.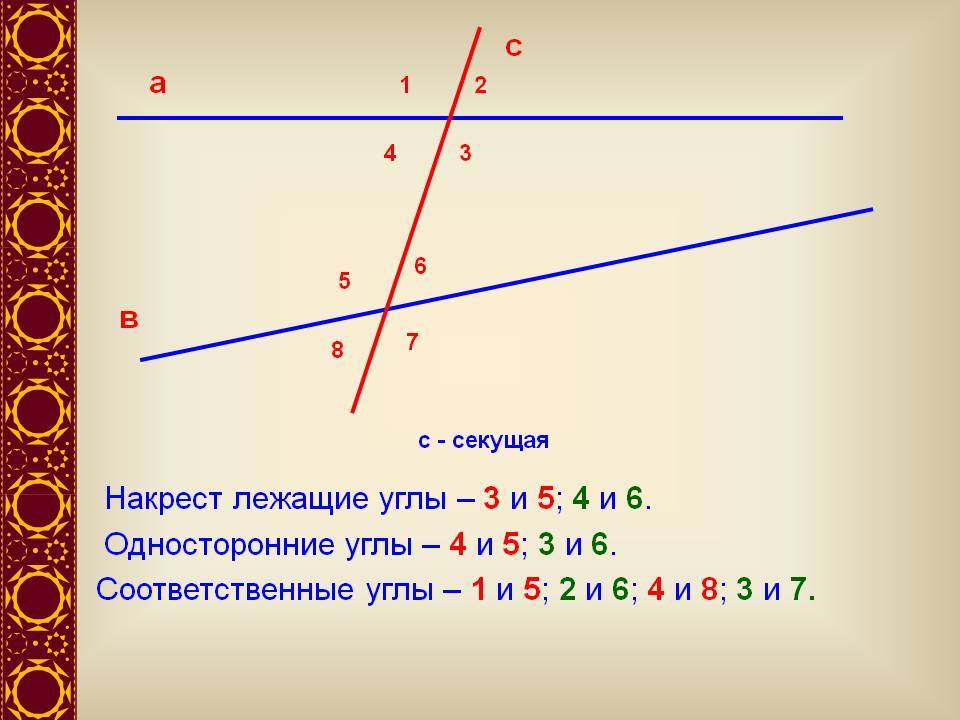
Все углы имеют отношения к другим углам, и именно эти отношения углов мы рассмотрим здесь.
Отношения углов
Помимо измерения градусов или радиан, вы также можете сравнивать углы и учитывать их отношения к другим углам. Мы говорим об отношениях углов, потому что мы сравниваем положение, измерение и конгруэнтность между двумя или более углами.
Типы углов — отношения угловНапример, когда две линии или отрезки пересекаются, они образуют две пары вертикальных углов. Когда две параллельные прямые пересекаются секущей, образуются сложные отношения углов, такие как чередующиеся внутренние углы, соответствующие углы и т. Д.
Умение определять взаимосвязь углов и уверенно находить конгруэнтные углы при пересечении линий поможет вам лучше изучить геометрию. Вы будете решать сложные задачи быстрее, когда будете досконально знакомы со всеми типами взаимосвязей углов.
Конгруэнтные углы
Любые два угла, независимо от их ориентации, которые имеют одинаковую меру (в радианах или градусах), конгруэнтны .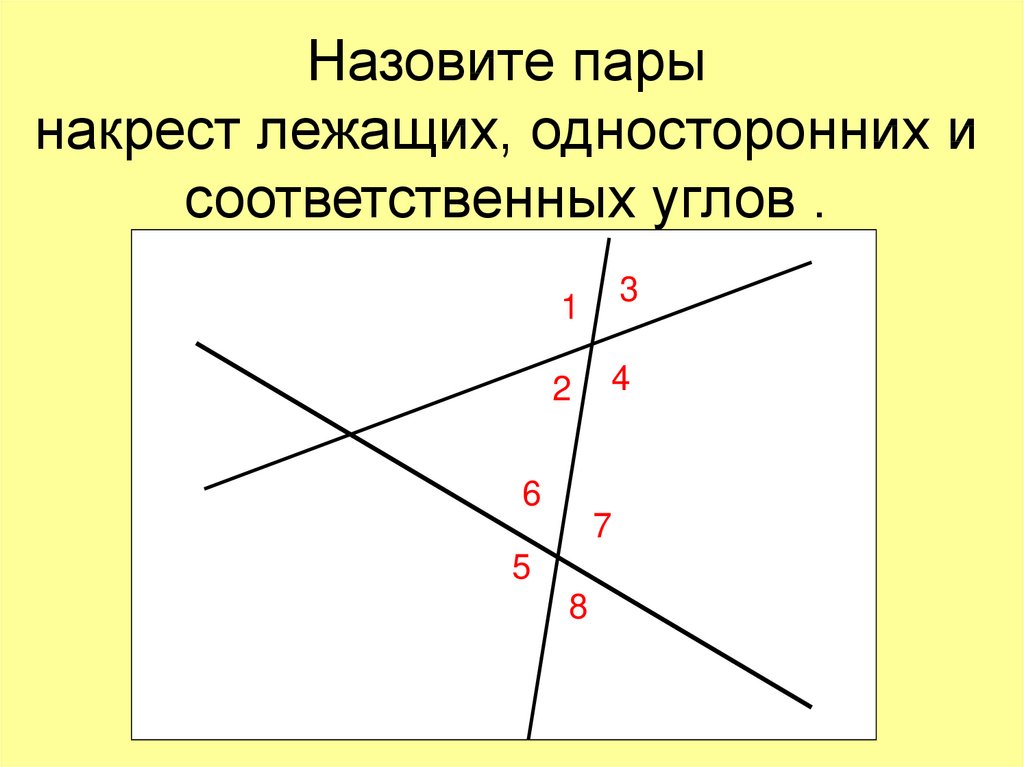
Они показывают одинаковую «открытость» между двумя лучами, отрезками или линиями, которые их образуют. Итак, эти два 35° углы конгруэнтны, даже если они не представлены одинаково и образованы разными конструкциями:
Смежные углы
Когда две прямые пересекаются, они образуют четыре угла. Любые два угла, имеющие общий луч, отрезок или прямую, являются смежными . На следующем рисунке линия JC пересекает линию OK , создавая четыре смежные пары и пересекаясь в точке Y . Ты можешь найти их всех?
Соотношение углов — смежные углыВы нашли ∠JYO рядом с ∠OYC ?
Как насчет ∠OYC рядом с ∠KYC ?
Вы видели ∠KYC рядом с ∠KYJ , верно?
И вы нашли ∠KYJ рядом с ∠JYO , конечно!
Вертикальные углы
На том же рисунке выше углы, которые пропускают угол, то есть углы, которые не касаются друг друга, кроме как в своей вершине, равны вертикальные углы .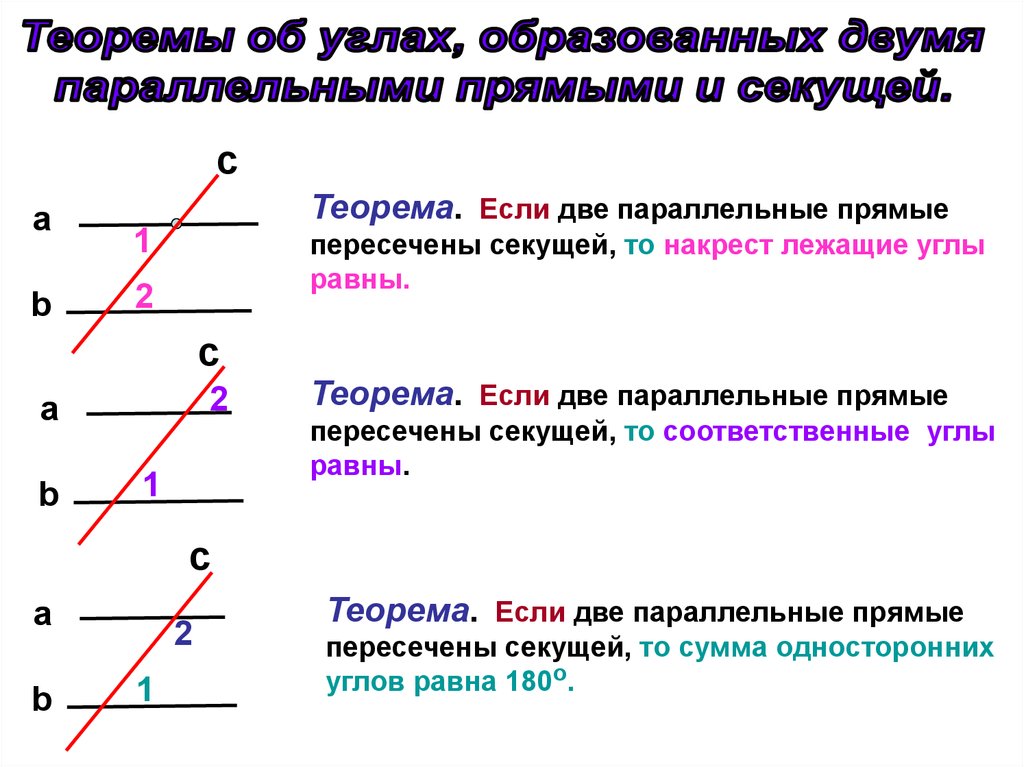
Здесь слово «вертикальный» означает «относящийся к вершине», а не «вверх и вниз». Вертикальные углы являются противоположными углами; они разделяют только свою точку вершины.
Две пересекающиеся линии создают две пары вертикальных углов. Посмотрите, сможете ли вы найти их на нашем рисунке.
Вы можете задаться вопросом, почему смежные углы не являются также вертикальными углами, ведь они тоже имеют общую вершину. Смежные углы имеют больше общего, чем вершина; они имеют общую сторону с углом.
Соответствующие углы
Каждый раз, когда секущая пересекает две другие прямые, мы получаем соответствующие углы. Чем более ограниченными становятся наши пересекающиеся линии, тем более ограниченными являются их угловые отношения. Когда линия пересекает две параллельные линии (поперечную), открывается совершенно новый уровень отношений углов:
Соотношения углов — соответствующие углы Мы можем ловко вытянуть из этой фигуры углы, похожие друг на друга.
Углы, которые имеют одинаковое положение относительно друг друга в двух наборах из четырех углов (четыре вверху, Строка AR ; четыре внизу, Line TO ) — соответствующие углы. Когда соответствующие углы лежат на параллельных прямых, они равны.
Наши поперечные и параллельные линии образуют четыре пары соответствующих углов. Можете назвать их всех?
Вы нашли ∠AYD соответствующее ∠TLY ?
Как насчет ∠DYR , соответствующего ∠YLO ?
Вы нашли ∠RYL соответствует ∠OLI , верно?
А вы не забыли, что ∠AYL соответствует ∠TLI , не так ли?
Во всех случаях, поскольку наши прямые AR и TO параллельны, их соответствующие углы равны.
Внешние углы
Те же самые параллельные прямые и их поперечные образуют внешние углы. Внешний угол среди линейных построений (не многоугольников) — это угол, лежащий вне параллельных прямых.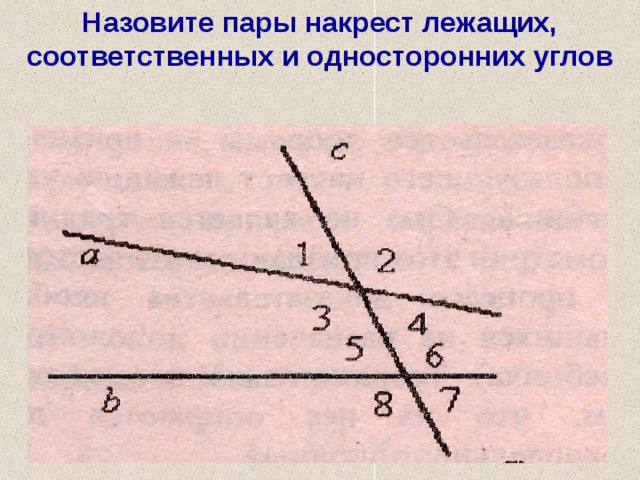
Вы можете увидеть два типа взаимосвязей внешних углов:
Последовательные внешние углы
Когда внешние углы находятся на одной стороне поперечной, они являются последовательными внешними углами, и дополнительными (добавляя к 180° ). На нашем рисунке выше ∠AYD и ∠TLI – это последовательные внешние углы. Единственная другая пара последовательных внешних углов — это ∠DYR и ∠OLI.
Взаимосвязи углов — последовательные углыЧередующиеся внешние углы
Альтернативные внешние углы подобны углам при вершине тем, что они являются противоположными углами (по обе стороны от поперечной). Альтернативные внешние углы находятся на противоположных сторонах поперечной (это альтернативная часть) и вне параллельных прямых (это внешняя часть). Сможете ли вы найти на нашем рисунке две пары альтернативных внешних углов?
Соотношения углов — альтернативные внешние углыВы записали ∠AYD и ∠OLI , а затем написали ∠DYR в паре с ∠TLI , несомненно!
Конгруэнтные альтернативные внешние углы используются для доказательства того, что прямые параллельны, с использованием (подходящей) теоремы о альтернативных внешних углах.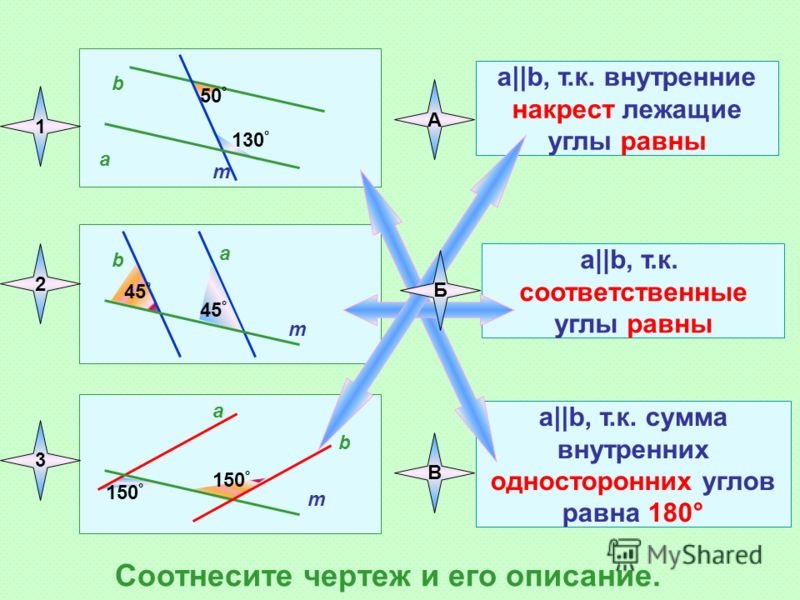
Внутренние углы
Углы между границами двух параллельных прямых являются внутренними углами , снова образованными секущей. Как и в случае с внешними углами, у нас могут быть последовательные внутренние углы и чередующиеся внутренние углы.
Последовательные внутренние углы
Внутренние углы на одной стороне поперечной составляют последовательных внутренних углов . На нашем рисунке вы можете найти две пары? Вы обнаружили, что ∠RYL сочетается с ∠YLO ? Вы видели, что ∠AYL сочетается с ∠TLY ?
Отношения углов — последовательные внутренние углыВ параллельных прямых последовательные внутренние углы являются дополнительными.
Альтернативные внутренние углы
Когда внутренние углы находятся на противоположных сторонах поперечной, они равны альтернативные внутренние углы . Они поддаются теореме о чередующихся внутренних углах, которая утверждает, что конгруэнтные чередующиеся внутренние углы доказывают параллельность прямых (так же, как это сделала теорема о чередующихся внешних углах).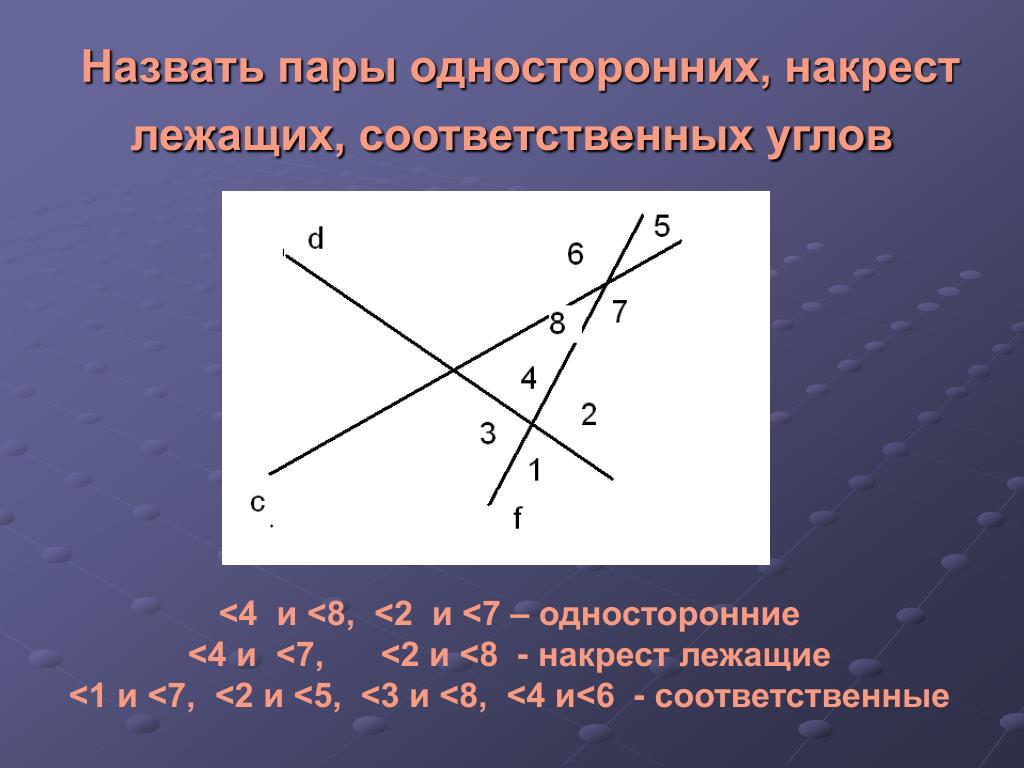
На нашем рисунке ∠ALY является альтернативным внутренним углом для ∠YLO , что делает их равными. И, конечно же, ∠RYL сочетается как альтернативный внутренний угол ∠TLY .
Примеры соотношения углов
Вы можете использовать свои новые знания об отношениях углов для решения алгебраических задач о геометрических фигурах. При просмотре любой новой фигуры просмотрите свой список и определите три вещи:
Относительное положение двух рассматриваемых углов
Находятся ли углы вне параллельных прямых (внешние) или внутри параллельных прямых (внутренние)
Находятся ли два исследуемых угла на одной стороне поперечной (последовательные) или на противоположных сторонах поперечной (чередующиеся)
Как только вы поймете взаимосвязь между двумя углами, вы можете предположить некоторые основные факты, такие как их совпадение или то, что они могут быть дополнительными.
Вы можете использовать эту осведомленность для решения кажущихся трудными алгебраических задач, таких как:
Нарисуйте параллельных линий MJ и TE и поперечных AS с пересечением 9029 Точки C 909030 с пересечением 909029 Точка I на Линия TE , написание по кругу MAJESTIC.
Пусть ∠MCA = 123° .
Учитывая число, найдите значение x , если ∠ MCA = 4x + 3° , а ∠EIS = 5x − 27° .
Сразу видно, что эти два угла, ∠MCA и ∠EIS , являются внешними углами по разные стороны от трансверсали. Таким образом, они являются альтернативными внешними углами, что делает их конгруэнтными и позволяет составить простое алгебраическое уравнение:
Далее мы вычитаем 4 x с обеих сторон:
Далее, мы добавим 27 ° к обеим сторонам:
, чтобы найти наши ракурсы, заменитель 30 ° для 29.3 . Если вы сможете решить это, вы совершите MAJESTIC некоторые математические вычисления!
Что вы можете рассказать нам о ∠JCI и ∠TIS ?
Что если мы скажем вам ∠JCI = 2y − 7° , а ∠TIS = y − 8° ?
Можете ли вы найти и ?
Ни один из углов не лежит по одну сторону от поперечной, и оба они не лежат вне параллельных прямых.
Они оба не находятся внутри параллельных линий! Кажется, что у них вообще нет отношений!
И все же по дедукции можно увидеть взаимосвязь:
Это означает, что наши два проблемных угла на самом деле дополняют друг друга, что является отличным намеком. Вместе их два уравнения должны составлять в сумме 180° :
Теперь упростим:
Необходимо 15° в обе стороны:
Обратно решая задачу, вы обнаружите, что ∠JCI = 123° и 9003 ∠TIS = 57° . Успех! Потренируйтесь сами, построив параллельные линии с пересечениями и определяя все отношения углов, которые они создают.
Помните также, что отношения остаются в силе, когда линии, пересекаемые секущей, не параллельны; вы просто не можете использовать теоремы, чтобы делать предположения об углах.
Соответствующие углы лежат на _________ стороне поперечной.
Последняя обновленная дата: 18 января 2023 г.
•
Общее представление: 162,6K
•
Просмотры сегодня: 5,60K
Ответ
Проверено
162.
6K+ виды
Хинт: Мы должны найти на поиск. лежат ли соответствующие углы по одну сторону от поперечной или по разные стороны. Сначала мы посмотрим, что такое соответствующие углы, а затем нарисуем схему и попытаемся выяснить, находятся ли они по одну сторону от поперечной или по разные стороны. Мы попробуем различить левую и правую стороны, используя разные цвета, а затем выясним, имеют ли соответствующие углы один и тот же цвет или разные цвета. Если они одного цвета, то они лежат на одной стороне, а если разного цвета, то на противоположной стороне поперечной.
Полный ответ:
Прежде всего обсудим, что такое соответствующие углы? Когда проведены две параллельные прямые и они пересекаются поперечной линией, то углы, которые образуются в соответствующих углах с поперечной линией и двумя прямыми соответственно. Давайте поймем это ясно, используя диаграмму.
На диаграмме выше мы видим, что m и n — две параллельные прямые, пересекаемые поперечной l.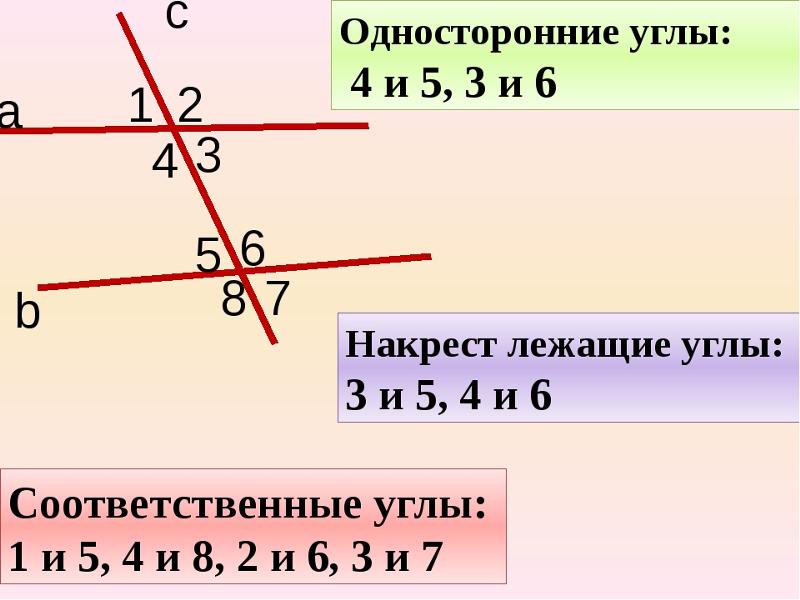
Теперь углы, образованные параллельными прямыми и секущей, нумеруются от \[1 — 8\]. Теперь мы видим, что \[\угол 1\] и \[\угол 5\] образованы в одном и том же углу, то есть в правом верхнем углу с поперечной линией и линией m и поперечной и линией n соответственно.
Итак, \[\угол 1\] и \[\угол 5\] образуют пару соответствующих углов. Точно так же мы видим, что \[\угол 2\] и \[\угол 6\] образуются в верхнем левом углу обеих линий с секущей. Итак, \[\угол 2\] и \[\угол 6\] образуют пару соответствующих углов. Мы также замечаем, что \[\угол 3\] и \[\угол 7\] образуются в нижнем левом углу обеих линий с секущей. Итак, \[\угол 3\] и \[\угол 7\] образуют пару соответствующих углов.
Наконец, мы видим, что \[\угол 4\] и \[\угол 8\] образуются в правом нижнем углу параллельных прямых. Следовательно, \[\угол 4\] и \[\угол 8\] образуют еще одну пару соответствующих углов. Соответственные углы между двумя параллельными прямыми равны по величине. Отсюда мы видим, что соответствующие углы образуются по одну и ту же сторону от секущей.