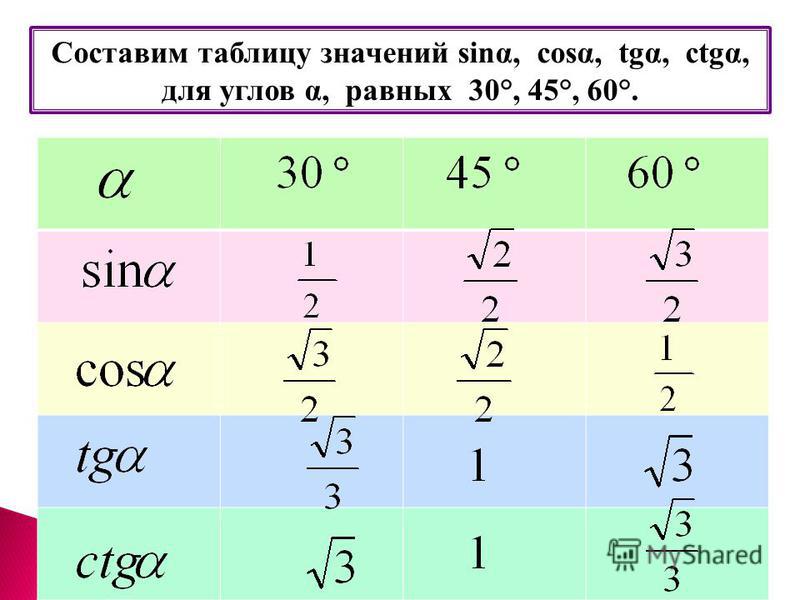
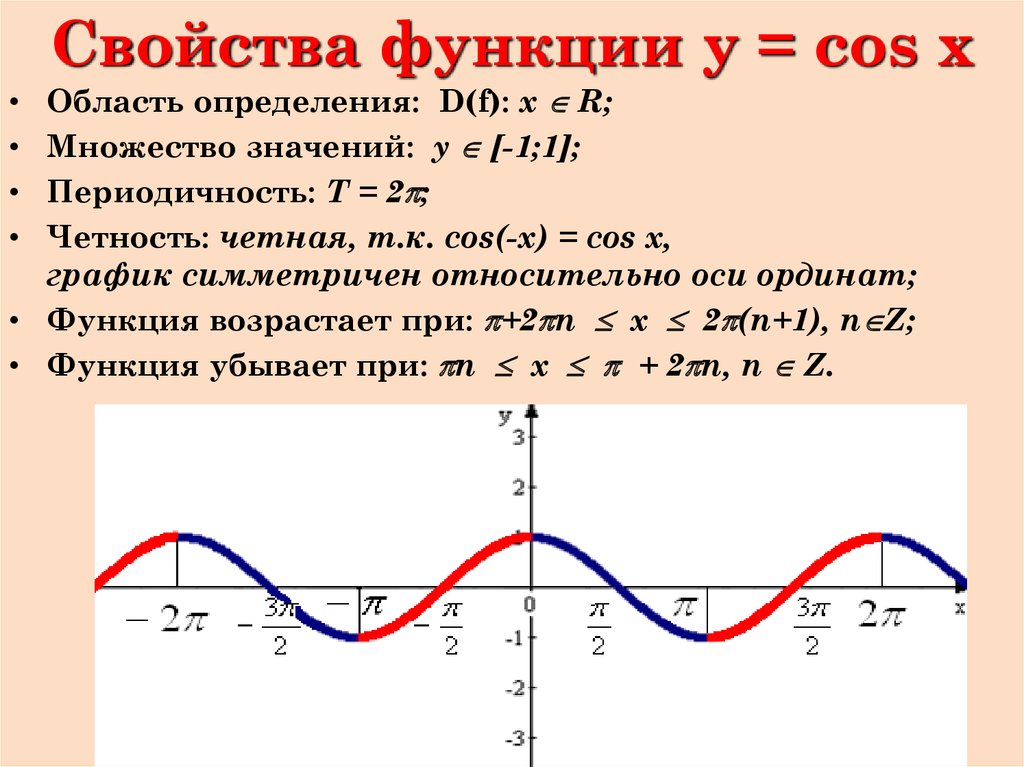
Чему равен косинус 30° градусов
математика тригонометрия
Только в сентябре: получи кредитку по акции с бонусом 2000р. и годом без % Получить карту
Мне нужно знать точное значение косинуса 30° градусов cos(30°) и косинус 60° градусов
Похвалить 4 Пожаловаться
3 ответа
Достаточно вспомнить определение косинуса:
«Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе.»
Наглядно это выглядит так (сторону «а» делим на строну «с», так как «а» — это катет, а «с» — это гипотенуза):
Какое значение косинуса 30 градусов?
- Точное значение косинуса 30 градусов (используется в реальных, нешкольных задачах) = 0.15425144988.
- В школьных задачах часто используют не точное значение косинуса 30 градусов, а не до конца посчитанное уравнение, чтобы школьники могли получить не страшный ответ из множества цифр, а точный.

Почему так вышло? А потому что угол в 30 градусов имеет равносторонний треугольник. Потому для многих косинусов, синусов, тангенсов и котангенсов можно определить подобное значение, удобное для использования в школьных задачках.
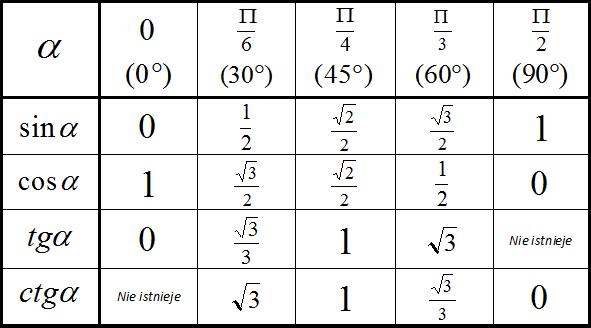
Полная таблица косинусов, синусов, тангенсов и котангенсов с указанием градусов в переводе в величину Pi:
Кому интересно, можете посмотреть похожие вопросы о косинусах, чтобы полностью разобраться в теме:
- «Какой косинус 15 градусов?»
- «Какой косинус 135 градусов?»
Также советую изучить статью о тригонометрических функциях из Википедии, ведь косинус — это тоже функция.
Похвалить 6 Пожаловаться
Пусть c — гипотенуза, a — катет, прилегающий к углу 30°, b — второй катет. Искомый косинус равен отношению прилегающего катета к гипотенузе (это одно из определений, см.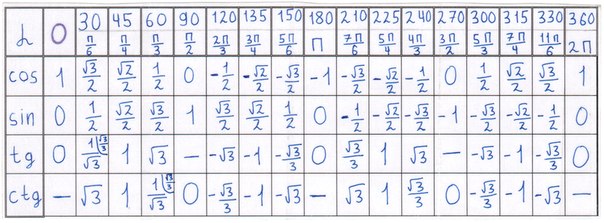
Cos(30°) = a/c (1)
По теореме Пифагора: а2 + b2 = c2 (2)
Если отразить треугольник относительно катета а, то у удвоенного треугольника все углы будут по 60°, то есть он будет равносторонним (см рис.). Следовательно,
c = 2b. (3)
Из уравнения (3) можно выразить катет b = c/2 и подставить его в уравнение (2). В итоге получится a2 + c2/4 = c2 или a2 = 3/4c2, откуда a = (√3/2)c. С учетом уравнения (1) получаем окончательно:
Cos(30°) = √3/2 или приблизительно 0,866.
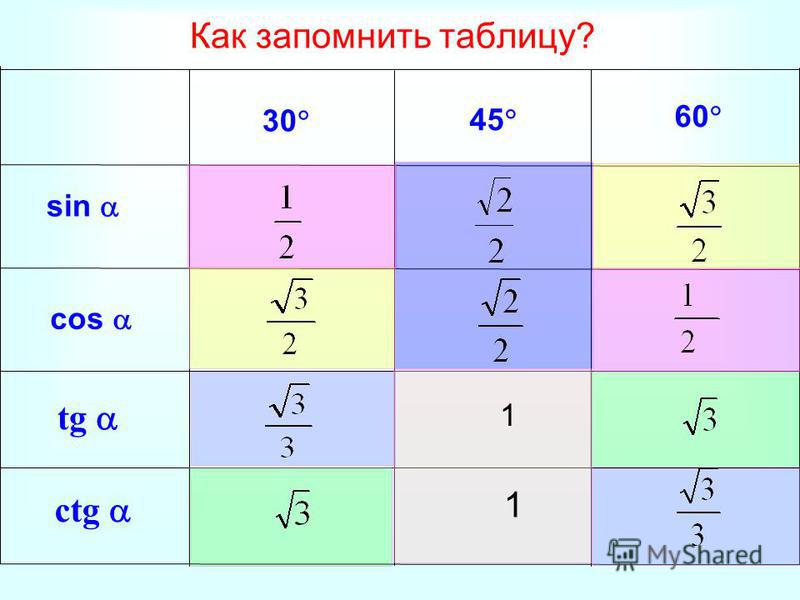
Это одно из немногих значений тригонометрических функций, которое легко запомнить.
Похвалить 3 Пожаловаться
Определение
Отношение прилежащего катета к гипотенузе является косинусом угла.
Тригонометрия изучает разные формулы, их закономерности и для упрощения обозначений используется «cos». Это значение легко найти в прямоугольном треугольнике, зная стороны фигуры или углы.
сos (30°) = cos (π/6), в расчётах используют другую формулу: сos (30°) = (√3)/2 = 0,866.
Как получить косинус 30° градусов?
Математика – точная наука, но сos (30°) считается одним из самых простых значений для запоминания.
К примеру, нужно найти косинус тридцати градусов в равностороннем треугольнике с одинаковыми сторонами. Все углы равны шестьдесят градусов. После проведения медианы на сторону ВС, которая является биссектрисой, получаем прямоугольный треугольник. В нём, очевидно, есть два угла по 60, 90°. Сумма углов треугольника равна 180°, в данном случае легко можно получить третий угол, он равен разнице 180° и суммы оставшихся углов, ∠ВАО = 30°. Косинус равен отношению стороны ОА к АВ.
Похвалить 3 Пожаловаться
Дать ответ и заработать:
Cимволов:
Обсудить на форуме |
Cos 30 градусов — Найдите значение Cos 30 градусов
LearnPracticeDownload
Значение cos 30 градусов равно 0,8660254. . . . Cos 30 градусов в радианах записывается как cos (30° × π/180°), т. е. cos (π/6) или cos (0,523598…). В этой статье мы обсудим методы нахождения значения cos 30 градусов на примерах.
- Cos 30°: 0,8660254. . .
- Cos 30° в дробях: √3/2
- Cos (-30 градусов): 0,8660254. . .
- Cos 30° в радианах: cos (π/6) или cos (0,5235987 . . .)
Каково значение Cos 30 градусов?
Значение cos 30 градусов в десятичной системе равно 0,866025403. . .. Cos 30 градусов также можно выразить с помощью эквивалента заданного угла (30 градусов) в радианах (0,52359 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (пи/ 180°)
⇒ 30 градусов = 30° × (π/180°) рад = π/6 или 0,5235. . .
∴ cos 30 ° = cos (0,5235) = √ 3/2 или 0,8660254. . .
Объяснение:
Для cos 30 градусов угол 30° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 30° = √3/2 или 0,8660254. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 30° как cos 30 градусов = cos(30° + n × 360°), n ∈ Z.
⇒ cos 30° = cos 390° = cos 750° и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-30°) = cos(30°).
Методы определения значения косинуса 30 градусов
Функция косинуса положительна в 1-м квадранте. Значение cos 30° равно 0,86602. . .. Мы можем найти значение cos 30 градусов по:
- Используя тригонометрические функции
- Использование единичного круга
Cos 30° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 30 градусов как:
- ± √(1-sin²(30°))
- ± 1/√(1 + tan²(30°))
- ± раскладушка 30°/√(1 + раскладушка²(30°))
- ±√(косек²(30°) — 1)/косек 30°
- 1/сек 30°
Примечание: Поскольку 30° лежит в 1-м квадранте, окончательное значение cos 30° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 30° как
- -cos(180° — 30°) = -cos 150°
- -cos(180° + 30°) = -cos 210°
- sin(90° + 30°) = sin 120°
- sin(90° — 30°) = sin 60°
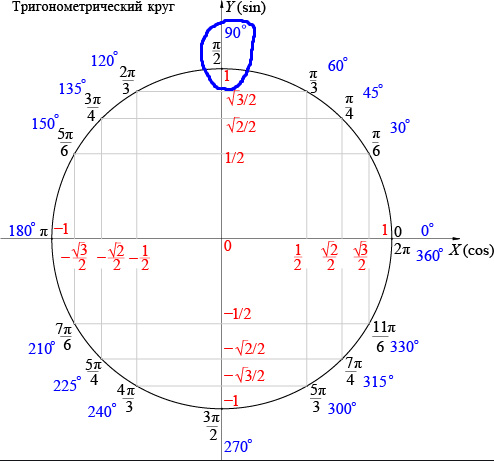
Cos 30 градусов с помощью единичной окружности
Чтобы найти значение cos 30 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 30° с положительной осью x.

- Космос 30 градусов равен x-координате (0,866) точки пересечения (0,866, 0,5) единичной окружности и r.
Отсюда значение cos 30° = x = 0,866 (приблизительно)
☛ Также проверьте:
- cos 11 градусов
- потому что 45 градусов
- потому что 180 градусов
- потому что 145 градусов
- , потому что 39 градусов
- потому что 115 градусов
Примеры использования Cos 30 градусов
Пример 1: Найдите значение cos 30°, если sec 30° равно 1,1547.
Решение:
Так как cos 30° = 1/сек 30°
⇒ cos 30° = 1/1,1547 = 0,866Пример 2: Упростить: 8 (cos 30°/sin 120°)
Решение:
Мы знаем, что cos 30° = sin 120°
⇒ 8 cos 30°/sin 120° = 8 (cos 30°/cos 30°)
= 8(1) = 8Пример 3.
 Найдите значение 2 cos(30°)/3 sin(60°).
Найдите значение 2 cos(30°)/3 sin(60°). Решение:
Используя тригонометрические тождества, мы знаем, что cos(30°) = sin(90° — 30°) = sin 60°.
⇒ cos(30°) = sin(60°)
⇒ Значение 2 cos(30°)/3 sin(60°) = 2/3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 30 Degrees
Что такое Cos 30 Degrees?
Косинус 30 градусов — значение тригонометрической функции косинуса для угла, равного 30 градусам. Значение cos 30° равно √3/2 или 0,866 (приблизительно)
Каково значение Cos 30 градусов в пересчете на Cot 30°?
Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 30° можно записать как cot 30°/√(1 + cot²(30°)). Здесь значение cot 30° равно 1,73205.
Здесь значение cot 30° равно 1,73205.
Как найти значение Cos 30 градусов?
Значение cos 30 градусов можно рассчитать, построив угол 30° с осью x и затем найдя координаты соответствующей точки (0,866, 0,5) на единичной окружности. Значение cos 30° равно координате x (0,866). ∴ cos 30° = 0,866.
Как найти косинус 30° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 30° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(30°))
- ± 1/√(1 + tan²(30°))
- ± раскладушка 30°/√(1 + раскладушка²(30°))
- ± √(косек²(30°) — 1)/косек 30°
- 1/сек 30°
☛ Также проверьте: тригонометрическую таблицу
Каково значение Cos 30° в пересчете на Cosec 30°?
Поскольку функцию косинуса можно представить с помощью функции косеканса, мы можем записать cos 30° как [√(cosec²(30°) — 1)/cosec 30°]. Значение cosec 30° равно 2.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядная программа
Опора 30 Анализ | Официальный информационный справочник для избирателей
- Перейти к основному содержанию
- Основной веб-сайт государственного секретаря
- Выборы и информация для избирателей
- Обратная связь
Всеобщие выборы в Калифорнии, 8 ноября 2022 г.
90 Официальный информационный справочник для избирателей
- Главная
- Предложения
- Кандидаты
- Судьи
- Краткое справочное руководство
- Информация для избирателей
- Аудио/PDF/крупный шрифт
Пожалуйста, сделайте выбор.
ОПОР
30
ОБЕСПЕЧИВАЕТ ФИНАНСИРОВАНИЕ ПРОГРАММ ПО СНИЖЕНИЮ ЗАГРЯЗНЕНИЯ ВОЗДУХА И ПРЕДОТВРАЩЕНИЮ ПОЖАРОВ ПУТЕМ ПОВЫШЕНИЯ НАЛОГА НА ЛИЧНЫЙ ДОХОД НА СВЫШЕ 2 МЛН ДОЛЛАРОВ США.
 ИНИЦИАТИВНЫЙ УСТАВ.
ИНИЦИАТИВНЫЙ УСТАВ.АНАЛИТИК ЗАКОНОДАТЕЛЬНЫХ ОРГАНИЗАЦИЙ
ОБЩИЕ СВЕДЕНИЯ
Подоходный налог с физических лиц штата Калифорния. Штат взимает налог на личный доход, полученный в штате. В прошлом году подоходный налог с населения собрал более 130 миллиардов долларов США. Большая часть доходов идет на оплату образования, тюрем, здравоохранения и других общественных услуг.
Программы для автомобилей с нулевым уровнем выбросов. У штата есть цели по ограничению выбросов парниковых газов, которые способствуют изменению климата, таких как углекислый газ при сжигании ископаемого топлива. Чтобы помочь в достижении этих целей, в штате есть программы, которые продвигают автомобили с нулевым уровнем выбросов (ZEV) — или автомобили, которые не выделяют загрязняющие вещества из выхлопной трубы. Примеры ZEV включают электромобили и автомобили на водородных топливных элементах. Государство требует от компаний, занимающихся райдшерингом (таких как Uber и Lyft), использовать все большее количество ZEV для своих услуг.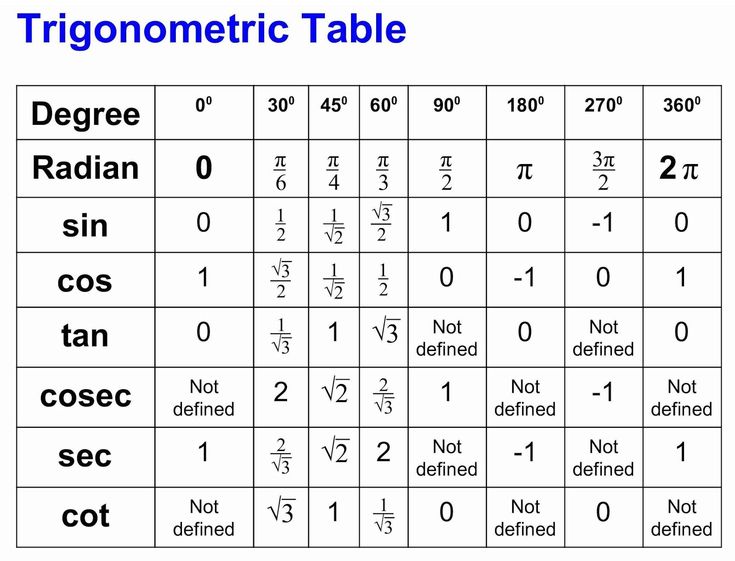 Государство также выделяет средства, чтобы помочь домохозяйствам, предприятиям и государственным учреждениям покупать новые ZEV и устанавливать заправочную инфраструктуру, такую как зарядные станции для электромобилей.
Государство также выделяет средства, чтобы помочь домохозяйствам, предприятиям и государственным учреждениям покупать новые ZEV и устанавливать заправочную инфраструктуру, такую как зарядные станции для электромобилей.
Программы реагирования и предотвращения лесных пожаров. Штат несет основную ответственность за действия по реагированию на лесные пожары, широко известные как тушение пожаров, примерно на одной трети территории Калифорнии. (Федеральное правительство и местные агентства несут основную ответственность за реагирование на лесные пожары повсюду в Калифорнии.) Мероприятия по реагированию на лесные пожары помогают ограничить распространение крупных лесных пожаров и предотвратить их нанесение ущерба населенным пунктам и жителям. Штат также реализует программы предотвращения лесных пожаров, чтобы снизить вероятность возникновения лесных пожаров и ограничить ущерб, который они наносят, когда они происходят. Некоторые примеры мероприятий по предотвращению лесных пожаров включают удаление деревьев из заросших лесов и удаление мертвых растений, которые могут загореться в районах вблизи зданий.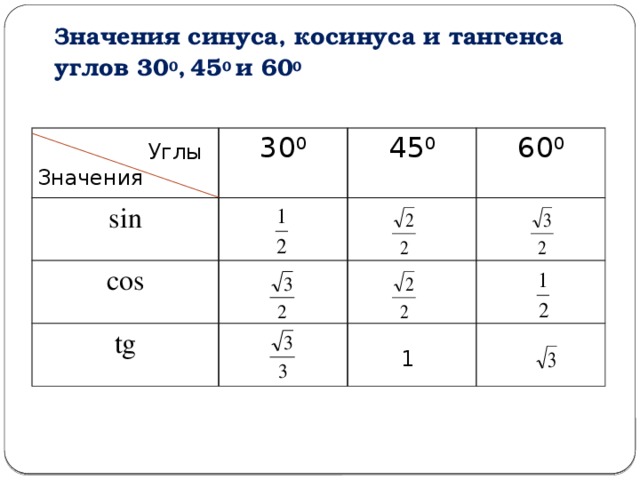
ПРЕДЛОЖЕНИЕ
СОЗДАЕТ НОВЫЙ НАЛОГ НА НАЛОГОПЛАТЕЛЬЩИКОВ С ВЫСОКИМ ДОХОДОМ
Начиная с января 2023 года, Предложение 30 требует, чтобы налогоплательщики с доходом выше 2 миллионов долларов США каждый год (ежегодно) платили дополнительный налог в размере 1,75 процента на долю их дохода выше 2 долларов США. млн. Этот дополнительный налог прекратится к январю 2043 года. Налог может быть отменен на несколько лет раньше, если Калифорния сможет до этого снизить выбросы парниковых газов по всему штату ниже определенного уровня.
ИСПОЛЬЗУЕТ ДОХОД ДЛЯ РАСШИРЕНИЯ ПРОГРАММ ZEV И МЕРОПРИЯТИЙ ПО ПОЖАРАМ
Предложение 30 требует, чтобы доходы от нового налога направлялись на увеличение финансирования программ ZEV и мероприятий по борьбе с лесными пожарами, как показано на рисунке 1. Деньги будут поступать в несколько государственных агентств для управления программами и мероприятиями.
Программы ZEV (80 процентов). Около 80% общего дохода приходится на две категории программы ZEV:
- Платежи для помощи в покупке новых автомобилей.
 Большая часть этих денег должна быть использована, чтобы помочь домохозяйствам, предприятиям и правительствам оплатить часть стоимости новых пассажирских ZEV (таких как легковые автомобили, фургоны и пикапы). Остальные деньги будут доступны для других программ. К ним относятся выплаты предприятиям и правительствам, чтобы помочь купить большие ZEV (такие как грузовики и автобусы), а также программы, которые поощряют меньше ездить и улучшают местное качество воздуха.
Большая часть этих денег должна быть использована, чтобы помочь домохозяйствам, предприятиям и правительствам оплатить часть стоимости новых пассажирских ZEV (таких как легковые автомобили, фургоны и пикапы). Остальные деньги будут доступны для других программ. К ним относятся выплаты предприятиям и правительствам, чтобы помочь купить большие ZEV (такие как грузовики и автобусы), а также программы, которые поощряют меньше ездить и улучшают местное качество воздуха. - Зарядные станции. Эти деньги будут использованы для установки и эксплуатации зарядных и заправочных станций ZEV в многоквартирных домах, частных домах и общественных местах.
Для каждой вышеперечисленной категории не менее половины средств должно быть потрачено на проекты, которые приносят пользу людям, живущим в районах с высоким уровнем загрязнения и/или с низким доходом или поблизости от них. Остальные деньги можно было потратить на проекты в любой точке штата.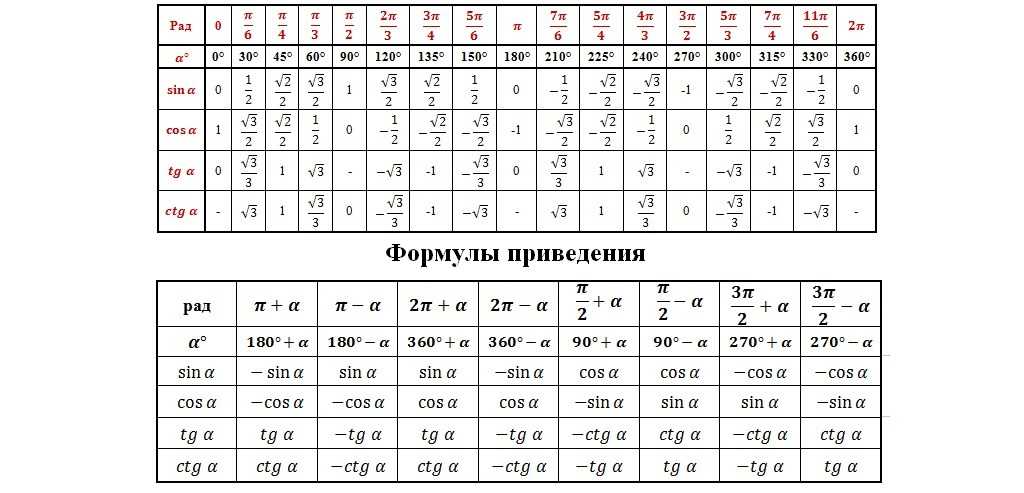
Мероприятия по ликвидации и предотвращению лесных пожаров (20 процентов). Около 20 % от общего дохода должно быть потрачено на мероприятия по ликвидации и предотвращению лесных пожаров. В целом штат должен был бы расставить приоритеты в расходах на наем, обучение и удержание государственных пожарных. Остальные деньги могут быть использованы для других мероприятий по ликвидации и предотвращению лесных пожаров.
ФИСКАЛЬНЫЕ ПОСЛЕДСТВИЯ
Увеличение государственных налоговых поступлений от нового налога для программ ZEV и противопожарных мероприятий. Новый налог на налогоплательщиков с высокими доходами обычно собирает от 3,5 млрд до 5 млрд долларов в год и со временем будет увеличиваться. Этот диапазон отражает изменения в доходах налогоплательщиков с высокими доходами. Их доходы часто сильно меняются из-за изменений в экономике и фондовом рынке. На основании требований к расходам, изложенных в Предложении 30, это финансирование будет поддерживать:
- Программы ZEV.
 Предложение увеличит государственное финансирование ZEV на 2,8–4 миллиарда долларов в год. Штат обычно ежегодно тратит сотни миллионов долларов на программы ZEV, а также недавно обязался потратить на эти программы около 10 миллиардов долларов в течение пятилетнего периода.
Предложение увеличит государственное финансирование ZEV на 2,8–4 миллиарда долларов в год. Штат обычно ежегодно тратит сотни миллионов долларов на программы ZEV, а также недавно обязался потратить на эти программы около 10 миллиардов долларов в течение пятилетнего периода. - Мероприятия по ликвидации и предотвращению лесных пожаров. Предложение увеличит государственное финансирование мероприятий по реагированию на лесные пожары и их предотвращению на 700 миллионов долларов США до 1 миллиарда долларов США в год. Штат обычно тратит от 2 до 4 миллиардов долларов в год на мероприятия по борьбе с лесными пожарами, в основном на тушение пожаров.
Потенциальные государственные и местные последствия увеличения расходов на ZEV. Дополнительное финансирование программ ZEV в соответствии с Предложением 30 может повлиять на количество ZEV, а также автомобилей с бензиновым или дизельным двигателем, используемых в Калифорнии.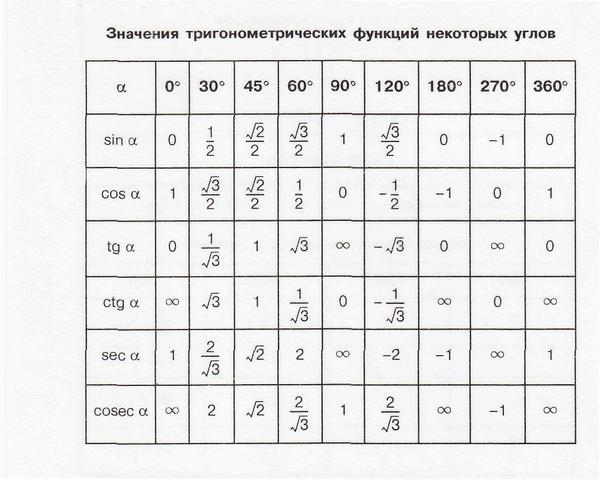 Однако фактический эффект, который это предложение имело бы, неясен по целому ряду причин. В частности, во время написания этого анализа государство рассматривало возможность потребовать, чтобы автомобильные компании продавали все большую долю ZEV в последующие годы до 2035 года, когда они смогут продавать только ZEV. (Штат должен был принять решение по этому требованию к августу 2022 года.) Это требование иногда называют «мандатом ZEV». Потенциальные финансовые последствия предложения, связанные с транспортом, для правительств штатов и местных органов власти зависят от того, будет ли утвержден мандат ZEV.
Однако фактический эффект, который это предложение имело бы, неясен по целому ряду причин. В частности, во время написания этого анализа государство рассматривало возможность потребовать, чтобы автомобильные компании продавали все большую долю ZEV в последующие годы до 2035 года, когда они смогут продавать только ZEV. (Штат должен был принять решение по этому требованию к августу 2022 года.) Это требование иногда называют «мандатом ZEV». Потенциальные финансовые последствия предложения, связанные с транспортом, для правительств штатов и местных органов власти зависят от того, будет ли утвержден мандат ZEV.
- Если штат одобрит мандат ZEV, то дополнительное финансирование от предложения помочь купить новые ZEV не окажет большого влияния на общее количество ZEV, эксплуатируемых в Калифорнии. Это связано с тем, что мандат ZEV уже требует значительного увеличения количества продаж ZEV даже без дополнительных расходов. Вместо этого основным эффектом предложения будет изменение того, кто платит за ZEV.
 То есть больше расходов будет покрываться за счет поступлений от нового налога на налогоплательщиков с высокими доходами, а не на продавцов и/или покупателей транспортных средств. Это не окажет большого влияния на государственные и местные финансы.
То есть больше расходов будет покрываться за счет поступлений от нового налога на налогоплательщиков с высокими доходами, а не на продавцов и/или покупателей транспортных средств. Это не окажет большого влияния на государственные и местные финансы. - Если штат не одобрит мандат ZEV, то финансирование от предложения помочь купить новые ZEV увеличит количество ZEV — и уменьшит количество автомобилей с бензиновым или дизельным двигателем — в Калифорнии. В результате количество используемого бензина будет меньше. В долгосрочной перспективе это изменение может иметь несколько различных финансовых последствий для правительств штатов и местных органов власти, включая более низкие доходы от налогов на бензин, которые используются для транспортных проектов, более высокие доходы от налогов на электроэнергию и другие эффекты, связанные с меньшим загрязнением воздуха. Чистый фискальный эффект этих изменений неясен, но, вероятно, незначителен по сравнению с сотнями миллиардов долларов, которые государственные и местные органы власти ежегодно тратят на все виды деятельности.

Потенциальное снижение государственных и местных расходов на реагирование на лесные пожары и восстановление. Предложение 30 может несколько сократить расходы правительства штата и местных органов власти, связанные с тушением пожаров, очисткой и восстановлением, если дополнительное финансирование лесных пожаров в конечном итоге снизит серьезность будущих лесных пожаров. Однако любое сокращение расходов будет зависеть от (1) того, какие конкретные мероприятия по борьбе с лесными пожарами будут в конечном итоге финансироваться, (2) насколько эффективно эти мероприятия уменьшат серьезность лесных пожаров, и (3) серьезности лесных пожаров, которые в противном случае произошли бы в любой конкретный год. Все эти факторы являются неопределенными, что делает неясным размер потенциальных финансовых последствий для правительств штатов и местных органов власти.
Снижение государственных доходов от других видов деятельности. Некоторые налогоплательщики, вероятно, предпримут шаги, чтобы уменьшить сумму подоходного налога, который они должны заплатить.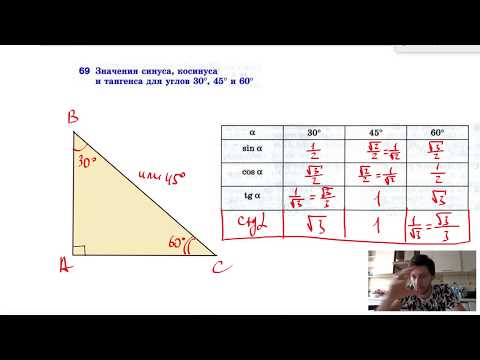 Это уменьшит существующие государственные доходы, используемые для оплаты деятельности, не финансируемой Предложением 30. Степень, в которой это произойдет, и сколько доходов государство может потерять в результате, неизвестно.
Это уменьшит существующие государственные доходы, используемые для оплаты деятельности, не финансируемой Предложением 30. Степень, в которой это произойдет, и сколько доходов государство может потерять в результате, неизвестно.
Возможные сокращения расходов на другие государственные программы в соответствии с лимитом государственных расходов. За некоторыми исключениями, такими как реагирование на чрезвычайные ситуации и строительство инфраструктуры, Конституция Калифорнии ограничивает расходы штата. В последние годы государственные расходы достигли этого предела. Некоторые из расходов, требуемых Предложением 30, — вероятно, сумма от 1,5 до 3 миллиардов долларов в год — будут учитываться в этом пределе. В результате, когда государственные расходы достигают предела, предложение потребует от штата сократить на равную сумму расходы на другие программы, чтобы «освободить место» для новых необходимых расходов на программы ZEV и мероприятия по ликвидации последствий лесных пожаров.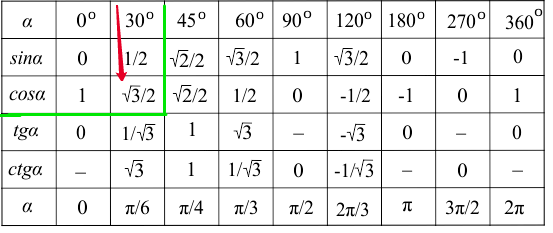




 Правильний чотирикутник (квадрат)
Правильний чотирикутник (квадрат)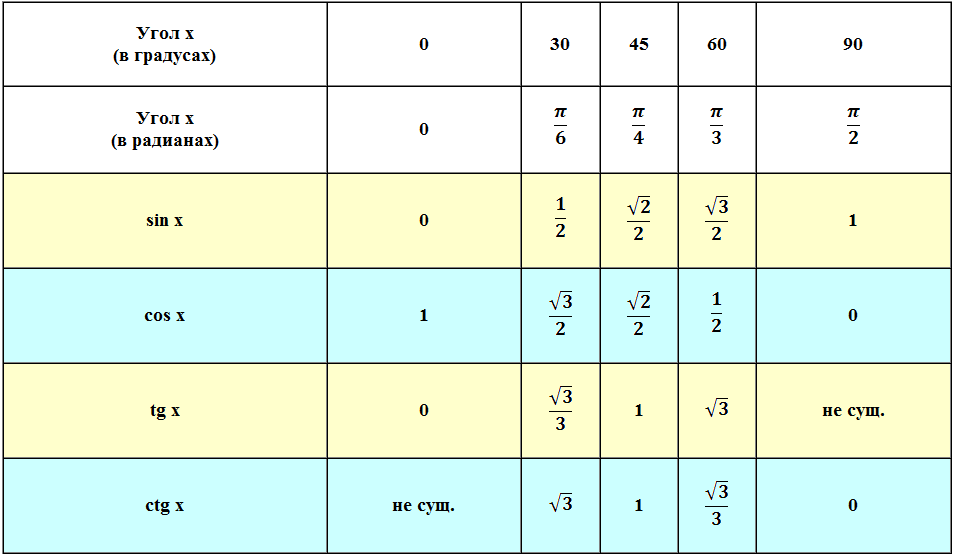
 Свойства и признаки параллельности.
Свойства и признаки параллельности.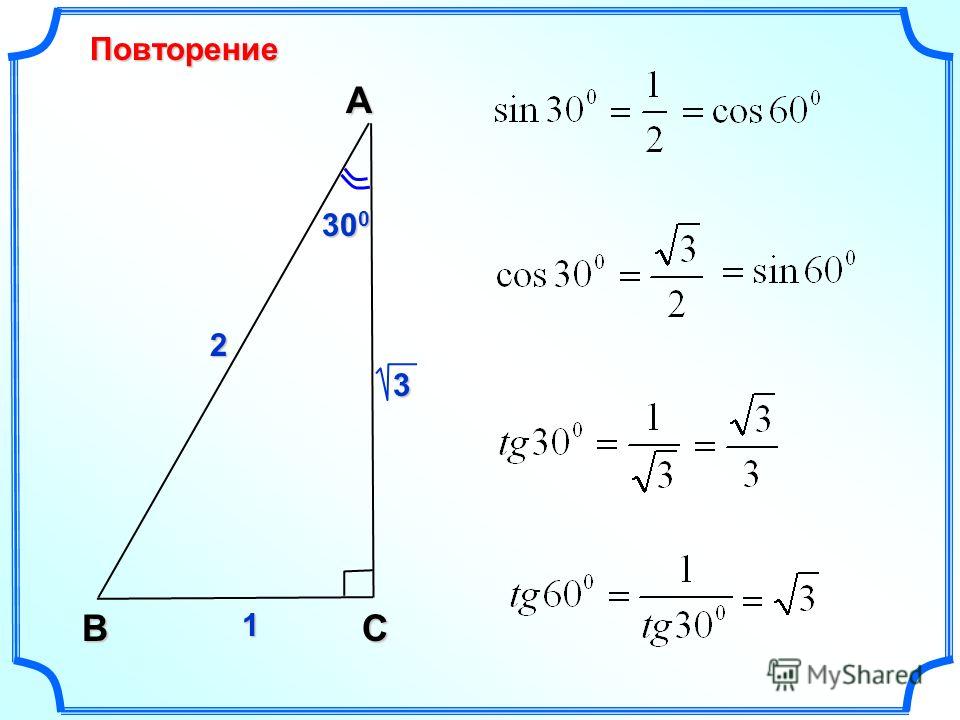 Решение задач
Решение задач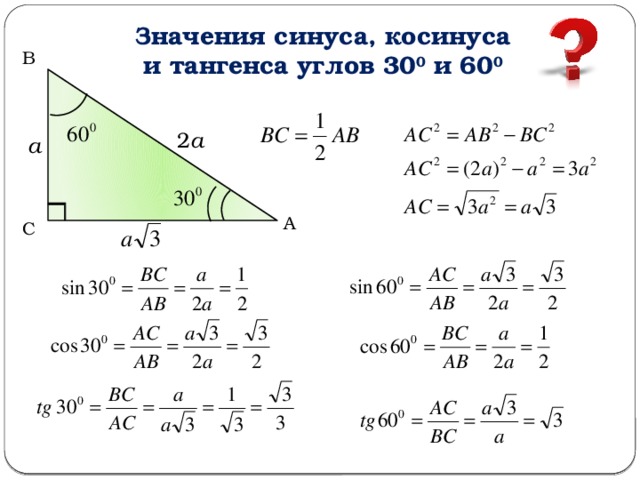 Шар. Куля
Шар. Куля См. также таблицу значений тригонометрических функций для всех углов.
См. также таблицу значений тригонометрических функций для всех углов.
 Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°.
Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°.
 Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°.
Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°.
 Сделаем это сначала для угла 30 градусов.
Сделаем это сначала для угла 30 градусов.
 В результате получаем табличные значения sin 30, cos 30 и tg 30 градусов
В результате получаем табличные значения sin 30, cos 30 и tg 30 градусов
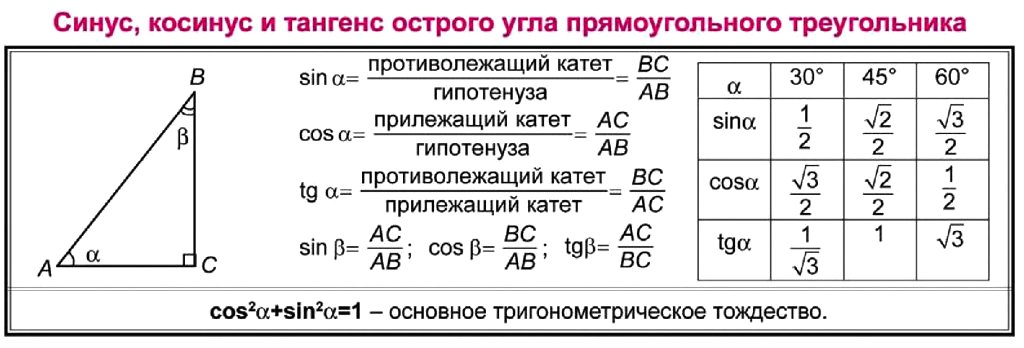
 Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса:
Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса:
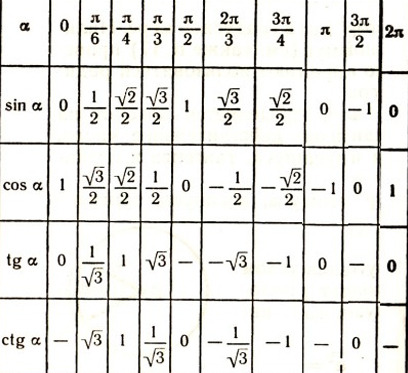 Здесь же приведены сами значения:
Здесь же приведены сами значения:
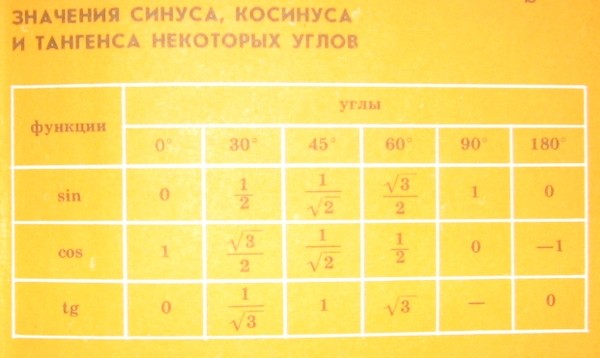 Поскольку все величины угла в радианах указываются через число пи, то для перевода в градусную меру достаточно заменить число пи на 180 градусов.
Поскольку все величины угла в радианах указываются через число пи, то для перевода в градусную меру достаточно заменить число пи на 180 градусов.

 Данная статья показывает, как вычисляется значение sin 60, cos 60 и подобных значений. Если Вы хотите посмотреть сводную справочную информацию — перейдите на таблицу значений тригонометрических функций
Данная статья показывает, как вычисляется значение sin 60, cos 60 и подобных значений. Если Вы хотите посмотреть сводную справочную информацию — перейдите на таблицу значений тригонометрических функций

 Найдите значение 2 cos(30°)/3 sin(60°).
Найдите значение 2 cos(30°)/3 sin(60°). 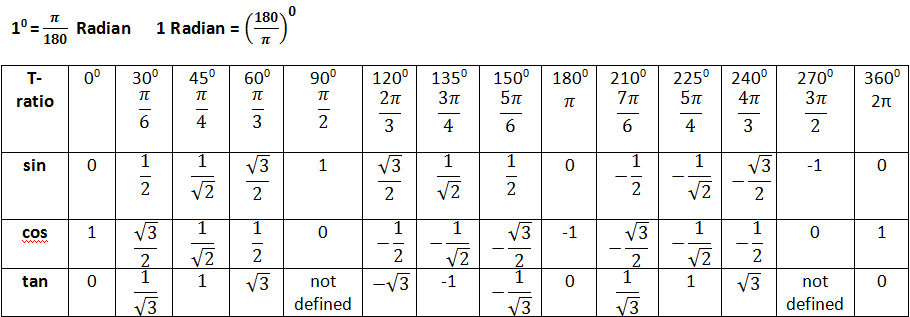 Большая часть этих денег должна быть использована, чтобы помочь домохозяйствам, предприятиям и правительствам оплатить часть стоимости новых пассажирских ZEV (таких как легковые автомобили, фургоны и пикапы). Остальные деньги будут доступны для других программ. К ним относятся выплаты предприятиям и правительствам, чтобы помочь купить большие ZEV (такие как грузовики и автобусы), а также программы, которые поощряют меньше ездить и улучшают местное качество воздуха.
Большая часть этих денег должна быть использована, чтобы помочь домохозяйствам, предприятиям и правительствам оплатить часть стоимости новых пассажирских ZEV (таких как легковые автомобили, фургоны и пикапы). Остальные деньги будут доступны для других программ. К ним относятся выплаты предприятиям и правительствам, чтобы помочь купить большие ZEV (такие как грузовики и автобусы), а также программы, которые поощряют меньше ездить и улучшают местное качество воздуха.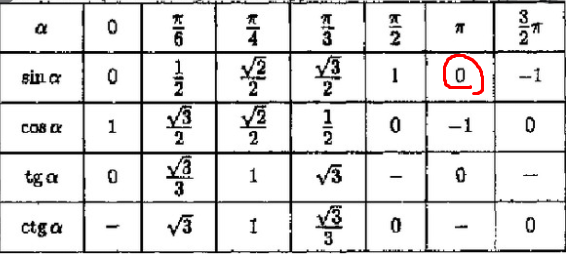 Предложение увеличит государственное финансирование ZEV на 2,8–4 миллиарда долларов в год. Штат обычно ежегодно тратит сотни миллионов долларов на программы ZEV, а также недавно обязался потратить на эти программы около 10 миллиардов долларов в течение пятилетнего периода.
Предложение увеличит государственное финансирование ZEV на 2,8–4 миллиарда долларов в год. Штат обычно ежегодно тратит сотни миллионов долларов на программы ZEV, а также недавно обязался потратить на эти программы около 10 миллиардов долларов в течение пятилетнего периода. То есть больше расходов будет покрываться за счет поступлений от нового налога на налогоплательщиков с высокими доходами, а не на продавцов и/или покупателей транспортных средств. Это не окажет большого влияния на государственные и местные финансы.
То есть больше расходов будет покрываться за счет поступлений от нового налога на налогоплательщиков с высокими доходами, а не на продавцов и/или покупателей транспортных средств. Это не окажет большого влияния на государственные и местные финансы.