Сравнение десятичных чисел: Сравнение десятичных дробей. Онлайн калькулятор

Сравнение десятичных дробей / Десятичные дроби / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Десятичные дроби
5. Сравнение десятичных дробей

Одно и то же натуральное число может быть представлено в виде обыкновенной дроби разными способами, например, . Для десятичных дробей также справедливо такое свойство, так, например, десятичные дроби 0,5, 0,50 и 0,500 обозначают одно и то же число.

Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.

Пример: 

1) 1,3 = 1,30 = 1,300 = …;

2) 3,67 = 3,670 = 3,6700 = … .

Если в десятичной дроби последние цифры — нули, то, отбросив их, получим дробь, равную данной.

Пример:

1) 3,40 = 3,4;           2) 0,50600 = 0,506;           3) 5,870000 = 5,87.

Любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой.

Пример:

1) 8 = 8,0 = 8,00 = 8,000 = …;

2) 125 = 125,0 = 125,00 = 125,000 = … .

Из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше.

Пример:

1) 3,5 2,96;          2) 0,567 4,2.

Из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение).

Пример:

1) 15,2 15,1;           2) 2,65 2,68;           3) 345,548 345,547.

Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (смотри правило выше).

Пример:

Сравнить десятичные дроби 45,6 и 45,498.

Решение:

У дроби 45,6 одна цифра после запятой, а у дроби 45,498 три цифры после запятой, для того, чтобы сравнить данные дроби, приписываем к дроби 45,6 справа два нуля, получим новую дробь 45,600. Теперь поразрядно сравниваем дроби 45,600 и 45,498, получим 45,

600 45,498, т.к. 6 4, значит, и 45,6 45,498.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Десятичная запись дробных чисел

Сложение и вычитание десятичных дробей

Приближенные значения чисел. Округление чисел

Умножение десятичных дробей

Деление десятичных дробей

Среднее арифметическое

Десятичные дроби

Правило встречается в следующих упражнениях:

5 класс

Задание 1172, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1174, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1249, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1419, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1472, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1738, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 826, Мерзляк, Полонский, Якир, Учебник

Номер 834, Мерзляк, Полонский, Якир, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 6, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 548, Мерзляк, Полонский, Якир, Учебник

Номер 916, Мерзляк, Полонский, Якир, Учебник

Номер 933, Мерзляк, Полонский, Якир, Учебник

Номер 955, Мерзляк, Полонский, Якир, Учебник

Номер 967, Мерзляк, Полонский, Якир, Учебник

Номер 993, Мерзляк, Полонский, Якир, Учебник

Номер 1108, Мерзляк, Полонский, Якир, Учебник

Задание 1505, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Задание 5, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

7 класс

Номер 172, Мерзляк, Полонский, Якир, Учебник

Номер 186, Мерзляк, Полонский, Якир, Учебник

---

Сравнение десятичных дробей — презентация онлайн

Сравнение десятичных
дробей
Устные задания:
Сколько единиц в каждом из разрядов в числе:
1) 16
1 десяток 6 единиц
2)234
2 сотни 3 десятка 4 единицы
3)4,7
4 единицы 7 десятых
4)52,68
5 десятков 2 единицы 6 десятых 8 сотых
5)10,19
1 десяток 1 десятая 9 сотых
6)3,507
3 единицы 5 десятых 7 тысячных
7)506,0506
5 сотен 6 единиц 5 сотых 6 десятитысячных
8)78,1002030
7 десятков 8 единиц 1 десятая 2
десятитысячных 3 миллионные
Какое из чисел больше: 5,3 или 4,988?
Из двух десятичных дробей больше та, у
которой целая часть больше.
Значит: 5,3 4,988
Как сравнить дроби с равными целыми?
В этом случае вначале сравнивают десятые.
Например, 11,23 11,19, так как 2 1.
Если же десятые оказались одинаковыми, то
сравнивают сотые.
Например, 2,84 2,86, так как 4 6.
Такой способ сравнения десятичных
дробей называют поразрядным.
Как сравнить десятичные дроби с равными
целыми частями, но с различным количеством
цифр после запятой?
Сравним отрезки длиной 5,4 м и 5,40 м. Имеем:
5,4 м = 5104 м = 5 м 4 дм = 540 см;
40
5,40 м = 5 100
м = 5 м 40 см=540
Получаем, что 5,4=5,40
Если к десятичной дроби справа приписать любое
количество нулей, то получится дробь, равная
данной.
Значение дроби, оканчивающейся нулями, не
изменится, если последние нули в её записи
отбросить.
Сравним дроби 3,2 и 3,198.
Поскольку, 3,2=3,200, а 3,200 3,198,то
3,2 3,198
Чтобы сравнить две десятичные дроби с равными
целыми частями и различным количеством цифр
после запятой, надо с помощью приписывания
нулей справа уравнять количество цифр в дробных
частях, после чего сравнить полученные дроби
поразрядно.
Запишите десятичную дробь:
1) С двумя цифрами после запятой, равную
числу 0,4
0,40
2) С четырьмя цифрами после запятой,
равную числу 3,26
3,2600
3) С тремя цифрами после запятой, равную
числу 42
42,000
4) С двумя цифрами после запятой, равную
числу 18,50000
18,50
Запишите несколько десятичных
дробей, равных данной:
1) 5,400
5,400 = 5,40000 = 5,40 = 5,4
2) 12,5080
12,5080 = 12,50800 = 12,508
3) 0,980
0,980 = 0,9800 = 0,98
Как сравнивают десятичные дроби с равными
целыми частями и одинаковым количеством
цифр после запятой?
Десятичные дроби с равными целыми
частями и одинаковым количеством
цифр после запятой сравнивают
поразрядно.
Какую дробь мы получим, если к данной
десятичной дроби припишем справа
несколько нулей?
Если к десятичной дроби справа
приписать любое количество нулей, то
получится дробь, равная данной.
Какую дробь мы получим, если у данной
десятичной дроби отбросим последние
нули её записи?
Если десятичная дробь оканчивается
нулями, то эти нули можно
отбросить, и при этом получится
дробь равная данной.
Сформулируйте правило сравнения двух
десятичных дробей с равными целыми
частями и различным количеством цифр
после запятой.
Чтобы сравнить две десятичные дроби с
равными целыми частями и различным
количеством цифр после запятой, нужно с
помощью приписывания нулей справа
уравнять количество цифр в дробных
частях, после чего сравнить полученные
дроби поразрядно.
Работа по учебнику
Письменно: № 323, 324, 325, 326
Устно: 329, 330, 331
Домашнее задание: п. 31, знать правила
сравнения десятичных дробей, № 348, 350

Сравнение десятичных дробей — определение, правила, примеры

Сравнение десятичных дробей означает нахождение большего и меньшего десятичного числа в данном наборе чисел. Десятичные числа можно сравнивать так же, как мы сравниваем другие числа. Однако нужно помнить, что цифры, которые ставятся после запятой, также необходимо учитывать. Эти цифры имеют разрядные значения, начинающиеся с десятых, за которыми следуют сотые, затем тысячные и так далее. Давайте узнаем больше о сравнении десятичных дробей в этой статье.

1.	Что такое сравнение десятичных дробей?
2.	Сравнение десятичных и дробных чисел
3.	Сравнение десятичных знаков в числовой строке
4.	Сравнение десятичных долей с сотыми долями
5.	Часто задаваемые вопросы о сравнении десятичных дробей

Что такое сравнение десятичных дробей?

Сравнение десятичных дробей аналогично сравнению других целых чисел, в которых мы начинаем сравнивать цифры с наибольшим разрядом. Помещаем заданные десятичные числа в таблицу стоимостных значений и начинаем сравнение. Если цифры на наибольшем разряде совпадают, мы переходим к цифрам на следующем месте справа. Мы продолжаем сравнивать цифры, пока не найдем цифры, которые отличаются. Давайте разберемся в этом с помощью следующего примера.

Пример: Сравните 0,64 и 0,362

Решение:

• Шаг 1: Сравните целую часть числа, которая является цифрой единиц. Если цифры совпадают, переходите к следующему шагу. В этом случае цифры единиц имеют 0 в обоих числах. Итак, переходим к следующему месту справа.
• Шаг 2: Сравните разряд десятых, то есть разряд справа от запятой. Когда мы сравниваем значение в десятом разряде, мы видим, что 6 больше, чем 3. На самом этом шаге мы узнаем, что 0,64 больше, чем 0,362. Поэтому нам не нужно переходить к сотым цифрам для дальнейшего сравнения.
• Шаг 3: Отсюда заключаем, что 0,64 > 0,362

Сравнение десятичных и дробных чисел

Когда нам нужно сравнить десятичные числа и дроби, мы сначала преобразуем данную дробь в десятичное число, а затем сравниваем числа, используя ту же процедуру.

Пример: Сравните 3/4 и 0,728

Решение: Сначала преобразуем 3/4 в десятичное число, разделив 3 на 4. Итак, 3 ÷ 4 = 0,75. Теперь у нас есть оба числа в десятичной форме. Итак, сравним 0,75 и 0,728 по приведенной выше методике.

• Шаг 1: Сравните целую часть числа, которая является цифрой единиц. В этом случае цифры единиц имеют 0 в обоих числах. Итак, мы перейдем к следующему значению разряда справа.
• Шаг 2: Сравните разряд десятых, который является первым разрядом справа от запятой. Когда мы сравниваем значение десятого разряда, мы видим, что оба числа имеют 7. Итак, мы переходим к сотому разряду.
• Шаг 3: Сравните сотые доли. Теперь, когда мы сравниваем значение в сотых долях, мы видим, что 5 больше, чем 2. На этом шаге мы узнаем, что 0,75 больше, чем 0,728. Поэтому нам не нужно переходить к разряду тысячных для дальнейшего сравнения.
• Шаг 3: Следовательно, мы заключаем, что 0,75 > 0,728, что означает 3/4 > 0,728

Сравнение десятичных знаков в числовой строке

Когда мы сравниваем десятичные дроби на числовой прямой, мы следуем основному правилу числовой строки, которое гласит, что по мере продвижения вправо значение чисел увеличивается. Например, если нам нужно сравнить 6,5 и 6,7, мы помечаем десятичные числа на числовой прямой таким образом, чтобы оба числа были включены.

Нам нужно сосредоточиться между 6 и 7, потому что оба заданных числа лежат между 6 и 7. Мы отмечаем 6 на левом конце и 7 на правом конце. Затем мы отмечаем все числа между ними в масштабе, записывая 6,5 посередине между 6 и 7. Отметив остальные десятые, мы видим, что 6,7 находится справа от 6,5, поэтому 6,5 < 6,7. Следовательно, можно сделать вывод, что 6,5 < 6,7, потому что 6,7 находится справа от 6,5 на числовой прямой.

Сравнение десятичных долей с сотыми долями

Мы уже видели, что мы сравниваем десятичные числа, начиная с целой части числа, а затем переходим к цифрам, указанным после запятой. Давайте посмотрим, как сравнивать десятичные дроби с сотыми долями.

Пример: Сравните 8,362 и 8,391, чтобы найти большее число.

Решение: Давайте проделаем те же шаги, что и выше.

• Шаг 1: Сравните целую часть числа. В этом случае целая часть числа имеет 8 в обоих числах. Итак, мы перейдем к следующему разряду.
• Шаг 2: Сравните разряд десятых, который является первым разрядом справа от запятой. Когда мы сравниваем значение десятого разряда, мы видим, что оба числа имеют 3. В этот момент мы переходим к сотому разряду.
• Шаг 3: Сравните сотые доли. Теперь, когда мы сравниваем значение в сотых долях, мы видим, что 9 больше, чем 6. Итак, мы узнаем, что 8,391 больше, чем 8,362. Поэтому нам не нужно переходить к разряду тысячных для дальнейшего сравнения.
• Шаг 3: Отсюда заключаем, что 8,362 < 8,391

Дополнительные ссылки

Ознакомьтесь со следующими страницами, посвященными сравнению десятичных дробей.

• Десятичные числа
• Десятичные числа и дроби
• Добавление десятичных знаков

 

Примеры сравнения десятичных дробей

1. Пример 1: Какое десятичное число больше: 5,612 или 5,071?

   Решение:

   Сравнение десятичных дробей начинается со сравнения целой части числа. Мы видим, что разряд единиц в обоих числах имеет одинаковое значение (5). Итак, мы переходим к разряду десятых, то есть 6 и 0 в соответствующих числах. На этом шаге мы можем сказать, что 5,612 больше, чем 5,071. Следовательно, 5,612 > 5,071

2. Пример 2: Сравните десятичные дроби от меньшего к большему: 17,102, 17,243 и 17,05

   Решение:

   Сравнение десятичных дробей от наименьшего к наибольшему означает упорядочивание чисел в порядке возрастания. Итак, когда мы начинаем сравнение с целой части числа, мы видим, что оно равно (17 во всех числах). Переходим к разряду десятых и обнаруживаем, что все числа разные, а среди 1, 2 и 0 наименьшее число — 0. Итак, 17,05 — наименьшее число среди этих. После этого сравниваем 17.102 и 17.243. Мы видим, что 17,102 < 17,243. Следовательно, данные числа можно расположить как 17,05, 17,102 и 17,243 в порядке от наименьшего к наибольшему.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

Часто задаваемые вопросы о сравнении десятичных дробей

Как сравнивать десятичные дроби?

Десятичные числа сравниваются так же, как мы сравниваем другие целые числа. Единственный момент, который следует помнить, это то, что нам также необходимо учитывать значения разрядов, указанные после десятичной точки. Эти разряды начинаются с десятых, затем следуют сотые, тысячные и так далее. Сначала мы сравниваем цифры до запятой. Если эти цифры равны, то переходим к сравнению цифр после запятой. Если они не равны, сравнение выполняется на самом этом шаге, и мы не продвигаемся дальше ни для какого сравнения. Другими словами, мы продолжаем сравнивать цифры справа до тех пор, пока не получим набор неравных цифр для сравнения.

Каковы правила сравнения десятичных дробей?

Существуют определенные правила сравнения десятичных дробей. Давайте разберемся в них с помощью следующего примера. Например, сравним 5,274 и 5,237

• Шаг 1: Сначала сравним целую часть числа. Если цифры совпадают, переходите к следующему шагу. В этом случае целая часть числа (цифра единиц) имеет 5 в обоих числах. Итак, переходим к следующему разрядному значению справа.
• Шаг 2: Сравните десятые доли, то есть цифру справа от запятой. Когда мы сравниваем значение десятого разряда, мы видим, что оба числа имеют 2. Итак, мы снова переходим к следующему разрядному значению, которое является сотым разрядом.
• Шаг 3: Сравните сотые доли. Теперь, когда мы сравниваем значение в сотых долях, мы видим, что 7 больше, чем 3. На самом этом шаге мы узнаем, что 5,274 больше, чем 5,237. Поэтому нам не нужно переходить к разряду тысячных для дальнейшего сравнения.
• Шаг 3: Отсюда заключаем, что 5,274 > 5,237

Как сравнивать десятичные дроби и дроби?

Когда нам нужно сравнить десятичные и дробные числа, мы сначала преобразуем данную дробь в десятичное число, а затем сравниваем их, используя ту же процедуру. Например, сравним 0,528 и 3/7. В этом случае мы преобразуем 3/7 в десятичное число, разделив 3 на 7. Итак, 3 ÷ 7 = 0,428. Теперь мы можем сравнить 0,428 и 0,528, потому что оба числа представлены в десятичной форме. Итак, мы начинаем сравнение с целой части числа, которая равна 0 в обоих числах. Итак, переходим к разряду десятых, который в обоих числах разный. На этом шаге мы можем сказать, что 0,528 больше, чем 0,428. Нам не нужно переходить к следующей цифре для дальнейшего сравнения. Следовательно, 3/7 < 0,528.

Как сравнивать десятичные дроби от наименьшего к наибольшему?

Сравнение десятичных дробей от наименьшего к наибольшему означает упорядочивание их в порядке возрастания, в котором сначала идет наименьшее число, а затем большее число. Например, давайте сравним заданный набор чисел от наименьшего к наибольшему. Приведены числа 1,002, 0,112, 1,102. Начнем сравнение с наибольшего разряда, в данном случае единиц. Итак, мы видим, что 0,112 имеет наименьшее значение в разряде единиц, а значит, это наименьшее число из всех, поэтому мы поместим его первым. Теперь мы сравним оставшиеся два числа, 1,002 и 1,102, в которых разряд единиц равен. Итак, мы сравниваем десятое место, которое равно 0 и 1 в соответствующих числах. Это показывает, что 1,002 — меньшее число. Итак, мы поместим его следующим номером в списке, за которым следует 1.102. Следовательно, данные числа можно расположить от меньшего к большему: 0,112, 1,002, 1,102.

Как сравнить десятичные дроби в числовой строке?

Когда мы сравниваем десятичные дроби на числовой прямой, мы следуем основному правилу числовой строки, которое гласит, что по мере продвижения вправо значение чисел увеличивается. Например, если нам нужно сравнить 4,3 и 4,7, мы помечаем десятичные числа на числовой прямой таким образом, чтобы оба числа были включены. Мы видим, что 4,7 находится справа от 4,3. Следовательно, 4,7 больше, чем 4,3

Как сравнивать десятичные дроби с сотыми?

Мы сравниваем десятичные дроби с сотыми долями, когда мы проверили все предшествующие разряды, то есть всю часть числа, и десятые доли. Если числа в этих местах равны, мы приходим к сотому месту для сравнения чисел. Давайте разберемся в этом на примере. Сравним 7.14 и 7.16

• Шаг 1: Сначала сравним целую часть числа. В этом случае целая часть числа имеет 7 в обоих числах. Итак, мы перейдем к следующему разряду.
• Шаг 2: Теперь, когда мы сравниваем десятые разряды, то есть первые разряды справа от запятой, мы обнаруживаем, что оба числа имеют 1. На этом этапе мы переходим к сотым разрядам.
• Шаг 3: Сравниваем сотые доли и видим, что 6 больше 4. Итак, мы узнаем, что 7,16 больше 7,14.
• Шаг 3: Отсюда заключаем, что 7,16 > 7,14

Как сравнить десятичные дроби с тысячными?

Сравнение десятичных долей с тысячными аналогично сравнению с сотыми. В этом случае, когда мы сравнили числа до разряда сотых и находим, что оба числа равны, мы приходим к разряду тысячных для сравнения. На этом месте, если цифры разные, мы можем сравнить числа и узнать большее число.

Скачать БЕСПЛАТНЫЕ учебные материалы

Сравнение десятичных дробей

Сравнение и упорядочивание десятичных дробей | Способы, примеры, определение

Что такое десятичные дроби?

Слово «десятичный» происходит от латинского слова «Decem», что означает 10. В алгебре десятичное число можно определить как число, полная и дробная части которого разделены десятичной точкой.

Десятичная система разрядов

Мы знаем, что каждое место в таблице разрядов имеет значение, в десять раз превышающее значение следующего справа от него места. Другими словами, ценность места составляет одну десятую ценности следующего места слева от него. Мы видим, что если одна цифра перемещается на одно место слева направо, ее значение становится одной десятой ($\frac{1}{10}$) ее предыдущего значения, а когда она перемещается на два места слева направо, ее значение становится на одну сотую ( $\frac{1}{100}$ ) своего предыдущего члена и так далее. Следовательно, если мы хотим выйти за пределы своего места, как в случае с десятичными дробями, нам придется расширить таблицу разрядов, введя разряды десятых ($\frac{1}{10}$ ), сотых ($\frac {1}{100}$ ), тысячные ( $\frac{1}{1000}$ ) и так далее.

Therefore, the place value table in case of a decimal number will be of the form –

11191111111119

Thousands ( 1000 )	Hundreds ( 100 )	Tens ( 10 )	Ones ( 1 )	Tenths ( $\frac{1}{10}$ )	Hundredths ( $ \ frac {1} {100} $ )	тысячи ( $ \ FRAC {1}	595)
	5)
403545)
403545)
	5)
	5)
	5)
	5)
) Например, десятичное число 257,32 в системе стоимости места будет записано как — 0007 3 Сотни TENS ОДИН Десятые сотни 2 5 2 70008 2 5 2 70007 2 2 2 2 Эту концепцию важно усвоить, так как перед сложением или вычитанием десятичные значения должны быть размещены в соответствии с их разрядными значениями. Теперь, давайте поймем, что мы подразумеваем под и в отличие от десятичных десятичных декораций , как и в отличие от десятичных десятиц Рассмотрим следующую группу десятичных десятичных 0,6, 0,98 Количество цифр справа от десятичной точки в числе называется количеством десятичных знаков. Десятичные дроби, имеющие одинаковое количество цифр справа от запятой, называются подобными десятичными дробями. Например, первая группа чисел выше — это группа одинаковых десятичных знаков. Точно так же десятичные дроби, имеющие разное количество цифр справа от запятой, называются похожими десятичными дробями. . Например, вторая группа чисел выше — это группа непохожих десятичных знаков. Можно ли преобразовать непохожие десятичные числа в подобные десятичные? Давайте узнаем. Преобразование непохожих десятичных дробей в одинаковые десятичные дроби Рассмотрим два непохожих десятичных дроби 3,5 и 4,75. Здесь важно отметить, что первое десятичное число 3,5 имеет одну цифру после запятой, а второе десятичное число 4,75 имеет две цифры после запятой. Чтобы преобразовать эти непохожие десятичные дроби в одинаковые десятичные дроби, у нас должно быть два десятичных разряда в числе 3.5. Мы знаем, что добавление нуля справа от крайних правых цифр в десятичной части числа не меняет его значения. Следовательно, 3,5 можно записать как 3,50 Итак, 3,50 и 4,75 подобны десятичным дробям. Таким образом, мы можем преобразовать разные десятичные числа в одинаковые десятичные числа, добавив нули справа от десятичной точки или найдя их эквивалентные десятичные числа. Как представляются десятичные числа в числовой строке? Теперь, когда мы знаем, что такое десятичные числа и что такое числовая строка, давайте перейдем к представлению десятичного числа в числовой строке. Представление десятичных чисел в числовой строке определяется как отображение десятичных чисел в числовой строке. Важным аспектом десятичных дробей, который необходимо понимать для нанесения их на числовую прямую, является то, что десятичные дроби располагаются между двумя целыми числами. Давайте разберемся на примере. Возьмем два числа 0 и 1 и проведем между ними числовую прямую. У нас будет, Далее, давайте разделим пробел между 0 и 1 на десятые доли. У нас будут дробные значения, такие как одна десятая, две десятых, три десятых и так далее. Его можно представить на числовой прямой следующим образом. Теперь мы знаем, что Одна десятая = 0,1 Две десятых = 0,2 Три десятых = 0,3 и так далее. Следовательно, если мы хотим представить вышеуказанные десятые значения в виде десятичных знаков, у нас будет  Кроме того, если мы хотим изобразить десятичное число, скажем, 0,6, мы пометим его как В приведенном выше примере у нас было простое десятичное число, и его было довольно легко построить. Но мы знаем, что в соответствии с разрядной системой десятичных знаков у нас есть десятичные числа, такие как одна десятая ($\frac{1}{10}$), одна сотая ($\frac{1}{100}$), один -тысячная ( $\frac{1}{1000}$ ) и т. д., так как же мы будем отображать эти числа? Представление десятых долей в числовой строке Мы уже знаем, как представлять дроби в числовой строке. Теперь представим десятые доли десятичной дроби на числовой прямой. Но, вспомним, что мы подразумеваем под десятыми долями? Рассмотрим следующий рисунок. Он разделен на десять равных частей и одна часть заштрихована. Заштрихованная часть представляет одну десятую всей фигуры. Записывается как $\frac{1}{10}$. $\frac{1}{10}$ также записывается как 0,1, что читается как «единица с запятой» или «десятичная единица». Таким образом, дробь $\frac{1}{10}$ называется одной десятой и записывается как 0,1. Теперь представим десятые доли на числовой прямой. Мы можем понять это на примере. Представим 0,4 на числовой прямой. Мы ясно видим, что в 0,4 содержится 4 десятых. Поэтому, чтобы представить 0,4 на числовой прямой, мы разделим единицу длины между 0 и 1 на 10 равных частей и возьмем 4 части, как показано ниже — Теперь мы знаем, что 0,4 в дробной форме равно 4/ 10. Следовательно, мы отметим 4/10 как 0,4, что является нашей желаемой отметкой на числовой прямой. Представление сотых в числовой строке Теперь представим сотые доли десятичного числа в числовой строке. Но, давайте вспомним, что мы понимаем под сотыми долями после запятой? Если предмет разделить на 100 равных частей, то каждая часть составляет одну сотую целого. Это означает, что – Одна тысячная = $\frac{1}{100}$ что в десятичной форме равно 0,01 Если из 100 равных частей объекта отнять 7 частей, то 7 частей составляют $\frac {7}{100}$ от целого и записывается как 0,07. Теперь представим сотые доли на числовой прямой. Мы можем понять это на примере. Представим тысячное значение числа 7,45 на числовой прямой. Чтобы представить 7,4 на числовой прямой, мы сначала проводим 10 линий, делящих общее расстояние между 7 и 8 на 10 равных частей. Мы видим, что стрелка находится на четыре части правее целого числа 7. Точно так же, чтобы представить 7,45 на числовой прямой, мы сначала проводим 10 линий, делящих общее расстояние между 7,4 и 7,5 на 10 равных частей. Представление тысячных в числовой строке Теперь представим тысячные доли десятичного числа в числовой строке. Но, давайте вспомним, что мы подразумеваем под тысячными долями после запятой? Если предмет разделить на 1000 равных частей, то каждая часть составляет одну тысячную целого. Это означает, что – Одна тысячная = $\frac{1}{1000}$ что в десятичной форме равно 0,001 Если из 1000 равных частей объекта отнять 7 частей, то 7 частей составляют $\frac {7}{1000}$ от целого и записывается как 0,007. Теперь представим тысячные на числовой прямой. Мы можем понять это на примере. Представим тысячное значение числа 7,456 на числовой прямой. Чтобы представить 7,4 на числовой прямой, мы сначала проводим 10 линий, делящих общее расстояние между 7 и 8 на 10 равных частей. Мы видим, что стрелка находится на четыре части правее целого числа 7. Точно так же, чтобы представить 7,45 на числовой прямой, мы сначала проводим 10 линий, делящих общее расстояние между 7,4 и 7,5 на 10 равных частей. Мы видим, что стрелка находится на пять частей правее десятичного числа 7,40. Далее, чтобы представить 7,456 на числовой прямой, мы сначала проводим 10 линий, делящих общее расстояние между 7,45 и 7,46 на 10 равных частей. Мы видим, что стрелка находится на шесть частей правее десятичного числа 7,45 Таким образом, мы представили число 7,456 на числовой прямой. Как сравнивать десятичные дроби? Для сравнения десятичных чисел необходимо выполнить следующие шаги – Получить десятичные числа. Далее мы будем сравнивать целые части чисел. Число с большей целой частью будет больше. Если все части равны, мы переходим к следующему шагу. Теперь сравним крайние левые цифры десятичных частей заданных десятичных чисел. Если крайние левые цифры десятичной части равны, то сравниваются следующие цифры и так далее. Давайте разберемся на примере. Пример Предположим, мы хотим сравнить десятичные числа 48,23 и 39,35 Если мы проделаем описанные выше шаги, то ясно увидим, что данные десятичные дроби состоят из разных частей целого числа. Это означает, что мы можем сравнивать только части целых чисел. В десятичном числе 48,23 целая часть числа равна 48 Аналогично, в десятичном числе 39,35 целая часть числа равна 39 Теперь мы знаем, что 48 > 39 Следовательно, 39,23 > 39,23.35 Возьмем другой пример. Пример Предположим, мы хотим сравнить десятичные числа 0,58 и 0,84. что нам придется сравнивать десятичные части. Теперь проверим, что крайние левые цифры в десятичных частях 0,58 и 0,84 равны 5 и 8 соответственно. Кроме того, 5 < 8 Следовательно, 0,58 < 0,84 Использование числовой прямой для сравнения десятичных дробей Мы можем использовать числовую прямую для сравнения десятичных дробей. Давайте разберемся на примере. Пример Обозначьте пропущенные десятичные числа в числовой строке и сравните их Нам даны четыре числа, отмеченные как A , B , C и D в числовой строке, и нам нужно выяснить, какие десятичные числа они представлять. Давайте отметим их один за другим. Начнем с завершения разметки строк, которые не были отмечены на данной числовой строке. Хорошо видно, что между двумя целыми числами на числовой прямой 10 линий. Это означает, что линии представляют одну десятую числа в десятичной форме. Поэтому строки между 7 и 8 будут помечены как  7 . 1 , 7 . 2 , 7 . 3 , 7 . 4 , 7  5 , 7 . 6 , 7 . 7 , 7 . 8 и d 7. 9. Аналогично, между целыми числами 8 и 9 у нас есть 8 . 1 , 8 . 2 , 8 . 3 , 8 . 4 , 8 . 5 , 8 . 6 , 8 . 7 , 8 . 8 и 8 . 9. Полученная таким образом числовая прямая будет –  . Теперь мы проверим положение четырех точек на этой числовой прямой. Из числовой строки выше видно, что точка А лежит на десятичном числе 8,7. Следовательно, А = 8. 7 Теперь давайте проверим положение точки B.  Мы видим, что из числовой строки выше точка B лежит на десятичном числе 8.2. Следовательно, В = 8. 2 Теперь давайте проверим положение точки C.  Мы видим, что из числовой строки выше точка C лежит на десятичном числе 7 . 1. Следовательно, С = 7. 1 Теперь давайте проверим положение точки D.  Из числовой строки выше видно, что точка D лежит на десятичном числе 7 . 8 . Следовательно, D = 7 . 8 Следовательно, имеем A = 8 . 7 В = 8 . 2 С = 7 . 1 Д = 8 . 8 Теперь мы знаем, что числа на числовой прямой увеличиваются слева направо. Следовательно, мы будем иметь, 7.1 < 8.2 < 8.7 < 8.8 Как расставить десятичные дроби по порядку? Теперь, когда мы научились сравнивать десятичные дроби, давайте научимся расставлять их по порядку.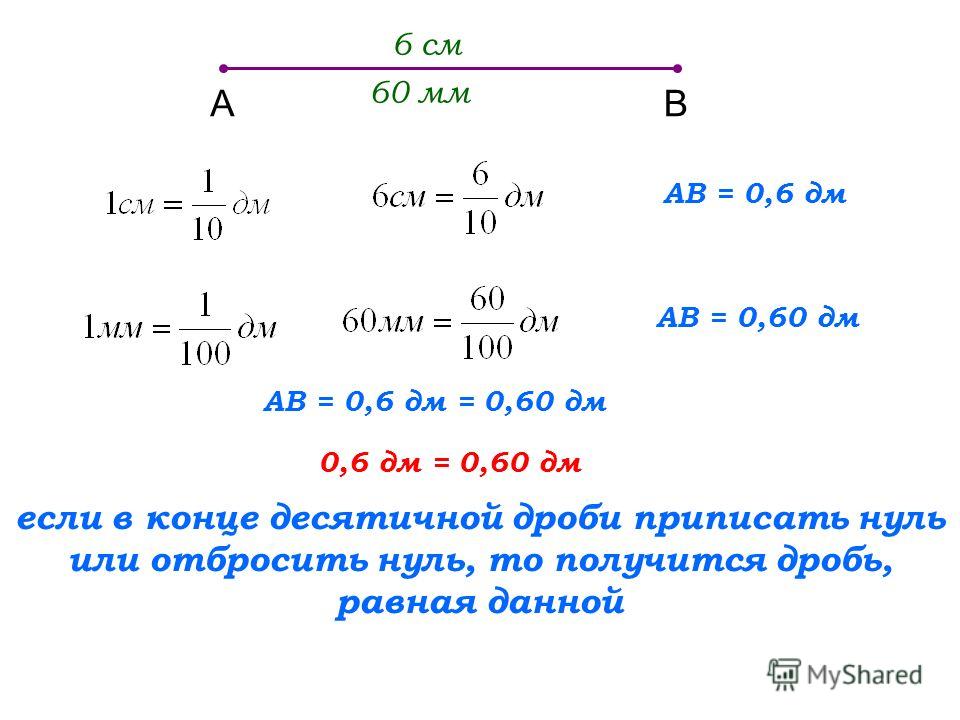 говоря, как расположить их по порядку, имеется в виду, что расположить их в порядке возрастания или в порядке убывания. Напомним, что восходящий порядок означает размещение чисел от наименьшего к наибольшему, а убывающий порядок означает размещение чисел от наибольшего к наименьшему порядку. Давайте посмотрим, как расположить десятичные числа по порядку. Мы можем использовать следующие шаги, чтобы расположить десятичные числа по порядку –  На первом этапе мы создали таблицу с десятичной точкой в ​​одном и том же месте для каждого числа. Теперь заполним пустые места нулями. Далее мы сравниваем десятичные числа, используя первый столбец слева. Если цифры равны, мы переходим к следующему столбцу справа. Чтобы разместить десятичные дроби в порядке возрастания, мы сначала выбираем наименьшее число, а если мы хотим расположить десятичные дроби в порядке убывания, мы выбираем наибольшее число. Давайте разберемся на примере. Пример Предположим, мы хотим расположить следующие десятичные дроби в порядке возрастания – 1,307, 1,36 и 0,7 Выполним для этой цели описанные выше шаги – На первом этапе мы создадим таблицу с десятичной точкой в ​​одном и том же месте для каждого числа. Итак, у нас будет 9. Единицы Десятичная точка 3 0 7 1 . 3 6 0 . 7 Теперь заполним пустые места нулями. У нас будет Единицы Десятичная точка Десятые доли Сотые доли Тысячные доли 1 1 . 3 0 7 1 . 3 6 0 0 . 7 0 0 Далее мы сравниваем десятичные числа, используя первый столбец слева. Мы видим, что два из них — «1», а другой — «0». В порядке возрастания сначала нужно наименьшее, поэтому мы сначала выберем «0». Так мы получим первое число 0,7 и удалим его из списка. Теперь сравним десятые. Мы видим, что для десятого значения «3» есть два значения. Итак, мы перейдем к сотому значению. Мы видим, что у нас есть «0» и «6» в сотом значении. Теперь 0 < 6, следовательно, 1,30 < 1,36 Таким образом, следующие числа по порядку будут 1,30, 1,36. Следовательно, порядок десятичных знаков по возрастанию будет 0,7 < 1,30 < 1,36 Ключевые факты и сводка точка. Местная система значений — это система, в которой позиция  цифры в числе определяет его значение. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт