Средние величины. Виды средних величин
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. ТЕМА: 5
СРЕДНИЕ ВЕЛИЧИНЫСредняя величина
это
обобщающий показатель,
характеризующий уровень или размер
варьирующего признака в расчёте
на единицу однородной совокупности
в конкретных условиях места и времени.
1. Средняя величина должна исчисляться
лишь для совокупности, состоящих из
Однородных единиц
4.

величину
целесообразно
исчислять не для
отдельных
единичных
фактов, взятых
изолировано друг
от
друга, а для
совокупности
фактов.
Условия
правильного
применения
средней
величины
2. Если совокупность
не однородной, то
необходимо
разделять ее на
однородные группы
и вычислять для
них групповые
типичные средние,
характеризующие
каждую из этих групп,
и в этом проявляется
связь между методом
группировок и
средних
величин.
3. Средняя величина сглаживает индивидуальные значения изучаемого
признака и тем самым может элиминировать различные тенденции в
развитии, скрыть передовое и отстающее, по этому Креме
средней величины следует исчислять и другие показатели.
виды средних величин
Степенные
средние величины
Структурные средние
величины
мода
средняя арифметическая величина
простой и взвешенной.
средняя гармоническая величина
простой и взвешенной
медиана
Квартили
Децили
средняя геометрическая величина
простой и взвешенной
средняя квадратическая величина
простой и взвешенной
Квинталы
Перцентили
Основные элементы средней степенной
величины
Варианта (X)
Это
варьирующий
признак,
для
которого
исчисляется
средняя
величина
Число единиц (n) Веса, частоты (f)
Это
Количество
вариантов
в
изучаемой
совокупности
Это
показатели
Повторяемости
Вариант в
изучаемой
совокупности
Типы средней степенной величины
Средняя степенная величина
простой
X
m
X
n
где x – это значение
варьирующего признака;
n – число единиц
совокупности;
m – показатель средней
степени.

Средняя степенная величина
взвешенная
m
X F
F
m
X m
показывающие, сколько раз
повторяется каждая варианта
признака.
Средняя арифметическая
Средняя арифметическая
простая
Средняя арифметическая
взвешенная
Средняя арифметическая
простая используется в тех
случаях, когда расчет
осуществляется по не
сгруппированным данным и
определяется по формуле:
Средняя арифметическая
взвешенная применяется
когда расчет проводиться по
сгруппированным данным или
по вариационным рядом, которые
могут быть дискретными или
интервальными и
Определяется по формуле:
X
X
n
i
X
X F
F
i
i
i
При наличии вариационного
непрерывного ряда распределения как с
равными так и с неравными
интервалами.
То для вычисления средней
арифметической взвешенной, находится
среднее значение каждого интервала,
как полусуммы его верхней и нижней
границы.
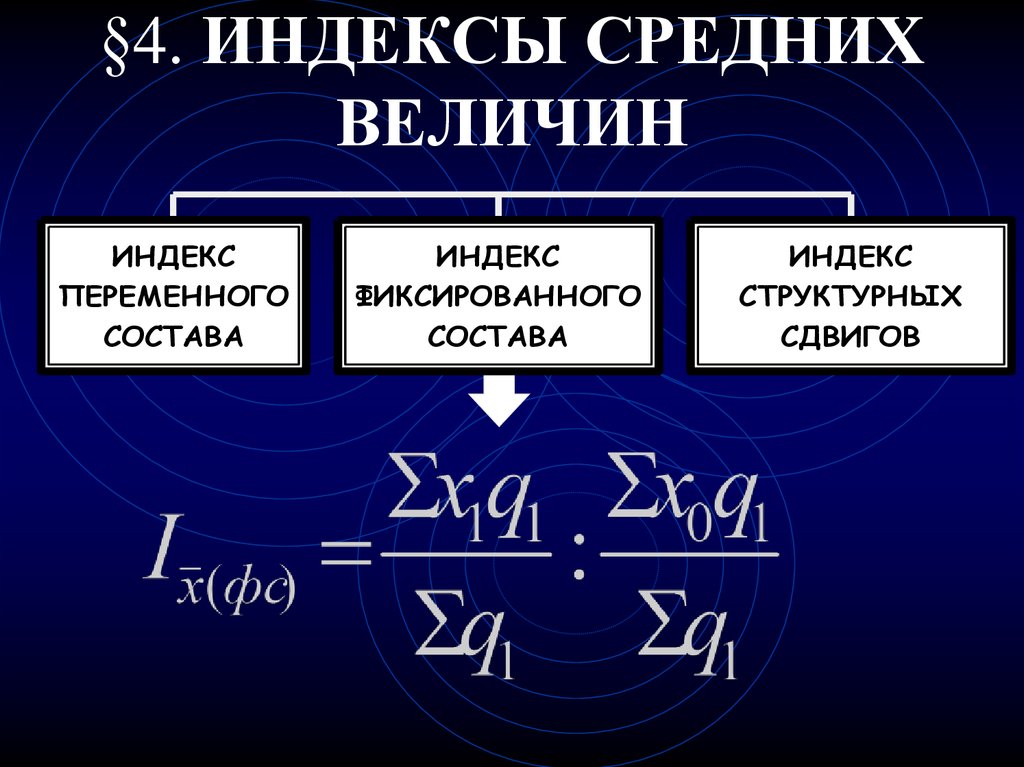
Эти средние значения интервалов
являются новыми значениями
вариантов, подлежащими усреднению.
Средняя гармоническая
Средняя гармоническая простая
Используется когда
статистическая информация не
содержит частот по отдельным
вариантов совокупности и когда
результаты произведения этих
вариантов на эти частоты везде
одинакова.
Определяется по формуле
X
n
1
X
Средняя гармоническая взвешенная
Используется когда в качестве весов
используются не единицы
совокупности, т.е. носители признака,
а произведения этих единиц на
значения признака (m=X*F), и когда
результаты произведения значения
признака на количество единиц
неодинаково.
X
m
m
X
Средняя геометрическая
Средняя геометрическая простая
Средняя геометрическая взвешенная
Применяются для определения средней величины
Простая
X X
n
либо
X n X1 X 2 .
 .. X n
.. X nВзвешенная
X
F
X
F
либо
F
F1
F2
X X X 2 … X
1
Fn
n
Средняя квадратическая
Средняя квадратическая простая
Средняя квадратическая взвешенная
Применяются, когда в место индивидуальных значений признака
представлены квадраты исходных величин
X 2
X
n
2
X F
F
2
X 2
Следует отметить, что средние квадратические,
кубические, биквадратические и т.д. имеют ограниченное
применение на практике в статистике.
Правило мажорантности средних величин
Предполагает строго определенные соотношения
Между разными видами средних величин
В частности:
Х гарманическая Х геометрическая Х арифметическая Х квадратическая
Исчисление средней величины способом
момента первого порядка
Средняя величина способом момента
первого порядка исчисляется при наличии
непрерывного вариационного ряда
распределения с равными интервалами и
определяется по формуле:
X m1 h
А — середина центрального интервала;
h – это ширина интервала;
m1 — это момент первого порядка.

Xi
h Fi
m1
Fi
Средняя структурная величина: Мода
Это
вариант, который чаще всего, встречается в изучаемой совокупности.
В вариационном дискретном ряду модой выступает вариант,
имеющий наибольшую частоту.
В интервальном ряду мода Определяется по формуле:
FМо FМо 1
Mо X 0 h
FМо FМо 1 FМо FМо 1
X 0 — нижняя граница модального интервала;
h – ширина модального интервала;
Fm — частота модального интервала;
Fm 1 — частота интервала, предшествующего модальному интервалу;
Fm 1- частота интервала – следующего за модальные.
это
вариант, который находится в середине ранжированного
вариационного ряда.
Медиана делит ряд пополам, где по обе стороны находится
одинаковое количество единиц совокупности.
В интервальном ряду медиана определяется по формуле:
F
Mе X 0 h
2
S Ме 1
FМе
Где X 0 — нижняя граница медианного интервала;
h – ширина медиана интервала;
F — сумма частот ряда;
S me 1 — сумма накопленных частот в интервалах, предшествующих медианному;
Fme — частота медианного интервала.

Квартили
значения признака, делящие ранжированную интервальный
ряд на четыре равные части
Нижний квартиль
Нижний квартиль отделяющий ¼
Часть совокупности с наименьшими
Значениями признака.
Q1 xQ1 hQ1
1
F S Q1 1
4
FQ1
Верхний квартиль
Верхний квартиль, отсекающий ¼
Часть с наибольшими значениями
Признака.
Q3 xQ 3 hQ 3
3
F S Q 3 1
4
FQ 3
гдеХ Q1 ( X Q3 ) нижняя граница интервала,
содержащег о нижний (вверхний) квартиль;
SQ1 -1 ( S Q3 1 ) накопленная частота интервала, предшествующего интервалу,
содержащем у нижний квартиль (вверхний) квартиль;
f Q1 ( f Q3 ) частота интервала, содержащег о нижний квартиль (вверхний) квартиль.
Децили
Значения признака, делящие ранжированный
Интервальный ряд на десять равных частей
Нижний дециль
d1 x d1 hd1
1
F S d1 1
10
Fd1
d 9 x d 9 hd 9
Верхний дециль
9
F S d 9 1
10
Fd 9
Квинтили
Значения признака, делящие интервальный ряд
На пять равных частей.

Квинтили вычисляются по той же схеме, что
квартили и децили.
Перцентили
Значения признака, делящие интервальный
English Русский Правила
ЛЕКЦИЯ №5. Средние величины и показатели вариации. Общая теория статистики: конспект лекции
ЛЕКЦИЯ №5. Средние величины и показатели вариации
1. Средние величины и общие принципы их исчисления
Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака. Для выяснения сущности средней величины необходимо рассмотреть особенности формирования значений признаков тех явлений, по данным которых исчисляют среднюю величину.
Известно, что единицы каждого массового явления обладают многочисленными признаками. Какой бы из этих признаков не был взят, его значения у отдельных единиц будут различными, они изменяются, или, как говорят в статистике, варьируют от одной единицы к другой.
Средняя величина отражает то общее, что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень (или размер) любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное для всех единиц изучаемой совокупности, которое и отражается в средней величине.
В совокупности индивидуальные значения признаков сливаются в общую массу и как бы растворяются. Отсюда и средняя выступает как «обезличенная» величина, которая может отклоняться от индивидуальных значений признаков, не совпадая количественно ни с одним из них. Таким образом, средняя отражает общее, характерное и типичное для всей совокупности благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц, так как ее величина определяется как бы общей равнодействующей из всех причин.
Однако для того чтобы средняя отражала наиболее типичное значение признака, она должна определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних и метода группировок в анализе социально-экономических явлений.
Следовательно, средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Определяя таким образом сущность средних величин, необходимо подчеркнуть, что правильное исчисление любой средней предполагает выполнение следующих требований:
1) качественная однородность совокупности, по которой исчислена средняя. Исчисление средней для разнокачественных (разнотипных) явлений противоречит самой сущности средней, так как развитие таких явлений подчиняется разным, а не общим закономерностям и причинам. Это означает, что исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;
Это означает, что исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;
2) исключение влияния на исчисление средней величины случайных, сугубо индивидуальных причин и факторов. Это достигается в том случае, когда исчисление средней основывается на достаточно массовом материале, в котором проявляется действие закона больших чисел, и все случайности взаимно погашаются;
3) при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показатель (свойство), на который она должна быть ориентирована. Определяющий показатель может выступать в виде суммы значений осредняемого признака, суммы его обратных значений, произведения его значений и т. п. Связь между определяющим показателем и средней выражается в следующем: если все значения осредняемого признака заменить их средним значением, то сумма или произведение в этом случае не изменят определяющего показателя. На основе этой связи определяющего показателя со средней величиной строят исходное количественное отношение для непосредственного расчета средней величины. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.
Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.
Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, – групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.
Способы расчета могут быть разные, и в связи с этим в статистике различают несколько видов средней величины, основными из которых являются средняя арифметическая, средняя гармоническая и средняя геометрическая.
В экономическом анализе использование средних величин является действенным инструментом для оценки результатов научно-технического прогресса, социальных мероприятий, изыскания скрытых и неиспользуемых резервов развития экономики.
В то же время следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.
Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.
Данный текст является ознакомительным фрагментом.
Глава 24 Прострация от экстраполяции Использовать средние показатели цены/прибыли – глупо
Глава 24 Прострация от экстраполяции Использовать средние показатели цены/прибыли – глупо Чтобы средние исторические показатели были полезны, данные, на основе которых они вычисляются, должны происходить из той же совокупности. В ином случае – если данные происходят из
ЛЕКЦИЯ № 15. Экономическое развитие Руси в средние века
ЛЕКЦИЯ № 15. Экономическое развитие Руси в средние века
1. Причины и последствия феодальной раздробленности. Рост феодального землевладения
Период политической раздробленности наступил в XII – XV вв. Это закономерный исторический этап в развитии феодализма. Одной из
Экономическое развитие Руси в средние века
1. Причины и последствия феодальной раздробленности. Рост феодального землевладения
Период политической раздробленности наступил в XII – XV вв. Это закономерный исторический этап в развитии феодализма. Одной из
23. Средние величины и общие принципы их исчисления
23. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количе–ства индивидуальных
26. Показатели вариации
26. Показатели вариации
Вариационными называют ряды распределени построенные по количественному признаку. Значени количественных признаков у отдельных единиц сов купности непостоянны, более или менее различают между собой. Такое различие в величине признака н сит
Такое различие в величине признака н сит
54. Средние показатели динамики
54. Средние показатели динамики С течением времени изменяются не только уров–ни явлений, но и показатели их динамики – абсолют–ные приросты и темпы развития. Поэтому для обоб–щающей характеристики развития, для выявления и измерения типичных основных тенденций и
ЛЕКЦИЯ № 4. Статистические величины и показатели
ЛЕКЦИЯ № 4. Статистические величины и показатели 1. Назначение и виды статистических показателей и величин Природа и содержание статистических показателей соответствуют тем экономическим и социальным явлениям и процессам, которые их отражают. Все экономические и
1. Средние величины и общие принципы их исчисления
1. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений
3.
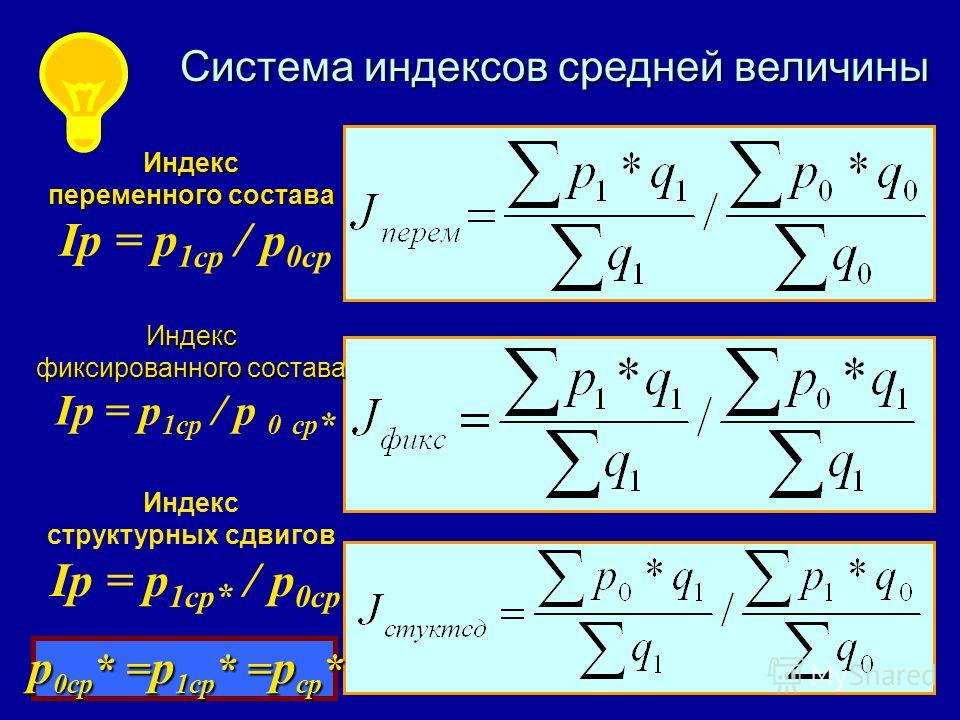 Показатели вариации
Показатели вариации3. Показатели вариации Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения. Различают два типа рядов
3. Средние показатели динамики
3. Средние показатели динамики С течением времени изменяются не только уровни явлений, но и показатели их динамики – абсолютные приросты и темпы развития. Поэтому для обобщающей характеристики развития, для выявления и измерения типичных основных тенденций и
59. Относительные и средние величины
59. Относительные и средние величины
Экономический анализ начинается по своей сути с исчисления величины относительной. Относительные величины незаменимы при анализе явлений динамики. Понятно, что эти явления можно выразить и в абсолютных величинах, но доходчивость,
Понятно, что эти явления можно выразить и в абсолютных величинах, но доходчивость,
31. Структурные средние величины. Мода и медиана
31. Структурные средние величины. Мода и медиана Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.Мода (Мо) – чаще всего встречающийся вариант.Модой называется
Правило № 5: улучшай свои средние показатели
Правило № 5: улучшай свои средние показатели Работая в страховом бизнесе, я понимал, что каждый раз, снимая трубку и разговаривая с любым клиентом, зарабатываю 30 долларов. Однако пятеро клиентов на каждые десять звонков казались мне не самым лучшим показателем, поскольку
ЛЕКЦИЯ № 7. Средние величины
ЛЕКЦИЯ № 7. Средние величины
1. Общая характеристика
В целях анализа и получения статистических выводов по результатом сводки и группировки исчисляют обобщающие показатели – средние и относительные величины.Задача средних величин – охарактеризовать все единицы
Средние величины
1. Общая характеристика
В целях анализа и получения статистических выводов по результатом сводки и группировки исчисляют обобщающие показатели – средние и относительные величины.Задача средних величин – охарактеризовать все единицы
3. Структурные средние величины. Мода и медиана
3. Структурные средние величины. Мода и медиана Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.Мода (Мо ) – чаще всего встречающийся вариант. Модой называется
ЛЕКЦИЯ № 8. Показатели вариации
ЛЕКЦИЯ № 8. Показатели вариации 1. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным
Средние показатели поведенческого профиля индивидуума
Средние показатели поведенческого профиля индивидуума
Усредненные показатели всегда скрывают различия. Предыдущие графики показывают среднее поведение команд продавцов и средний уровень поведенческих ожиданий и ценностей группы клиентов. На рис. 14.5 стиль продаж
Предыдущие графики показывают среднее поведение команд продавцов и средний уровень поведенческих ожиданий и ценностей группы клиентов. На рис. 14.5 стиль продаж
Средняя величина в статистике. Средние величины
Каждый человек в современном мире, планируя взять кредит или делая запасы овощей на зиму, периодически сталкивает с таким понятием, как «средняя величина». Давайте узнаем: что это такое, какие ее виды и классы существуют и зачем она применяется в статистике и других дисциплинах.
Средняя величина — это что такое?
Подобное название (СВ) носит обобщенная характеристика совокупности однородных явлений, определяемая по какому-либо одному количественному варьируемому признаку.
Однако люди далекие, от столь заумных определений, понимают это понятие, как среднее количество чего-то. Например, прежде чем взять кредит, сотрудник банка обязательно попросит потенциального клиента предоставить данные о среднем доходе за год, то есть общую сумму зарабатываемых человеком средств. Она вычисляется путем суммирования заработанного за весь год и разделения на количество месяцев. Таким образом, банк сможет определить, сумеет ли его клиент отдать долг в срок.
Она вычисляется путем суммирования заработанного за весь год и разделения на количество месяцев. Таким образом, банк сможет определить, сумеет ли его клиент отдать долг в срок.
Зачем она используется?
Как правило, средние величины широко применяются для того, чтобы дать итоговую характеристику определенных общественных явлений, носящих массовый характер. Также они могут быть использованы для менее масштабных расчетов, как в случае с кредитом, в приведенном выше примере.
Однако чаще всего средние величины все же применяются для глобальных целей. В качестве примера одного из них можно привести вычисление количества потребляемой гражданами электроэнергии на протяжении одного календарного месяца. На основе полученных данных в дальнейшем устанавливаются максимальные нормы для категорий населения, пользующихся льготами от государства.
Также с помощью средних величин разрабатывается гарантийный срок службы тех или иных бытовых приборов, автомобилей, зданий и т. п. На основе собранных таким способом данных когда-то были разработаны современные нормы труда и отдыха.
Фактически любое явление современной жизни, носящее массовый характер, тем или иным образом обязательно связано с рассматриваемым понятием.
Сферы применения
Данное явление широко применяется практически во всех точных науках, особенно носящих экспериментальный характер.
Поиск среднего значения величины имеет огромное значение в медицине, инженерных дисциплинах, кулинарии, экономике, политике и т. п.
Основываясь на данных, полученных от подобных обобщений, разрабатывают лечебные препараты, учебные программы, устанавливают минимальные прожиточные минимумы и зарплаты, строят учебные графики, производят мебель, одежду и обувь, предметы гигиены и многое другое.
В математике данный термин именуется «средним значением» и применяется для осуществления решений различных примеров и задач. Наиболее простыми из них являются сложение и вычитание с обычными дробями. Ведь, как известно, для решения подобных примеров необходимо привести обе дроби к общему знаменателю.
Также в царице точных наук часто применяется близкий по смыслу термин «значение среднее случайной величины». Большинству он более знаком как «математическое ожидание», чаще рассматриваемое в теории вероятности. Стоит отметить, что подобное явление также применяется и при произведении статистических вычислений.
Средняя величина в статистике
Однако чаще всего изучаемое понятие используется в статистике. Как известно, эта наука сама по себе специализируется на вычислении и анализе количественной характеристики массовых общественных явлений. Поэтому средняя величина в статистике используется в качестве специализированного метода достижения ее основных задач — сбора и анализа информации.
Суть данного статистического метода заключается в замене индивидуальных уникальных значений рассматриваемого признака определенной уравновешенной средней величиной.
В качестве примера можно привести знаменитую шутку о еде. Итак, на неком заводе по вторникам на обед его начальство обычно ест мясную запеканку, а простые рабочие – тушеную капусту. На основе этих данных можно сделать вывод, что в среднем коллектив завода по вторникам обедает голубцами.
На основе этих данных можно сделать вывод, что в среднем коллектив завода по вторникам обедает голубцами.
Хотя данный пример слегка утрирован, однако он иллюстрирует главный недостаток метода поиска средней величины – нивелирование индивидуальных особенностей предметов или личностей.
В статистике, данные средних величин применяются не только для анализа собранной информации, но и для планирования и прогнозирования дальнейших действий.
Также с его помощью производится оценка достигнутых результатов (например, выполнение плана по выращиванию и сбору урожая пшеницы за весенне-летний сезон).
Как правильно рассчитать
Хотя в зависимости от вида СВ существуют разные формулы ее вычисления, в общей теории статистики, как правило, применяется всего один способ расчета средней величины признака. Для этого нужно сначала сложить вместе значения всех явлений, а затем разделить получившуюся сумму на их количество. При произведении подобных вычислений стоит помнить, что средняя величина всегда имеет ту же размерность (или единицы измерения), что и отдельная единица совокупности.
Условия правильного вычисления
Рассмотренная выше формула весьма проста и универсальна, так что ошибиться в ней практически невозможно. Однако всегда стоит учитывать два аспекта, иначе полученные данные не будут отражать реальную ситуацию.
- Искомые индивидуальные значения (на основе которых вычисляются средние) всегда должны относиться к однородной совокупности, а количество их должно быть значительным.
В вышеупомянутой шутке мясная запеканка и капуста – относятся к одной категории – «еда». Однако если бы нужно было узнать, сколько килограмм капусты хранится в столовой завода, учитывать данные о мясе не было бы смысла, так как в данном случае они не относились бы к рассматриваемой однородной совокупности.
- В любом индивидуальном случае важно брать во внимание качественное содержания признака, среднюю величину которого необходимо рассчитать. При этом важно обращать внимание на взаимосвязь между изучаемыми признаками и имеющиеся для вычислений данные.

Классы СВ
Найдя ответы на основные вопросы: «Средняя величина — это что такое?», «Где применяется она?» и «Как можно вычислить ее?», стоит узнать, какие классы и виды СВ существуют.
Прежде всего это явление делится на 2 класса. Это структурные и степенные средние величины.
Виды степенных СВ
Каждый из вышеперечисленных классов, в свою очередь, делится на виды. У степенного класса их четыре.
- Средняя арифметическая величина – это наиболее распространенный вид СВ. Она являет собою среднее слагаемое, при определении коего общий объем рассматриваемого признака в совокупности данных поровну распределяется между всеми единицами данной совокупности.
Этот вид делится на подвиды: простая и взвешенная арифметическая СВ.
- Средняя гармоническая величина – это показатель, обратный средней арифметической простой, вычисляемый из обратных значений рассматриваемого признака.
Она применяется в тех случаях, когда известны индивидуальные значения признака и произведение, а данные частоты — нет.

- Средняя геометрическая величина чаще всего применима при анализе темпов роста экономических явлений. Она дает возможность сохранять в неизменном виде произведение индивидуальных значений данной величины, а не сумму.
Также бывает простой и взвешенной.
- Средняя квадратическая величина используется при расчете отдельных показателе показателей, таких как коэффициент вариации, характеризующего ритмичность выпуска продукции и т. п.
Также с ее помощью вычисляются средние диаметры труб, колес, средние стороны квадрата и подобных фигур.
Как и все остальные виды средних СВ, среднеквадратическая бывает простой и взвешенной.
Виды структурных величин
Помимо средних СВ, в статистике довольно часто используются структурные виды. Они лучше подходят для расчета относительных характеристик величин варьирующего признака и внутреннего строения рядов распределения.
Таких видов существует два.
- Мода. Данный вид чаще всего используется для определения наиболее популярных у покупателей размеров одежды и обуви.

Как правило, мода вычисляется по такой формуле.
В ней М0 – является значением моды, х0 – нижней границей интервала модального, h – величиной рассматриваемого интервала, fm – его частотой, fm-1 – частотой предшествующего модальному интервалу и fm+1 – частотой следующего. - Медианой именуется значение признака, лежащее в основе ранжированного ряда и делящее его на две части, равные между собою по численному показателю.
В формулах, данный вид обозначается, как Ме.
В зависимости от того в каком ряду определяется данный вид структурной СВ (дискретный или интервальный вариационный), применяются различные формулы его вычисления.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Пробег Тыс. км. | 4,8 | 5,1 | 5,1 | 6,5 | 6,5 | 6,5 | 6,5 | 7,0 | 7,0 | 7,0 | Число авто |
4,8 | 1 | |||||||||
5,1 | 2 | |||||||||
6,5 | 4 | |||||||||
7,0 | 3 | Число автомашин в данной группе | ||||||||
До 5,0 | 40 | |||||||||
5,0 — 7,0 | 80 | |||||||||
7,0 — 8,0 | 130 | |||||||||
8,0 и более | 50 | |||||||||
Итого | 300 | Середина интервала, тыс. км | Число автомашин | |||||||
До 5,0 | 4,0 | 40 | ||||||||
5,0-7,0 | 6,0 | 80 | ||||||||
7,0-8,0 | 7,5 | 130 | ||||||||
8,0 и более | 8,5 | 50 | Себестоимость одной детали Х, р | Затраты на всю партию деталей М, р | ||||||
1 | 1,8 | 180 | ||||||||
2 | 2,0 | 400 | ||||||||
3 | 2,3 | 165 | Число предприятий | Товарная продукция предприятия тыс. грн | ||||||
0,15 | 5 | 200 | ||||||||
0,2 | 7 | 460 | ||||||||
0,3 | 4 | 600 | ||||||||
Итого | 16 | 1260 |
|
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
⇐ ПредыдущаяСтр 9 из 35Следующая ⇒ Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимым инструментом анализа явлений и процессов в экономике. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Так, если мы рассчитаем средний курс по акциям всех предприятий, реализуемых в данный день на данной бирже, то получим фиктивную среднюю. На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу: ИСС = Суммарное значение признака / число единиц или объем совокупности Способы расчета средних величин. Простые и взвешенные средние. Порядок применения взвешенных средних. Количественные значения признаков, характеризующих единицы совокупности, могут варьироваться под влиянием разнообразных условий (факторов), одни из которых являются общими (типичными) для всех этил единиц, другие — индивидуальными (нетипичными) Применение средних величин как раз и позволяет количественно определить наиболее типичные признаки массовых явлений. Таким образом, средняя величина — это обобщающий показатель, характеризующий количественное значение признака в результате абстрагирования от его индивидуальных различий. Для правильного исчисления средних должна быть взята качественно однородная совокупность. «Средняя величина, — подчеркивал К. Маркс, — есть всегда средняя многих различных индивидуальных величин одного и того же вида»1. Приведенная формула используется в том случае когда значение признака у каждой единицы встречается лишь один раз. В тех случаях, когда статистическая совокупность представлена в сгруппированном виде и каждое значение признака, называемого вариантой, имеет свою частоту повторения (вес), то применяется средняя арифметическая взвешенная. Величина средней зависит не только от величины вариант, но и от величины их частот. Чем меньшие частоты имеют большие значения вариант, тем меньше величина средней, и наоборот. В статистике достаточно часто встречаются случаи, когда необходимо рассчитать среднюю по формуле средней гармонической, которая представляет собой величину, обратную средней арифметической. Среднюю гармоническую применяют в тех случаях, когда в качестве весов выступает сумма произведений осредняемого признака на частоту его повторения. Основной для применения рекомендуется экспоненциальная скользящая средняя. Способ построения простых скользящих средних («Moving Average — MA) сводится к формуле простой арифметической средней: МА = (Сумма цен за период времени) / порядок средней. ⇐ Предыдущая45678910111213Следующая ⇒
|
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 285. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда… |
Средние величины и показатели вариации
Средние величины и показатели вариации.
Понятие о средней величине
Средние величины используются
на этапе обработки и обобщения
полученных первичных статистических
данных. Потребность определения
средних величин связана с
тем, что у различных единиц исследуемых совокупностей индивидуальные
значения одного и того же признака, как
правило, неодинаковы.
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя. Например, для групп работников определенной отрасли с фиксированным уровнем дохода определяется типическая средняя расходов на предметы первой необходимости, т.е. типическая средняя обобщает качественно однородные значения признака в данной совокупности, каковым является доля расходов у работников данной группы на товары первой необходимости.
При исследовании совокупности с качественно
разнородными признаками на первый план
может выступить нетипичность средних
показателей. Такими, к примеру, являются
средние показатели произведенного национального
дохода на душу населения (разные возрастные
группы), средние показатели урожайности
зерновых культур по всей территории России
(районы разных климатических зон и разных
зерновых культур), средние показатели
рождаемости населения по всем регионам
страны, средние температуры за определенный
период и т. д. Здесь средние величины обобщают
качественно разнородные значения признаков
или системных пространственных совокупностей
(международное сообщество, континент,
государство, регион, район и т.д.) или динамических
совокупностей, протяженных во времени
(век, десятилетие, год, сезон и т.д.). Такие
средние величины называют системными средними.
д. Здесь средние величины обобщают
качественно разнородные значения признаков
или системных пространственных совокупностей
(международное сообщество, континент,
государство, регион, район и т.д.) или динамических
совокупностей, протяженных во времени
(век, десятилетие, год, сезон и т.д.). Такие
средние величины называют системными средними.
Таким образом, значение средних величин состоит в их обобщающей функции. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами.
Виды средних величин
Используются две категории средних величин: степенные средние; структурные средние.
Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.
Вторая категория (структурные
средние) — это мода и
медиана.
Введем следующие условные обозначения:
— величины, для которых исчисляется средняя;
— средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
— частота (повторяемость
Различные средние выводятся из
общей формулы степенной
при k = 1 — средняя арифметическая; k = -1 — средняя гармоническая; k = 0 — средняя геометрическая; k = -2 — средняя квадратическая.
Средние величины бывают простые и взвешенные.
Средняя арифметическая — самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Формула средней арифметической (простой) имеет вид
где n — численность совокупности.
При расчете средних
величин отдельные значения признака,
который осредняется, могут повторяться,
поэтому расчет средней величины производится по
сгруппированным данным. В этом случае
речь идет об использовании средней арифметической
взвешенной, которая имеет вид
В этом случае
речь идет об использовании средней арифметической
взвешенной, которая имеет вид
Средняя гармоническая. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы:
В статистической практике чаще используется гармоническая взвешенная:
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста).
Для простой средней геометрической
Для взвешенной средней геометрической
Показатели вариации
Для измерения вариации
признака используют как абсолютные,
так и относительные
Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:
Среднее линейное
отклонение d, которое вычисляют для того, чтобы учесть
различия всех единиц исследуемой совокупности.
Формула среднего линейного отклонения (простая)
Формула среднего линейного отклонения (взвешенная)
Среднее квадратическое отклонение: (простое)
Среднее квадратическое отклонение (взвешенное)
Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.
Формулы дисперсии взвешенной и простой :
Средний калькулятор
, созданный Mateusz Lighta
, рассмотренная Jack Bowater
Последнее будет вычислять среднее значение до тридцати чисел. Интересным аспектом калькулятора является то, что вы можете видеть, как среднее значение изменяется по мере ввода дополнительных значений. Прежде чем использовать калькулятор, вы должны знать, как рассчитать среднее значение, на тот случай, если у вас нет интернета и вы не можете получить доступ к этому калькулятору. Обратите внимание, что среднее значение совпадает со средним значением, и эти термины могут использоваться взаимозаменяемо.
Как вычислить среднее значение
Среднее значение набора чисел — это просто сумма чисел, деленная на общее количество значений в наборе. Например, предположим, что нам нужно среднее значение 24 , 55 , 17 , 87 и 100 . Просто найдите сумму чисел: 24 + 55 + 17 + 87 + 100 = 283 и разделите на 5 , чтобы получить 56,6 . Простую задачу, подобную этой, можно решить вручную без особых проблем, но для более сложных чисел, включающих много знаков после запятой, удобнее использовать этот калькулятор. Обратите внимание, что калькулятор среднего рейтинга выполняет аналогичную математику — он вычисляет средний рейтинг, учитывая количество голосов со значениями от 1 до 5.
Аналогичные концепции, связанные со средними значениями
Калькулятор средневзвешенного значения позволяет присвоить вес каждому числу. Взвешивание числа является показателем его важности. Распространенным типом вычисляемого средневзвешенного значения является средний балл успеваемости (GPA). Чтобы сделать это вручную, выполните следующие действия:
Распространенным типом вычисляемого средневзвешенного значения является средний балл успеваемости (GPA). Чтобы сделать это вручную, выполните следующие действия:
- Умножьте значение буквенной оценки на количество кредитов в классе.
- Сделайте это для всех классов и подсчитайте сумму.
- Разделите сумму на общее количество кредитов.
Предположим, что оценки представляют собой A для кредитного класса 3 , две B для кредитного класса 4 и C для кредитного класса 2 . Используя стандартное значение 4 для A, 3 для B и 2 для C, средний балл составляет GPA = [4(3) + 3(4) + 3(4) + 2(2)]/(3 + 4 + 4 + 2) = 40/13 = 3,08
Обратите внимание, что калькулятор среднего вычисляет среднее значение для всех значений с одинаковым весом. Для средневзвешенного, такого как GPA и других статистических приложений, калькулятор средневзвешенного значения, указанный выше, является инструментом, который вы хотите использовать. В статистике среднее значение известно как мера центральной тенденции.
В статистике среднее значение известно как мера центральной тенденции.
Часто задаваемые вопросы
Каковы 4 средние значения?
Четыре средних значения — это среднее значение, медиана, мода и диапазон . Среднее значение — это то, что вы обычно считаете средним значением , найденное путем суммирования всех значений и деления суммы на количество значений. Медиана — это среднее значение набора (или среднее двух средних значений, если набор четный). Режим** — это фрагмент данных, который встречается чаще всего**, а диапазон — это разница между самым высоким и самым низким значениями . Чтобы рассчитать все эти и другие средние значения, воспользуйтесь Калькулятором среднего среднего режима.
Почему мы считаем среднее?
Мы рассчитываем средние значения, потому что они очень полезны для представления большого количества данных . Вместо того, чтобы просматривать сотни или тысячи фрагментов данных, у нас есть одно число, которое кратко суммирует весь набор . Хотя со средними значениями возникают некоторые проблемы, такие как выбросы, показывающие неточное среднее значение, они полезно сравнивать данные с первого взгляда .
Хотя со средними значениями возникают некоторые проблемы, такие как выбросы, показывающие неточное среднее значение, они полезно сравнивать данные с первого взгляда .
Почему средние значения вводят в заблуждение?
Средние значения могут вводить в заблуждение по ряду причин . Они лучше всего представляют равномерно распределенные колоколообразные кривые , где большинство результатов находится в середине и мало на концах. Но даже одна очень крайняя точка может резко изменить среднее , поэтому эти аномалии часто исключаются, но не всегда. Далее, человека склонны интерпретировать средние значения как идеальные репрезентации 9.0074, что приводит к отсутствию желания разбираться в нюансах данных. Наконец, средние значения часто используются для предсказания отдельных случаев, которые часто бывают крайне неточными .
Как рассчитать средний балл?
- Умножьте каждую оценку на кредиты или вес, присвоенный ей .
 Если ваши оценки не взвешены, пропустите этот шаг.
Если ваши оценки не взвешены, пропустите этот шаг. - Сложите вместе все взвешенные оценки (или только оценки, если взвешивания нет).
- Разделите полученную сумму на количество сложенных оценок.
- Проверьте свой результат с помощью калькулятора среднего балла колледжа.
Как рассчитать средневзвешенное значение?
- Умножьте каждое число на его вес .
- Сложите все взвешенные числа вместе.
- Разделите сумму на количество точек данных.
- Проверьте свой результат с помощью калькулятора среднего веса.
Среднее лучше режима?
нет простого ответа на вопрос, лучше ли среднее значение, чем режим — это полностью зависит от данных установленных перед вами. Если данные распределены нормально, не имеют выбросов, то вам, вероятно, следует использовать среднее значение , так как оно представит вам наиболее репрезентативное значение. Однако режим является более надежным и будет представлять наиболее распространенное значение независимо от каких-либо выбросов. Этот режим следует всегда использовать с категориальными данными, т. е. данными с отдельными группами, поскольку группы не являются непрерывными.
Однако режим является более надежным и будет представлять наиболее распространенное значение независимо от каких-либо выбросов. Этот режим следует всегда использовать с категориальными данными, т. е. данными с отдельными группами, поскольку группы не являются непрерывными.
Как рассчитать средний процент в Excel?
Хотя проще использовать Omni Average Calculator, для расчета среднего процента в Excel:
- Введите нужные данные, например, из ячеек с A1 по A10.
- Выделите все ячейки, щелкните правой кнопкой мыши и выберите Формат ячеек .
- В поле Format Cells под Number выберите Percentages и укажите желаемое количество знаков после запятой.
- В другой ячейке введите =СРЗНАЧ(ячейка 1, ячейка 2,…) . В нашем примере это будет =СРЗНАЧ(A1:A10).
- Наслаждайтесь своим средним результатом!
Можете ли вы усреднить средние значения?
Вы можете усреднять средние значения, но это часто очень неточно и должно быть сделано осторожно.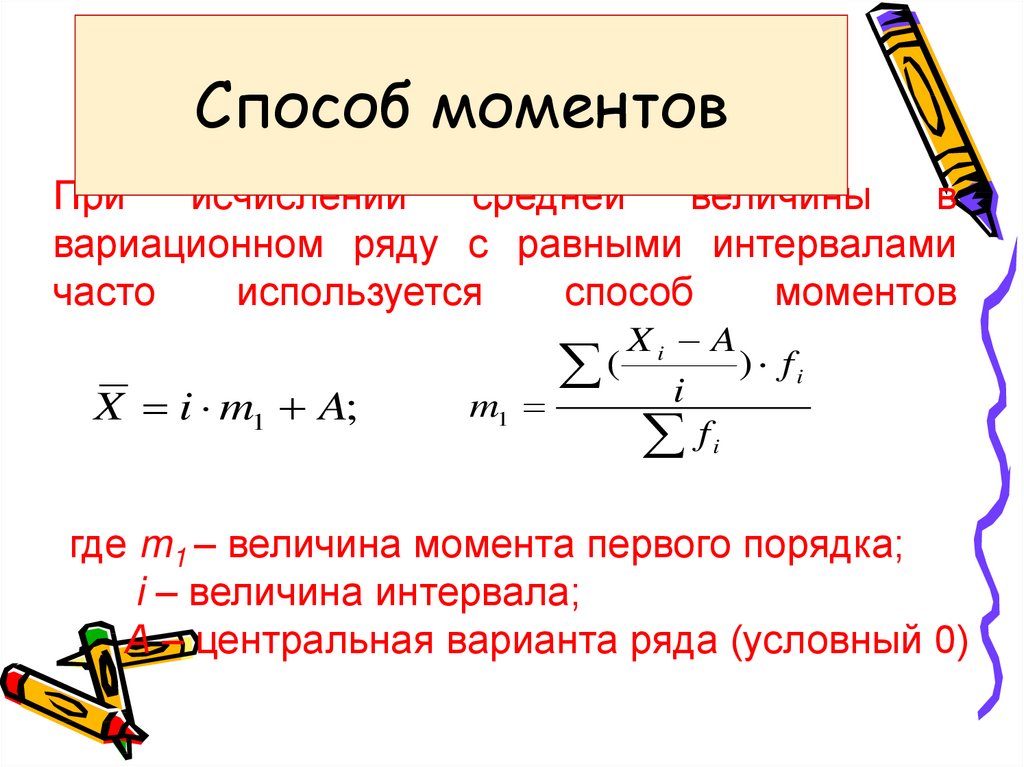 Допустим, у вас есть две страны: одна с населением 10 миллионов человек и ВВП 30 000 долларов, а другая с населением 10 000 человек и ВВП 2 000 долларов. Средний ВВП на страну составляет 16 000 долларов США, а средний ВВП на человека составляет ~ 30 000 долларов США, оба совершенно разные фигуры, показывающие совершенно разные вещи — так что будьте осторожны.
Допустим, у вас есть две страны: одна с населением 10 миллионов человек и ВВП 30 000 долларов, а другая с населением 10 000 человек и ВВП 2 000 долларов. Средний ВВП на страну составляет 16 000 долларов США, а средний ВВП на человека составляет ~ 30 000 долларов США, оба совершенно разные фигуры, показывающие совершенно разные вещи — так что будьте осторожны.
Что лучше, среднее или медиана?
Следует ли вам использовать среднее значение или медиану, зависит от данных, которые вы анализируете . Если данные нормально распределены, не имеют выбросов, то вам, вероятно, следует использовать среднее значение , хотя значение будет очень похоже на значение медианы. Если данные сильно искажены, следует использовать медиану , так как на нее меньше влияют выбросы.
Является ли среднее значение точным?
Среднее из средних неточно — большую часть времени . Данные могут быть вводящими в заблуждение из-за двух основных факторов, скрытых переменных и средневзвешенных . Скрытые переменные — это то место, где при усреднении средних значений теряется часть информации, которая обеспечивает более глубокое понимание рассматриваемой темы. Другая проблема заключается в том, что не взвешивает средние значения, когда это необходимо . Если, скажем, количество людей, посещающих сайт, меняется каждый месяц, если не учитывать количество людей, информация будет потеряна.
Скрытые переменные — это то место, где при усреднении средних значений теряется часть информации, которая обеспечивает более глубокое понимание рассматриваемой темы. Другая проблема заключается в том, что не взвешивает средние значения, когда это необходимо . Если, скажем, количество людей, посещающих сайт, меняется каждый месяц, если не учитывать количество людей, информация будет потеряна.
Матеуш Муха
Значения (можно ввести до 50 чисел)
Ознакомьтесь с 32 похожими калькуляторами справочника журналиста Excel
Формулы и функции
Формулы
Формулы
Вычислить среднее значение группы чисел
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно… Меньше
Предположим, вы хотите найти среднее количество дней, затрачиваемое на выполнение задачи разными сотрудниками. Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.
Или вы хотите рассчитать среднюю температуру в определенный день за 10-летний период времени. Существует несколько способов вычисления среднего значения группы чисел.
Функция СРЗНАЧ измеряет центральную тенденцию, которая является положением центра группы чисел в статистическом распределении. Тремя наиболее распространенными мерами центральной тенденции являются:
Среднее Это среднее арифметическое, которое рассчитывается путем сложения группы чисел и последующего деления на количество этих чисел. Например, среднее число 2, 3, 3, 5, 7 и 10 равно 30, делённому на 6, что равно 5.
Медиана Среднее число группы чисел. Половина чисел имеют значения больше медианы, а половина чисел имеют значения меньше медианы.
 Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.
Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.Режим Самое часто встречающееся число в группе чисел. Например, режим 2, 3, 3, 5, 7 и 10 равен 3.
Для симметричного распределения группы чисел все эти три меры центральной тенденции одинаковы. При асимметричном распределении группы чисел они могут быть разными.
Сделайте следующее:
Щелкните ячейку ниже или справа от чисел, для которых вы хотите найти среднее значение.
На вкладке Главная в группе Редактирование щелкните стрелку рядом с Автосумма , выберите Среднее и нажмите клавишу ВВОД.

Для выполнения этой задачи используйте функцию СРЗНАЧ . Скопируйте приведенную ниже таблицу на пустой рабочий лист.
Формула | Описание (Результат) |
=СРЕДНЕЕ(A2:A7) | Усредняет все числа в списке выше (9.5) |
=СРЕДНЕЕ(A2:A4,A7) | Усредняет первые три и последний номер в списке (7.5) |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например, ячейка A6 (11. |
Для выполнения этой задачи используйте функции СУММПРОИЗВ и СУММ . vВ этом примере вычисляется средняя цена, уплаченная за единицу по трем покупкам, где каждая покупка предназначена для разного количества единиц по разной цене за единицу.
Скопируйте приведенную ниже таблицу на пустой рабочий лист.
|
|
Для выполнения этой задачи используйте функции СРЗНАЧ и ЕСЛИ . Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Скопируйте приведенную ниже таблицу и помните, что этот пример может быть легче понять, если вы скопируете его на пустой лист.
Формула | Описание (Результат) |
=СРЗНАЧЕСЛИ(A2:A7, «<>0″) | Усредняет числа в списке, кроме тех, которые содержат ноль, например ячейка A6 (11.4) |
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
СРЕДНИЙ
СРЕДНЕЕСЛИ
СУММА
СУММПРОДУКТ
Разница между средним и средним
Среднее и среднее похожи, но различны. Среднее значение представляет собой сумму всех чисел, деленную на общее количество значений в наборе. Термин «среднее» означает нахождение среднего значения выборочных данных. Среднее значение находит центральное значение в математике, тогда как среднее значение находит центральное значение в статистике. Мы используем среднее, когда разница между значениями меньше, тогда как для набора значений, которые имеют большую разницу, мы предпочитаем находить среднее значение данных.
Среднее значение представляет собой сумму всех чисел, деленную на общее количество значений в наборе. Термин «среднее» означает нахождение среднего значения выборочных данных. Среднее значение находит центральное значение в математике, тогда как среднее значение находит центральное значение в статистике. Мы используем среднее, когда разница между значениями меньше, тогда как для набора значений, которые имеют большую разницу, мы предпочитаем находить среднее значение данных.
| 1. | Определение среднего |
| 2. | Определение среднего |
| 3. | Разница между средним и средним значением |
| 4. | Часто задаваемые вопросы о разнице между средним и средним значением |
Определение среднего
Среднее по определению представляет собой среднее арифметическое суммы всех значений, деленное на общее количество значений в заданном наборе.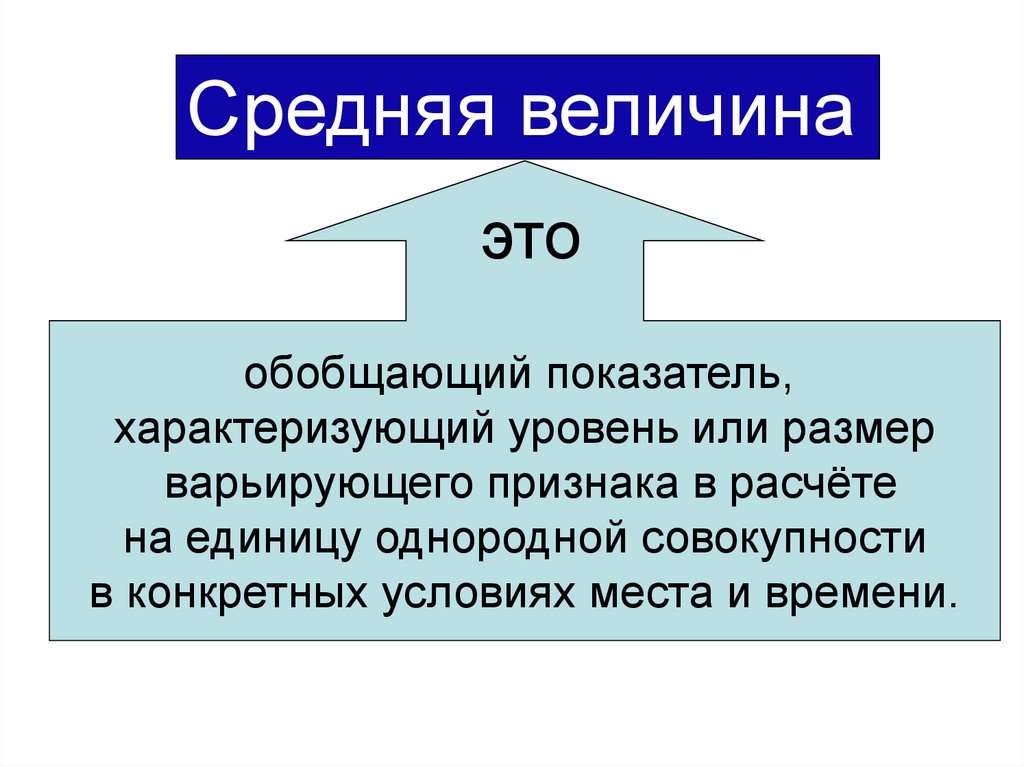 Среднее значение рассчитывается для тех наборов значений, которые более или менее одинаковы. Термин «среднее» описывает числовое значение, которое представляет большой объем данных. Среднее может быть получено путем вычисления отношения суммы всех значений к количеству единиц или значений.
Среднее значение рассчитывается для тех наборов значений, которые более или менее одинаковы. Термин «среднее» описывает числовое значение, которое представляет большой объем данных. Среднее может быть получено путем вычисления отношения суммы всех значений к количеству единиц или значений.
Давайте рассмотрим пример, чтобы лучше понять среднее: формула для нахождения среднего: сумма чисел/количество единиц
сумма чисел = 3 + 6 +14 + 18 + 20 + 35 + 44 = 140
количество единиц = 7
Следовательно, среднее = сумма числа/количество единиц
= 140/7
= 20
Следовательно, среднее значение набора чисел равно 20.
Определение среднего
Среднее значение — это математический термин, описывающий среднее значение выборки. В статистике определение среднего аналогично среднему, где оно представляет собой сумму всех заданных значений данных, деленную на общее количество значений данных, заданных в наборе. Среднее значение вычисляется для тех наборов значений, которые либо имеют большую разницу, либо те значения, которые близки друг к другу. Среднее значение имеет и другие формы, такие как среднее гармоническое и среднее геометрическое, которые используются в разных ситуациях.
Среднее значение имеет и другие формы, такие как среднее гармоническое и среднее геометрическое, которые используются в разных ситуациях.
Разница между средним и средним значением
Математически среднее и среднее похожи друг на друга, поскольку они используются для объяснения набора чисел. Ниже перечислены ключевые средние и средние значения, которые объясняют разницу в формате таблицы.
| Среднее | Среднее |
|---|---|
| Среднее можно определить как сумму всех чисел, деленную на общее количество значений. | Среднее можно определить как среднее значение набора значений в выборке данных. |
| Другими словами, среднее значение также называют средним арифметическим. | Описание среднего называется средним. Есть еще 2 вида среднего — гармоническое и среднее геометрическое. |
Среднее значение рассчитывается для набора чисел из одного диапазона значений. | Среднее в основном используется в статистике, где набор значений сильно различается или тесно связан друг с другом. |
| Среднее значение представляет собой одно число из списка чисел. | Среднее значение является центральной точкой среди набора чисел. |
| Среднее значение используется в повседневной жизни как разговор на английском языке. | Использование среднего значения рассматривается в основном в техническом и математическом смысле. |
| Через среднее мы также можем узнать значения медианы и моды. | С другой стороны, среднее не дает медиану и моду, хотя все три — среднее, медиана и мода тесно взаимодействуют в статистике. |
Связанные темы
Ниже перечислены несколько тем, связанных с разницей между средним и средним значением.
- Среднее значение, медиана и мода
- Среднее арифметическое
- Статистика
Важные моменты
- Среднее значение любого числового ряда или группы всегда находится между наименьшим и наибольшим значением.

- Среднее значение используется в повседневных расчетах, тогда как среднее значение в основном используется в статистике при решении математических задач.
Примеры разницы между средним и средним
Пример 1: Учащийся получил следующие оценки за тесты: 82, 93, 79 и 69. Он хочет получить в целом 75 или выше. Какую минимальную оценку он должен получить на последнем тесте, чтобы получить этот средний балл?
Решение:
Нам нужно узнать минимальную оценку, сложив все полученные оценки и разделив ее на количество оценок. Поскольку у нас нет результатов последнего теста, давайте воспользуемся переменной «x» для определения среднего значения.
(82 + 93 + 79 + 69 + х)/5 = 75
Переносим пятерку на другую сторону и умножаем 5 на 75.
82 + 93 + 79 + 69 + х = 375
323 + x = 375
x = 375 — 323
x = 52
Следовательно, учащийся должен набрать не менее 52 баллов за последний тест.

Пример 2: Найдите среднее значение для следующих данных: 45, 76, 2, 10, 33.
Решение:
Дан список 45, 76, 2, 10, 33
Среднее = Сумма наблюдений/общее количество наблюдений
= (45 + 76 + 2 + 10 + 33)/ 5
= 166/5
= 33,2
Следовательно, среднее значение для следующего списка равно 33,2
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы о разнице между средним и средним
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о разнице между средним и средним значением
В чем разница между средним и средним?
Среднее, также называемое средним арифметическим, представляет собой сумму всех значений, деленную на количество значений. Принимая во внимание, что среднее значение — это среднее значение в данных. В статистике среднее значение равно общему количеству наблюдений, деленному на количество наблюдений.
Принимая во внимание, что среднее значение — это среднее значение в данных. В статистике среднее значение равно общему количеству наблюдений, деленному на количество наблюдений.
Как рассчитать среднее и среднее?
Среднее значение — это среднее число, и для вычисления как среднего, так и среднего нам нужно сложить все значения, а затем разделить на общее количество значений. Другими словами, это сумма значений, деленная на количество значений. Формулы для обоих более или менее одинаковы. Среднее = Среднее = Сумма/счет
Всегда ли среднее отвечает взаимностью как среднее?
Поскольку и среднее, и среднее похожи, да, среднее обычно соответствует среднему. Среднее также называется средним арифметическим, а среднее — это среднее значение выборочных данных.
Какова формула среднего значения?
Среднее значение = сумма наблюдений/количество наблюдений. Например, среднее 2,5,7,9 и 7 равно 30, деленному на 5, что равно 6.
Почему среднее называется средним?
Среднее можно определить как среднее значение набора значений в выборке данных.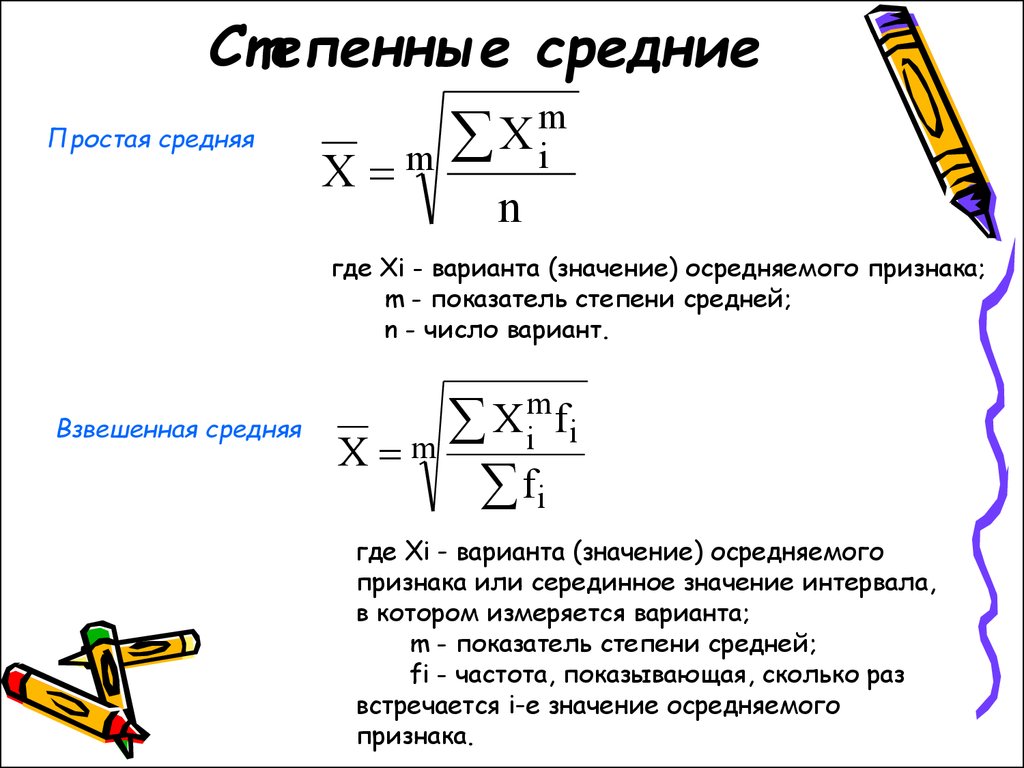 Среднее значение называется суммой всех значений, деленной на общее количество значений. В математике слова «среднее» и «среднее» связаны, но имеют свои отличия, как упоминалось в этой статье.
Среднее значение называется суммой всех значений, деленной на общее количество значений. В математике слова «среднее» и «среднее» связаны, но имеют свои отличия, как упоминалось в этой статье.
Среднее и среднее взаимозаменяемы?
Да, чаще всего среднее и среднее используются взаимозаменяемо. В статистике вместо слова «среднее» используется слово «среднее». Это, как правило, создает путаницу, поскольку основное значение слов «средний» и «средний» одинаково.
Скачать БЕСПЛАТНЫЕ учебные материалы
Разница между средним и средним
Средняя стоимость заказа — Optimizely
Оптипедия
- А
- Б
- С
- Д
- Е
- Ф
- грамм
- ЧАС
- я
- Дж
- К
- л
- М
- №
- О
- п
- Вопрос
- р
- С
- Т
- U
- В
- Х
- Y
- Z
Что такое средняя стоимость заказа (AOV)?
Средняя стоимость заказа (AOV) отслеживает среднюю сумму в долларах, потраченную каждый раз, когда клиент размещает заказ на веб-сайте или в мобильном приложении. Чтобы рассчитать среднюю стоимость заказа вашей компании, просто разделите общий доход на количество заказов.
Чтобы рассчитать среднюю стоимость заказа вашей компании, просто разделите общий доход на количество заказов.
Например, предположим, что в сентябре объем продаж вашего интернет-магазина составил 31 000 долларов США, и у вас было в общей сложности 1000 заказов. 31 000 долларов разделить на 1 000 = 31 доллар, поэтому месячная AOV в сентябре составила 31 доллар.
AOV — это ключевой показатель эффективности, который онлайн-компании измеряют, чтобы понять покупательские привычки своих клиентов. Как и другие ключевые показатели, AOV можно отслеживать за любой период времени, но большинство компаний отслеживают скользящее среднемесячное значение.
Почему средняя стоимость заказа имеет значение?
Зная среднюю стоимость заказа вашей компании, вы сможете оценить свои общие маркетинговые усилия в Интернете и стратегию ценообразования, предоставив вам показатели, необходимые для измерения долгосрочной ценности отдельных клиентов.
В качестве эталона поведения клиентов AOV помогает вам устанавливать цели и стратегии и оценивать, насколько хорошо эти стратегии работают.
Иногда маркетологи сосредотачивают большую часть своей энергии на увеличении посещаемости веб-сайта, когда было бы более эффективным и прибыльным увеличить их AOV. Увеличение трафика обычно стоит денег, а увеличение AOV — нет.
Поскольку каждый заказ связан с транзакционными издержками, увеличение AOV — это способ увеличить прямой доход и увеличить вашу прибыль, когда клиенты уже покупают в вашем магазине.
7 советов по увеличению средней стоимости заказа (AOV)
Существует ряд стратегий, которые могут увеличить среднюю стоимость заказа. Эти стратегии, по сути, представляют собой разные способы заставить вашего клиента тратить больше, либо покупая больше продуктов, чем они изначально планировали, либо покупая более дорогие продукты, чем они изначально планировали.
Оптимизация AOV может происходить на всех этапах воронки продаж. Вы можете подтолкнуть своего клиента к покупке дополнительных товаров, связанных с тем, что находится в его корзине, возможно, тех, о которых легко забыть, например, батарейки для электронного устройства или лампочки для лампы.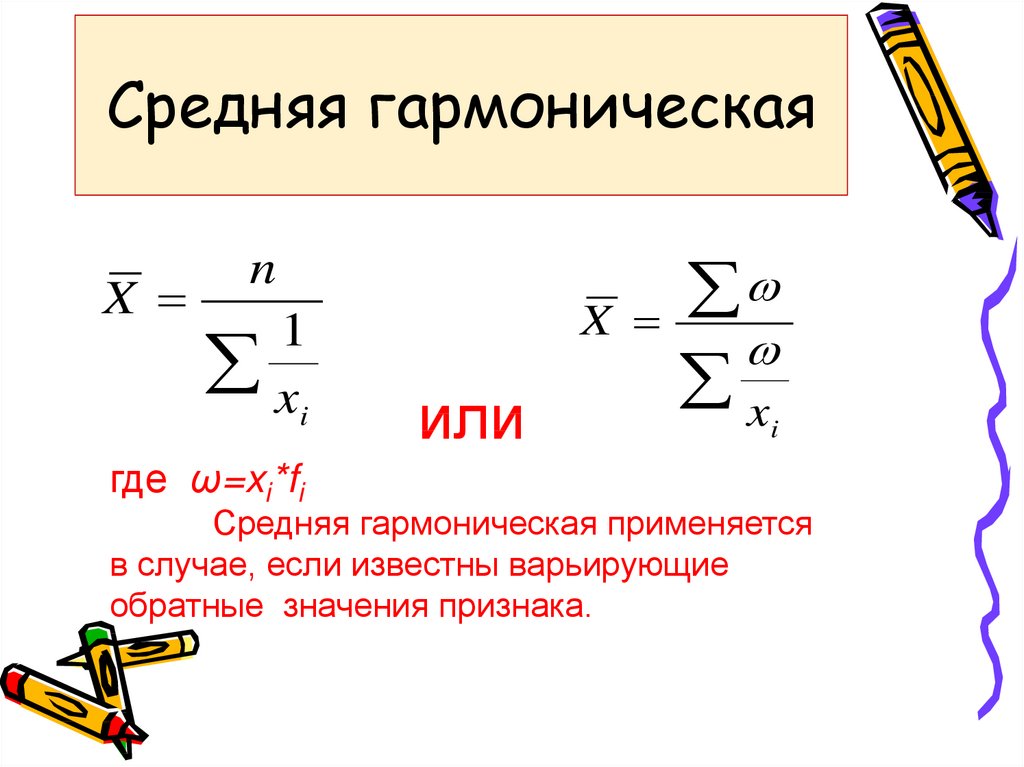 В качестве альтернативы вы можете предложить им рассмотреть более дорогую, возможно, даже самую продаваемую альтернативу.
В качестве альтернативы вы можете предложить им рассмотреть более дорогую, возможно, даже самую продаваемую альтернативу.
Побудить покупателя тратить больше можно с помощью грамотных методов мерчандайзинга — размещения перед покупателями заманчивого ассортимента товаров и демонстрации их таким образом, чтобы они были мотивированы к покупке, — или с помощью прямых стимулов, таких как бесплатная доставка.
Успешные стратегии увеличения AOV включают:
- Перекрестные продажи: «Как насчет носков к теннисным туфлям, которые вы только что заказали?»
- Дополнительные продажи: «Хотели бы вы купить эту пару теннисных туфель всего на 10 долларов дороже, чем пара в вашей корзине?»
- Оптовые скидки: «Это полотенце для рук стоит 9 долларов, но вы сэкономите 30%, если купите 3 или больше».
- Бесплатная доставка: (при более высокой минимальной покупке)
- Купоны: «Потратьте 50 долларов и получите скидку 5 долларов на следующую покупку!»
- Пожертвования: (некоммерческой организации на минимальную покупку)
- Политика возврата: «Не стесняйтесь отправлять их обратно, если вы не удовлетворены»
Отличный способ реализовать эти стратегии — разделить вашу клиентскую базу на несколько групп, таких как мелкие и крупные покупатели, покупатели с низкой и высокой частотой покупок, в зависимости от истории покупок. Таргетинг на каждую группу с различными предложениями. Например, чтобы увеличить AOV ваших постоянных покупателей, вы можете зарегистрировать их в программах лояльности.
Таргетинг на каждую группу с различными предложениями. Например, чтобы увеличить AOV ваших постоянных покупателей, вы можете зарегистрировать их в программах лояльности.
Помните об этих других ключевых показателях электронной коммерции
Простое сосредоточение внимания на увеличении средней стоимости заказа может быть отличным способом увеличить вашу валовую прибыль, но убедитесь, что вы также следите за парой других важных показателей:
- Коэффициент конверсии: Коэффициент конверсии определяется отношением количества конверсий к общему количеству посетителей. Вы не хотите увеличивать свой AOV только для того, чтобы обнаружить, что ваши общие коэффициенты конверсии падают!
- Доход на посетителя: Доход на посетителя (RPV) — это показатель суммы денег, получаемой каждый раз, когда клиент посещает ваш веб-сайт.
Как A/B-тестирование может помочь повысить среднюю стоимость заказа
У каждого веб-сайта и приложения есть уникальный набор клиентов и продуктов, и существуют десятки, если не сотни, методов увеличения средней стоимости заказа. В каждой конкретной стратегии есть несколько вариантов, которые вы можете протестировать, например заголовки, изображения и призывы к действию.
В каждой конкретной стратегии есть несколько вариантов, которые вы можете протестировать, например заголовки, изображения и призывы к действию.
Возьмем в качестве примера перекрестные продажи. Вы можете протестировать исходную корзину покупок с вариантом, который включает сообщение «Люди, которые купили это, также часто покупают это» и графику, чтобы увидеть, увеличивается ли AOV. Затем вы можете протестировать альтернативное сообщение, например «Рекомендуемые продукты для вас», чтобы увидеть, что приводит к наибольшему AOV.
Имея так много различных возможностей для улучшения AOV, вам необходимо разработать методическую серию A/B-тестов, которые позволят вам собрать достаточно данных для каждого теста, чтобы оптимизировать конверсию.
Optimizely ежемесячно оптимизирует миллиарды операций для клиентов из различных отраслей, включая средства массовой информации, розничную торговлю, путешествия и технологии. Платформа предлагает результаты в режиме реального времени, чтобы вы были уверены в своих бизнес-решениях.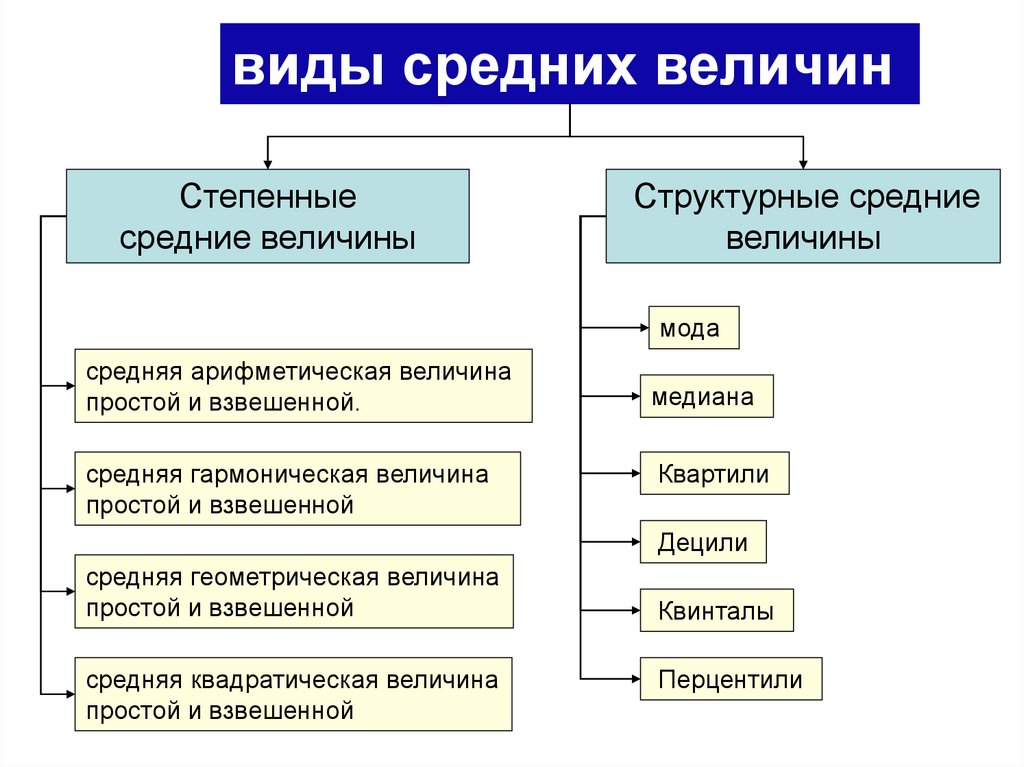 Начните использовать Optimizely сегодня, чтобы оптимизировать свой сайт или приложение и улучшить AOV.
Начните использовать Optimizely сегодня, чтобы оптимизировать свой сайт или приложение и улучшить AOV.
Готовы увеличить объем онлайн-заказов? Узнайте, как работает Optimizely B2C Commerce, чтобы получить максимальную отдачу от вашей онлайн-торговли
Узнайте, как это работает
Средние: среднее, медиана и мода
Термин « среднее» часто встречается в самых разных повседневных контекстах. Например, вы можете сказать « У меня сегодня обычный день », имея в виду, что ваш день не особенно хорош и не плох, он почти нормальный. Мы также можем называть людей, предметы и другие вещи « средними ».
Термин «среднее» относится к «средней» или «центральной» точке. При использовании в математике этот термин относится к числу, которое является типичным представлением группы чисел (или набора данных). Средние значения можно рассчитать разными способами — на этой странице рассматриваются среднее значение, медиана и мода. Мы включаем калькулятор средних значений, а также объяснение и примеры каждого типа среднего значения.
Мы включаем калькулятор средних значений, а также объяснение и примеры каждого типа среднего значения.
Наиболее широко используемый метод расчета среднего значения — «среднее». Когда термин «среднее» используется в математическом смысле, он обычно относится к среднему значению, особенно когда не дается никакой другой информации.
Краткое руководство:
Чтобы вычислить среднее значение
Сложите числа и разделите на количество чисел.
(Сумма значений, деленная на количество значений).
Для определения медианы
Расположите числа по порядку, найдите среднее число.
(Среднее значение при ранжировании значений) .
Для определения режима
Подсчитайте, сколько раз встречается каждое значение; значение, которое встречается чаще всего, является модой.
(Наиболее часто встречающееся значение)
Калькулятор среднего, медианы и моды
Используйте этот калькулятор для расчета среднего, медианы и моды набора чисел.
Среднее значение
Математический символ или обозначение среднего значения — «крестик». Этот символ появляется на научных калькуляторах, а также в математических и статистических обозначениях.
« среднее » или « среднее арифметическое » является наиболее часто используемой формой среднего. Чтобы вычислить среднее значение, вам нужен набор связанных чисел (или набор данных). Для вычисления среднего необходимо как минимум два числа.
Числа должны быть каким-то образом связаны друг с другом, чтобы получить какой-либо значимый результат – например, показания температуры, цена на кофе, количество дней в месяце, количество ударов сердца в минуту, данные о студентах. оценки за тесты и т. д.
Чтобы найти (среднюю) среднюю цену буханки хлеба в супермаркете, например, сначала запишите цену каждого вида буханки:
- Белая: 1 фунт стерлингов
- Цельнозерновой: 1,20 фунта стерлингов
- Багет: 1,10 фунта стерлингов
Затем сложите (+) цены вместе 1 фунт стерлингов + 1,20 фунта стерлингов + 1,10 фунта стерлингов = 3,30 фунта стерлингов
Затем разделите (÷) ваш ответ на количество буханок (3).
3,30 фунта стерлингов ÷ 3 = 1,10 фунта стерлингов.
Средняя цена буханки хлеба в нашем примере равна 1,10 фунта стерлингов .
Тот же метод применим к большим наборам данных:
Чтобы рассчитать среднее количество дней в месяце, мы должны сначала установить, сколько дней в каждом месяце (при условии, что это не високосный год):
| Месяц | дней |
| Январь | 31 |
| Февраль | 28 |
| Март | 31 |
| апрель | 30 |
| Май | 31 |
| июнь | 30 |
| июль | 31 |
| Август | 31 |
| Сентябрь | 30 |
| Октябрь | 31 |
| ноябрь | 30 |
| Декабрь | 31 |
Далее складываем все числа вместе: 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 30 + 31 = 365
Наконец, мы делим ответ на количество значений в нашем наборе данных, в этом случае их 12 ( по одному на каждый учитываемый месяц).
Таким образом, среднее значение равно 365 ÷ 12 = 30,42 .
Следовательно, среднее количество дней в месяце равно 30,42.
Тот же расчет можно использовать для расчета среднего значения любого набора чисел, например средней заработной платы в организации:
Предположим, что в организации 100 сотрудников одного из 5 классов:
| Класс | Годовой оклад | Численность сотрудников |
| 1 | 20 000 фунтов стерлингов | 21 |
| 2 | 25 000 фунтов стерлингов | 25 |
| 3 | 30 000 фунтов стерлингов | 40 |
| 4 | 50 000 фунтов стерлингов | 9 |
| 5 | 80 000 фунтов стерлингов | 5 |
В этом примере мы можем не добавлять зарплату каждого отдельного сотрудника, поскольку мы знаем, сколько их в каждой категории. Таким образом, вместо того, чтобы выписывать 20 000 фунтов двадцать один раз, мы можем умножить, чтобы получить ответы:
Таким образом, вместо того, чтобы выписывать 20 000 фунтов двадцать один раз, мы можем умножить, чтобы получить ответы:
| Оценка | Годовой оклад | Численность сотрудников | Заработная плата x Сотрудники |
| 1 | 20 000 фунтов стерлингов | 21 | 420 000 фунтов стерлингов |
| 2 | 25 000 фунтов стерлингов | 25 | 625 000 фунтов стерлингов |
| 3 | 30 000 фунтов стерлингов | 40 | 1 200 000 фунтов стерлингов |
| 4 | 50 000 фунтов стерлингов | 9 | 450 000 фунтов стерлингов |
| 5 | 80 000 фунтов стерлингов | 5 | 400 000 фунтов стерлингов |
Затем сложите значения в столбце Зарплата x Сотрудники, чтобы получить общую сумму: 3 095 000 фунтов стерлингов, и, наконец, разделите это число на количество сотрудников (100), чтобы найти среднюю зарплату:
3 095 000 фунтов стерлингов : 100 = 30 950 фунтов стерлингов.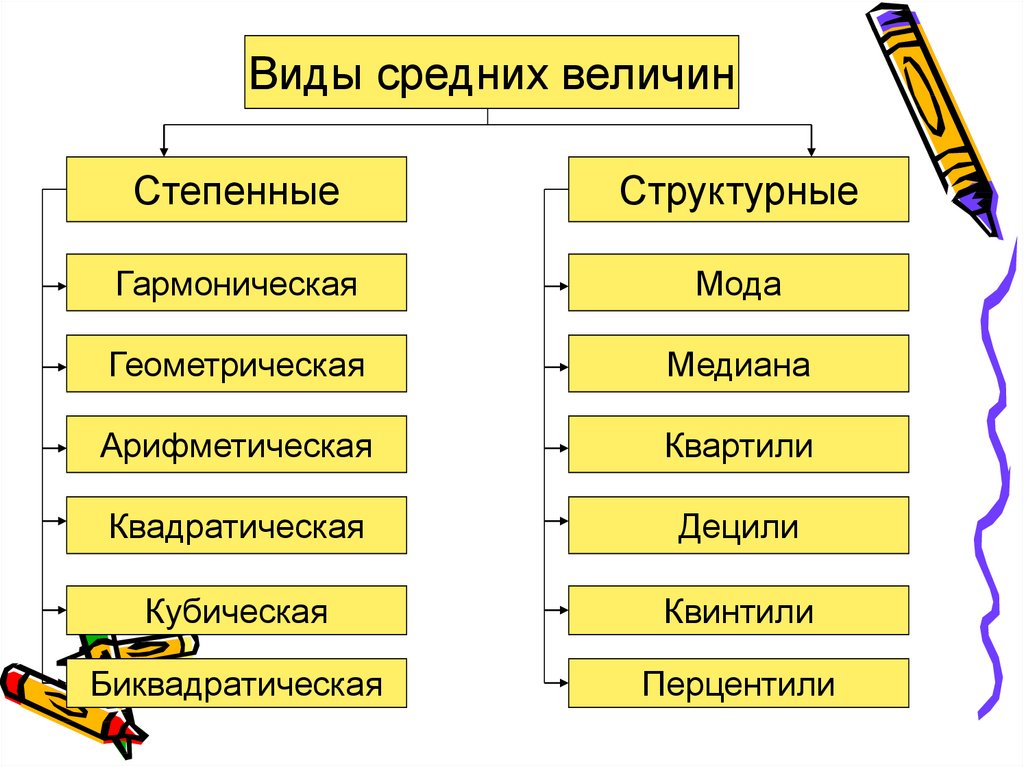
Подсказка:
Все зарплаты в приведенном выше примере кратны 1000 фунтов стерлингов — все они заканчиваются на ,000 .
Вы можете игнорировать 000 при расчете, если не забудете добавить их обратно в конце.
В первой строке таблицы выше мы знаем, что двадцать один человек получает зарплату в размере 20 000 фунтов стерлингов, вместо того, чтобы работать с 20 000 фунтов стерлингов, работая с 20:
21 x 20 = 420, затем замените 000, чтобы получить 420 000 .
Иногда мы можем знать сумму наших чисел, но не отдельные числа, из которых состоит сумма.
В этом примере предположим, что 122,50 фунта стерлингов были получены за неделю от продажи лимонада.
Мы не знаем, сколько денег было заработано каждый день, только общее количество на конец недели.
Мы можем рассчитать среднедневное значение: £122,50 ÷ 7 (общая сумма денег, разделенная на 7 дней).
122,5 ÷ 7 = 17,50 .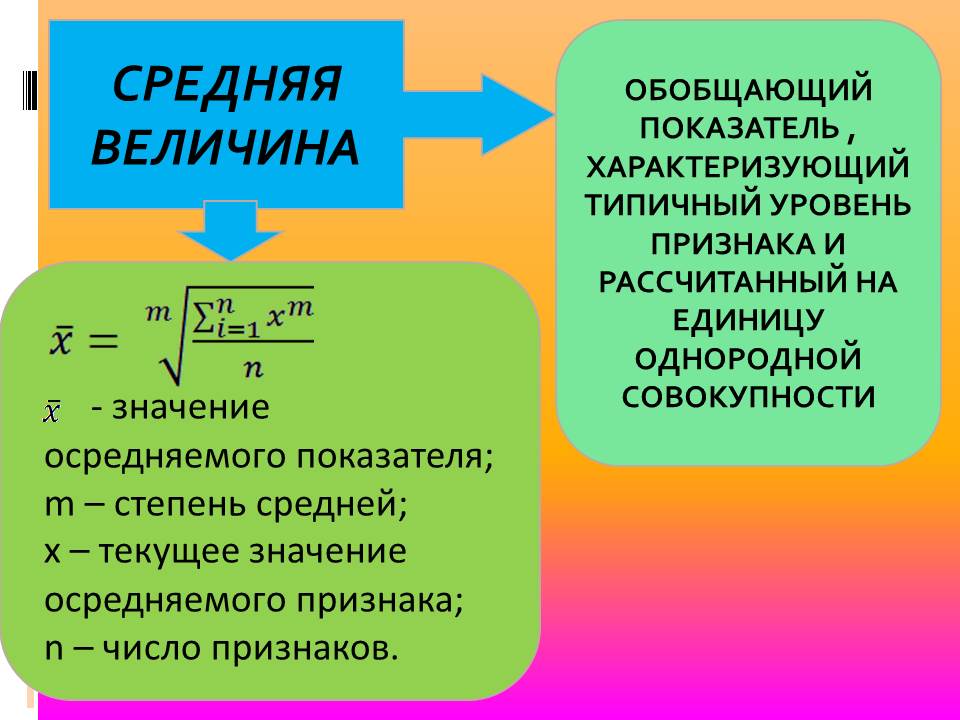
Итак, мы можем сказать, что в среднем мы зарабатывали 17,50 фунтов стерлингов в день.
Мы также можем использовать средние значения, чтобы дать нам представление о вероятных будущих событиях – если мы знаем, что в среднем зарабатывали 17,50 фунтов стерлингов в день, продавая лимонад за неделю, мы можем предположить, что за месяц мы заработаем:
£17,50 × количество дней в этом месяце
17,50 × 31 = 542,50 фунта стерлингов
Мы могли бы ежемесячно записывать средние показатели продаж, чтобы прогнозировать продажи на будущие месяцы и годы, а также сравнивать наши показатели. Мы могли бы использовать такие термины, как « выше среднего » — для обозначения периода времени, когда объем продаж был выше среднего, и также «ниже среднего», когда объем продаж был ниже среднего.
Используя данные о скорости и времени, чтобы найти среднее значение:
Если вы проедете 85 миль за 1 час 20 минут, какова будет ваша средняя скорость?
Первое, что нужно сделать с этой проблемой, — преобразовать время в минуты — время не работает в десятичной системе, так как в часе 60 минут, а не 100. Поэтому нам нужно стандартизировать наши единицы, прежде чем мы сможем начать:
Поэтому нам нужно стандартизировать наши единицы, прежде чем мы сможем начать:
1 час 20 минут = 60 минут + 20 минут = 80 минут.
Затем разделите пройденное расстояние на затраченное время: 85 миль ÷ 80 минут .
85 ÷ 80 = 1,0625.
Таким образом, наша средняя скорость составила 1,0625 мили в минуту.
Преобразуйте эту цифру обратно в часы, умножив ее на 60 (количество минут в часе).
1,0625 × 60 = 63,75 миль в час (миль в час).
Для пользователей электронных таблиц:
Используйте функцию
. =average(A1:A10)
Медиана
Медиана — это среднее число в списке отсортированных чисел.
Чтобы вычислить медиану: 6, 13, 67, 45, 2
Сначала расположите числа по порядку (это также известно как рейтинг )
2, 6, 13 , 45, 67
затем — найти среднее число
Медиана = 13, среднее число в ранжированном списке.
Когда имеется четное число чисел, то нет одного среднего числа, а есть пара средних чисел.
В таких случаях медианой является среднее двух средних чисел:
Например:
6,13,67,45,2,7 7 и 13.
Медиана относится к одному числу, поэтому мы вычисляем среднее двух средних чисел:
7 + 13 = 20
20 ÷ 2 = 10
Следовательно, медиана чисел 6, 13, 67, 45, 2, 7 равна 10 .
Режим
Режим — это наиболее часто встречающееся значение в наборе значений. Режим интересен тем, что его можно использовать для любого типа данных, а не только для чисел.
В этом примере предположим, что вы купили упаковку из 100 воздушных шаров, упаковка состоит из 5 разных цветов, вы считаете каждый цвет и обнаруживаете, что у вас есть:
18 Красный
12 Синий
24 Оранжевый
25 Фиолетовый
21 Зеленый
Цвет нашей выборки воздушных шаров фиолетовый, поскольку фиолетовых воздушных шаров (25) больше, чем любого другого цветного шара.
Чтобы узнать режим количества дней в каждом месяце:
| Месяц | дней |
| Январь | 31 |
| Февраль | 28 |
| Март | 31 |
| апрель | 30 |
| Май | 31 |
| июнь | 30 |
| июль | 31 |
| Август | 31 |
| Сентябрь | 30 |
| Октябрь | 31 |
| ноябрь | 30 |
| Декабрь | 31 |
В 7 месяцах 31 день, в 4 месяцах всего 30 дней и только в 1 месяце всего 28 дней (29 в високосном году).
Следовательно, режим равен 31.
Некоторые наборы данных могут иметь более одного режима:
1,3,3,4,4,5 — например, имеет два наиболее часто встречающихся числа (3 и 4), это известно как бимодальный набор .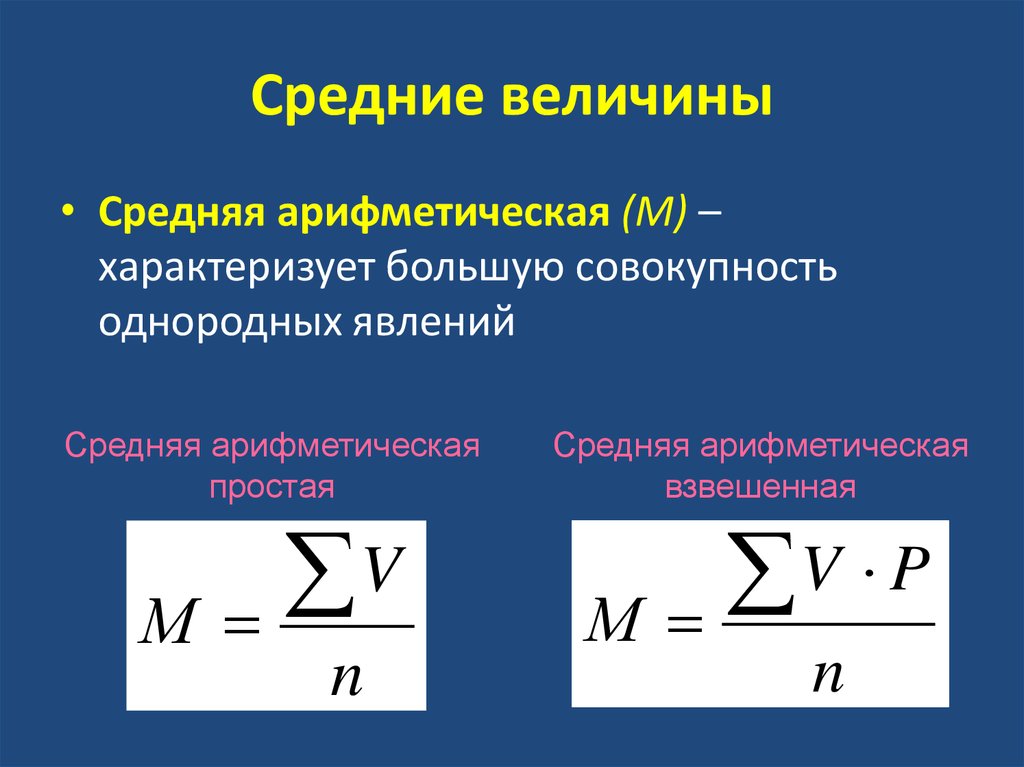 Наборы данных с более чем двумя режимами называются мультимодальными наборами данных .
Наборы данных с более чем двумя режимами называются мультимодальными наборами данных .
Если набор данных содержит только уникальных числа, то вычисление режима более проблематично.
Обычно вполне допустимо сказать, что мода отсутствует, но если нужно найти моду, то обычным способом является создание диапазонов чисел, а затем подсчет диапазона с наибольшим количеством точек в нем. Например, из набора данных, показывающих скорость проезжающих автомобилей, мы видим, что из 10 автомобилей зарегистрированные скорости составляют:
40, 34, 42, 38, 41, 50, 48, 49, 33, 47
Все эти числа уникальны (каждый встречается только один раз), режима нет. Чтобы найти моду, мы строим категории по четной шкале:
30—32 | 33—35 | 36—38 | 39—41 | 42—44 | 45—47 | 48—50
Затем определите, сколько значений попадает в каждую категорию, сколько раз встречается число от 30 до 32 и т. д.
30—32 = 0
33—35 = 2
36—38 = 1
39—41 = 2
42—44 = 1
45—47 = 1
48—50 = 3
Категория с наибольшим количеством значений: 48—50 с 3 значениями.
Мы можем взять среднее значение категории, чтобы оценить моду как 49.
Этот метод расчета моды не идеален, поскольку мода может меняться в зависимости от определяемых вами категорий.
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Обработка данных и алгебра
Часть «Навыки, которые вам нужны» Руководство по арифметике
Эта электронная книга охватывает основы обработки данных, визуализации данных, базового статистического анализа и алгебры. Книга содержит множество проработанных примеров для улучшения понимания, а также примеры из реальной жизни, чтобы показать вам, как эти концепции полезны.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Найти среднее значение списка в python
Предпосылки: функция sum(), функция len(), функция round(), reduce(), lambda и mean(). Учитывая список чисел, задача состоит в том, чтобы найти среднее значение этого списка. Среднее — это сумма элементов, деленная на количество элементов.
Среднее — это сумма элементов, деленная на количество элементов.
Ввод: [4, 5, 1, 2, 9, 7, 10, 8] Выход: среднее значение списка = 5,75. Объяснение : Сумма элементов 4+5+1+2+9+7+10+8 = 46 а общее количество элементов равно 8. Таким образом, среднее значение равно 46/8 = 5,75. Ввод: [15, 9, 55, 41, 35, 20, 62, 49] Выход: среднее значение списка = 35,75. Объяснение : Сумма элементов 15+9+55+41+35+20+62+49 = 286. а общее количество элементов равно 8. Таким образом, среднее значение равно 46 / 8 = 35,759.0002 Рекомендуется: сначала попробуйте свой подход на {IDE} , прежде чем переходить к решению.
Использование sum()
В Python мы можем найти среднее значение списка, просто используя функции sum() и len() .
- sum() : Используя функцию sum(), мы можем получить сумму списка.
- len() : функция len() используется для получения длины или количества элементов в списке.

Python3
|
Output:
Average of the list = 35.75
Using reduce() and lambda
Мы можем использовать reduce(), чтобы уменьшить цикл, и с помощью лямбда-функции можем вычислить суммирование списка. Мы используем len() для вычисления длины, как обсуждалось выше.
Python3
|
. списка.
списка.
Python3
|
Output:
Среднее значение списка = 35,75
Путем повторения списка
Повторение списка с использованием цикла for и выполнение операций над каждым элементом списка.





 Эти причины не связаны с природой изучаемого явления, их называют случайными причинами.
Эти причины не связаны с природой изучаемого явления, их называют случайными причинами. В действительности положение может быть следующим: один акционер имеет 1010 акций на сумму 505 тыс. грн, а 99 акционеров — 10 акций на сумму 495 тыс. грн. Таким образом существует две категории акционеров. К первой из них относится один акционер с величиной пакета, равной 505 тыс. грн. и ко второй группе — 99акционеров со средней величиной пакета акций 5 тыс. грн. Полученная средняя не может считаться надежной оценкой, так как она в два раза больше по своей величине, чем индивидуальные пакеты акций 99% акционеров.
В действительности положение может быть следующим: один акционер имеет 1010 акций на сумму 505 тыс. грн, а 99 акционеров — 10 акций на сумму 495 тыс. грн. Таким образом существует две категории акционеров. К первой из них относится один акционер с величиной пакета, равной 505 тыс. грн. и ко второй группе — 99акционеров со средней величиной пакета акций 5 тыс. грн. Полученная средняя не может считаться надежной оценкой, так как она в два раза больше по своей величине, чем индивидуальные пакеты акций 99% акционеров.


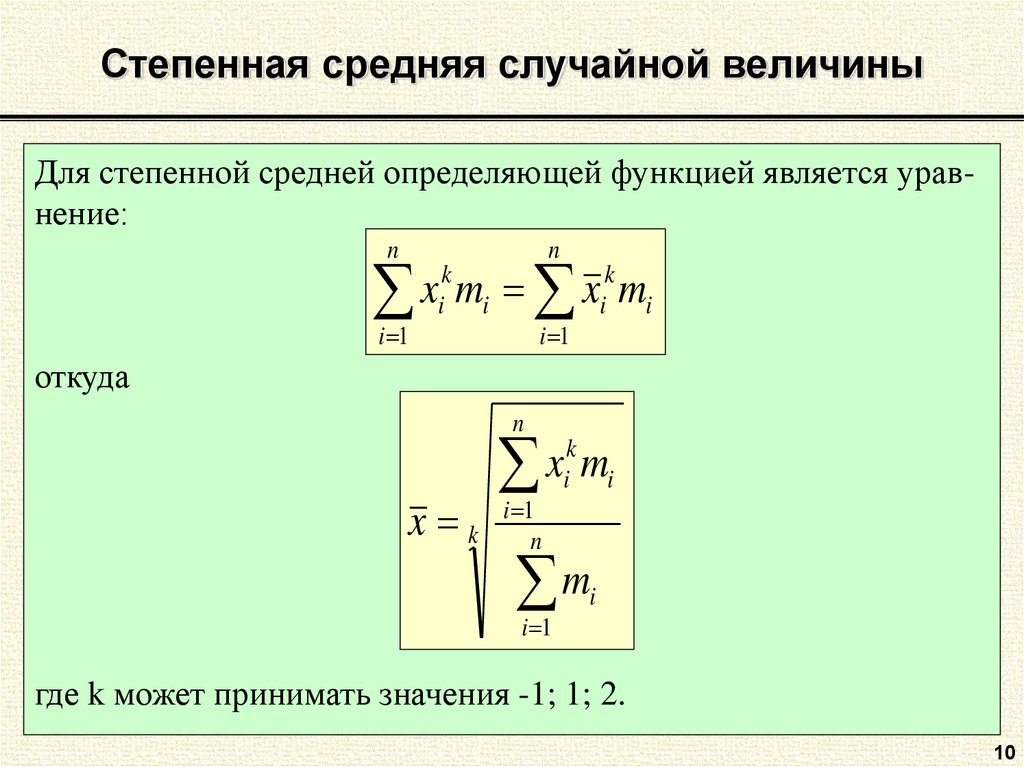
 км; две машины — по 5,1 тыс. км; четыре — по 6,5 тыс. км и три — по 7,0 тыс. км.
км; две машины — по 5,1 тыс. км; четыре — по 6,5 тыс. км и три — по 7,0 тыс. км. км.
км.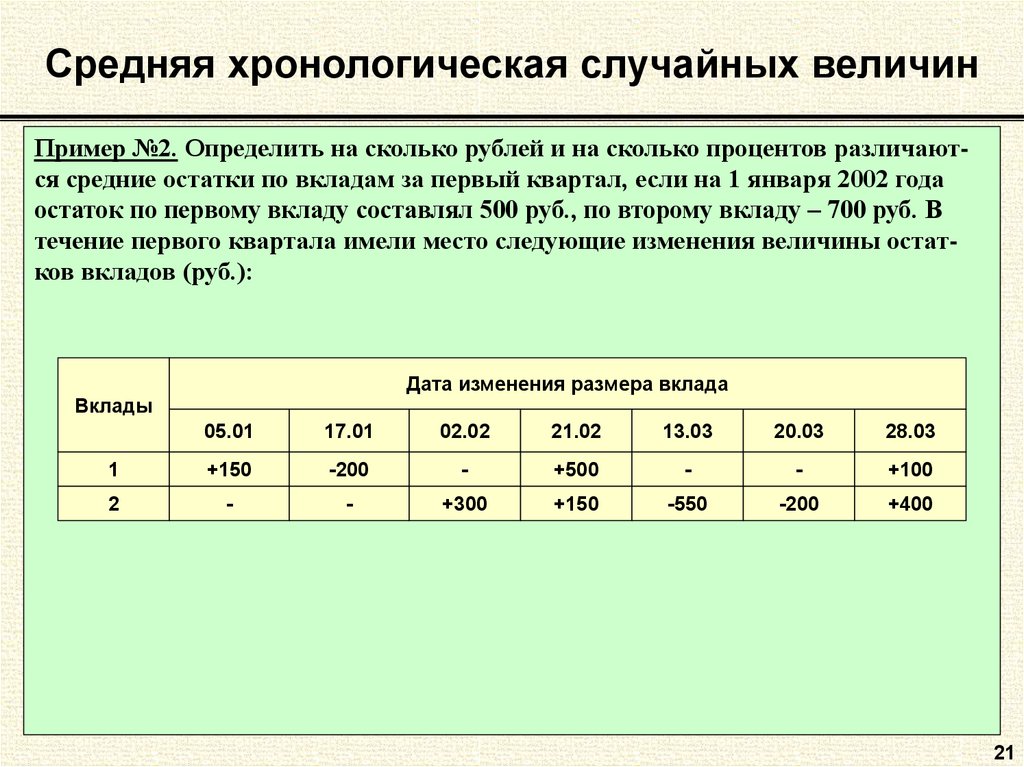
 е. второй группе), а при определении величины варианты для последней группы интервального ряда распределения — из предположения, что в последней группе величина интервала та же, что и в предыдущей группе.
е. второй группе), а при определении величины варианты для последней группы интервального ряда распределения — из предположения, что в последней группе величина интервала та же, что и в предыдущей группе. е. условные значения варианты каждой интервальной группы. Для второй и третей групп их определяют по формуле средней арифметической простой:
е. условные значения варианты каждой интервальной группы. Для второй и третей групп их определяют по формуле средней арифметической простой:
 к расчет основан на условном допущении равномерности распределения вариант в пределах каждого интервала.
к расчет основан на условном допущении равномерности распределения вариант в пределах каждого интервала.




 В зависимости от категорий медслучая, страховая сумма может изменяться от 100 до 10000грн. Средняя сумма выплат по страхованию 100*10000=1000грн.
В зависимости от категорий медслучая, страховая сумма может изменяться от 100 до 10000грн. Средняя сумма выплат по страхованию 100*10000=1000грн.
 Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью.
Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью. Например, курс акций корпорации в целом определяется ее финансовым положением. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
Например, курс акций корпорации в целом определяется ее финансовым положением. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Это будет объясняться тем, что используемая для расчета совокупность является крайне неоднородной. В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднородна — общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам.
Это будет объясняться тем, что используемая для расчета совокупность является крайне неоднородной. В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднородна — общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам. Предположим, что следователь в январе закончил расследование по трем уголовным делам, в феврале — по четырем, в марте — по шести, в апреле — — по пяти, в мае — — по двум, в июне —• по четырем. На полученные значения могли повлиять самые различные факторы и прежде всего сложность дел, объем работы по каждому из них и т. д. Но если абстрагироваться от всех частностей, вызвавших различия в количестве расследованных ва месяц дел, то можно оказать, что в среднем каждый месяц заканчиваются расследованием четыре дела (за полгода расследовано 3+4+6 + 5+2+4—24 дела, что при делении на шесть месяцев и дает указанную величину).
Предположим, что следователь в январе закончил расследование по трем уголовным делам, в феврале — по четырем, в марте — по шести, в апреле — — по пяти, в мае — — по двум, в июне —• по четырем. На полученные значения могли повлиять самые различные факторы и прежде всего сложность дел, объем работы по каждому из них и т. д. Но если абстрагироваться от всех частностей, вызвавших различия в количестве расследованных ва месяц дел, то можно оказать, что в среднем каждый месяц заканчиваются расследованием четыре дела (за полгода расследовано 3+4+6 + 5+2+4—24 дела, что при делении на шесть месяцев и дает указанную величину). Иными словами, исчисление средних должно основываться на методе научных группировок, который обеспечивает выделение однотипных, однородных совокупностей. В. И. Ленин, критикуя несостоятельность методологии средних при разработке материалов
Иными словами, исчисление средних должно основываться на методе научных группировок, который обеспечивает выделение однотипных, однородных совокупностей. В. И. Ленин, критикуя несостоятельность методологии средних при разработке материалов
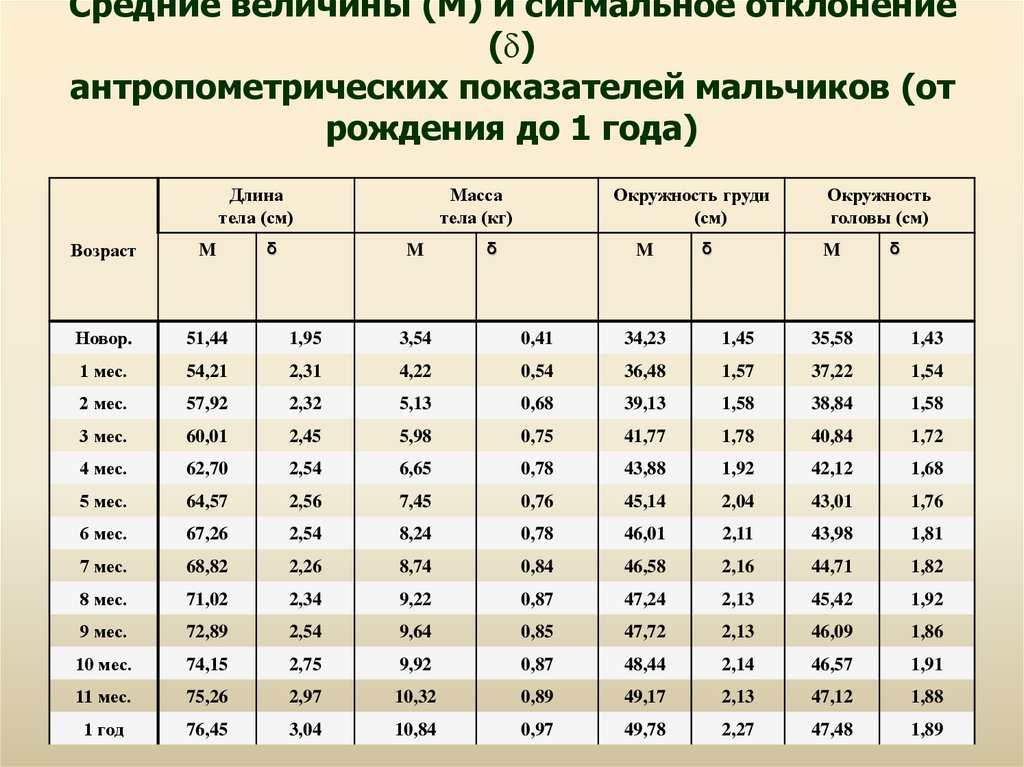 При анализе коротких промежутков времени (менее часа) возможно применение ЕМА или WMA. На средних промежутках времени (час и три часа) рекомендуется применение как МА, так и ЕМА и WMA.
При анализе коротких промежутков времени (менее часа) возможно применение ЕМА или WMA. На средних промежутках времени (час и три часа) рекомендуется применение как МА, так и ЕМА и WMA. Если ваши оценки не взвешены, пропустите этот шаг.
Если ваши оценки не взвешены, пропустите этот шаг. Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.
Например, медиана 2, 3, 3, 5, 7 и 10 равна 4.
 4)
4)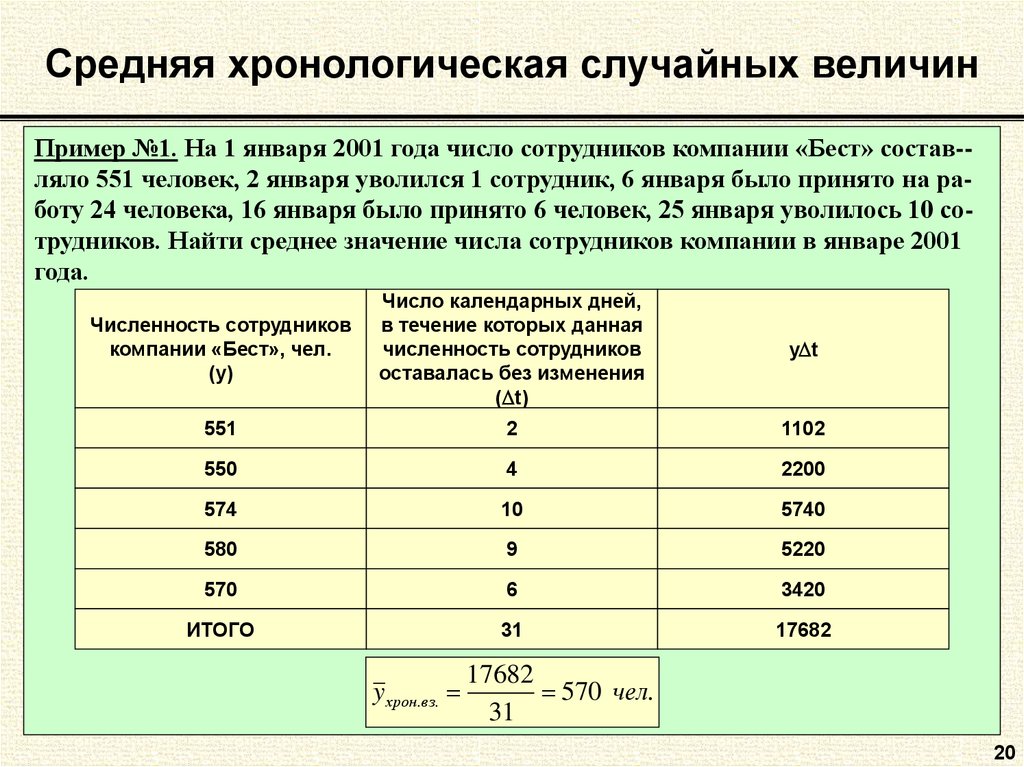


 75
75