Средняя линия трапеции задачи с решением: Решение задач по теме «Средняя линия трапеции»

Содержание

Решение задач по теме «Средняя линия трапеции»

Задачи по теме: средняя линия трапеции

9 класс Вариант 1

1) В равнобедренной трапеции средняя линия равна 10, а периметр 36 см. Найдите боковые стороны этой трапеции

2) В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

3) В равнобедренной трапеции острые углы , боковая сторона 10 см, а большее основание 15 см. Найдите меньшее основание и среднюю линию трапеции.

Задачи по теме: средняя линия трапеции

9 класс Вариант 2

1) Средняя линия трапеции равна 30 см, а одно из оснований в два раза меньше другого. Найдите основания трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

3) В равнобедренной трапеции острые углы 45, расстояние между основаниями 4 см, а меньшее основание 5см. Найдите большее основание и среднюю линию трапеции.

Задачи по теме: средняя линия трапеции

9 класс Вариант 3

1) Разность оснований трапеции равна 8 см, а средняя линия равна 20 см. Найдите основания этой трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.

3) В трапеции ABCD AD, Найдите среднюю линию трапеции, если известно, что ее диагональ перпендикулярна боковой стороне.

Задачи по теме: средняя линия трапеции

9 класс Вариант 4

1) Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

2) В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.

3) В трапеции MHKP MP, Найдите среднюю линию трапеции, если известно, что ее диагональ перпендикулярна боковой стороне.

Задачи по теме: средняя линия трапеции

9 класс Вариант 1

1) В равнобедренной трапеции средняя линия равна 10, а периметр 36 см. Найдите боковые стороны этой трапеции

Задачи по теме: средняя линия трапеции

9 класс Вариант 2

Задачи по теме: средняя линия трапеции

9 класс

Вариант 3

1) Разность оснований трапеции равна 8 см, а средняя линия равна 20 см. Найдите основания этой трапеции.

Задачи по теме: средняя линия трапеции

9 класс

Вариант 4

Найдите среднюю линию трапеции

В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания связанные с трапецией. На блоге уже рассмотрены задачи условия которых связаны с площадью трапеции, а также с углами. Кратко о средней линии:

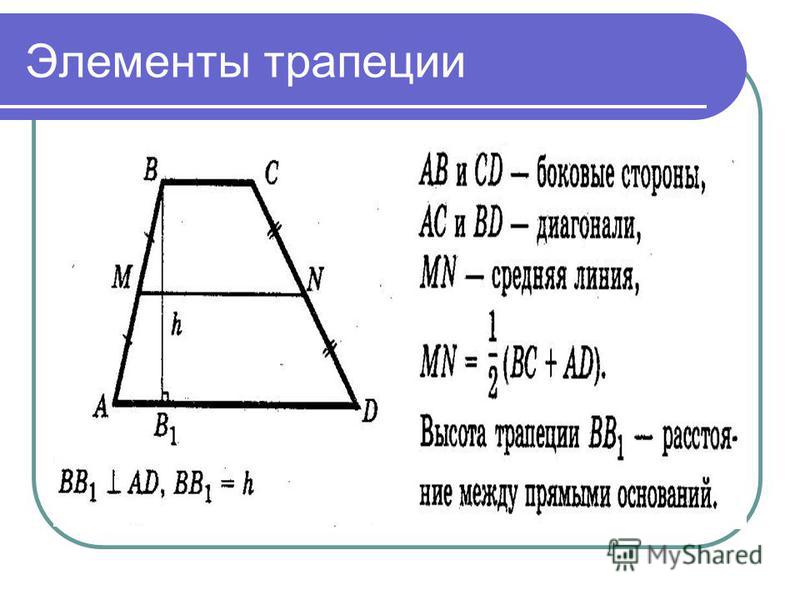
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.

Перед решением задач давайте рассмотрим теоретический пример.

Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.

Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.

Так же это основывается на теореме Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:

Можем теперь выразить отрезок KL через основания:

Доказано!

Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии.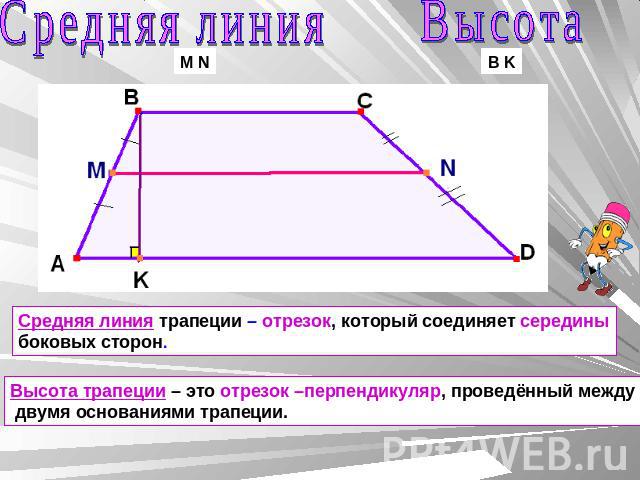 Рассмотрим задачи:

27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Вычисляем по формуле:

Ответ: 23

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Выразим большее основание:

Таким образом:

Ответ: 38

27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.

Построим второй перпендикуляр DF:

Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?

В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:

Таким образом DC=6. Вычисляем:

Ответ: 10

27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.

Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:

Следовательно меньшее основание равно 2∙2=4.

Ответ: 4

27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.

Исходя из условия можем записать:

Если обозначить среднюю линию через величину х, то получится:

Второе уравнение уже можно записать в виде:

Ответ: 20

27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать

Получили, что меньшее основание рано пяти, значит большее равно 9.

Ответ: 9

27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.

Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.

Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:

Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:

Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.

Ответ: 14

27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.

Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?

Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.

Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:

При чём:

Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:

Таким образом, средняя линия равна 12.

*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.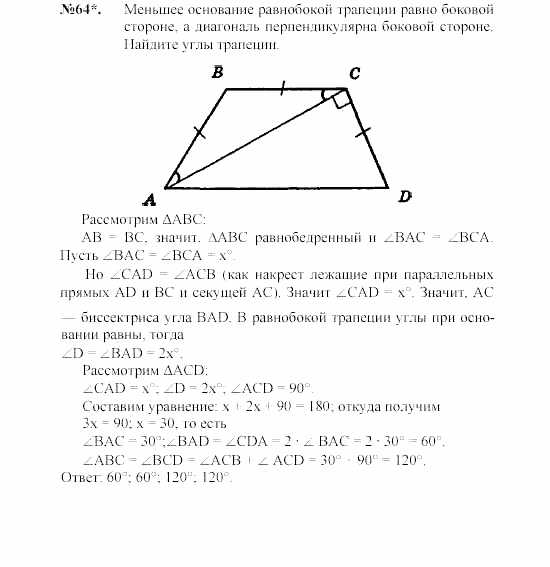

Ответ: 12

В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.

27848. Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.

Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3

Ответ: 3

Если же основания построены под углом к клеточной сетке, то есть два способа. Например!

28854.Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны √2.

В данном случае видно, что средняя линия трапеции равна трём диагоналям клетки. Диагональ одной клетки по теореме Пифагора будет равна:

Значит средняя линия равна 2∙3=6.

Конечно, есть и другой путь решения.

Если допустить мысль, что основания трапеции могут лежать по отношению к сетке под углом не 45 градусов, а например 30, или другим, то вполне применим следующий метод (таких задач на ЕГЭ не предвидится):

Вычисляем основания используя теорему Пифагора, а далее используем формулу средней линии.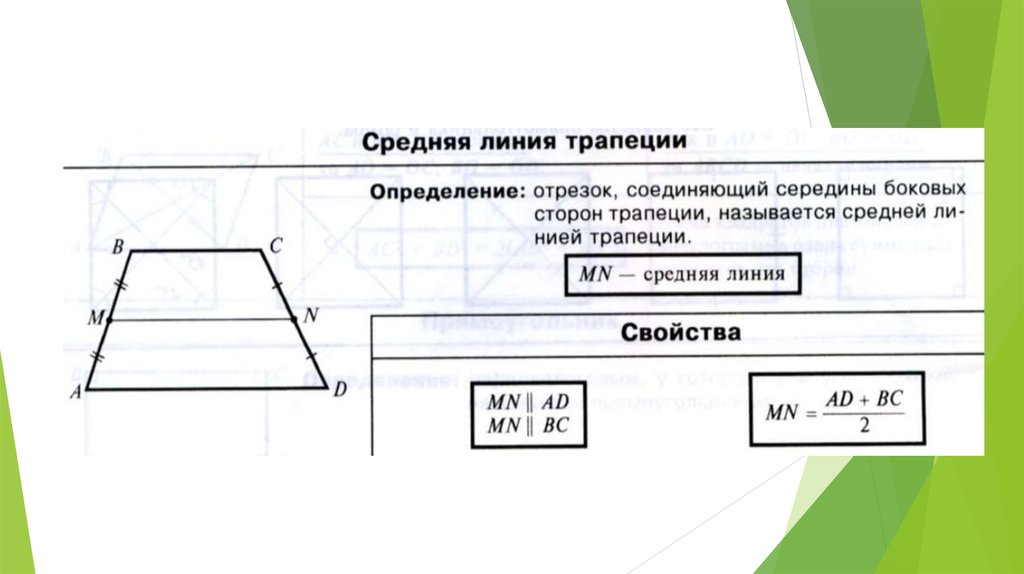

Основание AD при данных условиях это диагональ в прямоугольном треугольнике с катетами равными 4 сторонам клетки, вычисляем:

Основание BC это диагональ в прямоугольном треугольнике катетами равными 2 сторонам клетки, вычисляем:

Средняя линия будет равна (8+4)/2=6.

*То есть при данном подходе, как бы ни была построена трапеция всегда можно вычислить основания.

Ответ: 6

27853. Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны √2.

Высота трапеции равна диагонали клетки. Вычисляем по теореме Пифагора:

Ответ: 2

27821. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Посмотреть решение

27838.Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.

Посмотреть решение

27843. Основания трапеции равны 3 и 2.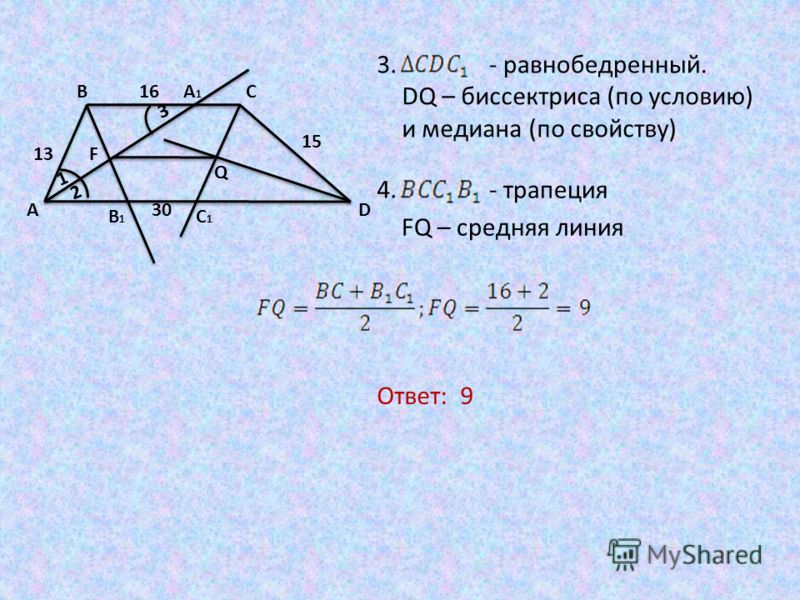 Найдите отрезок, соединяющий середины диагоналей трапеции.

Посмотреть решение

На этом всё, успеха вам!

С уважением, Александр Крутицких.

P,S: Расскажите о сайте в социальных сетях.

«Средняя линия трапеции». 8-й класс

Цели и задачи:

Образовательные – актуализировать субъективный опыт учащихся (опорные знания и способы действий, комплекс знаний), необходимый для изучения нового материала; организовать деятельность учащихся по восприятию, осмыслению и первичному закреплению знаний и способов действий.
Развивающие – развивать пространственного воображения учащихся, применять знания на практике, способствовать развитию логического мышления, воли и самостоятельности, умения работать в парах.
Воспитательные – создавать условия для воспитания интереса к изучаемой теме, воспитание мотивов учения, положительного отношения к знаниям, воспитания дисциплинированности, обеспечивать условия успешной работы в коллективе.

Тип урока: урок-открытие.

Методы обучения: беседа, фронтальный опрос, самостоятельная работа.

Средства обучения: доска, учебник, карточки, мультимедийный проектор.

Форма обучения: коллективная, индивидуальная.

Форма учебного занятия: классно-урочная.

Структура урока:

Организация класса и рабочий настрой _____ 2 мин
Повторение и актуализация знаний _____ 10 мин
Открытие новых знаний __________ 20 мин
Решение задач __________10 мин
Подведение итогов и домашнее задание ____ 3 мин

Итого ______________ 45 мин

ХОД УРОКА

Учитель: Здравствуйте, ребята, садитесь. [слайд 1] Сегодня мы продолжим разговор о средних линиях. И тема сегодняшнего урока «Средняя линия трапеции». Но прежде напомним о четырехугольниках и их свойствами, а также треугольнике, ее средней линии и свойствах средней линии треугольника.

Опрос:

– Что называется многоугольником?
– Что такое параллелограмм?
– Свойства параллелограмма?
– Что такое прямоугольник?
– Свойства прямоугольника?
– Что такое ромб?
– Свойства ромба?
– Что такое квадрат?
– Свойства квадрата?
– Что такое трапеция?
– Какая трапеция называется равнобокой?
– Свойства равнобокой трапеции?
– Чему равен периметр многоугольника?
– Сформулируйте теорему Фалеса.

– Что такое средняя линия треугольника?
– Какие свойства средней линии треугольника вы знаете?

– Решим задачи на готовых чертежах устно: (рис. 1) и (рис. 2)

Дано: EF || AC (рис. 1) [слайд 2]

Найти: P_BEF и P_ABC

Решение:

EF – средняя линия треугольника, значит EF = 5 см,
АЕ = ЕВ = 4 см (по условию)
BF = FC = 5 см ( по теореме Фалеса)
Тогда P_BEF = 4 + 5 + 5 = 14(см)
P_ABC = 8 + 10 + 10 = 28(см)

Ответ

: 14 см и 28 см

Дано: MN || AC (рис. 2) [слайд 3]

Найти: P_MBN и P_ABC

Решение:

АВ = 2МВ = 8 см
ВС = 2BN= 7 см (теорема Фалеса)
АС = 2MN = 6 см (средняя линия треугольника)
P_ABC = 8 + 7 + 6 = 21 (см)
P_MBN = 4 + 3 + 3,5 = 10,5 (см)

Ответ: 21 см и 10,5 см

Учитель: Итак, мы с вами сказали, что средней линией треугольника называется отрезок соединяющий середины двух сторон треугольника. Дадим определение средней линии трапеции.

Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 3).

[слайд 4]

Рис.3

На рисунке 3 средней линией трапеции является отрезок EF.

Учитель: Решим задачу: найти среднюю линию трапеции, зная ее основания. [слайд 5]

Решение: Пусть ABCD – трапеция, M – середина стороны АВ. BC = a, AD = b. Для решения задачи воспользуемся средней линией треугольника. Но у нас фигура трапеция, где же найти треугольник?

Учащиеся: Сделаем рисунок (рис.4) [слайд 6], дополнительное построение – проведем диагональ АС, она разобьет трапецию на два треугольника АВС и ACD. Проведем через точку М параллельно основаниям прямую, она пересечет отрезок АС в точке К, а отрезок CD – в точке N.

Учитывая следствие о средней линии треугольника (прямая, проходящая, через середину стороны треугольника параллельно другой ее стороне, делит третью сторону пополам) получим: К – середина АС и N середина CD. Тогда по определению МК – средняя линия треугольника АВС и KN – средняя линия треугольника ACD.
Учитывая теорему о средней линии треугольника получим:

Найдем длину средней линии:

Рис. 4

Ответ: .

Решенная задача является теоремой 1: средняя линия трапеции параллельна основаниям и равна их полусумме. [слайд 7]

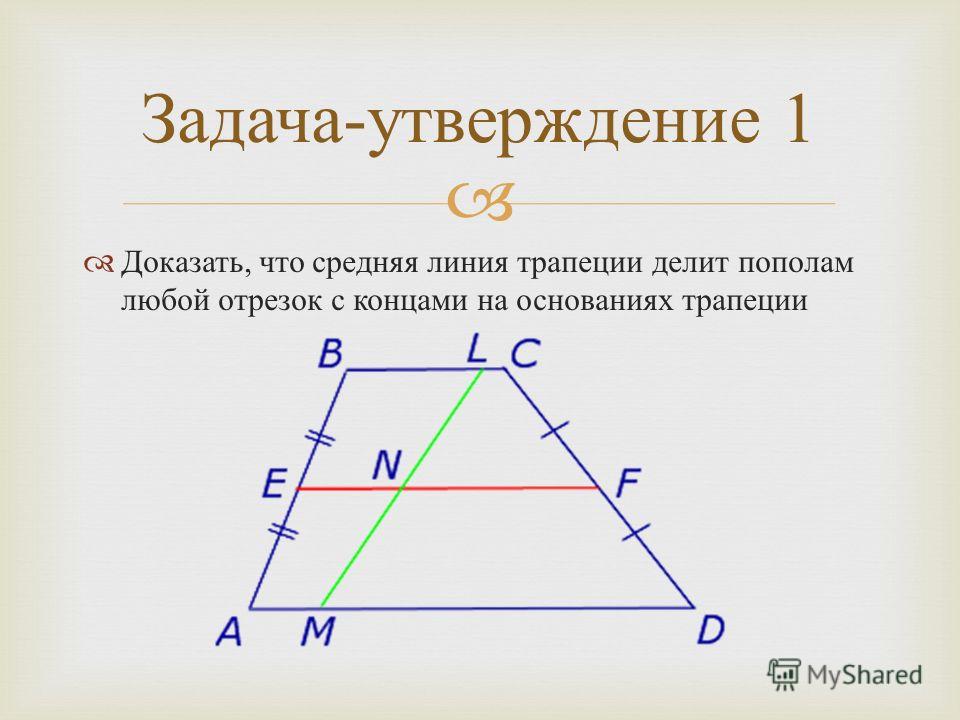
Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции. [слайд 8]

Рис. 5

Решение. Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.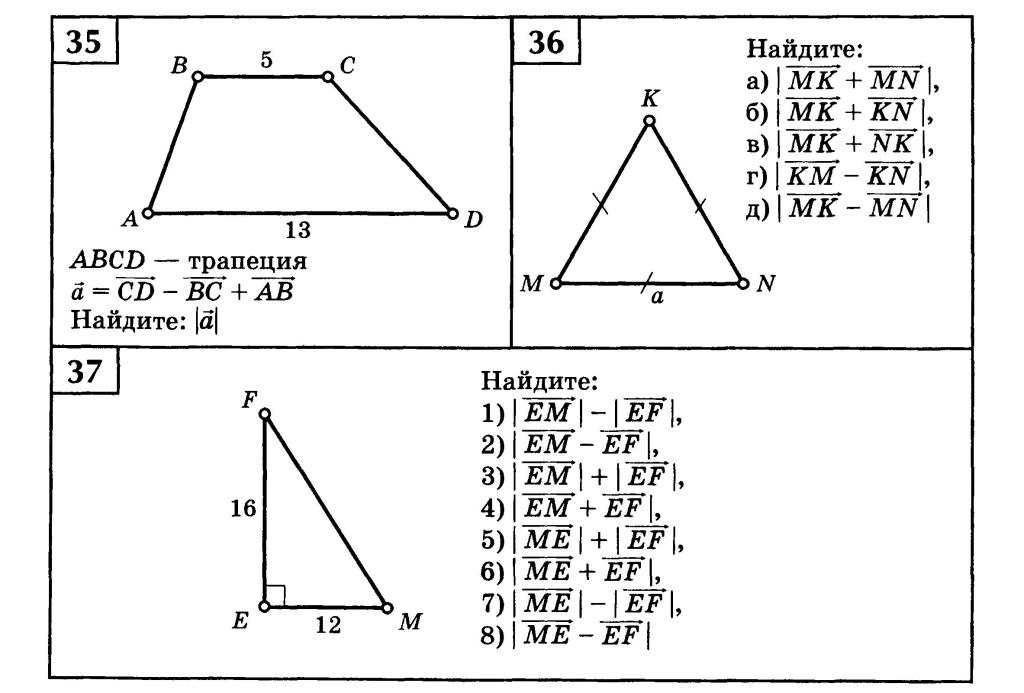 5). Поскольку AE = EB, то, в силу теоремы Фалеса, выполнено равенство: LN = NM, что и требовалось доказать.

Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции. [слайд 9]

Рис. 6

Решение. Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.6). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC, а точка L – середина отрезка BD. Поэтому отрезок

EK – средняя линия треугольника BAC, а отрезок EL – средняя линия треугольника ABD. Зная, что средняя линия треугольника параллельна третьей стороне и равна ее половине, получаем: , следовательно, , что и требовалось доказать.

Учитель: Проведем исследование: постройте произвольный четырехугольник.

Найдите середины сторон этого четырехугольника и соедините их последовательно. Какую фигуру вы получили? (Параллелограмм). Докажите, что это параллелограмм. Что вы при этом использовали? (признак параллелограмма)
Что вы можете сказать о длине сторон полученного параллелограмма? (Они равны половине соответствующей диагонали четырехугольника)

Теорема 2. Середины сторон четырехугольника являются вершинами параллелограмма. (теорема Вариньона) Стороны этого параллелограмма параллельны диагоналям четырехугольника, а их длины равны половинам длин диагоналей. [слайд 10]

Рис. 7

Доказательство: [слайд 11] В самом деле, если К и L – середины сторон АВ и ВС (рис. 7), то KL – средняя линия треугольника ABC, поэтому отрезок KLпараллелен диагонали АС и равен ее половине; если М и N – середины сторон CDи AD, то отрезок MNтакже параллелен АС и равен АС/2. Таким образом, отрезки KLи MN параллельны и равны между собой, значит, четырехугольник

KLMN – параллелограмм.

В качестве следствия из теоремы 2 получаем интересный факт (т. 2).

Теорема 3. В любом четырехугольнике отрезки, соединяющие середины противоположных сторон, делятся точкой пересечения пополам.[слайд 12]

В этих отрезках можно увидеть диагонали параллелограмма (см. рис. 7 [слайд 13]), а в параллелограмме диагонали делятся точкой пересечения пополам (эта точка – центр симметрии параллелограмма).

Учитель: Решим задачу на готовом чертеже [слайд 14]:

Дано: ABCD – трапеция.

Найти: х, у.

Рис. 8

Решение: В трапеции PBCK MK – средняя линия трапеции, тогда , и в трапеции AMND PK – средняя линия трапеции, значит

Тогда x = 4

Ответ: 4; 6

Итак, сегодня на уроке мы с вами узнали, что такое средняя линия треугольника и ее свойства, средняя линия трапеции и ее свойства. Я очень довольна, как вы сегодня работали, особенно хочу отметить…

Домашнее задание: выучить определение и свойства средней линии трапеции. И решить задачи 1 и 2 на готовых чертежах (учащимся раздаются карточки с задачами):

1. Дано: P_ABC = 40.

Найти: P_A₁B₁C₁

2. Дано: ABCD – трапеция

Найти: x, y, z.

[слайд 15]

Использованная литература:

Геометрия 7-9 Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Е.М. Рабинович Геометрия Задачи и упражнения на готовых чертежах
Геометрия 8. Дополнительные главы к учебнику. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Шестаков С.А., Юдина И.И.
Геометрия в таблицах 7-11. Звавич Л.И., Рязановский А.Р.

Средняя линия трапеции

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Понятие средней линии трапеции

2. Теорема о средней линии трапеции

3. Примеры задач на понятие средней линии трапеции

Понятие средней линии трапеции

Для начала вспомним, какую фигуру называют трапецией.

Определение 1

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.

Определение 2

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем её векторным методом.

Теорема 1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).

Рисунок 1. Средняя линия трапеции

Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.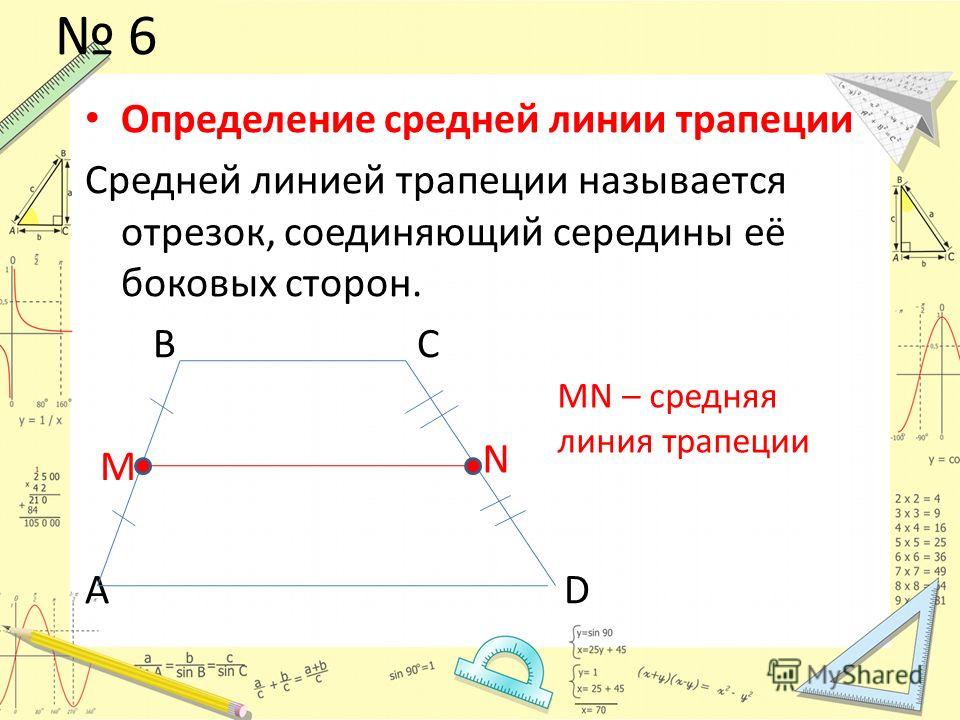

Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что

С другой стороны

Сложим два последних равенства, получим

Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь

Получаем:

Следовательно

Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.

Теорема доказана.

Примеры задач на понятие средней линии трапеции

Пример 1

Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

\[15\ см+17\ см=32\ см\]

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

\[52\ см-32\ см=20\ см\]

Значит, по теореме 1, получаем

\[n=\frac{20\ см}{2}=10\ см\]

Ответ: $10\ см$.

Пример 2

Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.

Решение.

Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

Рисунок 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем

\[OH=\frac{AD+BC}{2}=\frac{9\ см+5\ см}{2}=7\ см.\]

Значит

\[d=2OH=2\cdot 7\ см=14\ см.\]

Ответ: $14$ см.

Пример 3

Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.

Доказательство.

Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ — точку пересечения средней линии с этой диагональю (Рис. 3).

Рисунок 3.

Докажем, что $AK=KC$.

Так как $MN$ — средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ — средняя линия треугольника $ABC$. Значит $AK=KC$.

ч. т. д.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 01.04.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Средняя линия трапеции

Урок 10.

Геометрия 9 класс ФГОС

Данный урок познакомит учащихся с определением средней линии трапеции, а так же будут проведены доказательства её свойств. На протяжении урока рассматриваются примеры решения разнообразных задач, что позволит учащимся успешно усвоить новый материал.

Конспект урока «Средняя линия трапеции»

Вспомним, какую фигуру называют трапецией.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называют её основаниями, а две другие — боковыми сторонами.

Известны два частных случая трапеции. Равнобокая трапеция, у которой боковые стороны равны. И прямоугольная трапеция, у которой один из углов прямой.

К слову, у такой трапеции будет два прямых угла.

Повторив определение трапеции, введём понятие средней линии трапеции.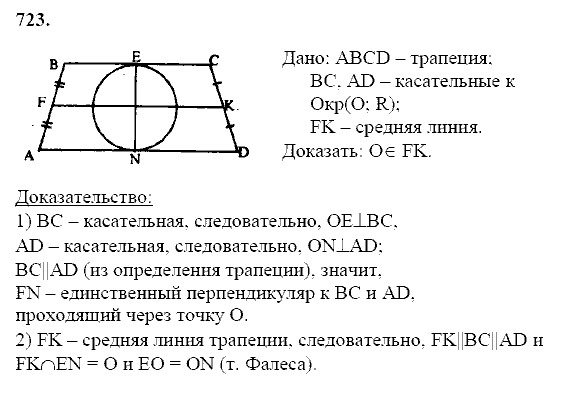

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Изобразим средние линии трапеций изображённых на рисунке.

Для этого сначала найдём их боковые стороны. Далее отметим точками их середины. Ну, а потом проведем средние линии.

Выполним задание. Пользуясь данными рисунков, указать пункты, в которых является средней линией трапеции .

На первом рисунке точка М не является серединой боковой стороны AB, поэтому МN не является средней линией трапеции.

На втором рисунке точки М и N — середины сторон BC и AD, но они являются основаниями трапеции. А по определению средняя линия трапеции соединяет середины боковых сторон. Значит, в данном случае МN не является средней линией.

На третьем рисунке видим, что точки М и N — середины боковых сторон. Причём по рисунку понятно, что эта трапеция — равнобокая.

Так получаем, что МN в данном случае — средняя линия трапеции ABCD.

Посмотрев на следующий рисунок, не трудно заметить, что МN соединяет середину одного из оснований и середину одной из боковых сторон, а не середины боковых сторон. Поэтому МN не является средней линией.

На рисунке под номером 5 точки М и N середины боковых сторон АB и CD трапеции ABCD. Значит, МN — её средняя линия.

В последнем случае точки М и N не поровну делят боковые стороны трапеции, поэтому МN не является её средней линией.

Мы получили, что только на рисунках под номерами 3 и 5 изображены средние линии трапеции.

Как и средняя линия треугольника, средняя линия трапеции обладает определёнными свойствами.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Что и требовалось доказать.

Выполним задание, где, пользуясь этой теоремой и данными рисунков, найдём длины средних линий трапеций.

Длина средней линии трапеции равна полусумме оснований.

На рисунке а известны длины оснований. Поэтому не составит никакого труда найти, что .

Перейдём к рисунку б.

Известен периметр трапеции, тогда можем записать,

В последнем случае также дан периметр трапеции и известны боковые стороны.

Записав периметр через стороны, и, подставив известные значения, можем выразить сумму оснований.

Задача. В трапеции найти длины оснований и , если в два раза больше и длина средней линии равна .

Решение.

Ответ: мм, мм.

Задача. В прямоугольной трапеции . Найти длину средней линии , если , а угол .

Решение.

Ответ: .

Подведём итоги нашего урока.

Сегодня мы познакомились с понятием средней линии трапеции. Это отрезок, соединяющий середины её боковых сторон.

При этом мы выяснили, что средняя линия трапеции обладает следующими свойствами: она параллельна основаниям трапеции и равна их полусумме.

Так же мы рассмотрели примеры применения этих знаний при решении задач.

Предыдущий урок 9 Применение векторов к решению задач

Следующий урок 11 Разложение вектора по двум неколлинеарным векторам

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Подготовка школьников к ЕГЭ и ОГЭ Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Средние линии

Средние линии треугольника

Средняя линия трапеции

Средние линии четырехугольников.

Теорема Вариньона

Средние линии тетраэдра

Средние линии треугольника

Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис.1

На рисунке 1 средней линией является отрезок DE.

Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

Доказательство. Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Рис.2

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Рис.3

Поскольку

DE | | FC , DF | | EC ,

то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно, DE = FC .

Поскольку

DE | | AF , AD | | FE ,

то четырёхугольник DEFA – параллелограммчетырёхугольник DEFA – параллелограмм, следовательно, DE = AF .

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

Следствие.

Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5.

Рис.4

Средняя линия трапеции

Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

Рис.5

На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

Рис.6

Доказательство. Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Рис.7

Решение. Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Рис.8

Решение. Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

Следовательно,

что и требовалось доказать.

Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Рис.9

Доказательство. Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Заметим также, что треугольник KMC подобен треугольнику NMD . Поэтому

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

Рис.10

На рисунке 10 средние линии – это отрезки EF и GH .

Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.

Доказательство. Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Рис.12

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

Рис.13

Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.

Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Рис.14

Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис.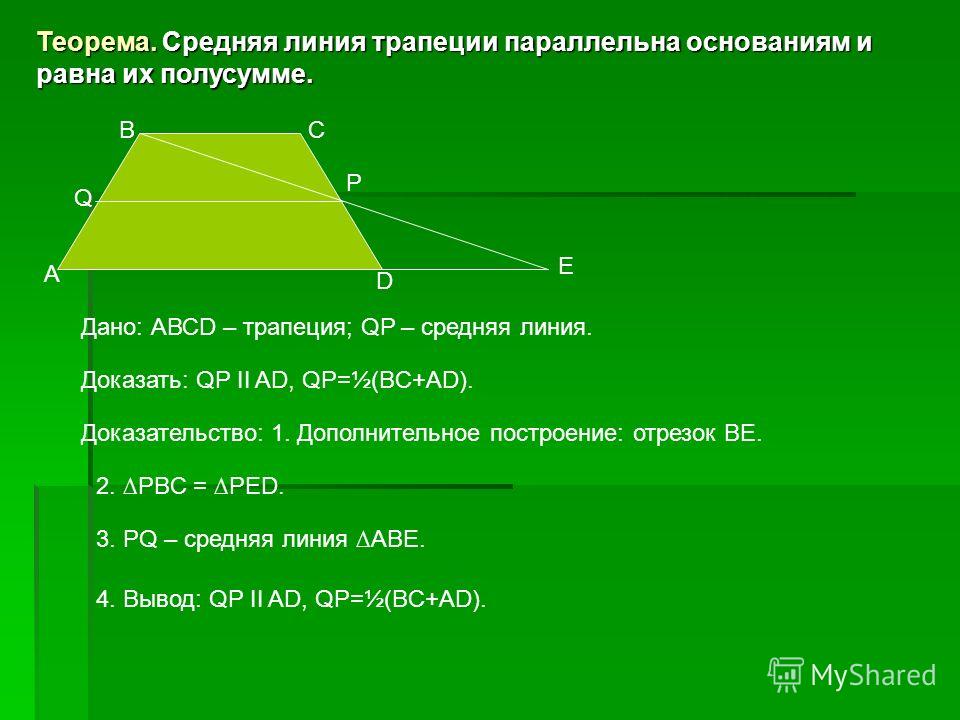 15). Тогда будет выполнено векторное равенство:

Рис.15

Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке O (рис. 16).

Рис.16

В соответствии со свойствами векторов справедливы следующие равенства:

что и требовалось доказать.

Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.

Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

Рис.18

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Рис.19

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Отрезок GF является средней линией треугольника ACB , поэтому

Отсюда вытекает, что отрезки EH и GF равны и параллельны, следовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограмм. Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.

Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.

Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

Рис.20

Доказательство. По свойствам векторов

что и требовалось доказать.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Диагонали трапеции. Средняя линия трапеции

Четырехугольник, у которого параллельны только две стороны, называется трапецией .

Параллельные стороны трапеции называются ее основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.

Средняя линия трапеции

Средняя линия — это отрезок, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.

Теорема:

Если прямая, проходящая через середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.

Теорема:

Длина средней линии равна среднему арифметическому длин ее оснований

МН || АБ || DC
утра = МД; БН = НЗ

МН средняя линия, АВ и CD — основания, AD и ВС — стороны

МН = (АВ + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин его оснований.

Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине основания трапеции.

Центральная линия треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и составляет половину длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне этого треугольника, то она делит третью сторону пополам.

AM = MC и BN = NC =>

Применение свойств средней линии треугольника и трапеции

Деление сегмента на определенное количество равных частей.
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч с началом в точке A, не лежащий на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Соединяем А 5 с В и проводим через А 4, А 3, А 2 и А 1 такие прямые, которые параллельны А 5 В. Они пересекают АВ соответственно в точках В 4, В 3, В 2 и В 1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции ВВ 3 А 3 А 5 видим, что ВВ 4 = В 4 В 3. Точно так же из трапеции В 4 В 2 А 2 А 4 получаем В 4 В 3 = В 3 В 2

Тогда как из трапеции B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем :
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных отрезков на луч р. А затем продолжить, как описано выше.

Понятие средней линии трапеции

Для начала вспомним, какая фигура называется трапецией.

Определение 1

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.

Определение 2

Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.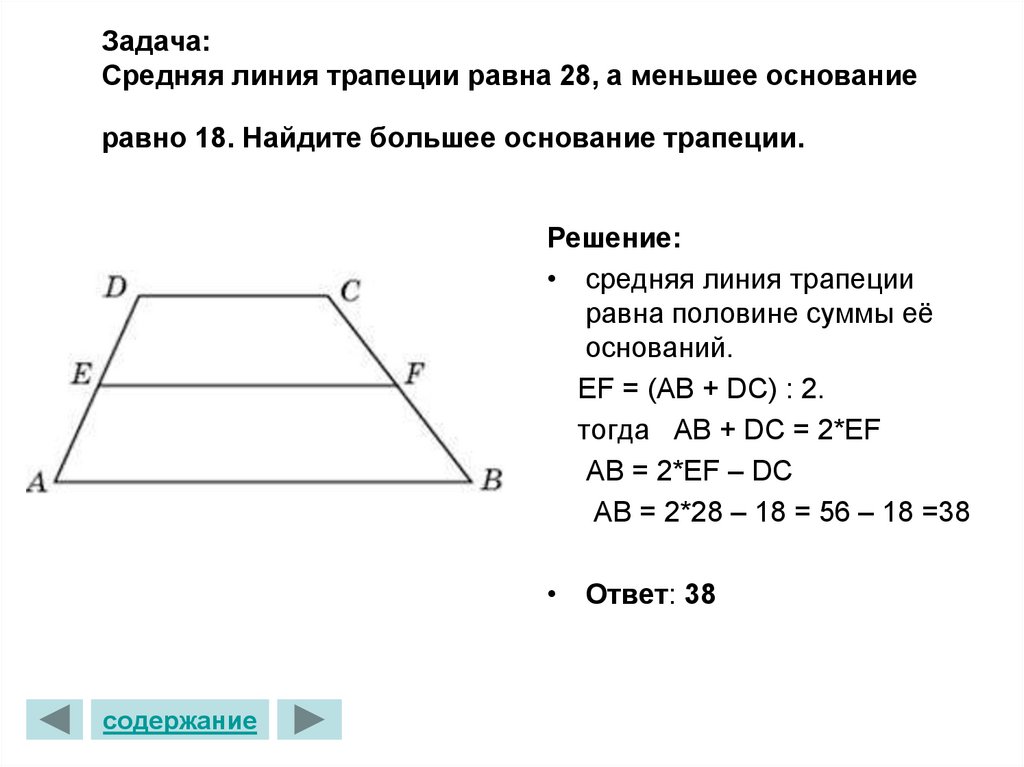

Теорема 1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Дана трапеция $ABCD$ с основаниями $AD\ и \BC$. И пусть $MN$ будет средней линией этой трапеции (рис. 1).

Рис. 1. Средняя линия трапеции

Докажем, что $ MN || AD\ и \MN = \frac(AD+BC)(2)$.

Рассмотрим вектор $\overrightarrow(MN)$. Затем мы используем правило многоугольника для добавления векторов. С одной стороны получаем что

С другой стороны

Сложим два последних равенства, получим

Так как $M$ и $N$ являются серединами боковых сторон трапеции, то будем иметь

Получаем:

Отсюда

Из того же равенства (так как $\overrightarrow(BC)$ и $\ (AD) $ сонаправлены и, следовательно, коллинеарны) получаем $ MN || АД $.

Теорема доказана.

Примеры заданий на понятие средней линии трапеции

Пример 1

Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен 52$\см$. Найдите длину средней линии трапеции.

Раствор.

Обозначим среднюю линию трапеции через $n$.

Сумма сторон равна

Следовательно, так как периметр равен 52$\см$, то сумма оснований равна

Отсюда по теореме 1 получаем

Ответ: $10\см$.

Пример 2

Концы диаметра окружности удалены от ее касательной на $9$ см и $5$ см соответственно. Найдите диаметр этого круга.

Раствор.

Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\см$ и $BC=5\см$. Проведем радиус $ОН$ (рис. 2).

Рис. 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH \bot l $, следовательно, $OH | \ слева | AD \ справа || БК $. Из всего этого получаем, что $ABCD$ — это трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем

Трапеция — это частный случай четырехугольника с одной парой параллельных сторон. Термин «трапеция» происходит от греческого слова τράπεζα, означающего «стол», «стол». В этой статье мы рассмотрим виды трапеций и их свойства. Кроме того, мы разберемся, как рассчитать отдельные элементы этого Например, диагональ равнобедренной трапеции, среднюю линию, площадь и т. д. Материал представлен в стиле элементарной популярной геометрии, то есть в легкодоступной форме. .

Общая информация

Для начала разберемся, что такое четырехугольник. Эта фигура представляет собой частный случай многоугольника с четырьмя сторонами и четырьмя вершинами. Две несмежные вершины четырехугольника называются противоположными. То же самое можно сказать и о двух несмежных сторонах. Основные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтовидная форма.

Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны параллельны. Они называются базами. Две другие (непараллельные) — стороны. В экзаменационных материалах и различных контрольных работах очень часто можно встретить задачи, связанные с трапециями, решение которых часто требует от студента знаний, не предусмотренных программой. Школьный курс геометрии знакомит учащихся со свойствами углов и диагоналей, а также со средней линией равнобедренной трапеции. Но кроме этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…

Типы трапеций

Есть много типов этой фигуры. Однако чаще всего принято рассматривать две из них – равнобедренную и прямоугольную.

1. Прямоугольной трапецией называется фигура, у которой одна из боковых сторон перпендикулярна основаниям. Два его угла всегда равны девяноста градусам.

2. Равнобедренная трапеция – геометрическая фигура, стороны которой равны между собой. Это означает, что углы при основаниях также попарно равны.

Основные принципы методики изучения свойств трапеции

Основным принципом является использование так называемого задачного подхода. В принципе, нет необходимости вводить в теоретический курс геометрии новые свойства этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных).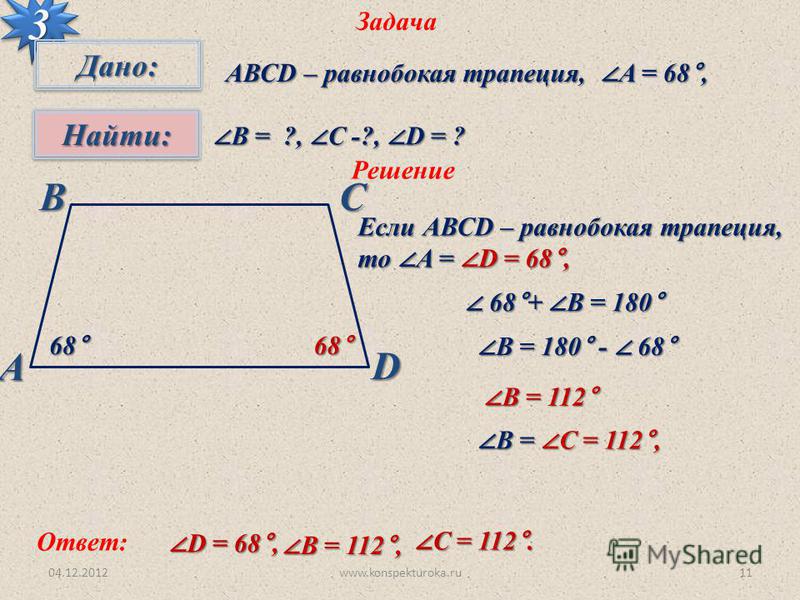 При этом очень важно, чтобы учитель знал, какие задачи нужно ставить перед школьниками в тот или иной момент. учебный процесс . При этом каждое свойство трапеции можно представить как ключевую задачу в системе задач.

Второй принцип – так называемая спиральная организация изучения «замечательных» свойств трапеции. Это предполагает возврат в процессе обучения к отдельным признакам заданной геометрической фигуры. Это облегчает обучающимся их запоминание. Например, свойство четырех точек. Это можно доказать как изучением подобия, так и последующим использованием векторов. А равновеликость треугольников, примыкающих к боковым сторонам фигуры, можно доказать, применяя не только свойства равновеликих треугольников, проведенных к сторонам, лежащим на одной прямой, но и используя формулу S = 1/2 (аб*синα). Кроме того, можно работать на вписанной трапеции или прямоугольном треугольнике на описанной трапеции и т. д.

Использование «внеклассных» признаков геометрической фигуры в содержании школьного курса – задача технологии их обучения.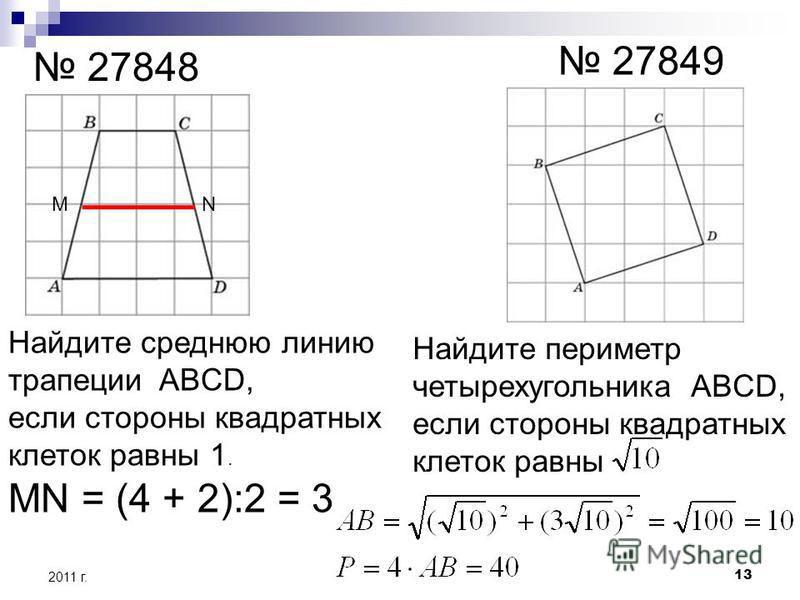 Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже понять трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.

Элементы и свойства равнобедренной трапеции

Как мы уже отмечали, эта геометрическая фигура имеет равные стороны. Его также называют правильной трапецией. И чем он так примечателен и почему получил такое название? К особенностям этой фигуры относится то, что равны не только стороны и углы при основаниях, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусов. Но это не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов этой фигуры равна 180 градусам, и только при этом условии вокруг четырехугольника можно описать окружность. Следующее свойство рассматриваемой геометрической фигуры состоит в том, что расстояние от вершины основания до проекции противоположной вершины на прямую, содержащую это основание, будет равно центральной линии.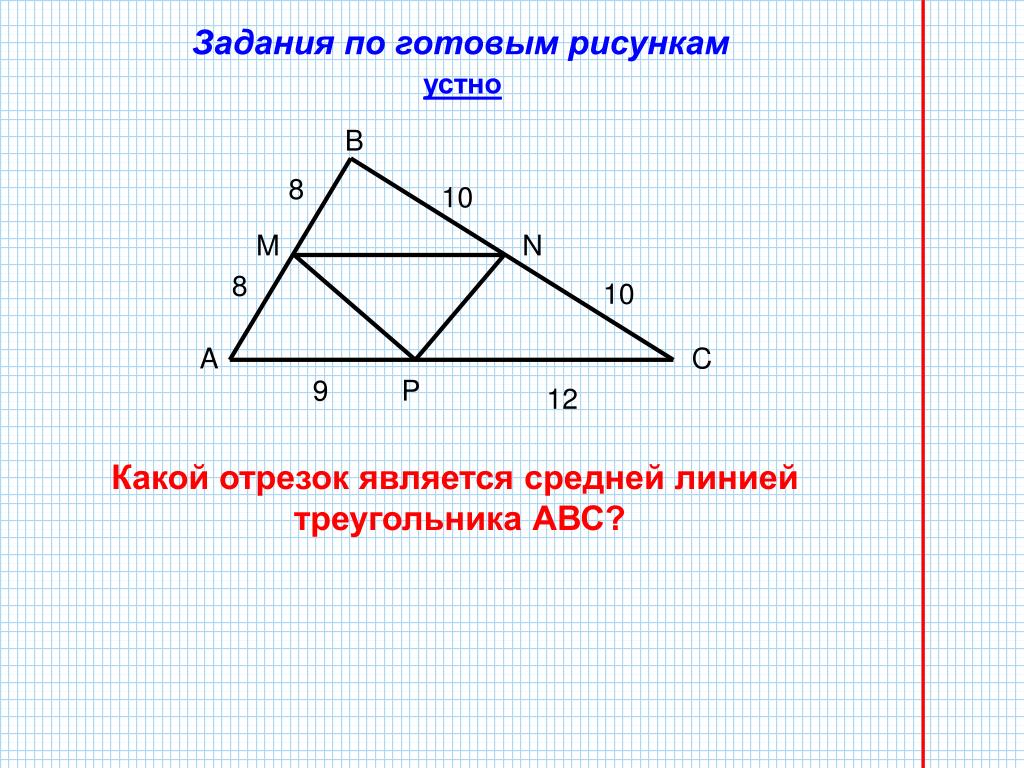

Теперь разберемся, как найти углы равнобедренной трапеции. Рассмотрим решение этой задачи при условии, что известны размеры сторон фигуры.

Решение

Обычно четырехугольник принято обозначать буквами A, B, C, D, где BS и AD — основания. У равнобедренной трапеции стороны равны. Будем считать, что их размер равен X, а размеры оснований равны Y и Z (меньше и больше соответственно). Для проведения расчета необходимо из угла В провести высоту Н. В результате получится прямоугольный треугольник АВН, где АВ — гипотенуза, а ВН и АН — катеты. Вычисляем размер катета AH: из большего основания вычитаем меньшее, а результат делим на 2. Записываем в виде формулы: (Z-Y)/2=F. Теперь вычисляем острый угол треугольника, мы используем функцию cos. Получаем следующую запись: cos(β) = X/F. Теперь вычисляем угол: β = arcos(X/F). Далее, зная один угол, мы можем определить второй, для этого выполняем элементарное арифметическое действие: 180 — β. Все углы определены.

Есть и второе решение этой проблемы. В начале опускаем высоту Н. от угла. Рассчитайте значение ножки BN. Мы знаем, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: BN = √(X2-F2). Далее воспользуемся тригонометрической функцией tg. В итоге имеем: β = arctg (BN/F). Найден острый угол. Далее определяем так же, как и в первом способе.

Свойство диагоналей равнобедренной трапеции

Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:

Высота фигуры будет равна сумме оснований, деленной на два;

Его высота и средняя линия равны;

Центром круга является точка их пересечения;

Если боковая сторона делится точкой касания на отрезки Н и М, то она равна произведениям квадратных корней этих отрезков;

Четырехугольник, образованный точками касания, вершиной трапеции и центром вписанной окружности, представляет собой квадрат, сторона которого равна радиусу;

Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.

Аналогичная трапеция

Эта тема очень удобна для изучения свойств этой. Например, диагонали делят трапецию на четыре треугольника, причем прилежащие к основаниям подобны, а к боковым сторонам равны. Это утверждение можно назвать свойством треугольников, на которые трапеция делится своими диагоналями. Первая часть этого утверждения доказывается через признак подобия двух углов. Для доказательства второй части лучше использовать способ, описанный ниже.

Доказательство теоремы

Примем, что фигура АБСД (ВР и BS — основания трапеции) делится диагоналями ВД и AS. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АВО и СОД у боковых сторон. Треугольники SOD и BFB имеют общую высоту, если их основаниями являются отрезки BO и OD. Получаем, что разность их площадей (Р) равна разнице между этими отрезками: ПБОС/ПСОД=БО/ОД=К. Следовательно, ПБОС=ПБОС/К. Аналогично, треугольники БФВ и АОВ имеют общую высоту.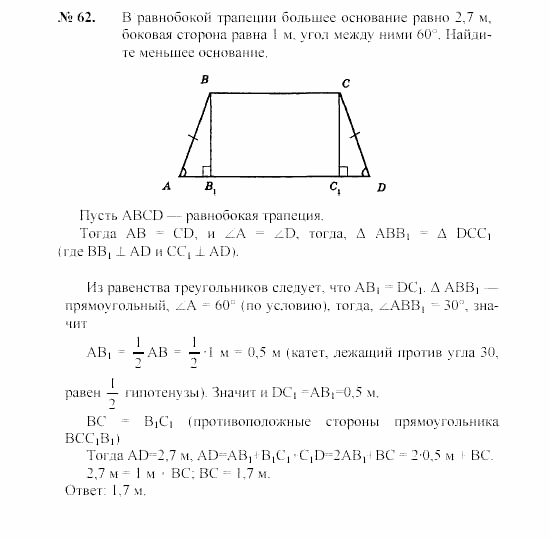 За их основания возьмем отрезки SB и OA. Получаем PBOS/PAOB=SO/OA=K и PAOB=PBOS/K. Отсюда следует, что PSOD=PAOB.

Для закрепления материала учащимся предлагается найти связь между площадями полученных треугольников, на которые трапеция делится своими диагоналями, решая следующую задачу. Известно, что площади треугольников биологической обратной связи и АОЗ равны; надо найти площадь трапеции. Поскольку PSOD = PAOB, это означает, что PABSD = PBOS + PAOD + 2 * PSOD. Из подобия треугольников BFB и AOD следует, что BO/OD = √(PBOS/PAOD). Следовательно, ПБОС/ПСОД=БО/ОД=√(ПБОС/ПАОД). Получаем PSOD=√(PBOS*PAOD). Тогда PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2,

Подобие свойств

Продолжая развивать эту тему, можно доказать и другие интересные особенности трапеции. Итак, с помощью подобия можно доказать свойство отрезка, проходящего через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка RK, который проходит через точку O. Из подобия треугольников AOD и BFB следует, что AO/OS = AD/BS . Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО = БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК = БС * АД / (БС + АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две стороны, делится точкой пересечения пополам. Его длина есть среднее гармоническое основания фигуры.

Рассмотрим следующее свойство трапеции, которое называется четырехточечным свойством. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Г) всегда лежат на одной прямой. Это легко доказывается методом подобия. Получившиеся треугольники BES и AED подобны, и в каждом из них медианы ET и EZ делят угол при вершине E на равные части. Следовательно, точки E, T и Ж лежат на одной прямой. Точно так же точки Т, О и Ж расположены на одной прямой.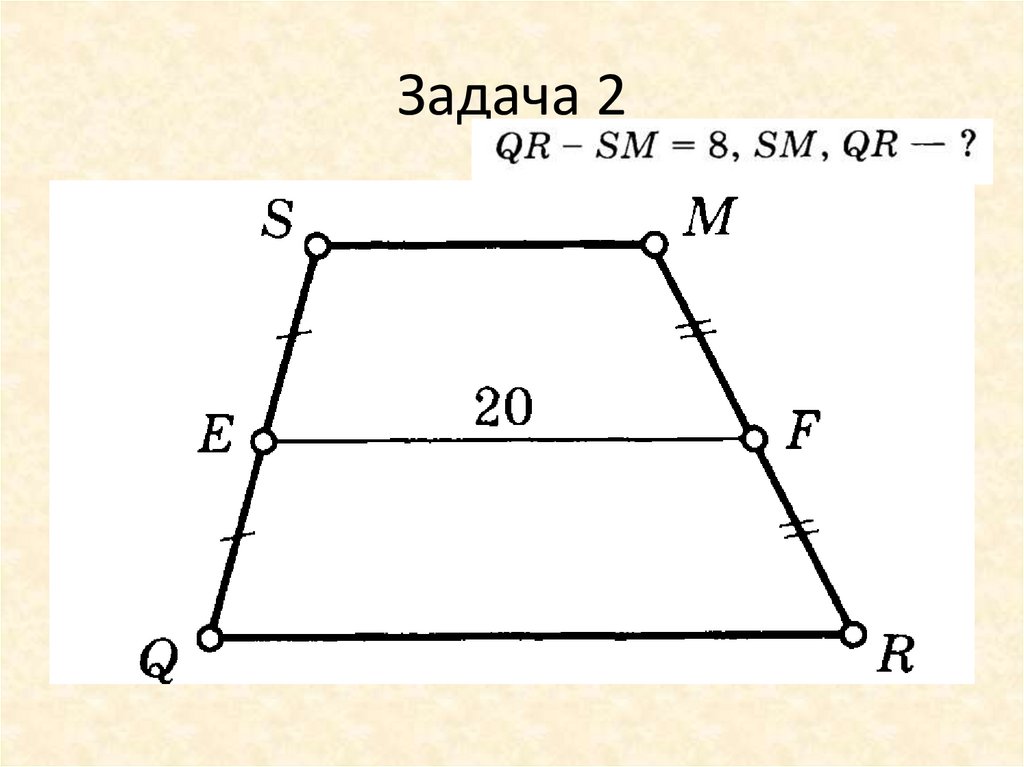 Все это следует из подобия треугольников BFB и AOD. Отсюда делаем вывод, что все четыре точки — Е, Т, О и F — будут лежать на одной прямой.

Используя такие трапеции, можно попросить учащихся найти длину отрезка (LF), который разбивает фигуру на две подобные. Этот отрезок должен быть параллелен основаниям. Так как полученные трапеции ALPD и LBSF подобны, то BS/LF = LF/BP. Отсюда следует, что ЛФ = √(БС*АД). Получаем, что отрезок, делящий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две фигуры одинакового размера. Считаем, что трапеция ABSD разделена отрезком ЕН на две подобные. Высота сбрасывается с вершины B, которая делится отрезком EH на две части — B1 и B2. Получаем: ПАБСД/2=(БС+ЭХ)*Б1/2=(АД+ЭХ)*Б2/2 и ПАБСД=(БС+АД)*(Б1+Б2)/2. Далее составляем систему, первое уравнение которого (БС+ЭН)*В1=(АД+ЭН)*В2 и второе (БС+ЭН)*В1=(БС+АД)*(Б1+В2)/2. Отсюда следует, что В2 /Б1=(БС+ЭХ)/(АД+ЭХ) и БС+ЭХ=((БС+АД)/2)*(1+Б2/Б1). Получаем, что длина отрезка, делящего трапецию на две равные по размеру, равна среднему квадрату длин оснований: √ ((BS2 + AD2)/2).

Находки подобия

Итак, мы доказали, что:

1. Отрезок, соединяющий середины боковых сторон трапеции, параллелен ВР и ВР и равен среднему арифметическому между ВР и ВР (длина основание трапеции).

2. Прямая, проходящая через точку О пересечения диагоналей, параллельных АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).

3. Отрезок, делящий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.

4. Элемент, делящий фигуру на два равных размера, имеет длину средних квадратов чисел BP и BS.

Для закрепления материала и понимания связи между рассматриваемыми отрезками учащемуся необходимо построить их для конкретной трапеции. Он легко может отобразить среднюю линию и отрезок, проходящий через точку О — пересечение диагоналей фигуры — параллельно основаниям.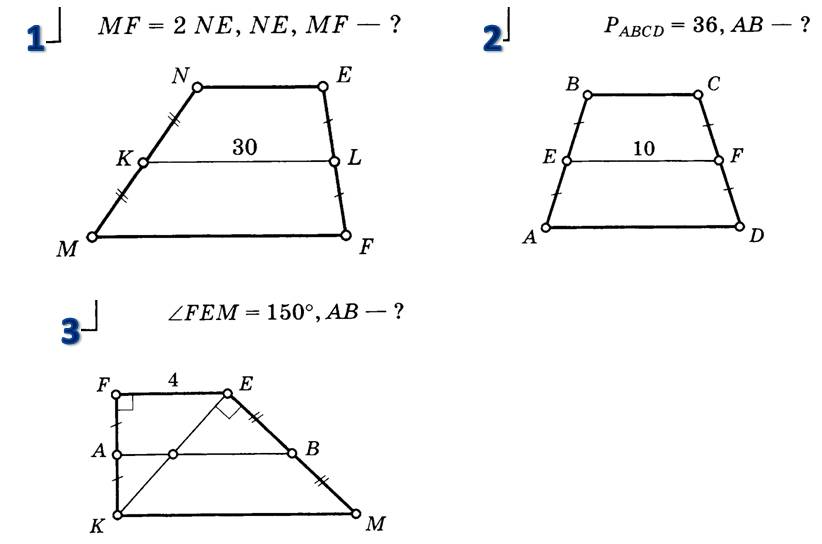 Но где будут находиться третий и четвертый? Этот ответ приведет студента к обнаружению желаемого соотношения между средними значениями.

Отрезок, соединяющий середины диагоналей трапеции

Рассмотрим следующее свойство этой фигуры. Предположим, что отрезок MH параллелен основаниям и делит диагонали пополам. Точки пересечения будем называть Ш и Ш. Этот отрезок будет равен половине разности оснований. Давайте посмотрим на это поближе. МШ — средняя линия треугольника АБС, она равна БС/2. МЧ — средняя линия треугольника АБД, равна ВР/2. Тогда получаем, что ШШ = МШ-МШ, следовательно, ШШ = АД/2-БС/2=(АД+ВС)/2.

Центр тяжести

Давайте посмотрим, как определяется этот элемент для данной геометрической фигуры. Для этого необходимо вытянуть основания в противоположные стороны. Что это значит? К верхнему основанию необходимо добавить нижнее — в любую сторону, например, вправо. И удлинить нижний на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры является центром тяжести трапеции.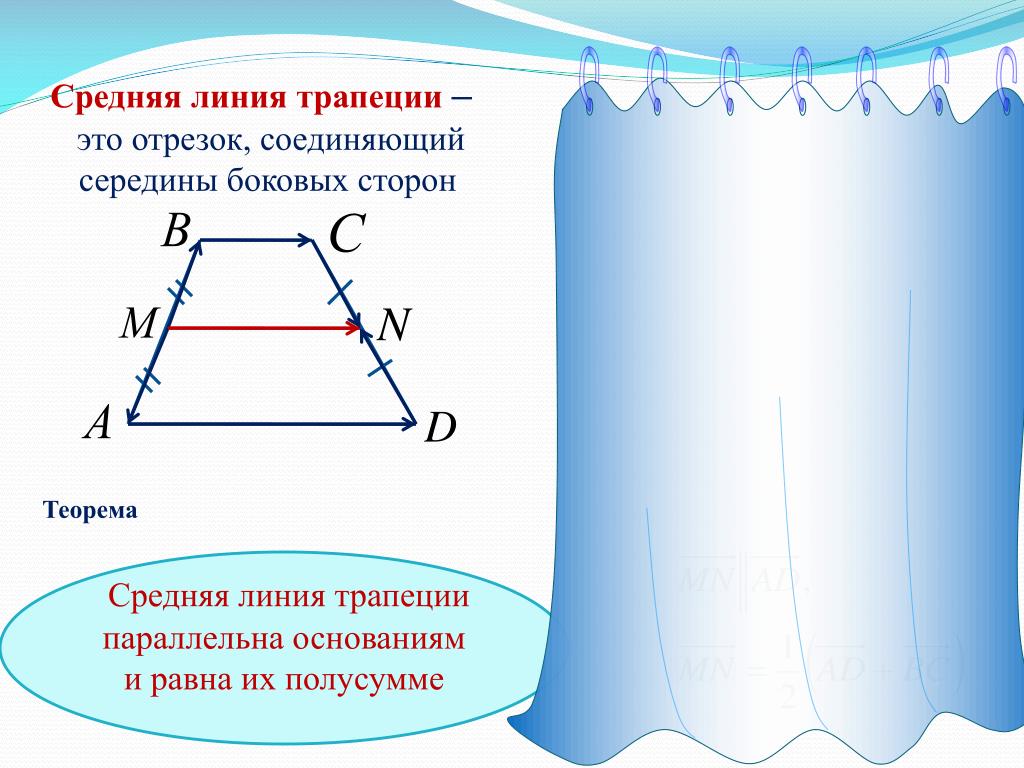

Вписанные и описанные трапеции

Перечислим признаки таких фигур:

1. Трапецию можно вписать в окружность, только если она равнобедренная.

2. Трапецию можно описать по окружности при условии, что сумма длин их оснований равна сумме длин боковых сторон.

Последствия вписанной окружности:

1. Высота описываемой трапеции всегда равна двум радиусам.

2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.

Первое следствие очевидно, но для доказательства второго требуется установить, что угол СОД прямой, что, собственно, тоже не составит труда. Но знание этого свойства позволит использовать прямоугольный треугольник при решении задач.

Теперь конкретизируем эти следствия для равнобедренной трапеции, вписанной в окружность. Получаем, что высота есть среднее геометрическое основания фигуры: H = 2R = √(BS*АД). При отработке основного приема решения задач на трапеции (принцип удержания двух высот) учащийся должен решить следующую задачу. Будем считать, что ВТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки AT и TD. Используя формулу, описанную выше, сделать это не составит труда.

Теперь разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем высоту от вершины Б к основанию АД. Так как окружность вписана в трапецию, то БС+АД=2АВ или АВ=(БС+АД)/2. Из треугольника АБН находим sinα=БН/АВ=2*БН/(БС+АД). ПАБСД=(БС+АД)*БН/2, БН=2Р. Получаем ПАБСД=(БС+АД)*R, отсюда следует, что R=ПАБСД/(БС+АД).

Все формулы средней линии трапеции

Теперь пришло время перейти к последнему элементу этой геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):

1. Через основания: М = (А+В)/2.

2. Через высоту, основание и углы:

М = А-Н* (ctgα + ctgβ)/2;

M = B + H * (ctgα + ctgβ) / 2.

3. Через высоту, диагонали и угол между ними. Например, D1 и D2 — диагонали трапеции; α, β — углы между ними:

М = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.

4. По площади и высоте: M = P/N.

ЧЕТЫРЕ УГЛА.

§ 49. ТРАПЕЦИЯ.

Четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны, называется трапецией.

На рис. 252 четырехугольник ABDC AB || компакт-диск, переменный ток || БД. ABDC — трапеция.

Параллельные стороны трапеции называются ее основаниями ; АВ и CD — основания трапеции. Две другие стороны называются боковые стороны трапеция; АС и ВD — стороны трапеции.

Если стороны равны, то трапеция называется равнобедренной .

Трапеция АВОМ равнобедренная, так как АМ = VO (рис. 253).

Трапецию, у которой одна из боковых сторон перпендикулярна основанию, называют прямоугольной (рис. 254).

Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.

Теорема. Средняя линия трапеции параллельна каждому из ее оснований и равна их полусумме.

Дано: OS — средняя линия трапеции ABDK, то есть OK = OA и BC = CD (рис. 255).

Необходимо доказать:

1) ОС || КД и ОС || АБ;
2)

Доказательство. Через точки A и C проведем прямую, пересекающую продолжение основания KD в некоторой точке E.

В треугольниках ABC и DCE:
ВС = СD — по условию;
/ 1 = / 2 вертикально,
/ 4 = / 3, как внутренний крест-накрест с параллельными АВ и КЕ и секущей BD. Следовательно, /\ АВС = /\ ДСЕ.

Следовательно, AC = CE, т.е. OS – средняя линия треугольника КАЕ. Следовательно (§ 48):

1) ОС || КЭ и, следовательно, ОС || КД и ОС || АБ;
2) , но DE = AB (из равенства треугольников ABC и DCE), поэтому отрезок DE можно заменить равным ему отрезком AB. Тогда получаем:

Теорема доказана.

Упражнения.

1. Докажите, что сумма внутренних углов трапеции, примыкающих к каждой стороне, равна 2 d .

2. Докажите, что углы при основании равнобедренной трапеции равны.

3. Докажите, что если углы при основании трапеции равны, то эта трапеция равнобедренная.

4. Докажите, что диагонали равнобедренной трапеции равны.

5. Докажите, что если диагонали трапеции равны, то эта трапеция равнобедренная.

6. Докажите, что периметр фигуры, образованной отрезками, соединяющими середины сторон четырехугольника, равен сумме диагоналей этого четырехугольника.

7. Докажите, что прямая, проходящая через середину одной из боковых сторон трапеции параллельно ее основаниям, делит другую боковую сторону трапеции пополам.

просмотров

Площадь трапеции — формула, примеры, определение, вывод

Площадь трапеции — это количество единичных квадратов, которые могут быть вписаны в нее, и измеряется в квадратных единицах (например, см ², м ², ² и т. д.). Например, если внутрь трапеции можно поместить 15 единичных квадратов длиной 1 см каждый, то ее площадь будет равна 15 см ² . Трапеция — это тип четырехугольника с одной парой параллельных сторон (которые известны как основания). Это означает, что другая пара сторон может быть непараллельной (известной как ноги). Не всегда возможно нарисовать единичные квадраты и измерить площадь трапеции. Итак, давайте узнаем о формуле для нахождения площади трапеции на этой странице.

1.	Какова площадь трапеции?
2.	Площадь трапеции Формула
3.	Площадь трапеции без высоты
4.	Как вывести формулу площади трапеции?
5.	Калькулятор площади трапеции
6.	Часто задаваемые вопросы по площади трапеции

Какова площадь трапеции?

Площадь трапеции равна площади, занимаемой ее сторонами. Здесь следует отметить интересный момент: если мы знаем длины всех сторон, мы можем просто разделить трапецию на более мелкие многоугольники, такие как треугольники и прямоугольники, найти их площади и сложить их, чтобы получить площадь трапеции. Однако есть прямая формула, которая используется для нахождения площади трапеции, если известны определенные размеры.

Формула площади трапеции

Площадь трапеции можно вычислить, если известны длины ее параллельных сторон и расстояние (высота) между ними. Формула площади трапеции выражается следующим образом:

A = ½ (a + b) h

, где (A) — площадь трапеции, а и b — основания. (параллельные стороны), а «h» — высота (перпендикулярное расстояние между a и b)

Пример:

Найдите площадь трапеции, параллельные стороны которой равны 32 см и 12 см соответственно, а высота равна 5 см.

Решение:

Основания даны как, a = 32 см; б = 12 см; высота h = 5 см.

Площадь трапеции = A = ½ (a + b) h

A = ½ (32 + 12) × (5) = ½ (44) × (5) = 110 см ² .

Площадь трапеции без высоты

Зная все стороны трапеции и не зная высоту, можно найти площадь трапеции. В этом случае нам сначала нужно вычислить высоту трапеции. Давайте разберемся в этом с помощью примера.

Пример: Найдите площадь трапеции, у которой основания (параллельные стороны) равны 6 и 14 единицам соответственно, а непараллельные стороны (катеты) равны 5 единицам каждая.

Решение: Вычислим площадь трапеции, используя следующие шаги.

Шаг 1: Мы знаем, что площадь трапеции = ½ (a + b) h; где h — высота трапеции, которая в данном случае не приводится; a = 6 единиц, b = 14 единиц, непараллельные стороны (ножки) = по 5 единиц.
Шаг 2: Итак, если мы найдем высоту трапеции, мы сможем вычислить площадь. Если мы начертим высоту трапеции с обеих сторон, мы увидим, что трапеция разбита на прямоугольник ABQP и 2 прямоугольных треугольника, ADP и BQC.
Шаг 3: Поскольку прямоугольник имеет равные противоположные стороны, это означает, что AP = BQ, и известно, что стороны AD = BC = 5 единиц. Итак, высоты AP и BQ можно вычислить по теореме Пифагора.
Шаг 4: Теперь найдем длину DP и QC. Поскольку ABQP — прямоугольник, AB = PQ и DC = 14 единиц. Это означает, что PQ = 6 единиц, а оставшуюся общую длину DP + QC можно рассчитать следующим образом. DC — PQ = 14 — 6 = 8. Итак, 8 ÷ 2 = 4 единицы. Следовательно, DP = QC = 4 ед.
Шаг 5: Теперь можно вычислить высоту трапеции по теореме Пифагора. Взяв прямоугольный треугольник ADP, мы знаем, что AD = 5 единиц, DP = 4 единицы, поэтому AP = √(AD ² — DP ² ) = √(5 ² — 4 ² ) = √(25 — 16) = √9 = 3 единицы. Поскольку ABQP — прямоугольник, у которого противоположные стороны равны, AP = BQ = 3 единицы.
Шаг 6: Теперь, когда мы знаем все размеры трапеции, включая высоту, мы можем вычислить ее площадь по формуле: площадь трапеции = ½ (a + b) h; где h = 3 ед., a = 6 ед., b = 14 ед. После подстановки значений в формулу получаем, площадь трапеции = ½ (a + b) h = ½ (6 + 14) × 3 = ½ × 20 × 3 = 30 ед. ² .

Как вывести формулу площади трапеции?

Мы можем доказать формулу площади трапеции, используя здесь треугольник. Взяв трапецию с основаниями «а» и «b» и высотой «h», докажем формулу.

Шаг 1: Разделите одну из ножек на две равные части и вырежьте треугольную часть трапеции, как показано на рисунке.
Шаг 3: Прикрепите его снизу, как показано, так, чтобы получился большой треугольник.

Шаг 4: Таким образом, трапеция преобразуется в треугольник. Даже после того, как мы присоединим его таким образом, мы знаем, что площади трапеции и нового большого треугольника остаются прежними. Мы также можем видеть, что основание нового большого треугольника равно (a + b), а высота треугольника равна h.
Шаг 5: Итак, можно сказать, что площадь трапеции = площади треугольника
Шаг 6: Это можно записать как площадь трапеции = ½ × основание × высота = ½ (a + b) h

Итак, мы доказали формулу нахождения площади трапеции.

Калькулятор площади трапеции

Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Калькулятор площади трапеции — это онлайн-инструмент, который помогает найти площадь трапеции. Если доступны определенные параметры, такие как значение основания или высоты, мы можем напрямую ввести входные данные и рассчитать площадь. Попробуйте калькулятор площади трапеции Куэмата и рассчитайте площадь трапеции за несколько секунд. Для большей практики проверьте площадь листа трапеции и решите задачи с помощью калькулятора.

☛ Статьи по теме

Площадь равностороннего треугольника
Площадь квадрата
Площадь параллелограмма
Площадь прямоугольника
Площадь ромба
Район Пентагона
Площадь круга

Площадь трапеции Примеры

Пример 1: Если одно из оснований трапеции равно 8 единицам, высота 12 единиц, а площадь 108 квадратных единиц, найдите длину другого основания.
Решение:
Одно из оснований равно «а» = 8 единиц.
Пусть другое основание будет ‘b’.
Площадь трапеции A = 108 квадратных единиц.
Его высота ‘h’ = 12 единиц.
Подставить все эти значения в область формулы трапеции,
A = ½ (a + b) h
108 = ½ (8 + b) × (12)
108 = 6 (8 + b)
Разделив обе части на 6,
18 = 8 + b
b = 10
Ответ: Длина другого основания данной трапеции = 10 ед.
Пример 2: Найдите площадь равнобедренной трапеции, у которой длина каждого катета равна 8 единицам, а основания равны 13 единицам и 17 единицам соответственно.
Решение:
Базы a = 13 единиц и b = 17 единиц. Предположим, что его высота равна h.
Данную трапецию можно разделить на два конгруэнтных прямоугольных треугольника и прямоугольник следующим образом:
На приведенном выше рисунке
x + x + 13 = 17
2x + 13 = 17
2x = 4
x = 2
с использованием теоремы Pythagoras,
x ² + H ^{. 2} = 8 ²
2 ² + H ² = 64
4 + H ² = 64
H ² = 60
H = √60 = × a ². = 2√15
Площадь данной трапеции равна,
A = ½ (a + b) h
A = ½ (13 + 17) × (2√15) = 30√15 = 116,18 квадратных единиц
Ответ: Площадь данной трапеции = 116,18 квадратных единиц.
Пример 3: Найдите площадь трапеции, у которой основания равны 7 единицам и 9 единицам, а высота равна 5 единицам.
Решение: Площадь трапеции = ½ (a + b) h; где a = 7, b = 9, h = 5.
Подставляя эти значения в формулу, получаем:
A = ½ (a + b) h
A = ½ (7 + 9) × 5
A = ½ × 16 × 5 = 40 единиц ²
Следовательно, площадь трапеции равна 40 кв. единицы.

перейти к слайдуперейти к слайдуперейти к слайду

Развивайте логическое мышление и укрепляйте его уверенность!

Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!

Забронировать бесплатный пробный урок

Практические вопросы по площади трапеции

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по площади трапеции

Что такое площадь трапеции в математике?

Площадь трапеции — это количество единичных квадратов, которые могут в нее поместиться. Мы знаем, что трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. Площадь трапеции рассчитывается по формуле Площадь трапеции = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — перпендикулярная высота. Он представлен в квадратных единицах.

Как найти площадь трапеции?

Площадь трапеции находится по формуле A = ½ (a + b) h, где «a» и «b» — основания (параллельные стороны), а «h» — высота (перпендикулярное расстояние между основания) трапеции.

Почему площадь трапеции равна ½ (a + b) h?

Формулу площади трапеции можно легко доказать. Рассмотрим трапецию с основаниями «а» и «b» и высотой «h». Мы можем отрезать от трапеции треугольную часть и прикрепить ее внизу, чтобы вся трапеция превратилась в треугольник. Тогда полученный треугольник имеет основание (a + b) и высоту h. Применяя формулу площади треугольника, площадь трапеции (или треугольника) = ½ (a + b) h. Для получения дополнительной информации вы можете обратиться к статье Как вывести формулу площади трапеции? раздел этой страницы.

Как найти недостающее основание трапеции, если известна площадь?

Мы знаем, что площадь трапеции с основаниями а и b и высотой h равна A = ½ (a + b) h. Если одно из оснований (скажем, «а»), высота и площадь заданы, то мы просто подставим эти значения в приведенную выше формулу и решим ее для отсутствующего основания (а) следующим образом:

A = ½ (a + b) h

Умножение обеих частей на 2,

2A = (a + b) h

Деление обеих частей на h,

2A/h = a + b

Вычитание b с обеих сторон,

a = (2A/h) — b

Как найти высоту трапеции с площадью и основанием?

Если площадь и основания трапеции известны, то мы можем вычислить ее высоту по формуле Площадь трапеции = ½ (a + b) h; где «а» и «b» — основания, а «h» — высота. Другими словами, мы можем найти высоту трапеции, подставив заданные значения площади и двух оснований.

Как найти площадь равнобедренной трапеции без высоты?

Если высота трапеции не задана и известны все ее стороны, то мы можем разделить трапецию на два конгруэнтных прямоугольных треугольника и прямоугольник. Используя теорему Пифагора в прямоугольных треугольниках, мы можем вычислить высоту. После того, как мы получим высоту, мы можем использовать формулу A = ½ (a + b) h, чтобы получить площадь трапеции.

Какая формула площади трапеции?

Формула, используемая для нахождения площади трапеции, выглядит следующим образом: Площадь трапеции = ½ (a + b) h; где а и b — основания (параллельные стороны), а h — высота трапеции.

Площадь трапеции – объяснение и примеры

Напомним, трапеция , также называемая трапецией , , представляет собой четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция тоже плоская. Следовательно, это 2D.

В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — катетами. Расстояние по перпендикуляру между двумя параллельными сторонами трапеции известно как высота трапеции.

Проще говоря, основание и высота трапеции перпендикулярны друг другу.

Трапеции могут быть как прямыми трапециями (два угла по 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, чтобы он одновременно образовывал два прямых угла.

Из этой статьи вы узнаете:

Как найти площадь трапеции,
Как вывести формулу площади трапеции и,
Как найти площадь трапеции, используя формулу площади трапеции.

Как найти площадь трапеции?

Площадь трапеции — это область, покрытая трапецией в двумерной плоскости. Это пространство, заключенное в двумерную геометрию.

На приведенном выше рисунке трапеция состоит из двух треугольников и одного прямоугольника. Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.

Получите формулу трапеции

Область трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x 2 CD. x ) ) + (½ x 2 CD x ). ¹/₂ × AB × H ) + ( до н.э. × H ) + (¹/₂ × CD × H )

= ₂ H )

= ₂ H ) = ₂ H ). + 2 BC + CD )
= ¹/₂ × h × ( FE + AD )
Но, FE = b ₁ и AB = B ₂
Следовательно, площадь трапеции ADEF ,
= ¹/ ₂ × h × (B 9082 1
33333333333 333 33333333 333 33333333 333 3333333 3333 333333 3333 333333 3333 333333 33333 33333333339 гг. ………. (Это формула площади трапеции)
Формула площади трапеции
Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.
Площадь = ½ x (сумма параллельных сторон) x (перпендикулярное расстояние между параллельными сторонами).
Площадь = ½ h (b ₁ + b ₂ )
Где h — высота, а b _1, и b ₂ — параллельные стороны трапеции.
Как найти площадь неправильной трапеции?
Неправильная трапеция имеет непараллельные стороны разной длины. Чтобы найти его площадь, нужно найти сумму оснований и умножить ее на половину высоты.
В вопросе иногда отсутствует высота, которую можно найти с помощью теоремы Пифагора.
Как найти периметр трапеции?
Вы знаете, что периметр — это сумма всех длин внешнего края фигуры. Следовательно, периметр трапеции равен сумме длин всех 4-х сторон.
Пример 1
Вычислите площадь трапеции, высота которой 5 см, а основания 14 см и 10 см.
Solution
Пусть b ₁ = 14 см и b ₂ = 10 см
Площадь трапеции = ½ h (b ₁ + b ₂ ) cm ²
= ½ x 5 (14 + 10) cm ²
= ½ x 5 x 24 cm ²
= 60 cm ²
Пример 2
Найдите участок трапеции высотой 30 мм, основания которого равны 60 мм и 40 мм.
Solution
Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. единиц
= ½ x 30 x (60 + 40) мм 2 900Пример 3 Если длины двух параллельных сторон трапеции равны 19 и 27 дюймов, найдите высоту трапеции.
Решение
Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. единицы.
⇒ 322 квадратных дюйма = ½ x высота x (19 + 27) кв. дюймов
⇒ 322 квадратных дюйма = ½ x высота x 46 кв. дюймов
⇒ 322 = 23h
Разделите обе стороны на 23.
h = 14
Итак, высота трапеции 14 дюймов.
Пример 4
Учитывая, что высота трапеции 16 м, а длина одного основания 25 м. Вычислите размер другого основания трапеции, если ее площадь равна 352 м ² .
Решение
Пусть b ₁ = 25 м
Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. шт.
⇒ 352 м ² = ½ x 16 м x (25 м + b ₂ ) кв. шт.
⇒ 352 = 200 + 8b ₂
Вычтите по 200 с обеих сторон.
⇒ 152 = 8b ₂
Разделите обе части на 8, чтобы получить;
b ₂ = 19
Следовательно, длина другого основания трапеции равна 19 м.
Пример 5
Вычислите площадь трапеции, показанной ниже.
Решение
Поскольку катеты (непараллельные стороны) трапеции равны, то высоту трапеции можно рассчитать следующим образом;
Чтобы получить основания двух треугольников, вычтите 15 см из 27 см и разделите на 2.
⇒ (27 – 15)/2 см
⇒ 12/2 см = 6 см
12 ^{2 = h ² + 6 ² По теореме Пифагора высота (h) рассчитывается как;}
144 = h ² + 36.
Вычесть 36 с обеих сторон.
ч ² = 108.
ч = 10,39 см.
Отсюда высота трапеции 10,39 см.
Теперь вычислите площадь трапеции.
Площадь трапеции = ½ h (b ₁ + b ₂ ) кв. единицы.
= ½ x 10,39 x (27 + 15) см ² .
= ½ x 10,39 x 42 см ² .
= 218,19 см ² .
Пример 6
Одно основание трапеции на 10 м больше высоты. Если другое основание равно 18 м, а площадь трапеции 480 м ² , найдите высоту и основание трапеции.
Решение
Пусть высота = x
Другое основание равно 10 м, чем высота = x + 10.
Площадь трапеции = ½ h (b ₁ + b _{2) Sq. единицы.}
Подстановкой,
480 = ½ * x * (x + 10 + 18)
480 = ½ *x * (x + 28)
Используйте свойство распределения, чтобы удалить скобки.
480 = ½x ² + 14x
Умножение каждого члена на 2.
960 = x ² + 28x
x ² + 28x — 960 = 0
Solive Quadratic уравнение, чтобы получить;
x = – 48 или x = 20
Подставьте положительное значение x в уравнение высоты и основания.
Высота: x = 20 м.
Другая база = х + 10 = 10 + 20 = 30 м.
Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.

Центроид трапеции Формула
Трапеция — это тип четырехугольника с двумя параллельными сторонами. Четырехугольник — это тип многоугольника с четырьмя сторонами. Сумма четырех внутренних углов четырехугольника равна 360°. Центроид относится к центральной точке любой фигуры. Он также известен как геометрический центр. В 2D-системе координат центроид всегда измеряется относительно осей x и y. В трапеции центр тяжести также измеряется относительно этих двух осей.
Центроид трапеции Формула
Центроид — это центр трапеции. Центроид представляется в виде координат центра трапеции. Горизонтальная или вертикальная линия, проходящая через центроид, делит его на две равные части. Это означает, что для высоты «h» центральная точка будет «h/2». Точно так же вычисляется другая центральная точка. Эти две точки образуют центр тяжести.
Схема трапеции показана ниже:
Центр тяжести фигуры определяется как:
C = [X _C , Y _C ]
Где
X _C — точка на оси X
88 точка на оси Y
Формула для расчета центра тяжести трапеции:
C = [h/2, ]
Где
h – высота
p – основание
q — противоположная параллельная сторона
Сравнивая значения, получаем:
X _C = h/2
Y _C =
Примеры задач
Вопрос 1. Найдите центр тяжести трапеции высотой 4 м и двумя параллельными сторонами по 5 м.
Решение:
Формула для расчета центра тяжести трапеции:
C = [h/2, ]
параллельные стороны
h = 4 м
p = 5m
q = 3m
C = [4/2,]
C = [2, 52/24]
C = [2, 2.17]
Таким образом, центр тяжести равен [2, 2.17 ] или 2 м по оси x и 2,17 м по оси y.
Вопрос 2: Найдите центр тяжести трапеции высотой 2 см и двумя параллельными сторонами 6 см и 4 см.
Решение :
Формула для вычисления центра тяжести трапеции:
C = [h/2,]
Где
h = высота
p и q две параллельные стороны
h = 2 см
p = 6 см
q = 4 см
C = [2/2, ] 90 , 32/30]
C = [1, 1,07]
Таким образом, центроид равен [1, 1,07] или 1 см по оси x и 1,07 см по оси y.
Вопрос 3: Найдите центр тяжести трапеции высотой 10 м и двумя параллельными сторонами 7 м и 4 м.
Решение :
Формула для расчета центра тяжести трапеции:
C = [h/2, ]
h = 10 м
p = 7 м
q = 4 м
C = [10/2, ]
C = [5, 180/33]
90 Таким образом, 002 C = [5, 5,45] 9000 центроид равен [5, 5,45] или 5 м по оси x и 5,45 м по оси y.
Вопрос 4: Найдите центр тяжести трапеции высотой 11 см и двумя параллельными сторонами 3 см и 2 см.
Решение :
Формула для расчета центра тяжести трапеции: параллельные стороны
h = 1 см
p = 2 см
q = 3 см
C = [1/2, ]
C = [0,5, 7/15]
C = [0,5, 90,47]0005
Таким образом, центр тяжести составляет [0,5, 0,47] или 0,5 см по оси X и 0,47 см по оси Y.
Вопрос 5: Найдите центр тяжести трапеции высотой 8 м и двумя параллельными сторонами 5 м и 3 м.
Решение :
Формула для расчета центра тяжести трапеции: параллельные стороны
h = 8 м
p = 5 м
q = 3 м
C = [8/2, ]
C = [4, 104/24]
C = [4, 4.33]
,
составляет [4, 4.33] или 4 м по оси x и 4,33 м по оси y.
Вопрос 6: Найдите центр тяжести трапеции высотой 5 м и двумя параллельными сторонами 7 м и 9 м.
Решение:
Формула для вычисления центра тяжести трапеции:
C = [h/2, ]
Где
h = высота
p и q две параллельные стороны
h = 5 м /2, ]
C = [2,5, 115/48]
C = [2,5, 2,4]
Таким образом, центроид равен [2,5, 2,4] или 2,5 м по оси x и 2,4 м по оси X. относительно оси Y.
Вопрос 7: Найдите центр тяжести трапеции высотой 20 см и двумя параллельными сторонами 15 см и 12 см.
Решение :
Формула для расчета центра тяжести трапеции:
C = [h/2, ]
параллельные стороны , центроид равен [10, 10,37] или 10 см по оси x и 10,37 см по оси y.

Основания трапеций, катеты, углы и площади, правила и формулы
К сожалению, в прошлом году рекламный блок начал отключать загрузку почти всех изображений на нашем сайте, что привело к тому, что mathwarehouse стало непригодным для использования пользователями adlbock.
Трапеция – это четырехугольник с одной парой параллельных прямых
Основания. Две параллельные прямые называются основаниями.
Ноги — две непараллельные линии — это ноги.
Диаграмма 1
Диаграмма 2
Свойства
Свойство №1) Углы с одной стороны катета называются смежными и являются дополнительными ( 9еще 1536 )
Свойство № 2) Площадь трапеции = $$ Площадь = высота \cdot \left( \frac{ \text{сумма оснований} }{ 2 } \right) $$ ( еще )
Свойство №3) У трапеций есть средний сегмент, который соединяет точки середины сторон (еще )
Смежные углы трапеции 907:50
Углы с одной и той же стороны катета называются смежными, например, $$\угол A $$ и $$\угол D $$ являются дополнительными. По той же причине $$ \angle B $$ и $$ \angle C $$ являются дополнительными.
Практика Проблемы
Проблема 1
Используйте теорему о смежных углах, чтобы определить m $$ \angle ZWX $$.
$$ \угол ZWX = 180 − 44 = 136° $$
Проблема 2
Используйте теорему о смежных углах для вычисления m $$ \angle MLO $$.
$$ \угол MLO = 180-124 = 56° $$
Проблема 3
Найдите значение x в трапеции ниже, затем определите меру углов $$ \angle WXY $$ и $$ \angle XYZ $$.
Проблема 4
Что не так с трапецией LMNO, изображенной ниже? (Объясните, почему LMNO не может быть трапецией на основе предоставленной информации) .
Если LMNO трапеция и ее основания LO и MN параллельны, то $$ \угол MNO $$ и $$ \угол NOL $$ должны быть дополнительными, но сумма этих углов не равна 180 111 + 68 ≠ 180.
Площадь трапеции
Проблема 5
$ Площадь = высота \cdot \left( \frac{ \text{сумма оснований} }{ 2 } \right) \\ = 7 \cdot \left( \frac{ 4 + 8 }{ 2 } \right) \\ =7 \cdot \left( \frac{ 12 }{ 2 } \right) \\ = 7 \cdot 6 \\ = \fbox {42 } футов^2 $
Средняя часть трапеции
Средняя часть трапеции:
параллельна обоим основаниям
мера его длины равна средней длине оснований
Проблема 6
Используйте теорему о среднем отрезке, чтобы определить длину среднего отрезка ON.
Чтобы вычислить длину среднего отрезка, найдите среднее значение длины основания среднего отрезка = (6 + 4) / 2 = 5.
Средняя часть трапеции 907:50
Краткий обзор Midpoint
Самое важное, что нужно помнить, это то, что середина делит линию пополам (делит линию на две равные половины).
Середина красного сегмента, изображенного ниже, — это точка $$(A, 2b)$$ (нажмите кнопку ниже, чтобы увидеть).
Средняя линия трапеции — это отрезок, соединяющий середины непараллельных сторон трапеции.
В приведенной ниже трапеции середины непараллельных сторон — это точки S и V. Середина — это отрезок красной линии от S до V.
Пример среднего сегмента
Трапеция #10
Шаг 1
Вычисление длины оснований. Верхняя база:
35$ — 16 = 9$$
Шаг 2
Расчет низкой базы:
45$ — 0 = 45 $$
Шаг 3
Вычисление суммы оснований
$$ 9 + 45 = 54 $$
Шаг 4
Разделите сумму на 2
$$ \frac {54}{2} = \boxed{27}$$
Проблема 8
Какова длина среднего отрезка SV в трапеции внизу?
Шаг 1
Вычисление длины оснований. Верхняя база:
$$ 17 — 8 = 9 $$
Шаг 2
Расчет низкой базы:
20$ — 0 = 20 $$
Шаг 3
Вычисление суммы оснований
$$ 9 + 20 = 29 $$
Шаг 4
Разделите сумму на 2
$$ \frac {29}{2} = \boxed{14. 5}$$
Проблема 9
Красный сегмент находится ниже среднего сегмента?
Это не настоящий средний отрезок, потому что его длина не равна половине суммы длин оснований.
2.5: Численное интегрирование — средняя точка, трапеция, правило Симпсона
Последнее обновление
Сохранить как PDF
Идентификатор страницы
10269
Эта страница является черновиком и находится в активной разработке.
Первообразные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть через известные функции). Следовательно, вместо непосредственного вычисления определенных интегралов этих функций мы прибегаем к различным приемам численного интегрирования для аппроксимации их значений. В этом разделе мы рассмотрим некоторые из этих методов. Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов. 9n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком $f(x)$ и осью $x$ над $[ а, б]$. На графике показаны прямоугольники, соответствующие $M_4$ для неотрицательной функции на замкнутом интервале $[a,b].$
Рисунок $\PageIndex{1}$: Правило средней точки аппроксимирует площадь между график $f(x)$ и оси $x$ путем суммирования площадей прямоугольников со средними точками, являющимися точками на $f(x)$.
Пример $\PageIndex{1}$: использование правила средней точки с $M_4$ 92\,dx\) с использованием четырех подынтервалов. Сравните результат с действительным значением этого интеграла.
Решение: Каждый подинтервал имеет длину $ Δx=\dfrac{1−0}{4}=\dfrac{1}{4}. $ Следовательно, подынтервалы состоят из
\[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber\]
Середины этих подинтервалов являются $\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right \}.$ Таким образом, 92_1\frac{1}{x}\,dx.\)
Подсказка
$ Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.$
Ответить
$\dfrac{24}{35}$
Правило трапеций
Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке $\PageIndex{2}$ область под кривой аппроксимирована трапециями, а не прямоугольниками.
Рисунок $\PageIndex{2}$: Трапеции можно использовать для аппроксимации площади под кривой, таким образом, аппроксимируя определенный интеграл.
Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке $\PageIndex{2}$. Мы предполагаем, что длина каждого подынтервала равна $Δx$. Во-первых, напомним, что площадь трапеции с высотой $h$ и длинами оснований $b_1$ и $b_2$ определяется выражением $\text{Area}=\frac{1}{ 2}h(b_1+b_2)$. Мы видим, что первая трапеция имеет высоту $Δx$ и параллельные основания длины $f(x_0)$ и $f(x_1)$. Таким образом, площадь первой трапеции на рисунке $\PageIndex{2}$ равна 9b_af(x)\,dx≈\frac{Δx}{2}\big(f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f( x_4)\big).\nonumber\]
Обобщая, сформулируем формально следующее правило.
Правило трапеций
Предположим, что $f(x)$ непрерывно над $[a,b]$. Пусть $n$ — натуральное число и $Δx=\dfrac{b−a}{n}$. Пусть $[a,b]$ разбит на $n$ подынтервалов, каждый длиной $Δx$, с концами в $ P=\{x_0,x_1,x_2…,x_n\}. \ )
Набор
\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\big).\] 9nf(x_i)Δx.$
То есть $L_n$ и $R_n$ аппроксимируют интеграл, используя левую и правую конечные точки каждого подинтервала соответственно. Кроме того, внимательное изучение рисунка $\PageIndex{3}$ позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)
Подсказка
Множество $Δx=\dfrac{1}{2}.$ Концы подынтервалов являются элементами множества $P=\left\{1,\frac{3}{2},2\right \}.$
Ответить
$\dfrac{17}{24}$
Абсолютная и относительная погрешность
Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла. Сначала нам нужно определить абсолютную ошибку и относительную ошибку.
Определение: абсолютная и относительная ошибка
Если $B$ является нашей оценкой некоторой величины, имеющей действительное значение $A$, то абсолютная ошибка определяется выражением $|A−B|\ ).
Относительная ошибка представляет собой ошибку в процентах от фактического значения и определяется как \[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. 2\,dx$, используя правило средней точки, найденное в Пример $\PageIndex{1}$. 92_1\frac{1}{x}\,dx\) в $\frac{24}{35}$ с использованием $T_2$. Фактическое значение этого интеграла равно $\ln 2$. Используя $\frac{24}{35}≈0,6857$ и $\ln 2≈0,6931,$, вычислите абсолютную ошибку и относительную ошибку.
Подсказка
Используйте предыдущие примеры в качестве руководства.
Ответить
абсолютная ошибка $\приблизительно 0,0074,$ и относительная ошибка $\приблизительно 1,1\%$
Границы погрешности для средней точки и правил трапеций
В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши. В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла. 2\,dx.\)
Подсказка
$f»(x)=2,$ поэтому $M=2.$
Ответить
$\dfrac{1}{192}$
Правило Симпсона
С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через $ (x_2,f(x_2)), \,(x_3,f(x_3)),$ и $(x_4,f(x_4)).$ Этот процесс продолжается с каждой последующей парой подынтервалов.
Рисунок $\PageIndex{4}$: С помощью правила Симпсона мы приближаем определенный интеграл, интегрируя кусочно-квадратичную функцию.
Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этого приближения для первых двух подынтервалов. Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]
Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.
Правило Симпсона
Предположим, что $f(x)$ непрерывно над $[a,b]$. Пусть $n$ — четное положительное число и $Δx=\dfrac{b−a}{n}$. Пусть $[a,b]$ разбит на $n$ подынтервалов, каждый длиной $Δx$, с концами в $P=\{x_0,x_1,x_2,…,x_n\}. $ Набор 9b_af(x)\,dx.\nonumber\]
Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что $S_{2n}=(\dfrac{2}{3})M_n+(\dfrac{1}{3})T_n$.
Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла. Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)
Подсказка
\[S_2=(\frac{1}{3}Δx(f(x_0)+4f(x_1)+f(x_2))\]
Ответить
$\фракция{25}{36}$
Основные понятия
Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда сложно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла.
Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона.
Правило средней точки аппроксимирует определенный интеграл с помощью прямоугольных областей, тогда как правило трапеций аппроксимирует определенный интеграл с помощью трапециевидной аппроксимации.
Правило Симпсона аппроксимирует определенный интеграл, сначала аппроксимируя исходную функцию с помощью кусочно-квадратичных функций.
No related posts.