Как находится средняя линия треугольника. Как найти середину треугольника: задачка по геометрии
Средняя линия треугольника – это отрезок, соединяющий середины 2-х его сторон. Соответственно, каждого у треугольника три средних линии. Зная качество средней линии, а также длины сторон треугольника и его углы, дозволено обнаружить длину средней линии.
Вам понадобится
- Стороны треугольника, углы треугольника
Инструкция
1. Пускай в треугольнике ABC MN – средняя линия, соединяющая середины сторон AB (точка M) и AC (точка N).По свойству средняя линия треугольника, соединяющая середины 2-х сторон, параллельна третьей стороне и равна её половине. Значит, средняя линия MN будет параллельна стороне BC и равна BC/2.Следственно, для определения длины средней линии треугольника довольно знать длину стороны именно этой третьей стороны.
2. Пускай сейчас вестимы стороны, середины которых соединяет средняя линия MN, то есть AB и AC, а также угол BAC между ними. 2/4) = 0.
2/4) = 0.
Квадратный треугольник больше верно именуется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры детально рассматриваются в математической дисциплине тригонометрии.
Вам понадобится
- – лист бумаги;
- – ручка;
- – таблицы Брадиса;
- – калькулятор.
Инструкция
1. Обнаружьте сторону прямоугольного треугольника с поддержкой теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника , a и b – его катеты. Дабы применить это уравнение, надобно знать длину всяких 2-х сторон прямоугольного треугольника .
2. Если по условиям заданы размеры катетов, разыщите длину гипотенузы. Для этого с поддержкой калькулятора извлеките квадратный корень из суммы катетов, всякий из которых заранее возведите в квадрат.
3. Вычислите длину одного из катетов, если вестимы размеры гипотенузы и иного катета.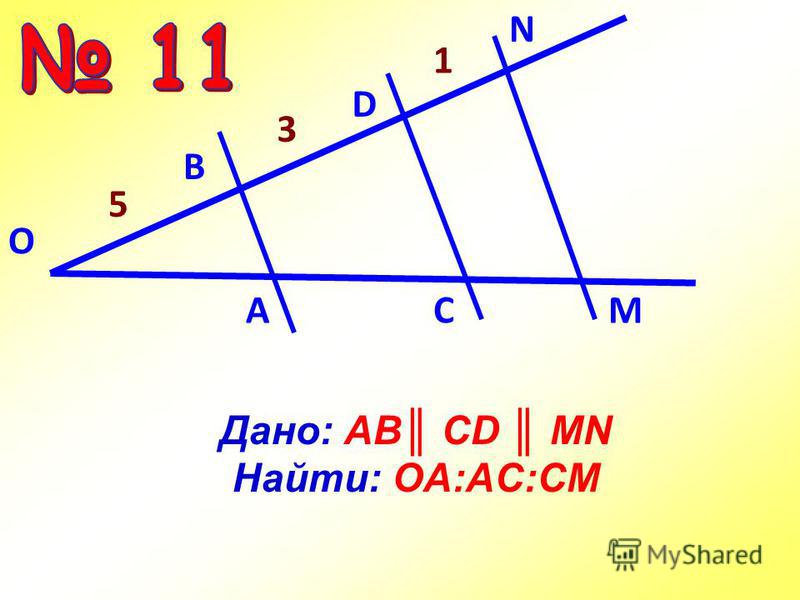
4. Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника .
5. Обнаружьте катеты при помощи основных тригонометрических функций: a = c*sin ?, b = c*cos ?, где а – катет, противолежащий к углу?, b – катет, прилежащий к углу?. Сходственным образом посчитайте размер сторон треугольника , если заданы гипотенуза и иной острый угол: b = c*sin ?, a = c*cos ?, где b – катет, противолежащий к углу?, а – катет, прилежащий к углу?.
6. В случае, когда вестим катет a и прилежащий к нему острый угол?, не забывайте, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: ? + ? = 90°. Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.
Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.
7. Если вестим катет а и противолежащий к нему острый угол?, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin ?, катет: b=a*tg ?.
Видео по теме
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…
Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…
Что такое средняя линия треугольника и каковы её свойства?
Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.
Понятно, что средних линий в треугольнике три. Покажем их:
Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.
Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Доказательство:
1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:
Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:
По признаку параллельности прямых MN||AC.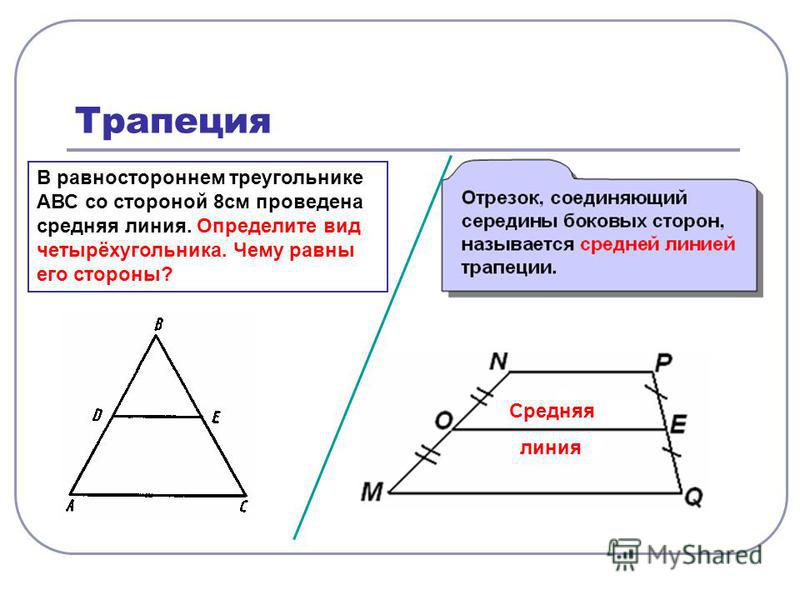
2. Также из подобия треугольников следует, что
То есть MN в два раза меньше. Доказано!
Решим типичную задачу.
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.
Построим эскиз:
Таким образом периметр треугольника АВС равен 24+20+16=60.
*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:
Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что
Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.
Есть такие типы, в которых речь идет о треугольной призме.
Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.
Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот с такими задачами.
На этом всё! Всего доброго!
Скачать материал статьи
С уважением, Александр Крутицких.
1
Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.
И она равна половине гипотенузы .
Следствие 1.
Следствие 2.
2 Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
3
Пример дополнительного построения — высота, опущенная на гипотенузу.
Отсюда видно, что
1
Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому откуда
Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:
Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия!
2 Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.
Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:
Отсюда видно, что .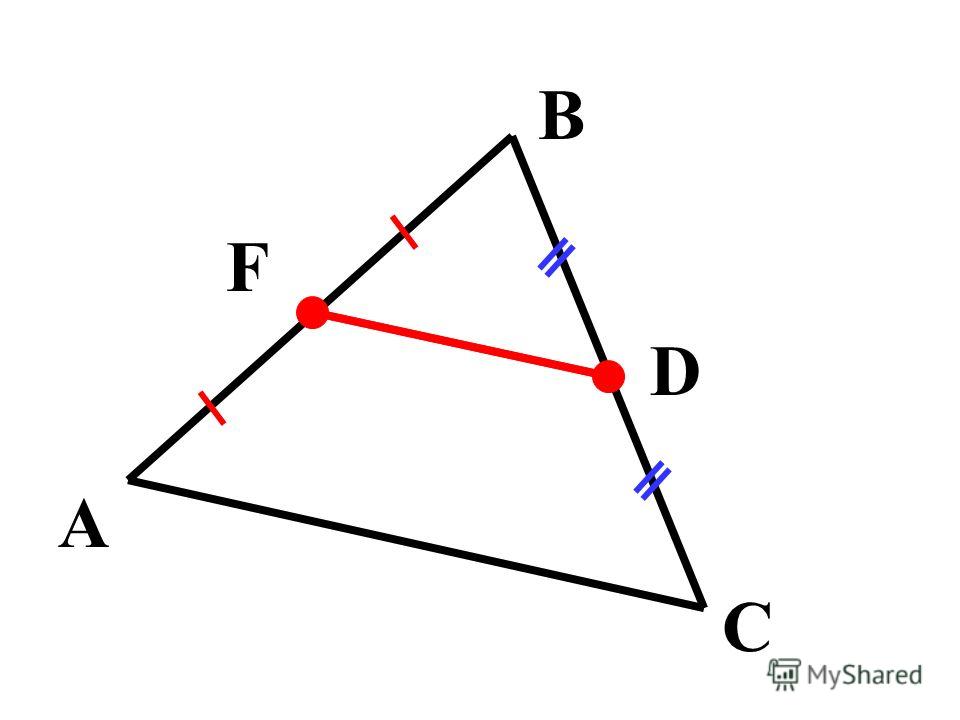 Складывая, получаем теорему Пифагора, поскольку :
Складывая, получаем теорему Пифагора, поскольку :
Другое доказательство теоремы Пифагора см.в комментарии к задаче 4.
3
Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.
Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.е. MC – медиана, проведенная к гипотенузе прямоугольного треугольника , и она равна половине гипотенузы
Следствие 1. Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.

Следствие 2. Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.
Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.
Задачи
Использование свойств подобия -1
Использование основных свойств — 2
Использование дополнительного построения 3-4
1 2 3 4
Высота, опущенная из вершины прямого угла прямоугольного треугольника равна корню квадратном из длин отрезков, на которые она делит гипотенузу. 2=c_1c_2\).
2=c_1c_2\).
Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.
Точка пересечения медиан любого треугольника отсекает от медианы одну треть, считая от точки ее пересечения с соответствующей стороной. В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Поэтому искомое ГМТ есть окружность радиуса, равной 1/6 от длины гипотенузы, с центром в середине этой (фиксированной) гипотенузы.
На рисунке 1 показаны два треугольника. Треугольник ABC подобен треугольнику A1B1C1. И прилежащие стороны пропорциональны, то есть AB относится к A1B1 также как AC относится к A1C1. Их этих двух условий и следует подобие треугольников.
Как найти среднюю линию треугольника — признак параллельности прямых
На рисунке 2 показаны прямые a и b, секущая c. При этом образуются 8 углов. Углы 1 и 5 соответственные, если прямые параллельны, то соответственные углы равны, и наоборот.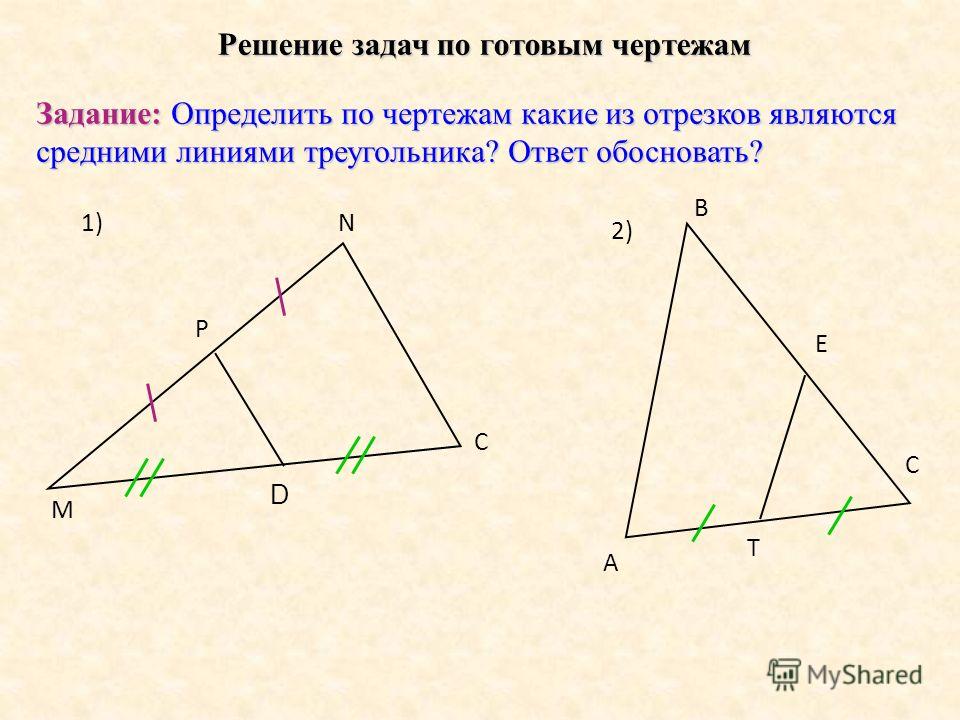
Как найти среднюю линию треугольника
На рисунке 3, M середина AB, а N середина AC, BC основание. Отрезок MN — называется средней линии треугольника. Сама же теорема гласит — Средняя линия треугольника параллельная основанию и равна его половине.
Для того чтобы доказать, что MN — средняя линия треугольника, нам понадобится второй признак подобия треугольников и признак параллельности прямых.
Треугольник AMN подобен треугольнику ABC, по второму признаку. В подобных треугольниках соответственные углы равны, угол 1 равен углу 2, а эти углы являются соответственными при пересечении двух прямых секущей, следовательно, прямые параллельны, MN параллельно BC. Угол A общий, AM/AB = AN/AC = ½
Коэффициент подобия этих треугольников ½, из этого следует что ½ = MN/BC, MN = ½ BC
Вот мы и нашли среднюю линию треугольника, и доказали теорему о средней линии треугольника, если вам до сих пор не понятно, как найти среднюю линию, смотрите видео ниже.
Средняя линия треугольника — это отрезок, соединяющий середины 2-х его сторон. 2/4) = 0.
2/4) = 0.
Квадратный треугольник больше верно именуется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры детально рассматриваются в математической дисциплине тригонометрии.
Вам понадобится
- — лист бумаги;
- — ручка;
- — таблицы Брадиса;
- — калькулятор.
Инструкция
1. Обнаружьте сторону прямоугольного треугольника с поддержкой теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника , a и b – его катеты. Дабы применить это уравнение, надобно знать длину всяких 2-х сторон прямоугольного треугольника .
2. Если по условиям заданы размеры катетов, разыщите длину гипотенузы. Для этого с поддержкой калькулятора извлеките квадратный корень из суммы катетов, всякий из которых заранее возведите в квадрат.
3. Вычислите длину одного из катетов, если вестимы размеры гипотенузы и иного катета.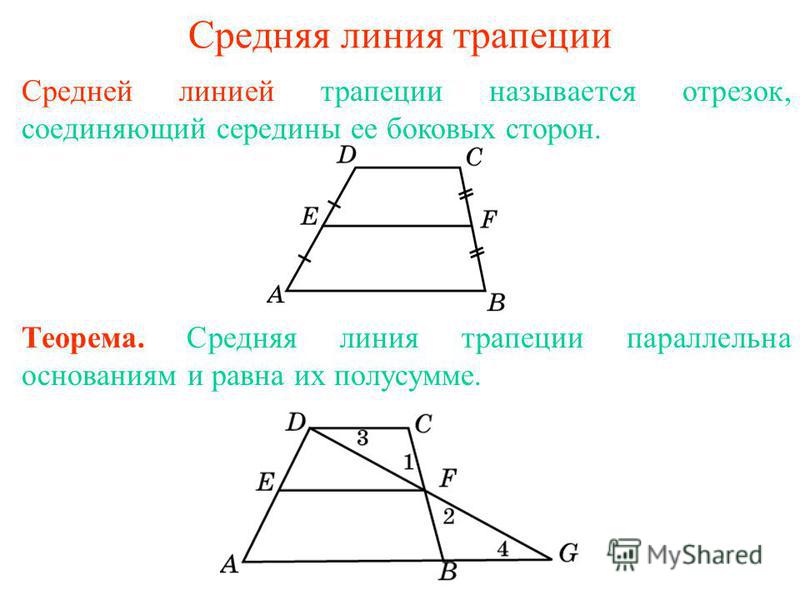 При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и вестимого катета, также возведенного в квадрат.
При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и вестимого катета, также возведенного в квадрат.
4. Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника .
5. Обнаружьте катеты при помощи основных тригонометрических функций: a = c*sin ?, b = c*cos ?, где а – катет, противолежащий к углу?, b – катет, прилежащий к углу?. Сходственным образом посчитайте размер сторон треугольника , если заданы гипотенуза и иной острый угол: b = c*sin ?, a = c*cos ?, где b – катет, противолежащий к углу?, а – катет, прилежащий к углу?.
6. В случае, когда вестим катет a и прилежащий к нему острый угол?, не забывайте, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: ? + ? = 90°.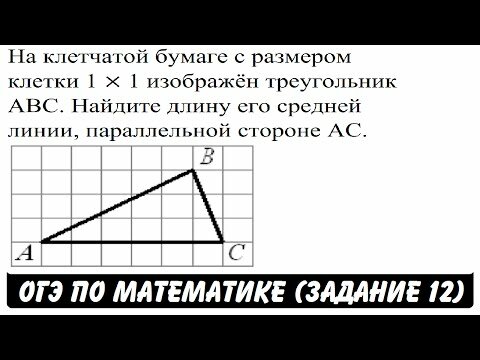 Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.
Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.
7. Если вестим катет а и противолежащий к нему острый угол?, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin ?, катет: b=a*tg ?.
Видео по теме
Как найти среднюю линию треугольника. Средняя линия как найти треугольника
Автор Historian Просмотров 98 Опубликовано
Решение. Пусть ABCD — таблица, а ее средняя линия, lm — определенное сечение (рис. 7). Поскольку AE = EB, по теории Талиса выполняется следующее равенство: ln= nm, что и требовалось доказать.
Содержание
- Понятие треугольника
- Понятие средней линии треугольника
- Понятие средней линии прямоугольного треугольника
- Видео
- Средняя линия
- Важные свойства
- Решение задачи
- Формула для расчета
- Средние линии четырехугольника.
 Теорема Вариньона
Теорема Вариньона - Средние линии тетраэдра
- Что такое средняя линия треугольника
- Свойства средней линии треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Признак средней линии треугольника
- Длина средней линии треугольника
- Треугольник и его характеризующие отрезки
- Свойства средней линии
Понятие треугольника
Треугольники — это геометрические фигуры, возникающие из трех отрезков. Они соединены с тремя точками, которые не лежат на прямой линии. Отрезки называются сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник является равнобедренным, если две его стороны равны. Эти стороны называются боковыми сторонами, а третья сторона называется основанием.
Треугольник, у которого все стороны равны, называется равносторонним или прямоугольным.
Треугольник называется прямоугольным, если он имеет прямой угол, т.е. угол, равный 90°. Сторона прямоугольного треугольника, противоположная прямому углу, является подчиненной; две другие стороны — катеты.
Прямоугольный (равносторонний или эквивалентный) треугольник — это прямоугольный многоугольник, у которого все стороны равны и все углы также равны 60°. В равносторонних треугольниках высота является одновременно биссектрисой и медианой.
Свойство треугольника:.
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро систематизировать свои знания перед экзаменом? Запишитесь на урок математики Use Maths на SkySmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для каждого типа этой фигуры.
Средняя линия треугольника — это часть треугольника, которая соединяет центры двух сторон. Для каждого треугольника можно разработать три средние линии.
Основание — это сторона с параллельными средними линиями.
Как найти средние линии треугольника — мы объясним далее, но сначала давайте разберемся со всеми определениями немного подробнее.
Понятие средней линии прямоугольного треугольника
Математики говорят: в каждом треугольнике можно провести три средние линии. В прямоугольном треугольнике этот отрезок равен половине основания. Это тип средней линии для прямоугольных треугольников.
Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.
В прямоугольном треугольнике две средние линии перпендикулярны перпендикуляру, а третья равна медиане, призванной быть подчиненной. Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.
Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.
Выделяя срединные линии, мы говорили о вторичных свойствах отрезков. Мы привели свойства центральной линии и рассказали об особенностях формулировки этих свойств. Мы обсудили, как типы проявляются в длине центральной линии треугольника и как средняя линия делит треугольник. Все эти свойства используются при разрешении треугольника.
Видео
Математики говорят: в каждом треугольнике можно провести три средние линии. В прямоугольном треугольнике этот отрезок равен половине основания. Это тип средней линии для прямоугольных треугольников.
Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.
В прямоугольном треугольнике две средние линии перпендикулярны перпендикуляру, а третья равна медиане, призванной быть подчиненной. Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.
Средние линии кислотных и неправильных треугольников не обладают аналогичными свойствами.
Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.
Средняя линия
Чтобы понять, как найти центр треугольника, можно воспользоваться простой линейкой. Для этого выделите две любые стороны фигуры. Затем отметьте каждую точку, равноудаленную от каждой из вершин, примыкающих к этой стороне. Чтобы спроектировать центральную часть, эти две точки необходимо соединить. Их названия интуитивно понятны всем, поскольку они соединяют носителей информации с обеих сторон.
Важные свойства
Этот компонент имеет три основных свойства Предположим, у нас есть произвольный треугольник типа ABC, с P и Q в серединах AB и AC соответственно. Учитывая эту запись, PQ является средней линией ABC. Применяются следующие геометрические свойства.
- Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям.
 Таким образом, выполняется один из признаков подобия.
Таким образом, выполняется один из признаков подобия. - Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
- Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.
Пункт №3 списка применим к любому треугольнику. Для доказательства используйте формулу Герона. В соответствии с этим, площадь этой фигуры можно рассчитать следующим образом:.
где p = (a + b + c)/2 — полуокружность диаграммы. Пусть α, β и γ — длины его сторон. Символизируйте стороны ABC таким же образом. Тогда длины отрезка APQ равны a / 2, b / 2 и c / 2. Полупериметр APQ равен p1 = (a + b + c)/4 = ½*p. Подставив все известные величины в формулу Герона, получим площадь S1.
Другими словами, площадь треугольника APQ составляет одну четверть от данной величины ABC. 0,5.
0,5.
Тогда длина стороны BC становится равной
Из цитаты этих двух уравнений следует, что уравнение, которое необходимо доказать, следующее
Поскольку в доказательстве использовались произвольные координаты вершин треугольника, полученные выводы являются общими и универсальными для каждого типа рассматриваемой фигуры.
Формула для расчета
Центральная линия треугольника параллельна основанию и равна его половине.
ЭВИДЕНЦИЯ.
\Рассмотрим dž (dž треугольник BA_1C_1 \) и dž (dž треугольник BAC \).
Мы видим, что треугольники похожи по двум соответствующим сторонам и углу между ними.
Следовательно, ἀ (ἀ угол BA_1C_1 = ἀ угол BAC \) является соответствующим элементом подобного треугольника. Поэтому, согласно принципу параллелизма \(A_1C_1 \ параллельно AC \).
Подобие также показывает, что ǁ(ǁ frac = \ frac12 \)
Это уравнение работает для любого треугольника, включая изоклетки, изоклетки и правильные треугольники.
Проведите центральные линии см, см и см на заданном треугольнике.
Найдите периметр треугольника. Решение Средняя линия равна половине параллельных сторон, поэтому можно найти длины всех сторон треугольника. см см см см см см см Теперь можно найти периметр треугольника как сумму всех длин. Его стороны: см см Ответ: см см см.
Средние линии четырехугольника. Теорема Вариньона
Значение. Средняя линия четырехугольника соединяет середины непересекающихся сторон четырехугольника.
Поскольку каждый четырехугольник имеет две пары непересекающихся сторон, каждый четырехугольник имеет две средние линии (рис. 10).
Средние линии на рисунке 10 — это отрезки EF и GH.
Примечание 1: Приведенное выше определение средней линии применимо не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис. 11). Пространственный четырехугольник» — это замкнутая четырехсвязная линия, не имеющая самопересечений и не находящаяся на одном уровне.
На рис. 11 показан «пространственный четырехугольник» ABCD. Его середины — отрезки EF и GH.
Его середины — отрезки EF и GH.
Замечание 2. Хотя таблица является четырехугольником, принято называть среднюю линию банкира единственной частью, соединяющей середины ее сторон.
Замечание 3. В этом разделе книги невыпуклые четырехугольники и четырехугольники с независимыми сечениями не рассматриваются.
Теорема Валлиньона. Середины сторон любого плоского или «пространственного» четырехугольника являются вершинами прямоугольника.
Доказательство Рассмотрим плоский четырехугольник ABCD, изображенный на рисунке 12. Точки E, G, F и H являются средними точками, а отрезок AC — диагональю четырехугольника.
Отрезок EG — перпендикулярная биссектриса треугольника ABC, поэтому отрезок EG параллелен и равен половине диагонали AC. Отрезок FH — перпендикулярная биссектриса треугольника CDA, поэтому отрезок FH параллелен диагонали AC и составляет ее половину. Таким образом, в четырехугольнике EGFH противоположные стороны EG и FH одинаково параллельны. Знак прямоугольника указывает на то, что четырехугольник EGFH является прямоугольным, что и требуется доказать.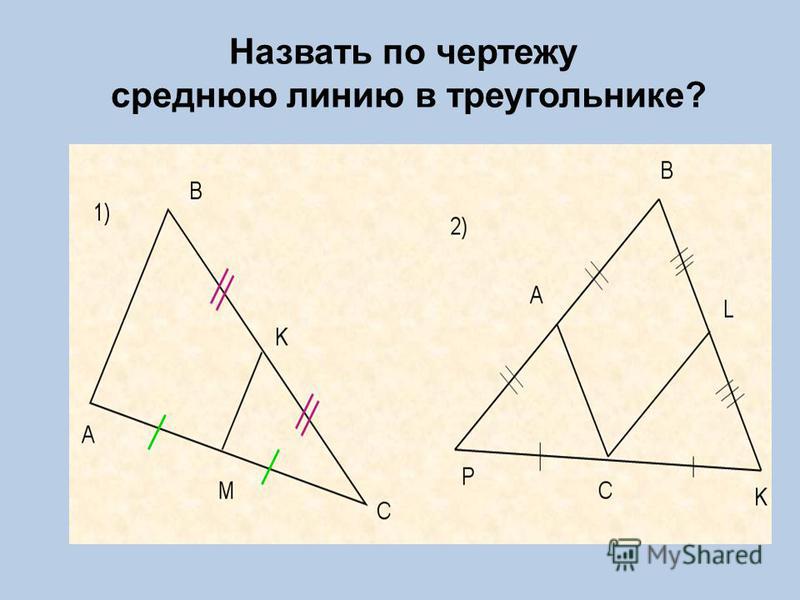
Замечание 4. Для «пространственного четырехугольника» ABCD доказательство остается прежним (рис. 13).
Пункт 5. Средние линии любого четырехугольника пересекаются и делятся пополам в точке пересечения (рис. 14).
Средние линии тетраэдра
Тетраэдры представляют собой произвольные треугольники (рис. 17).
Каждый тетраэдр имеет четыре вершины, четыре поверхности и шесть ребер, разделенных на три пары непересекающихся ребер. На рисунке 17 каждая пара непересекающихся ребер показана другим цветом. Все две непересекающиеся грани тетраэдра располагаются на пересекающихся линиях пересечения.
Значение. Центральная линия тетраэдра (с обеих сторон) — это часть, соединяющая середины двух непересекающихся граней тетраэдра.
Каждый тетраэдр имеет три центральные линии. Часть EF на рис. 18 является одной из центральных линий тетраэдра.
Утверждение 7. Все центральные линии тетраэдра пересекаются в одной точке и делятся посередине этой точкой.
ДОКАЗАТЕЛЬСТВА Выберите среднюю линию тетраэдра. Например, EF и докажите, что остальные средние линии тетраэдра проходят через центр отрезка EF. Для этого рассмотрим, например, медиану GH, соединяющую средние точки AC и BD и соединяющую точки E, H, F и G с отрезком (рис. 19).
Так как отрезок EH является средней линией треугольника ADB, он является
Значение. Точка пересечения средних точек тетраэдра называется центростремительной силой тетраэдра.
Пункт 8. Рассмотрим декартову систему координат с началом в точке O и произвольный тетраэдр ABCD. Если центр этого тетраэдра обозначить буквой М (рис. 20), то векторное равенство выполняется.
Прямые углы помогают применять другие точки равенства и подобия. Геометрическое тождество можно использовать для углов прямоугольного треугольника без дополнительной структуры, а по теореме Пифагора можно найти любую сторону.
Что такое средняя линия треугольника
В данной публикации рассматриваются определения, качества и признаки треугольников.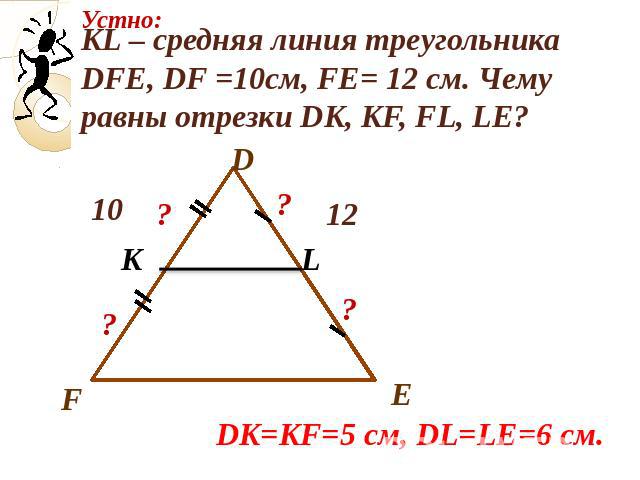 Вы также получите примеры решений для лучшего понимания теоретического материала.
Вы также получите примеры решений для лучшего понимания теоретического материала.
Часть треугольника, соединяющая центры двух сторон треугольника, называется средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (не пересекается) и вдвое меньше этой стороны.
Свойство 2
Средняя линия треугольника разрезает аналогичный треугольник (1:2), который в четыре раза меньше исходного треугольника.
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC: AB = 2KB, BC = 2BL, AC = 2KL .
- Sabc. =4⋅s△KBL
Свойство 3
Для каждого треугольника можно разработать три средние линии.
KL, KM и ML — средние линии треугольника ABC.
Свойство 4
Три центральные линии треугольника делят его на четыре треугольника равной площади.
Признак средней линии треугольника
Отрезок, проходящий через середину одной стороны треугольника, пересекает вторую и параллелен третьей — это центральный класс треугольника.
Дан треугольник, стороны которого равны 6 см и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, а известные величины — длинами перпендикуляров. Средняя линия, соединяющая катетеры, параллельна нижней и равна половине ее длины.
Для нахождения подчиненных можно использовать теорему Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100. bc = 10.
Поэтому центральная линия lm = 1 /2 de bc = 1 /2 ⋅ 10 = 5.
Теорема Валлиньона. Середины сторон любого плоского или «пространственного» четырехугольника являются вершинами прямоугольника.
Длина средней линии треугольника
Средняя линия треугольника — интересный классификационный отрезок, так как он обладает рядом свойств, позволяющих находить простые решения, казалось бы, сложных задач. Давайте рассмотрим основные свойства средней линии и поговорим о том, как длину этого отрезка можно найти в треугольнике.
Давайте рассмотрим основные свойства средней линии и поговорим о том, как длину этого отрезка можно найти в треугольнике.
Треугольник и его характеризующие отрезки
Треугольник — это фигура, состоящая из трех сторон и трех углов. В зависимости от величины углов треугольник делится на
Основные характеристики треугольника следующие
- Медиана – отрезок, соединяющий вершину с серединой противоположной стороны.
- Биссектриса – отрезок, проведенный из вершины угла к противоположной стороне и делящий угол пополам
- Высота – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
Рисунок 2.Высота, межстрочный и биссектрисальный треугольники
За каждый раздел характеристики начисляется балл. Когда три центральных пересечения класса, бисквит и возвышение, соединяются, возникает золотое пересечение треугольников.
Однако существует несколько дополнительных классифицированных разделов.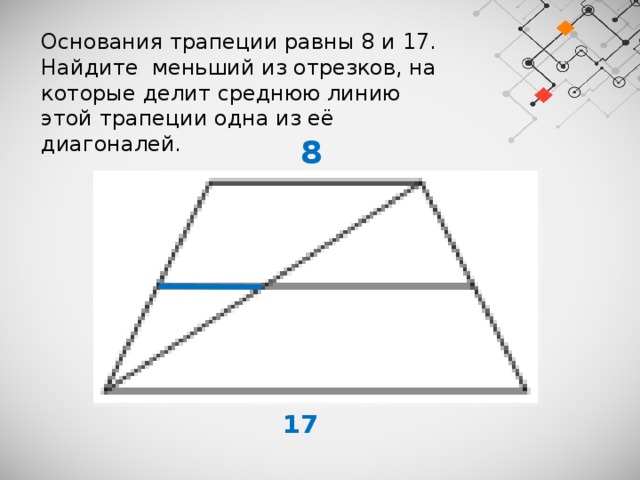
- Серединный перпендикуляр – перпендикуляр восстановленный из середины стороны. Как правило серединный перпендикуляр продлевается до пересечения с другой стороной.
- Средняя линия – отрезок, соединяющий середины смежных сторон.
- Радиус вписанной окружности. Вписанная окружность – окружность, которая касается каждой из сторон треугольника. Центр вписанной окружности – точка пересечения биссектрис треугольника
- Радиус описанной окружности. Описанная окружность – окружность, содержащая в себе все вершины треугольника. Центр описанной окружности – точка пересечения серединных перпендикуляров треугольника.
Смежные стороны треугольника — это стороны с общей вершиной. В геометрии существует понятие противоположных сторон, то есть сторон, противоположных друг другу и не имеющих общей вершины. Однако это понятие не применимо к треугольникам — все стороны треугольника смежные.
Свойства средней линии
Средняя линия не обладает многими свойствами, все из которых важны для решения задачи. Дело в том, что лишь немногие задачи связаны с нахождением длины средней линии, некоторые из них, несмотря на свою простоту, могут привести учащихся в апатию.
Дело в том, что лишь немногие задачи связаны с нахождением длины средней линии, некоторые из них, несмотря на свою простоту, могут привести учащихся в апатию.
Давайте теперь приведем и обсудим все свойства средней линии треугольника.
- Средняя линия треугольника равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить. В общем случае по этому свойству и определяется длина средней линии треугольника.
- Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в предыдущем свойстве.
- Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
- Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5
Фактический вид длины срединной линии вытекает из второго свойства.
$ m = 1 \ над * a $-, где m — средняя линия, а a — сторона, противоположная средней линии.
ее свойства, признаки, формула нахождения длины
Содержание:
- Определение средней линии треугольника
- Средняя линия треугольника — свойства, признаки и формулы
- Теорема о средней линии треугольника
- Задачи на использование теоремы
Содержание
- Определение средней линии треугольника
- Средняя линия треугольника — свойства, признаки и формулы
- Теорема о средней линии треугольника
- Задачи на использование теоремы
Использование понятия «средняя линия треугольника» помогает решить многие задачи по геометрии. Ее можно провести в любом треугольнике, независимо от соотношения длин его сторон и видов имеющихся углов.
Ее можно провести в любом треугольнике, независимо от соотношения длин его сторон и видов имеющихся углов.
Определение средней линии треугольника
Средней линией треугольника называется отрезок, который располагается внутри него таким образом, что соединяет точки, являющиеся серединами двух сторон, лежащих противоположно.
Источник: nauka.clubТакое определение не является единственным. Исходя из доказательства теоремы Фалеса:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если отрезок, начинающийся на середине одной из сторон треугольника, заканчивается на другой стороне и параллелен третьей, то это средняя линия этого треугольника.
В любом треугольнике можно провести три срединные линии, поскольку он имеет три стороны, в т.ч. две — лежащие друг против друга.
Доказательством этого утверждения является теорема Фалеса:
Источник: nauka. club
clubСредняя линия треугольника — свойства, признаки и формулы
Cвойства средних линий могут различаться. Так, в прямоугольном треугольнике две из трех средних линии перпендикулярны катетам. В то же время третья — по длине аналогична медиане, которую провели к гипотенузе.
Для треугольника, имеющего острые углы и стороны различной длины, средние линии таким свойством не обладают.
Источник: nauka.clubДля прямоугольного треугольника является справедливым утверждение, что его средняя линия делит площадь на 4 треугольника, имеющие прямые углы.
В геометрии к свойствам средней линии относят:
- Найти длину средней линии можно разделив длину основания пополам. При этом основание треугольника и его средняя линия являются параллельными.
- Проведя в треугольнике среднюю линию, можно смело утверждать, что он отсек еще один треугольник, который с коэффициентом ½ подобен основному — большому. Вычислить его площадь можно, разделив площадь основного треугольника на 4.

- Проведя в треугольнике все три средние линии, получают четыре треугольника равной площади. При этой центральный из них получил название дополнительного.
- Три средние линии, проведенные в прямоугольном треугольнике, также делят его на 4 меньших треугольника. При этом все они имеют прямые углы.
свойство 1
Из приведенного списка позволяет находить длину средней линии через длину стороны, которая ей параллельна.
Рассмотрим треугольник: Формулу для такого действия, исходя из ниже приведенной схемы, можно выразить так:
Источник: uztest.ruФормулу для такого действия, исходя из выше приведенной схемы, можно выразить так:
nb=1/2b
Свойство
Это же свойство № 1 лежит в основе следующей формулы — для нахождения площади треугольника, который образуется в результате отсекания части основного средней линией (S1) нужно площадь основного треугольника (S) разделить на 4:
S1=S/4
Теорема о средней линии треугольника
Утверждение, что средняя линия треугольника параллельна его основанию (либо третьей стороне) и по длине составляет половину этого основания, носит название теоремы о средней линии. Доказать ее можно с помощью трех способов:
Доказать ее можно с помощью трех способов:
- Рассмотрим треугольник.
Из рисунка видно, что прямая MK параллельна AC. Исходя из теоремы Фалеса понятно, что точкой пересечения стороны BC является ее половина. Так как MN∈MK, значит MN параллельна AC.
Это доказательство первой части теоремы.
Приступаем к доказательству второй части: длина средней линии равна половине длины основания треугольника.
Предположим, что NP параллельна AB. По этому признаку она является средней линией треугольника (согласно теореме Фалеса). Если это так, то AP=PC.
Из рисунка видно, что фигура AMNP является параллелограммом, поэтому AP=MN. Из приведенных фактов следует, что MN=1/2AC
Второй способ основывается на том, что угол B — общий для треугольников MBN и ABC.
По известному признаку, лежащему в основе подобия треугольников, можно утверждать, что ΔMBN∼ΔABC.
Отсюда следует равенство углов BMN и BAC. Данные углы соответственные, поэтому прямые MN и AC являются параллельными.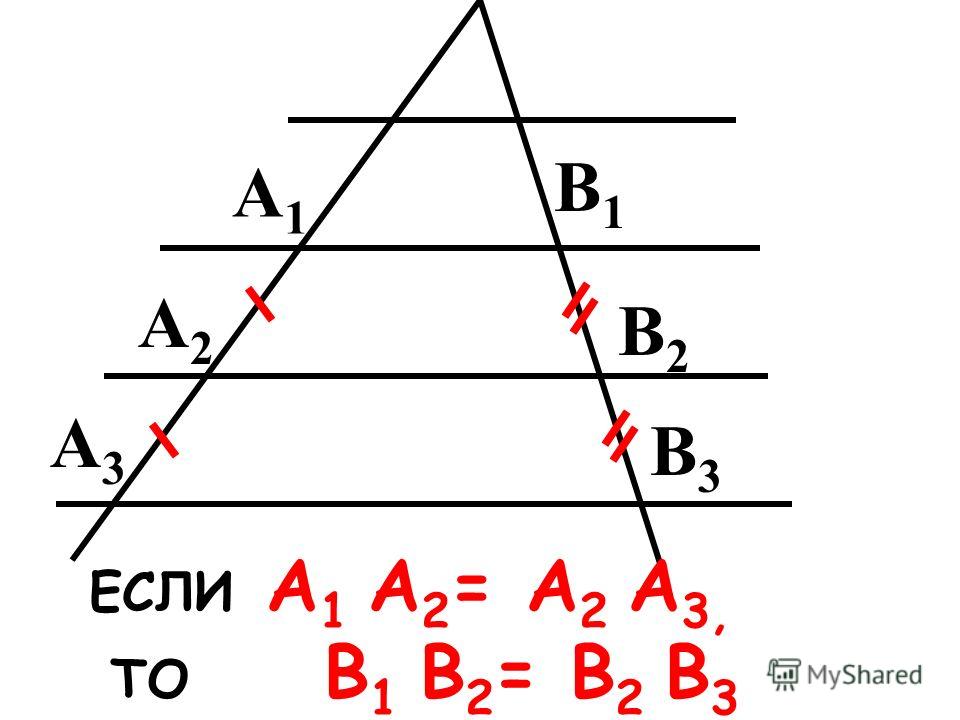
Поскольку MN является средней линией треугольника, ее длина — равная половине AC.
Правильным является утверждение, что пропорциональность двух пар сторон обуславливает аналогичное отношение, касающееся третьей пары сторон.
Источник: auka.clubТретий вариант доказательства теоремы средней линии использует такое понятие, как сумма векторов: CA, AM, MN, NC. Из вышеприведенного рисунка можно узнать, что последовательно сменяющие друг друга обозначенные векторы образуют замкнутую линию. Поэтому их сумма равна нулю.
Проведя простые математические действия, получаем формулу:
Источник: nauka.clubДля решения задач по нахождению параметров равнобедренных, равносторонних, прямоугольных треугольников важно знать следствия из теоремы средней линии. К ним относятся:
- С помощью средней линии можно отсечь в основном треугольнике второй, меньший по размеру, но подобный треугольник. Его площадь составляет четверть основного, а коэффициент подобия равен ½.

Данное утверждение может быть доказано исходя из следующего:
Согласно своим особенностям средняя линия треугольника пересекается с двумя его сторонами в их серединах. Следовательно, она делит стороны AB и BC пополам. Можно записать, что MB/AB=BN/BC=1/2
В то же время сама теорема средней линии утверждает, что ее длина составляет половину основания (третьей стороны треугольника). Значит MN/AC=1/2
Искать продолжение доказательства следствия теоремы следует в третьем признаке подобия. Установлено, что площади фигур, являющихся подобными, относятся друг к другу как коэффициента подобия в квадрате. То есть приходим ко второй части свойства: площадь меньшего треугольника находится по отношению к площади большего как дробь ¼.
Поэтому записываем:
SΔMBN/SΔABC=1/4
Это результат, какой и следовало доказать.
Существует еще одно следствие из теоремы средней линии. Оно звучит следующим образом:
Если в треугольнике провести три средние линии, то они разделят его на четыре одинаковых по площади треугольника, которые будут подобными исходному с коэффициентом подобия 0,5.
Для доказательства рассмотрим рисунок.
Источник: nauka.clubНа рисунке отрезок MN является средней линией треугольника. Поэтому по одному из своих свойств он параллелен AC. Вытекающий признак: угол BMN равен углу BAP, а угол BNM равен углу BCA, поскольку они прилегают к параллельным прямым и линиям, которые являются секущими (AB и BC).
Аналогичная ситуация по линии MP. Она параллельна BC, откуда следует, что угол MPA равен углу BCA. Это углы соответственные с учетом параллельности прямых и секущей AC.
Из вышеприведенного следует, что углы BNM, BCA, MPA равны.
MN — средняя линия треугольника, поэтому ее длина составляет половину AC и равна AP.
Поэтому треугольники AMP и MBN равны (согласно второму признаку равенства).
Факт, что остальные пары треугольников равны, можно доказать аналогичным образом.
Треугольники MBN и ABС подобны с коэффициентом 0,5. Поскольку все образовавшиеся треугольники равны, то любой из них является подобным основному (большому) с одним и тем же коэффициентом.
Задачи на использование теоремы
Задача 1
Дан рисунок. Необходимо доказать, что в произвольном выпуклом четырехугольнике середины сторон — вершины параллелограмма.
Источник: nauka.clubПри проведении диагонали в четырехугольнике образуется два треугольника. В обоих необходимо построить средние линии, которые по определению будут параллельными диагонали (являющейся основанием).
Существует правило: если две прямые параллельны третьей, то они параллельны между собой. В тот же время стороны, которые лежат противоположно и образованы средними линиями в 4-х угольнике, также параллельны.
Это и есть запрашиваемое по условию задачи доказательство.
Касательно параллельности двух других сторон вновь образованного 4-х угольника, то ее можно доказать аналогичным путем. Четырехугольник, который образовался в результате соединения середин сторон первоначально данного четырехугольника, называется параллелограммом.
Задача 2
На рисунке изображен треугольник. Его сторона имеют длины 6 и 8 см. В треугольнике провели среднюю линию, соединив две стороны. Какой размер она имеет?
Источник: microexcel.ruИзобразив схематически треугольник с заданными сторонами (катетами), видим, что он прямоугольный. По своему определению средняя линия, соединяющая эти катеты, параллельна основанию (гипотенузе) и составляет половину ее длины.
Для дальнейшего решения обратимся к теореме Пифагора, которая говорит: «для прямоугольного треугольника справедливо выражение: квадрат гипотенузы равняется сумме квадратов катетов».
Записываем данное утверждение математически применительно для имеющегося треугольника:
BC2=AB2+AC2=62+82=100
Проведя несложные вычисления, получаем ответ задачи:
BC=√100=10
Отсюда длина средней линии LM составляет половину длины BC и равна 10/2=5 см
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Поиск по содержимому
Средняя линия треугольника / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Средняя линия треугольника
Средняя линия треугольника — отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия . На рисунке 1 изображен треугольник АВС, отрезки МЕ, МК и КЕ являются средними линиями данного треугольника, ВМЕ =АМК =СЕК =МЕК.
Теорема
| Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. |
Доказательство
Дано: АВС, МЕ — средняя линия.
Доказать: МЕАС, МЕ = АС.
Доказательство:
В треугольниках МВЕ и АВС:
- В — общий;
- ВА = 2ВМ, т.к. МЕ — средняя линия, значит, М — середина АВ, тогда , аналогично, , т.е. .
Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 1 =2 и .
Прямые МЕ и АС пересечены секущей АВ, углы 1 и 2 — соответственные, при этом 1 =2, следовательно, МЕАС (по признаку параллельности двух прямых).
Из равенства следует, что МЕ = АС. Теорема доказана.
Задача:
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Дано: АВС, АА1 и ВВ1, СС1 — медианы, АА1ВВ1 = О.
Доказать: АА1ВВ1СС1 = О, АО : ОА1 = ВО : ОВ1 = СО : ОС1 = 2 : 1.
Доказательство:
Проведем среднюю линию В1А1 треугольника АВС (В1А1 — средняя линия, т.к. по условию АА1 и ВВ1 — медианы, значит точки А1 и В1 — середины сторон АС и СВ).
А1В1АВ (по теореме, доказанной выше), АА1 и ВВ1 — секущие, 1 и 2, 3 и 4 — накрест лежащие, значит, 1 =2, 3 =4 (по теореме о накрест лежащих углах). Следовательно, треугольники АОВ и А1ОВ1подобны (по 1 признаку подобия), тогда сходственные стороны данных треугольников пропорциональны:
. (1)
(1)
Так как А1В1 — средняя линия, А1В1 = АВ, откуда АВ = 2А1В1, поэтому АО = 2А1О и ВО = 2В1О. Подставляя три последних равенства в (1), получим:
.
Следовательно, точка О, в которой пересекаются медианы АА1 и ВВ1 делит каждую из них в отношении 2 : 1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.
Итак, все три медианы АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 616, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 618, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 733, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 792, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 794, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 797, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 866, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 867, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1003, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Средняя линия треугольника онлайн разными способами
Треугольник — геометрическая фигура, составленная из трёх отрезков. Они объединены тремя точками, не
лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами.
Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.
Они объединены тремя точками, не
лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами.
Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.
Во всяком треугольнике можно проложить три средних линии. В прямоугольном многоугольнике такой отрезок равняется половине основания. Средняя линия прямоугольного треугольника разделяет его на четыре прямоугольных треугольника. Существует и признак срединного отрезка треугольника: если отрезок в многоугольнике пролегает через средину одной из его сторон, пересекает вторую и параллелен ей, тогда такой отрезок называется средней линией.
Выделяют свойства срединного отрезка:
- Средняя линия равняется половине длины основания и параллельна ему;
- Этот отрезок отделяет треугольник, подобный заданному с коэффициентом 0.
 5, а его площадь
равняется четверти площади заданной фигуры;
5, а его площадь
равняется четверти площади заданной фигуры; - Три средние линии дробят заданный многоугольник на четыре других, эквивалентных друг другу. Находящуюся по центру фигуру именуют дополнительной.
- Средняя линия треугольника через сторону
- Средняя линия равностороннего треугольника через высоту
- Средняя линия равностороннего треугольника через радиус вписанной окружности
- Средняя линия равностороннего треугольника через радиус описанной окружности
- Средняя линия треугольника через площадь и высоту
- Средняя линия равнобедренного треугольника через боковую сторону и высоту
- Средняя линия равностороннего треугольника через площадь
Через сторону
Срединный отрезок равняется половине противолежащей стороны.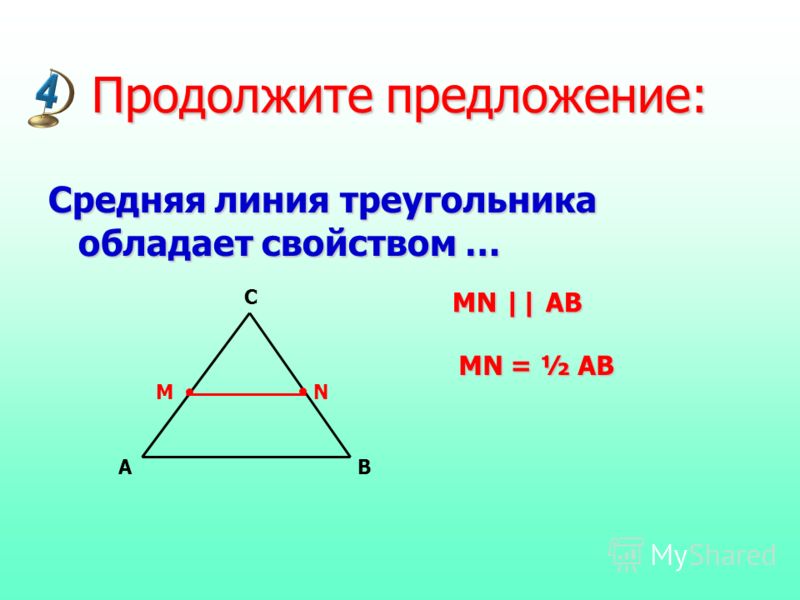 Следовательно, формула выглядит так:
Следовательно, формула выглядит так:
m = a/2
где a — противолежащая сторона.
Сторона (a):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Следовательно, если такая сторона будет равна 50, то срединный отрезок будет равен m = 50/2 = 25. Если же сторона будет равна 20, тогда срединный отрезок будет рассчитываться так: m = 20/2 = 10.
Средняя линия равностороннего треугольника через радиус вписанной окружности
Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается так:
m = r√3
где r — радиус вписанной окружности.
Радиус (R):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Таким образом, если радиус такой окружности равняется 5, тогда m= 5√3 ≈ 8,66.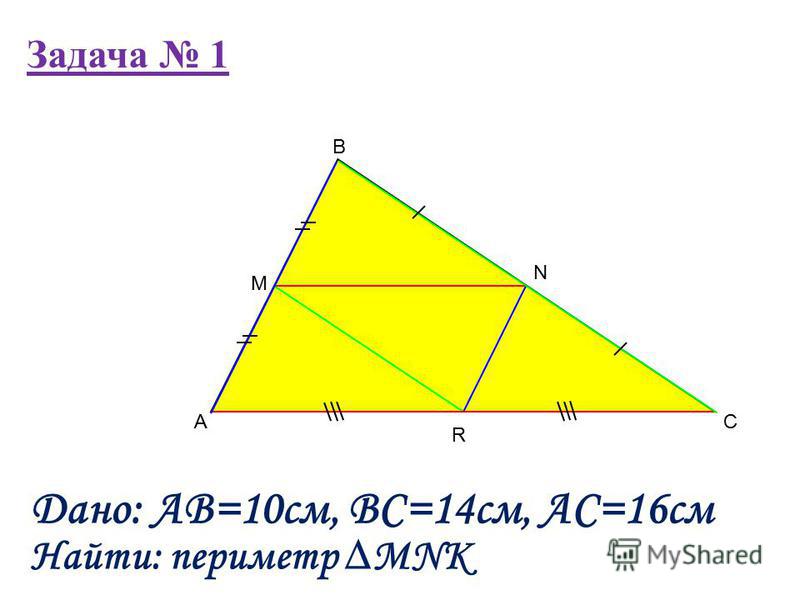 Если же радиус будет равен, допустим, 9, в таком случае
m = 9√3 ≈ 15,59.
Если же радиус будет равен, допустим, 9, в таком случае
m = 9√3 ≈ 15,59.
Средняя линия треугольника через площадь и высоту
Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней линии. Таким образом, тождество имеет такой вид:
m = S/h
где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.
Площадь (S):
мм²см²дм²м²
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Если площадь некоторого многоугольника будет равна 25, а перпендикуляр — 5, тогда m = 25/5 = 5. Если же в качестве площади взять число 60, а в качестве перпендикуляра — 3, получится следующий срединный отрезок: m = 60/3 = 20.
Средняя линия равностороннего треугольника через высоту
Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим образом:
m = h/√3
где h — перпендикуляр равностороннего многоугольника.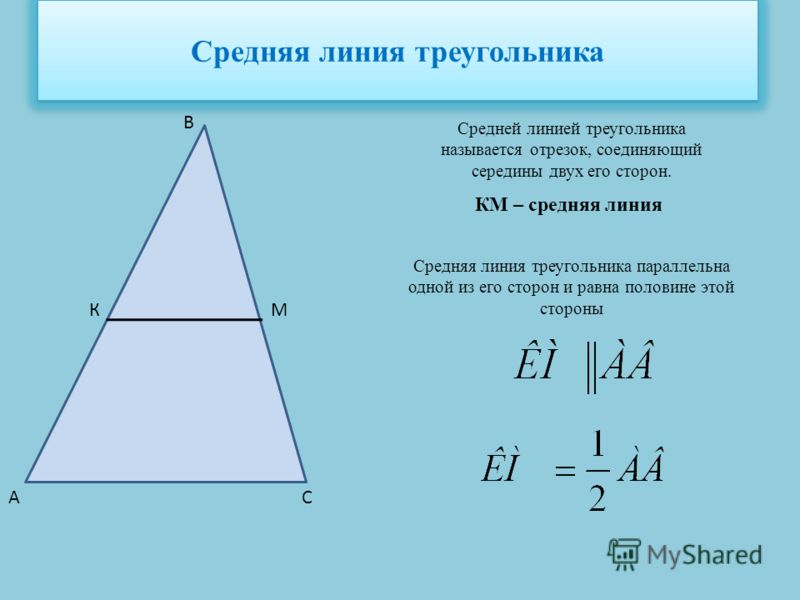
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
К примеру, если перпендикуляр равностороннего многоугольника равен 5, тогда срединный отрезок будет
такой: m = 5/√3 ≈ 2,89.
Если же перпендикуляр будет равен 10, тогда
срединный отрезок будет около m = 10/√3 ≈ 5,77.
Средняя линия равнобедренного треугольника через боковую сторону и высоту
Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим образом:
m = a2 – h2
где a — боковая сторона, а h — перпендикуляр.
Сторона (b):
ммсмдмм
Высота (h):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Допустим, если боковая сторона многоугольника равна 5, а перпендикуляр — 3, тогда m = 25 – 9 = 16.
Если же в качестве боковой стороны взять число 8, а в качестве перпендикуляра равнобедренного
многоугольника — 2, в таком случае m = 64 – 4 = 60.
Средняя линия равностороннего треугольника через площадь
Срединный отрезок равнобедренного многоугольника через площадь находится по следующей формуле:
m = 1/4 √(√3/S)
где S — это площадь равностороннего многоугольника.
Площадь (S):
мм²см²дм²м²
Цифр после запятой:
012345678910Результат в: ммсмдмм
Допустим, если площадь равностороннего многоугольника будет равна 5, тогда m = 1/4 √(√3/5) ≈ 0,15.
Если выбрать равносторонний многоугольник побольше, к примеру, с площадью 25, в таком случае m = 1/4 √(√3/25) ≈ 0,065.
Средняя линия равностороннего треугольника через радиус описанной окружности
Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается так:
m = R√3/2
где R — радиус описанной окружности.
Радиус (R):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Следовательно, если радиус такой окружности будет равен 15, тогда m = 15√3/2 =12,99. Если в качестве радиуса взять число 24, в таком случае m = 24√3/2 = 20,78.
Средняя линия фигур в планиметрии — отрезок, который объединяет средины двух сторон представленной фигуры. Такой термин используется при описании треугольников, четырёхугольников и трапеций. В некоторых случаях рассматривается вырожденный треугольник, три вершины которого пролегают на единственной прямой. Треугольник считается одной из основных геометрических фигур, повсюду применяемых в науке и технике, потому изучение его качеств велось с давних времён.
Средняя линия треугольника — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
Средняя линия треугольника — это сегмент, соединяющий середины двух сторон треугольника.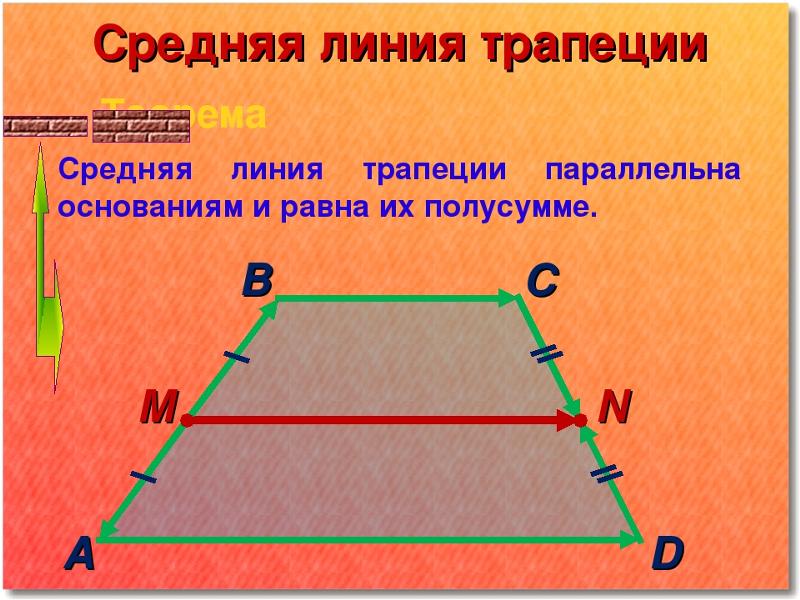
Формулы и свойства центральной линии треугольника
Средняя линия треугольника параллельна одной стороне и равна половине ее:
\(\ K N \| A C, K N=\frac{1}{2} A C \)
В любом треугольнике вы можете нарисовать три средних линии, на пересечении которых образуются 4 равных треугольника, аналогичные оригинальному с коэффициентом 1/2.
Средняя линия обрезает треугольник, который похож на этот, и его площадь равна одной четверти исходного треугольника.
Примеры решения проблем
ПРИМЕР 1
В треугольнике \(\ \mathrm{ABC} \) была проведена средняя линия \(\ \mathrm{MN} \), параллельная \(\ \mathrm{AC} \). Найдите область треугольника \(\ \mathrm{MBN} \), если известно, что \(\ \mathrm{MN = 6 см.} \), а высота \(\ \mathrm{BK} \), опущенная на сторону переменного тока, составляет 5 см.
В треугольнике \(\ \mathrm{ABC} \) (см. Рис.1) средняя линия \(\ \mathrm{MN} \) равна половине стороны \(\ \mathrm{AC} \), поэтому
Найдите область треугольника \(\ \mathrm{ABC} \):
\(\ S_{A B C}=\frac{1}{2} A C \cdot B K=\frac{1}{2} \cdot 12 \cdot 5=30 \mathrm{cm}^{2} \)
Так как средняя линия \(\ \mathrm{MN} \) разрезает треугольник \(\ M B N \), площадь которого равна одной четверти исходного треугольника \(\ \mathrm{ABC} \), площадь треугольника \(\ M B N \) равна:
\(\ S_{M B N}=\frac{1}{4} S_{A B C}=\frac{1}{4} \cdot 30=7,5 \mathrm{cm}^{2} \)
\(\ S_{M B N}=7,5 \)
ПРИМЕР 2
В треугольнике \(\
\mathrm{ABC}
\) мы построили средние линии \(\
\mathrm{KN = 4 см}
\), \(\
\mathrm{NL = 5 см}
\) и \(\
\mathrm{KL = 8 см}
\). Найдите периметр треугольника \(\
\mathrm{ABC}
\).
Найдите периметр треугольника \(\
\mathrm{ABC}
\).
Так как средняя линия находится на половине стороны, в которой она параллельна, мы можем найти длины всех сторон треугольника \(\ \mathrm{ABC} \):
\(\ \mathrm{AC}=2 \mathrm{KN}=8 \mathrm{см.} \), \(\ \mathrm{AB}=2 \mathrm{NL}=10 \mathrm{см.} \), \(\ \mathrm{BC}=2 \mathrm{KL}=16 \mathrm{см.} \)
Теперь вы можете найти периметр треугольника \(\ \mathrm{ABC} \) как сумму длин всех его сторон:
\(\ \ P_{A B C}=A C+A B+B C=8+10+16=34 \mathrm{см.} \)
\(\ P_{A B C}=34 \mathrm{см.} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Промежутки выпуклости и вогнутости функции Точки перегиба функции Наибольшее и наименьшее значение функции Монотонность функции. Возрастание и убывание
Возрастание и убывание
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Теорема о средней точке — Утверждение, Доказательство, Обратное, Примеры
В геометрии теорема о средней точке помогает нам найти пропущенные значения сторон треугольников. Он устанавливает отношение между сторонами треугольника и отрезком, проведенным из середины любых двух сторон треугольника. Теорема о средней точке утверждает, что отрезок, проведенный из середины любых двух сторон треугольника, параллелен третьей стороне и составляет половину длины третьей стороны треугольника.
Он устанавливает отношение между сторонами треугольника и отрезком, проведенным из середины любых двух сторон треугольника. Теорема о средней точке утверждает, что отрезок, проведенный из середины любых двух сторон треугольника, параллелен третьей стороне и составляет половину длины третьей стороны треугольника.
В этой статье мы рассмотрим концепцию теоремы о средней точке и ее обращение. Мы изучим применение теоремы с помощью нескольких решенных примеров для лучшего понимания концепции.
| 1. | Что такое теорема о средней точке? |
| 2. | Определение теоремы о средней точке |
| 3. | Доказательство теоремы средней точки |
| 4. | Обратная теорема о средней точке |
| 5. | Формула теоремы о средней точке |
| 6. | Часто задаваемые вопросы по теореме о средней точке |
Что такое теорема о средней точке?
Теорема о средней точке утверждает, что отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне и равен половине длины третьей стороны.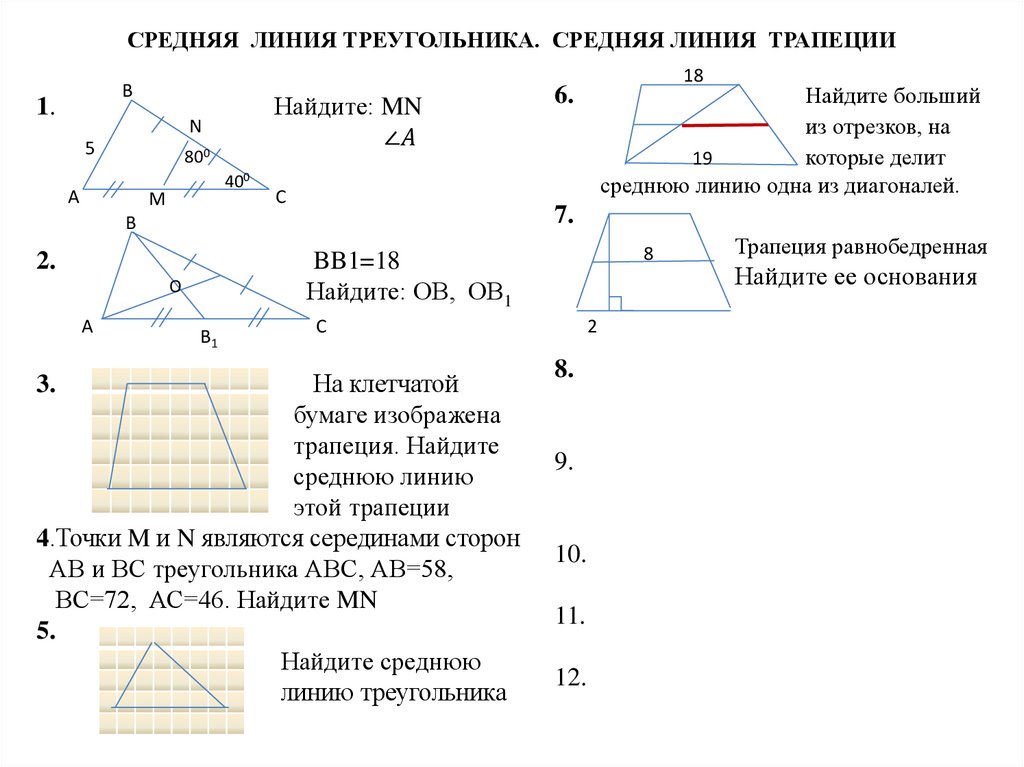 Эта теорема используется в разных местах в реальной жизни, например, при отсутствии измерительного инструмента мы можем использовать теорему о средней точке, чтобы разрезать палку пополам.
Эта теорема используется в разных местах в реальной жизни, например, при отсутствии измерительного инструмента мы можем использовать теорему о средней точке, чтобы разрезать палку пополам.
Определение теоремы о средней точке
Теорема о средней точке утверждает, что отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне и равен половине третьей стороны. Рассмотрим произвольный треугольник ΔABC. Пусть D и E — середины отрезков AB и AC соответственно. Предположим, что вы соединяете D с E. Теорема о средней точке говорит, что DE будет параллелен BC и равен ровно половине BC. Посмотрите на изображение, приведенное ниже, чтобы понять теорему о средней точке треугольника.
Доказательство теоремы о средней точке
Теперь сформулируем и докажем теорему о средней точке. Прямая линия, соединяющая середины любых двух сторон треугольника, считается параллельной и составляет половину длины третьей стороны.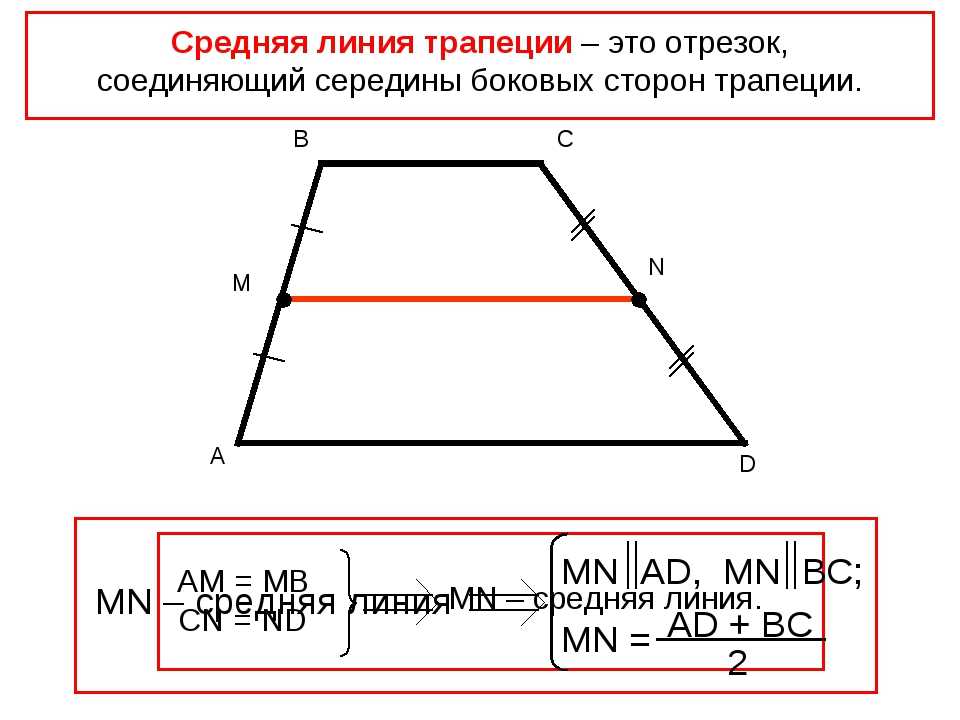 Рассмотрим треугольник ABC, как показано на рисунке ниже. Пусть E и D — середины сторон AC и AB соответственно. Тогда говорят, что прямая DE параллельна стороне BC, тогда как сторона DE составляет половину стороны BC, т. е.
Рассмотрим треугольник ABC, как показано на рисунке ниже. Пусть E и D — середины сторон AC и AB соответственно. Тогда говорят, что прямая DE параллельна стороне BC, тогда как сторона DE составляет половину стороны BC, т. е.
Немецкий || BC
DE = 1/2 × BC
Это формулировка теоремы о средней точке. Теперь давайте посмотрим на его доказательство.
Дано: D и E — середины сторон AB и AC треугольника ΔABC соответственно.
Построение: В ΔABC через C провести линию, параллельную BA, и продолжить DE так, чтобы она пересекалась с этой параллельной линией в точке F, как показано ниже:
Доказательство:
- AE = EC (E — середина AC)
- ∠DAE = ∠FCE (альтернативные внутренние углы)
- ∠DEA = ∠FEC (вертикально противоположные углы)
По критерию ASA два треугольника равны. Таким образом, DE = EF и AD = CF. Но AD также равно BD, а это означает, что BD = CF (также BD || CF по нашей конструкции).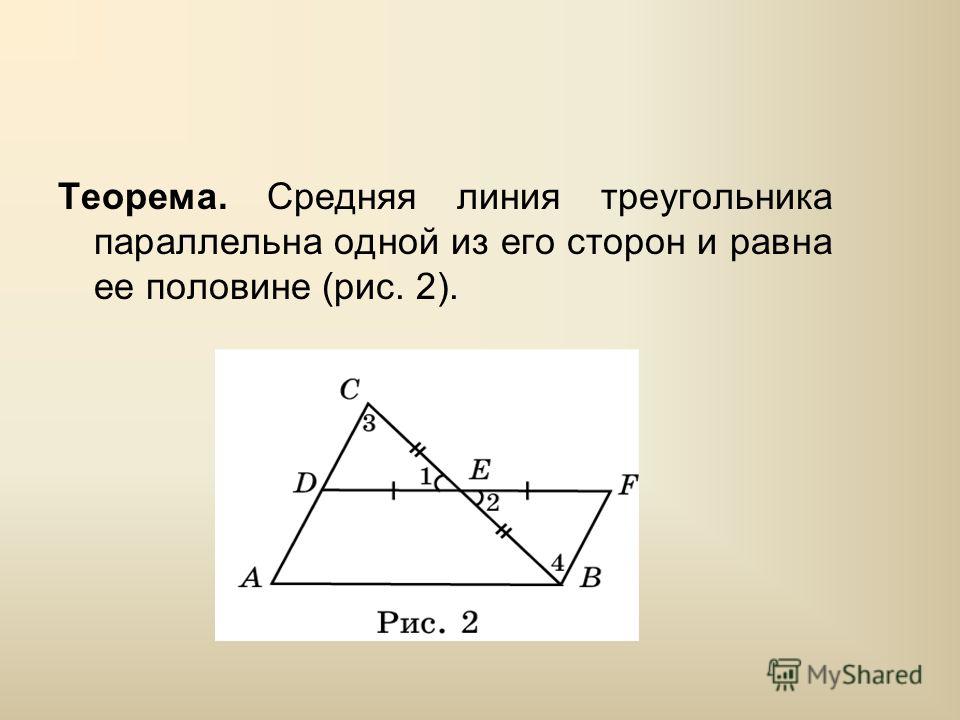 Отсюда следует, что BCFD является параллелограммом. Таким образом,
Отсюда следует, что BCFD является параллелограммом. Таким образом,
DF || БК ⇒ DE || BC
и, DF = BC
⇒ DE + EF = BC
⇒ 2DE = BC (как, DE = EF, доказано выше)
⇒ DE = 1/2 × BC
Это завершает наше доказательство. Будет ли верна обратная теорема о средней точке? Да, будет, и далее будет представлено доказательство обратного.
Обратная теорема о средней точке
Обратная теорема о средней точке утверждает, что прямая, проведенная через середину одной стороны треугольника, параллельная другой стороне, делит третью сторону пополам. Рассмотрим треугольник ABC, и пусть D будет серединой треугольника AB. Линия, проходящая через D параллельно BC, пересекает AC в точке E, как показано ниже. Теперь предположим, что E не является серединой AC. Пусть F — середина АС. Соедините D с F, как показано ниже:
По теореме о средней точке DF || ДО Н.Э. Но у нас также есть DE || ДО Н.Э. Этого не может быть, потому что через данную точку (в данном случае D) к данной прямой (в данном случае BC) можно провести ровно одну параллель.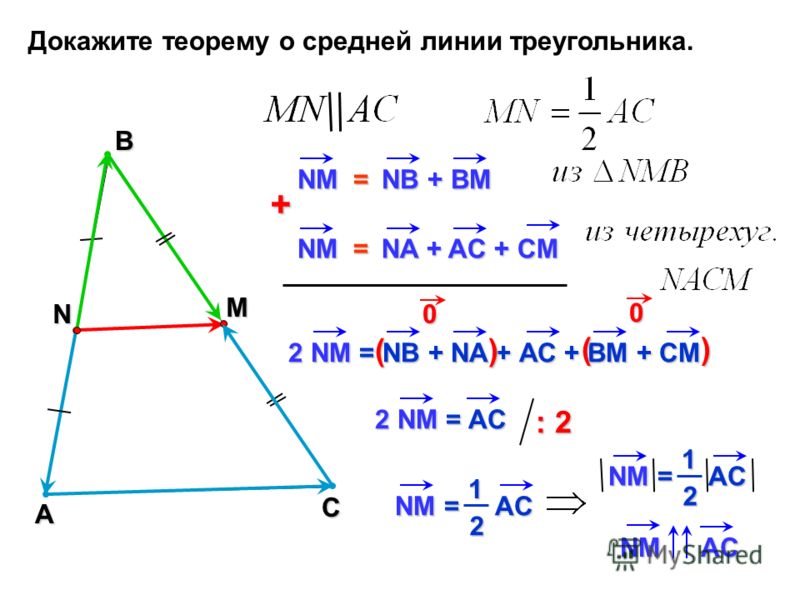 Таким образом, E должна быть серединой AC. Это завершает доказательство обратной теоремы о средней точке.
Таким образом, E должна быть серединой AC. Это завершает доказательство обратной теоремы о средней точке.
Формула теоремы о средней точке
В математике у нас также есть формула теоремы о средней точке, которая находит применение в координатной геометрии. Это также может быть известно как теорема о средней точке отрезка. В нем говорится, что если у нас есть отрезок, чьи конечные точки координаты заданы как (x 1 , y 1 ) и (x 2 , y 2 ), то мы можем найти координаты середины отрезка, используя следующую формулу:
Пусть (x m , y m ) — координаты середины отрезка. Тогда
(x м , y м ) = ((x 1 + x 2 )/2, (y 1 + y 2 )/2 известно как формула теоремы о средней точке.
Стороны, соединяющие середины треугольника
Интересным следствием теоремы о средней точке является то, что если мы соединим середины трех сторон любого треугольника, мы получим четыре (меньших) конгруэнтных треугольника, как показано на рисунке ниже:
Имеем: ΔADE ≅ ΔFED ≅ ΔBDF ≅ ΔEFC.
Доказательство: Рассмотрим четырехугольник DEFB. По теореме о средней точке имеем:
- DE = 1/2 × BC = BF
- Германия || БФ
Таким образом, DEFB является параллелограммом, а значит, ΔFED ≅ ΔBDF. Точно так же мы можем показать, что AEFD и DECF являются параллелограммами, и, следовательно, все четыре треугольника, образованные таким образом, конгруэнтны друг другу (убедитесь, что когда вы записываете отношение конгруэнтности между этими треугольниками, вы получаете правильный порядок вершин).
Статьи по теме
- Формула средней точки
- Середина треугольника
- Медиана треугольника
- Основная теорема о пропорциональности
Важные замечания по теореме о средней точке
- Теорема о средней точке утверждает, что отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне и равен половине длины третьей стороны.

- Обратная теорема о средней точке утверждает, что линия, проведенная через середину одной стороны треугольника, параллельная другой стороне, делит третью сторону пополам.
Примеры теоремы о средней точке
Пример 1: Рассмотрим треугольник ABC, и пусть D — любая точка на BC. Пусть X и Y — середины отрезков AB и AC соответственно.
Покажите, что XY делит AD пополам.
Решение: Дано, что X и Y являются серединами AB и AC. По теореме о средней точке XY || ДО Н.Э. Теперь рассмотрим ΔABD. Отрезок XE параллелен основанию BD, а X — середина AB. Согласно обратной теореме о средней точке, E должна быть серединой AD. Таким образом, XY делит AD пополам.
Пример 2: Докажите, что если три параллельные прямые пересекают на одной секущей равные точки, то и на любой другой секущей они пересекаются одинаково.
Решение: Давайте сначала лучше разберемся в этой проблеме.
 Рассмотрим три прямые и две секущие, как показано ниже:
Рассмотрим три прямые и две секущие, как показано ниже:Предположим, что пересечения на левой секущей равны, то есть AB = BC. Затем нам нужно доказать, что пересечения на правой секущей также будут равны, т. е. DE = EF.
Чтобы доказать это, соедините A с F:
Рассмотрим ΔACF. Так как B — середина AC и BG || CF, обратная теорема о средней точке говорит нам, что G является серединой AF. Теперь рассмотрим ΔAFD. Мы показали, что G является серединой AF. Кроме того, ГЭ || ОБЪЯВЛЕНИЕ. Таким образом, обратная теорема о средней точке говорит нам, что E должна быть серединой FD. Следовательно, ДЭ = ЭФ.
Пример 3: Рассмотрим параллелограмм ABCD. E и F — середины отрезков AB и CD соответственно. Докажите, что отрезки AF и EC пересекают диагональ BD пополам.
Решение: Рассмотрим следующую фигуру:
Нам нужно показать, что BX = XY = YD = BD/3.
Прежде всего отметим, что AECF является параллелограммом, так как ABCD является параллелограммом, что означает AB = CD и, следовательно, AE = CF (поскольку E и F — середины), и, таким образом, EC || АФ.
 Теперь рассмотрим ΔBAY. Так как E — середина AB, а EX || AY, обратная теорема о средней точке говорит нам, что X является серединой BY, а это означает, что BX = XY. Аналогично можно доказать, что XY = YD. Таким образом, BX = XY = YD = BD/3. Значит доказано.
Теперь рассмотрим ΔBAY. Так как E — середина AB, а EX || AY, обратная теорема о средней точке говорит нам, что X является серединой BY, а это означает, что BX = XY. Аналогично можно доказать, что XY = YD. Таким образом, BX = XY = YD = BD/3. Значит доказано.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы по теореме о средней точке
Что такое теорема средней точки?
Теорема о средней точке утверждает, что в любом треугольнике линия, соединяющая середины любых двух сторон треугольника, параллельна половине длины третьей стороны. Он имеет множество применений в математике при вычислении сторон треугольника, нахождении координат середин и т. д.
Как доказать теорему о средней точке?
Чтобы доказать теорему о средней точке, мы используем правила конгруэнтности. Построим треугольник вне заданного треугольника так, чтобы он касался стороны треугольника. А затем докажем, что оно конгруэнтно любой части треугольника. Это помогает нам доказать равенство сторон, используя правила CPCTC.
Построим треугольник вне заданного треугольника так, чтобы он касался стороны треугольника. А затем докажем, что оно конгруэнтно любой части треугольника. Это помогает нам доказать равенство сторон, используя правила CPCTC.
Как доказать обратную теорему о средней точке?
Чтобы доказать обратную теорему о средней точке, рассмотрим треугольник ABC, и пусть D будет серединой треугольника AB. Прямая через D, параллельная ВС, пересекает АС в точке Е. Теперь предположим, что Е не является серединой АС. Пусть F — середина АС. Соедините D с F. По теореме о средней точке DF || ДО Н.Э. Но у нас также есть DE || ДО Н.Э. Этого не может быть, потому что через данную точку (в данном случае D) к данной прямой (в данном случае BC) можно провести ровно одну параллель. Таким образом, E должна быть серединой AC. Это доказательство обратной теоремы о средней точке.
Как найти теорему о средней точке?
Теорему о средней точке можно применить к любому треугольнику. Когда линия проводится между серединами любых двух сторон треугольника, она всегда параллельна половине длины третьей стороны. Эта теорема применима ко всем типам треугольников.
Эта теорема применима ко всем типам треугольников.
Что такое формулировка теоремы о средней точке?
Утверждение теоремы о средней точке состоит в том, что «Линия, проведенная между серединами любых двух сторон треугольника, параллельна половине третьей стороны треугольника». Это может быть математически представлено как,
Предположим, что DE — это прямая, соединяющая середины треугольника ABC и параллельная BC.
⇒ DE || BC и DE = 1/2 × BC
Где используется теорема о средней точке?
Теорема о средней точке используется для определения отношений между сторонами треугольника. Полезно найти недостающие длины сторон, доказать конгруэнтность четырех треугольников, образованных соединением середины треугольника, найти координаты и т. д. Все это приложения теоремы о средней точке в математике.
Скачать БЕСПЛАТНЫЕ учебные материалы
Скачать рабочие листы с важными формулами для классов 7-8
Скачать образцы рабочих листов для классов 7-8
Скачать рабочие листы с важными формулами для класса 9
Скачать теорему средней точки | Решенные вопросы Рабочие листы
Рабочие листы по средней точке Теорема
Средняя линия треугольника.
 Теорема Фалеса. Полные уроки
Теорема Фалеса. Полные урокиО параллели и секущей.
Вне русскоязычной литературы теорему Фалеса иногда называют другой теоремой планиметрии, а именно утверждением, что вписанный угол, исходя из диаметра окружности, прямой. Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.
Формулировка
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то на второй прямой они отрежут равные отрезки.
Более общая формулировка, также называемая теоремой о пропорциональных отрезках
Параллельные прямые отсекаются на секущих пропорциональных отрезках:
A 1 A 2 B 1 B 2 = A 2 A 3 B 2 B 3 = A 1 A 3 B 1 B 3. (\ displaystyle (\ frac (A_ (1) A_ (2)) (B_ (1) B_ ( 2))) = (\ frac (A_ (2) A_ (3)) (B_ (2) B_ (3) )) = (\ frac (A_ (1) A_ (3)) (B_ (1) B_ ( 3))).)
Замечания
- Теорема не имеет ограничений на взаимное расположение секущих (справедлива как для пересекающихся, так и для параллельных прямых).
 Также не имеет значения, где находятся отрезки линии.
Также не имеет значения, где находятся отрезки линии.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A A 1 | | Б Б 1 | | С С 1 | | D D 1 (\ displaystyle AA_ (1) || BB_ (1) || CC_ (1) || DD_ (1)) и где AB = C D (\ displaystyle AB = CD).
Доказательство в случае параллельных прямых
Проведем прямую BC … Углы ABC и BCD равны как внутренние крест-накрест для параллельных прямых AB и CD и секущая 3 BC и секущая и углы ACB и CBD равны как внутренние перекрещивающиеся для параллельных прямых AC и BD и секущей BC … Тогда по второму критерию равенства треугольников треугольники ABC и DCB равны.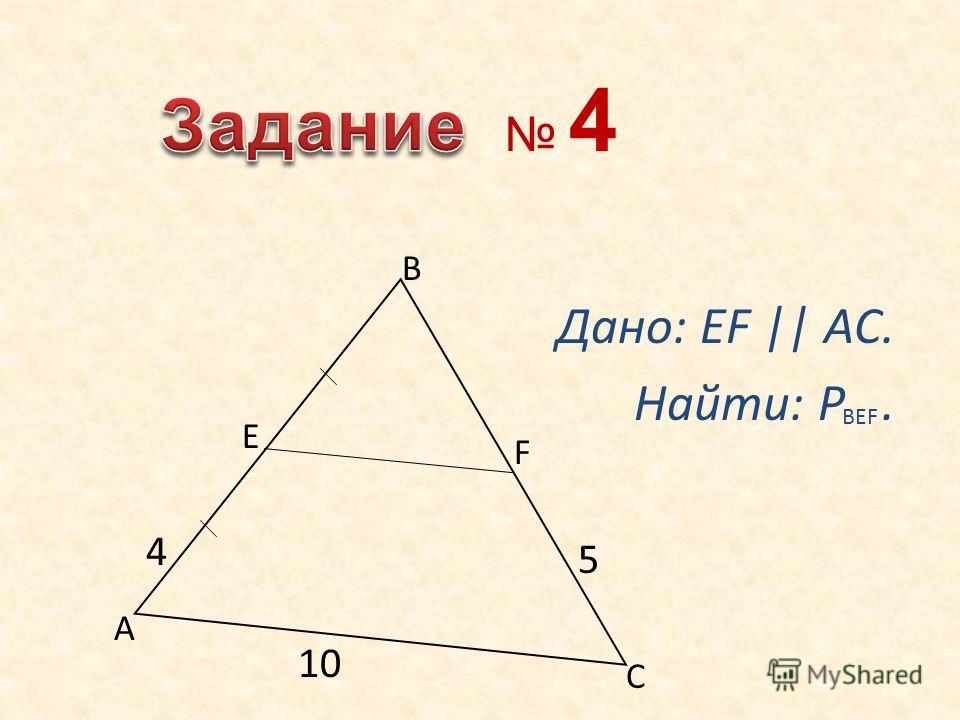 Отсюда следует, что AC = BD и AB = CD . ■
Отсюда следует, что AC = BD и AB = CD . ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются с вершины (часто в школьной литературе используется следующая формулировка), то оказывается справедливой и обратная теорема. Для пересекающихся секущих оно формулируется следующим образом:
В обратной теореме Фалеса важно, чтобы равные отрезки начинались с вершины
Таким образом (см. рис.) Из того, что CB 1 CA 1 = B 1 B 2 A 1 A 2 =… (\ displaystyle (\ frac (CB_ (1)) (CA_ (1))) = (\ frac (B_ (1) B_ (2)) (A_ (1) A_ (2))) = \ ldots), следует, что A 1 B 1 | | А 2 Б 2 | | … (\ Displaystyle A_ (1) B_ (1) || A_ (2) B_ (2) || \ ldots).
Если секущие параллельны, то необходимо требовать равенства отрезков на обоих секущих друг другу, иначе это утверждение становится неверным (контрпримером является трапеция, пересеченная прямой, проходящей через середины оснований).
Эта теорема используется в навигации: столкновение кораблей, движущихся с постоянной скоростью, неизбежно, если сохраняется направление от одного корабля к другому.
Лемма Соллертинского
Следующее утверждение двойственно лемме Соллертинского:
Пусть f(\displaystyle f)- проективное соответствие между точками прямой l(\displaystyle l) и прямой m(\displaystyle m) . Тогда множество прямых будет множеством касательных к некоторому коническому сечению (возможно дегенерат). |
В случае теоремы Фалеса коникой называется бесконечно удаленная точка, соответствующая направлению параллельных прямых.
Этот оператор, в свою очередь, является предельным случаем следующего оператора:
Пусть f (\displaystyle f)- проективное коническое преобразование. Тогда огибающая множества прямых X f(X)(\displaystyle Xf(X)) будет коникой (возможно, вырожденной). |
Эта гробница мала, но слава над ней огромна.
В нем, перед вами, скрыт многоразумный Фалес.
Надпись на гробнице Фалеса Милетского
Представьте себе эту картину. 600 г. до н.э. Египет. Перед вами огромная египетская пирамида. Чтобы удивить фараона и остаться в его фаворитах, нужно измерить высоту этой пирамиды. У тебя ничего нет. Можно впасть в отчаяние, а можно действовать как Фалес Милетский : используйте теорему подобия треугольников. Да, оказывается все достаточно просто. Фалес Милетский подождал, пока длина его тени и его высота совпадут, а затем, используя теорему о подобии треугольников, нашел длину тени пирамиды, которая, соответственно, была равна тени, отбрасываемой пирамида.
600 г. до н.э. Египет. Перед вами огромная египетская пирамида. Чтобы удивить фараона и остаться в его фаворитах, нужно измерить высоту этой пирамиды. У тебя ничего нет. Можно впасть в отчаяние, а можно действовать как Фалес Милетский : используйте теорему подобия треугольников. Да, оказывается все достаточно просто. Фалес Милетский подождал, пока длина его тени и его высота совпадут, а затем, используя теорему о подобии треугольников, нашел длину тени пирамиды, которая, соответственно, была равна тени, отбрасываемой пирамида.
Кто этот Фалес Милетский ? Человек, снискавший себе славу одного из «семи мудрецов» древности? Фалес Милетский — древнегреческий философ, прославившийся своими успехами в астрономии, а также в математике и физике. Годы его жизни оценивались лишь приблизительно: 625-645 до н.э.
Среди доказательств познаний Фалеса в астрономии можно привести следующий пример. 28 мая 585 г. до н.э. предсказание Милецким солнечного затмения помогло положить конец 6-летней войне между Лидией и Мидией. Это явление так напугало мидийцев, что они согласились на невыгодные для себя условия заключить мир с лидийцами.
Это явление так напугало мидийцев, что они согласились на невыгодные для себя условия заключить мир с лидийцами.
Довольно широко известна легенда, характеризующая Фалеса как находчивого человека. Фалес часто слышал нелестные отзывы о своей бедности. Однажды он решил доказать, что философы тоже могут жить в достатке, если захотят. Еще зимой Фалес, наблюдая за звездами, определил, что лето будет хорошим урожаем оливок. В то же время он нанял маслобойни в Милете и на Хиосе. Это обошлось ему достаточно дешево, так как спроса на них зимой практически нет. Когда маслины дали богатый урожай, Фалес стал сдавать в аренду свои маслобойни. Большая сумма денег, собранная таким методом, рассматривалась как доказательство того, что философы могут зарабатывать умом, но их призвание выше таких земных проблем. Эту легенду, кстати, повторил и сам Аристотель.
Что касается геометрии, то многие его «открытия» были заимствованы у египтян. И все же эта передача знаний в Грецию считается одной из главных заслуг Фалеса Милетского.
Достижениями Фалеса считаются формулировка и доказательство следующих теорем:
- вертикальные углы равны;
- равных треугольников — это те, у которых сторона и два смежных угла соответственно равны;
- углы при основании равнобедренного треугольника равны;
- диаметр делит окружность пополам;
- вписанный угол, основанный на диаметре, прямой.
Фалес назван в честь еще одной теоремы, которая полезна при решении геометрических задач. Есть обобщенный и частный вид, обратная теорема, формулировки также могут незначительно отличаться в зависимости от источника, но смысл у них у всех остается один. Рассмотрим эту теорему.
Если параллельные прямые пересекают стороны угла и отсекают равные отрезки с одной его стороны, то они отсекают равные отрезки и с другой его стороны.
Допустим, точки А 1, А 2, А 3 — точки пересечения параллельных прямых с одной стороны угла, а В 1, В 2, В 3 — точки пересечения параллельных прямых с другой стороны угла.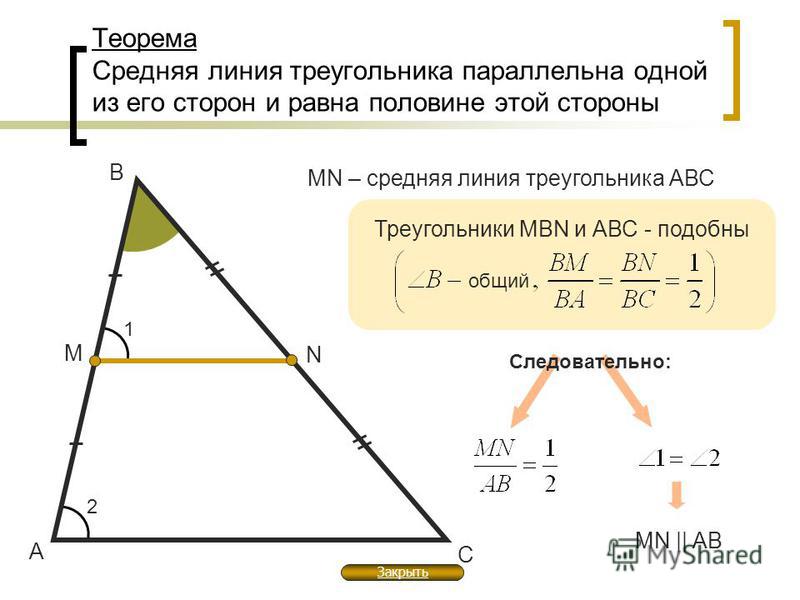 угол. Необходимо доказать, что если A 1 A 2 = A 2 A 3, то B 1 B 2 = B 2 B 3.
угол. Необходимо доказать, что если A 1 A 2 = A 2 A 3, то B 1 B 2 = B 2 B 3.
Через точку B 2 проведем прямую, параллельную прямой A 1 A 2. Обозначим новую прямая С 1 С 2. Рассмотрим параллелограммы A 1 C 1 B 2 A 2 и A 2 B 2 C 2 A 3.
Свойства параллелограмма позволяют утверждать, что A1A2 = C 1 B 2 и A 2 A 3 = B 2 C 2. А так как по нашему условию A 1 A 2 = A 2 A 3, то C 1 B 2 = B 2 C 2,
Наконец, рассмотрим треугольники Δ C 1 B 2 B 1 и Δ C 2 B 2 B 3.
C 1 B 2 = B 2 C 2 (доказано выше).
А это значит, что Δ C 1 B 2 B 1 и Δ C 2 B 2 B 3 будут равны по второму признаку равенства треугольников (по стороне и смежным углам).
Таким образом, теорема Фалеса доказана.
Использование этой теоремы значительно облегчит и ускорит решение геометрических задач. Удачи в освоении этой занимательной науки математики!
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Тема урока
Цели урока
- Познакомьтесь с новыми определениями и вспомните уже выученные.

- Сформулируйте и докажите свойства квадрата, докажите его свойства.
- Научитесь применять свойства фигур при решении задач.
- Развивающая — для развития у учащихся внимания, усидчивости, усидчивости, логического мышления, математической речи.
- Воспитательная — через урок воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручку, самостоятельность.
Цели урока
- Проверьте способность учащихся решать задачи.
План урока
- Справочник по истории.
- Фалес как математик и его работы.
- Приятно помнить.
История истории
- Теорема Фалеса до сих пор используется в морском мореплавании как правило о том, что столкновение кораблей, движущихся с постоянной скоростью, неизбежно, если корабли остаются курсами друг на друга.
- Вне русскоязычной литературы теорему Фалеса иногда называют другой теоремой планиметрии, а именно утверждением, что вписанный угол, исходя из диаметра окружности, прямой.
 Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.
Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.
- Фалес изучил основы геометрии в Египте.
Открытия и заслуги автора
Знаете ли вы, что Фалес Милетский был одним из семи самых известных в то время мудрецов Греции. Он основал Ионическую школу. Идея, которую Фалес продвигал в этой школе, заключалась в единстве всех вещей. Мудрец считал, что существует единое начало, из которого произошли все вещи.
Великая заслуга Фалеса Милетского — создание научной геометрии. Это великое учение смогло создать из египетского искусства измерения дедуктивную геометрию, основу которой составляет общий фундамент.
Помимо своих обширных познаний в геометрии, Фалес также неплохо разбирался в астрономии. Эму первым предсказал полное солнечное затмение. Но произошло это не в современном мире, а в далеком 585 году, еще до нашей эры.
Фалес Милетский был человеком, который понял, что север можно точно определить по созвездию Малой Медведицы. Но это было не последнее его открытие, так как он смог точно определить продолжительность года, разбить его на триста шестьдесят пять дней, а также установить время равноденствий.
Но это было не последнее его открытие, так как он смог точно определить продолжительность года, разбить его на триста шестьдесят пять дней, а также установить время равноденствий.
На самом деле Фалес был всесторонне развитым и мудрым человеком. Помимо того, что он был известен как прекрасный математик, физик, астроном, он был еще и настоящим метеорологом, он умел довольно точно предсказывать урожай оливок.
Но самое замечательное то, что Фалес никогда не ограничивал свои знания только научно-теоретической областью, а всегда старался закрепить доказательства своих теорий на практике. И самое интересное, что великий мудрец не зацикливался на какой-то одной области своих знаний, его интерес имел разные направления.
Имя мудреца Фалеса уже тогда стало нарицательным. Значение и значение его для Греции было столь же велико, как имя Ломоносова для России. Конечно, его мудрость можно трактовать по-разному. Но можно определенно сказать, что ему были присущи изобретательность, практическая смекалка и, в какой-то мере, беспристрастность.
Фалес Милецкий был прекрасным математиком, философом, астрономом, любил путешествовать, был купцом и предпринимателем, занимался торговлей, а также был хорошим инженером, дипломатом, провидцем и активно участвовал в политической жизни.
Ему даже удалось определить высоту пирамиды с помощью посоха и тени. И это было так. В один прекрасный солнечный день Фалес поставил свой посох на границе, где заканчивалась тень пирамиды. Затем он подождал, пока длина тени его посоха сравняется с его ростом, и измерил длину тени пирамиды. Вот так, казалось бы, Фалес просто определил высоту пирамиды и доказал, что длина одной тени связана с длиной другой тени, как высота пирамиды связана с высотой посоха. Что поразило самого фараона Амасиса.
Благодаря Фалесу все известные на тот момент знания были перенесены в область научных интересов. Он смог довести результаты до уровня, пригодного для научного потребления, выделив определенный набор понятий. И, возможно, с помощью Фалеса началось последующее развитие античной философии.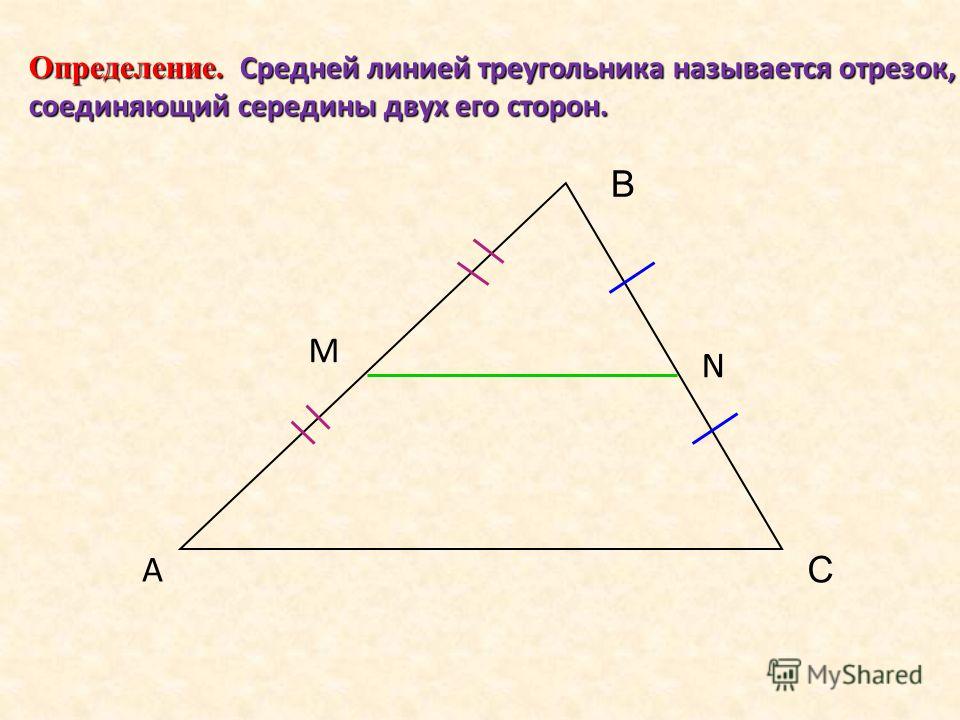
Теорема Фалеса играет важную роль в математике. Она была известна не только в Древнем Египте и Вавилоне, но и в других странах и явилась основой развития математики. И в быту, при строительстве зданий, сооружений, дорог и т. д. без теоремы Фалеса не обойтись.
Теорема Фалеса в культуре
Теорема Фалеса прославилась не только в математике, но и была введена в культуру. Однажды аргентинский музыкальный коллектив Les Luthiers (исп.) представил публике песню, которую они посвятили знаменитой теореме. Участники Les Luthiers в своем видеоклипе специально на эту песню представили доказательства прямой теоремы для пропорциональных отрезков.
Вопросы
- Какие прямые называются параллельными?
- Где на практике применяется теорема Фалеса?
- Что говорит теорема Фалеса?
Список использованных источников
- Энциклопедия для детей. Т.11. Математика / Главный редактор М.Д.
 Аксенова.-м.: Аванта+, 2001.
Аксенова.-м.: Аванта+, 2001. - «ЕГЭ 2006. Математика. Учебно-методические материалы для обучения студентов / Рособрнадзор, ИСОП — М.: Интеллект-Центр, 2006″
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Е.Г., Юдина И.И. «Геометрия, 7 — 9: учебник для общеобразовательных учреждений»
Теорема не имеет ограничений на взаимное расположение секущих (справедлива как для пересекающихся прямых, так и для параллельных прямых). Также не имеет значения, где находятся отрезки линии.
Доказательство в случае параллельных прямых
Проведем линию ВС. Углы ABC и BCD равны как внутренние крест-накрест с параллельными прямыми AB и CD и секущей BC, а углы ACB и CBD равны как внутренние углы, лежащие с параллельными прямыми AC и BD и секущей BC. Тогда по второму критерию равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Существует также теорема о пропорциональных отрезках :
.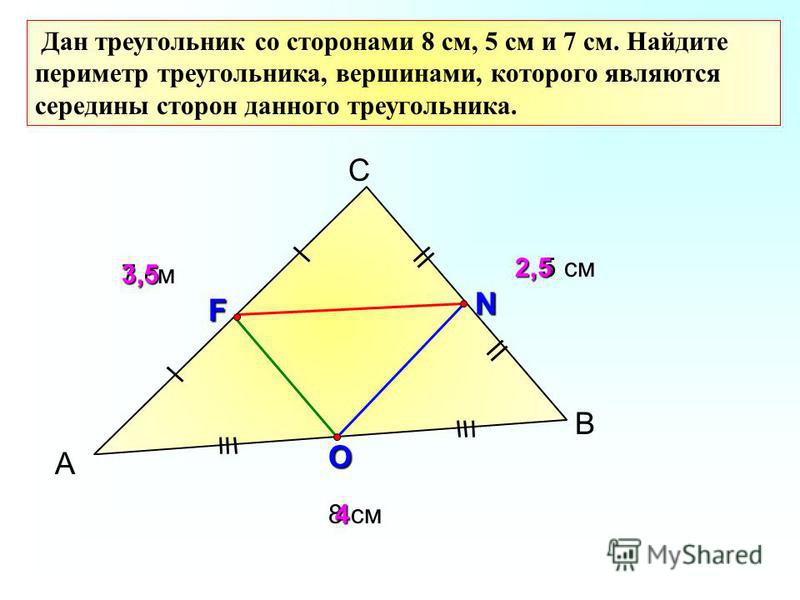 Параллельные прямые отсекаются на секущих пропорциональных отрезках:
Параллельные прямые отсекаются на секущих пропорциональных отрезках: \ гидроразрыв (A_1A_2) (B_1B_2) = \ гидроразрыв (A_2A_3) (B_2B_3) = \ гидроразрыв (A_1A_3) (B_1B_3).
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Обратная теорема
Если в теореме Фалеса из вершины начинаются равные отрезки (такая формулировка часто используется в школьной литературе), то верна и обратная теорема. Для пересекающихся секущих формулируется следующим образом:
Таким образом (см. рис.) Из того, что \frac(CB_1)(CA_1)=\frac(B_1B_2)(A_1A_2)=\ldots=(\rm idem) следует что прямые линии A_1B_1 || А_2В_2 || \ лдочки.
Если секущие параллельны, то необходимо требовать равенства отрезков на обоих секущих друг другу, иначе это утверждение становится неверным (контрпримером является трапеция, пересеченная прямой, проходящей через середины оснований).
Вариации и обобщения
Следующее утверждение двойственно лемме Соллертинского:
Написать рецензию на статью «Теорема Фалеса»Литература
Примечания (редактирование)см. также
Отрывок, характеризующий теорему Фалеса— Ничего не думаю, просто не понимаю.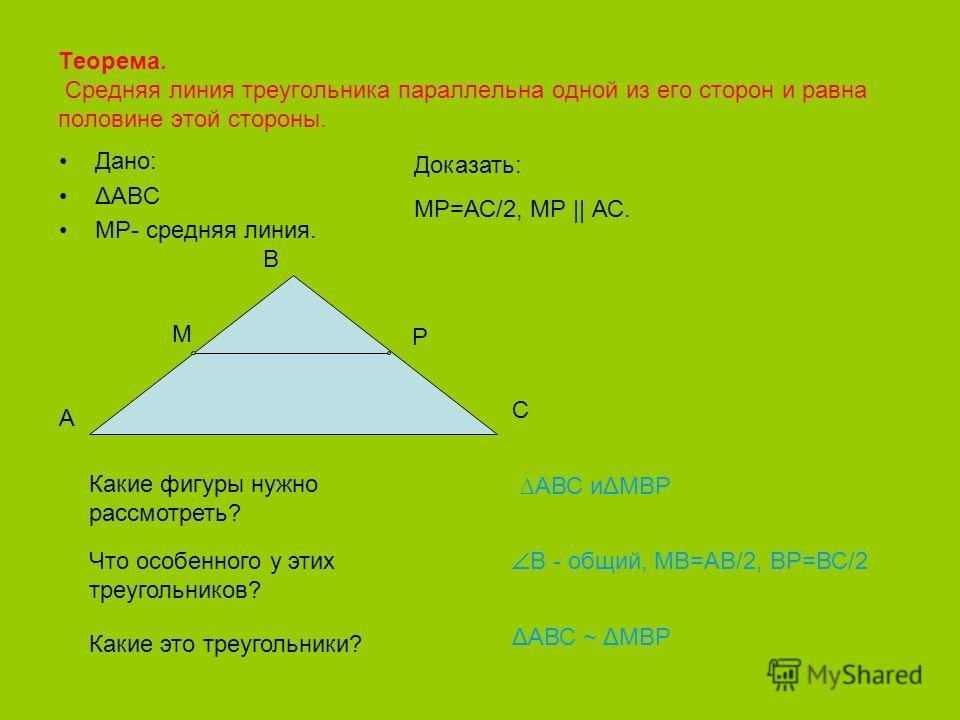 .. .. — Подожди, Соня, ты все поймешь. Вы увидите, что он за человек. Не думай плохо ни обо мне, ни о нем. — Я ни о ком плохо не думаю: всех люблю и всех жалею. Но что мне делать? Соня не отказалась от ласкового тона, с которым обратилась к ней Наташа. Чем мягче и пытливее становилось выражение лица Наташи, тем серьезнее и суровее было лицо Сони. – Наташа, – сказала она, – ты просила меня не говорить с тобой, я не говорила, теперь ты сама начала. Наташа, я ему не верю. Почему это секрет? — Опять, опять! — прервала Наташа. — Наташа, я боюсь за тебя. — Чего бояться? — Боюсь, что ты себя погубишь, — решительно сказала Соня, сама испугавшись сказанного. Лицо Наташи снова выразило гнев. — И погублю, погублю, погублю себя поскорее. Не твое дело. Не тебе, а мне будет плохо. Оставь, оставь меня. Я ненавижу тебя. — Наташа! — испуганно вскрикнула Соня. — Ненавижу, ненавижу! И ты мой враг навсегда! Наташа выбежала из комнаты. 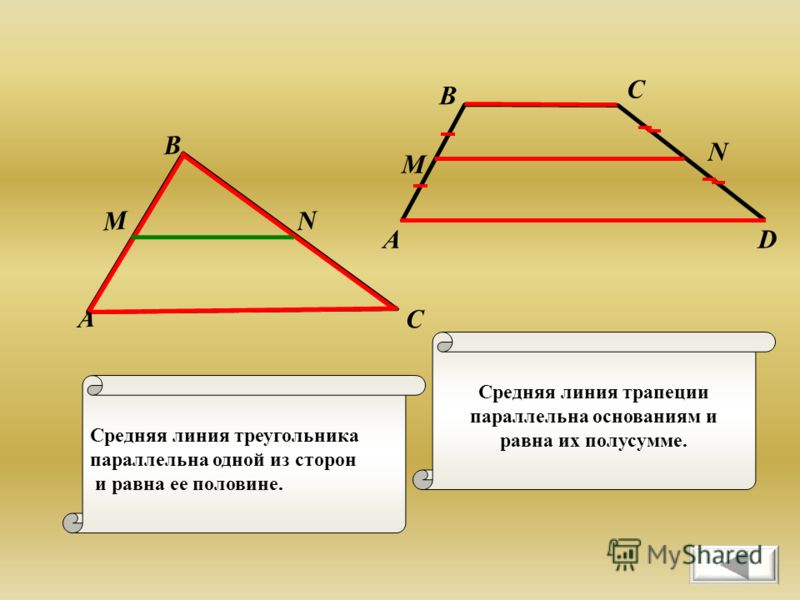 Наташа больше не разговаривала с Соней и избегала ее. С тем же выражением взволнованного удивления и преступности ходила она по комнатам, то и дело берясь за другое занятие и тотчас же покидая их. Как ни тяжело было Соне, она, не отрывая глаз, следила за подругой. Накануне того дня, когда граф должен был вернуться, Соня заметила, что Наташа все утро сидела у окна гостиной, как бы чего-то ожидая, и что она сделала какой-то знак проходившему солдату, которого Соня взяла с собой. для Анатоля. Соня стала еще внимательнее наблюдать за своей подругой и заметила, что Наташа все время обеда и вечера находилась в странном и неестественном состоянии (она отвечала неадекватно на заданные ей вопросы, начинала и не заканчивала фразы, смеялась над всем ). После чая Соня увидела робкую горничную, которая ждала ее у Наташиной двери. Она впустила ее и, подслушав в дверях, узнала, что письмо опять передано. И вдруг Соне стало ясно, что у Наташи на этот вечер есть какой-то ужасный план. 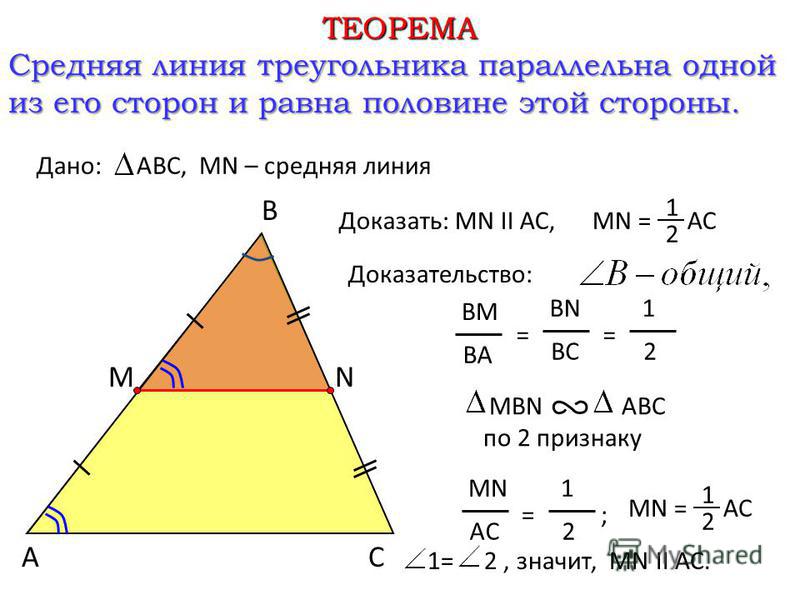 Соня постучала в дверь. Наташа не пустила ее. Соня постучала в дверь. Наташа не пустила ее. «Она убежит с ним! подумала Соня. Она способна на все. Сегодня в ее лице было что-то особенно жалостное и решительное. Она расплакалась, прощаясь с дядей, вспоминала Соня. Да, она с ним бежит, но что мне делать? — подумала Соня, припоминая теперь те признаки, которые ясно доказывали, почему у Наташи было какое-то страшное намерение. — Графа нет. Что мне делать, писать Курагину, требуя от него объяснений? как просил князь Андрей на случай несчастья?… А может быть, и в самом деле она уже отказала Болконскому (она вчера послала письмо княгине Марье). Дядя нет!» Сказать Марье Дмитриевне, так верившей в Наташу , показался Соне ужасным. «Но так или иначе, думала Соня, стоя в темном коридоре: сейчас или никогда самое время доказать, что я помню добрые дела их семьи и люблю Николя. Нет, я не буду спать хоть три ночи, но я не выйду из этого коридора и не впущу ее насильно, и не позволю позору пасть на их семью», — думала она. Анатолий недавно переехал в Долохов. |
О параллели и секущей.
Вне русскоязычной литературы теорему Фалеса иногда называют еще одной теоремой планиметрии, а именно утверждением, что вписанный угол, исходя из диаметра окружности, прямой. Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.
Формулировка
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то на второй прямой они отрежут равные отрезки.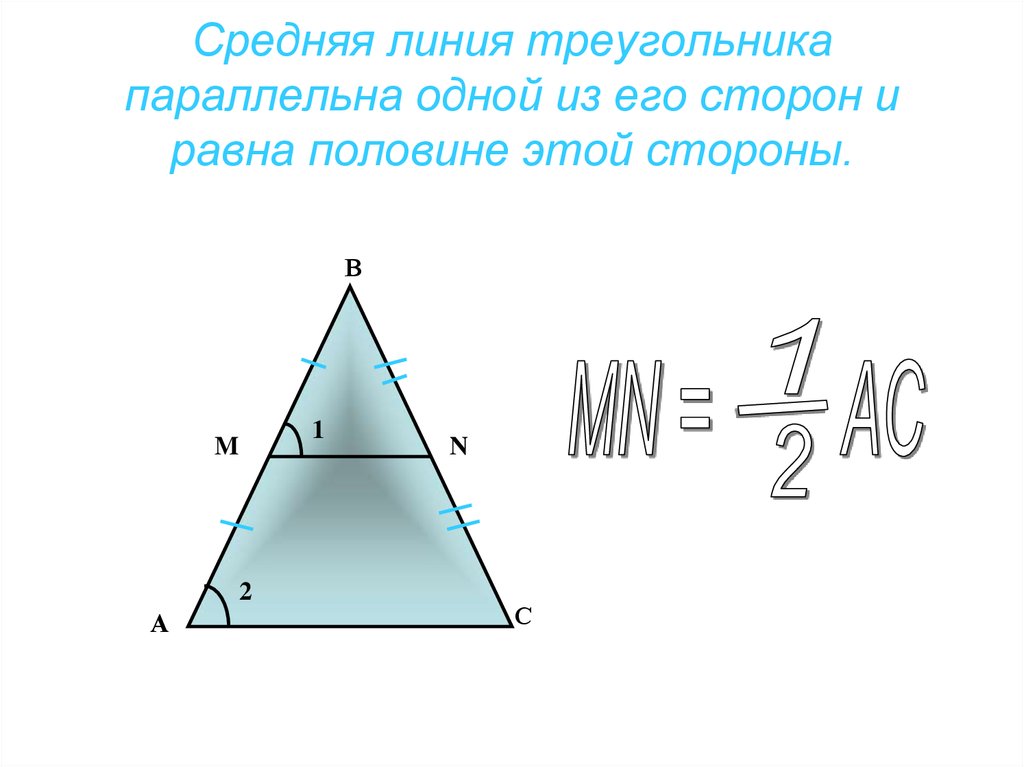
Более общая формулировка, также называемая теоремой о пропорциональных отрезках
Параллельные прямые линии отсекаются на секущих пропорциональных отрезках:
A 1 A 2 B 1 B 2 = A 2 A 3 B 2 B 3 = A 1 A 3 B 1 B 3. (\ displaystyle (\ frac (A_ (1) A_ (2)) (B_ (1) B_ ( 2))) = (\ frac (A_ (2) A_ (3)) (B_ (2) B_ (3) )) = (\ frac (A_ (1) A_ (3)) (B_ (1) B_ ( 3))).)
Замечания
- Теорема не имеет ограничений на взаимное расположение секущих (справедлива как для пересекающихся, так и для параллельных прямых). Также не имеет значения, где находятся отрезки линии.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A A 1 | | Б Б 1 | | С С 1 | | D D 1 (\ displaystyle AA_ (1) || BB_ (1) || CC_ (1) || DD_ (1)) и где AB = C D (\ displaystyle AB = CD).
- Проведем через точки A (\displaystyle A) и C (\displaystyle C) прямые, параллельные другой стороне угла. A B 2 B 1 A 1 (\ displaystyle AB_ (2) B_ (1) A_ (1)) и C D 2 D 1 C 1 (\ displaystyle CD_ (2) D_ (1) C_ (1))… Согласно свойство параллелограмма: A B 2 = A 1 B 1 (\ displaystyle AB_ (2) = A_ (1) B_ (1)) и C D 2 = C 1 D 1 (\ displaystyle CD_ (2) = C_ (1) D_ ( 1)).
- Треугольники △ A B B 2 (\displaystyle\bigtriangleup ABB_(2)) и △C D D 2 (\displaystyle\bigtriangleup CDD_(2)) равны на основании второго знака равенства треугольников
Доказательство в случае параллельных прямых
Проведем прямую BC … Углы ABC и BCD равны внутренним крестам для параллельных прямых AB и CD и секущая 3 и углы ACB и CBD равны как внутренние перекрещивающиеся для параллельных прямых AC и BD и секущей BC … Тогда по второму критерию равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD . ■
Отсюда следует, что AC = BD и AB = CD . ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются с вершины (эта формулировка часто используется в школьной литературе), то обратная теорема также будет верна. Для пересекающихся секущих формулируется следующим образом:
Таким образом (см. рис.) Из того, что CB 1 CA 1 = B 1 B 2 A 1 A 2 =… (\displaystyle(\frac(CB_(1))( CA_ (1))) = (\ frac (B_ (1) B_ (2)) (A_ (1) A_ (2))) = \ ldots), следует, что A 1 B 1 | | А 2 Б 2 | | … (\ Displaystyle A_ (1) B_ (1) || A_ (2) B_ (2) || \ ldots).
Если секущие параллельны, то необходимо требовать равенства отрезков на обоих секущих друг другу, иначе это утверждение становится неверным (контрпримером является трапеция, пересеченная прямой, проходящей через середины оснований).
Эта теорема используется в мореплавании: столкновение судов, движущихся с постоянной скоростью, неизбежно, если сохраняется направление от одного корабля к другому.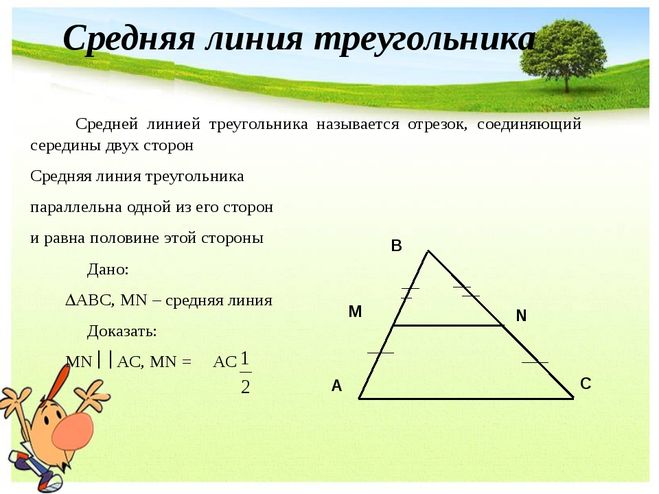
Лемма Соллертинского
Следующее утверждение двойственно лемме Соллертинского:
Пусть f(\displaystyle f)- проективное соответствие между точками прямой l(\displaystyle l) и прямой m(\displaystyle m) . Тогда множество прямых X f(X)(\displaystyle Xf(X) ) будет набором касательных к некоторым |
Трапеция, средняя линия трапеции, треугольник. Средняя линия треугольника
Четырехугольник только с двумя параллельными сторонами называется трапецией .
Параллельные стороны трапеции называются ее основания , а те стороны, которые не параллельны, называются сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.
Средняя линия трапеции
Срединная линия представляет собой отрезок, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.
Теорема:
Если прямая, проходящая через середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.
Теорема:
Длина средней линии равна среднему арифметическому длин ее оснований
МН || АБ || DC
AM=MD; БН=НЗ
MN — средняя линия, AB и CD — основания, AD и BC — стороны
MN=(AB+DC)/2
Теорема:
длины его оснований.
Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат на середине оснований трапеции.
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Он параллелен третьей стороне и его длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC и BN = NC =>
Применение свойств средней линии треугольника и трапеции
Деление сегмента на определенное количество равных частей.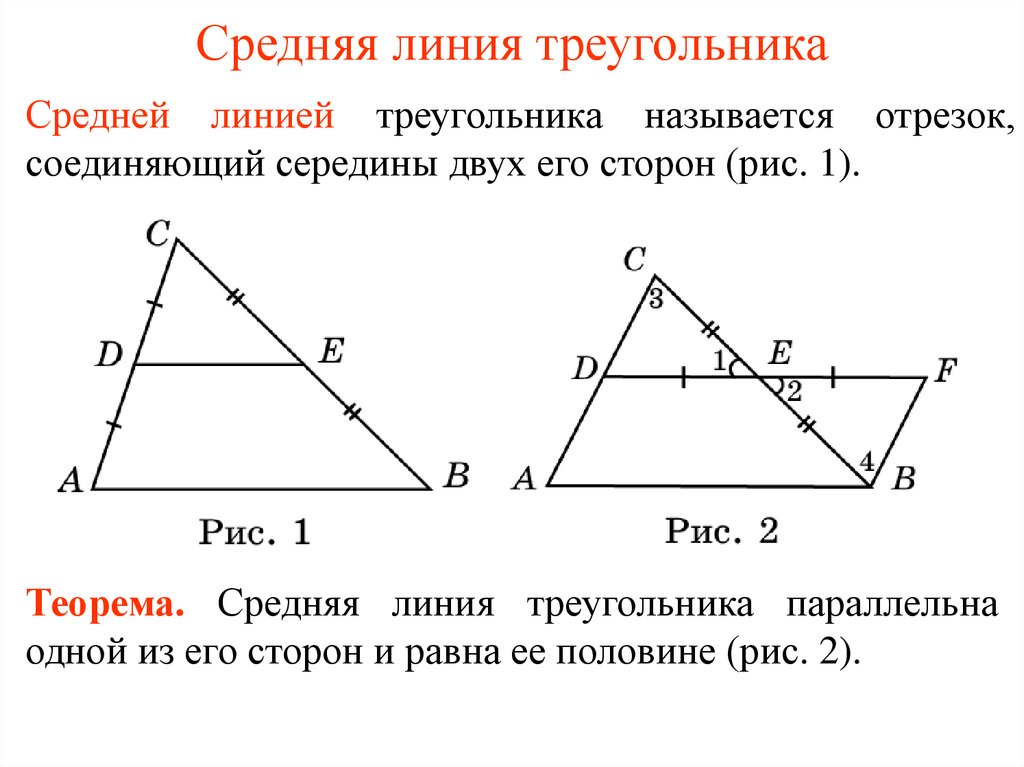
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч, начало которого — точка A и который не лежит на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Соединяем А 5 с В и проводим прямые через А 4 , А 3 , A 2 и A 1 параллельны A 5 B. Они пересекают AB в точках B 4 , B 3 , B 2 и B 1 соответственно. Эти точки делят отрезок АВ на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Точно так же из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Это Ясно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных отрезков на луч p. А затем продолжить в порядке, описанном выше.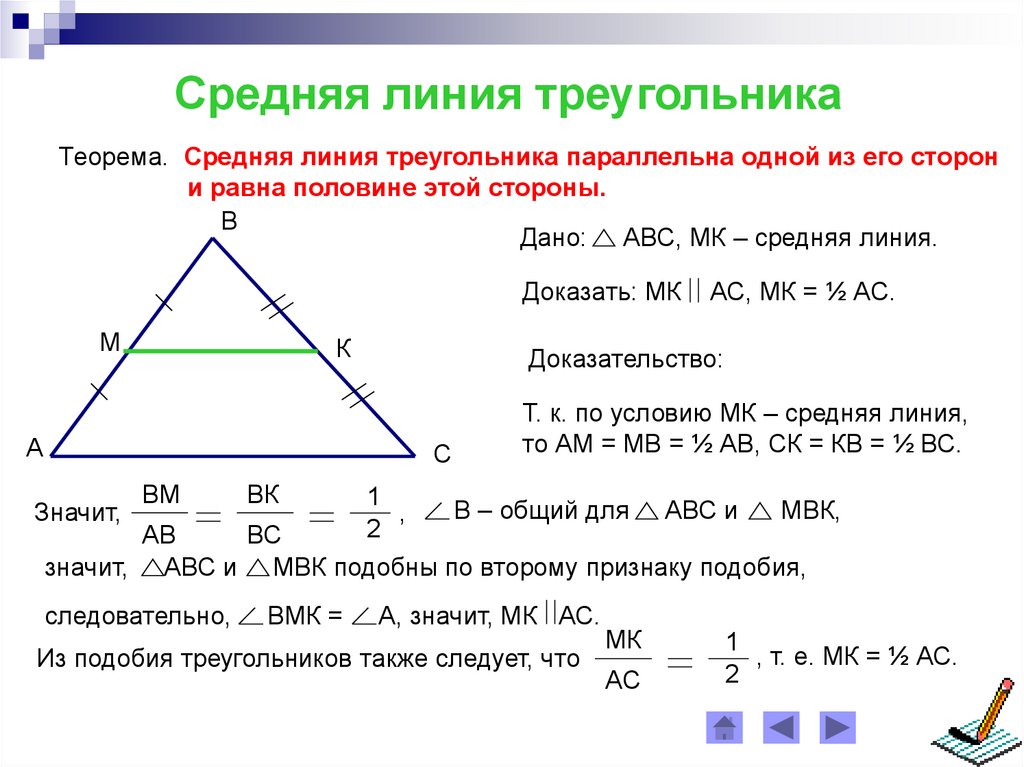
Средняя линия треугольника. Привет друзья! Сегодня теоретический материал связан с треугольником. В составе экзамена имеется группа заданий, использующих свойство его средней линии. И не только в задачах с треугольниками, но и с трапециями. Был такой, в котором я предлагал просто запомнить эти факты, теперь подробнее…
Что такое средняя линия треугольника и каковы ее свойства?
Определение. Средняя линия треугольника — это отрезок, соединяющий середины сторон треугольника.
Ясно, что в треугольнике три средние линии. Покажем их:
Без всяких доказательств вы, наверное, уже заметили, что все четыре образовавшихся треугольника равны. Это правда, но об этом мы поговорим позже.
Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна половине ее.
Доказательство:
1. Рассмотрим треугольники BMN и BAC. По условию имеем BM=MA, BN=NC. Можно написать:
Рассмотрим треугольники BMN и BAC. По условию имеем BM=MA, BN=NC. Можно написать:
Следовательно, треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А вот то что:
На основе параллельных линий MN||AC.
2. Из подобия треугольников также следует, что
То есть МН в два раза меньше. Доказано!
Решим типовую задачу.
В треугольнике ABC точки M, N, K являются серединами сторон AB, BC, AC. Найдите периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, в первую очередь нужно проверить существование треугольника MNK (а значит, и существование треугольника ABC). Сумма двух меньших сторон должна быть больше третьей стороны, пишем 10+8>12. Выполнить, следовательно, треугольник существует.
Построим эскиз:
Таким образом, периметр треугольника ABC равен 24+20+16=60.
*Теперь подробнее о треугольниках, полученных при построении всех трех средних линий.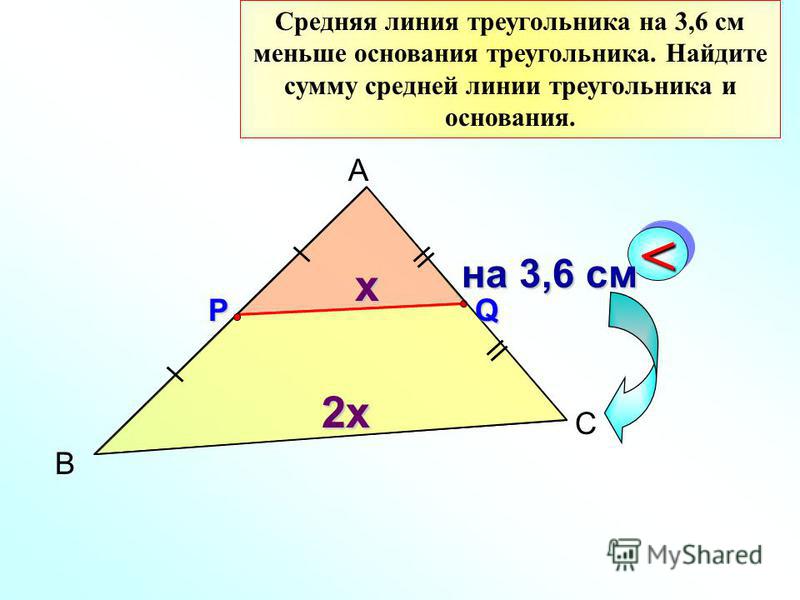 Их равенство легко доказывается. Смотрите:
Их равенство легко доказывается. Смотрите:
Они равны с трех сторон. Конечно, здесь применимы и другие признаки. Получаем, что
Как это свойство используется в заданиях, включенных в экзамен? Особо хотелось бы остановиться на задачах стереометрии. Есть виды, в которых речь идет о треугольной призме.
Например, говорят, что плоскость проходит через середины сторон основания и параллельна третьему краю основания. Ставятся вопросы об изменении площади поверхности призмы, ее объема и др.
Так. Зная и понимая изложенную выше информацию, вы сразу определите, что эта плоскость отсекает от основания одну четвертую часть указанной призмы и решите задачу устно. Вот с такими задачами.
Вот и все! Всего наилучшего!
Скачать материал статьи
С уважением, Александр Крутицких.
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Это отрезок, соединяющий середины двух сторон треугольника (рис. 1).
1).
Рис. 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна половине ее.
Доказательство.
Дан треугольник $ABC$. $MN$ — средняя линия (как на рис. 2).
Рис. 2. Иллюстрация к теореме 1
Так как $\frac(AM)(AB)=\frac(BN)(BC)=\frac(1)(2)$, то треугольники $ABC$ и $MBN$ подобны по второму критерию подобия треугольников. Значит
Также отсюда следует, что $\angle A=\angle BMN$ означает $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1: Медианы треугольника пересекаются в одной точке и делят точку пересечения в отношении $2:1$, начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где $(AA)_1,\ (BB)_1,\ (CC)_1$ — его медиана. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (рис. 3). Рис. 3. Иллюстрация следствия 1 Следовательно, треугольники $ABM$ и $A_1B_1M$ подобны по первому критерию подобия треугольников. Затем
3). Рис. 3. Иллюстрация следствия 1 Следовательно, треугольники $ABM$ и $A_1B_1M$ подобны по первому критерию подобия треугольников. Затем
Аналогично доказывается, что
Теорема доказана.
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac(1)(2)$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ (\ A)_1C_1,\ B_1C_1$ (рис. 4)
Рис. 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то
Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму критерию подобия треугольников с коэффициентом подобия $k=\frac(1)(2)$.
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, а также треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac(1)(2)$.
Рассмотрим треугольник $A_1B_1C_1$. Поскольку $A_1B_1,\ (\ A)_1C_1,\ B_1C_1$ — средние линии треугольника, то
Поскольку $A_1B_1,\ (\ A)_1C_1,\ B_1C_1$ — средние линии треугольника, то
Следовательно, по третьему критерию подобия треугольников треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac(1)(2)$.
Теорема доказана.
Примеры задания на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найдите периметр треугольника, вершины которого лежат на серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в середине сторон данного треугольника, то его стороны являются средними линиями исходного треугольника. По следствию 2 получаем, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и \ M$ являются серединами сторон $BC$ и $AB$ соответственно (рис. 5).
Рисунок 5
Периметр треугольника $BMN=14$ см. Найдите периметр треугольника $ABC$.
Найдите периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
По теореме 1 $AC=2MN$. Получаем:
Объяснение урока: Параллельные прямые в треугольнике
В этом объяснителе мы узнаем, как найти недостающие длины в треугольнике, содержащем две или три параллельные прямые, используя пропорциональность.
Напомним, что при пересечении двух параллельных прямых секущей получается соответствующие углы равны.
Добавив вторую поперечную, как показано на рисунке ниже, мы можем сформировать два треугольника.
Присвоив каждой вершине метку, мы можем определить больший треугольник △𝐴𝐷𝐸 и меньший треугольник △𝐴𝐵𝐶.
Поскольку две пары соответствующих углов равны, треугольник 𝐴𝐷𝐸 похож на треугольник 𝐴𝐵𝐶: △𝐴𝐷𝐸∼△𝐴𝐵𝐶.
Поскольку эти треугольники подобны, отношения их соответствующих сторон
длины должны быть равны. Другими словами, мы имеем
𝐴𝐵𝐴𝐷=𝐴𝐶𝐴𝐸=𝐵𝐶𝐷𝐸.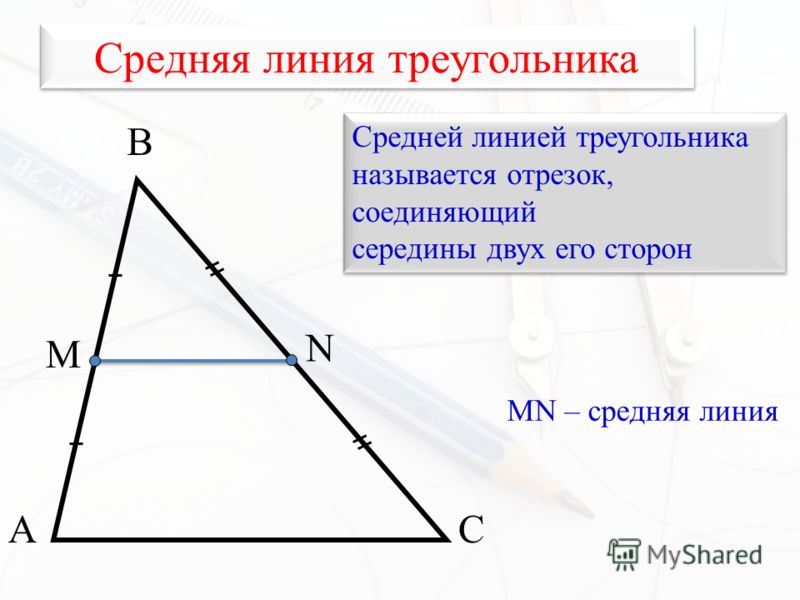
В первом примере мы покажем, как использовать это определение подобия треугольников, чтобы определить, какие пары длин сторон имеют равные пропорции при разрезании треугольника линией, параллельной одной из его сторон.
Пример 1. Определение пропорций в треугольниках
Используя диаграмму, какое из следующего равно 𝐴𝐵𝐴𝐷?
- 𝐴𝐶𝐸𝐶
- 𝐴𝐵𝐷𝐵
- 𝐴𝐷𝐷𝐵
- 𝐴𝐶𝐴𝐸
- 𝐴𝐸𝐸𝐶
Ответ
Диаграмма показывает, что 𝐸𝐷 параллельно 𝐶𝐵. Поскольку соответствующие углы равны, то есть ∠𝐷𝐸𝐴=∠𝐵𝐶𝐴 и ∠𝐸𝐷𝐴=∠𝐶𝐵𝐴,𝐸𝐷 создает треугольник 𝐴𝐷𝐸, который подобен большему треугольнику 𝐴𝐵𝐶.
Поскольку эти треугольники подобны, отношения их соответствующих длины сторон должны быть равны. Особенно, 𝐴𝐸𝐴𝐶=𝐴𝐷𝐴𝐵.
Чтобы найти дробь, эквивалентную 𝐴𝐵𝐴𝐷, мы можем найти
величина, обратная обеим частям этого уравнения:
𝐴𝐶𝐴𝐸=𝐴𝐵𝐴𝐷.
𝐴𝐶𝐴𝐸 равно 𝐴𝐵𝐴𝐷.
Пример 2. Нахождение неизвестной длины треугольника с помощью пропорций
Найдите значение 𝑥.
Ответ
𝐴𝐶 и 𝐴𝐵 — трансверсали, которые пересекают параллельные прямые ⃖⃗𝐷𝐸 и ⃖⃗𝐵𝐶. Поскольку две пары соответствующих углов, образованные этим пересечением равны, то есть ∠𝐷𝐸𝐴=∠𝐵𝐶𝐴,∠𝐸𝐷𝐴=∠𝐶𝐵𝐴, можно сказать, что треугольник 𝐴𝐷𝐸 подобен треугольнику 𝐴𝐵𝐶: △𝐴𝐵𝐶∼△𝐴𝐷𝐸.
Если два треугольника подобны, отношения длин их соответствующие стороны равны. Особенно, 𝐴𝐷𝐴𝐵=𝐷𝐸𝐵𝐶.
Путем подстановки известных значений для длины 𝐴𝐷, 𝐷𝐸, и 𝐴𝐵 (где мы должны отметить, что 𝐴𝐵 является суммой 𝐴𝐷 и 𝐷𝐵), мы можем найти значение 𝑥: 1010+11=10𝑥. Решение для 𝑥, 𝑥=21.
В предыдущих двух примерах мы отметили, что если линия, пересекающая две стороны
треугольника параллельна третьей стороне, то образован меньший треугольник
параллельной линией подобен исходному треугольнику. Вспомним схему, которую мы представили ранее.
Вспомним схему, которую мы представили ранее.
Поскольку треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐸 подобны, получаем равные пропорции: 𝐴𝐵𝐴𝐷=𝐴𝐶𝐴𝐸.
На этой диаграмме мы также отмечаем, что отрезки линии 𝐴𝐷 и 𝐴𝐸 могут разделить следующим образом: 𝐴𝐷=𝐴𝐵+𝐵𝐷𝐴𝐸=𝐴𝐶+𝐶𝐸.and
Подставляя эти выражения в наше предыдущее уравнение и переставляя, 𝐴𝐵𝐴𝐷 = 𝐴𝐶𝐴𝐸𝐴𝐵𝐴𝐵+𝐵𝐷 = 𝐴𝐶𝐴𝐶+𝐶𝐸𝐴𝐵 (𝐴𝐶+𝐶𝐸) = 𝐴𝐶 (𝐴𝐵+𝐵𝐷) 𝐴𝐵om𝐴𝐶+𝐴𝐵om𝐶𝐸 = 𝐴𝐶om𝐴𝐵+𝐴𝐶om𝐵𝐷.
Теперь мы можем вычесть 𝐴𝐵⋅𝐴𝐶 с обеих сторон, чтобы найти 𝐴𝐵⋅𝐶𝐸=𝐴𝐶⋅𝐵𝐷,𝐴𝐵𝐵𝐷=𝐴𝐶𝐶𝐸.
Это приводит нас к определению теоремы, связывающей прямую сегменты, созданные при добавлении параллельной стороны к треугольнику.
Теорема: Теорема о разделении сторон
Если прямая, параллельная одной стороне треугольника, пересекает две другие стороны треугольника, то линия пропорционально делит эти стороны.
Примечание:
Теорема о боковых разделителях может быть расширена для включения параллельных прямых, которые
лежат вне треугольника. Когда прямая лежит вне треугольника
и параллельна одной стороне треугольника, она образует другой треугольник,
похож на первый. Это показано на следующей диаграмме. В этом случае аналог теоремы о боковом разветвителе может быть выведен непосредственно
из подобных треугольников.
Когда прямая лежит вне треугольника
и параллельна одной стороне треугольника, она образует другой треугольник,
похож на первый. Это показано на следующей диаграмме. В этом случае аналог теоремы о боковом разветвителе может быть выведен непосредственно
из подобных треугольников.
В следующем примере мы увидим, как использовать эту теорему для определения пропорциональные сегменты треугольников для вычисления недостающей длины.
Пример 3. Использование пропорций в треугольнике для вычисления неизвестной длины
На рисунке 𝑋𝑌 и 𝐵𝐶 параллельны. Если 𝐴𝑋=18, 𝑋𝐵=24 и 𝐴𝑌=27, какова длина 𝑌𝐶?
Ответ
Нам дано, что 𝑋𝑌 параллельно 𝐵𝐶. Теорема бокового делителя говорит, что если прямая, параллельная одной стороне треугольника, пересекает другую две стороны треугольника, то линия пропорционально делит эти стороны.
В частности,
𝐴𝑌𝑌𝐶=𝐴𝑋𝑋𝐵.
Замена 𝐴𝑋=18, 𝑋𝐵=24 и 𝐴𝑌=27 в это уравнение и решение для 𝑌𝐶, 27𝑌𝐶=1824𝑌𝐶27=2418𝑌𝐶=2418×27=36.
Длина 𝑌𝐶 равна 36.
В нашем следующем примере мы покажем, как решать многоэтапные задачи. с участием треугольников и параллельных прямых.
Пример 4: Поиск неизвестных в прикладной задаче
На данном рисунке изображен треугольник 𝐴𝐵𝐶.
- Определите значение 𝑥.
- Определите значение 𝑦.
Ответ
Часть 1
На рисунке линия параллельна стороне 𝐵𝐶 это пересекает две другие стороны треугольника. Теорема о боковых разделителях говорит нам, что эта линия делит эти стороны пропорционально.
Обозначив этот отрезок как 𝐷𝐸, мы получаем 𝐴𝐷𝐷𝐵=𝐴𝐸𝐸𝐶.
Это дает нам уравнение, которое можно решить относительно 𝑥: 32𝑥+3=2𝑥+53(𝑥+5)=2(2𝑥+3)3𝑥+15=4𝑥+615=𝑥+6𝑥=9.
Часть 2
Теперь, когда мы знаем значение 𝑥, мы можем использовать эту информацию, чтобы найти
значение 𝑦. Поскольку две пары соответствующих углов, образованные
пересечения 𝐷𝐸 равны,
треугольник 𝐴𝐵𝐶 подобен треугольнику 𝐴𝐷𝐸:
△𝐴𝐵𝐶∼△𝐴𝐷𝐸.
Поскольку две пары соответствующих углов, образованные
пересечения 𝐷𝐸 равны,
треугольник 𝐴𝐵𝐶 подобен треугольнику 𝐴𝐷𝐸:
△𝐴𝐵𝐶∼△𝐴𝐷𝐸.
В частности, 𝐴𝐷𝐴𝐵=𝐷𝐸𝐵𝐶.
Длина 𝐴𝐵 равна сумме длин из 𝐴𝐷 и 𝐷𝐵. Нам дано, что 𝐴𝐷=3 и 𝐷𝐵=2𝑥+3. Поскольку 𝑥=9, 𝐷𝐵=21. Следовательно, 𝐴𝐵=3+21=24.
Подставив эти значения в наше предыдущее уравнение и найдя 𝑦, 324=2𝑦𝑦24=23𝑦=23×24=16.
Следовательно, 𝑦=16.
В следующем примере мы покажем, как применить боковой разделитель теорема о треугольнике, состоящем из нескольких пар параллельных прямых.
Пример 5. Нахождение длины стороны треугольника по соотношению между параллельными прямыми
Найдите длину 𝐶𝐵.
Ответ
Из приведенной схемы отметим, что 𝐷𝐹
параллельно
𝐴𝐸 в треугольнике 𝐶𝐴𝐸 и
𝐷𝐸
параллелен 𝐴𝐵 в треугольнике 𝐶𝐴𝐵. Теорема о боковых разделителях говорит нам, что если линия, параллельная одной стороне
треугольник пересекает две другие стороны треугольника,
то линия делит эти стороны пропорционально. Применяя эту теорему к треугольнику 𝐶𝐴𝐸, где 𝐷𝐹 равно
параллельно одной из сторон треугольника, получаем
𝐶𝐹𝐹𝐸=𝐶𝐷𝐷𝐴.
Применяя эту теорему к треугольнику 𝐶𝐴𝐸, где 𝐷𝐹 равно
параллельно одной из сторон треугольника, получаем
𝐶𝐹𝐹𝐸=𝐶𝐷𝐷𝐴.
Так как 𝐷𝐸 параллелен одной стороне больший треугольник 𝐶𝐴𝐵, мы также можем получить 𝐶𝐸𝐸𝐵=𝐶𝐷𝐷𝐴.
Оба 𝐶𝐹𝐹𝐸 и 𝐶𝐸𝐸𝐵 равны 𝐶𝐷𝐷𝐴. Это означает, что мы можем установить 𝐶𝐹𝐹𝐸=𝐶𝐸𝐸𝐵.
Мы можем заменить данные значения 𝐶𝐹=15, 𝐹𝐸=6 и 𝐶𝐸=15+6=21 в это уравнение чтобы получить уравнение, которое можно решить относительно 𝐸𝐵: 156=21𝐸𝐵𝐸𝐵=21×615.
Следовательно, 𝐸𝐵=8.4.cm
Так как 𝐶𝐵=𝐶𝐹+𝐹𝐸+𝐸𝐵, 𝐶𝐵=15+6+8,4=29.4.см
Длина 𝐶𝐵 составляет 29,4 см.
Вспомним, что теорема о боковых разделителях говорит нам, что если линия, параллельная одной
сторона треугольника пересекает две другие стороны треугольника, то прямая
делит эти стороны пропорционально. Более того, мы узнали, что эта теорема
можно расширить, включив в него параллельные прямые, лежащие за пределами треугольника. Оказывается, верно и обратное этому результату, что очень хорошо доказывает
полезно при решении задач такого типа.
Оказывается, верно и обратное этому результату, что очень хорошо доказывает
полезно при решении задач такого типа.
Теорема: обратная теорема о разветвителе сторон
Если прямая пересекает две стороны треугольника и делит эти стороны на равные части пропорции, то эта линия должна быть параллельна третьей стороне треугольника.
На всех трех приведенных выше диаграммах 𝐴𝐵𝐶 представляет собой треугольник и ⃖⃗𝐷𝐸 пересекает ⃖⃗𝐴𝐵 в 𝐷 и ⃖⃗𝐴𝐶 в 𝐸.
Если 𝐴𝐷𝐷𝐵=𝐴𝐸𝐸𝐶, то ⃖⃗𝐷𝐸 должен быть параллелен ⃖⃗𝐵𝐶.
Применяя обратную теорему о делителях сторон, мы можем доказать, что прямая параллельна одной стороне треугольника из-за пропорциональных частей. В нашем последнем примере мы продемонстрируем этот процесс.
Пример 6. Нахождение неизвестных длин в треугольнике по длинам других сторон с использованием соотношений параллельных прямых
Зная, что 𝐴𝐵𝐶𝐷 — параллелограмм, найдите длину
из 𝑌𝑍.
Ответ
Чтобы найти длину 𝑌𝑍, начнем с определение релевантной информации о треугольниках 𝑋𝑌𝑍 и 𝑋𝐷𝐶. Нам дано, что 𝑋𝑌=𝑌𝐷 и 𝑋𝑍=𝑍𝐶. Мы также помним, что теорема о боковых делителях говорит нам, что если прямая, параллельная одной стороне треугольника, пересекает две другие его стороны треугольника, то линия пропорционально делит эти стороны. И наоборот, если линия делит две стороны треугольника на равные части, то эта линия должна быть параллельна в третью сторону. Поскольку стороны 𝑋𝐷 и 𝑋𝐶 большего треугольника 𝑋𝐷𝐶 были разделены на равные части, мы можем применить обращение этой теоремы, чтобы вывести, что 𝐷𝐶 и 𝑌𝑍 должны быть параллельны.
Напомним также, что если прямая, параллельная стороне треугольника, пересекает
две другие стороны, то меньший треугольник, образованный параллельной линией, равен
аналогично исходному треугольнику. Следовательно, мы получаем
△𝑋𝑌𝑍∼△𝑋𝐷𝐶.
Так как 𝐷𝐶 является противоположной стороной 𝐴𝐵 в параллелограмме 𝐴𝐵𝐶𝐷 эти две стороны должны иметь одинаковую длину. Следовательно длина 𝐷𝐶 составляет 134,9 см. Обозначая длину 𝑋𝑌 неизвестной константой 𝑥, мы можем нарисовать следующую схему.
Поскольку треугольники 𝑋𝑌𝑍 и 𝑋𝐷𝐶 подобны, мы можем составить уравнение, связывающее длины сторон 𝑋𝑌, 𝑋𝐷, 𝑌𝑍, и 𝐷𝐶: 𝑋𝑌𝑋𝐷=𝑌𝑍𝐷𝐶𝑥2𝑥=𝑌𝑍134,912=𝑌𝑍134,9.
Решая 𝑌𝑍, находим 𝑌𝑍=134,92=67,45.
Длина 𝑌𝑍 67,45 см.
Теперь мы повторим ключевые моменты этого объяснения.
Ключевые точки
- Если линия, пересекающая две стороны треугольника, параллельна оставшейся стороне, то меньший треугольник, созданный параллельной линией, подобен большему исходному треугольнику.
- Теорема о делителях сторон говорит нам, что если прямая, параллельная одной стороне треугольника, пересекает две другие стороны треугольника, то эта прямая делит эти стороны пропорционально.

- Теорему о боковых делителях можно расширить, включив в нее параллельные прямые, лежащие вне треугольника. Если прямая, лежащая вне треугольника, параллельна одной стороне треугольника и пересекает продолжения двух других сторон треугольника, то линия пропорционально делит продолжения этих сторон.
- Теорема, обратная теореме о делителях сторон, утверждает, что если линия пропорционально делит две стороны треугольника, то линия параллельна оставшейся стороне.
Основы геометрии, точки, прямые и треугольники
Основы геометрии, точки, прямые и треугольники: Прямые линии, параллельные линии, углы, треугольники, свойства треугольников с примерами и упражнениями.
Охватываемые концепции базовой геометрии,
- Точки и линии: Прямая и изогнутая линия, Замкнутая форма, Параллельные линии, Расстояние между двумя линиями, Угол между двумя линиями, Законы пересечения, Линия, пересекающая пару параллельных линий,
- Уголки и виды уголков ,
- Треугольники: Основные понятия о треугольниках, Внешний угол треугольника, Типы треугольников, Теорема Пифагора, Равнобедренные и равнобедренные треугольники, Прямоугольные треугольники, Подобие и конгруэнтность треугольников, Условия подобия и конгруэнтности, Медианы треугольников и биссектрисы треугольников , Инцентр, Ортоцентр и Центроид треугольника.

- Десять выбранных тестовых вопросов для упражнений по основам геометрии, точек, линий и треугольников с ответами.
Точки и линии
Чтобы сформировать фигуру, вам нужны строительные блоки. Любая форма образована поверхностями, любая поверхность образована линиями и, наконец, любая линия образована точками. Это все равно, что построить твердый объект из атомных частиц.
Точка:
Точка в пространстве (3D или 2D) определяется как уникальное местоположение без каких-либо измерений. Точка не имеет ни длины, ни ширины, ни высоты. Это просто местоположение, определяемое параметрами относительно контрольной точки. В геометрии координатной плоскости вы используете две перпендикулярно пересекающиеся оси $x$ и $y$ и определяете положение любой точки относительно кратчайшего расстояния точки от оси $x$ и оси $y$ как пары значений $(x, y)$. Точкой отсчета в этом случае является точка пересечения двух осей. Оно называется началом координат и имеет координаты $(0,0)$.
На листе бумаги или на плоскости вы можете разместить начало координат в любом удобном месте и определить все остальные точки на плоскости относительно этого начала.
Но не всегда нужен ориентир для изучения свойств фигур. Другими словами, не всегда нужна координатная геометрия. В основном мы будем обсуждать здесь чистую геометрию, но иногда для ясности будем использовать две оси.
В реальном мире какой бы маленькой ни была точка, которую вы нарисуете на листе бумаги, она все равно будет иметь размер. Итак, определение точки, что она безразмерна, является идеальным и называется Аксиома.
Линия:
При соединении двух точек получается линия. Линии бывают двух типов:
Прямая линия и изогнутая линия:Вы соединяете две точки множеством линий, фактически бесконечным числом линий.
Кратчайшая линия, соединяющая две точки, — прямая.
Все другие линии, соединяющие две точки, являются изогнутыми линиями, и длина этих линий больше, чем длина прямой линии, соединяющей те же две точки.
Точки составляют линию:
Линия состоит из бесконечного числа точек, следующих друг за другом. Следуя этим точкам, вы достигаете от одного конца линии до другого.
Концы линии и замкнутые формы:Линия, прямая или изогнутая, имеет два конца, если эти два конца не встречаются. Линия может иметь конечную длину, или вы можете представить, что каждый конец линии простирается бесконечно.
Если два конца линии встречаются, линия должна быть изогнутой линией, и дает замкнутую форму с изогнутым периметром.
Примеры: Круги или Эллипсы .
Такие замкнутые формы с изогнутым периметром имеют только одну линию, ограничивающую площадь, и эта единственная линия не имеет концов.
Любая фигура, ограниченная только прямыми линиями, состоит из более чем двух линий (не менее 3), и точки пересечения этих линий называются вершинами.
Замкнутая фигура, ограниченная наименьшим количеством прямых линий, равна Треугольник и является одной из важнейших геометрических фигур в математике, причем не только в геометрии, но и в других дисциплинах тоже.
Примеры прямой и изогнутой линий между двумя точками:
Все три изогнутые линии, соединяющие две точки $A$ и $B$, длиннее, чем расстояние по прямой линии $AB$ между точками $A$ и $ Б$. Между двумя точками может быть такое бесконечное количество изогнутых линий, но только одна прямая линия, соединяющая две точки.
Прямая может иметь фиксированную определенную длину $AB$, но также оба ее конца могут быть бесконечно продолжены в две стороны.
Использование прямых линий в реальной жизни:
Прямые линии — это края столов, вертикальный край, где встречаются две стены комнаты, края вашего блокнота и так далее. Для производства прямой кромки расходуется наименьшее количество материала, а также ее легко создать в любом производственном процессе. Вот почему вокруг мы видим прямые линии краев.
Параллельные линии:
Если две линии никогда не пересекаются, если они продолжаются в обоих концах на неопределенный срок, могут быть две причины: либо линии не находятся в одной плоскости, либо линии находятся в одной плоскости, но параллельны.
Две параллельные прямые на плоскости никогда не пересекаются.
Пример пары параллельных линий:
Расстояние между двумя линиями:
Расстояние между двумя линиями обычно варьируется от точки к точке. Он определяется как кратчайшее расстояние от точки на одной линии до другой линии.
В случае двух параллельных прямых $AB$ и $PQ$ кратчайшим расстоянием от точки $P$ на прямой $PQ$ до второй прямой $AB$ будет длина перпендикуляра, проведенного из $P$ на $AB$, то есть $PC$. Это расстояние от точки $P$ до прямой $AB$. Точно так же расстояние от точки $B$ на прямой $AB$ до прямой $PQ$ будет равно длине перпендикуляра $BD$.
Для пары параллельных линий эти две длины всегда будут одинаковыми. Таким образом, для любой точки $P$ на $PQ$ и любых точек $B$ и $AB$ перпендикулярные расстояния $PC = BD$.
Поскольку расстояния между параллельными линиями не меняются, они никогда не смогут сблизиться и встретиться.
Напротив, для двух пересекающихся линий расстояние между двумя линиями уменьшается по мере приближения к точке пересечения, в которой оно становится равным нулю.
Две линии $AC$ и $BC$ пересекаются в точке $C$, где расстояние между ними становится равным нулю. После пересечения в точке $C$ межстрочное расстояние снова продолжает увеличиваться.
Угол между двумя линиями:
До сих пор мы не говорили об углах, так как впервые столкнулись с пересекающимися прямыми, а вопрос об угле возникает только при пересечении двух прямых. Вот почему мы говорим угол между двумя линиями.
На этом этапе мы просто определяем угол как
Величина наклона одной линии по отношению к другой.
Очевидно, угол между двумя параллельными прямыми равен нулю.
Когда две прямые $ACE$ и $BCD$ пересекаются в точке $C$, пересечение образует четыре угла, а именно: $\угол BCE$, $\угол ECD$, $\угол DCA$ и $\угол ACB$. 90 = \pi $
90 = \pi $
Прямая линия, пересекающая две параллельные линии:
Теперь мы рассмотрим важные аспекты прямой линии, пересекающей две параллельные линии.
Здесь также действуют два закона пересечения для восьми (8) углов, образованных прямой линией, пересекающей две параллельные линии.
Закон 3: Углы между двумя параллельными прямыми с пересекающейся прямой по одну сторону от пересекающейся прямой: Внешний угол $\angle DCQ$ и внутренний угол второй прямой $\angle CFH$ равны . Этот закон приводит к четырем равенствам,
$ \angle DCQ = \angle GFC, \quad \angle BCF = \angle EFP, \quad \angle QCB = \angle CFE, \quad \angle FCD = \angle PFH $
Закон 4: Внутри противоположные углы, удерживаемые двумя параллельными прямыми с пересекающейся линией , $\угол BCF = \угол GFC$.
На самом деле это не отдельный независимый закон — это производный закон от Закона 1 о пересечении линий и Закона 3 о пересечении параллельных линий.
$\angle BCF = \angle QCD$, по закону 1, $\angle QCD = \angle GFC$, по закону 3 и суммируя,
$\угол BCF = \угол GFC$. Вот почему мы называем это Законом 4, поскольку он получен из Закона 1 и Закона 3.
Эти два Закона, Закон 3 и Закон 4, в итоге дают только два уникальных различных значения восьми углов, образованных пересекающейся прямой,
$ \angle DCQ = \angle GFC = \angle BCF = \angle EFP = \theta, $
и,
$\angle QCB = \angle FCD = \angle CFE = \angle PFH = \gamma $
Углы:
Традиционно углы измеряются 90$ — тупой угол.
Треугольники
Основные понятия о треугольнике
- Треугольник можно определить как — три точки на плоскости, не лежащие на одной прямой и соединенные друг с другом тремя прямыми линиями, охватывающими пространство на плоскости.
- Таким образом, треугольник имеет три вершины, соединенные тремя ребрами.
- Треугольник — это замкнутая фигура, ограниченная наименьшим числом ребер или сторон.
 У четырехугольника 4 стороны, у пятиугольника 5 сторон, у шестиугольника 6 сторон и так далее. 90$.
У четырехугольника 4 стороны, у пятиугольника 5 сторон, у шестиугольника 6 сторон и так далее. 90$. - Суммарная длина любых двух сторон треугольника больше длины третьей стороны.
- Общая длина двух ребер становится все меньше и меньше по мере того, как вершина, являющаяся точкой соединения двух сторон, опускается к третьей стороне. Сумма этих двух длин становится равной длине третьей стороны, когда вершина, содержащая две стороны, падает на третью сторону — но тогда треугольник уже не остается треугольником, он становится прямой линией.
В третьем треугольнике $\треугольник PQR$ вершина $P$ почти попала на основание $QR$, но сумма двух меньших сторон $PQ$ и $PR$ все равно больше большей стороны $QR$. Таким образом, самая длинная сторона $QR$ никогда не может быть больше, чем сумма длин двух других меньших сторон треугольника.
Внешний угол равен двум противоположным внутренним углам:
В любом треугольнике внешний угол равен сумме двух его противоположных углов.
В прямоугольном треугольнике все три стороны могут быть не равны. Единственное условие: один из трех углов должен быть прямым.
И $\треугольник ABC$, и $\треугольник EDF$ являются прямоугольными треугольниками, у которых все три стороны не равны.
Теорема Пифагора:Это одна из важнейших и основных теорем геометрии, устанавливающая определенное соотношение между длинами сторон прямоугольного треугольника.
92 $
В прямоугольном треугольнике $\треугольник EDF основание$ равно $DE$, $высота$ равно $DF$ и $гипотенуза$ равно $FE$.
Общий треугольник, все стороны которого не равны — Разносторонний треугольник:В разностороннем треугольнике нет особых характеристик сторон. У него все стороны разной длины и все углы разной степени.
Нет двух сторон одинаковой длины и нет двух одинаковых углов.
Если все три стороны не равны, а все три угла не равны, то даже прямоугольный треугольник может быть разносторонним. Примером может служить $\triangle DEF$ из трех разносторонних треугольников, показанных ниже.
Примером может служить $\triangle DEF$ из трех разносторонних треугольников, показанных ниже.
Равнобедренный треугольник:
Это тип треугольника,
Две его стороны имеют одинаковую длину. Два угла, прилежащие к равным сторонам, также равны.
Перпендикуляр из вершины $A$, содержащей равные стороны, на неравную сторону $BC$ делит пополам неравную сторону, угол при вершине $\угол A$ и площадь треугольника $\треугольника ABC$, как показано ниже.
Единственный другой вывод, который можно сделать из этих двух основных свойств 92 \qquad \text{или, } PB=PC $
Таким образом, в двух треугольниках $\треугольник APB$ и $\треугольник APC$ все соответствующие стороны равны. Это делает два треугольника конгруэнтными и, следовательно, все соответствующие углы двух треугольников равны. Таким образом,
$ \angle ABP = \angle ACP = \alpha \qquad \text{and, } \angle BAP = \angle CAP = \theta $
Равносторонний треугольник: В равностороннем треугольнике $\triangle ABC$ все три стороны равны. 0$.
0$.
Как и в равнобедренном треугольнике, в равнобедренном углу также перпендикуляр из вершины $A$ на основание $BC$ делит пополам и $\угол A$, и основание $BC$.
Сравнение двух треугольников
Два треугольника могут быть связаны друг с другом двумя особыми способами: Подобные и Конгруэнтные .
Подобные треугольники:В двух подобных треугольниках
- Три угла одного треугольника $\треугольника ABC$ равны трем соответствующим углам второго треугольника $\треугольника DEF$. То есть $\угол A=\угол D$, $\угол B=\угол E$ и $\угол C=\угол F$, и,
- Соотношение соответствующих сторон двух треугольников также одинаково. То есть $ \displaystyle\frac{AB}{DE}=\displaystyle\frac{BC}{EF}=\displaystyle\frac{CA}{FD}$.
$\треугольник ABC$ и $\треугольник DEF$ подобны . Если вы посмотрите на них и сравните, вы сможете заметить сходство. Говоря более конкретно, все три пары соответствующих углов равны: $\угол A=\угол D$, $\угол B=\угол E$ и $\угол C=\угол F$. Таким образом, первое условие выполняется.
Говоря более конкретно, все три пары соответствующих углов равны: $\угол A=\угол D$, $\угол B=\угол E$ и $\угол C=\угол F$. Таким образом, первое условие выполняется.
Кроме того, отношения соответствующих сторон равны:
$ \displaystyle\frac{AB}{DE}=\displaystyle\frac{BC}{EF}=\displaystyle\frac{CA}{FD}=1,4 $
Это как если бы меньший треугольник был увеличен без изменения соотношения сторон , , который является знакомым термином при работе с растровыми изображениями. Если бы углы не были одинаковыми, этого нельзя было бы достичь.
Любой из этих треугольников можно было бы повернуть на любой угол, но сходство не нарушилось бы.
Если отношение соответствующих сторон равно 1, мы получаем треугольники точно равные или конгруэнтные.
Конгруэнтные треугольники: Это частный случай подобных треугольников, в которых соответствующие стороны равны, или, другими словами, отношение соответствующих сторон равно 1.
Кроме того, из-за сходства соответствующие углы также равны. Фактически один треугольник дублирует другой.
Проверка сходства двух треугольников:
Есть три теста. Если два треугольника проходят любой из этих тестов, они подобны друг другу.
1. AA: или угол-угол : Если две пары соответствующих углов двух треугольников равны, треугольники должны быть подобны. Равенство двух пар соответствующих углов приводит к равенству и третьей пары соответствующих углов, и тест можно назвать подобием AAA.
2. SSS: или Side-Side-Side : Если отношения трех пар соответствующих сторон равны, два треугольника подобны.
3. SAS: или Сторона-Угол-Сторона : Если две соответствующие стороны имеют одинаковое отношение и углы между ними равны, то два треугольника подобны. Соответствующие стороны AB, DE и AC, DF находятся в равном отношении и заключают в себе углы $\угол A = \угол D$.
Причина: Поскольку прилежащий угол такой же, как и отношение двух сторон прилежащего угла, меньший треугольник можно наложить на больший треугольник таким образом, что вершины под равными углами накладываются друг на друга совпадающим образом, и две включающие стороны меньшего треугольника также лежат вдоль двух включающих сторон большего треугольника.
Ситуация была бы такой, как если бы два треугольника $\треугольник ABC$ и $\треугольник DEF$ наложены друг на друга с $\углом D$, объединенным с общим $\углом A$ и отношением включающих сторон равным, $AB : AE = AC : АФ$.
После наложения угол при вершине $\угол A$ будет одинаковым (при объединении $\угла D$) и отношение сторон AB и AE будет равно отношению сторон AC и AF. Это автоматически сделает EF параллельным BC.
Тогда два треугольника $\triangle ABC$ и $\triangle DEF$ будут подобны $EF || до н.э.$. Следовательно, в двух треугольниках $\angle A=\angle A$, $\angle B= \angle E$ и $\angle C=\angle F$. Кроме того, отношение соответствующих сторон также будет равным,
Кроме того, отношение соответствующих сторон также будет равным,
$ \displaystyle\frac{AB}{AE}=\displaystyle\frac{AC}{AF}=\displaystyle\frac{BC}{EF} $.
Проверка на соответствие:
Если два треугольника проходят любой из следующих тестов, они считаются конгруэнтными.
1. Тест SSS: Если три стороны равны, треугольники конгруэнтны. Это очевидно.
2. Тест SAS: Если две стороны равны, как и угол между ними, треугольники конгруэнтны.
Это следует из теста подобия SAS.
3. Тест ASA: Если два угла равны, а также сторона, заключенная между ними, треугольники конгруэнтны.
Если два угла равны, то и третий угол тоже будет равен, и треугольники будут подобны с соответствующими сторонами в фиксированном соотношении. Поскольку две соответствующие стороны равны (с отношением 1), две другие пары соответствующих сторон также будут равны (с отношением 1).
Таким образом, четвертый тест на конгруэнтность становится возможным.
4. Тест AAS: Если два угла равны и любая другая смежная сторона, два треугольника конгруэнтны.
5. Тест RHS: Это частный случай прямоугольного треугольника. Если гипотенуза и любая другая сторона в паре прямоугольных треугольников равны, треугольники конгруэнтны.
Причина: По теореме Пифагора третья сторона тоже будет равна и это будет трансформировано в тест SSS.
Особые точки треугольника
В треугольнике есть несколько важных особых точек.
Пересечение серединных перпендикуляров трех сторон треугольника — центр окружности
Серединные перпендикуляры к трем сторонам треугольника пересекаются в одной точке, центре окружности треугольника.
Окружность, на которой лежат три вершины треугольника, есть Окружность треугольника; радиус окружности — любая из длин AO, BO или CO равна Радиус окружности треугольника и центральная точка $O$ являются центром окружности треугольника.
Так как расстояние от центра описанной окружности до трех вершин одинаковое, то окружность также может быть определена как
Метод получения центра окружности и окружности:Точка, равноудаленная от трех вершин треугольника.
- Нарисуйте три перпендикулярные биссектрисы на трех сторонах треугольника.
- Обнаружить, что три серединных перпендикуляра всегда пересекаются в точке внутри треугольника. Это центр окружности треугольника.
- Соедините вершины $A$, $B$ и $C$ с этой новой точкой $O$. Длины $AO$, $BO$ и $CO$ будут равны.
- Нарисуйте окружность с центром в точке $O$ и радиусом, равным любому из трех значений $AO$, $BO$ или $CO$
Причина:
Сторонами треугольника являются три хорды описанной окружности, а перпендикуляр из центра окружности к хорде всегда делит хорду пополам. Таким образом, серединные перпендикуляры к трем сторонам треугольника $\треугольника ABC$ сойдутся в центре окружности, на которой лежат вершины треугольника.
В треугольнике $\треугольник BOC$ $OQ$ является перпендикуляром к $BC$. Так как $OB=OC$, радиусы, а общая сторона $OQ$, то в двух прямоугольных треугольниках, $\треугольнике BOQ$ и $\треугольнике COQ$, третьи стороны также совпадают по теореме Пифагора, то есть $ БК=КК$.
Итак, перпендикуляр из центра окружности к хорде делит хорду пополам.
Пересечение перпендикуляров из вершин к противоположным сторонам — ортоцентр :Перпендикуляры из трех вершин к противоположным сторонам пересекаются в точке, которая является0003 Ортоцентр треугольника.
- В остроугольном треугольнике, как в примере, ортоцентр лежит внутри треугольника.
- В тупоугольном треугольнике ортоцентр лежит вне треугольника, и
- в прямоугольном треугольнике ортоцентр совпадает с вершиной прямого угла.
Ниже приведен пример ортоцентра в тупоугольном треугольнике.
$AP$ — высота треугольника на стороне основания $CB$ в расширенном виде, $BQ$ — высота на стороне основания $AC$ и $CR$ — высота треугольника в расширенном основании $AB$.
Эти три высоты или высоты не пересекаются внутри треугольника. Они пересекаются в точке $O$ вне треугольника после продолжения через тупой угол $\угол B$ вершины $B$.
Пересечение медиан – центроидМедиана – это линия, соединяющая вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке Центроид.
Это называется центром тяжести треугольника.
Центроид делит каждую медиану в соотношении 2:1.
В результате имеем
$ \displaystyle\frac{AO}{OQ}=\displaystyle\frac{BO}{OP}=\displaystyle\frac{CO}{OR}=2 $.
Пересечение биссектрисы угла — центр вписанной части:
Три биссектрисы внутреннего угла пересекаются в точке, обозначенной как в центре . Это центр окружности, вписанной внутрь треугольника. Три стороны треугольника касаются окружности.
Это центр окружности, вписанной внутрь треугольника. Три стороны треугольника касаются окружности.
Биссектрисы углов $AI$, $BI$ и $CI$ делят пополам углы $\angle A$, $\angle B$ и $\angle C$ соответственно и пересекаются в точке $I$, являющейся центр вписанной окружности радиуса $IP$ или $IR$. Это центра треугольника $\треугольника ABC$.
Поскольку радиус окружности перпендикулярен касательной, когда две касательные $BC$ и $AC$ пересекаются в точке $C$, $IP$ и $IQ$ перпендикулярны к $CB$ и $CA$, а также равны, являясь радиусами вписанной окружности.
Итак, два треугольника $\triangle ICQ\equiv\triangle ICP$. В результате $\angle ICQ=\angle ICP$, то есть $CI$ является биссектрисой угла $\angle C$.
По той же логике $BI$ и $AI$ являются биссектрисами углов $\angle B$ и $\angle A$.
Таким образом, центр вписанной окружности треугольника, центр вписанной окружности , является точкой пересечения трех его биссектрис.
0$, то $\угол BAD$ равен 90$
Задача 2.
В равнобедренном треугольнике $\треугольник FGH$, $FG \lt 3$ см и $GH = 8$см. Тогда правильное соотношение:
- $GH = FH$
- $GH\ltFH$
- $ GF =
GH $- $FH\gt GH$
Задача 3.
Сумма трех высот треугольника
- равна сумме трех сторон
- удвоенная сумма сторон
- больше суммы сторон
- меньше суммы сторон 90$
Задача 9.
В $\треугольнике ABC$ на прямых $AB$ и $BC$ взяты две точки $D$ и $E$ соответственно так, что $AC$ параллелен $DE$ . Тогда $\треугольник ABC$ и $\треугольник DBE$
- всегда подобны
- всегда совпадают
- аналогично, только если $D$ лежит вне отрезка $AB$
- конгруэнтны, только если $D$ лежит вне отрезка $AB$
Задача 10.
$AD$ — медиана $\треугольника ABC$, а $O$ — центроид такой, что $AO = 10см$.
Длина $OD$ (в см) составляет, 90$.
Задача 9: а: всегда похожи.
Проблема 10: B: 5.
Эти вопросы образуют SSC CGL. Набор вопросов 18 на геометрии 1.
Стоимость. набор 18 по геометрии 1.
Пошаговая помощь по геометрии в Suresolv
Чтобы получить наилучшие результаты из обширного ассортимента статей учебники , вопросы и решения по Geometry в Suresolv, следуйте руководству,
Suresolv SSL Compitive Geometry Reading and Practice Guide, Экзамены.
Список статей руководства включает ВСЕ статьи по геометрии и соответствующим темам в Suresolv, и является актуальным.
→
Знак треугольника на ладони Значение
- Домашняя страница
- Китайская хиромантия
- Знак треугольника
Значения треугольника в разных местах на ладони
Треугольник, который формируется на вашей ладони беспорядочными линиями на ладони.
Четкие и правильные треугольники всегда имеют благоприятные последствия. Давайте посмотрим на различные значения треугольника в разных местах на ладони.
В центре ладони
Правильный большой треугольник в центре вашей ладони является признаком удачи и указывает на то, что вы сделаете карьеру, будете иметь удачу в зарабатывании денег и станете широко известным; вы можете даже стать лидером. Кроме того, у вас будет муж/жена в хорошем состоянии. Однако треугольник на горе Нептуна, к сожалению, является плохим знаком, предполагающим наказание за одиночество на всю жизнь.На линии Брака или Сердца
Треугольник на линии брака или линии сердца указывает на то, что вы получите удачу в богатстве или получите имущество от брака или любви.На линии головы
Если хиромантический треугольник находится на линии головы, это говорит о том, что вы не только добьетесь академических и теоретических успехов, но и будете обладать хорошим красноречием.На линии жизни
Эта ситуация подразделяется на две категории. Если треугольник находится на линии жизни, это указывает на то, что вы более энергичны, чем в среднем, и у вас есть утонченная дирижерская манера, поэтому другие всегда помогают вам и высоко ценят ваше начальство и коллеги; у вас будет хорошее развитие, будь то чиновник, займитесь бизнесом или начните свой собственный бизнес, и у вас будут большие достижения в карьере, что очень благословляет. Если треугольник находится на конце линии жизни, это говорит о том, что в старости вами будут восхищаться.Если треугольник находится очень близко к линии жизни, это говорит о недопустимых заболеваниях внутренних органов, таких как сердце, печень и желудок, и их следует остерегаться и предупреждать заранее, а также обратиться на обследование в больницу, т.к. как можно скорее, как только вы почувствуете дискомфорт.
На линии запястья
Треугольник на линии запястья также является благоприятным знаком.Если треугольник находится в центре линии запястья, это говорит о том, что вы родились благословленным и вам очень повезло в непредвиденной ситуации; вы можете унаследовать наследие предков или стать главой подразделения, таким образом, известным своей славой или властью. Если другие линии на линии запястья образуют правильную форму с острыми углами (не треугольник), это говорит о том, что вы очень умны и обладаете особыми способностями в чем-то, благодаря которым вы получите большое богатство.
Ниже указательного пальца (холм Юпитера )
Указывает на то, что вы талантливы в военном и политическом плане, энергичны, предусмотрительны, самодисциплинированы и способны выдерживать большое давление, поэтому можете иметь успешная карьера и успешная жизнь.Ниже среднего пальца (холм Сатурна )
Это указывает на то, что вы сделаете карьеру и достигнете того, чего желали, после среднего возраста.Под безымянным пальцем (гора Аполлона )
Это говорит о том, что вы разносторонне развиты и обладаете хорошей способностью к обучению, необыкновенным темпераментом и талантом, поэтому вы можете добиться определенных успехов в жизни.Под мизинцем (холм Луны)
Благоприятный знак успешной карьеры и удачи в богатстве. Этот треугольник говорит о том, что вы очень умны и обладаете управленческим талантом, поэтому обязательно добьетесь определенных успехов в бизнесе.Больше признаков в Palmistry:
● Моли под рукой ● Крест ● Звезда ● Остров ● КвадратСвязанное чтение:
→ Aspeyciple Prics and Symbles в Palmystistionчеловек также читают
1человек. пятна или родинки на линиях на ладони
2
что означает звезда на ладони?
3
что цвет рук говорит о вашем здоровье и судьбе
4
китайская хиромантия
5
川 ладонь в хиромантии: личность, любовь, карьера, брак, судьба
6
может ли операция на ладони изменить ваше будущее?
Линия жизни и линия ума (0 Отвечать ) Вопрос задан J***o | 26.
07.2022 8:31:39
Что означает линия, соединяющая линию жизни и линию ума, образующая треугольник с линией судьбы
линия здоровья (1 Отвечать ) Вопрос задан V***s | 08.04.2021 2:50:31
Если линия здоровья неудачна, а та, которая касается линии жизни, очень неудачна, то как образуется треугольник между здоровьем,…
Большой треугольник на равнине Марса, образованный линией жизни и головой (1 Отвечать ) Вопрос от C***S | 03.01.2021 20:11:09
На моей левой ладони линия головы и линия жизни, а также некоторые другие линии ладони образуют большой треугольник на равнине области Марса (центральная область…
Треугольник между линией солнца и линией судьбы (1 Отвечать ) Вопрос задан C***S | 03.

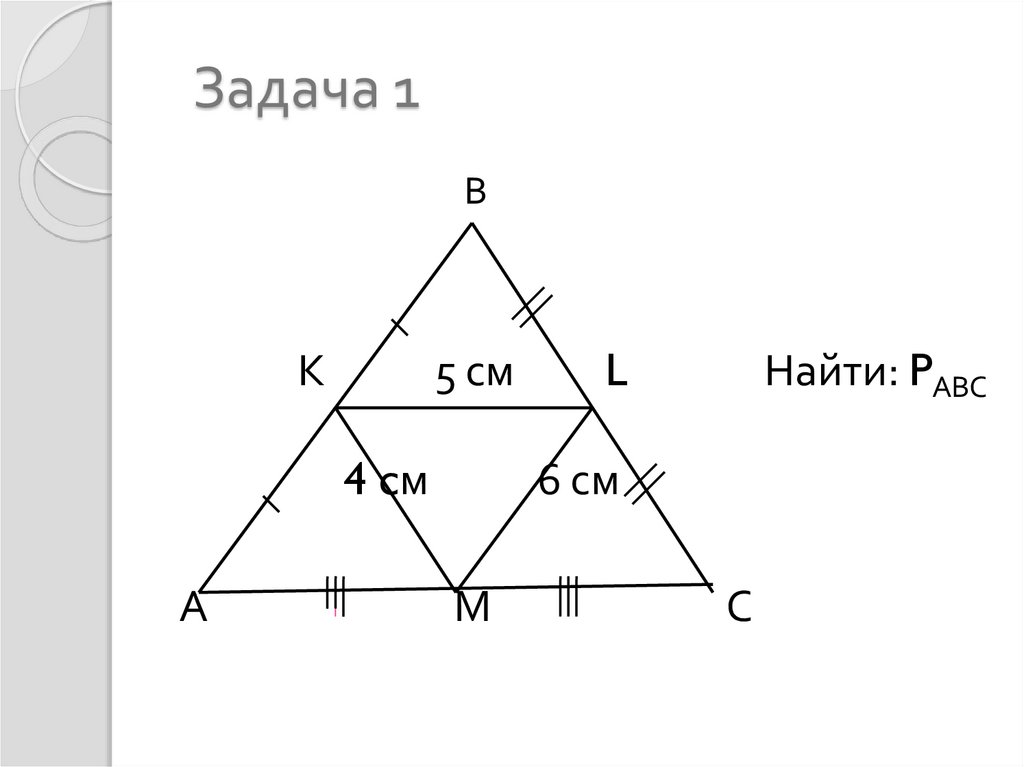 Теорема Вариньона
Теорема Вариньона Таким образом, выполняется один из признаков подобия.
Таким образом, выполняется один из признаков подобия. Найдите периметр треугольника. Решение Средняя линия равна половине параллельных сторон, поэтому можно найти длины всех сторон треугольника. см см см см см см см Теперь можно найти периметр треугольника как сумму всех длин. Его стороны: см см Ответ: см см см.
Найдите периметр треугольника. Решение Средняя линия равна половине параллельных сторон, поэтому можно найти длины всех сторон треугольника. см см см см см см см Теперь можно найти периметр треугольника как сумму всех длин. Его стороны: см см Ответ: см см см.
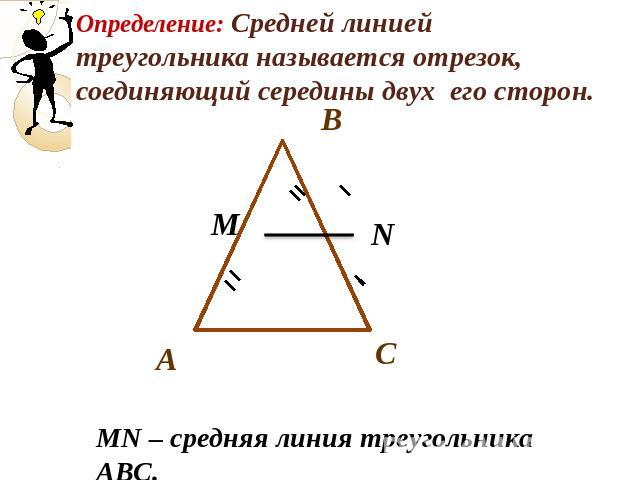
 5, а его площадь
равняется четверти площади заданной фигуры;
5, а его площадь
равняется четверти площади заданной фигуры;
 Рассмотрим три прямые и две секущие, как показано ниже:
Рассмотрим три прямые и две секущие, как показано ниже: Теперь рассмотрим ΔBAY. Так как E — середина AB, а EX || AY, обратная теорема о средней точке говорит нам, что X является серединой BY, а это означает, что BX = XY. Аналогично можно доказать, что XY = YD. Таким образом, BX = XY = YD = BD/3. Значит доказано.
Теперь рассмотрим ΔBAY. Так как E — середина AB, а EX || AY, обратная теорема о средней точке говорит нам, что X является серединой BY, а это означает, что BX = XY. Аналогично можно доказать, что XY = YD. Таким образом, BX = XY = YD = BD/3. Значит доказано.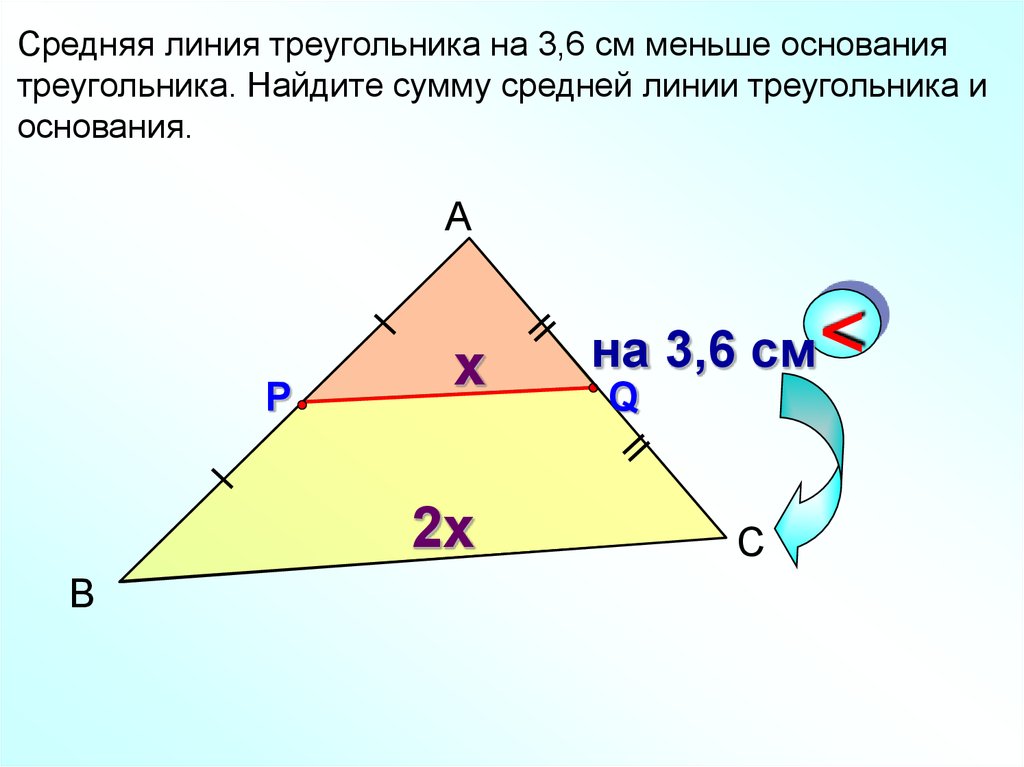 Также не имеет значения, где находятся отрезки линии.
Также не имеет значения, где находятся отрезки линии.
 Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.
Открытие этой теоремы фактически приписывается Фалесу, о чем свидетельствует Прокл.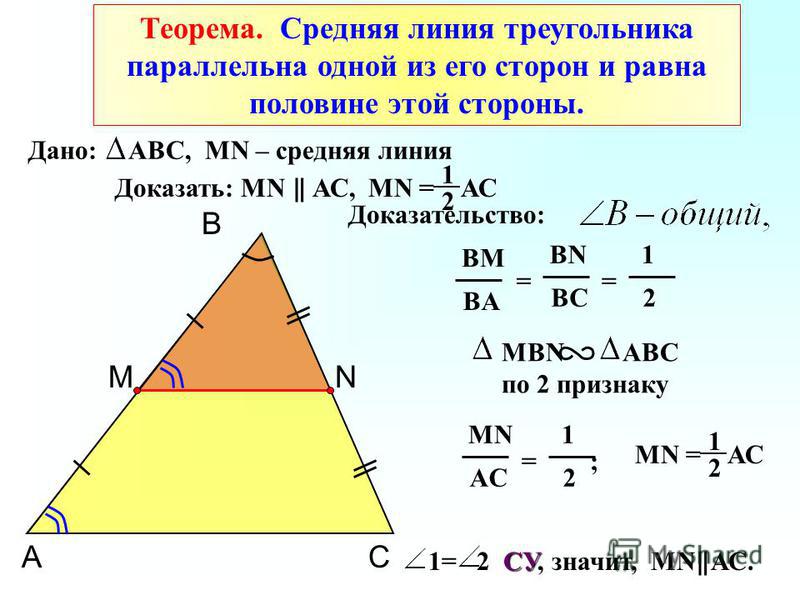 Аксенова.-м.: Аванта+, 2001.
Аксенова.-м.: Аванта+, 2001. 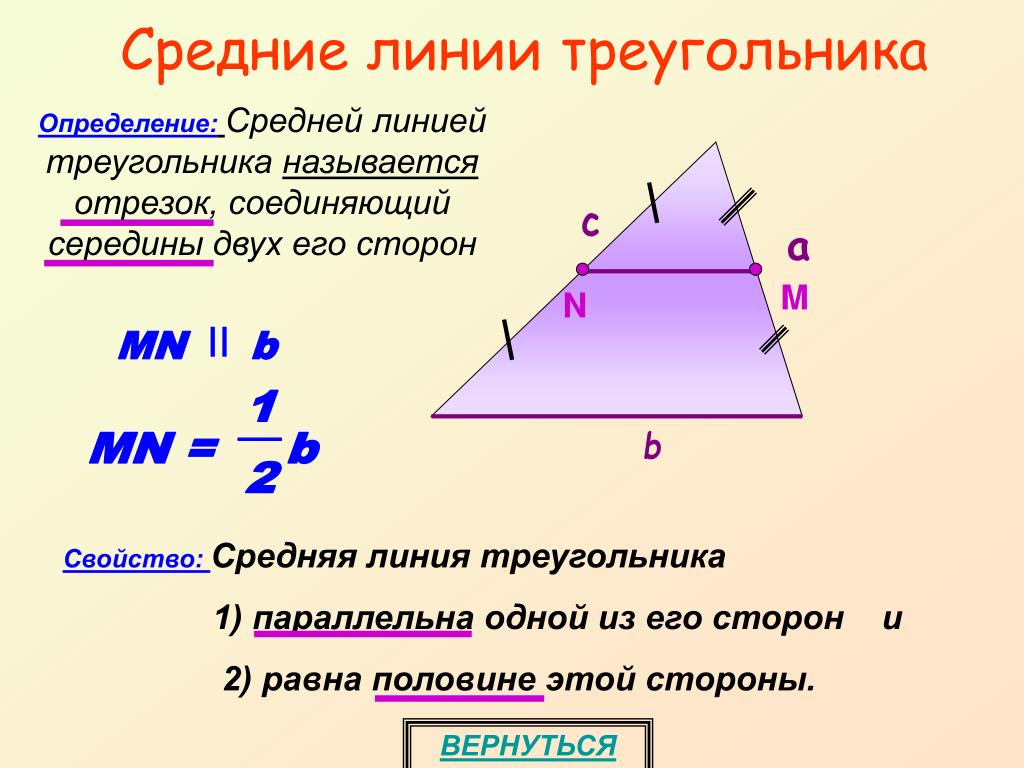 План похищения Ростовой уже несколько дней обдумывался и готовился Долоховым, и в тот день, когда Соня, подслушав Наташу в дверях, решила ее защитить, этот план должен был быть осуществлен. Наташа в десять часов вечера обещала выйти на Курагиново заднее крыльцо. Курагин должен был посадить ее в подготовленную тройку и отвезти за 60 верст от Москвы до села Каменки, где был приготовлен остриженный священник, который должен был их обвенчать. В Каменке была готова подстава, которая должна была вывезти их на Варшавскую дорогу, а там им предстояло скакать за границу на почте.
План похищения Ростовой уже несколько дней обдумывался и готовился Долоховым, и в тот день, когда Соня, подслушав Наташу в дверях, решила ее защитить, этот план должен был быть осуществлен. Наташа в десять часов вечера обещала выйти на Курагиново заднее крыльцо. Курагин должен был посадить ее в подготовленную тройку и отвезти за 60 верст от Москвы до села Каменки, где был приготовлен остриженный священник, который должен был их обвенчать. В Каменке была готова подстава, которая должна была вывезти их на Варшавскую дорогу, а там им предстояло скакать за границу на почте. 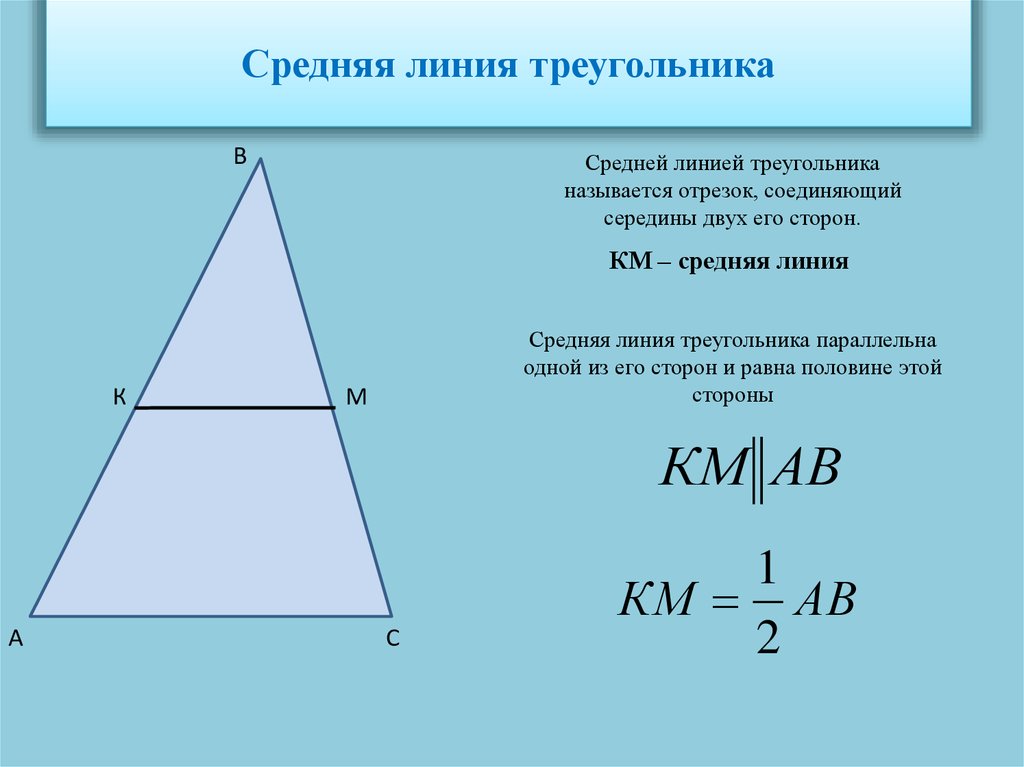 Анатоль в расстегнутом мундире прошел из комнаты, где сидели свидетели, через кабинет в заднюю комнату, где его лакей-француз с другими упаковывал последние вещи. Долохов пересчитал деньги и записал.
Анатоль в расстегнутом мундире прошел из комнаты, где сидели свидетели, через кабинет в заднюю комнату, где его лакей-француз с другими упаковывал последние вещи. Долохов пересчитал деньги и записал.