Средняя линия треугольника параллельна основанию и равна его половине: Средняя линия треугольника и её свойства — доказательство

Содержание

Чему равна средняя линия треугольника определение. Как найти среднюю линию треугольника

Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…

Что такое средняя линия треугольника и каковы её свойства?

Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.

Понятно, что средних линий в треугольнике три. Покажем их:

Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.

Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

Доказательство:

1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:

Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:

По признаку параллельности прямых MN||AC.

2. Также из подобия треугольников следует, что

То есть MN в два раза меньше. Доказано!

Решим типичную задачу.

В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.

Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.

Построим эскиз:

Таким образом периметр треугольника АВС равен 24+20+16=60.

*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:

Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что

Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.

Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.

Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот с такими задачами.

На этом всё! Всего доброго!

Скачать материал статьи

С уважением, Александр Крутицких.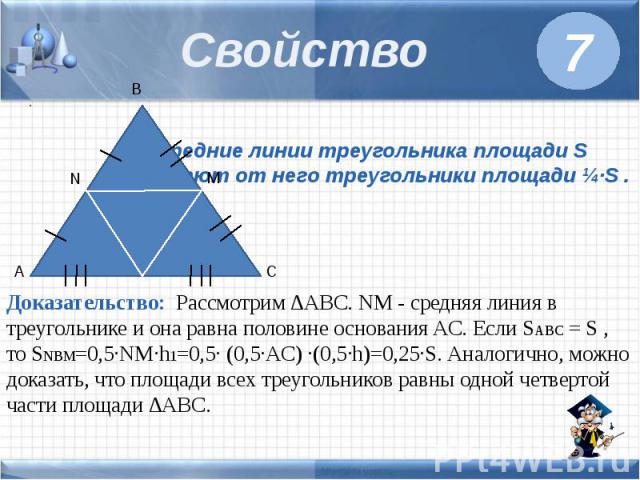

На рисунке 1 показаны два треугольника. Треугольник ABC подобен треугольнику A1B1C1. И прилежащие стороны пропорциональны, то есть AB относится к A1B1 также как AC относится к A1C1. Их этих двух условий и следует подобие треугольников.

Как найти среднюю линию треугольника — признак параллельности прямых

На рисунке 2 показаны прямые a и b, секущая c. При этом образуются 8 углов. Углы 1 и 5 соответственные, если прямые параллельны, то соответственные углы равны, и наоборот.

Как найти среднюю линию треугольника

На рисунке 3, M середина AB, а N середина AC, BC основание. Отрезок MN — называется средней линии треугольника. Сама же теорема гласит — Средняя линия треугольника параллельная основанию и равна его половине.

Для того чтобы доказать, что MN — средняя линия треугольника, нам понадобится второй признак подобия треугольников и признак параллельности прямых.

Треугольник AMN подобен треугольнику ABC, по второму признаку. В подобных треугольниках соответственные углы равны, угол 1 равен углу 2, а эти углы являются соответственными при пересечении двух прямых секущей, следовательно, прямые параллельны, MN параллельно BC.

Угол A общий, AM/AB = AN/AC = ½

Коэффициент подобия этих треугольников ½, из этого следует что ½ = MN/BC, MN = ½ BC

Вот мы и нашли среднюю линию треугольника, и доказали теорему о средней линии треугольника, если вам до сих пор не понятно, как найти среднюю линию, смотрите видео ниже.

Средняя линия треугольника — это отрезок, соединяющий середины 2-х его сторон. Соответственно, каждого у треугольника три средних линии. Зная качество средней линии, а также длины сторон треугольника и его углы, дозволено обнаружить длину средней линии.

Вам понадобится

Стороны треугольника, углы треугольника

Инструкция

1. Пускай в треугольнике ABC MN — средняя линия, соединяющая середины сторон AB (точка M) и AC (точка N).По свойству средняя линия треугольника, соединяющая середины 2-х сторон, параллельна третьей стороне и равна её половине. Значит, средняя линия MN будет параллельна стороне BC и равна BC/2.Следственно, для определения длины средней линии треугольника довольно знать длину стороны именно этой третьей стороны.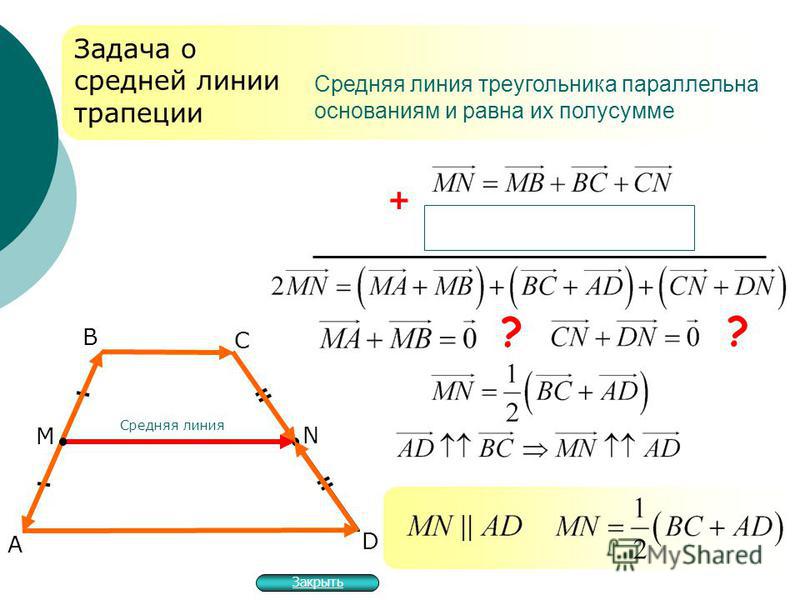

2/4) = 0.

Квадратный треугольник больше верно именуется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры детально рассматриваются в математической дисциплине тригонометрии.

Вам понадобится

— лист бумаги;
— ручка;
— таблицы Брадиса;
— калькулятор.

Инструкция

1. Обнаружьте сторону прямоугольного треугольника с поддержкой теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника

, a и b – его катеты. Дабы применить это уравнение, надобно знать длину всяких 2-х сторон прямоугольного треугольника .

2. Если по условиям заданы размеры катетов, разыщите длину гипотенузы. Для этого с поддержкой калькулятора извлеките квадратный корень из суммы катетов, всякий из которых заранее возведите в квадрат.

3. Вычислите длину одного из катетов, если вестимы размеры гипотенузы и иного катета. При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и вестимого катета, также возведенного в квадрат.

4. Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного

треугольника .

5. Обнаружьте катеты при помощи основных тригонометрических функций: a = c*sin ?, b = c*cos ?, где а – катет, противолежащий к углу?, b – катет, прилежащий к углу?. Сходственным образом посчитайте размер сторон треугольника , если заданы гипотенуза и иной острый угол: b = c*sin ?, a = c*cos ?, где b – катет, противолежащий к углу?, а – катет, прилежащий к углу?.

6. В случае, когда вестим катет a и прилежащий к нему острый угол?, не забывайте, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: ? + ? = 90°. Разыщите значение угла, противолежащего к катету а: ? = 90° – ?. Либо воспользуйтесь тригонометрическими формулами приведения: sin ? = sin (90° – ?) = cos ?; tg ? = tg (90° – ?) = ctg ? = 1/tg ?.

7. Если вестим катет а и противолежащий к нему острый угол?, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin ?, катет: b=a*tg ?.

Видео по теме

1 Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.

И она равна половине гипотенузы .
Следствие 1.
Следствие 2.

2 Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.

3 Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.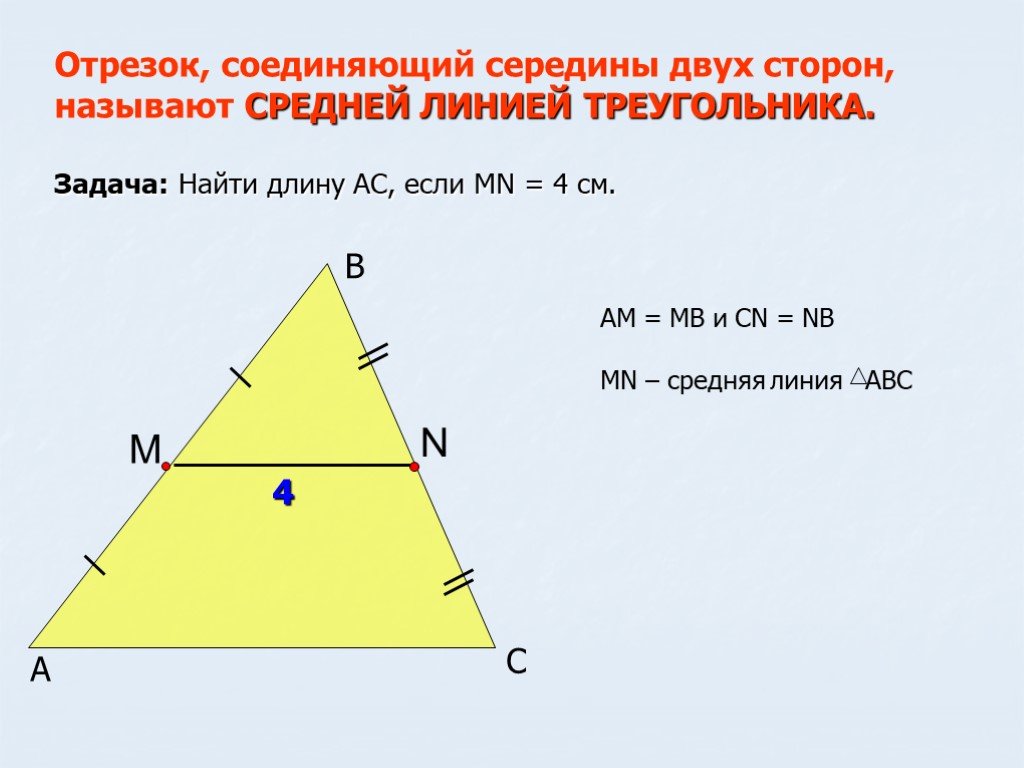

Отсюда видно, что

1 Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.

Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому откуда

Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:

Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия!

2 Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.

Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:

Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :

Другое доказательство теоремы Пифагора см.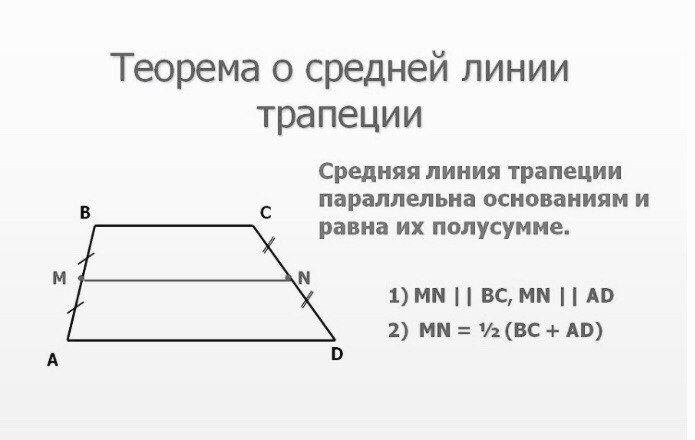

в комментарии к задаче 4.
3 Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.

Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.е. MC – медиана, проведенная к гипотенузе прямоугольного треугольника , и она равна половине гипотенузы .
Следствие 1. Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.

Следствие 2. Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.

Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.

Задачи
Использование свойств подобия -1
Использование основных свойств — 2
Использование дополнительного построения 3-4

1 2 3 4

Высота, опущенная из вершины прямого угла прямоугольного треугольника равна корню квадратном из длин отрезков, на которые она делит гипотенузу.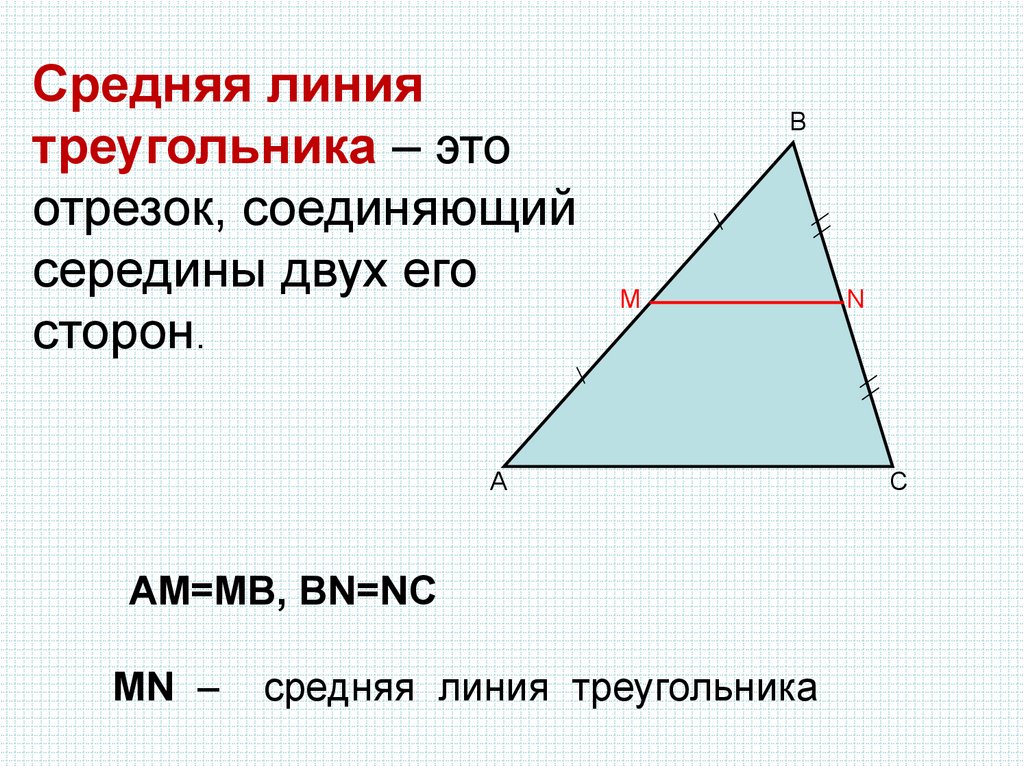 2=c_1c_2\).

Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.

Точка пересечения медиан любого треугольника отсекает от медианы одну треть, считая от точки ее пересечения с соответствующей стороной. В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Поэтому искомое ГМТ есть окружность радиуса, равной 1/6 от длины гипотенузы, с центром в середине этой (фиксированной) гипотенузы.

Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т. д. В чем же состоит сущность этого геометрического ребуса?

Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.

Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.

Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.

Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.

Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.

Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и «физическую» середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия несет в себе множество подобных захватывающих «тайн», знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.

\[{\Large{\text{Подобие треугольников}}}\]

Определения

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).

Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

Определение

Периметр треугольника – это сумма длин всех его сторон.

Теорема

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

Доказательство

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$ со сторонами $a,b,c$ и $a_1, b_1, c_1$ соответственно (см. \circ — \angle A_1 — \angle B_1 = \angle C_1\) , то есть углы треугольника $ABC$ соответственно равны углам треугольника $A_1B_1C_1$ .

Так как $\angle A = \angle A_1$ и $\angle B = \angle B_1$ , то $\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}$ и $\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}$ .

Из этих равенств следует, что $\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}$ .

Аналогично доказывается, что $\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}$ (используя равенства $\angle B = \angle B_1$ , $\angle C = \angle C_1$ ).

В итоге, стороны треугольника $ABC$ пропорциональны сходственным сторонам треугольника $A_1B_1C_1$ , что и требовалось доказать.

Теорема (второй признак подобия треугольников)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство

Рассмотрим два треугольника $ABC$ и $A»B»C»$ , таких что $\dfrac{AB}{A»B»}=\dfrac{AC}{A»C»}$ , $\angle BAC = \angle A»$ . Докажем, что треугольники $ABC$ и $A»B»C»$ – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что $\angle B = \angle B»$ .

Рассмотрим треугольник $ABC»»$ , у которого $\angle 1 = \angle A»$ , $\angle 2 = \angle B»$ . Треугольники $ABC»»$ и $A»B»C»$ подобны по первому признаку подобия треугольников, тогда $\dfrac{AB}{A»B»} = \dfrac{AC»»}{A»C»}$ .

С другой стороны, по условию $\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»}$ . Из последних двух равенств следует, что $AC = AC»»$ .

Треугольники $ABC$ и $ABC»»$ равны по двум сторонам и углу между ними, следовательно, $\angle B = \angle 2 = \angle B»$ .

Теорема (третий признак подобия треугольников)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство

Пусть стороны треугольников $ABC$ и $A»B»C»$ пропорциональны: $\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}$ . Докажем, что треугольники $ABC$ и $A»B»C»$ подобны.

Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что $\angle BAC = \angle A»$ .

Рассмотрим треугольник $ABC»»$ , у которого $\angle 1 = \angle A»$ , $\angle 2 = \angle B»$ .

Треугольники $ABC»»$ и $A»B»C»$ подобны по первому признаку подобия треугольников, следовательно, $\dfrac{AB}{A»B»} = \dfrac{BC»»}{B»C»} = \dfrac{C»»A}{C»A»}$ .

Из последней цепочки равенств и условия $\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}$ вытекает, что $BC = BC»»$ , $CA = C»»A$ .

Треугольники $ABC$ и $ABC»»$ равны по трем сторонам, следовательно, $\angle BAC = \angle 1 = \angle A»$ .

\[{\Large{\text{Теорема Фалеса}}}\]

Теорема

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство

Докажем сначала лемму: Если в $\triangle OBB_1$ через середину $A$ стороны $OB$ проведена прямая $a\parallel BB_1$ , то она пересечет сторону $OB_1$ также в середине.

Через точку $B_1$ проведем $l\parallel OB$ . Пусть $l\cap a=K$ . Тогда $ABB_1K$ — параллелограмм, следовательно, $B_1K=AB=OA$ и $\angle A_1KB_1=\angle ABB_1=\angle OAA_1$ ; $\angle AA_1O=\angle KA_1B_1$ как вертикальные. Значит, по второму признаку $\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1$ . Лемма доказана.

Перейдем к доказательству теоремы. Пусть $OA=AB=BC$ , $a\parallel b\parallel c$ и нужно доказать, что $OA_1=A_1B_1=B_1C_1$ .

Таким образом, по данной лемме $OA_1=A_1B_1$ . Докажем, что $A_1B_1=B_1C_1$ . Проведем через точку $B_1$ прямую $d\parallel OC$ , причем пусть $d\cap a=D_1, d\cap c=D_2$ . Тогда $ABB_1D_1, BCD_2B_1$ — параллелограммы, следовательно, $D_1B_1=AB=BC=B_1D_2$ . Таким образом, $\angle A_1B_1D_1=\angle C_1B_1D_2$ как вертикальные, $\angle A_1D_1B_1=\angle C_1D_2B_1$ как накрест лежащие, и, значит, по второму признаку $\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1$ .

Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство

Пусть параллельные прямые $p\parallel q\parallel r\parallel s$ разбили одну из прямых на отрезки $a, b, c, d$ . Тогда вторую прямую эти прямые должны разбить на отрезки $ka, kb, kc, kd$ соответственно, где $k$ – некоторое число, тот самый коэффициент пропорциональности отрезков.

Проведем через точку $A_1$ прямую $p\parallel OD$ ($ABB_2A_1$ — параллелограмм, следовательно, $AB=A_1B_2$ ). Тогда $\triangle OAA_1 \sim \triangle A_1B_1B_2$ по двум углам. Следовательно, $\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb$ .

Аналогично проведем через $B_1$ прямую $q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc$ и т.д.

\[{\Large{\text{Средняя линия треугольника}}}\]

Определение

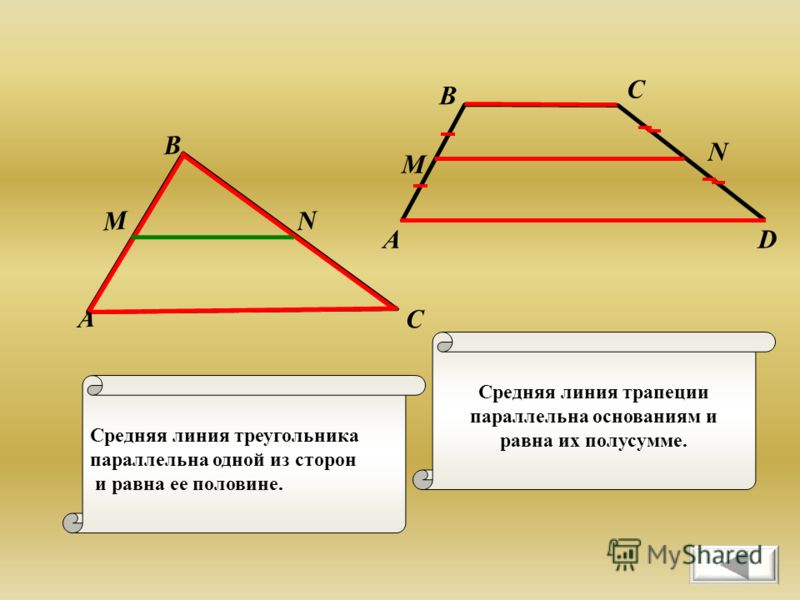
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.

Теорема

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Доказательство

1) Параллельность средней линию основанию следует из доказанной выше леммы .

2) Докажем, что $MN=\dfrac12 AC$ .

Через точку $N$ проведем прямую параллельно $AB$ . Пусть эта прямая пересекла сторону $AC$ в точке $K$ . Тогда $AMNK$ — параллелограмм ($AM\parallel NK, MN\parallel AK$ по предыдущему пункту). Значит, $MN=AK$ .

Т.к. $NK\parallel AB$ и $N$ – середина $BC$ , то по теореме Фалеса $K$ – середина $AC$ . Следовательно, $MN=AK=KC=\dfrac12 AC$ .

Следствие

Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом $\frac12$ .

Средняя линия треугольника — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Средняя линия треугольника

Средней линией треугольника называется
соединяющий середины двух его сторон.
отрезок,

2. Теорема о средней линии треугольника

Теорема. Средняя линия треугольника параллельна
одной из его сторон и равна ее половине.
Доказательство. Пусть DE – средняя
линия треугольника АВС. Докажем, что
DE параллельна АВ и равна ее
половине. Отложим на прямой DE
отрезок EF = DE и соединим отрезком
точки B и F.
Треугольники ECD и EBF равны по первому признаку равенства
треугольников.

Следовательно, BF = CD, значит, BF = AD. Угол 3
равен углу 4, значит, прямые AC и BF параллельны. Таким
образом, по признаку параллелограмма, четырехугольник ABFD –
параллелограмм. Итак, сторона АВ параллельна и равна стороне
DF. Средняя линия DE равна половине DF и, следовательно,
половине АВ.

3. Упражнение 1

Проведите средние линии треугольника ABC,
изображенного на рисунке.
Ответ:

4. Упражнение 2

Изобразите треугольник, середины
которого отмечены на рисунке.
Ответ:
сторон

5. Упражнение 3

Изобразите треугольник, середины
которого отмечены на рисунке.
Ответ:
сторон

6. Упражнение 4

Углы треугольника равны 50о, 60о и 70о. Найдите
углы треугольника, вершинами которого
являются
середины
сторон
данного
треугольника.
Ответ: 50о, 60о и 70о.

7. Упражнение 5

Стороны треугольника равны 8 см, 10 см и 12
см. Найдите стороны треугольника, вершинами
которого являются середины сторон данного
треугольника.

Ответ: 4 см, 5 см и 6 см.

8. Упражнение 6

Стороны треугольника равны 2 см, 3 см и 4 см.
Его вершины являются серединами сторон
второго треугольника. Найдите периметр
второго треугольника.
Ответ: 18 см.

9. Упражнение 7

Периметр треугольника равен 12 см, середины
сторон соединены отрезками. Найдите периметр
получившегося треугольника.
Ответ: 6 см.

10. Упражнение 8

Периметр равностороннего треугольника равен
72 см. Найдите его среднюю линию.
Ответ: 12 см.

11. Упражнение 9

Периметр треугольника равен 12 см. Найдите
периметр треугольника, отсекаемого от данного
какой-нибудь его средней линией.
Ответ: 6 см.

12. Упражнение 10

Средняя линия равнобедренного треугольника,
параллельная основанию, равна 3 см. Найдите
стороны треугольника, если его периметр равен
16 см.
Ответ: 5 см, 5 см, 6 см.

13. Упражнение 11

Через вершины треугольника проведены
прямые, параллельные его противоположным
сторонам.

Найдите периметр треугольника,
ограниченного этими прямыми, если периметр
исходного треугольника равен 6 см.
Ответ. 12 см.

14. Упражнение 12

Диагонали четырехугольника равны а и b.
Найдите
периметр
четырехугольника,
вершинами которого являются середины сторон
данного четырехугольника.
Ответ: a + b.

15. Упражнение 13

В прямоугольнике меньшая сторона равна 20 см
и образует с диагональю угол в 60о. Середины
сторон
прямоугольника
последовательно
соединены. Найдите периметр полученного
четырехугольника.
Ответ: 80 см.

16. Упражнение 14

Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Решение: Пусть ABCD – четырехугольник, E, F, G, H – середины его
сторон. Проведем диагональ AC. EF – средняя линия треугольника
ABC и, следовательно, параллельна AC и равна ее половине.
Аналогично, HG – средняя линия треугольника ACD и,
следовательно, параллельна AC и равна ее половине.

Таким
образом, стороны EF и HG четырехугольника EFGH равны и
параллельны. Значит, этот четырехугольник – параллелограмм.

17. Упражнение 15

Докажите, что середины сторон
являются вершинами ромба.
прямоугольника
Решение. Пусть ABCD – прямоугольник, E, F, G, H – середины
соответствующих сторон. Проведем диагонали AC и BD.
Отрезок EF является средней линией треугольника ABC,
следовательно, он равен половине диагонали AC. Аналогично,
остальные стороны четырехугольника EFGH равны половинам
соответствующих диагоналей. Так как диагонали
прямоугольника равны, то равны и стороны этого
четырехугольника, т.е. он является ромбом.

18. Упражнение 16

Докажите, что середины сторон ромба являются
вершинами прямоугольника.
Решение. Пусть ABCD – ромб, E, F, G, H – середины
соответствующих сторон. Проведем диагонали AC и BD.
Отрезок EF является средней линией треугольника ABC,
следовательно, он параллелен диагонали AC.

Аналогично,
остальные стороны четырехугольника EFGH параллельны
соответствующим диагоналям. Так как диагонали ромба
перпендикулярны, то перпендикулярны и соседние стороны этого
четырехугольника, т.е. он является прямоугольником.

19. Упражнение 17

Вершинами какого четырехугольника
середины сторон квадрата?
Ответ. Квадрата.
являются

English Русский Правила

Что такое теорема о средней линии? – Reviews Wiki

Теорема о средней линии утверждает, что разрезание по средней линии треугольника создает отрезок, параллельный основанию и вдвое длиннее . … Два треугольника должны иметь одинаковый размер и форму, поэтому все три стороны имеют одинаковую длину и все три угла имеют одинаковую меру.

Аналогично, что такое теорема о средней точке класса 10? Теорема о средней точке утверждает, что ” Отрезок в треугольнике, соединяющий середины двух сторон треугольника, называется параллельным его третьей стороне, а также составляет половину длины третьей стороны ».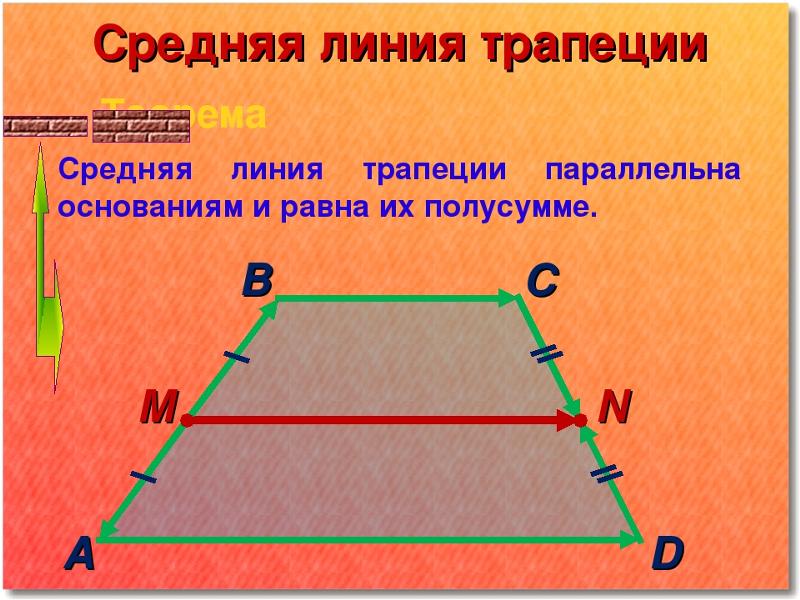

Во-вторых Что такое теорема подобия? В евклидовой геометрии: Подобие треугольников. Фундаментальная теорема подобия утверждает , что отрезок прямой делит две стороны треугольника на пропорциональные отрезки тогда и только тогда, когда этот отрезок параллелен третьей стороне треугольника.

Что такое 9-й класс теоремы о средней точке?

Эта теорема утверждает, что -й отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и составляет ее половину ”

то Что такое середина CV? Середина относится к точке, которая находится в середине линии, соединяющей две точки. Две опорные точки являются конечными точками линии, а средняя точка лежит между двумя точками.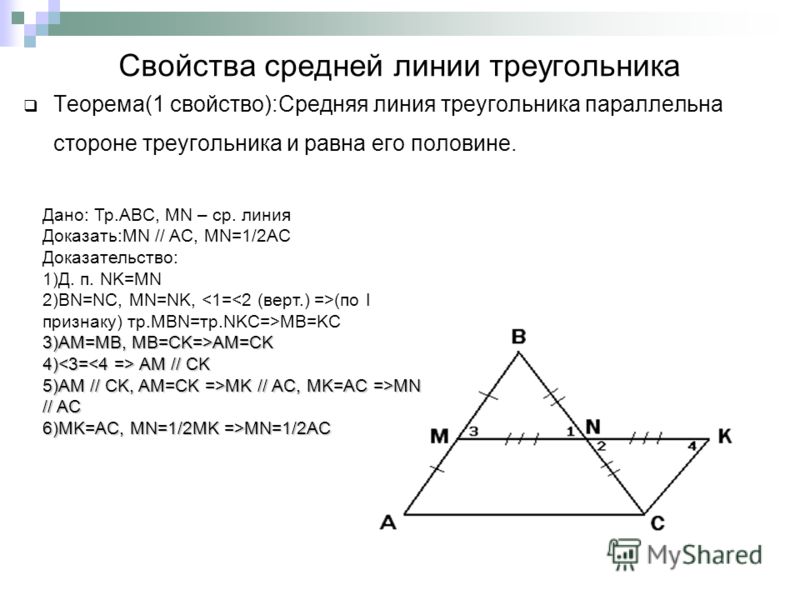
…
Формула средней точки.

1.	Что такое средняя точка?
4.	Формулы, относящиеся к средней точке
5.	Часто задаваемые вопросы

Кто изобрел теорему о средней точке? Архимед «Теорема о средней точке» — из Wolfram MathWorld.

Что такое средняя линия треугольника?

Каждая сторона медиального треугольника называется средним сегментом (или средней линией). В общем случае середина треугольника — это отрезок, соединяющий середины двух сторон треугольника. Он параллелен третьей стороне и имеет длину, равную половине длины третьей стороны.

Какой сегмент является средней линией? середина треугольника (также называемая средней линией) — это отрезок, соединяющий середины двух сторон треугольника.

Почему важно изучать теорему Ближний?

Эта теорема позволяет нам доказать некоторые вещи о треугольнике .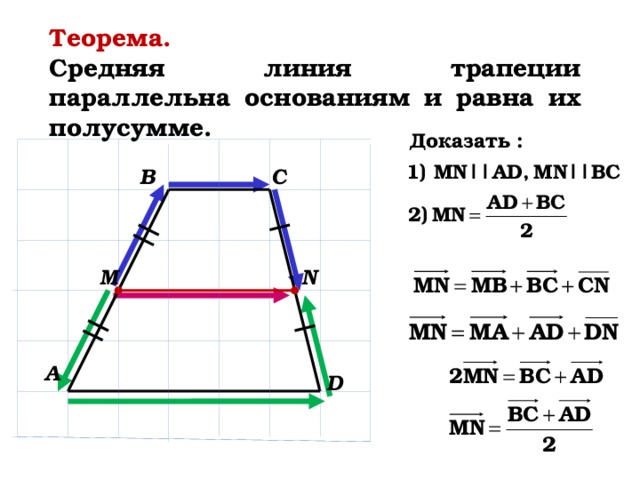 Во-первых, если мы знаем длину TV, то можем вычислить длину RS, и наоборот, поскольку RS = ½(TV). Это также позволяет нам найти длины AS, VS, TR и AR.

Что такое средняя линия в геометрии?

Каждая сторона медиального треугольника называется средним сегментом (или средней линией). В общем, средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника . Он параллелен третьей стороне и имеет длину, равную половине длины третьей стороны.

Каковы 3 условия подобия?

Эти три теоремы, известные как Угол — Угол (AA), Сторона — Угол — Сторона (SAS) и Сторона — Сторона — Сторона (SSS) , являются надежными методами определения сходства в треугольниках.

Что такое теорема подобия ААА? Евклидова геометрия

может быть переформулирована как теорема подобия ААА (угол-угол-угол): соответствующие углы двух треугольников равны тогда и только тогда, когда их соответствующие стороны пропорциональны .

В какой главе находится теорема о средней точке?

Теорема 8.9 – Глава 8 Класс 9 Четырехугольники (Термин 2)

Какова середина линии с концами 3 4 и 10 5? Середина линии (-3, 4) и (10, -5) равна (7/2, -1/2) .

Почему важна средняя точка?

Формула средней точки применяется , когда требуется найти точную центральную точку между двумя определенными точками . Таким образом, для линейного сегмента используйте эту формулу для вычисления точки, которая делит пополам линейный сегмент, определяемый двумя точками.

Сколько средних точек в утверждении? Отрезок прямой имеет ровно одну среднюю точку .

Как доказать теорему BPT?

Давайте теперь сформулируем основную теорему пропорциональности, которая выглядит следующим образом:

Если провести прямую, параллельную одной стороне треугольника, пересекающую две другие стороны в различных точках, то две другие стороны делятся в том же отношении.
Таким образом, основная теорема о пропорциональности доказана.
Значит, доказано.

Что такое теорема о равнобедренном треугольнике? Если две стороны треугольника равны, то и углы, лежащие против этих сторон, равны.

Как найти теорему о средней линии треугольника?

Как работают средние сегменты? — All Famous Faqs

Средняя линия треугольника определяется как отрезок, образованный соединением средних точек любых двух сторон треугольника. Проще говоря, делит две стороны треугольника на поровну. Середина стороны делит сторону на два равных отрезка.

Как вы используете теорему о средней линии?

https://www. youtube.com/watch?v=Wkq8jQ-43vw

Почему работает теорема о срединном отрезке?

Теорема о среднем отрезке утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче . А поскольку у треугольника три стороны, значит, у треугольника есть и три середины. Но на этом удивительность заканчивается!

Что такое средние сегменты?

Середина — это отрезок, соединяющий середины двух сторон треугольника . Поскольку у треугольника три стороны, каждый треугольник имеет три середины. Средняя линия треугольника параллельна третьей стороне треугольника и составляет половину длины третьей стороны.

Какие две вещи говорит нам теорема о срединном отрезке?

Теорема о средней линии утверждает, что средняя линия, соединяющая середины двух сторон треугольника, параллельна третьей стороне треугольника, а длина этой средней линии составляет половину длины третьей стороны .

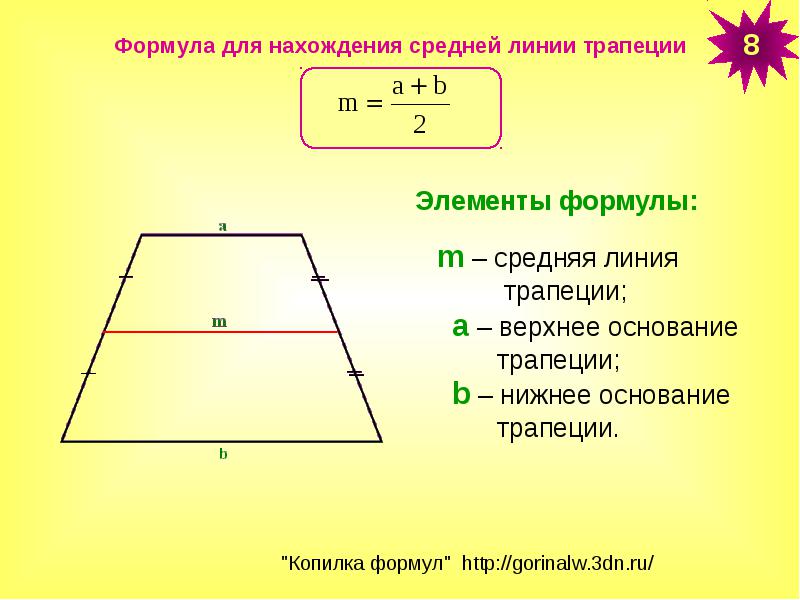
Как рассчитать средние сегменты?

Длина средней части сумма двух оснований, деленная на 2 .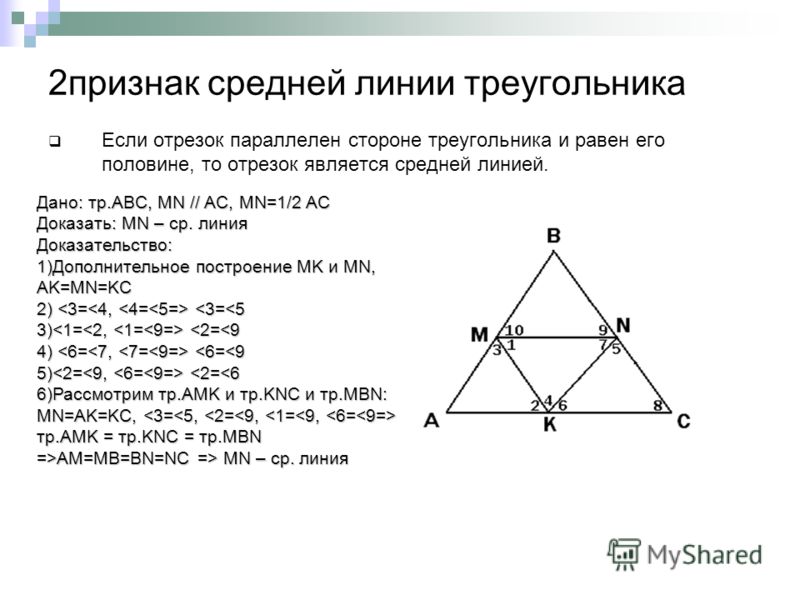 Помните, что основания трапеции – это две параллельные стороны.

Как устранить проблемы среднего сегмента?

Как доказать теорему о средней линии?

Доказательство этой теоремы — это просто использование свойств подобных треугольников и соответствующих углов для логического вывода, что оба свойства теоремы верны. Если в треугольнике ABC соединить середины D и E любых двух сторон, то верны следующие факты: AD = BD и CD = BE.

Совпадают ли средние сегменты треугольника?

Все четыре типа линий или отрезков внутри треугольников являются параллельными , что означает, что три медианы треугольника имеют общие точки пересечения, как и три высоты, средние сегменты, биссектрисы угла и биссектрисы перпендикуляра. Точка пересечения называется точкой совпадения.

Почему важно изучать теорему о средней линии?

Теорема о средней точке используется для получения конкретной информации о длинах сторон треугольников . Теорема о средней точке утверждает, что отрезок, соединяющий две стороны треугольника в середине этих сторон, параллелен третьей стороне и составляет половину длины третьей стороны.

Что такое теорема о средней точке доказать это?

Доказательство теоремы о средней точке

Если отрезок прямой пересекает середины любой из сторон треугольника, то говорят, что отрезок параллелен всем остальным сторонам и измеряет примерно половину оставшихся сторон.

Сколько средних сегментов у трапеции?

Сколько средних сегментов у трапеции? У трапеции только одного срединного отрезка. Срединный отрезок — это линия, проходящая от одной непараллельной стороны к другой, параллельная основаниям и проходящая посередине между ними.

Средняя часть трапеции?

Середина трапеции параллельна каждому основанию , а ее длина составляет половину суммы длин оснований.

Что такое уравнение средней линии?

Для y = sin x средняя линия равна y = 0 (ось x). Средняя линия параллельна оси x и расположена посередине между максимальным и минимальным значениями графика. На среднюю линию влияют любые вертикальные переводы на график. Например, y = sin(x) + 2 имеет среднюю линию в точке y = 2.

Какова длина викторины на середине сегмента?

Средняя часть равна половине длины соответствующей стороны . Средняя линия соединяет середины двух сторон треугольника.

Как решить треугольник со средними сегментами?

Что такое постулат подобия SAS?

Устанавливает ли теорема о середине треугольника конгруэнтные сегменты?

Поскольку средние сегменты составляют половину длины сторон, которым они параллельны, они конгруэнтны половине каждой из сторон (как отмечено).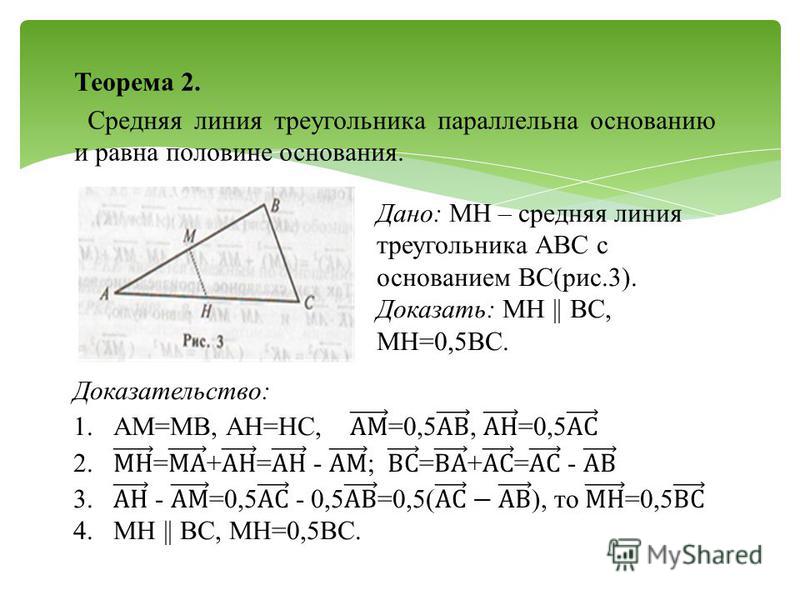 Кроме того, это означает, что все четыре треугольника в @$begin{align*}треугольнике ABCend{align*}@$, созданные средними сегментами, конгруэнтны SSS.

Что такое теорема подобия?

Основная теорема подобия утверждает, что отрезок прямой делит две стороны треугольника на пропорциональные отрезки тогда и только тогда, когда отрезок параллелен третьей стороне треугольника .

Какова длина среднего сегмента?

Пояснение: Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника. Этот сегмент имеет два особых свойства. Он всегда параллелен третьей стороне, а длина его середины составляет и составляет половину длины третьей стороны .

Является ли средний сегмент половиной основания?

Средняя часть составляет половину длины основания .

Как найти недостающую сторону треугольника?

если сторона а отсутствует, то преобразуем уравнение к виду, когда а находится на одной стороне, и извлекаем квадратный корень: а = √(c² – b²)
если ветвь b неизвестна, то. б = √(с² – а²)
для гипотенузы c отсутствует, формула есть. с = √(а² + b²)

Что говорит теорема об угле при основании?

Теорема об углах при основании утверждает, что в равнобедренном треугольнике углы, противоположные конгруэнтным сторонам, равны .

Что вы узнали о теореме о средней линии?

Теорема о средней линии — это теорема о треугольнике, которая утверждает, что отрезок, соединяющий две середины треугольника, будет параллелен третьей стороне, а длина среднего отрезка будет равна половине длины третьей стороны .

Образуют ли середины прямые углы?

По определению середины отрезок AD конгруэнтен отрезку BD. Отрезок DE параллелен отрезку AC, поэтому угол и угол ADE равны . Это делает треугольник ADE и треугольник BDE прямоугольными.

Что верно в теореме о средней линии?

Отрезок, соединяющий середины двух сторон треугольника, равен третьей стороне . Б. Отрезок, соединяющий середины двух сторон треугольника, равен половине длины третьей стороны и перпендикулярен ей.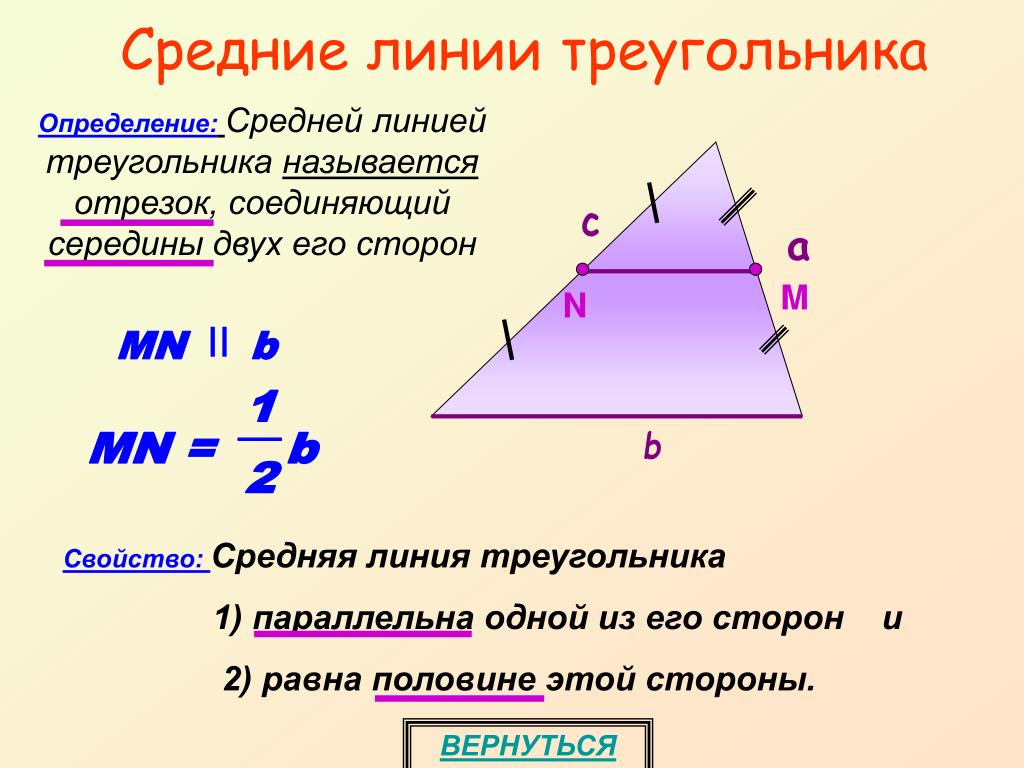

Что такое теорема о средней точке и обратная ей класс 9?

Что такое обратная теорема о средней точке? Линия, проведенная через середину одной стороны треугольника параллельно основанию треугольника, делит пополам третью сторону треугольника .

Как узнать срок действия степени?

Период функций синуса и косинуса составляет 2π (пи) радиан или 360 градусов . Для функции тангенса период составляет π радиан или 180 градусов.

Что такое теорема о средней линии трапеции?

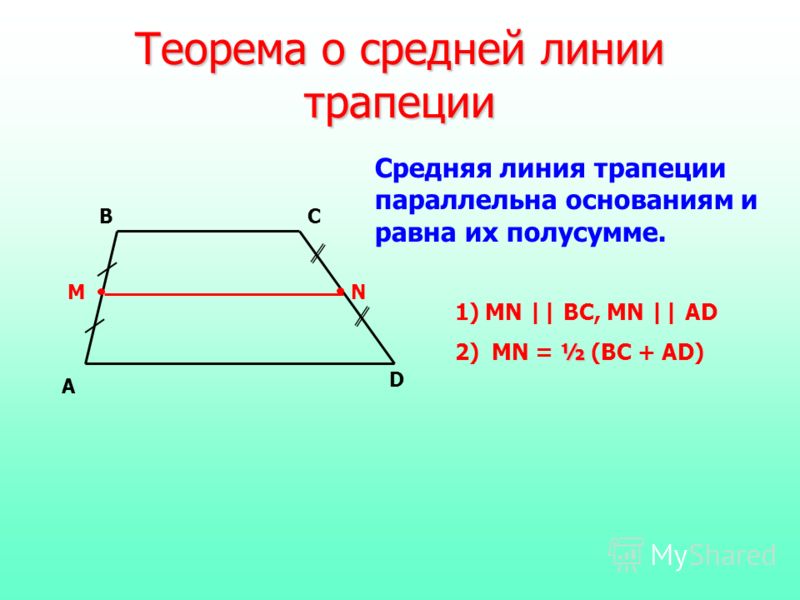
Теорема 1: Если прямая, проходящая через середину катета трапеции, параллельна ее основаниям, то эта прямая проходит через середину другого катета. Теорема 2: Середина трапеции равна половине длины двух параллельных сторон .

Что такое формула среднего сегмента трапеции?

Средняя часть трапеции параллельна каждому основанию, а ее длина составляет половину суммы длин оснований. Если MN — середина трапеции ABCD, то MN||AB и MN||DC и МН = 2(AB+CD) .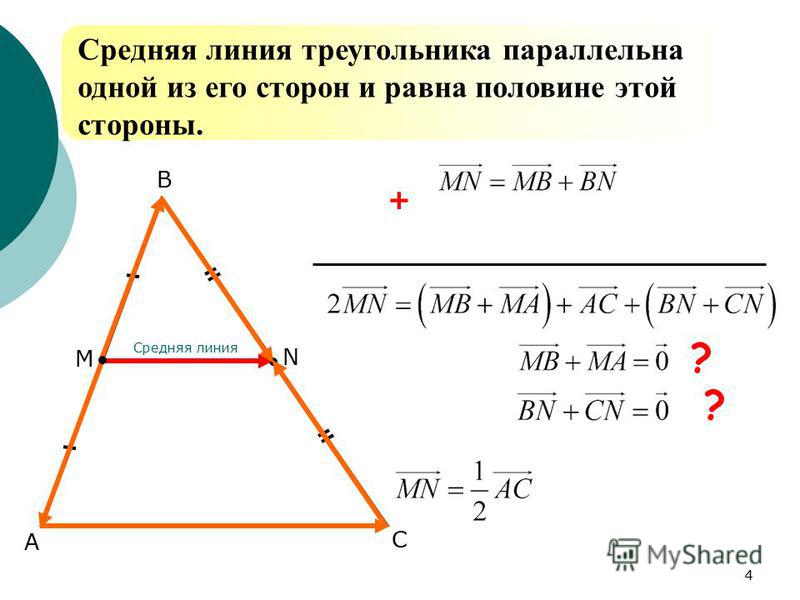

Что такое амплитуда и средняя линия?

Амплитуда — это расстояние по вертикали от средней линии до минимума или максимума . Итак, если вам дан минимум, добавьте амплитуду к координате y.

Представляет ли средняя линия среднее значение?

Напомним, что средняя линия описывает среднее или среднее значение синусоидальной функции .

Какой отрезок соединяет середины непараллельных сторон трапеции?

Середина трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции. Середина трапеции параллельна множеству параллельных прямых трапеции и равна среднему значению длин оснований.

EF выглядит параллельно основанию трапеции?

EF — прямая, параллельная основаниям (EF||AB||CD), образующая две подобные трапеции: ABFE ∼ EFCD. Найдите формулу длины FE через длины AB и CD.

Является ли трапеция параллелограммом?

У трапеции одна пара параллельных сторон, а у параллелограмма две пары параллельных сторон. Таким образом, параллелограмм также является трапецией .

Какие стороны трапеции?

Катетами трапеции являются непараллельные стороны . Медиана трапеции — это отрезок, соединяющий середины двух катетов. Высота трапеции — это отрезок перпендикулярной прямой из вершины одного основания к другому основанию (или к продолжению этого основания).

Что верно для любой средней линии треугольника?

Средняя часть вдвое короче соответствующей стороны . Средняя линия соединяет середины двух сторон треугольника. Средний сегмент в два раза длиннее соответствующей стороны.

Что такое теорема о шарнирах в геометрии?

Геометрия. Теорема о шарнирах утверждает, что если две стороны двух треугольников равны, а прилежащие к ним углы различны, то больший угол лежит против более длинной стороны .

Как работает подобие SAS?

Теорема подобия SAS утверждает, что если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а прилежащие к ним углы конгруэнтны, то эти два треугольника подобны . Преобразование подобия — это одно или несколько жестких преобразований, за которыми следует расширение.

Что такое критерий подобия SSS?

Критерий сходства треугольников SSS утверждает, что если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны .

Что такое сходство SSS?

Критерий сходства треугольников SSS утверждает, что если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны .

Средние сегменты параллельны основанию?

Теорема о средней линии треугольника говорит нам, что средняя линия равна половине длины третьей стороны (основания) и также параллельна основанию .

Средние сегменты параллельны?

Средняя линия, соединяющая две стороны треугольника, параллельна третьей стороне и вдвое короче.

Что такое теорема бокового делителя?

Теорема о делителях сторон Если прямая параллельна одной стороне треугольника и пересекает две другие стороны, то она делит эти стороны пропорционально .

Как вы делаете средние сегменты?

Какими двумя способами средний сегмент связан с противоположным сегментом в треугольнике?

Обратите внимание, что здесь есть две важные идеи. Один из них заключается в том, что средняя линия параллельна стороне треугольника . Другая состоит в том, что средний сегмент всегда составляет половину длины этой стороны.

Как найти меру среднего сегмента?

Как решить теорему подобия?

1. Если отрезок параллелен одной стороне треугольника и пересекает две другие стороны, то образованный треугольник подобен исходному и отрезок, который делит две пересекаемые стороны, пропорционален. 2. Если три параллельные прямые пересекают две секущей, то они делят секущую пропорционально.

Как доказать теорему подобия?

Если две пары соответствующих углов в паре треугольников равны, то треугольники подобны .