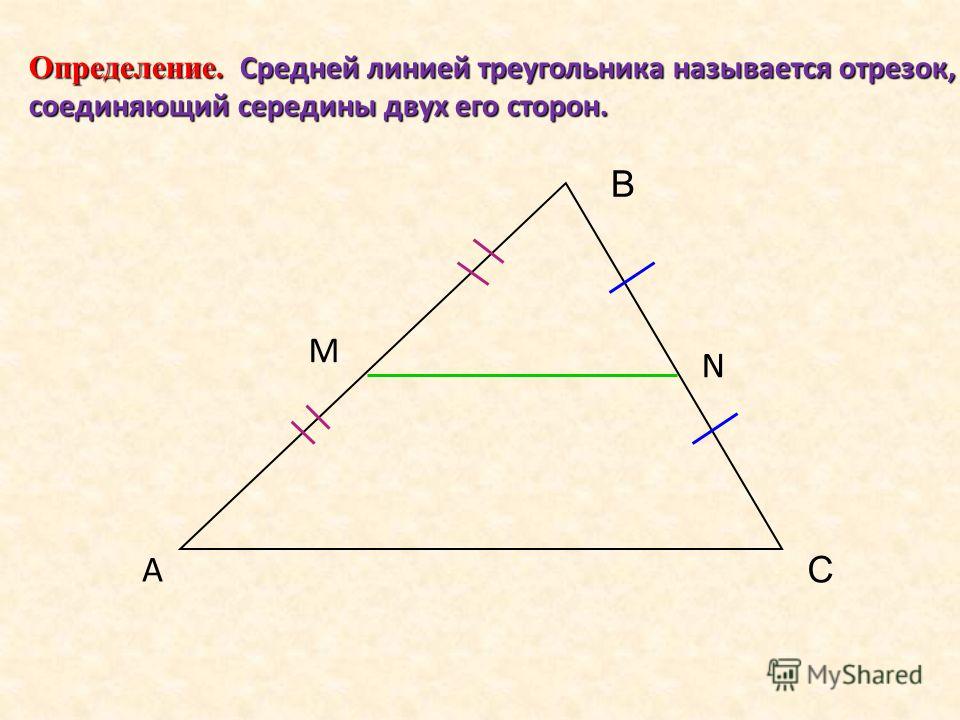
Средняя линия треугольника
Урок 21. Геометрия 8 класс ФГОС
На этом уроке мы введем понятие средней линии треугольника. Изучим её свойства. Рассмотрим, каким свойством обладают медианы треугольника. А также закрепим полученные знания при решении задач различного уровня сложности.
Конспект урока «Средняя линия треугольника»
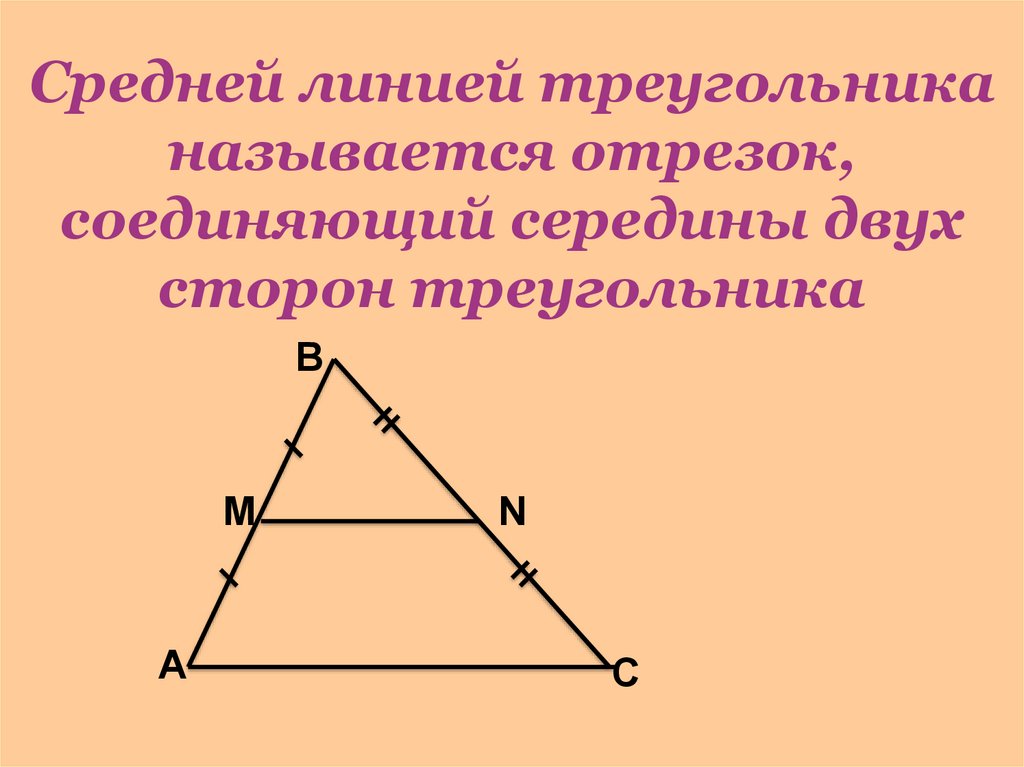
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Пользуясь этим определением, изобразим для прямоугольного, остроугольного и тупоугольного прямоугольников по одной средней линии.
Попробуем ответить на вопрос. Как средняя линия расположена относительно третьей стороны треугольника?
Похоже, что они параллельны. А теперь измерим линейкой каждую среднюю линию и параллельные им стороны треугольников.
Получаем, что каждая средняя линия в два раза меньше
параллельной ей стороны треугольника.
Действительно имеют место следующие свойства.
Теорема. Средняя линия треугольника параллельна одной из его сторон
и равна половине этой стороны.
Доказательство.
средняя линия
Что и требовалось доказать.
Задача. Укажите, какие из изображённых отрезков являются средними линиями,
и найдите их длину.
Решение.
Решим ещё одну задачу.
Задача. Дан треугольник, стороны которого соответственно равны см, см и см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Решение.
Ответ: 14 см.
Задача. Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении два к одному, считая от вершины
Доказательство.
1. 𝐴_1 𝐵_1∥𝐴𝐵
2. △𝐴𝑂𝐵∼△𝐴_1 𝑂𝐵_1 (по двум углам)
⟹ 𝐴𝐵/(𝐴_1 𝐵_1 )=𝐴𝑂/(𝐴_1 𝑂)=𝐵𝑂/(𝐵_1 𝑂)=2
3. 𝐴𝑂:𝑂𝐴_1=𝐵𝑂:𝑂𝐵_1=2:1
4. Аналогично п.1-3:𝐵𝑀:𝑀𝐵_1=𝐶𝑀:𝑀𝐶_1=2:1
5. Точка 𝑀 совпадает с точкой 𝑂 ⟹𝐴𝐴_1∩𝐵𝐵_1∩𝐶𝐶_1=𝑂
Решим ещё несколько задач.
Задача. В треугольнике , через точки и — середины отрезков и соответственно, проведена прямая .. Найти и .
Решение.
1. 𝐾𝑀−средняя линия (по определению)
2. 𝐴𝐵=8 см, 𝐵𝐶=12 см
Ответ: 8 см, 16 см.
Задача. В четырёхугольнике ABCD точки M, N, P и Q являются серединами сторон AB, BC, CD и AD соответственно. Докажите, что MNPQ — параллелограмм.
Решение.
:
:
:
Что и требовалось доказать.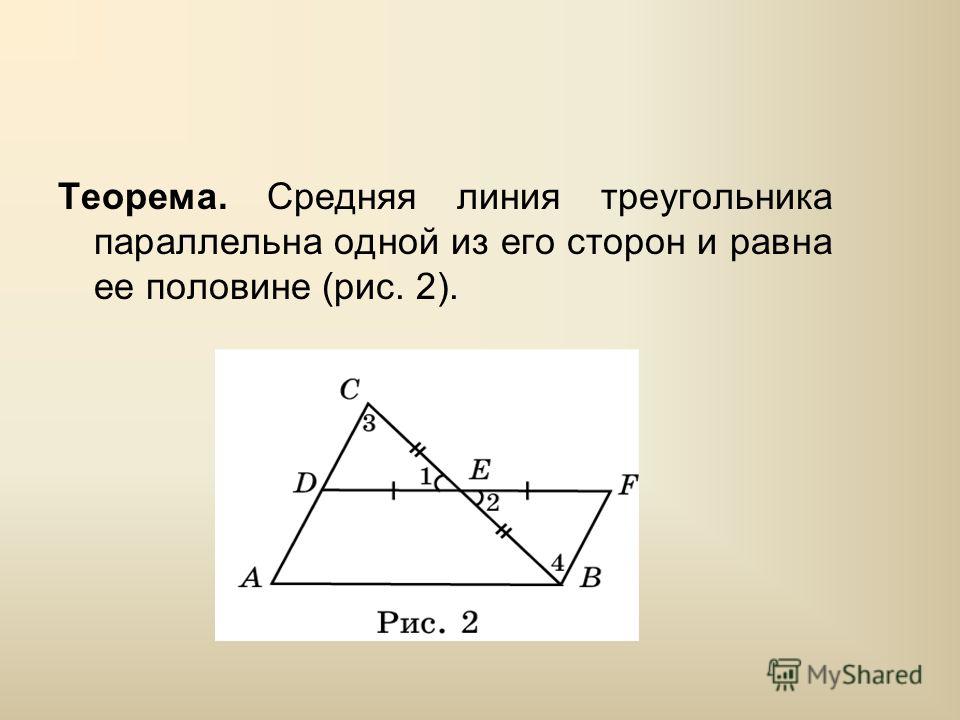
Подведём итоги урока.
Сегодня вы узнали, что средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С помощью этой теоремы мы также доказали, что медианы любого треугольника пересекаются в одной точке, которая делит каждую медиану в отношении два к одному, считая от вершины.
Полученные знания мы применили при решении задач.
Предыдущий урок 20 Третий признак подобия треугольников
Следующий урок 22 Пропорциональные отрезки в прямоугольном треугольнике
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Средняя линия треугольника
Методическая разработка урока математики в 8 классе. Тема урока «Средняя линия треугольника».
Тема урока «Средняя линия треугольника».
Тип урока: урок усвоения новых знаний
Цели урока:
Образовательные:
Развивающие:
совершенствовать графическую культуру.
Воспитательные:
Мотивировать детей к самообразованию.
Воспитывать интерес к геометрии, расширять кругозор учащихся
Прививать аккуратность в оформлении геометрических задач, культуру устной речи.
Оборудование, наглядность, электронные приложения к уроку:
Компьютер. Мультимедийный проектор. Документ камера.
Презентация Microsoft PowerPoint.
Структура урока.
Вид деятельности. | № слайдов. | мин. |
1. | 1-3 | 2 |
2. Проверка домашнего задания | 2 | |
3. Повторение изученного материала. Признаки подобия треугольников. | 4-6 | 3 |
4. Понятие средней линии треугольника и её свойство. Математический диктант | 7-9 10-14 | 12 |
5. Физкультминутка. | 1 | |
6. Свойство медиан треугольника. Следствия. | 15-17 18-21 | 15 |
7. Закрепление нового материала. Решение задач. | 22-23 | 8 |
8. | 24 | 2 |
9. Домашнее задание. | 25 | 1 |
Ход урока.
1. Вступительное слово учителя.
Эпиграфом к сегодняшнему уроку взяты слова французского писателя XIX столетия. Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом” (сайд №2).
Давайте последуем совету писателя и на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Многие известные мыслители и писатели прошлого обращались к темам о замечательных точках и линиях треугольника. Сегодня мы тоже займемся этим интересным исследованием.
Тема нашего урока «Средняя линия треугольника». Давайте сформулируем, какие цели мы должны достичь: (учащиеся самостоятельно формулируют цели, слайд №3)
Дать определение средней линии треугольника.

Доказать теорему о средней линии треугольника.
Доказать теорему о пересечении медиан треугольника.
2. Проверка домашнего задания.
С помощью документ камеры решение домашнего задания (№ 568 б) из тетради учащегося проектируется на экран. Учащийся комментирует решение.
3. Устная работа. Повторение изученного материала.
Цель: систематизировать базовые знания по теме «Подобие треугольников»; развивать логическое мышление; формировать умение четко и ясно излагать свои мысли.
Чтобы успешно выполнить цели сегодняшнего урока, нам не раз придется обращаться к признакам подобия треугольников. Какие признаки подобия треугольников вы знаете? Учащиеся формулируют признаки подобия треугольников (слайд 4-6).
4. Понятие средней линии треугольника и ее свойства.
Цели: сформулировать определение средней линии треугольника и доказать ее свойство; развивать умение сравнивать и анализировать.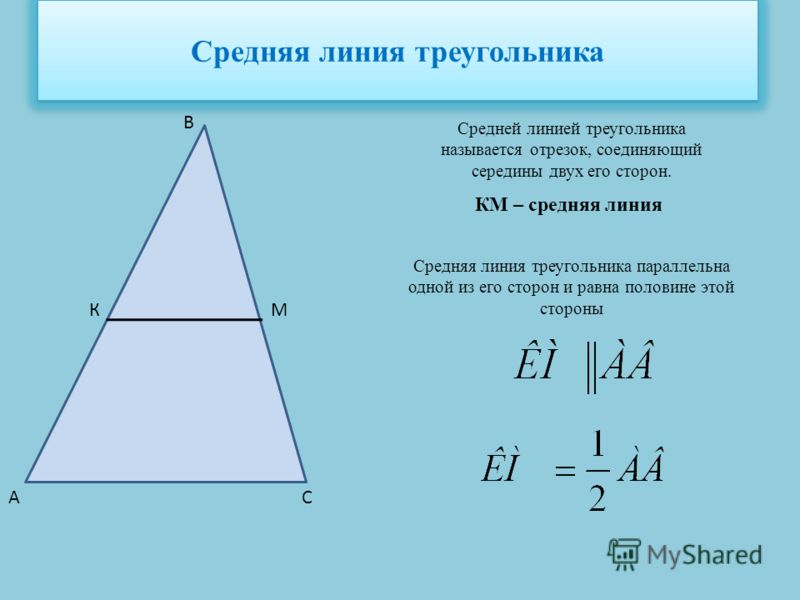
— Что общего у треугольников, изображенных на рисунке? (слайд №7)
Учащиеся самостоятельно дают определение средней линии треугольника(слайд №8).
— Сколько средних линий можно построить в треугольнике?
—Средняя линия треугольника — это замечательная линия треугольника. А чем же она замечательна? Давайте сформулируем и докажем свойство средней линии треугольника (слайд №9).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно). С целью закрепления понятия и свойства средней линии треугольника проводится математический диктант (решение задач по готовым чертежам; слайд № 10-14). Учащиеся получают карточки, выполняют математический диктант.
Математический диктант
Вариант 1 | Вариант 2 |
1)Две стороны треугольника соединили отрезком, непараллельным третьей стороне. | 1)Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ? |
2)В ∆АВС сторона АВ=7 см. Чему равна средняя линия треугольника, параллельная этой стороне? | 2)Средняя линия треугольника АВD, параллельная стороне ВD, равна 4 см. Чему равна сторона ВD? |
3) Дано: МК=3, KN=4, MN=5. Найти периметр треугольника АВС. | 3) Дано: АВ=3м, ВС=5м, АС=4м. Найти периметр треугольника MNK. |
4) Концы отрезка АВ лежат на сторонах треугольника, а его длина равна половине третьей стороны. Обязательно ли: АВ – средняя линия этого треугольника? | 4)Концы отрезка MN лежат на сторонах треугольника. Отрезок MN параллелен третьей стороне и равен его четверти. Обязательно ли: MN – средняя линия этого треугольника? |
5) Периметр треугольника равен 5,9 см. Найти периметр треугольника, отсекаемого одной из его средних линий. | 5)Периметр треугольника равен 7,3 см. Найти периметр треугольника, отсекаемого одной из его средних линий. |
5. Физкультминутка
6. Свойство медиан треугольника
Цель: развивать логическое мышление; способность к исследовательской деятельности, к синтезу и анализу.
Вспомните, что называется медианой треугольника? (слайд №15) Укажите рисунок, на котором изображена медиана.
Свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины (слайд № 16).
Теорему учащиеся доказывают самостоятельно (задание получено сильным учащимся предварительно).
-Медиану тоже считают замечательной линией треугольника. Как вы считаете, почему? Вспомните, какие треугольники называются равновеликими (слайд 17)?Давайте, исследуем следующие предположения. В треугольнике провели медиану. Как изменится площадь? (слайд № 18)
Утверждение: медиана треугольника делит его на два равновеликих треугольника. |
—В параллелограмме, площадь которого равна S, проведены диагонали. Чему равны площади образовавшихся треугольников (слайд №19)?
Следствие 1: диагонали параллелограмма делят его на четыре равновеликих треугольника.
— В треугольнике проведены три медианы. Являются ли они равновеликими (слайд № 20)?
Следствие 2: медианы треугольника делят его на шесть равновеликих треугольников.
— В треугольнике проведены средние линии. Чему равна площадь треугольника BMN (слайд № 21)?
Следствие 3: средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного треугольника.
7. Закрепление нового материала. Решение задач
Цель: научить учащихся применять приобретенные на уроке знания при решении задач; развивать логическое мышление; прививать аккуратность в оформлении геометрических задач; совершенствовать графическую культуру.
Задача 1. Медианы ВК и ЕМ, треугольника ВСЕ, пересекаются в точке О. Найти SMOK:SCMK (слайд №22).
Задача 2. Решите задачу устно по готовому чертежу (слайд № 23).
АА1, ВВ1, СС1 – медианы треугольника. Доказать:
|
8. Подведение итогов
Рефлексия.
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного.

Три средние линии треугольника разбивают его на 4 равоновеликих треугольника, площадь каждого из них равна ¼ площади исходного.
Оценки за урок.
9. Домашнее задание
П. 62, вопросы 8, 9 (стр. 160). Задачи № 616, 571.
Литература
Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений. / Л.С. Атанасян, В.Ф Бутузов, С.Б. Кадомцев и др. – 5-е изд. – М.: Просвещение, 1995. – 335 с.: ил. – ISBN 5-09-006554-3
Лысенко Ф. Ф. Математика. Подготовка к ЕГЭ. – Ростов – на –Дону: «Легион М», 2012.
Алтынов П.И. Геометрия. Тесты. 7-9 кл.
Гилярова М. Г. Поурочные разработки по геометрии: 8 класс. Волгоград: « Учитель — АСТ», 2003.
As4dspark
As4dsparkНазначение 4
по
Дэвид С.
 Парк
ПаркЧто такое центроид?
Центроид треугольника — это точка, в которой сходятся три медианы треугольника. Медиана треугольника — это отрезок прямой от одной вершины до середины противоположной стороны треугольника.
Центроид также называется центром тяжести треугольника. Если у вас треугольная тарелка, попробуйте сбалансировать тарелку на пальце. Как только вы найдете точку, в которой он будет балансировать, это будет центр тяжести этого треугольника.
Центр тяжести треугольника ABC
1. Совпадают ли три медианы?
Теперь кто-то может задать вопрос, откуда мы знаем, что три медианы действительно пересекаются в одной точке. Это очень хороший вопрос, и давайте проверим пару разных треугольников, чтобы убедиться, что это так. Нажмите ЗДЕСЬ , чтобы открыть файл GSP и поэкспериментировать самостоятельно.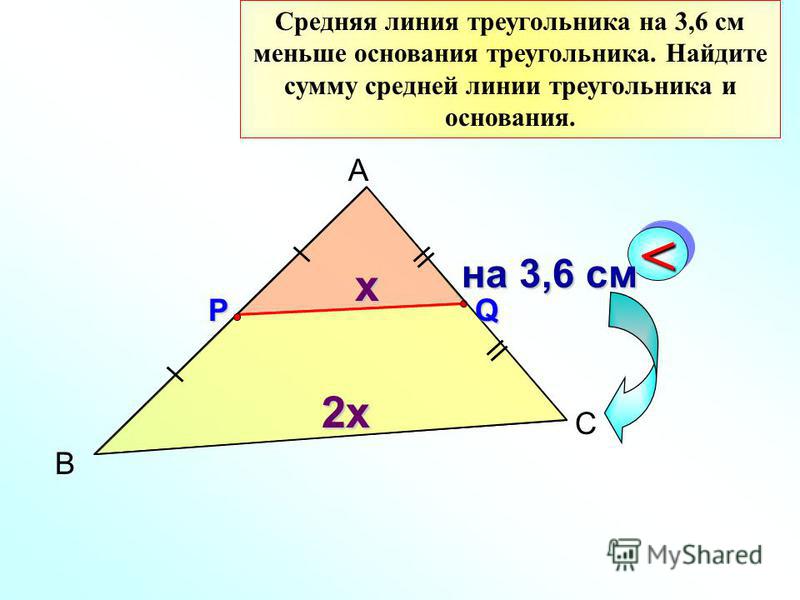
Чтобы проверить, совпадают ли три медианы, давайте сначала построим середины D, E и F на каждой стороне треугольника. Затем соединим точки B и E, C и F и обозначим точку пересечения G.
Затем построим луч из точки A в точку G и проверим, проходит ли этот луч (выделенный оранжевым цветом) через середину точки D для треугольников разной формы.
Проверка пересечения трех медиан в одной точке
Из этих образцов видно, что луч AG проходит точно через среднюю точку D, и три медианы действительно пересекаются в одной точке. Чтобы доказать совпадение трех медиан, нам нужно будет использовать теорему Чевы.
Теорема Чевы
Эта теорема была доказана Джованни Чева (1648-1734). Чтобы получить полное введение в эту теорему, НАЖМИТЕ ЗДЕСЬ , и чтобы увидеть доказательство теоремы Чевы, НАЖМИТЕ ЗДЕСЬ .
Теорема : В треугольнике ABC три прямые AD, BE и CF пересекаются в одной точке K тогда и только тогда, когда
Доказательство параллелизма трех медиан
Теперь, используя теорему Чевы, будет несложно доказать, что три медианы пересекаются в одной точке. Поскольку медианы делят каждую сторону треугольника пополам, отсюда следует, что AF = FB = 1/2, BD = DC = 1/2 и CE = EA = 1/2. Следовательно, AF/FB = 1, BD/DC = 1, CE/EA = 1, а произведение трех отношений равно 1,9.0003
Поскольку медианы делят каждую сторону треугольника пополам, отсюда следует, что AF = FB = 1/2, BD = DC = 1/2 и CE = EA = 1/2. Следовательно, AF/FB = 1, BD/DC = 1, CE/EA = 1, а произведение трех отношений равно 1,9.0003
2. Особое свойство центроида
Есть еще одна особенность центроида. Видите ли вы какие-либо закономерности на диаграммах ниже?
Вы видите что-нибудь особенное в Centroid?
Центроид делит каждую медиану в особом отношении 2:1. На диаграммах выше я вставил средние точки AG, BG и CG, чтобы упростить сравнение длин. Теперь докажем, что центроид делит каждую медиану в отношении 2:1.
ТеоремаЦентроид делит каждую медиану в отношении 2:1.
Доказательство:
Соединим две середины E и F,
Тогда треугольники AEF и ACB подобны, так как
Из этого следует, что поскольку треугольники AEF и ACB подобны, прямые EF и CB параллельны и CB = 2 * EF.
Теперь посмотрим на треугольники EGF и BGC. Поскольку прямые EF и CB параллельны,
Кроме того, угол GDE равен углу GBC, потому что они противоположны друг другу.
Таким образом, треугольники EGF и BGC подобны. Кроме того, поскольку CB = 2 * EF, это означает, что длины сторон треугольников BGC и EGF относятся как 2:1, и мы имеем
Аналогично, проведя прямую из точки D в F и используя два подобных треугольника DFG и AGC, мы можем доказать, что
Возвращение в дом Дэвида
Свойства треугольника | Бесплатная помощь с домашними заданиями
Свойства треугольника https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 ШколаРепетиторская Академия ШколаРепетиторская Академия https://secure.gravatar.com/avatar/983a20e95a059722e4981790f518b20b?s=96&d=mm&r=g
Треугольник:
Треугольник представляет собой замкнутую кривую, состоящую из трех отрезков. Отрезки, из которых образован треугольник, называются сторонами треугольника. Точки пересечения сторон треугольника называются вершинами треугольника. Углы, образованные при вершинах, называются углами треугольника.
Треугольник — это базовая форма, которая имеет несколько свойств, основанных на сторонах, внутренних углах и внешних углах.
а)
Медианы треугольника:Линия, проведенная из любой вершины к середине противоположной стороны, называется медианой относительно этой вершины. Таким образом, треугольник имеет 3 медианы, и все 3 медианы пересекаются в одной точке. то есть медианы треугольника совпадают.
Точка совпадения медиан называется центр тяжести треугольника.
Отрезок перпендикулярной линии, проведенный из вершины к противоположной стороне, называется высотой треугольника относительно этой вершины. Таким образом, треугольник имеет 3 высоты, и все 3 высоты пересекаются в одной точке. . то есть высот треугольника совпадают.
Точка совпадения высот называется ортоцентр треугольника.
c)
Биссектрисы углов:Биссектрисы углов треугольника пересекаются в одной точке. то есть биссектрисы треугольника совпадают.
Точка совпадения высот называется центром треугольника.
d)
Свойство внешнего угла:Внешний угол в треугольнике равен сумме двух противоположных внутренних углов.
Здесь ∠4 = ∠1 + ∠2.
e)
Свойство суммы углов: Сумма всех внутренних углов треугольника равна 180 0 .

 Постановка цели урока. Эпиграф к уроку.
Постановка цели урока. Эпиграф к уроку. Подведение итогов.
Подведение итогов.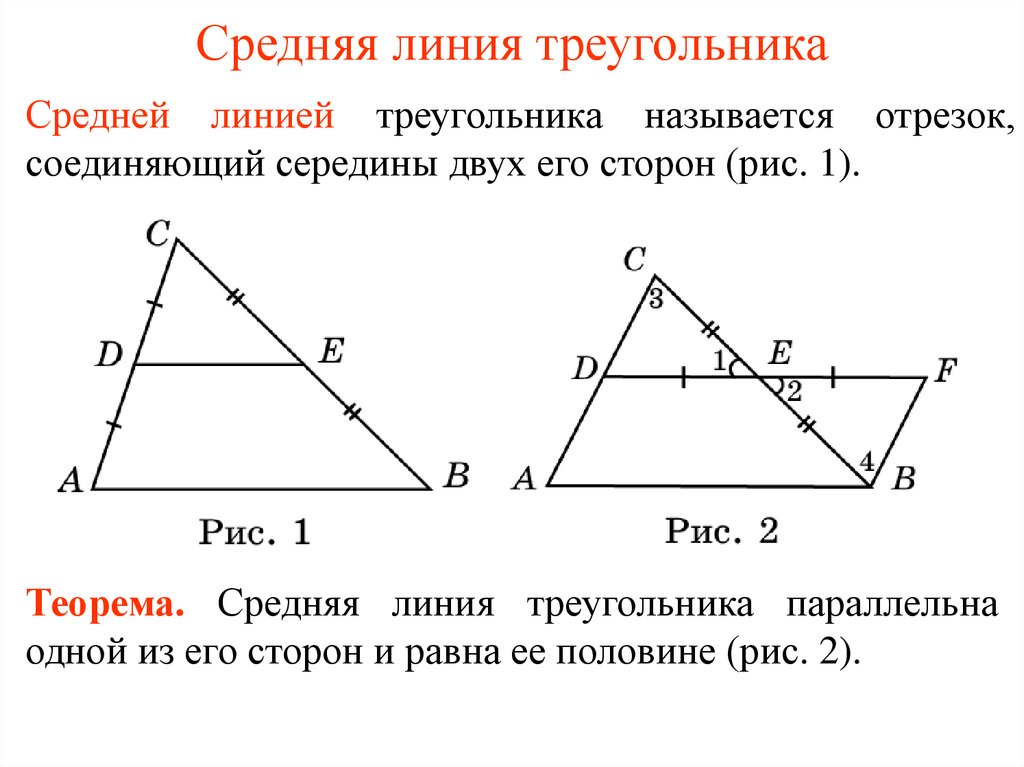
 Является ли этот отрезок средней линией данного треугольника?
Является ли этот отрезок средней линией данного треугольника?