самостоятельная работа «Степень числа» | Материал (5 класс):
Опубликовано 23.12.2021 — 9:45 — Зиборова Ирина Александровна
2 варианта
Скачать:
Предварительный просмотр:
Самостоятельная работа по теме «Степень числа» Вариант1 1. Сравните числа: а) 23 и 32 б) 42 и 32 в) 43 и 53 2.Вычислите: а)3 ∙ 42 ;б) (3 ∙ 8)2 ; в) 27 — 32 ; г) 250 — 53 ;д) (98 — 18)3∙18 ; е) 600 — 750 : 53 ; ж) 2 ∙ 152 + 5 3. Определите показатель степени числа и запишите его вместо звездочки: а) 8* = 512 б) 2* = 64 в) 6* = 1296 | Самостоятельная работа по теме «Степень числа» Вариант2 1. Сравните числа: а) 34 и 43 б) 62 и 53 в) 34 и 24 2. а)2 ∙ 52 ;б) (7 ∙ 2)2 в) 72 — 62 ;г) 352 — 53 д) (76 — 66)3∙23;е) 800 — 750 : 52 ж) 3 ∙ 132 — 15 3. Определите показатель степени числа и запишите его вместо звездочки: а) 3* = 81 б) 7* = 343 в) 5* = 3125 |
Самостоятельная работа по теме «Степень числа» Вариант1 1. Сравните числа: а) 23 и 32 б) 42 и 32 в) 43 и 53 2.Вычислите: а)3 ∙ 42 ; б) (3 ∙ 8)2 ; в) 27 — 32 ; г) 250 — 53 ; д) (98 — 18)3∙18 ; е) 600 — 750 : 53 ; ж) 2 ∙ 152 + 5 3. Определите показатель степени числа и запишите его вместо звездочки: а) 8* = 512 б) 2* = 64 в) 6* = 1296 | Самостоятельная работа по теме «Степень числа» Вариант2 1. а) 34 и 43 б) 62 и 53 в) 34 и 24 2.Вычислите: а)2 ∙ 52 ; б) (7 ∙ 2)2 в) 72 — 62 ; г) 352 — 53 д) (76 — 66)3∙23 ; е) 800 — 750 : 52 ж) 3 ∙ 132 — 15 3. Определите показатель степени числа и запишите его вместо звездочки: а) 3* = 81 б) 7* = 343 в) 5* = 3125 |
Самостоятельная работа по теме «Степень числа» Вариант 1 1. Сравните числа: а) 23 и 32 б) 42 и 32 в) 43 и 53 2.Вычислите: а)3 ∙ 42 ; б) (3 ∙ 8)2 ; в) 27 — 32 ; г) 250 — 53 ; д) (98 — 18)3∙18 ; е) 600 — 750 : 53 ; ж) 2 ∙ 152 + 5 3. Определите показатель степени числа и запишите его вместо звездочки: а) 8* = 512 б) 2* = 64 в) 6* = 1296 | Самостоятельная работа по теме «Степень числа» Вариант2 1. а) 34 и 43 б) 62 и 53 в) 34 и 24 2.Вычислите: а)2 ∙ 52 ; б) (7 ∙ 2)2 в) 72 — 62 ; г) 352 — 53 д) (76 — 66)3∙23 ; е) 800 — 750 : 52 ж) 3 ∙ 132 — 15 3. Определите показатель степени числа и запишите его вместо звездочки: а) 3* = 81 б) 7* = 343 в) 5* = 3125 |
По теме: методические разработки, презентации и конспекты
Самостоятельная работа по теме «Орфография имён числительных, обозначающих целые числа».
Данная самостоятельная работа может быть использована при закреплении темы в 7 классе и при повторении в 9-10 классах. Необходимо записать числовые выражения и математические задачи, заменя…
Самостоятельная работа «Квадрат и куб числа»
Данная самостоятельная работа позволит проверить знания таблицы по математике в 5 классе по теме «Квадрат и куб числа»…
Самостоятельная работа по теме «Отрицательные числа»
Самостоятельная работа по теме «Отрицательные числа» для 6 класса. ..
..
Самостоятельная работа по теме: «Натуральные числа»
Данная самостоятельная работа предназначена для учащихся 5 класса и состоит из двух вариантов. В работе проверяются такие темы, как выполнение действий над числами, решение уравнений, составление букв…
«Подготовка выпускников колледжа из числа детей-сирот и детей, оставшихся без попечения родителей, к самостоятельной жизни»
Статья об организации работы социальной службы колледжа в рамках подготовки учащихся выпускных групп из числа детей-сирот и дтей, оставшихся без попечения родителей, к самостоятелльной жизни и трудово…
Самостоятельные работы по алгебре и началам математического анализа для 10 профильного класса по теме «Действительные числа»
Самостоятельные работы по темам из главы 1 «Действительные числа» — для тех, кто работает по УМК А.Г.Мордковича по программе 4 ч алгебры в неделю.1. Натуральные и целые числа2. Рациональные и иррацион…
Комплексные числа самостоятельная работа №1.

10 класс Мордкович А.Г. профильный уровень…
Поделиться:
простых чисел и степени двойки. Связь степеней двойки с простыми числами… | Хоакин де Кастро
Связь степеней двойки с простыми и совершенными числами
Взгляните на суммы первых нескольких степеней двойки.
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
1 + 2 + 4 + 8 +16 = 31
1 + 2 + 4 + 16 + 32 = 63
1 + 2 + 4 + 8 + 16 + 32 + 64 = 127
Интересно, что многие из этих сумм являются простыми числами. И это не случайность. Далее по строке мы получаем еще несколько простых чисел. На самом деле, эти простые числа настолько распространены, что у нас есть для них название: простые числа Мерсенна. 9m — 1. Заметим, что обратное утверждение неприменимо; простые значения m (к сожалению) не всегда дают простое число Мерсенна.
Совершенные числа — это числа, которые могут быть представлены в виде суммы своих собственных делителей (не включая сами числа).
n — 1,
существует четное совершенное число
Теорема Евклида-Эйлера выражает корреляцию между простыми числами Мерсенна и совершенными числами в обоих направлениях. В этой статье мы только покажем, что существует совершенное число для каждого простого числа Мерсенна.
Мы можем рассмотреть конкретный пример и сделать из него обобщения. Возьмите простое число Мерсенна 31 и соответствующее ему совершенное число 496. Правильные делители последнего:
496 => 248, 124, 62, 31, 16, 8, 4, 2, 1
Из этого мы видим, что оно включает простое число Мерсенна (согласно соотношению) и все степени двойки, меньшие указанного простого числа.
248, 124, 62, 31 , 16, 8, 4, 2, 1
Кроме того, делители слева от простого числа Мерсенна получаются путем его умножения на другие степени двойки. Это, конечно, не включает те, которые дают само Совершенное число (31 * 16 = 496) и дубликаты (31 * 1 = 31).
248 = 31 * 8 , 124 = 31 * 4 , 62 = 31 * 2 , 31 , 16, 8, 4, 2,
Мы можем сказать, что идеальное число будет есть три «категории» факторов.
1.) Степени двух меньших, чем указанное простое число Мерсенна
2.) Произведение 1.) и само простое число Мерсенна (которое включает фактическое простое число Мерсенна)
Обобщение
Для любого совершенного числа, которое отзыв может быть выражен как 9n — 1, что дает нам:
И деление этого числа на два действительно дает исходное совершенное число:
Как видите, мы пришли к нашему исходному выражению. Выражение также равно удвоенной сумме своих множителей, что делает его совершенным числом. Итак, мы доказали, что для каждого простого числа Мерсенна существует совершенное число, которое представляет собой простое число Мерсенна, умноженное на степень двойки.
Из-за своей простоты степени двойки можно найти в самых разных местах теории чисел. По степени они также соединяют эти разные поля. Легкость, с которой ими можно манипулировать, и их элегантные свойства позволяют нам связать два, казалось бы, несвязанных набора чисел. Точно так же наша жажда правды и справедливости объединяет нас даже в эти ужасные времена.

 Вычислите:
Вычислите: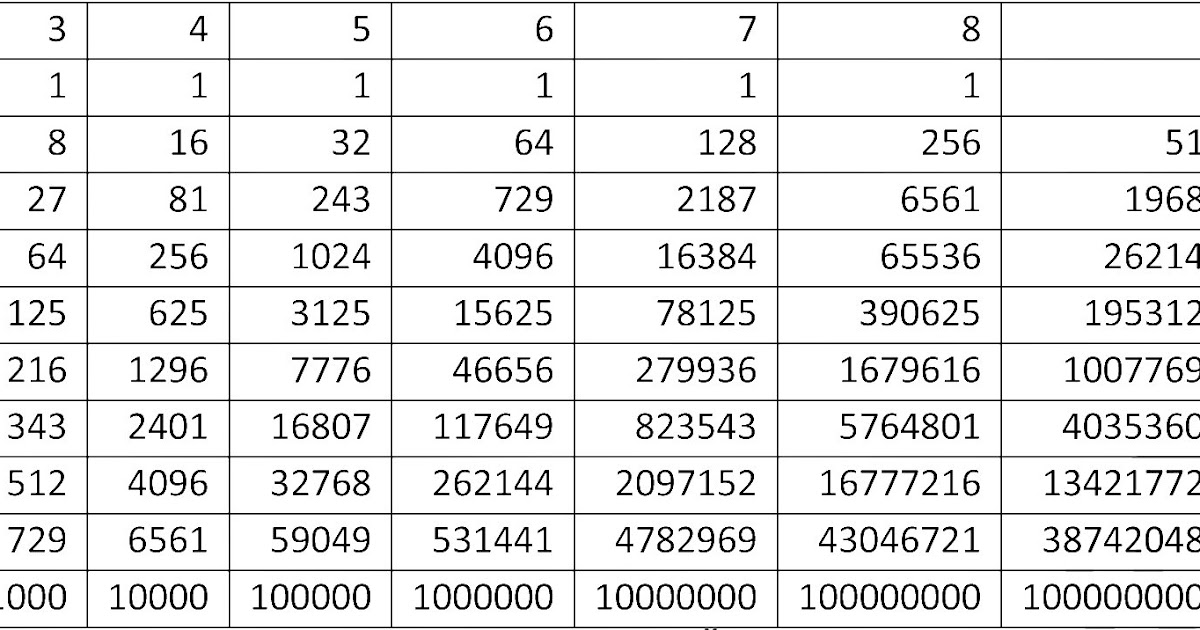 Сравните числа:
Сравните числа: Сравните числа:
Сравните числа: n — 1,
n — 1,