Сумма степеней с одинаковым основанием: Сложение степеней с одинаковыми показателями. Сложение, вычитание, умножение, и деление степеней

Действия со степенями | СПАДИЛО

Что такое степень?

Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть аⁿ=a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.

Пример №1.

• 3⁴=3×3×3×3 число 3 берем 4 раза (показатель 4)
• 21³=21×21×21 число 21 берем 3 раза (показатель 3)

Свойства степени (применимы для степеней с одинаковым основанием)

Умножение степеней

При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:

aⁿ× a^m=a^n+m

Пример №2.

а²×а⁸=а²⁺⁸=а¹⁰

5⁵×5³×5⁴=5⁵⁺³⁺⁴=5¹²

Деление степеней

При делении степеней с одинаковым основанием  основание оставляют тем же, а показатели вычитают:

aⁿ : a^m=a^n–m

Пример №3.

с¹²:с⁵=с^12-5= с⁷

3²³:3²⁰=3^23-20= 3³

Возведение степени в степень

При возведении степени в степень основание оставляют тем же, а показатели умножают:

(aⁿ)^m=a^n×m

Пример №4.

(с¹⁰)²=с²⁰

(6³)⁵=6¹⁵

Степень произведения

При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:

(a×b×c)^m=a^m×b^m×c^m

Пример №5.

(сmn)⁵=c⁵m⁵n⁵

(3²5⁴)⁶=3¹²5²⁴

Степень дроби  (степень частного)

При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:

Важные правила для работы со степенями

Запомните!

1. Любое число в нулевой степени равно 1 (а⁰=1).
2. Нуль в любой степени равен нулю (0ⁿ=0).
3. Свойства степени с натуральным показателем применимы для степени с целым отрицательным показателем.

Пример №6.

с^-21× с^-2=с^-21+(-2)=с^-23

х¹² : х^-2= х^12-(-2)=х¹⁴

(с^-3)⁵=с^-15

Правила для степени с целым отрицательным показателем

1. Степень с целым отрицательным показателем можно представить в виде обыкновенной дроби, числитель которой равен единице, а знаменатель степени с натуральным показателем.
2. Если дана дробь, в знаменателе которой есть степень с целым отрицательным показателем, то ее можно представить в виде степени с натуральным показателем.
3. Если дана дробь, в числителе и знаменателе которой есть степень с целым отрицательным показателем, то можно заменить её дробью, содержащей степень с натуральным показателем, просто поменяв числитель и знаменатель местами.

Задание OM2004 Сократите дробь 36n4n−2∙32n−1 .

---

Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.

(3∙3∙4)n4n−2∙32n−1 ..

Теперь представим каждый множитель в виде степени:

3n∙3n∙4n4n−2∙32n−1 ..

Разложим знаменатель дроби на множители по свойству степеней

3n∙3n∙4n4n∙4−2∙32n∙3−1 ..

Теперь можно сократить числитель и знаменатель на 3n и в 4n степени

Получим дробь, которую преобразуем по свойству степеней:

. .14−2∙3−1 ..= 42∙311..=16∙3=48

Ответ: 48

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 8OM21R Найти значение выражения

(3∙8)737∙85..

 

---

В числителе дроби возведем в степень каждый множитель:

(3∙8)737 ∙85..=37∙8737∙85.

Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.

 (3∙8)737 ∙85..=37∙8737∙85..=82=64

Ответ: 64

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1302o

Найдите значение выражения:

при a = 13, b = 6,8

---

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить.

Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

 Сокращаем (a-b):

 И получаем:

a/2

Подставляем значение a = 13:

13 / 2 = 6,5

Ответ: 6,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1301o

Найдите значение выражения: (x + 5)² — x (x- 10) при x = — 1/20

---

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5)² – x (x – 10) = x² + 2 • 5 • x + 25 – x² + 10x

Затем приведем подобные слагаемые:

x² + 2 • 5 • x + 25 – x² + 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24

Ответ: 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0807o Найдите значение выражения:

---

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

Ответ: 81

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0806o

Найдите значение выражения:

---

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:   По аналогии извлекаем и 2-й корень: В итоге получаем:

Ответ: 70,7

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0805o

Значение какого из выражений является рациональным числом?

1. √6-3
2. √3•√5
3. (√5)²
4. (√6-3)²

---

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ:

3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0804o

Какое из данных ниже чисел является значением выражения?

---

Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:

16 – 14 = 2

Суммарно наши действия выглядят так:

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0801o

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ ?

1. 121ⁿ
2. 11ⁿ⁺²
3. 11²ⁿ
4. 11ⁿ⁺³

---

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

• при умножении степени складываются
• приделении степени вычитаются
• при возведении степени в степень степени перемножаются
• при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ = 11² • 11ⁿ

С учетом правила умножения, складываем степени:

  11² • 11ⁿ = 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0606o Найдите значение выражения:

–0,3·(–10)⁴+4·(–10)²–59

---

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

–0,3·(–10)⁴+4·(–10)²–59 =

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

= –0,3·10000+4·100–59 =

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

= –3000+400–59 =

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

= –2600–59 =

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

= –(2600+59) = –2659

Ответ: -2659

pазбирался: Даниил Романович | обсудить разбор | оценить

Алла Василевская | Просмотров: 7.5k

Что делать со степенями при сложении чисел?

Что делать со степенями при сложении чисел?

Как складывать числа с одинаковыми степенями Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень. Сначала возводим каждое число в степень и затем выполняем сложение. В уравнениях это будет происходить немного иначе.

Что происходит с показателями степени при сложении?

Свойство № 1 При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются. am · an = am + n, где «a» — любое число, а «m», «n» — любые натуральные числа. Данное свойство степеней также действует на произведение трёх и более степеней. Примеры.

Как разделить степени с одинаковыми основаниями?

Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.

Что нужно делать со степенями при делении?

При делении степеней с одинаковым основанием их показатели вычитаются. … Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

Как умножать и делить числа с разными основаниями и степенями?

Как перемножить степени с разными основаниями в виде чисел?

1. Если надо умножить два числа с одинаковыми основаниями, но разными показателями степеней, то общее основание возводится в сумму степеней. …
2. Если основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.

Как решить число в степени?

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.

Как считается степень числа?

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a». Запись «an» читается так: «а в степени n» или «n-ая степень числа a».

Когда умножаются степени?

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

Как разделить число в отрицательной степени?

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя. Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью: a 5 : a 8 = a5 — 8 = a -3. = x -2.

Как умножить число на степень?

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто: 23 = 2·2·2, где

Почему любое число в нулевой степени равно единице?

Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя. …

Почему число в нулевой степени равно единице?

Известно, что абсолютно любое число в нулевой степени равно единице. Почему 0 в степени 0 равно 1? Доказать это просто, при умножении степеней с одинаковым основанием их показатели складываются, а при делении – вычитаются. … Но ведь мы делим число на себя, это всегда будет равно единице!

Чему равно число е в первой степени?

Возведение числа е в степень означает возведение в степень числа Эйлера e x = exp (x). Число е в 1-й степени, как и любое число в этой степени, будет равно самому себе, т. е. 2.

Как посчитать е в минусовой степени?

При возведении экспоненты в отрицательную степень нужно 1 делить на число е в заданной степени, но со знаком плюс.

Чему будет равно число в минус первой степени?

Степень с отрицательным показателем К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1). Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины.

Что такое е в математике?

Само число e — иррациональное, то есть выражается бесконечной непериодической десятичной дробью.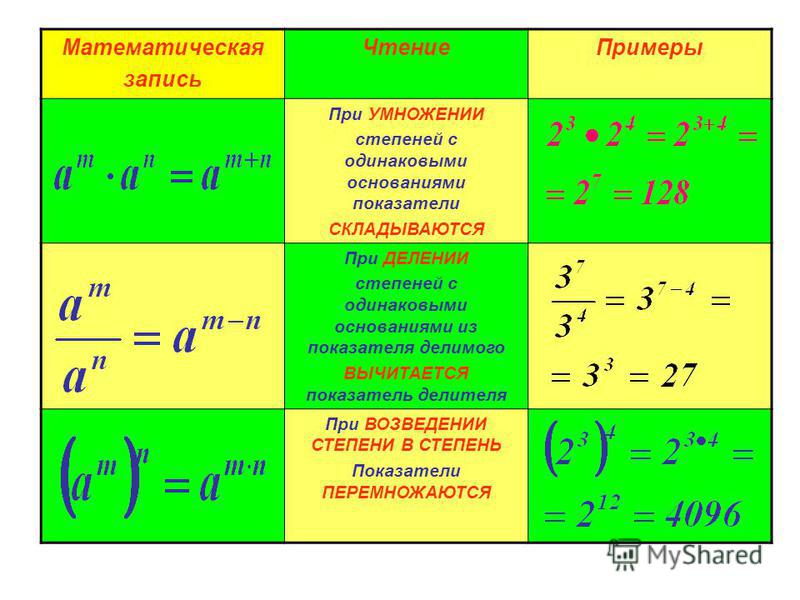 Приблизительно оно равно 2,718. … Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.

Что значит 1е 5?

1e5 — это 100000. 5 обозначает количество нулей, которые вы добавляете за этим числом. Например, предположим, что у меня есть 1e7. Я бы поставил 7 нулей за 1, так что он станет

Что значит 1е 9?

e (или e ) означает «times 10-to-the», поэтому 1e9 «один раз десять до девятой мощности», а 1e-9 означает «один раз десять до отрицательного девятой власти». В математических научных обозначениях это обычно обозначается надстрочным индексом: 1 × 10 —9 или —1 × 10 9 .

Что значит 1 е7?

В большинстве случаев код ошибки 1Е / 1C / E7 прямо указывает на поломку прессостата, однако, в некоторых случаях, исправить возникшую неполадку можно своими силами.

Как на калькуляторе посчитать экспоненту?

В виндовом калькуляторе есть неприметная галочка Inv, выставив которую, пользователь информирует калькулятор, что хочет применить функцию, обратную вызываемой. Функцией, обратной экспоненте, является натуральный логарифм — следовательно, чтобы вычислить экспоненту числа, нужно нажать сначала Inv, потом ln.

Сложение показателей степени — определение, шаги, метод, примеры

Сложение показателей степени относится к простому сложению чисел, но в виде показателей степени или степени. Другими словами, добавление основания и показателей степени — это добавление показателей степени. Показатель степени также называется степенью числа и показывает, сколько раз число умножается само на себя. В общем, x ⁿ означает, что x умножается сам на себя n раз. Добавление показателей выполняется в разных типах, давайте посмотрим, что это за типы, и решим несколько примеров, чтобы лучше понять эту концепцию.

1.	Что такое добавление показателей?
2.	Шаги добавления экспоненты
3.	Добавление методов экспоненты
4.	Часто задаваемые вопросы о добавлении экспонентов

Что такое добавление показателей?

Сложение показателей степени — это процесс сложения показателей степени или степени числа независимо от того, совпадает ли основание или нет. Показатель степени также можно назвать степенью числа, поскольку он представляет собой количество раз, когда число умножается само на себя. Например, 3 ² = 3 × 3, где 3 — основание, а 2 — показатель степени.

Здесь в члене x ⁿ ,

• x называется основанием
• n называется показателем степени или степенью
• x ⁿ читается как x в степени n (или) x в степени n

При сложении показателей следует помнить одно главное правило: основание и показатель степени должны совпадать, а сложение выполняется с коэффициентом. Переменные, которые объединяются, имеют одно и то же основание и одинаковую мощность. Это правило применимо и ко всем другим формам показателей степени, то есть к вычитанию, умножению и делению.

Шаги добавления показателей

Добавление показателей степени может быть выполнено, когда основание и степень совпадают. Бывают случаи, когда основание и показатели степени различаются, но мы все равно можем выполнять сложение для этих выражений. Давайте посмотрим на шаги добавления показателей.

• Шаг 1: Проверьте члены в выражении, имеют ли они одинаковое основание и одинаковые показатели степени. Например, 2 ² + 2 ² . Как мы видим, и основание, и показатель степени равны 2,9.0050
• Шаг 2: Если основание и показатели различны, вычислите выражение с отдельными членами. Например, 5 ³ + 4 ² . База и показатели разные.
• Шаг 3. Сложите результаты.

Добавление методов экспоненты

Сложение показателей может выполняться различными способами. Основное правило при добавлении показателей степени состоит в том, что основание и степень должны быть одинаковыми. Однако иногда основание и показатели могут не совпадать, поэтому нам нужно вычислять члены по отдельности, чтобы вычислить выражение. Давайте посмотрим на различные методы.

Метод 1: Сложение показателей степени с одинаковым основанием и показателями степени

Сложение показателей степени, когда основание и показатели степени совпадают, выполняется очень простым методом. Общая форма сложения показателей с одинаковым основанием и показателями такова: ⁿ + ⁿ = 2a ⁿ . Давайте посмотрим на пример, чтобы понять это лучше. Например: 4 ³ + 4 ³ = 2(4 ³ ) = 2 × 4 × 4 × 4 = 128.

Метод 2. Сложение показателей степени с разным основанием и степенью

Если основание и показатель степени имеют разные значения, мы сначала добавляем каждый показатель степени, а затем вычисляем все выражение. Общая форма вычисления различных оснований и показателей такова: a ⁿ + b ^m . Давайте посмотрим на пример, чтобы понять это лучше. Например: 3 ³ + 5 ² = 3 × 3 × 3 + 5 × 5 = 27 + 25 = 52.

Метод 3: сложение отрицательных показателей с разными основаниями

Сложение отрицательных показателей выполняется путем вычисления каждого срок по отдельности, а затем добавить общее количество. Термины записываются в дробной форме, а затем добавляются. Общая форма вычисления отрицательных показателей с разными основаниями — это ^-n + b ^-m = 1/a ⁿ + 1/b ^m . Давайте применим общую форму в примере, чтобы понять это лучше. Например: 6 ^-2 + 3 ^-3 = 1/6 ² + 1/3 ³ = 1/36 + 1/27 = 0,0648.

Метод 4: Добавление дробных показателей степени с одинаковым основанием и показателями степени

Показатели степени также могут быть выражены в форме дроби. Таким образом, сложение этих дробей в виде показателей степени может быть выполнено с использованием этой общей формы, ^н/м + а ^н/м = 2а ^н/м . Для дробей мы можем преобразовать дробные показатели в форму корня, то есть либо квадратный корень, либо кубический корень, в зависимости от дроби. Давайте применим эту общую форму в примере для лучшего понимания. Например: 4 ^1/2 + 4 ^1/2 = 2(4 ^1/2 ) = 2 × √4 = 2 × 2 = 4.

Метод 5. Сложение дробных показателей с разным основанием и Показатель степени

Показатель степени, записанный в дробной форме с разным основанием и разными показателями степени, выражается в общей форме как ^н/м + б ^д/к . Здесь сначала вычисляется каждый член, а затем вычисляется весь результат. Дробная форма преобразуется в ее корень, а затем вычисляется. Давайте рассмотрим пример: 27 ^1/3 + 4 ^1/2 = ³ √27 + √4 = 3 + 2 = 5.

Метод 6: добавление переменных с одинаковыми показателями степени

Это аналогично методу сложения показателей степени с одинаковым основанием и одинаковыми показателями степени. Общий вид: x ⁿ + x ⁿ = 2x ⁿ . Рассмотрим пример: 7 ² + 7 ² = 2(7 ² ) = 2 × 7 × 7 = 98.

Метод 7: добавление переменных с разными показателями степени

Общая форма для вычисления переменных с разными показателями составляет x ⁿ + x ^m . Давайте рассмотрим пример: 4 ² + 4 ³ = 4 ^{2 × 3} = 4 ⁶ = 4096. Взглянем.

• Как определить степени и степени
• Экспоненциальные функции
• Иррациональные Показатели

Часто задаваемые вопросы о добавлении экспонентов

Что означает добавление показателей?

Добавление показателей степени — это процесс добавления терминов, имеющих одинаковые основание и показатель степени. Сложение возможно только в том случае, если основание и показатель степени совпадают. Есть случаи, когда это не так, это можно решить, увидев, одинаковы ли показатели двух терминов или одинаковое основание двух терминов. В противном случае добавление показателей степени невозможно.

Каковы шаги по добавлению показателей?

Добавление степеней выполняется в 3 простых шага, а именно:

• Проверьте члены в выражении, если они имеют одно и то же основание и одинаковые степени.
• Если основание и показатели различны, вычислить выражение с отдельными элементами.
• Сложите результаты вместе.

Каково правило добавления показателей?

Наиболее важным правилом сложения показателей степени является то, что основание и показатели степени членов, которые помещаются для сложения, должны быть одинаковыми. Если они одинаковые, коэффициенты будут складываться вместе, при этом основание и показатель степени одинаковы.

Можно ли складывать числа с разными показателями степени?

Нет, сложение чисел с разными показателями степени применимо, поскольку правило сложения показателей степени заключается в том, что основание и показатель степени должны быть одинаковыми. В то время как что-то основание и показатель степени могут быть разными, но только одно отличие не применимо.

Добавляете ли вы показатели при добавлении?

Для сложения показателей степени основание и показатель степени должны совпадать. Коэффициент переменной добавляется, оставляя показатель степени неизменным. В выражение добавляются члены с одинаковыми переменными и степенями. Это правило применимо как к умножению, так и к делению.

Как складывать одночлены с показателями степени?

При сложении двух или более одночленов мы сначала складываем коэффициенты, пока переменные и показатели степени у переменной одинаковы. Мы можем получить результат, добавляя подобные одночлены.

Сложение и вычитание степеней

Введение в сложение степеней

Дата последнего обновления: 19 апреля 2023

•

Всего просмотров: 46,2 тыс. 16к 92=4 \times 4$, где 4 — основание, а 2 — показатель степени. Сложение степеней — это процесс сложения показателей или степеней числа независимо от того, совпадает ли основание.