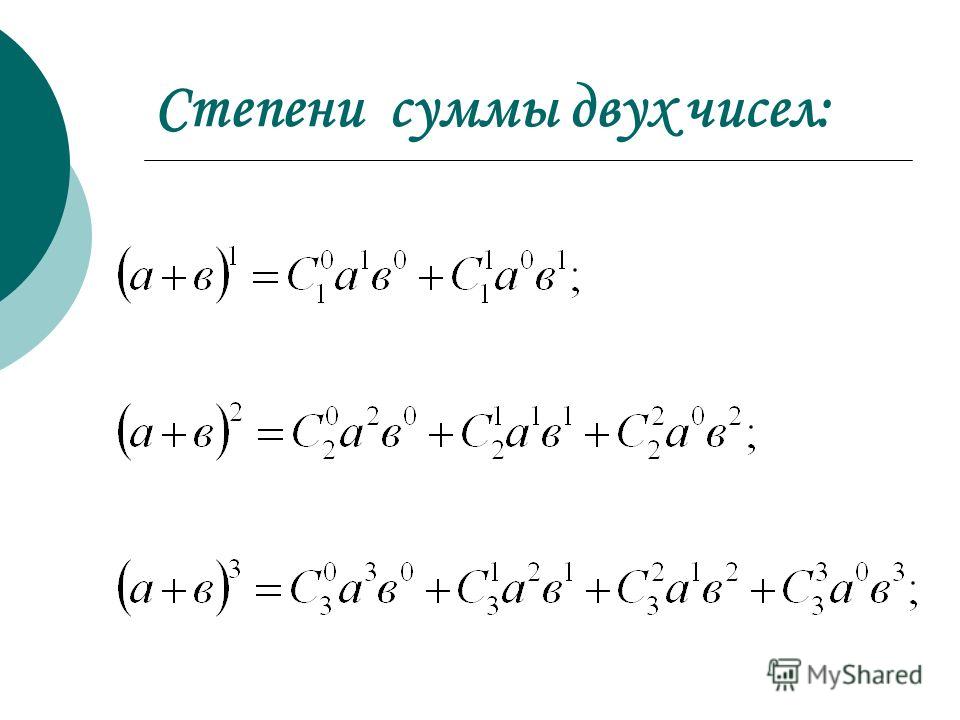Сумма в степени 3: Формулы сокращенного умножения

Формула сумм энных степеней

Опубликовано 31 декабря 2016 г. Джон

Есть известная формула суммы первых

1 + 2 + 3 + … + n = n ( n + 1) / 2

формула суммы первых n квадратов

1 ² + 2 ² + 3 ² + … + n ² = n ( n + 1)(2 n + 1) / 6

2 и 008 кубов:

1 ³ + 2 ³ + 3 ³ + … + n ³ = n ^{) 2 0 9 ( 0 9 0023 2} / 4

Естественно спросить существует ли общая формула для всех показателей. Есть, но не совсем устраивает. Есть единая формула для суммы p -я степень первых n положительных целых чисел, но она включает загадочные коэффициенты, известные как числа Бернулли. Таким образом, существует довольно простая формула для сумм степеней в терминах чисел Бернулли, но простой формулы для чисел Бернулли не существует.

На первый взгляд это может показаться бесполезным, потому что у нас есть формула для суммы через другую сумму, но обратите внимание, что суммы находятся в разных диапазонах. Первоначальная сумма достигает n , а в приложении n может быть очень большим. Сумма справа доходит до показателя степени p , а в приложении p обычно довольно мала.

Первые несколько чисел Бернулли B _j , начиная с j = 0, равны 1, -1/2, 1/6, 0, -1/30, 0, …. Этот краткий список может дать вам некоторую надежду найти хорошую формулу для чисел Бернулли, но он полон сюрпризов. Например, 12-е число Бернулли равно -69.1/2730.

Так как же определить числа Бернулли? Эти числа встречаются во многих контекстах, поэтому существует множество способов их определения. Один из способов — сказать, что экспоненциальная производящая функция чисел Бернулли равна

Есть несколько способов взглянуть на это определение. Первая реакция, наверное, разочарование. «Вы не будете просто рассказывать мне, что такое числа Бернулли. Вы говорите мне, что я должен вычислять еще один член этого уродливого степенного ряда каждый раз, когда мне нужно новое число Бернулли?! Но с более продвинутой точки зрения вы можете быть благодарны за то, что громоздкие числа Бернулли имеют такую ​​простую экспоненциальную производящую функцию. Часто наиболее полезными способами изучения специальных чисел являются их производящие функции.

В следующем посте мы рассмотрим, что произойдет, если мы допустим, что p

Похожие : Сообщения на специальные номера

Категории : Математика

Метки : Математика

Добавить в закладки постоянную ссылку

Суммы степеней положительных целых чисел

Автор(ы): 

Джанет Бири (Университет Редлендса)

Томас Хэрриот был английским математиком и ученым, который жил в Лондоне и работал под покровительством сэра Уолтера Рэли и Генри Перси, графа Нортумберленда. Рэли отправил Харриота в путешествие в колонию Вирджиния в 1585–1586 годах, что позволило Харриоту применить на практике свою навигационную теорию, а также собрать обширные заметки для своей книги . опубликовано в 1588 году.

Харриот никогда не публиковал ни одной своей математической или научной работы, но оставил более 5000 рукописных листов с заметками на различные темы. В своих заметках по математике он гораздо больше использовал символические обозначения, чем его современники и многие из его последователей, включая Ферма и Паскаля (см.

Ниже). Он также часто использовал таблицы разностей, применяя их для изучения пифагорейских троек и, как мы увидим, сумм степеней натуральных чисел.

Харриот написал формулы для сумм квадратов, кубов и четвертых степеней на листе рукописи, озаглавленном «Ad aggregata Z.C.ZZ. и т. д.» («Для сумм квадратов, кубов, квадратов-квадратов и т. д.») (Харриот, лист 240). В этом заголовке мы заменили Z, C и ZZ на символы квадратов, кубов и четвертых степеней (квадрат-квадраты), которые Харриот, вероятно, позаимствовал из знаменитой книги по алгебре Роберта Рекорда, Whetstone of Witte (1557), и мы заменили «и т. д.» для символа Harriot, используемого для «et cetera».

Рис. 8. Коссистское обозначение степеней Роберта Рекорда можно увидеть в списке, начинающемся слева внизу и заканчивающемся в середине правой страницы, наряду с упрощенными версиями, записанными читателем. Символы R для «корень» (первая степень), Z для «квадрат», C для «кубайк» (куб) и ZZ для «квадрат квадратов» (четвертая степень). ) находятся слева. Дополнительные изображения из книги Рекорда по алгебре, Точильный камень Витте, см. Роберт Рекорд Точильный камень Витте в «Математических сокровищах». (Воспроизведено с разрешения библиотеки Колумбийского университета). ф. 239), как показано на рисунке 9.

Рисунок 9. Таблицы разностей для сумм квадратов, кубов и квадратов-квадратов

 

Эти таблицы называются таблицами «разностей», потому что, например, в треугольнике чисел

$$\matrix{ 14 & {}\cr 30 & 16\cr}$$

в верхней левой таблице на рисунке 9 разница между 30 и 14 составляет 16 (30 – 14 = 16). Это отношение разности сохраняется для каждого такого треугольника чисел в таблицах на рисунке 9 и характеризует эти таблицы как таблицы разностей. Если мы применим это свойство разности повторно, то увидим, что элементы любого столбца можно суммировать, чтобы получить элементы столбца слева. Например, в двух крайних левых столбцах верхней левой таблицы на рисунке 9, мы видим, что 14 + 16 + 25 = 55, 5 + 9 + 16 + 25 = 55, 1 + 4 + 9 + 16 + 25 = 55 и 1 + 4 + 9 + 16 = 30. Последние две суммы равны , соответственно, сумма первых пяти квадратов положительных целых чисел и сумма первых четырех квадратов положительных целых чисел, и это следует непосредственно из определения таблицы разностей и выбора Харриотом 1 в качестве первой записи столбца, помеченного

p ³ и последовательные положительные целые квадраты в качестве элементов столбца с пометкой 9.0007 p

Эти таблицы различий на самом деле называются «постоянными» таблицами различий, потому что различия становятся постоянными в столбце с надписью « e ». У Харриота были общие формулы для записей в таблицах постоянных разностей, и он мог применить эти формулы к крайним левым столбцам своих таблиц на рис. 9, чтобы получить общие формулы для сумм квадратов, кубов и четвертых степеней последовательных положительных целых чисел. Формулы Харриота, данные в терминах первой строки записей в таблице постоянных разностей, были следующими (Harriot, ff. 234, 246). 95  \cr} $$

Здесь, v ¹  дает n -й элемент столбца, помечен р ²  , v ³   n -й элемент столбца с меткой p ³  , v ^{7 0 0} ая запись столбца с пометкой p ⁴ , и против ^{5 95  = 24nnnnn + 120nnnn + 120nnn — 120nn — 144n  \cr   & \quad \quad \quad \quad \quad \quad \quad  — 60nnnn — 120nnn + 60nn + 120n  \cr  & \quad \quad \quad \quad \quad \ quad \quad \quad \quad \quad \quad  + 40nnn — 0 — 40n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 60nn — 60n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120n — 120  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad  + 120 \кр} $$ 93 } \over 3} — {n \over {30}}. $$}

(Во всех этих вычислениях показатели степени n являются современными. Харриот всегда писал, например, nnn , где мы должны были писать n ³ .)

Когда Хэрриот перечислил свои полученные формулы для сумм единиц, натуральных чисел, квадратов, кубов и квадратов-квадратов, он заменил v ⁰ , 72 v 4 0,

3 v ² , v ³ и v ⁴  с « s » (для суммы), за которыми следуют, соответственно, точка, отрезок, маленький квадрат, маленький куб и его символ квадрат-квадрат из Recorde. Он записал свою формулу для суммы квадратов, например, как s (квадрат): 6 = 2 nnn + 3 nn + 1 n . Несмотря на то, что вычисления долгие, они простые, и Харриот не показал столько работы, сколько мы. Он уже проделал тяжелую работу по выводу формул для записей в таблицах постоянных разностей. Для суммы кубов, например, на листе 239Харриот написал только

$$\eqalign{  & 6nnnn + 12nnn — 6nn — 12n  \cr   & \quad \quad \quad \quad \quad \quad  + 12nn — 12n  \cr   & \quad \quad \quad \quad \quad \quad \quad \quad \quad  + 24n \cr} $$

_______________________________________________ 

$$6nnnn + 12nnn + 6nn + 0n$$

а также проверил, что его формула для v ⁴ с = 6, р = 0, р ² = 1, р ³ = 1, p ⁴ = 1 и n = 5 дадут правильное значение 225 в пятой строке, прежде чем записать его окончательный результат на листе 240.   

На листе 239 рукописный лист на которых появляются таблицы различий на рис. 9, Харриот процитировал три страницы из Maurolico Arithmeticorum Libri Duo, , страницы 52, 63 и 67. Что общего у этих трех страниц, так это список первых пяти различий четвертых степеней, 1 (= 1 ⁴   – 0 ⁴ ), 15 (= 2 ⁴   – 1 ⁴ ), 65, 175 и 369 = (5 ⁴   – 4 ⁴     , которые Хэрриот сам скопировал на листе 239. на листе 154 того же тома рукописи, что разности квадратов, кубов, четвертой и более высоких степеней в конечном счете постоянны, и иллюстрирует это свойство на рис. кубов или четвертых степеней можно расширить до таблицы постоянных разностей, изучая 9-е число Мауролико.0007 Арифметика.

Английский математик Генри Бриггс (1561-1631), прославившийся своим изобретением логарифмов совместно с Джоном Нейпиром, жил в Лондоне в то же время, что и Хэрриот. Бриггс отметил в своем 1624 Arithmetica Logarithmica , что разности квадратов, кубов, четвертых и более высоких степеней в конечном счете постоянны (Briggs, стр. 29-30, или Hutton, стр. 386-387), но не распространил свое наблюдение на формулы сумм этих степеней. Мы так и не нашли никаких доказательств контакта между Бриггсом и Хэрриотом. После смерти Харриота Бриггс уведомил Иоганна Кеплера в 1625 г. о готовящейся публикации некоторых работ Харриота (Фриш, стр. 661-662), а позже, в 1630 г. или чуть раньше, похвалил работу Харриота по «телесным углам» или сферической тригонометрии (Хейквилл , стр. 263-264), но ни разу не ссылался ни на какую другую работу Харриота.

Упражнение 13. Напишите таблицу постоянных разностей, в которой второй столбец слева содержит пятые степени, а крайний левый столбец содержит суммы пятых степеней, начиная с 1.  Включите не менее четырех строк. (Вам потребуется как минимум семь записей во втором столбце, чтобы получить по крайней мере две копии постоянной разности, 120, в крайнем правом столбце только путем взятия разностей.) Используйте формулу Харриота для v ⁶ , 96  \cr}$$

Упражнение 14: Чтобы использовать метод Харриота для получения формулы для суммы первых n шестых степеней, нам потребуется как таблица постоянных разностей, так и крайний левый столбец, содержащий первые несколько сумм шестых степеней и формула для v ⁷ , n -я запись крайнего левого столбца восьмистолбцовой таблицы разностей констант, с точки зрения записей, p ⁷ , стр.