график, основание, функции, предел, формулы и область определения. Натуральный логарифм, функция ln x
Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»
Что такое натуральный логарифм
Ребята, на прошлом уроке мы с вами узнали новое, особенное число – е. Сегодня мы продолжим работать с этим числом.Мы с вами изучили логарифмы и знаем, что в основании логарифма может стоять множество чисел, которые больше 0. Сегодня мы также рассмотрим логарифм, в основании которого стоит число е. Такой логарифм принято называть натуральным логарифмом.
 x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:
x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные: Свойства функции $y=\ln{x}$
1. $D(f)=(0;+∞)$.2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.
В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции .
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.
Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять. 6=1$.
6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:
Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
| ||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||
Разница между Log и Ln – определение, свойства и правила
Log и Ln обозначают логарифм и натуральный логарифм соответственно. Логарифмы необходимы для решения уравнений, в которых неизвестная переменная появляется как показатель степени некоторой другой величины. Они важны во многих разделах математики и научных дисциплин и используются для решения задач, связанных со сложными процентами, которые широко связаны с финансами и экономикой.
В математике логарифм можно определить как обратную функцию возведения в степень.
Проще говоря, логарифм можно определить как степень, в которую нужно возвести число, чтобы получить любое другое число.
Он также известен как логарифм по основанию 10 или десятичный логарифм.

Общая форма логарифма может быть представлена как:
0031 |
Вышеуказанная форма также может быть записана как: 9{x} = y\]
В этой статье мы собираемся обсудить, что такое log, что такое ln в математике, правила Log и ln, разница между Log и Ln x, разница между log и natural log. и разница между логарифмом и графиком ln.
Ниже приведены четыре основных свойства логарифма, которые помогут вам легко решать задачи, основанные на логарифмировании.
Свойства логарифма
Logb(mn) = Logb m + Logb n Это свойство логарифма означает, что умножение двух значений логарифма эквивалентно сложению отдельного логарифма. |
Logb (m/n) = Logb m — Logb n Это свойство логарифма говорит о том, что деление двух значений логарифма эквивалентно вычитанию отдельного логарифма. |
Logb (mn) = n logbm Вышеприведенное свойство известно как экспоненциальное правило логарифма. Логарифм m вместе с рациональным показателем эквивалентен показателю, умноженному на его логарифм. |
Logb m = loga m / loga При делении двух чисел по одному основанию степени вычитаются. |
Журнал Значение от 1 до 10
Журнал | Значение журнала |
Протокол 1 | 0 |
Журнал 2 | 0,3010 |
Журнал 3 | 0,4771 |
Журнал 4 | 0,6020 |
Журнал 5 | 0,6989 | Журнал 6 | 0,7781 |
Журнал 7 | 0,8450 |
0,9030 | |
Журнал 9 | 0,9542 |
Журнал 10 | 1 |
Что такое Ln в математике?
Ln называется натуральным логарифмом. Его также называют логарифмом по основанию e. Здесь константа e обозначает число, которое является трансцендентным числом и иррациональным числом, приблизительно равным значению 2,71828182845. Натуральный логарифм (ln) может быть представлен как ln x или \[\log_{e}x\].
Его также называют логарифмом по основанию e. Здесь константа e обозначает число, которое является трансцендентным числом и иррациональным числом, приблизительно равным значению 2,71828182845. Натуральный логарифм (ln) может быть представлен как ln x или \[\log_{e}x\].
Рассмотрим различные правила Ln
Частное правило | 9 0002 ln(x/y) равно ln(x) — ln(y) Естественный log деления x и y равен разности ln x и ln of y. Пример: ln(10/5) = ln(10) — ln(5) |
Правило взаимного обмена | ln(1/x) равно − ln(x) 9000 3 Натуральный log обратной величины x равен обратному значению ln x. 9{y})\] равно \[y \times \ln x\] Натуральный логарифм x, возведенный в степень y, равен y, умноженному на ln x. Пример: ln(4²) равно 2 * ln(4) |
Выше мы обсуждали правила log и ln.
Значения журнала от 1 до 10 по основанию e приведены ниже-
Таблица, показывающая значения Ln от 1 до 10.
0 | |
В (2) | 0,693147 |
В (3) | 1.098612 |
В (4) | 1.386294 |
В (5) | 1.609438 |
В (6) | 90 002 1.791759 |
В (7) | 1.94591 |
В (8) | 2.079442 |
В (9) | 2.197225 |
В (10) | 2. |
Разница между логарифмическим и линейным графиком
Эти графики покажут вам разницу между логарифмическим и линейным графиком.
(Изображения будут загружены в ближайшее время)
Давайте обсудим некоторые из ключевых различий между Log и Ln:
Чтобы решить логарифмические задачи, нужно знать разницу между логарифмом и натуральным логарифмом. Ключевое понимание экспоненциальных функций также может оказаться полезным для понимания различных концепций. Некоторые из важных различий между логарифмическим и естественным логарифмом приведены ниже в табличной форме:0025
Log
Ln
Log обычно относится к логарифму по основанию 10.
Ln в основном относится к логарифму по основанию e.
Это также известно как десятичный логарифм.
Также известен как натуральный логарифм.
Общий журнал может быть представлен как log10 (x).
Вопросительное утверждение для десятичного логарифма записывается как «На какое число нужно возвести 10, чтобы получить y?»
Вопросительное утверждение для натурального логарифма записывается как «На какое число мы должны возвести постоянное число Эйлера, чтобы получить y?»
Логарифмическая функция более широко используется в физике по сравнению с ln.
Поскольку логарифмы в физике обычно берутся за основание, ln используется гораздо реже. 9{6}\] = 2 x 2 x 2 x 2 x 2 x 2 = 64 или y = 64
Вопрос 2) Упростите log(98).
Ответ) Мы будем использовать правила Log и ln, которые мы обсуждали. Поскольку мы знаем, что число 98 не является степенью числа 10 (в отличие от 100), поэтому мы можем найти значение, подключив его к калькулятору, не забывая использовать клавишу «LOG» (а не клавишу «LN» ), и мы получаем log(98) = 1,99122607569… или log(98) = 1,99, округленное до двух знаков после запятой.
Поскольку мы знаем, что число 98 не является степенью числа 10 (в отличие от 100), поэтому мы можем найти значение, подключив его к калькулятору, не забывая использовать клавишу «LOG» (а не клавишу «LN» ), и мы получаем log(98) = 1,99122607569… или log(98) = 1,99, округленное до двух знаков после запятой.
Интересные факты
Первым человеком, который привнес понятие логарифма в наше время, был немецкий математик Михаэль Штифель (около 1487-1567 гг.).
Логарифм с основанием 10 называется обычным или бриггсовским логарифмом и может также записываться как log n. Обычно они пишутся без базы.
Дата последнего обновления: 25 апреля 2023 г. Обновлены страницы
НОК 3 и 4 и как найти наименьшее общее кратное
Что такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — Определение, решенные примеры и практические задачи
Числа прописью
Доля в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
НОК из 3 и 4, и Как найти наименьшее общее кратное
Что такое простой процент? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Дробь в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
Свойства логарифмов
Свойства логарифмов
|
Содержание: Эта страница соответствует § 4. 3
(стр. 341) текста.
3
(стр. 341) текста.
Предлагаемые проблемы из текста:
р. 345 #3, 7, 9, 11, 13, 25, 27, 33, 35, 45, 49, 53, 91
Смена базы
Свойства логарифмов
Смена базы
В то время как большинство научных калькуляторов имеют кнопки только для десятичного и натурального логарифмов, другие логарифмы могут быть вычислены с помощью следующей формулы замены основания.
Замена базовой формулы
Пример 1 .Оценить журнал 5 3. Формула изменения базы позволяет нам оценить это выражение, используя любой другой логарифм, поэтому мы решим эту задачу двумя способами, используя сначала натуральный логарифм, затем десятичный логарифм.
Натуральный логарифм:
десятичный логарифм:
Упражнение 1 :
Из логарифмического тождества 1 следует, что log 2 8 = 3,
(a) Используйте калькулятор и формулу изменения основания с натуральным логарифмом, чтобы убедиться, что log 2 8 = 3,
(b) Используйте калькулятор и формулу замены основания с десятичным логарифмом, чтобы проверить, что log 2 8 = 3,
Ответить
Упражнение 2 :
Из логарифмического тождества 2 следует, что .
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень. Ответить
Вернуться к содержанию
Свойства логарифмов
| 1. log a (ув) = log a у + лог а в | 1. ln (ув) = ln u + ln v |
| 2. log a (u/v) = log a u — log a v | 2. ln (u / v) = ln u — ln v |
| 3. журнал a u n = n log a u | 3. лн у н = н пер у |
Свойства слева справедливы для любого основания a.
Свойства справа являются переформулировкой общих свойств натурального логарифма.
Многие логарифмические выражения могут быть переписаны в расширенном или сокращенном виде с использованием трех указанных выше свойств.
Расширение — это разбиение сложного выражения на более простые компоненты.
Пример 2 .
Расширение выражения.
переписать с использованием экспоненциальной записи недвижимость 3 имущество 1
Пример 3 .
Расширение выражения.
собственность 2 собственность 1 собственность 3
Пример 4 .
Сжатие выражения.
собственность 3 собственность 1 собственность 2
Распространенные ошибки
- Логарифмы разбивают произведения на суммы по свойству 1, но логарифм суммы нельзя переписать .



 Но ряд:
Но ряд: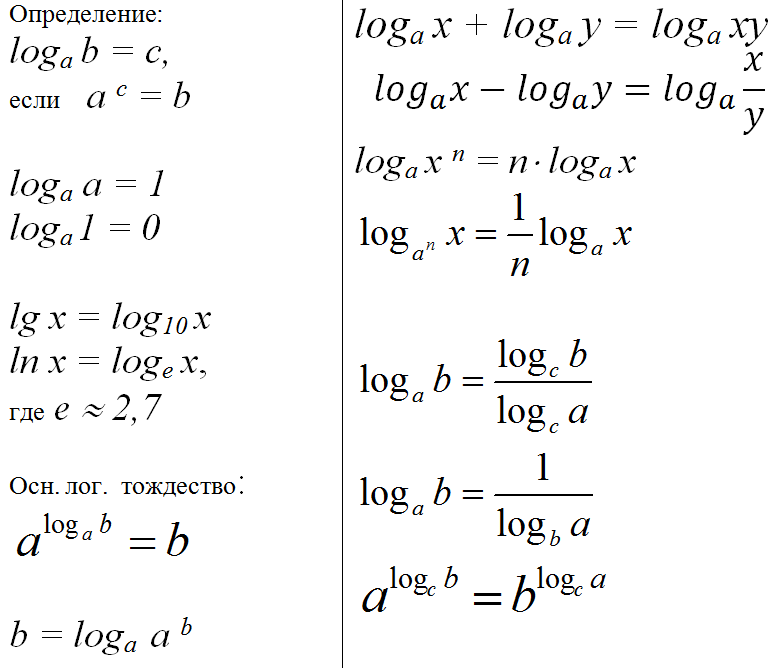 Введите свой запрос:
Введите свой запрос:

 302585
302585
