Свойства тригонометрических функций: Свойства тригонометрических функций

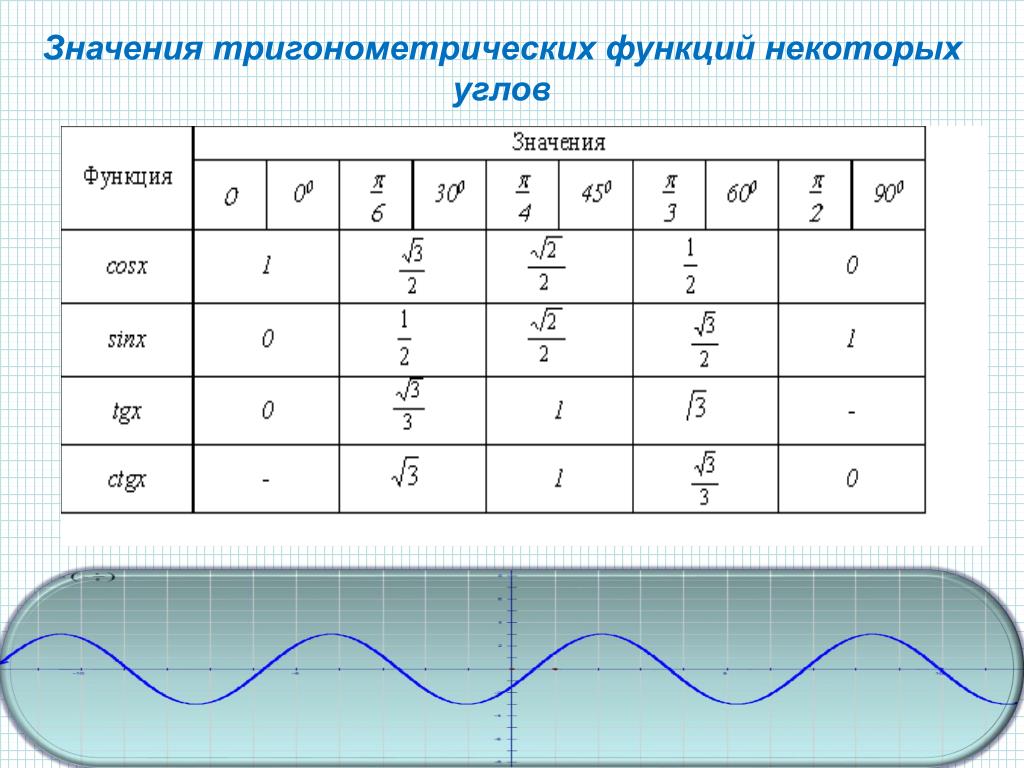
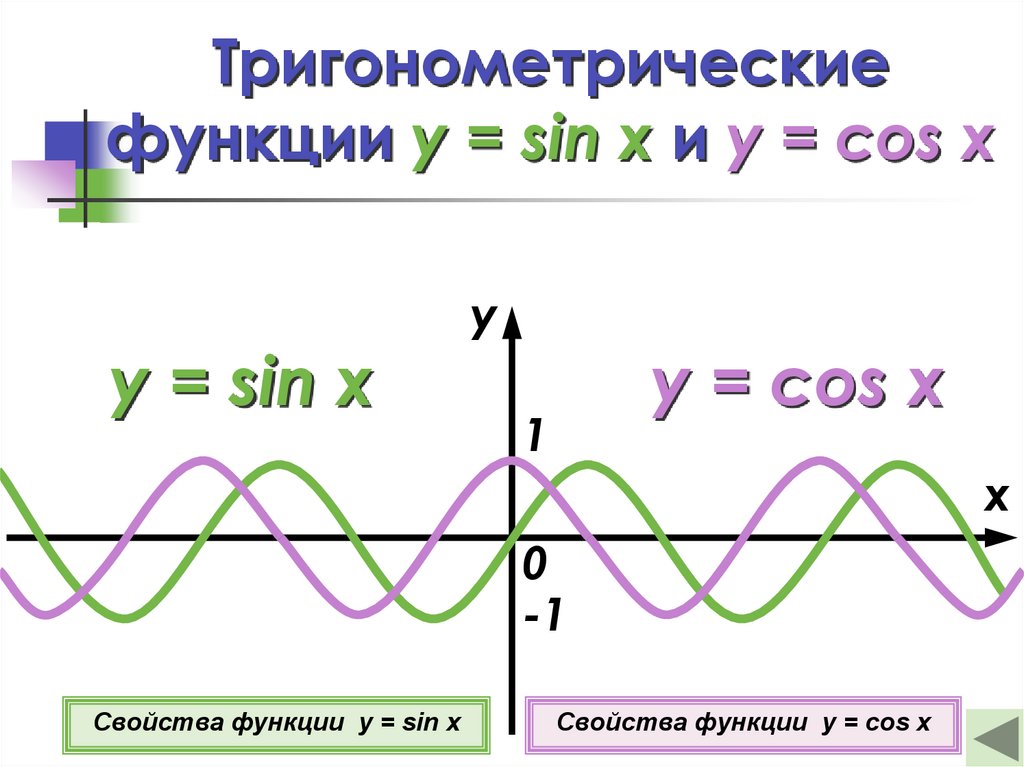
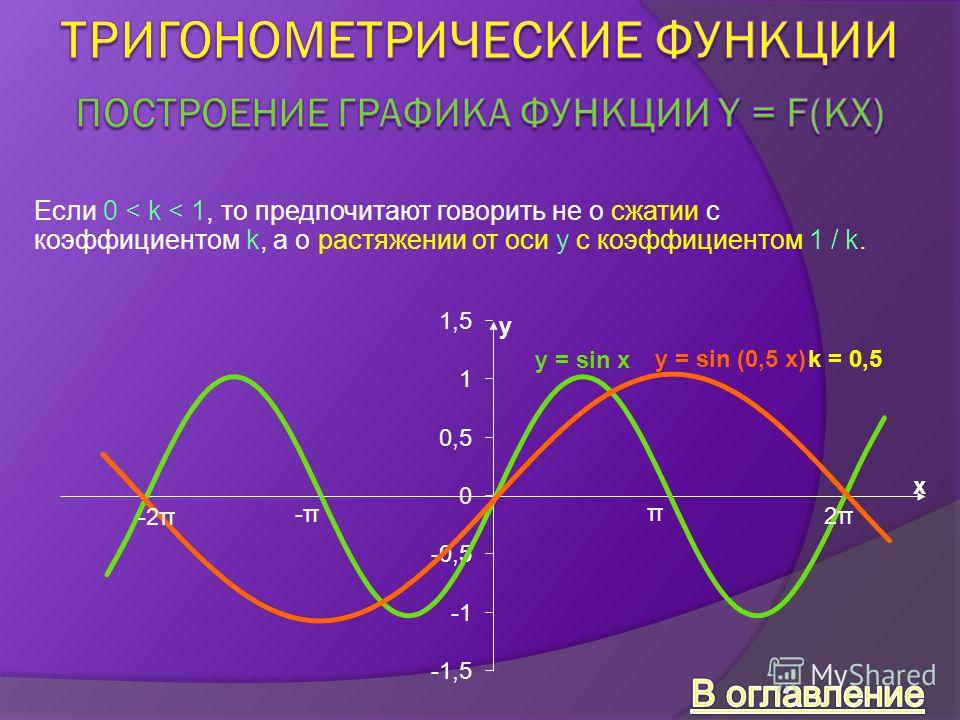
Свойства обратных тригонометрических функций

• Главная
• Справочник
• Тригонометрия
• Свойства обратных тригонометрических функций

• Арксинус
• Арккосинус
• Арктангенс
• Арккотангенс
• Основные соотношения
• Решение простейших тригонометрических уравнений
• Частные случаи

Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

Арксинус

Арксинусом числа называется такое значение угла для которого

• Областью определения функции арксинус является отрезок
• Областью значений функции арксинус является отрезок
• Арксинус строго возрастающая функция.
• Арксинус является нечетной функцией:

Арккосинус

Арккосинусом числа называется такое значение угла для которого

• Областью определения функции арккосинус является отрезок
• Областью значений функции арккосинус является отрезок
• Арккосинус строго убывающая функция.
• Арккосинус является индифферентной функцией: Функция центрально-симметрична относительно точки

Арктангенс

Арктангенсом числа называется такое значение угла для которого

• Областью определения функции арктангенс является вся числовая прямая:
• Областью значений функции арктангенс является интервал
• Арктангенс строго возрастающая функция.
• Арктангенс является нечетной функцией:

Арккотангенс

Арккотангенсом числа называется такое значение угла для которого

• Областью определения функции арккотангенс является вся числовая прямая:
• Областью значений функции арккотангенс является интервал
• Арккотангенс строго убывающая функция.
• Арккотангенс является индифферентной функцией: Функция центрально-симметрична относительно точки

Основные соотношения

Решение простейших тригонометрических уравнений

В общем виде

или

Частные случаи

a = – 1

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Тригонометрия Математика Тригонометрия Формулы Теория 11657

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

• Меры углов

  Для измерения углов используются градусы или радианы.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Соотношения между тригонометрическими функциями

  Знак тригонометрической функции в левой части должен совпадать со знаком правой части.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Периодичность тригонометрических функций

  Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π. Тригонометрические функции tg(x) и ctg(x) являются периодическими, с наименьшим периодом равным π.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Четность и нечетность тригонометрических функций

  Четной называется функция, которая не меняет своего значения при изменении знака независимой переменной. Нечетной называется функция, которая меняет свое значение при изменении знака независимой переменной.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Тригонометрические функции суммы и разности углов

  Тригонометрические функции суммы и разности углов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Соотношения между обратными тригонометрическими функциями

  Тригонометрия Математика Тригонометрия Формулы Теория

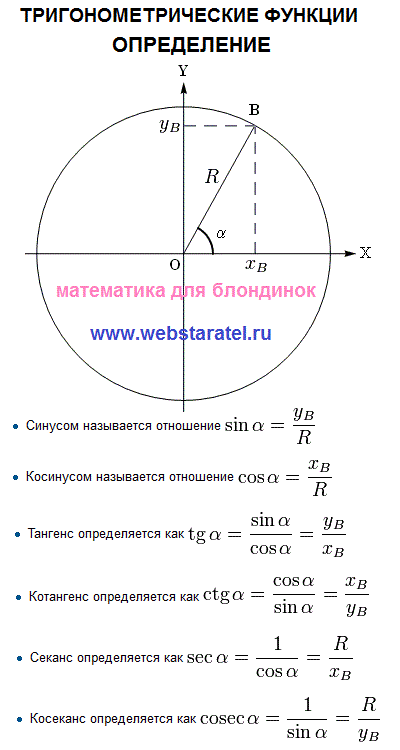
• Определения тригонометрических функций в прямоугольном треугольнике

  Тригонометрия Математика Тригонометрия Формулы Теория 8 класс

• Сколько километров в узле?

  Один морской узел равен одной тысяче восемьсот пятьдесят двум метрам или одному километру восемьсот пятьдесят двум метрам

  Размеры и расстояния Формулы

• Закон Дальтона

  Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.

  Законы Уравнение Формулы Физика Химия Закон Термодинамика

• Что такое Ампер

  1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.

  Электротехника Формулы Физика Теория Электричество

• 1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?

  Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.

  Разное Единицы измерения Деньги Справочник

• Солько весит ведро?

  Ведро́ — сосуд для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния.

  Масса и вес Масса Теория Единицы измерения

• Что такое дюйм? Чему равен 1 дюйм?

  Дюйм — это длина, которая соответствует 2,54 сантиметра (приблизительно 25 миллиметров)

  Размеры и расстояния Длина Формулы

• ЕГЭ: обязательные предметы для сдачи экзамена

  ЕГЭ Экзамены

• Переводчик азбуки Морзе онлайн

  Азбука Морзе — перечень сигналов из точек и тире, воспроизводящихся с помощью радиосигналов или прерыванием постоянного электрического тока.

  Работа с текстом Инструмент Текст

Свойства тригонометрических функций | План-конспект урока по алгебре (10 класс) по теме:

Аннотация

     Данное занятии е является продолжением изучения раздела «Тригонометрические функции».Урок предназначен для учащихся 10 классов. Урок является интегрированным с дисциплиной информатика по теме «Применение информационных технологий». Позволит педагогу развить идеи программированного обучения.

Методические рекомендации.

    Преподаватель математики в своей работе постоянно сталкивается с различными трудностями и проблемами6 как научить логично мыслить, правильно ставить вопросы, как сделать учебный процесс сделать интересным. Попытки решить эти проблемы традиционным методом не дают желаемого результата, не способствуют развитию творческой личности. Необходимо обратить внимание на интеграцию дисциплин.           Применение новых информационных технологий требует от преподавателя и ученика компьютерной грамотности.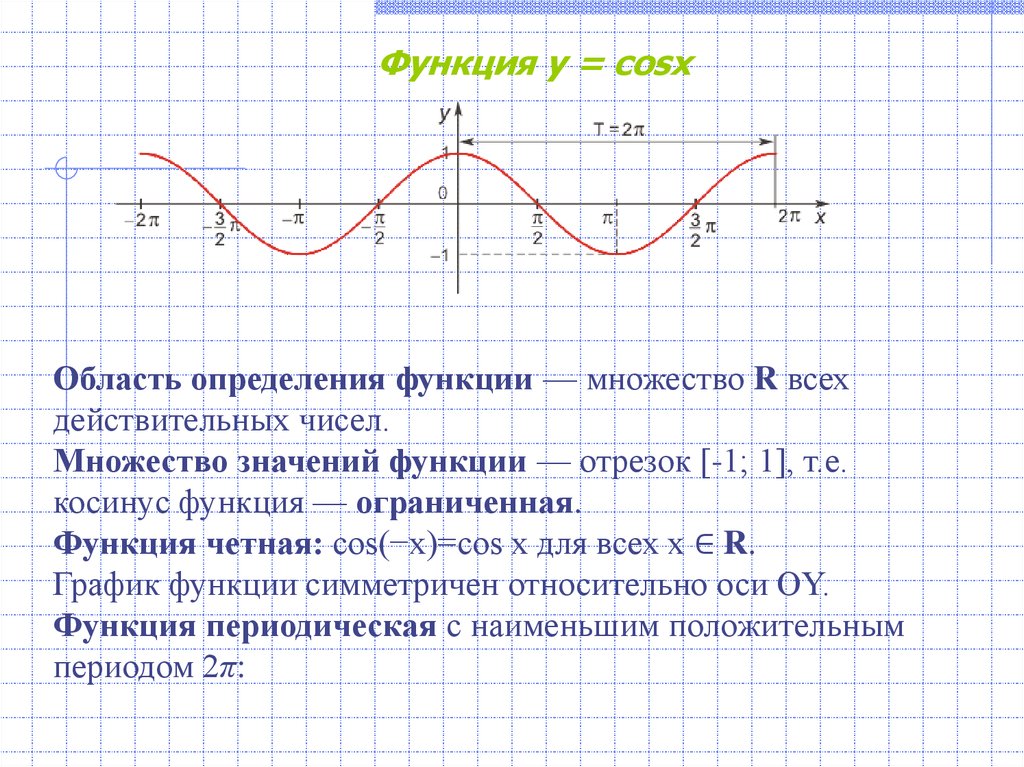  Применение ИТ  способствует:

-закреплению, совершенствованию знаний и умений, применению их на практике с использованием ИТ;

-освоению системы базовых знаний ;

-приобретению опыта использования ИТ в индивидуальной и коллективной учебно-познавательной деятельности.

      Всё выше сказанное ,является методическим обоснованием проведения предлагаемого мною занятия с использованием ИТ.

Тема: Свойства  и графики тригонометрических функций

Тип занятия: урок -закрепление

Место проведения: компьютерный класс.

Учитель: Дорофеева Лилия Ильинична.

Цели:

1)Обучающие:

-углубление, закрепление полученных знаний и умений

-изучение свойств основных тригонометрических функций и их свойств;

-совершенствование знаний , умений ,навыков с использованием информационных

2)развивающие:

-развитие навыков самоконтроля;

-развитие памяти, внимания, логического мышления;

-развитие умение  наблюдать и сравнивать

3) воспитательные:

-стимулирование потребностей  в самообразовании;

-формирование умения работы в коллективе, слушать, аргументированно высказывать свои мысли;

4)мотивационные:

-пробудить интерес к изучению математики;

-повышение интереса к вопросам современных компьютерных технологий;

-совершенствование навыков работы с программами прикладного обеспечения.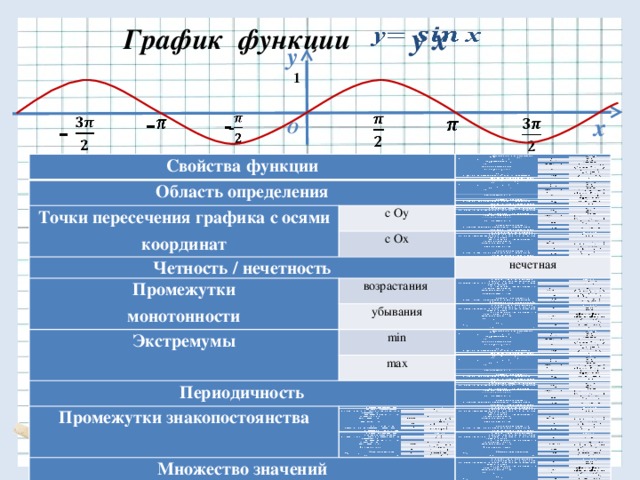

Обеспечение и оборудование к занятию:

-персональный компьютер;

-мультимедийный проектор;

-раздаточный материал.

Ход занятия

I. Организационный момент(3 мин)

2) Сообщение темы и целей занятия;

3)Сообщение форм работы .

II.Актуализация опорных знаний ( 7 мин)

1)Чтение графиков.

1. График, какой функции изображен на рисунке?

1) y = 1/2 sin x
2) y = 2cos x
3) y = cos 2x
4) y = 2sinx

2. График, какой функции изображен на рисунке?

1) y = – sin x
2) y = cos x
3) y = sin x
4) y = – cos x

3. График, какой функции изображен на рисунке?

1) y = – 2cos x
2) y = – 2sin x
3) y = 1/2 cos x
4) y = sin 2x

4. График, какой функции изображен на рисунке?

1) y = – cos x
2) y = cos x
3) y = sin x
4) y = – sin x

5. График, какой функции изображен на рисунке?

1) y = – cos x
2) y = cos x
3) y = – sin x
4) y = sin x

6.  График, какой функции изображен на рисунке?

1) y = – 3 cos x
2) y = – 1/3 sin x
3) y = cos 3x
4) y = 3 sin x

7. График, какой функции изображен на рисунке?

1) y = – cos x
2) y = – sin x
3) y = cos x
4) y = sin x

8. График, какой функции изображен на рисунке?

1) y = – sin 2x
2) y = 1/2 cos x
3) y = 2 sin x
4) y = – 2 cos x

9. График, какой функции изображен на рисунке?

1) y = 3 cos x
2) y = – 3 sin x
3) y = – cos 3x
4) y = 1/3 sin x

10. График, какой функции изображен на рисунке?

1) y = 2 cos x
2) y = – 2 sin x
3) y = – 1/2 cos x
4) y = sin 2x

2) Сообщение темы и целей занятия;

3)Сообщение форм работы .

II.Самостоятельная работа ( 15 мин)

Работа даётся по двум вариантам:

первый вариант даёт характеристику функции sinx, второй -cosx.

Характеристика
Область определения
Область значения
Чётность(нечётность)
Наименьший положительный период
Координаты пересечения графика с осями координат -с осью ОХ -с осью ОУ
f(x)>0 f(x)
Промежутки возрастания функции
Промежутки убывания функции
Точки минимума Минимумы функции
Точки максимума Максимумы функции

III. Закрепление(12 мин)

Решить номера по учебнику Колмогорова:№112(а)

IV. Подведение итогов(3 мин)

V.Задание на дом.№113(а,г)

Изучить самостоятельно свойства и график функции тангенс(по учебнику).

Тригонометрические функции и их свойства. Урок 57

По способу организации познавательной деятельности: объяснительно-иллюстративные, репродуктивные.

Методы воспитания: Организация деятельности, формирование мировоззрения, стимулирование деятельности, осуществление контроля, взаимоконтроля, самоконтроля.

Этапы урока	Содержание этапа
Оргмомент. Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению	Приветствие Проверка подготовленности к уроку Организация внимания школьников Ознакомление с планом проведения урока
Проверка домашнего задания. Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы	Выявление степени усвоения заданного учебного материала Ликвидация обнаруженных недостатков. Проверка выполнения домашнего задания у доски
Вызов. Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.	Сообщение темы урока Формулируют цели: сформировать навыки применения знаний по данной теме
Актуализация знаний и умений Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т. д.	1.Определите какой четверти принадлежат данные углы 3800 ; 2800 ; 1600 ; 3220 ; 990 ; 4600 ; 1900 ; ; . I IV II IV II II III III II 2.Что называется единичной окружностью? Единичным радиусом? Какие направления поворота единичного радиуса известны? В каких единицах измеряется угол поворота единичного радиуса? Что такое угол в один радиан? Сколько приблизительно градусов содержит угол в 1 радиан ? Сформулировать правила перевода из градусной меры угла в радианную меру и наоборот. Определение основных тригонометрических функций. Что является аргументом для всех тригонометрических функций? От чего зависит значение тригонометрических функций?
Осмысление Изучение нового материала. Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации	Работа по учебнику. 1Выражения sin х и cos x определены для любых x, поскольку для любого числа х можно найти координаты точки , единичного круга. Выражение tg х имеет смысл при любом x, кроме чисел вида х = , n  Ζ. Выражение ctg x имеет смысл при любом x, кроме чисел вида х = πn, n  Ζ. 2. Поскольку sin х и cos х — это ордината и абсцисса точки  единичного круга, то областью значений синуса и косинуса является промежуток [-1; 1]. Поскольку tg α — это ордината точки  линии тангенсов, то областью значений тангенса является R. Поскольку ctg α — это абсцисса точки  линии котангенсов, то областью значений котангенса является R. 3. Поскольку точки Рα и Г-α единичного круга (рис. 75) симметричны относительно оси ОХ, то эти точки имеют одинаковые абсциссы и ординаты противоположны, т.е. sin (-α) = -sin α; cos (-α) = cos α. Какие знаки имеют тригонометрические функции в каждой координатной плоскости? ) Какие функции называются периодическими и почему? Объясните нахождение неотрицательного угла большего 3600) Какие тригонометрические функции нечетные, четные? ) Изучи примеры применения четности (нечетности) тригонометрических функций. Приведи свои примеры
Закрепления новых знаний и умений. Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения	Задание для группы 1) После выполнения этого задания вы вспомните это свойство; тригонометрических функций . ВЕРНО О Н Б К   cos0,1  tg12° 0 ctg4 0 НЕВЕРНО З Е А Т 2) Указать номера верных равенств: 1. sin ( — 3x) = sin 3x 2. cos 5x = cos (- 5x) 3. tg 0,6x = — tg 0,6x 4. ctg (- 2,4x) = — ctg 2,4x 5. sin (x-) = sin (–x) 6. cos (1,7  –x) = cos ( x-1,7 ) По номерам верных ответов легко сделать вывод о таком свойстве тригонометрических функций как чётность (нечётность).
Проверка новых знаний Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления	Работа с учебником № 383(чет),385 Уровень В № 391
Коррекция знаний. Задачи: скорректировать выявленные проблемы	Организация деятельности учащихся по коррекции выявленных недостатков Индивидуальное задание. Повторное разъяснение учителя.
Подведение итогов. Рефлексия. Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса	Мобилизация учащихся на рефлексию Стратегия «Телеграмма»  Кратко написать самое важное, что уяснил с урока с пожеланиями соседу по парте и отправить. — Чему научил вас урок? — Какое впечатление осталось у вас от урока? .Выставление оценок.

Важные свойства обратных тригонометрических функций

Обратные тригонометрические функции определяются как обратные функции некоторых основных тригонометрических функций, таких как функции синуса, косинуса, тангенса, секанса, косеканса и котангенса.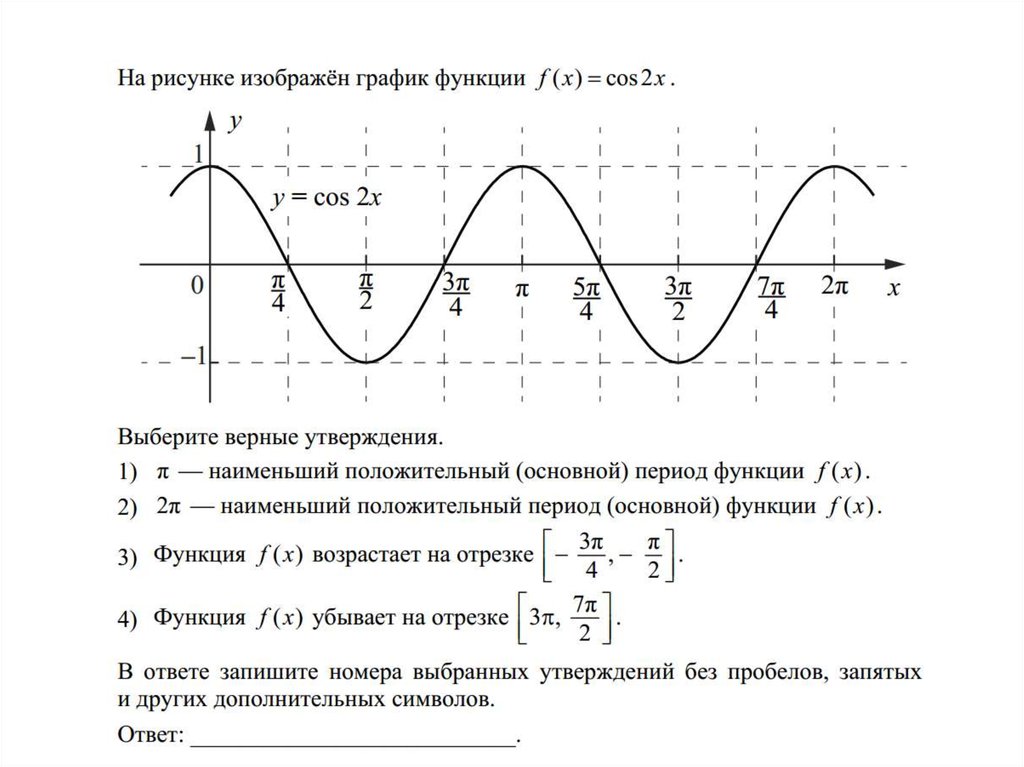 Обратные тригонометрические функции также известны как антитригонометрические функции, функции дуги и циклометрические функции. Эти формулы обратных тригонометрических функций позволяют нам найти любые углы с любым из соотношений тригонометрии. Эти формулы получены из свойств тригонометрических функций. В этой статье мы узнаем о концепциях обратной тригонометрии, свойствах обратных тригонометрических функций, проблемах обратных тригонометрических функций и т. д.

Диапазон и область определения обратных тригонометрических функций преобразуются из области определения и области значений тригонометрических функций. Мы изучаем отношения между углами и сторонами в прямоугольном треугольнике в тригонометрии. Также существуют функции обратной тригонометрии. Sin, cos, tan, cosec, sec и cot — основные тригонометрические функции. Обратные тригонометрические функции обозначаются sin-1x, cos-1x, cot-1x, tan-1x, cosec-1x и sec-1x соответственно.

Формулы обратной тригонометрии

Следующие формулы были объединены в список обратных тригонометрических формул. Эти формулы можно использовать для преобразования одной функции в другую, вычисления значений главного угла функций и выполнения различных арифметических операций с этими обратными тригонометрическими функциями. Кроме того, все основные формулы тригонометрических функций были преобразованы в формулы обратных тригонометрических функций и организованы в четыре группы ниже.

• Arbitrary Values ​​

• Reciprocal and Complementary functions

• Sum and difference of functions

• Double and triple of a function

Inverse Trigonometric Functions also termed as “Arc functions” or anti Trigonometric functions are функции, обратные некоторым основным тригонометрическим функциям.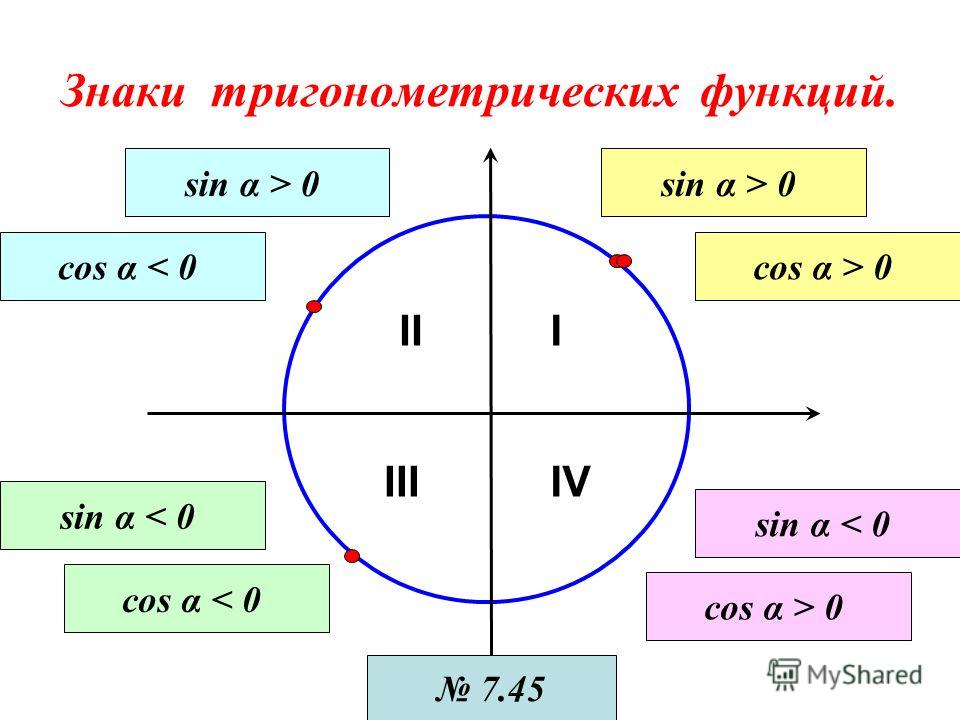 С их помощью находят неизвестные значения углов прямоугольного треугольника при любом из соотношений тригонометрии. Мы знаем, что тригонометрические функции обычно применяются к прямоугольному треугольнику. Они широко используются в области машиностроения, физики, геометрии и навигации. Шесть тригонометрических функций используются для определения измерения угла прямоугольного треугольника, когда известны измерения двух сторон треугольника.

 

Для каждого тригонометрического соотношения существует шесть тригонометрических функций. The inverse of those six Trigonometric functions are:

• Arcsine

• Arccosine

• Arctangent

• Arcsecant

• Arcosecant

• Arccontangent

Properties of Inverse Trigonometry

Inverse Тригонометрические функции обладают качествами, которые определяются областью и диапазоном функций. Есть несколько аспектов обратных тригонометрических функций, которые необходимы не только для решения проблем, но и для лучшего понимания этой темы. Диапазон значений, которые обратная функция может получить с определенной областью определения функции, определяется как диапазон значений, которые может получить обратная функция. Область определения функции определяется как совокупность всех мыслимых независимых переменных, в которых может существовать функция. Обратные тригонометрические функции имеют фиксированный диапазон значений.

Свойство 1:

• Sin−1(x) = cosec−1(\[\frac{1}{x}\]), x ∈ [−1,1]−{0}

• Cos−1(x) = sec−1(\[\frac{1}{x}\]), x ∈ [−1,1]−{0}

• Tan−1(x) = cot− 1(\[\frac{1}{x}\]), если x > 0  (или)  cot−1(\[\frac{1}{x}\]) −π, если x < 0

• Cot−1(x) = tan−1(\[\frac{1}{x}\]), если x > 0 (или) tan−1(\[\frac{1}{x}\]) + π, если x < 0

Свойство 2:

• Sin−1(−x) = −Sin−1(x)

• Tan−1(−x) = −Tan−1(x)

• Cos−1(−x) = π − Cos−1(x)

• Cosec−1(−x) = — Cosec-1(x)

• Sec-1(-x) = π — Sec-1(x)

• Cot-1(-x) = π — Cot-1(x)

Свойство 3:

• Sin−1(\[\frac{1}{x}\]) = cosec−1x, x≥1 или x≤−1

• Cos−1(\[\ frac{1}{x}\]) = sec−1x, x≥1 или x≤−1

• Tan−1(\[\frac{1}{x}\]) = −π + cot− 1(х)

Свойство 4:

• Sin−1(cos θ) = π/2 − θ, если θ ∈ [0,π]

• Cos−1(sin θ) = π/2 − θ , если θ ∈ [−π/2, π/2]

• Tan−1(ctg θ) = π/2 − θ, θ ∈ [0,π]

• Cot−1(tan θ) = π/2 − θ, θ ∈ [−π/2, π/2]

• Sec−1(cosec θ) = π/2 − θ, θ ∈ [−π/2, 0] ∪ [0 , π/2]

• Cosec−1(sec θ) = π/2 − θ, θ ∈ [0,π]−{π/2}

• Sin−1(x) = cos−1 \[\sqrt{(1−x^2)}\], 0 ≤ x ≤ 1

Свойство 5:

• Sin−1x + Cos−1x = π/2

• Tan−1x + Cot−1(x) = π/2

  −

1 Sec 1x = π/2

Решенные примеры

1.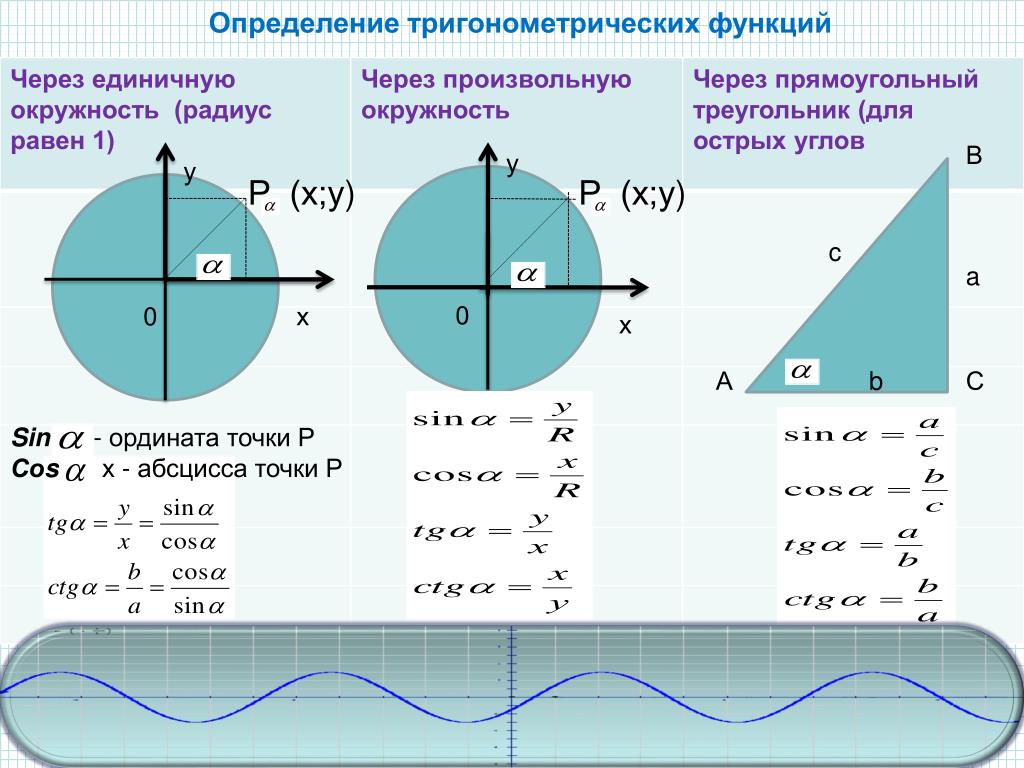 Докажите приведенное ниже уравнение: «Sin-1 (-x) = — Sin-1 (x), x ϵ (-1, 1)»

 

Решение: Пусть Sin-1 (-x) = y

 

Тогда -x = sin y

x = — sin y

x = sin (-y)

sin-1 -x = arcsin ( sin( -у))

sin-1 -x = y

Следовательно, Sin-1 (-x) = — Sin-1 (x), x ϵ (-1, 1)

 

2. Докажите, что Cos-1 (4×3 — 3 x) = 3 Cos-1 x , ½ ≤ x ≤ 1.

 

Решение: Пусть x = Cos ϴ

 

Где ϴ = Cos-1 (-x)

LHS = Cos-1 ( -x) (4×3 -3x)

Подставляя значение x, получаем

= Cos-1 (-x) (4 Cos3ϴ — 3 Cosϴ)

 

Соответственно получаем,

Cos-1 (Cos 3ϴ) = 3ϴ

 

, заменив значение θ, мы получаем

= 3 COS-1 x

= RHS

Следовательно, доказано

Время викторины

1. Что является основной стоимость (−680°) ?

а. 2 π/9

б. -2 π/9

в. №/9

д. 34 π/9

 

2. Tan-1 (sin- π/2) равен

а. -1

б. 1

в. π/2

д. – π/4

Использование обратной тригонометрии

Это обратные функции синуса, косинуса, тангенса, котангенса, секанса и косеканса, и они используются для вычисления угла из любого из его тригонометрических соотношений. Инженерия, навигация, физика и геометрия требуют обратных тригонометрических функций.

Если вы плотник, например, и хотите убедиться, что конец деревянного профиля обрезан под углом 45 градусов, вы можете использовать обратные тригонометрические функции. Вы можете определить угол разреза, измерив длины сторон в конце молдинга и используя обратную тригонометрическую функцию. В результате обратные триггерные функции можно использовать для различных плотницких работ, таких как строительство.

Применение обратной тригонометрии

В инженерии, строительстве и архитектуре часто используются обратные тригонометрические отношения. Обратные тригонометрические отношения — это самый простой способ получить неизвестный угол, поэтому мы используем их в местах, где нам нужно знать угол для нашей помощи и быстрого получения желаемого результата. Ниже приведены несколько примеров использования обратных тригонометрических соотношений:

1. Неизвестные углы прямоугольного треугольника измеряются с помощью этой формулы.

2. Используется для определения глубины отверстия или угла наклона.

3. Используется архитекторами для определения угла моста и его опор.

4. Плотники используют этот инструмент для достижения определенного угла среза.

Факты

• Гиппарх — отец тригонометрии, составивший первую тригонометрическую таблицу0003

• Эйлер написал «A t» для арктангенса в 1736 году.

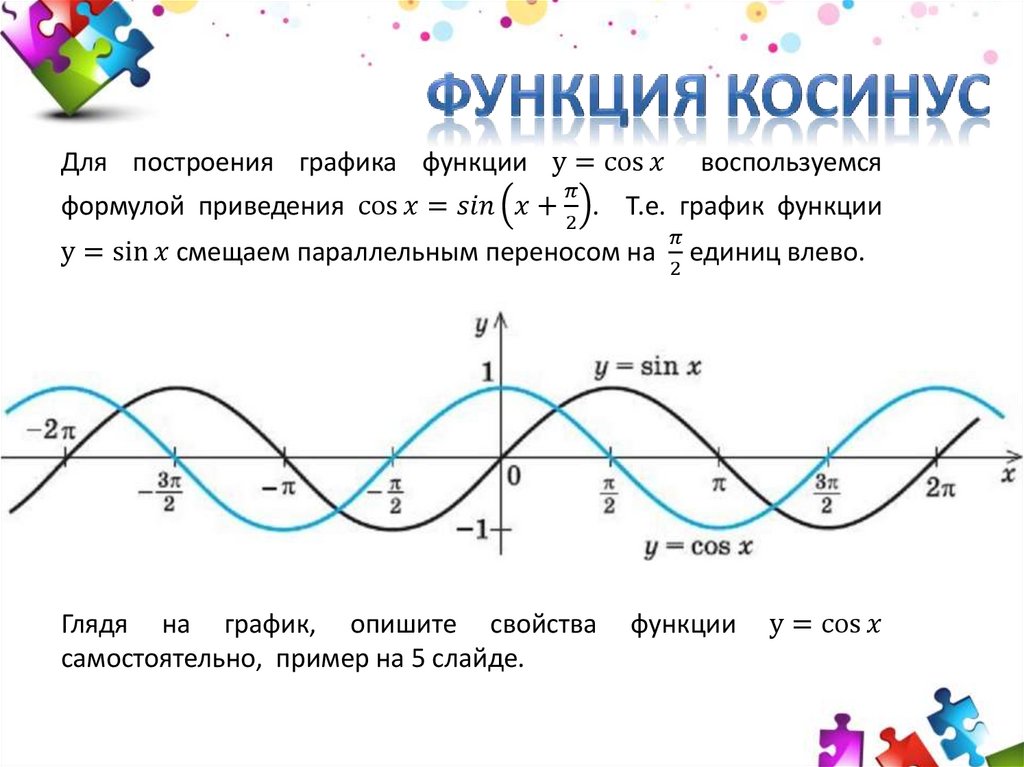
Графики тригонометрических функций. При этом мы часто сталкиваемся с

тригонометрическими значениями , которые нам нужно вычислить, чтобы получить наш результат. Например, мы можем обнаружить, что недостающую длину треугольника можно найти, вычислив . Итак, мы просто берем наш удобный калькулятор, набираем , и Боб становится вашим дядей. Однако вы могли или не могли задаться вопросом, почему значение таково, какое оно есть; откуда номер? В этой статье мы рассмотрим графики тригонометрических функций помогут нам ответить на этот вопрос.

Напомним, что когда мы изучали тригонометрические соотношения, мы смотрели на функции , и . Тригонометрическая функция — это функция, которая связывает величину угла в прямоугольном треугольнике с длинами его сторон.

Свойства тригонометрических графиков

При изучении графиков тригонометрических функций нас интересуют три графика: графики sin(x) , cos (x ) и tan(x) . Для математики GCSE вам нужно запомнить, как выглядят эти графики. Тем не менее, у них есть некоторые ключевых свойств , которые делают их довольно простыми в рисовании. Начнем с графика .

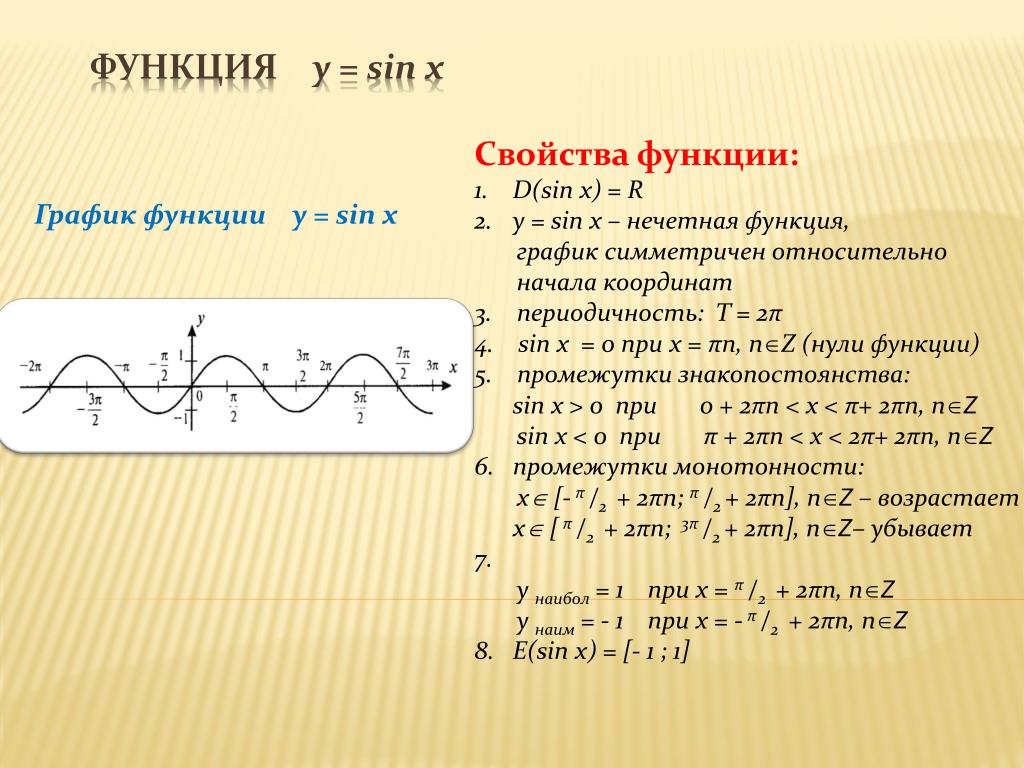
График y=sin(x)

Графики тригонометрической функции — график y=sin(x), Jordan Madge — StudySmarter Originals

Ключевые свойства

• Мы видим, что график y=sin(x) имеет максимальное значение 1 и минимальное значение -1. Отсюда мы можем сделать вывод, что значение sin(x) может быть только между 1 и -1. Таким образом, если у нас есть уравнение где , уравнение не имеет решений.

• Значения x увеличиваются с интервалом в 90 градусов и периодически повторяют в цикле 360 градусов. Другими словами, через каждые 360 градусов мы замечаем, что график повторяет .

• В различных точках граф симметричен . Например, у нас есть симметрия относительно линии . Это пригодится нам в дальнейшем при поиске множественных решений тригонометрических уравнений.

Допустим . Глядя на график, мы видим, что при , и . Поскольку график будет продолжать бесконечно осциллировать , мы можем заключить из этого, что уравнение имеет бесконечное число решений. Если тригонометрическое уравнение имеет одно решение, оно будет иметь бесконечное число решений, и позже мы будем использовать свойство симметрии, чтобы попытаться найти такие решения.

Официальное название графика, имеющего форму синусоиды, — синусоидальная волна . Многие вещи естественным образом принимают форму синусоиды, например, движение планет вокруг Солнца.

График y=cos(x)

Графики тригонометрической функции – график y=cos(x), Jordan Madge – StudySmarter Originals

Ключевые свойства

• раздел, вы можете подумать, что этот график почти такой же, как график . Однако, если вы вернетесь назад и поиграете в нахождение различий, вы заметите, что график — это всего лишь график сдвинул 90 градусов на влево .

• Подобно , график также имеет максимум при , минимум при , а также свойство симметрии . Мы должны просто помнить, что график начинается с , тогда как график начинается с .

График y=tan(x)

Графики тригонометрической функции – график y=tan(x), Jordan Madge – StudySmarter Originals

Ключевые свойства

• График выглядит немного иначе, чем и . Однако это похоже в том смысле, что это 90 315 периодических 90 316, и мы можем видеть, что оно повторяется каждые 90 315 градусов 90 316.

• На графике есть эти вещи, называемые асимптотами , которые представляют собой точки, к которым график стремится, но никогда не достигает их. На графике они представлены пунктирными линиями. Мы видим, что первая положительная асимптота появляется при , а затем они повторяются через каждые градусы.

• В отличие от и , график не имеет максимума или минимума плюс или минус ; у него есть максимум и минимум плюс-минус бесконечность . Таким образом, уравнение может быть решено для получения бесконечного числа действительных значений x.

Графики тригонометрических функций Методы

Нахождение решений тригонометрических уравнений

В предыдущем разделе мы вкратце коснулись того факта, что если тригонометрическое уравнение имеет одно решение, то оно будет иметь бесконечное число решений.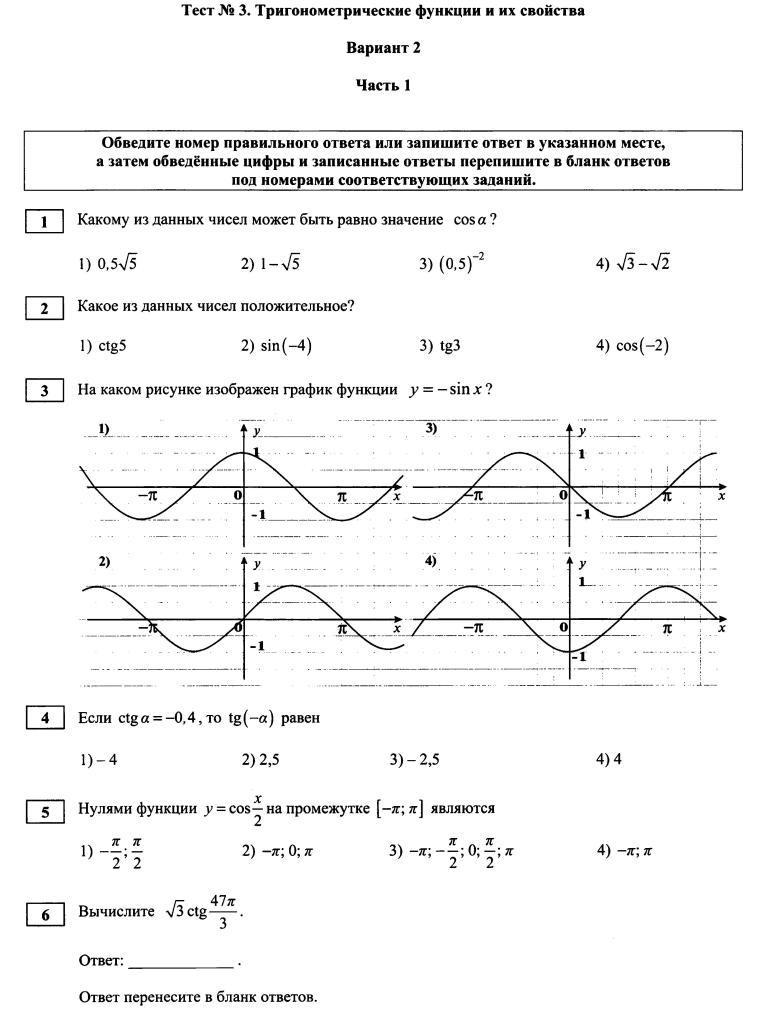 В следующем разделе мы разберемся, как найти несколько решений тригонометрических уравнений.

Поскольку тригонометрические уравнения могут иметь бесконечное число решений, нам нужно указать границу при формулировании ответов, чтобы мы не тратили бесконечное количество времени на поиск каждого последнего решения. Эта граница обычно выражается в виде интервала, например, или . Обязательно обратите внимание на эту границу, отвечая на вопросы.

Графики тригонометрических функций Примеры

Найдите решения для , для интервала .

Решение:

Первый шаг — начертить график и на одной оси для интервала .

Графики тригонометрических функций — График, показывающий решения sin(x) = 0,9, Jordan Madge — StudySmarter Originals

Точки пересечения отмечены оранжевым цветом как 1 и 2, это решения, которые мы ищем, чтобы найти точное значения.

Второй шаг — найти точное значение начального решения.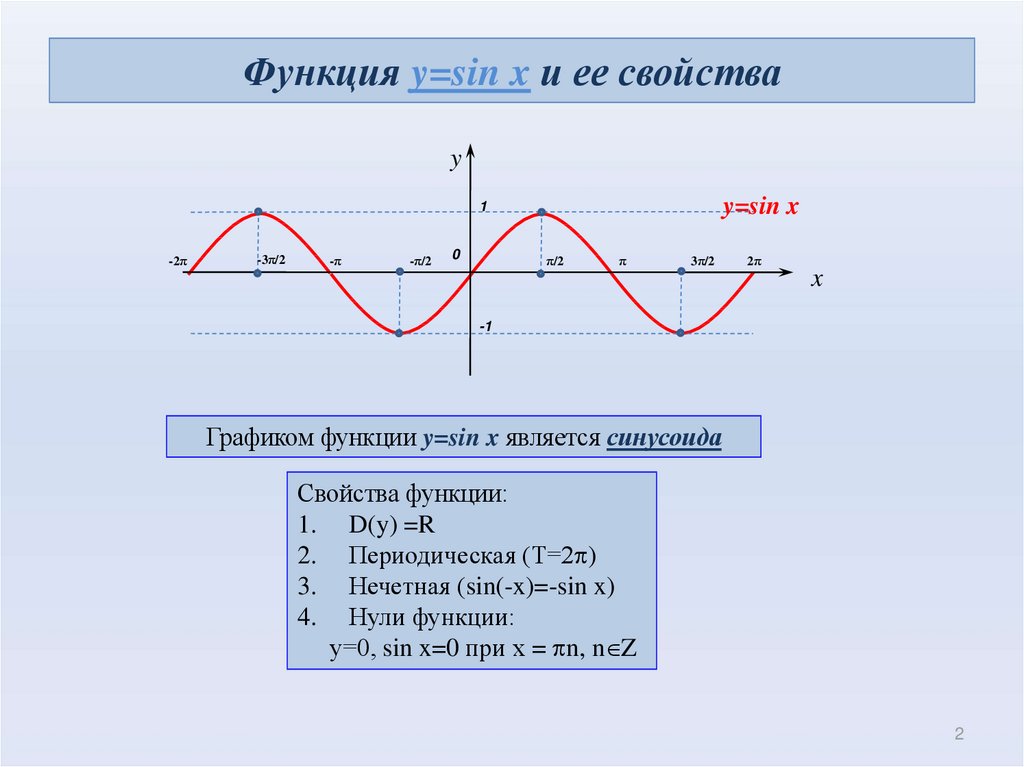 Это можно сделать, введя данные в наш калькулятор. Сделав это, мы получим . Очевидно, это первое решение, отмеченное на диаграмме, поскольку оно находится между и .

Важно отметить, что ваш калькулятор должен быть в режиме градусов при расчете тригонометрических значений, так как мы работаем в градусах. Если ваш калькулятор находится в режиме радиан , ответ может отличаться, и вы можете получить неверный ответ. Вы знаете, что ваш калькулятор находится в режиме градусов, когда в верхней части экрана появляется маленькая буква D. Если вы видите букву R или любую другую букву, это означает, что выбран неправильный режим, и его необходимо изменить.

Следующий шаг — найти другое решение, используя свойство симметрии графика sin(x). Если мы заметим, график симметричен относительно . Таким образом, мы можем найти второе решение, вычислив расстояние между и и затем добавив это значение к . Это можно проиллюстрировать на диаграмме ниже:

Графики тригонометрических функций — График, показывающий решения sin(x) = 0,9, Jordan Madge — StudySmarter Originals

Поскольку расстояние между и равно , второе решение равно .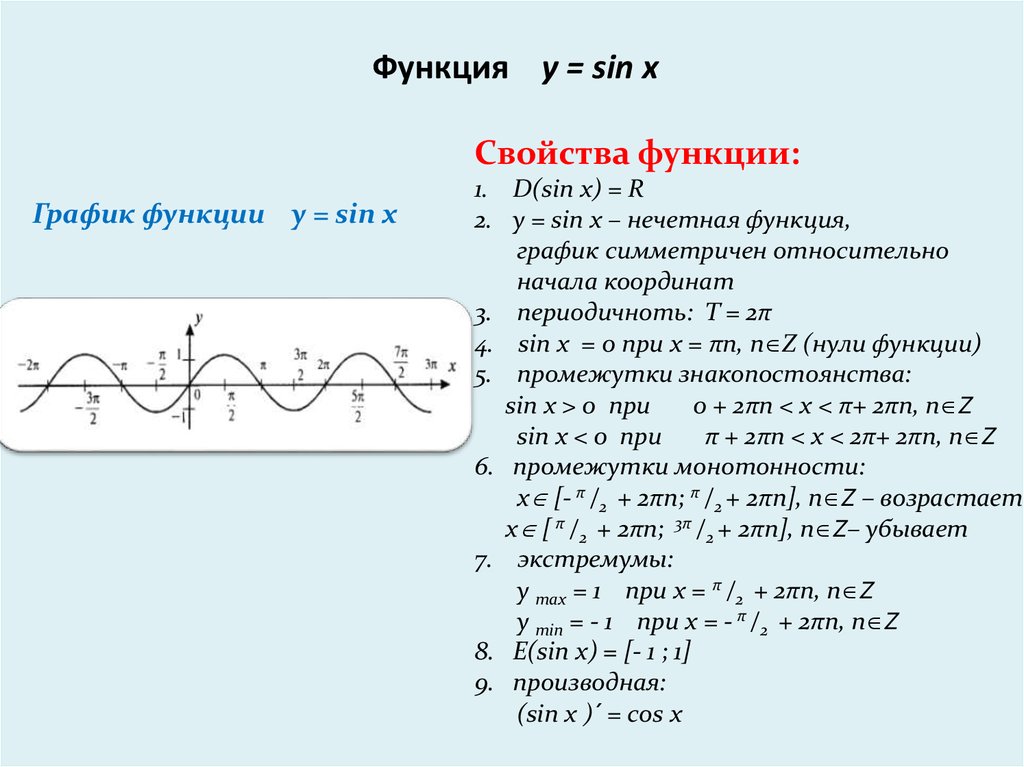 Следовательно, два решения уравнения в интервале равны и .

Найдите решения для интервала .

Решение:

Первым шагом является набросок графиков и на тех же осях для интервала, чтобы мы могли видеть решения, которые мы пытаемся найти.

Графики тригонометрических функций – График, показывающий решения cos(x)=-0,2, Джордан Мэдж – StudySmarter Originals

Следующий шаг – найти начальное решение, введя его в наш калькулятор. Мы получаем . Ясно, что это решение, отмеченное на диаграмме цифрой 2, так как оно немного больше, но меньше .

Теперь нам нужно найти другое решение, изображенное на диаграмме. Поскольку график симметричен относительно линии , мы можем видеть, что другое решение должно быть при . Таким образом, два решения в интервале и .

Найдите решения для интервала .

Решение:

Первым шагом, как обычно, является набросок графиков и на тех же осях для интервала .

Графики тригонометрических функций. График, показывающий решения tan(x)=2.3, Jordan Madge- StudySmarter Originals

Мы видим, что есть две точки пересечения и, следовательно, два решения для . Первое решение можно найти, введя в наш калькулятор. Делая это, мы получаем Это явно первое решение, так как оно находится между и степенями.

График периодически повторяется после градусов. Следовательно, мы можем найти следующее решение, прибавив множители 180 к исходному решению. Итак, второе решение находится в . Таким образом, два решения в интервале и .

Решения любых уравнений, содержащих tan(x), можно найти, прибавив к исходному решению число, кратное 180.

Найдите решения для интервала .

Решение:

Мы не можем решить это уравнение в его текущей форме. Сначала нам нужно разделить обе стороны на то, чтобы получить само по себе. Мы получаем . Теперь мы можем найти первое решение уравнения, взяв обратный тангенс обеих сторон, чтобы получить .

Теперь, поскольку он коричневый, мы знаем, что решения можно найти, прибавляя или вычитая кратные исходному решению. Таким образом, следующее решение будет при , однако это выходит за пределы допустимого диапазона. Мы можем получить другое решение, вычитая из, чтобы получить то, что находится в диапазоне. Дальнейшее вычитание даст решение вне диапазона, поэтому два решения в интервале равны и .

Графики тригонометрических функций. Ключевые выводы

• При изучении графиков тригонометрических функций нас интересуют три графика: графики sin(x), cos(x) и tan(x).
• Графики sin(x) и cos(x) имеют максимальное значение 1 и минимальное значение -1, график tan(x) имеет максимум и минимум плюс или минус бесконечность.
• График cos(x) — это просто график sin(x), сдвинутый влево на 90 градусов.
• Графики sin(x) и cos(x) обладают свойствами симметрии, которые позволяют нам находить несколько решений при решении уравнений.
• Для уравнений, включающих tan(x), мы можем получить каждое решение, прибавив к каждому решению число, кратное 180.

Объяснение урока: Графики тригонометрических функций

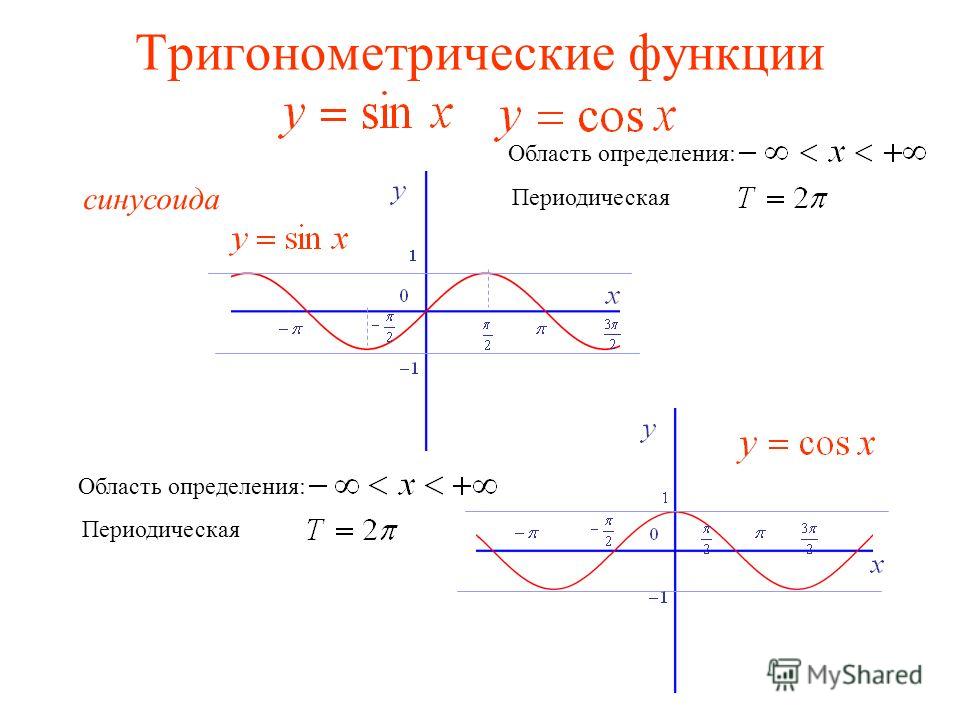
В этом объяснении мы научимся строить графики тригонометрических функций, таких как синус, косинус и тангенс, и выводить их свойства.

Начнем с рассмотрения специальных углов единичной окружности.

Мы знаем, что 𝑦-координаты этих точек представляют собой значения синусов соответствующих углов. Используя степени, мы можем построить вход-выход таблица для функции sin𝑥.

𝑥	0∘	30∘	45∘	60∘	90∘	120∘	135∘	150∘	180∘	210∘	⋯
sin𝑥	0	12	√22	√32	1	√32	√22	12	0	−12	⋯

222222. 0, когда 𝑥=0∘, и увеличивается до максимального значения 1, когда 𝑥=90∘. Построив точки из приведенной выше таблице ввода-вывода, мы можем аппроксимировать график sin𝑥.

Как отмечалось ранее, график sin𝑥 начинается с нуля, когда 𝑥=0∘, и увеличивается до максимального значения 1, когда 𝑥=90∘.

Поскольку 𝑥 представляет собой угол на диаграмме единичного круга, мы знаем, что каждое из этих значений повторяется каждые 360∘ или 2𝜋 радианы. Это приводит к тому, что sin𝑥 является периодическим с периодом 360∘, или 2𝜋 радианы. График греха𝑥 можно расширить за пределы интервала [0,360]∘∘, создав копии графика этого интервала. Например, график sin𝑥 над [−1080,1080]∘∘ показано ниже.

Из этого графика видно, что sin𝑥 имеет корни через каждые 180∘ начиная с 0∘. Заметим также, что функция синуса нечетная, а это означает, что его график осесимметричен относительно начала координат. Это свойство алгебраически выражается формулой грех(-𝑥)=-𝑥, для любого действительного числа 𝑥.

Свойства: синусоидальная функция и ее график

График синусоидальной функции демонстрирует следующие характеристики:

• 𝑦-пересечение sin𝑥 равно 0 и увеличивается до максимального значения 1.
• Корни sin𝑥 180𝑛∘, или 𝑛𝜋 для любого 𝑛∈ℤ.
• Максимальное значение функции равно 1, а минимальное значение равно −1.
• Функция периодическая, с периодом 360∘ или 2𝜋 радианы.
• sin𝑥 — нечетная функция; то есть sinsin(−𝑥)=−𝑥.

Аналогичным образом можно определить график функции косинуса. Мы знаем, что 𝑥-координаты точек на единичной окружности представляют косинусные значения соответствующих углов. Затем мы можем получить таблицу ввода-вывода.

𝑥	0∘	30∘	45∘	60∘	90∘	120∘	135∘	150∘	180∘	210∘	⋯
потому что	1	√32	√22	12	0	−12	−√22	−√32	−1	−√32	⋯

By plotting these точек, мы можем аппроксимировать график функции косинуса.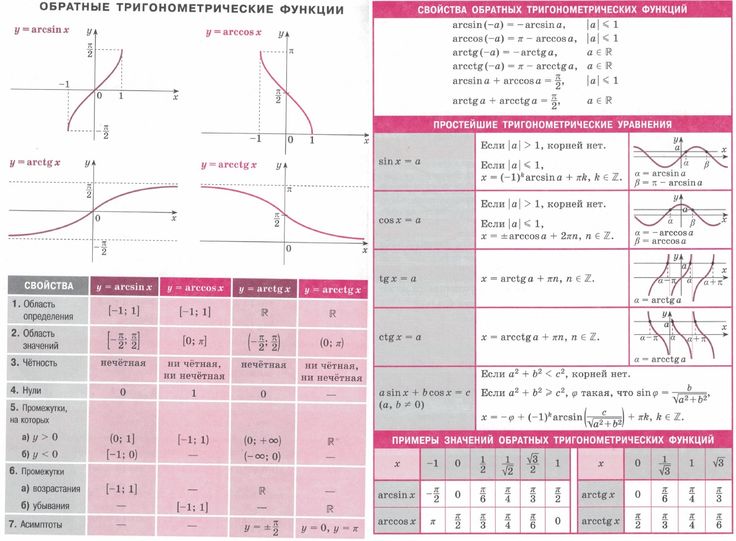

В отличие от графика синуса, косинус начинается с максимального значения 1 при 𝑥=0∘ и уменьшается до минимального значения −1 при 𝑥=180∘. Как синус, косинус является периодической функцией с периодом 360∘, или 2𝜋 радиан, и мы можем расширить этот график до больший интервал, делая копии графика поверх [0,360]∘∘. График cos𝑥 по [−1080,1080]∘∘ показано ниже.

Корни cos𝑥 начинаются на 90∘ и повторяются каждые 180∘. В отличие от синуса, мы можем видеть, что косинус является четной функцией, что означает что он имеет отражательную симметрию относительно оси 𝑦. Алгебраически это означает coscos(−𝑥)=𝑥.

Свойства: функция косинуса и ее график

График функции косинуса демонстрирует следующие характеристики:

• 𝑦-перехват функции равен 1, и он уменьшается до минимального значения −1.
• Корни cos𝑥 равны (90+180𝑛)∘ или 𝜋2+𝑛𝜋 для любого 𝑛∈ℤ.
• Максимальное значение функции равно 1, а минимальное значение равно −1.
• Функция периодическая, с периодом 360∘ или 2𝜋 радианы.
• cos𝑥 — четная функция; то есть coscos(−𝑥)=𝑥.

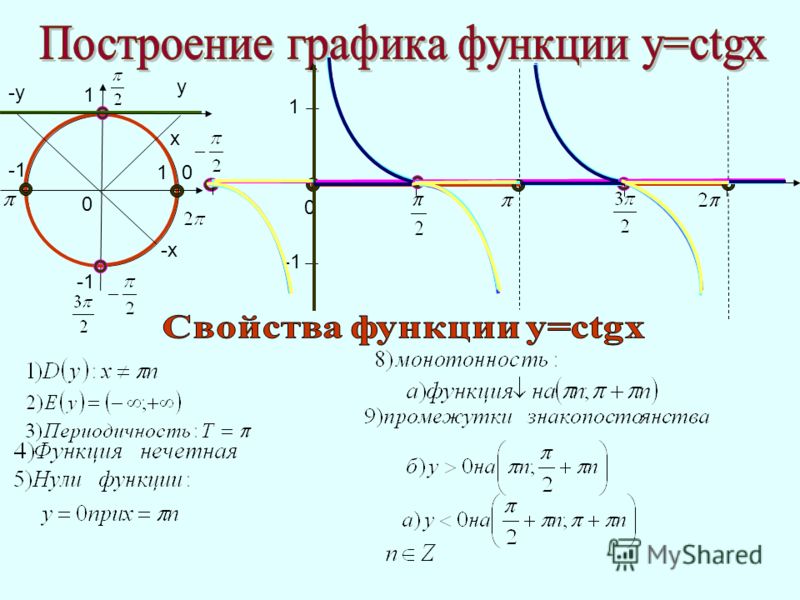
Наконец, рассмотрим график функции тангенса. Мы знаем, что тансинкос𝑥=𝑥𝑥. Это означает, что касательная функция не определена, когда cos𝑥 равен нулю, то есть когда 𝑥=(90+180𝑛),𝜋2+𝑛𝜋.∘orinradians

Используя таблицу ввода-вывода для синуса и косинуса, мы можем построить таблицу для тангенса.

𝑥	0∘	30∘	45∘	60∘	90∘	120∘	135∘	150∘	180∘	210∘	⋯
рыжевато-коричневый𝑥	0	√33	1	√3	Не определено	−√3	−1	−√33	0	√33	⋯

Построив эти точки, мы можем аппроксимировать график функции тангенса.

Опять же стоит подчеркнуть, что функция не определена на 90∘ и 270∘, так как cos𝑥=0 при этих углах.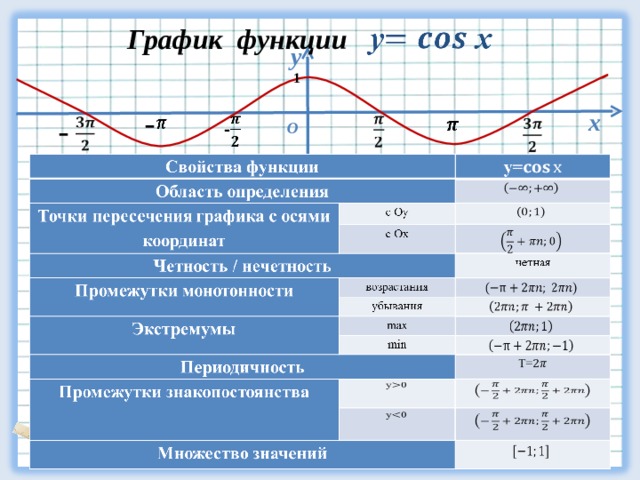 В отличие от синуса и косинуса, график функции тангенса неограничен и включает вертикальные асимптоты. Подобно синусу и косинусу, мы может периодически расширять этот график на больший интервал, [−990 990]∘∘.

Из этого графика видно, что период касательной функции равен 180∘, в отличие от функций синуса и косинуса, которые имеют периоды 360∘. Также, как и синус, график функции тангенса имеет вращательную симметрию относительно начала координат, что означает, что функция тангенса нечетна; то есть, тантан(-𝑥)=-𝑥.

Свойства: функция тангенса и ее график

График функции тангенса демонстрирует следующие характеристики:

• 𝑦-перехват функции равен 0, и он неограниченно возрастает до 𝑥=90∘.
• Корни загара𝑥 такие же, как и у греха𝑥. Это 180𝑛∘, или 𝑛𝜋, для любого 𝑛∈ℤ.
• График tan𝑥 имеет вертикальные асимптоты в корнях cos𝑥, которые равны (90+180𝑛)∘, или 𝜋2+𝑛𝜋 для любого 𝑛∈ℤ.
• Граф tan𝑥 не ограничен.
• Функция периодическая, с периодом 180∘ или 𝜋 радианы.
• tan𝑥 — нечетная функция; то есть тантан(-𝑥)=-𝑥.

В первых трех примерах определим, какая из тригонометрических функций соответствует данному графику, и рассмотрим какая часть графика тригонометрической функции является результатом каждого квадранта на единичной круговой диаграмме.

Пример 1. Распознавание тригонометрических функций по их графикам

Рассмотрим следующие рисунки.

1. Какую функцию представляет график на графике (а)?
   1. Косинус
   2. Синус
   3. Тангенс
2. Назначьте каждую область графика на рисунке (a) соответствующему квадранту единичного круга на рисунке (b).

Ответ

Часть 1

Напомним, что график функции тангенса имеет вертикальные асимптоты на каждом интервале длины 𝜋. Поскольку этот граф не имеет вертикальных асимптот на интервале длины больше 𝜋, это не может быть график функции тангенса. Следовательно, это должен быть график либо синуса, либо косинуса. Давайте сравним значения обозначены графиком со значениями функций синуса и косинуса.

Координаты точек на единичной окружности задаются (𝜃,𝜃) косинусом, где 𝜃 — угол радиуса против часовой стрелки относительно точки относительно положительной 𝑥-ось. На данном графике мы видим, что значение функции равно 0, когда угол равен 2𝜋 радианы. Мы знаем это 2𝜋 — это угол полного оборота, который приводит точку обратно к положительной оси 𝑥.

Координата точки единичной окружности, соответствующей углу 2𝜋, равна (1,0), что говорит нам cossin2𝜋=1,2𝜋=0.

Данный график показывает, что эта функция принимает значение 0 в 2𝜋, так что это согласуется с функцией синуса.

Это вариант B.

Часть 2

Мы знаем, что значения функции синуса задаются 𝑦-координатами точек на единичной окружности. Чтобы найти область единичного круга, соответствующую каждой части данного графа, мы проводим эти углы на единичном круге. Область A включает углы между 3𝜋2 и 2𝜋. Мы знаем, что 2𝜋 это полный оборот против часовой стрелки. В единичном круге эти углы можно изобразить, как показано ниже.

Следовательно, углы между этими двумя значениями лежат в четвертом квадранте, а это означает, что область A относится к квадранту IV.

Аналогично можно нарисовать углы области B.

Значит, эти углы лежат в первом квадранте. Следовательно, регион B относится к квадранту I.

Давайте посмотрим на остальные регионы.

Мы видим, что область C соответствует квадранту II, а область D соответствует квадранту III. В итоге имеем задания A:IVB:IC:II и D:III,.

Рассмотрим другой пример, в котором мы определим тригонометрическую функцию, представленную данным графиком, и свяжем области графа с частями единичного круга.

Пример 2. Распознавание тригонометрических функций по их графикам

Рассмотрим следующие рисунки.

1. Какую функцию представляет график на графике (а)?
   1. Косинус
   2. Синус
   3. Тангенс
2. Назначьте каждую область графика на рисунке (a) соответствующему квадранту единичного круга на рисунке (b).

Ответ

Часть 1

Напомним, что график функции тангенса имеет вертикальные асимптоты на каждом интервале длины 𝜋. Поскольку этот граф не имеет вертикальных асимптот на интервале длины больше 𝜋, это не может быть график функции тангенса. Следовательно, это должен быть график либо синуса, либо косинуса. Давайте сравним значения обозначены графиком со значениями функций синуса и косинуса.

Координаты точек на единичной окружности задаются (𝜃,𝜃) косинусом, где 𝜃 — угол радиуса против часовой стрелки относительно точки относительно положительной 𝑥-ось. На данном графике мы видим, что значение функции равно 0, когда угол равен −7𝜋2 радиан. Мы знаем, что негатив углы — это углы по часовой стрелке от положительной оси 𝑥. Поскольку −7𝜋2=−3𝜋−𝜋2, этот угол получается вращением по часовой стрелке от положительной оси 𝑥 на 3𝜋 (полтора оборота) и еще четверть оборота по часовой стрелке.

Координаты точки на единичной окружности, соответствующей углу −7𝜋2, равны (0,1), что говорит нам cossin−7𝜋2=0,−7𝜋2=1.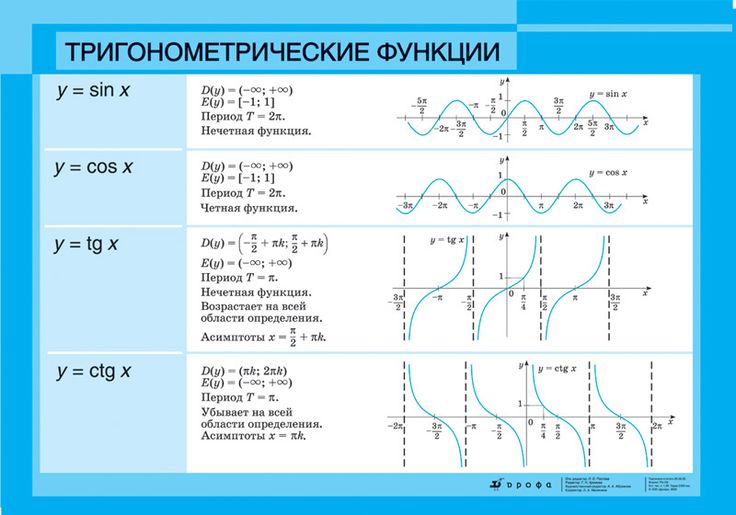

Данный график показывает, что эта функция принимает значение 0 при −7𝜋2, так что это согласуется с функция косинуса.

Это вариант А.

Часть 2

Мы знаем, что значения функции косинуса задаются 𝑥-координатами точек на единичной окружности. Чтобы найти область единичного круга, соответствующую каждой части данного графа, мы проводим эти углы на единичном круге. Область A включает углы между −11𝜋2 и −5𝜋. Мы знаем, что отрицательные углы отсчитываются по часовой стрелке от положительной оси 𝑥, а −2𝜋 — это полный оборот по часовой стрелке. Мы можем написать −11𝜋2=−2𝜋−2𝜋−𝜋−𝜋2.

Таким образом, этот угол представляет собой два с половиной оборота по часовой стрелке, за которыми следует дополнительная четверть оборота. Также −5𝜋=−2𝜋−2𝜋−𝜋, так что этот угол представляет собой два с половиной оборота по часовой стрелке. Эти углы нарисованы ниже.

Следовательно, углы между этими двумя значениями лежат во втором квадранте, а это означает, что область А относится к квадранту II.

Точно так же мы можем рисовать углы в других регионах.

Мы видим, что область B соответствует квадранту III, область C соответствует квадранту IV, а область D соответствует квадранту I. В заключение имеем присвоения A:IIB:IIIC:IVandD:I,.

Рассмотрим другой пример, где дан график тригонометрической функции с вертикальными асимптотами.

Пример 3. Распознавание тригонометрических функций по их графикам

1. Какую функцию представляет график на графике (а)?
   1. Косинус
   2. Синус
   3. Тангенс
2. Назначьте каждую область графика на рисунке (a) соответствующему квадранту единичного круга на рисунке (b).

Ответ

Часть 1

Среди функций синуса, косинуса и тангенса только функция тангенса имеет неограниченное возрастание. Другими словами, график функции тангенса содержит вертикальные асимптоты, а графики функций синуса и косинуса ограничены между −1 и 1. Следовательно, этот график представляет функцию тангенса.

Это вариант C.

Часть 2

Область A содержит углы между −𝜋2 и 0. Угол 0 представляет положительную ось 𝑥. Мы также знаем, что отрицательные углы отсчитываются по часовой стрелке от положительной оси 𝑥, поэтому угол −𝜋2 представляет собой четверть оборота по часовой стрелке от положительной оси 𝑥, что помещает этот угол на отрицательной оси 𝑦. Это говорит нам о том, что углы в области А лежат между отрицательными 𝑦-ось и положительная 𝑥-ось. Следовательно, область А соответствует четвертому квадранту.

Углы в области B лежат между 0 и 𝜋2. Мы знаем, что 0 представляет положительную 𝑥-ось, а 𝜋2 представляет собой положительную ось 𝑦, поскольку это четверть против часовой стрелки. оборот от положительной 𝑥-оси. Эти углы лежат в квадранте I.

Область C имеет углы между 𝜋2 и 𝜋. Так как 𝜋 является на пол-оборота против часовой стрелки, он представляет собой отрицательную 𝑥-ось. Следовательно, углы в области C лежат между положительная 𝑦-ось и отрицательная 𝑥-ось, которая является квадрантом II.

Наконец, область C имеет углы между 𝜋 и 3𝜋2. Последний угол составляет три четверти. оборот против часовой стрелки, который приземляется на отрицательную 𝑦-ось. Итак, квадрант между отрицательным 𝑥-ось, а отрицательная 𝑦-ось — это квадрант III.

В заключение у нас есть задания A:IVB:IC:II и D:III,.

В следующем примере мы распознаем правильный график тригонометрической функции по ее характеристикам.

Пример 4. Идентификация графика касательной функции

Что из следующего является графиком 𝑦=𝑥tan?

Ответ

Напомним несколько важных характеристик касательного графика:

• tan𝑥 является периодическим, с периодом 180∘.
• tan𝑥 имеет вертикальные асимптоты в корнях cos𝑥, которые 90+180𝑛∘∘ для любого 𝑛∈ℤ.
• Корни загара𝑥 такие же, как и у греха𝑥, которые 180𝑛∘ для любого 𝑛∈ℤ.

Давайте начнем с изучения первого свойства, которое говорит нам, что период загара𝑥 равен 180∘.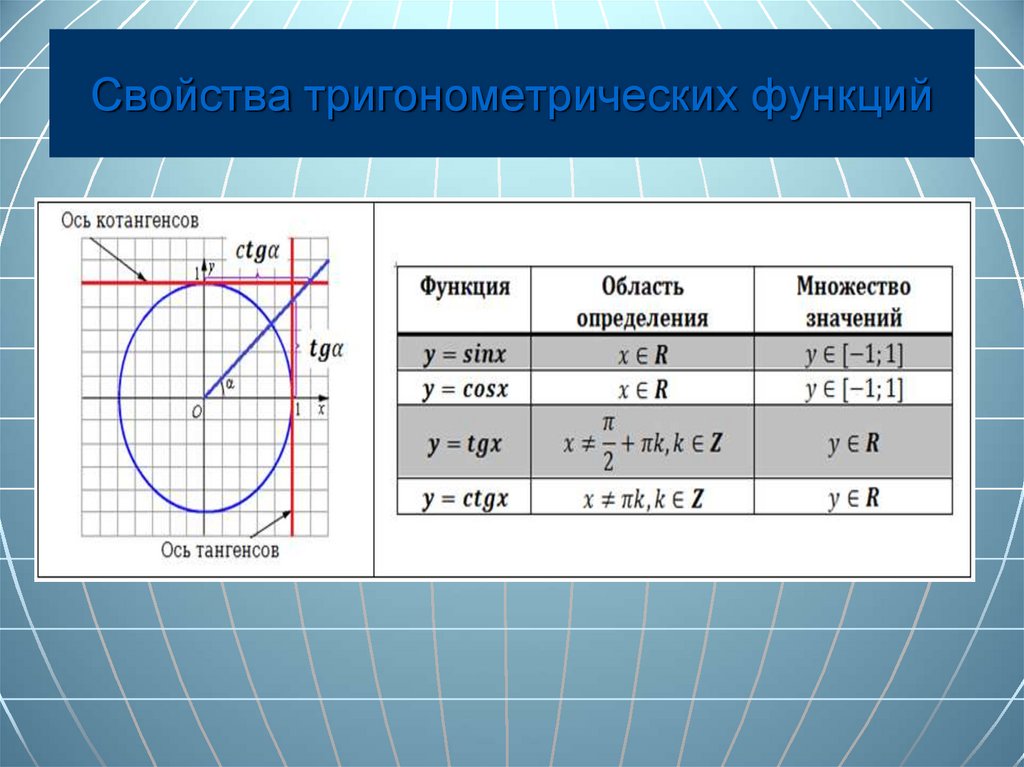 Мы видим, что вариант А имеет период 90∘, поэтому мы можем это исключить. Все остальные графы являются периодическими, т.е. период 180∘.

Вторая характеристика говорит нам о том, что мы должны видеть вертикальные асимптоты при 90+180𝑛∘∘. Поскольку мы уже проверяли периодичность 180∘, достаточно будет увидеть можем ли мы найти вертикальную асимптоту при 𝑥=90∘. Вариант Б не имеет вертикальной асимптоты при 𝑥=90∘, поэтому мы можем этот вон. Остальные варианты C, D и E имеют вертикальную асимптоту при 𝑥=90∘.

Далее рассмотрим корни. Мы знаем, что корни функции тангенса равны 180𝑛∘. Еще раз, поскольку мы уже проверили периодичность, достаточно проверить, есть ли на графе корень при 𝑥=0∘. Вариант C не имеет корня в точке 𝑥=0∘, поэтому мы исключаем этот вариант. Два оставшихся варианта, D и E, оба имеют корень в 𝑥=0∘.

Сравним оставшиеся два графика, D и E. Заметим, что функция в D отрицательна на интервале 𝑥∈(0,90)∘∘, в то время как функция в E положительна в этом интервале. Мы знаем, что 𝑥∈(0,90)∘∘ представляет собой острые углы или углы в первом квадранте. Поскольку функция тангенса положительна для острых углов, мы видим, что D равно а не график функции тангенса.

Это приводит к варианту E.

В нашем следующем примере мы идентифицируем график касательной функции после преобразования функции.

Пример 5. Определение графика тригонометрической функции после преобразования

Что из следующего является графиком 𝑦=−𝑥tan?

Ответ

Начнем с рисования графика tan𝑥. Напомним несколько важных характеристик график касательной:

• tan𝑥 периодический, с периодом 180∘.
• tan𝑥 имеет вертикальные асимптоты в корнях cos𝑥, которые 90+180𝑛∘∘ для любого 𝑛∈ℤ.
• Корни загара𝑥 такие же, как и у греха𝑥, которые 180𝑛∘ для любого 𝑛∈ℤ.

Кроме того, мы знаем, что tan𝑥 положителен для острых углов; то есть 𝑥∈(0,90)∘∘. Это приводит к графику функции тангенса.

Мы знаем, что умножение функции на −1 приводит к отражению по оси 𝑥.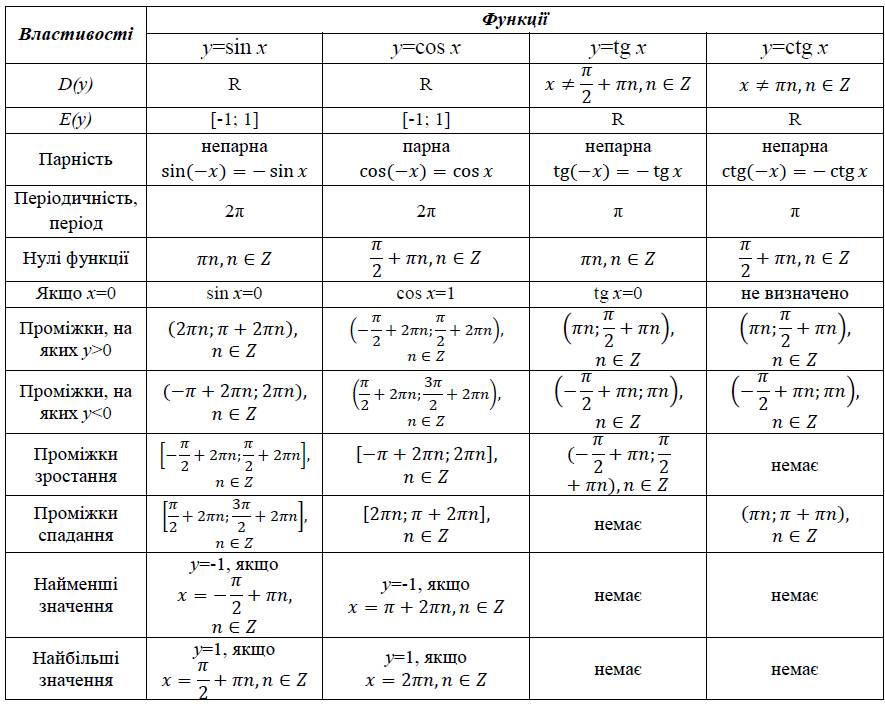 Так как мы умножая tan𝑥 на −1, чтобы получить заданную функцию −𝑥tan, нам нужно чтобы перевернуть этот график по оси 𝑥.

На приведенном выше графике сплошной синий график представляет исходную функцию tan𝑥, а пунктирный график представляет отраженная функция, −𝑥tan.

В частности, отметим, что и корни, и вертикальные асимптоты после отражения остаются прежними. Следовательно, график −𝑥tan должен иметь корни на 180𝑛∘ и вертикальные асимптоты при 90+180𝑛∘∘ для любого 𝑛∈ℤ.

Мы можем исключить варианты B, D и E, так как эти графики не демонстрируют корней в точках 180𝑛∘, особенно при 𝑥=0∘.

Мы видим, что разница между графиками в двух оставшихся вариантах, A и C, заключается в том, что функция отрицательна для 𝑥∈(0,90)∘∘ в A, в то время как положительно на этом интервале в C. На построенном нами отражающем графике −𝑥tan мы видим, что наша функция принимает отрицательные значения в течение (0,90)∘∘.

Это приводит к варианту A.

В нашем последнем примере мы применим функциональные преобразования к синусоидальной функции, чтобы получить новый график.

Пример 6. Нахождение максимального значения заданной синусоидальной функции

Найдите максимальное значение функции 𝑓(𝜃)=11𝜃sin.

Ответ

Напомним, что график sin𝜃 начинается с 0 при 𝜃=0∘ и колеблется между максимальным значением 1 и минимальное значение −1.

Мы знаем, что умножение положительной константы на 𝑎>0 приводит к вертикальному расширению (растяжению или сокращение) с масштабным коэффициентом 𝑎. Здесь мы умножаем sin𝜃 на 11, поэтому новый график этой функции можно получить, растянув приведенный выше график в 11 раз.

Здесь сплошной синий график представляет исходную функцию sin𝜃, а пунктирная кривая представляет функция 11𝜃sin. Двусторонние красные стрелки указывают вертикальное расширение. Мы можем видеть из этого график, показывающий, что функция 11𝜃sin колеблется между −11 и 11,

Мы также можем прийти к этому выводу алгебраически. Мы знаем это −1≤𝜃≤1.sin

Умножая это неравенство на 11, получаем −11≤11𝜃≤11.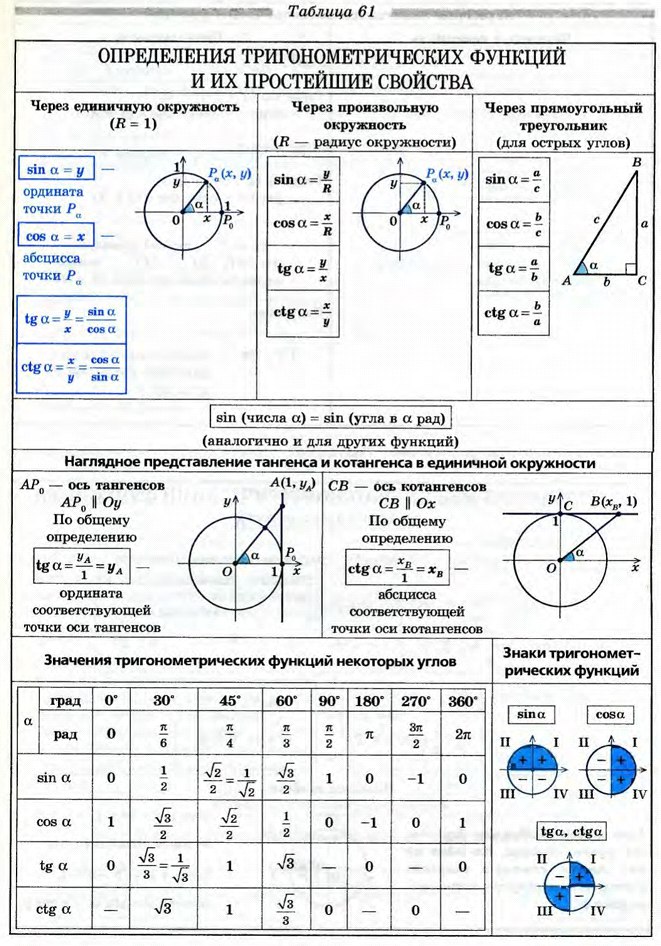 sin

Это приводит к максимальному значению 11.

Следовательно, максимальное значение 𝑓(𝜃)=11𝜃sin равно 11.

Давайте закончим, повторив несколько важных понятий из этого объяснения.

Ключевые моменты

• График синусоидальной функции демонстрирует следующие характеристики:
  • 𝑦-пересечение sin𝑥 равно 0 и увеличивается до максимального значения 1.
  • Корни греха𝑥 180𝑛∘, или 𝑛𝜋 для любого 𝑛∈ℤ.
  • Максимальное значение функции равно 1, а минимальное значение равно −1.
  • Функция периодическая, с периодом 360∘ или 2𝜋 радианы.
  • sin𝑥 — нечетная функция; то есть sinsin(−𝑥)=−𝑥.
• График функции косинуса демонстрирует следующие характеристики:
  • 𝑦-пересечение функции равно 1 и уменьшается до минимального значения −1.
  • Корни cos𝑥 равны (90+180𝑛)∘ или 𝜋2+𝑛𝜋 для любого 𝑛∈ℤ.
  • Максимальное значение функции равно 1, а минимальное значение равно −1.

    No related posts.