Таблица синусов, косинусов, тангенсов, котангенсов
Таблицы Брадиса для sin, cos, tg, ctg.
Таблица синусов, косинусов, тангенсов, котангенсов содержит вычисленные значения тригонометрических функций для определенного угла от 0 до 360 градусов в виде простой таблицы и в виде таблицы Брадиса. Так же приведены значения тригонометрических функций в радианах для наиболее распространённых углов, применяемых при вычислениях.
Таблицы с вычисленными значениями sin, cos, tg, ctg применяются для упрощения и ускорения математических вычислений, когда нет возможности воспользоваться калькулятором или компьютером.
- sin
- cos
- tg
- ctg
- триг. функции
- Брадиса sin и cos
- Брадиса tg и ctg
sin 0° = sin 360° = 0
| α° | sin α | α° | sin α | sin α | α° | sin α | |
|---|---|---|---|---|---|---|---|
| α° | sin α | α° | sin α | α° | sin α | α° | sin α |
|---|---|---|---|---|---|---|---|
cos 0° = cos 360° = 1
| α° | cos α | α° | cos α | α° | cos α | α° | cos α |
|---|---|---|---|---|---|---|---|
| α° | cos α | α° | cos α | α° | cos α | α° | cos α |
|---|---|---|---|---|---|---|---|
tg 0° = tg 360° = 0
| α° | tg α | α° | tg α | α° | tg α | α° | tg α |
|---|---|---|---|---|---|---|---|
| α° | tg α | α° | tg α | α° | tg α | α° | tg α |
|---|---|---|---|---|---|---|---|
ctg 0° = ctg 360° = ∞
| α° | ctg α | α° | ctg α | α° | ctg α | α° | ctg α |
|---|---|---|---|---|---|---|---|
| α° | ctg α | α° | ctg α | α° | ctg α | α° | ctg α |
|---|---|---|---|---|---|---|---|
Значения тригонометрических функций в радианах для наиболее распространённых углов.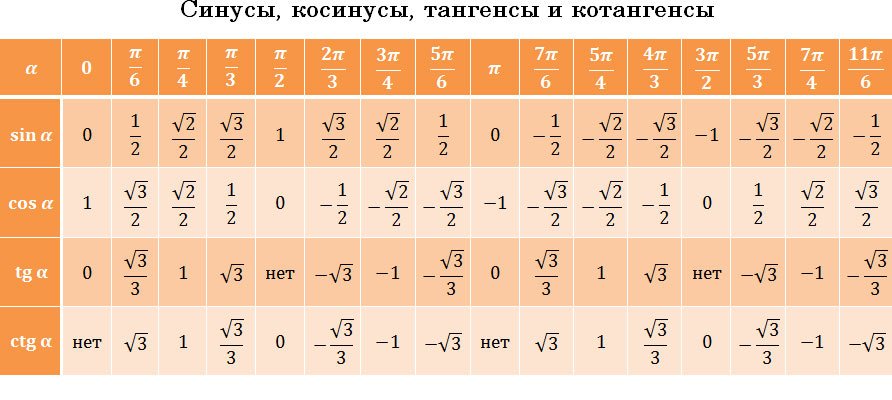
Таблица Брадиса для синусов и косинусов
| sin | 0′ | 6′ | 12′ | 18′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ | |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85° | 3 | 6 | 9 | |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1719 | 0. 1736 1736 | 80° | 3 | 6 | 9 | |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 | |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0. 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0. 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0. 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.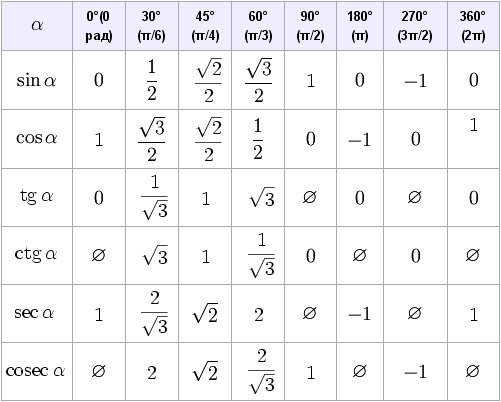 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0. 8192 8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0. 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0. 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0. 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.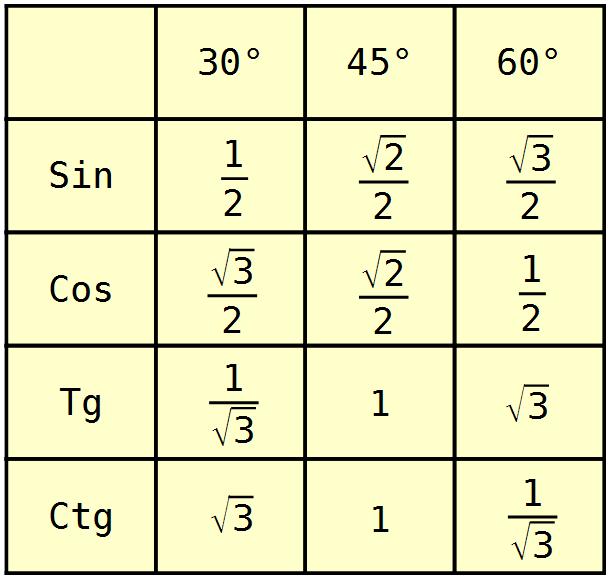 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0. 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Таблица Брадиса для тангенсов и котангенсов
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Тригонометрия и тригонометрические функции
Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.
Функция – это правило, описывающее зависимость одной величины от другой.
Угол — это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.
Углы по своему виду могут быть:
- острыми – меньше 90 градусов
- тупыми – больше 90 градусов
- прямыми – равными 90 градусов (прямые или отрезки перпендикулярны)
Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.
В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:
Прямоугольный треугольник
гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.
катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.
Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.
К базовым тригонометрическим функциям относятся:
То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.
Таблицы с вычисленными значениями синусов, косинусов, тангенсов, котангенсов.
Для ускорения расчетов, когда нет под рукой калькулятора, смартфона или компьютера, раньше были очень популярны таблицы с заранее вычисленными соотношениями сторон треугольников, выраженными в вычисленных значениях sin, cos, tg.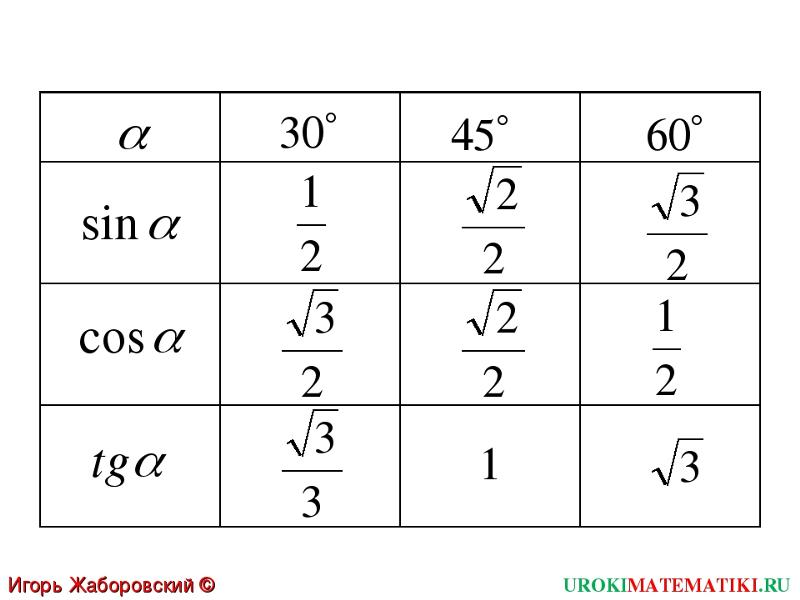
Например, зная из таблицы значения вычисленных заранее тригонометрических функций известного угла треугольника и длину одной из его сторон, можно быстро вычислить длины других сторон треугольника и величины неизвестных углов.
|
Вашему вниманию представлена тригонометрическая таблица синусов косинусов и тангенсов из таблицы Брадиса. Она дает данные с точностью до четвертого знака после запятой. Причем все численные величины углов идут с кратностью шесть минут. Промежуточные значения углов находятся методом поправок. Для того, чтобы узнать величину SIN мы выбираем значения угла слева, а чтобы узнать величину COS угол выбираем справой стороны, при этом значения минут для SIN будут сверху, а для COS снизу. Таблица Брадиса синусов и косинусов практически незаменима если вы проводите свои вычисления без инженерного калькулятора, поэтому постарайтесь овладеть всеми правилами использования предоставленных нами материалов. 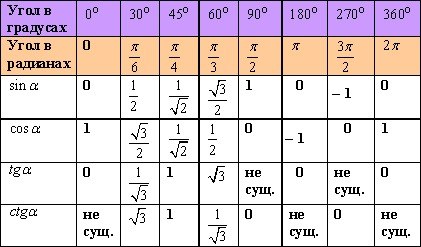
|
Как пользоватся таблицей Брадиса ⇒
| ||||||||||||||
Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)
Как найти значения тригонометрических функций для угла 15 градусов
Найдем значения синуса, косинуса и тангенса для угла 15 градусов аналитическим способом.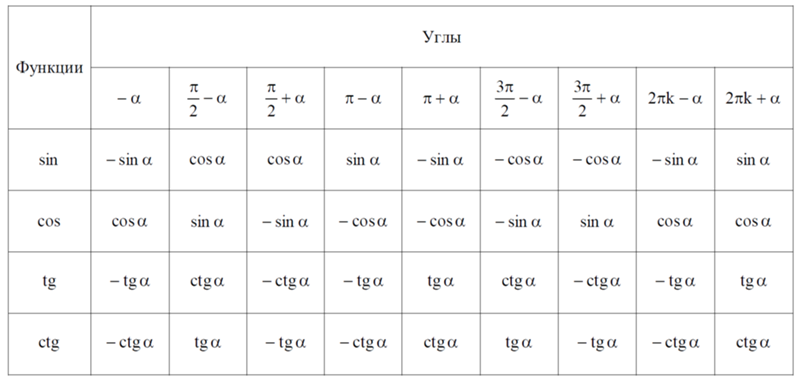
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 15 градусов — задача сложная. Однако, это не совсем так.
Нам на помощь придут формулы преобразования двойного угла тригонометрических функций.
Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).
Тогда, отталкиваясь от тождества:
cos 2α = 1 — 2sin2α
Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 — 2sin215
sin215 = ( 1 — cos 30 ) / 2
Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin215 = ( 1 — √3/2 ) / 2
sin 15 = √ (( 1 — √3/2 ) / 2 )
верхнюю часть дроби под корнем приведем к общему знаменателю (2)
sin 15 = √ (( (2 — √3) /2 ) / 2 ) = √( (2 — √3) / 4 )
теперь у нас одна дробь под знаком корня. Умножим числитель и знаменатель на два
sin 15 = √( (2 — √3) / 4 ) = √( (4 — 2√3) / 8 )
самый интересный момент, мы можем представить 4 — 2√3 как (√3-1)2
тогда
sin 15 = √( (√3-1)2 / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)
путем несложных агебраических преобразований получаем:
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 15 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 15 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
π/12 |
синус 15 sin 15 |
косинус 15 cos 15 |
тангенс 15 tg 15 |
котангенс 15 ctg 15 |
|
Значение |
0.2588190451 |
0.96592582628 |
0. |
3.73205080757 |
Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
Примечание: см. также таблицу значений тригонометрических функций других углов.
Табличные значения синуса 45, косинуса 45 и тангенса 45 градусов указаны ниже. Далее по тексту следует пояснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника.
45 градусов — это π/4 радиан. Формулы для значений косинуса, синуса и тангенса пи/4 радиан указаны ниже (хотя они и тождественны).
То есть, например, tg π/4 = tg 45 градусов
Как самостоятельно вычислить значения sin cos tg 45 градусов?
Построим и рассмотрим прямоугольный треугольник АВС у которого угол ∠В = 45°. На основании соотношения его сторон, вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный, то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.
На основании соотношения его сторон, вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный, то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.
Поскольку значение функций синуса, косинуса и тангенса зависят исключительно от градусной меры угла (или значения, выраженного в радианах), то найденные нами соотношения и будут значениями функции синуса 45, косинуса 45 и тангенса 45 градусов.
Согласно свойствам прямоугольного треугольника, угол С — прямой и равен 90 градусам. Угол B мы изначально построили с градусной мерой 45 градусов. Найдем значение угла А. Так как сумма углов треугольника равна 180 градусам, то
∠А + ∠В + ∠С = 180°
Угол C прямой и равен 90 градусам, угол B мы изначально определили как 45 градусов, таким образом:
∠А = 180° —∠С — ∠В = 180° — 90° — 45° = 45°
Поскольку у данного треугольника два угла равны между собой, то треугольник АВС – прямоугольный, и, одновременно, равнобедренный, в котором оба катета равны между собой: AC = BC.
Допустим, что длина сторон равна некому числу АС = ВС = а. Зная длины катетов, вычислим длину гипотенузы.
По теореме Пифагора: АВ2=АС2+ВС2
Заменим длины AC и BC на переменную а, тогда получим:
АВ2 = а2 + а2 = 2а2,
тогда АВ=а√2.
В результате мы выразили длины всех сторон прямоугольного треугольника с углом 45 градусов через переменную а.
Согласно свойств тригонометрических функций в прямоугольном треугольнике соотношение соответствующих сторон треугольника будет равным значению соответствующих функций. Таким образом для угла α = 45 градусов:
sin α = BC / AB (согласно определению синуса для прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, BC — катет, AB — гипотенуза)
cos α = AC / AB (согласно определению косинуса — это отношение прилежащего катета к гипотенузе, AC — катет, AB — гипотенуза)
tg α = BC / AC (аналогично, тангенс для угла α будет равен отношению противолежащего катета к прилежащему)
Вместо обозначений сторон подставим значения их длин через переменную а.
Исходя из этого (см. таблицу значений sin 45, cos 45, tg 45) получаем:
Табличные значения sin 45, cos 45, tg 45 (то есть значение синуса 45, косинуса 45 и тангенса 45 градусов можно вычислить как соотношение соответствующих сторон данного треугольника), подставим вычисленные выше значения длин сторон в формулы и получим результат на картинке ниже.
Табличные значения: синус 45, косинус 45 и тангенс 45 градусов
Таким образом:
- тангенс 45 градусов равен единице
- синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)
Как видно из вычислений, приведенных выше, для вычисления значений соответствующей тригонометрической функции важны не длины сторон треугольника, а их соотношение, которое всегда одно и то же для одинаковых углов, независимо от размеров конкретного треугольника.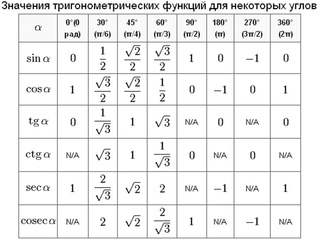
Синус, косинус и тангенс угла π/4 радиан
В задачах, предлагаемых для решения в старших классах и на ЗНО/ЕГЭ вместо градусной меры угла часто встречается указание на его величину, измеренную в радианах. Мера угла, выраженная в радианах, базируется на числе пи, которое выражает зависимость длины окружности от ее диаметра.
Для простоты понимания, рекомендую запомнить простой принцип перевода градусов в радианы. Диаметр окружности охватывает дугу, равную 180 градусам. Таким образом, пи радиан будет равно 180 градусам. Откуда легко пересчитать любую градусную меру угла в радианы и обратно.
Учтем, что угол 45 градусов, выраженный в радианах, равен (180 / 45 = 4) π/4 ( пи на четыре). Поэтому найденные нами значения верны для той же самой градусной меры угла, выраженной в радианах:
- тангенс π/4 ( пи на четыре) равен единице
- синус π/4 ( пи на четыре) градусов равен косинусу π/4 градусов и равен корню из двух пополам
Для удобства зрительного восприятия эти значения приведены на рисунке ниже.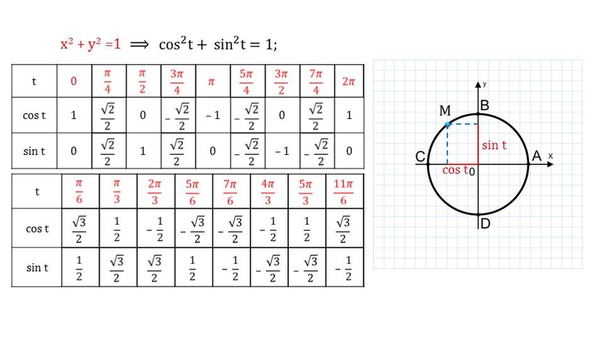
Примечание. В поисковых запросах часто встречается нечто типа «тангенс р/4 или p/4». Это неграмотно. Используйте запрос, например «тангенс пи/4».
Примечание: см. также таблицу значений тригонометрических функций остальных углов.
Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) — таблица значений | Описание курса | Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60)
6 ctg
Вы искали 6 ctg? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos 0 sin, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «6 ctg».
Например, «6 ctg».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 6 ctg,cos 0 sin,cos 0 sin 0,cos sin 0,cos sin tg ctg таблица,cos sin tg углов таблица,cos sin таблица,cos sin таблица значений,cos и sin таблица,cos таблица брадиса,ctg 0 чему равен,ctg 180,ctg 30,ctg 30 градусов,ctg 40,ctg 44,ctg 45,ctg 45 градусов,ctg 5,ctg 5 2,ctg 6,ctg 6 pi,ctg 60,ctg 60 градусов,ctg п 2,ctg таблица,ctg30,sin 0 cos,sin cos 0,sin cos tg ctg таблица,sin cos tg ctg таблица значений,sin cos tg ctg таблица значения,sin cos tg таблица,sin cos tg углов таблица,sin cos таблица,sin и cos таблица,tg и ctg таблица,брадиса таблица cos,значение тангенса и котангенса таблица,значения cos и sin таблица,значения sin,значения sin cos,значения sin cos tg ctg таблица,значения sin и cos таблица,значения синуса косинуса тангенса таблица,значения синусов и косинусов таблица,значения синусов косинусов тангенсов котангенсов таблица,кос син табл,косинус и синус таблица,косинус синус и тангенс таблица,косинус синус таблица,косинусы синусы таблица,косинусы синусы тангенсы котангенсы таблица,котангенс 10,котангенс 15,котангенс 15 градусов,котангенс 225,котангенс 30,котангенс 35,котангенс 360,котангенс 4,котангенс 40,котангенс 45,котангенс 5,котангенс 60 градусов,котангенс 75,котангенс таблица,полная таблица sin cos tg ctg,полная таблица косинусов и синусов,полная таблица косинусов синусов,полная таблица синусов и косинусов,полная таблица синусов косинусов,син кос табл,син кос таблица,син кос танг таблица,син кос тг ктг таблица,синус и косинус 20 градусов,синус и косинус тангенс таблица,синус косинус и тангенс таблица,синусы косинусы таблица,синусы косинусы таблица значений,синусы косинусы тангенсы котангенсы таблица брадиса,табл кос и син,табл кос син,табл син и кос,табл син кос,таблица cos sin,таблица cos sin tg,таблица cos sin tg ctg,таблица cos sin tg ctg полная,таблица cos sin углов,таблица cos брадиса,таблица cos и sin,таблица ctg,таблица sin cos,таблица sin cos tg,таблица sin cos tg ctg,таблица sin cos tg ctg значения,таблица sin cos tg ctg полная,таблица sin и cos,таблица брадиса косинусы синусы тангенсы котангенсы,таблица брадиса котангенс,таблица брадиса синусы и косинусы тангенсы котангенсы,таблица брадиса синусы косинусы тангенсы котангенсы,таблица всех синусов косинусов тангенсов и котангенсов,таблица градусов,таблица градусов синус косинус тангенс котангенс,таблица градусов тангенсов синусов косинусов тангенсов,таблица значений cos sin,таблица значений cos sin tg,таблица значений sin cos,таблица значений sin cos tg,таблица значений sin cos tg ctg,таблица значений sin cos tg ctg таблица,таблица значений tg cos sin,таблица значений tg sin cos,таблица значений косинус синус,таблица значений косинусов синусов тангенсов,таблица значений котангенса,таблица значений синус косинус тангенс,таблица значений синуса и косинуса,таблица значений синусов и косинусов,таблица значений синусов косинусов,таблица значений синусов косинусов тангенсов,таблица значений синусов косинусов тангенсов котангенсов,таблица значений синусы косинусы,таблица значений тангенса и котангенса,таблица значения cos sin tg ctg,таблица значения cos и sin,таблица значения sin cos tg ctg,таблица значения sin и cos,таблица значения углов,таблица кос син,таблица кос син тг ктг,таблица кос тг син,таблица косинус синус,таблица косинуса и синуса и тангенса,таблица косинуса синуса,таблица косинуса синуса и тангенса,таблица косинуса синуса тангенса котангенса,таблица косинусов и синусов в радианах,таблица косинусов и синусов тангенсов,таблица косинусов и синусов тангенсов котангенсов,таблица косинусов и синусов тангенсов котангенсов в радианах,таблица косинусов и тангенсов,таблица косинусов синусов и тангенсов,таблица косинусов синусов полная,таблица косинусов синусов тангенсов,таблица косинусов синусов тангенсов и котангенсов в радианах,таблица косинусов синусов тангенсов котангенсов,таблица косинусов синусов тангенсов котангенсов полная,таблица косинусов тангенсов,таблица косинусы синусы,таблица котангенса,таблица котангенсов,таблица котангенсов углов от 0 до 90,таблица син кос,таблица син кос тан катан,таблица син кос танг,таблица син кос тг ктг,таблица синус косинус,таблица синус косинус и тангенс,таблица синус косинус тангенс,таблица синус косинус тангенс и котангенс таблица,таблица синуса и косинуса и тангенса,таблица синуса косинуса,таблица синуса косинуса и тангенса,таблица синуса косинуса тангенса и котангенса,таблица синуса косинуса тангенса котангенса,таблица синуса тангенса и косинуса,таблица синусов и косинусов в радианах,таблица синусов и косинусов всех углов,таблица синусов и косинусов полная,таблица синусов и косинусов тангенсов,таблица синусов и косинусов тангенсов котангенсов,таблица синусов и косинусов тангенсов котангенсов в радианах,таблица синусов косинусов,таблица синусов косинусов и тангенсов,таблица синусов косинусов полная,таблица синусов косинусов тангенсов,таблица синусов косинусов тангенсов и котангенсов,таблица синусов косинусов тангенсов и котангенсов от 0 до 360 и,таблица синусов косинусов тангенсов котангенсов,таблица синусов косинусов тангенсов котангенсов от 0 до 360,таблица синусов косинусов тангенсов котангенсов полная,таблица синусов косинусов тангенсов котангенсов полная таблица,таблица синусов тангенсов,таблица синусы косинусы,таблица тангенса синуса и косинуса,таблица тангенсов и косинусов,таблица тангенсов и котангенсов синусов и косинусов,таблица тангенсов котангенсов косинусов синусов в радианах,таблица тангенсов котангенсов синусов косинусов в радианах,таблица тангенсов синусов,таблица тангенсов синусов и косинусов,таблица тг ктг син кос,таблица тригонометрии,таблица тригонометрическая углов,таблица тригонометрические,таблица тригонометрических значений с градусами,таблица углов,таблица углов cos sin,таблица углов sin cos tg,таблица углов косинусов синусов,таблица углов синусов и косинусов,таблицу синусов и косинусов,таблицы косинусов синусов,таблицы синусов косинусов,таблицы синусов косинусов тангенсов и котангенсов,таблицы синусов косинусов тангенсов котангенсов,таблицы тригонометрических функций,таблиця кутів,табличные значения синусов косинусов,табличные значения синусов косинусов тангенсов котангенсов,тангенс синус и косинус таблица,тригонометрическая таблица,тригонометрическая таблица косинусов синусов,тригонометрическая таблица синусов косинусов,тригонометрические таблица,тригонометрические таблицы,тригонометрия таблица косинусов и синусов. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 6 ctg. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos 0 sin 0).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 6 ctg. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos 0 sin 0).
Где можно решить любую задачу по математике, а так же 6 ctg Онлайн?
Решить задачу 6 ctg вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
синусы, косинусы, тангенсы и котангенсы
- Главная
- Справочник
- Таблицы
- Таблицы по геометрии
- Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы
Таблица Брадиса — это таблица, которая поможет вычислить значения
синусов, косинусов, тангенсов и котангенсов углов с точностью до одной
минуты без калькулятора.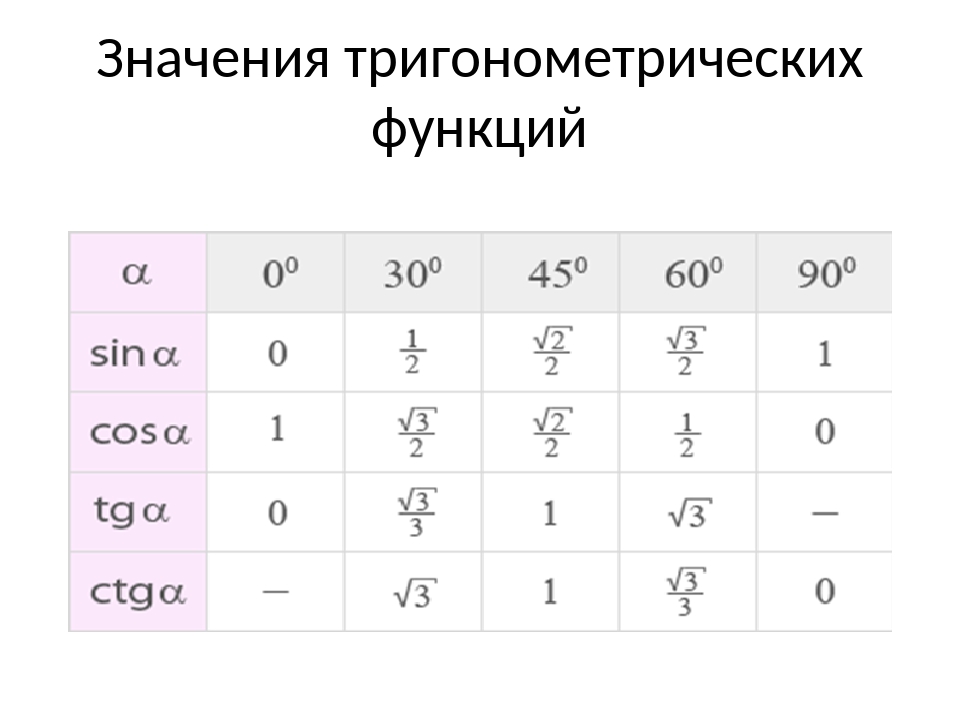
Для таблиц Брадиса в качестве аргумента функций используется значение
угла, заданное в градусах. Если же значение аргумента дано в радианах,
то для перевода в градусы его следует умножить на 180 и разделить на
3.1415926.
Как пользоваться таблицей Брадиса?
В таблице Брадиса представлены значения углов кратных 6 минутам. Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение. И добавить (отнять) к нему поправку соответствующую разнице, которая может быть равна 1′, 2′, 3′.
Примеры:
- sin(15°25′) = sin(15°24′) + поправка 1′ = 0.2656 + 0.0003 = 0.2659
- sin(15°28′) = sin(15°30′) — поправка 2′ = 0.2672 — 0.0006 = 0.2666
При вычислении значений синуса поправка имеет положительный знак, для косинуса поправку необходимо брать с отрицательным знаком:
- cos(15°25′) = sin(15°24′) + поправка 1′ = 0.
 9641 — 0.0001 = 0.9640
9641 — 0.0001 = 0.9640 - cos(15°28′) = sin(15°30′) — поправка 2′ = 0.9636 + 0.0002 = 0.9638
Таблица Брадиса для синуса и косинуса
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0.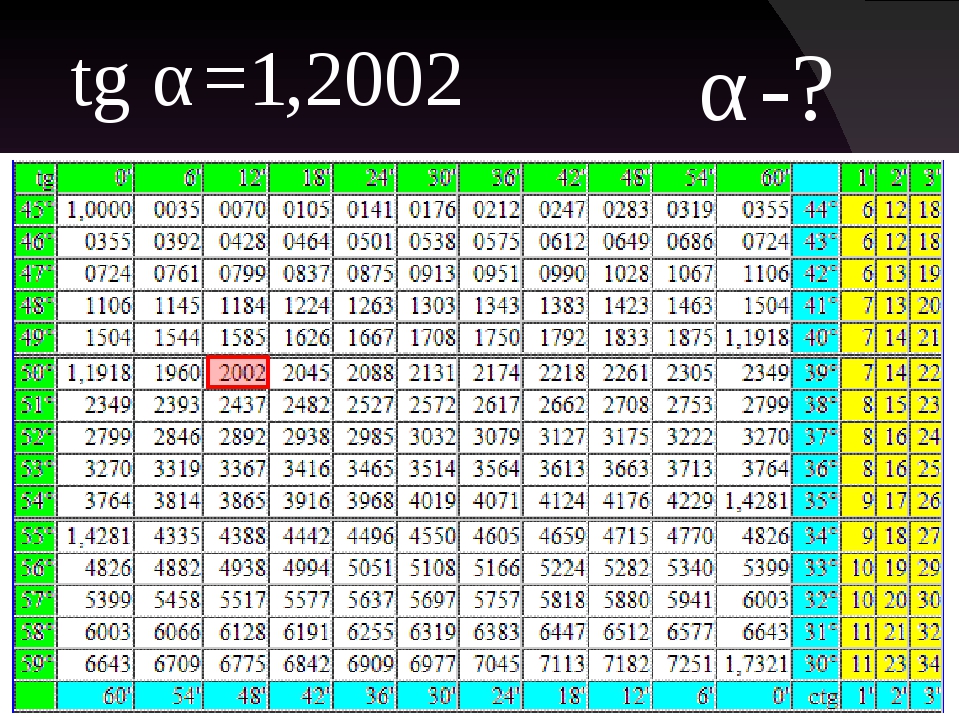 0872 0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.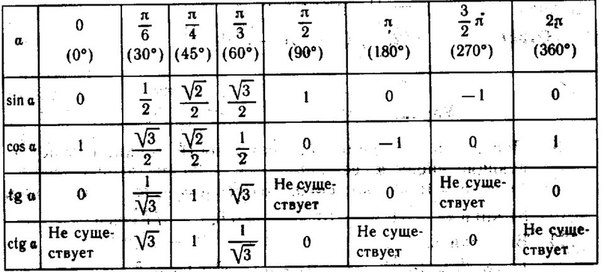 1736 1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.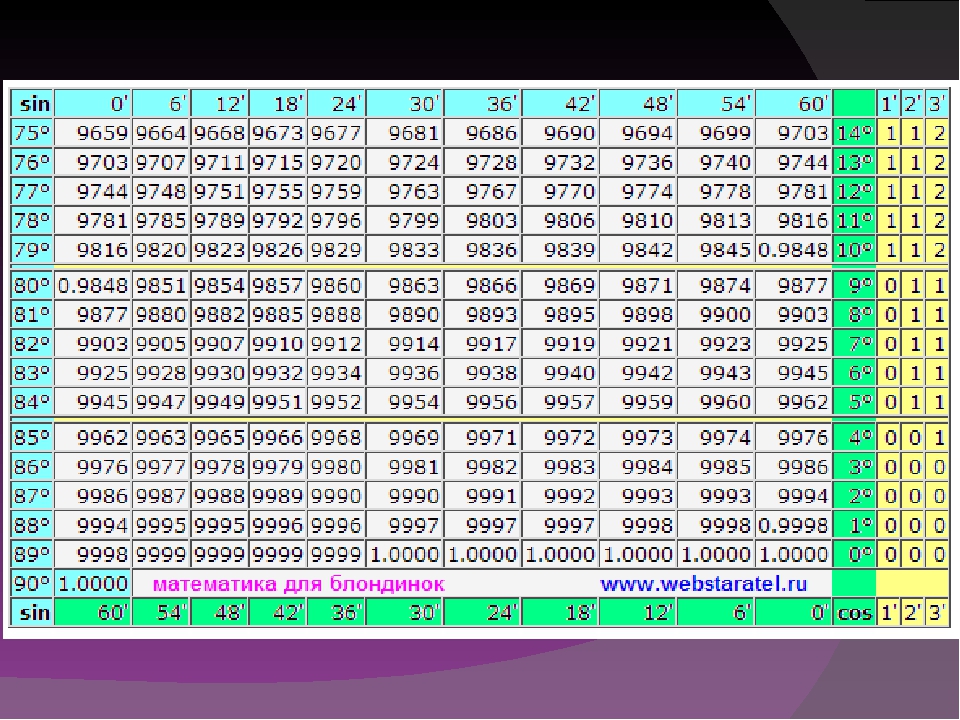 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.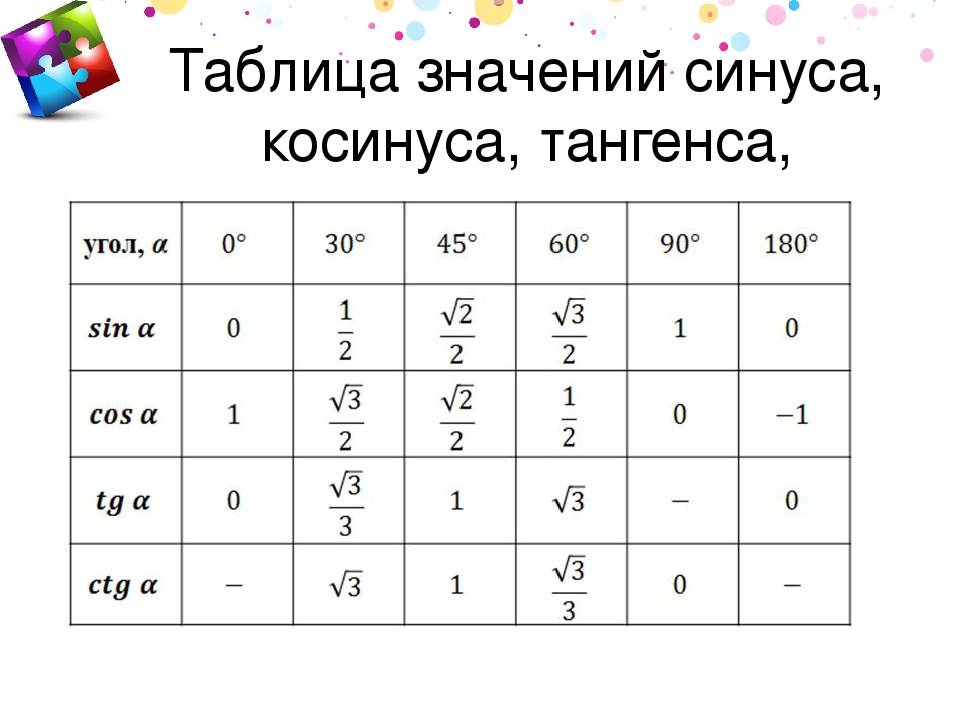 5736 5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.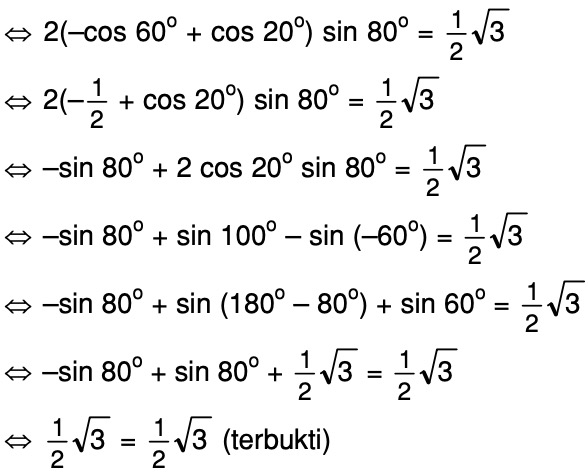 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.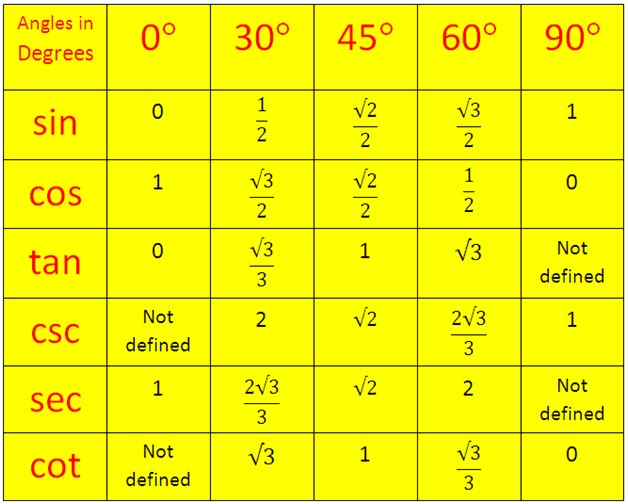 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0. 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.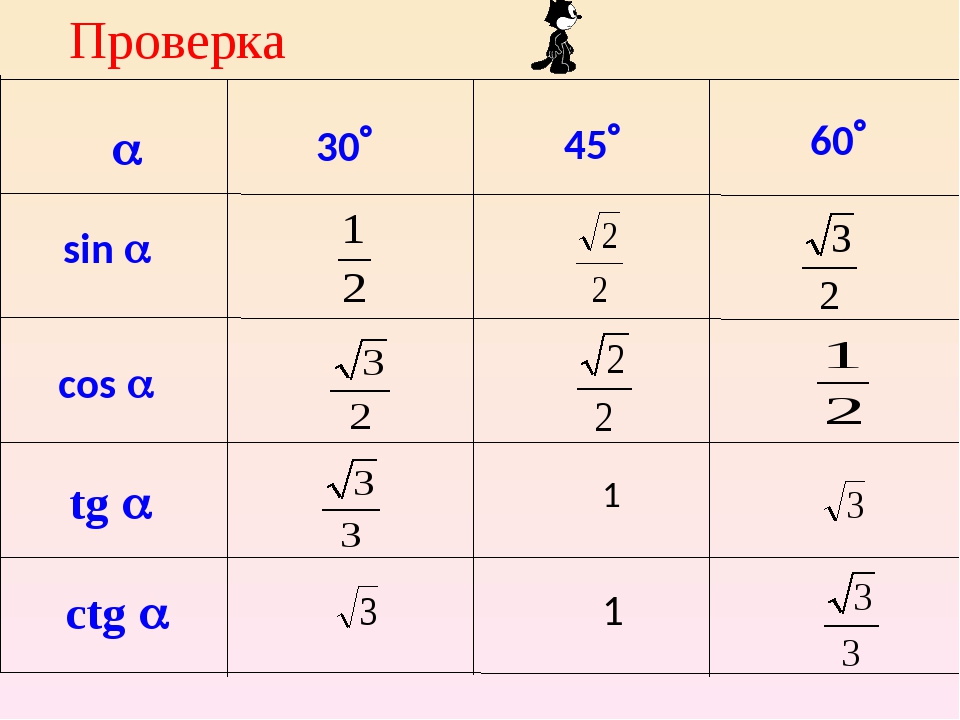 8192 8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.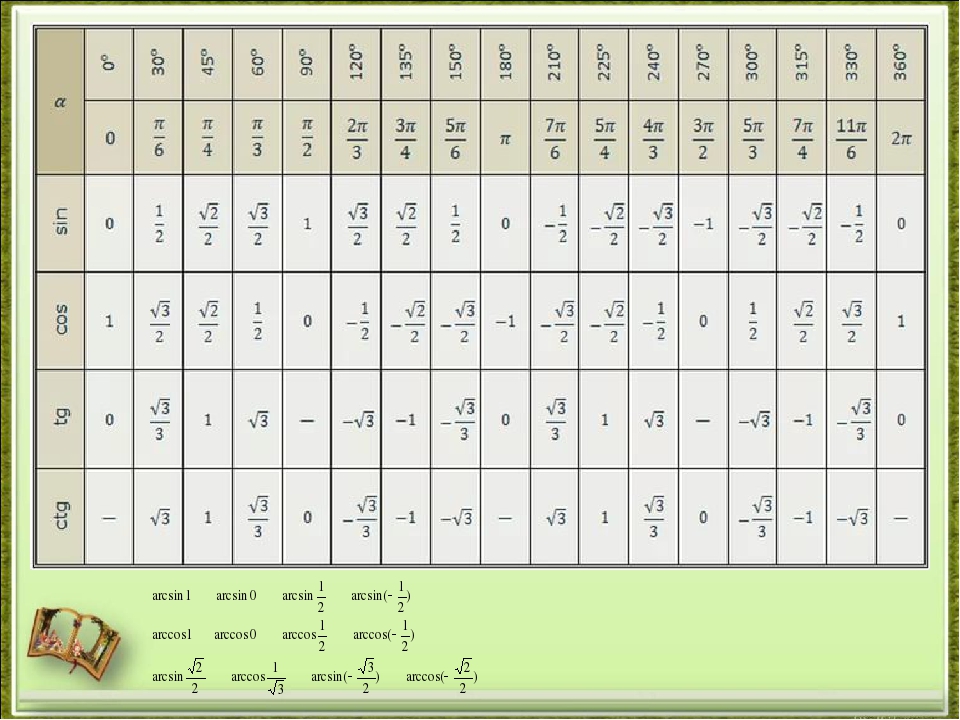 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0. 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0. 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0. 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0. 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
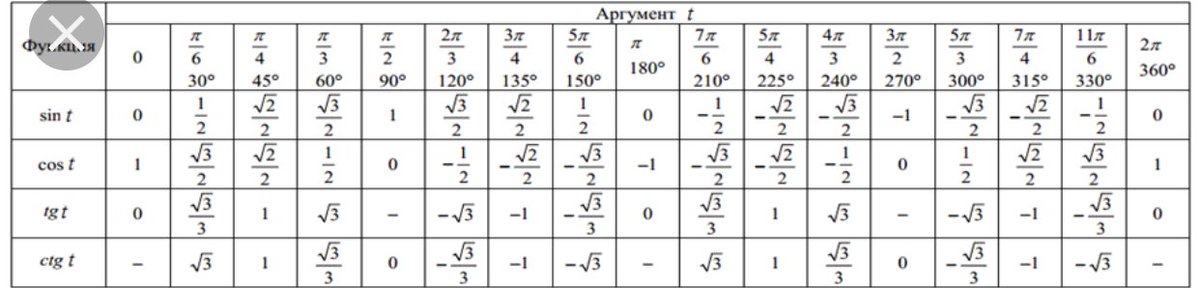
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его. Коэффициент мощности для трехфазного электродвигателя.
На шильдиках многих электромоторов (электродвигателей и др. устройств) указывают активную мощность в Вт и cosφ / или λ /или PF. Что тут к чему см. ниже.
Подразумеваем,что переменное напряжение в сети синусоидальное — обычное, хотя все рассуждения ниже верны и для всех гармоник по отдельности других периодических напряжений.
Полная, или кажущаяся мощность S (apparent power) измеряется в вольт-амперах (ВА или VA) и определяется произведением переменных напряжения и тока системы. Удобно считать, что полная мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой.
Удобно считать, что полная мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой.
|
Активная мощность P (active power = real power =true power) измеряется в ваттах (Вт, W) и это та мощность, которая потребляется электрическим сопротивлением системы на тепло и полезную работу. Для сетей переменного тока:
Для сетей переменного тока:
- P=U*I*cosφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Реактивная мощность Q (reactive power) измеряется в вольт-амперах реактивных (вар, var) и это электромагнитная мощность, которая запасается и отдается обратно в сеть колебательным контуром системы. Реактивная мощность в идеале не выполняет работы, т.е. название вводит в заблуждение. Легко догадаться глядя на рисунок, что:
- P=U*I*sinφ, где U и I — действующие=эффективные=среднеквадратичные значения напряжения и тока, а φ- сдвиг фаз между ними
Сама концепция активной и реактивной мощности актуальна для устройств (приемников) переменного тока. Она малоактуальна=никогда не упоминатеся для приемников постоянного тока в силу малости (мизерности) соответствующих эффектов, связанных только с переходными процессами при включении/выключении.
Любая система, как известно, имеет емкость и индуктивность = является неким колебательным контуром. Переменный ток в одной фазе накачивает электромагнитное поле этого контура энергией а в противоположной фазе эта энергия уходит обратно в генератор ( в сеть). Это вызывает в РФ 3 проблемы (для поставщика энергии!)
- Хотя теоретически, при нулевых сопротивлениях передачи, на выработку реактивной мощности не тратится мощность генератора, но практически для передачи реактивной мощности по сети требуется дополнительная, активная мощность генератора (потери передачи).
- Сеть должна пропускать и активные и реактивные токи, т.е иметь запас по пропускным характеристикам.
- Генератор мог бы, выдавая те же ток и напряжение, поставлять потребителю электроэнергии больше активной мощности.
попробуем догадаться, что делает поставщик электроэнергии? Правильно, пытается навязать Вам различные тарифы для разлиных значений cos φ. Что можно сделать: можно заказать компенсацию реактивной мощности ( т.е. установку неких блоков конденсаторов или катушек), которые заставят реактивную нагрузку колебаться внутри Вашего предприятия/устройства. Стоит ли это делать? Зависит от стоимости установки, наценок за коэффициент мощности и очень даже часто не имеет экономического смысла. В некоторых странах качество питающего напряжения тоже может пострадать от избытка реактивной мощности, но в РФ проблема неактуальна в силу изначально очень низкго качества в питающей сети.
Что можно сделать: можно заказать компенсацию реактивной мощности ( т.е. установку неких блоков конденсаторов или катушек), которые заставят реактивную нагрузку колебаться внутри Вашего предприятия/устройства. Стоит ли это делать? Зависит от стоимости установки, наценок за коэффициент мощности и очень даже часто не имеет экономического смысла. В некоторых странах качество питающего напряжения тоже может пострадать от избытка реактивной мощности, но в РФ проблема неактуальна в силу изначально очень низкго качества в питающей сети.
Естественно, хотелось бы ввести величину, которая характеризовала бы степень линейности нагрузки. И такая величина вводится под названием коэффициент мощности («косинус фи», power factor, PF), как отношение активной мощности к полной, естественно сразу в 2-х видах, в РФ это:
- λ=P/S*100% — то есть, если в %, то это лямбда, P в (Вт), S в (ВА)
- cosφ=P/S — более распространенная величина , P в (Вт), S в (ВА)
Коэффициент мощности для трехфазного асинхронного (обычного) электродвигателя.
cosφ = P / (√3*U*I)
где
cosφ = косинус фи
√3 = квадратный корень из трех
P = активная мощность (Вт)
U = Напряжение (В)
I = Ток (А)
Табель Sin Cos Tan Dari 0 Sampai 360 Semua Sudut Trigonometri
Tabel Sin Cos Tan — Sahabat Rumus Rumus setelah dipertemuan sebelumnya telah saya bahas tentang rumus dan sizesi trigonometri secara lebih detail dan lengkap, maka dipertemuan sekarang ini Saya member cosan kaña para máscoba 0 дераджат сампай 360 дераджат.
Karena tidak bisa dipungkiri bahwa sin cos tan ini merupakan salah satu sizesi trigonometri itu sendiri sehingga bisa dikatakan bahwa trigonometri sangat berkaitan dengan sin cos tan.
Fungsi trigonometri seperti sin cos dan tan ini sangatmbantu untuk kalian dalam menghitung perhitungan sudut bangun terutama didalam perhitungan sudut istimewa trigonometri dasar.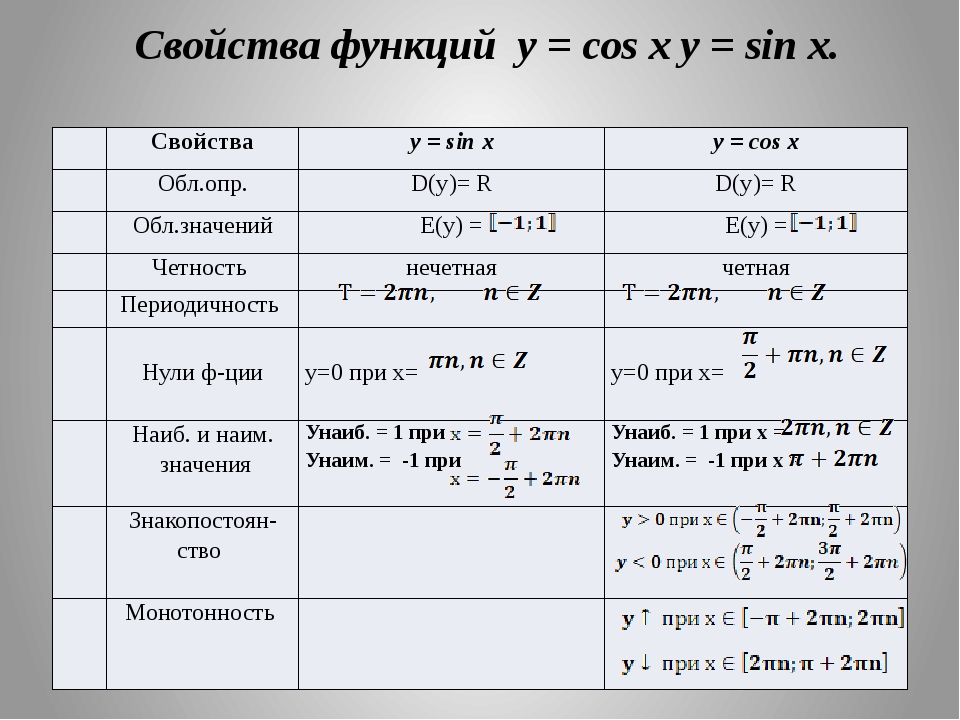
Oleh karena itu sudah sangat bijak sekali bagi kalian para pelajar siswa dan siswi khususnya tingkat sekolah menengah atas (SMA) untuk lebih mengetahui dan lebih mengenal tentang nilai sin cos sin cos tan dalamon dimetri is tan dalamon diometri is tan dalamon diometre соал удзян, термасук джуга келуар ди соал удзян националь (ООН) тингкат СМА.
Dengan adanya tabel trigonometri ini maka akan sangatmbantu dalam mengerjakan nilai trigonometri dalam sebuah sudut.
Nilai trigonometri yang akan dijabarkan ini ialah sinus, cosinus, dan juga tangen. Ян Биаса Дебют Джуга Денган Сингкатан Син cos Тан .
Pengertian Sin Cos Tan
Sebelum memahami ke tabel nilai cos sin tan trigonometri, lebih baiknya pahamlah terlebih dahulu dengan pengertian atau istilah sin cos tan dan trigonometri
- Sin (синус) ialah perbandingan panjang sebuah segitiga yakni antara sisi depan sudut dengan sisi miring segitiga, y / z.

- Cos (косинус) ialah perbandingan panjang sebuah segitiga yakni antara sisi samping sudut dengan sisi miringnya, x / z.
- Тан (танген) ialah perbandingan panjang sebuah segitiga antara sisi depan sudut дан sisi samping segitiga, y / x.
- Trigonometri adalah salah satu cabang dari ilmu matematika yang membersahas tentang hubungan antara panjang dan sudut pada sebuah segitiga.
Untuk lebih jelasnya tentan penjelasan diatas, lihatlah gambar dibawah ini:
Кататан: Seluruh perbandingan trigonometri sin cos tan diatas terbatas yakni hanya berlaku untuk objek segitiga siku siku atau segitiga dimana salah satu sudutnya nilainya 90 derajat.
Табель Sin Cos Tan
Untuk itu dibawah ini telah kami buatkan tabel cos sin tan seluruh sudut yang terbentuk dalam satu lingkaran penuh atau yang sering Disbut dengan lingkaran 360 derajat.
Rumus sin cos tan sudut istimewa sampai 360 didalam tabel tersebut sangat berguna bagi kalian Untuk mempermudah dalam menjawab pertanyaan — pertanyaan terkait rumus dan persamaan trigonometri, langsung saja dibawah ini tabel sinus ter cosinus tangrien is.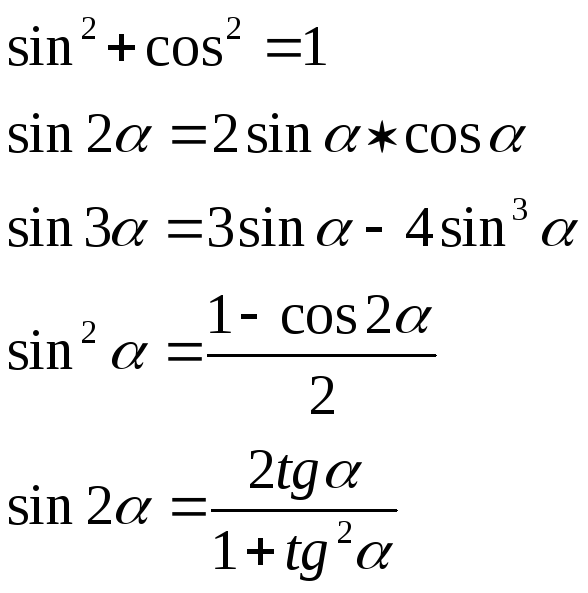
| 0 дераджат | 30 дераджатов | 45 дераджат | 60 дераджат | 90 дераджат | |
| Грех | 0 | ½ | ½√2 | ½√3 | 1 |
| Cos | 1 | ½√3 | ½√2 | ½ | 0 |
| Желто-коричневый | 0 | ½√3 | 1 | √3 | ∞ |
Табель Sin Cos Tan Kuadran 2 дня 90º сампай 180º
| 90 дераджат | 120 дераджат | 135 дераджат | 150 дераджат | 180 дераджат | |
| Грех | 1 | ½√3 | ½√2 | ½ | 0 |
| Cos | 0 | -½ | -½√2 | -½√3 | -1 |
| Желто-коричневый | ∞ | -√3 | -1 | -½√3 | 0 |
Табель Sin Cos Tan Kuadran 3 дня 180º сампай 270º
| 180 дераджат | 210 дераджат | 225 дераджат | 240 дераджат | 270 дераджат | |
| Грех | 0 | -½ | -½√2 | -½√3 | -1 |
| Cos | -1 | -½√3 | -½√2 | -½ | 0 |
| Желто-коричневый | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Табель Sin Cos Tan Kuadran 4 дня 270º сампай 360º
| 270 дераджат | 300 дераджат | 315 дераджат | 330 дераджат | 360 дераджат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Грех | -1 | -½√3 | -½√2 | -½ | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cos | 0 | ½ | ½√2 | ½√3 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Желто-коричневый | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
| Судут | Радиан | Грех | Cos | Желто-коричневый | |
| 0 ° | 0 | 0 | 1 | 0 | |
| 1 ° | 0,01746 | 0,01746 | 0,99985 | 0,01746 | |
| 2 ° | 0.03492 | 0,03491 | 0,99939 | 0,03494 | |
| 3 ° | 0,05238 | 0,05236 | 0,99863 | 0,05243 | |
| 4 ° | 0,06984 | 0,06979 | 0,99756 | 0,06996 | |
| 5 ° | 0,0873 | 0,08719 | 0, | 0,08752 | |
| 6 ° | 0,10476 | 0,10457 | 0. | 0,10515 | |
| 7 ° | 0,12222 | 0,12192 | 0, | 0,12283 | |
| 8 ° | 0,13968 | 0,13923 | 0, | 0,1406 | |
| 9 ° | 0,15714 | 0,1565 | 0, | 0,15845 | |
| 10 ° | 0,1746 | 0,17372 | 0,9848 | 0,1764 | |
| 11 ° | 0. 19206 19206 | 0,19089 | 0, | 0,19446 | |
| 12 ° | 0,20952 | 0,20799 | 0, | 0,21265 | |
| 13 ° | 0,22698 | 0,22504 | 0, | 0,23096 | |
| 14 ° | 0,24444 | 0,24202 | 0, | 0,24943 | |
| 15 ° | 0,26191 | 0.25892 | 0,9659 | 0,26806 | |
| 16 ° | 0,27937 | 0,27575 | 0, | 0,28687 | |
| 17 ° | 0,29683 | 0,29249 | 0, | 0,30586 | |
| 18 ° | 0,31429 | 0,30914 | 0, | 0,32506 | |
| 19 ° | 0,33175 | 0,32569 | 0. | 0,34448 | |
| 20 ° | 0,34921 | 0,34215 | 0, | 0,36413 | |
| 21 ° | 0,36667 | 0,35851 | 0, | 0,38403 | |
| 22 ° | 0,38413 | 0,37475 | 0, | 0,40421 | |
| 23 ° | 0,40159 | 0,39088 | 0, | 0. 42467 42467 | |
| 24 ° | 0,405 | 0,40689 | 0, | 0,44543 | |
| 25 ° | 0,43651 | 0,42278 | 0, | 0,46652 | |
| 26 ° | 0,45397 | 0,43854 | 0,89871 | 0,48796 | |
| 27 ° | 0,47143 | 0,45416 | 0,89092 | 0,50976 | |
| 28 ° | 0.48889 | 0,46965 | 0,88286 | 0,53196 | |
| 29 ° | 0,50635 | 0,48499 | 0,87452 | 0,55458 | |
| 30 ° | 0,52381 | 0,50018 | 0,86592 | 0,57763 | |
| 31 ° | 0,54127 | 0,51523 | 0,85706 | 0.60116 | |
| 32 ° | 0,55873 | 0.53011 | 0,84793 | 0,62518 | |
| 33 ° | 0,57619 | 0,54483 | 0,83854 | 0,64974 | |
| 34 ° | 0,59365 | 0,55939 | 0,8289 | 0,67486 | |
| 35 ° | 0,61111 | 0,57378 | 0,81901 | 0,70057 | |
| 36 ° | 0,62857 | 0,58799 | 0. 80887 80887 | 0,72693 | |
| 37 ° | 0,64603 | 0.60202 | 0,79848 | 0,75396 | |
| 38 ° | 0,66349 | 0,61587 | 0,78785 | 0,78172 | |
| 39 ° | 0,68095 | 0,62953 | 0,77697 | 0,81024 | |
| 40 ° | 0,69841 | 0,643 | 0,76586 | 0,83958 | |
| 41 ° | 0.71587 | 0,65628 | 0,75452 | 0,86979 | |
| 42 ° | 0,73333 | 0,66935 | 0,74295 | 0, | |
| 43 ° | 0,75079 | 0,68222 | 0,73115 | 0, | |
| 44 ° | 0,76825 | 0,69488 | 0,71913 | 0, | |
| 45 ° | 0,78571 | 0.70733 | 0,70688 | 1.00063 | |
| 46 ° | 0. 80318 80318 | 0,71956 | 0,69443 | 1.0362 | |
| 47 ° | 0,82064 | 0,73158 | 0,68176 | 1.07308 | |
| 48 ° | 0,8381 | 0,74337 | 0,66888 | 1,11137 | |
| 49 ° | 0,85556 | 0,75494 | 0,6558 | 1.15117 | |
| 50 ° | 0,87302 | 0,76627 | 0,64252 | 1,1926 | |
| 51 ° | 0,89048 | 0,77737 | 0,62904 | 1,2358 | |
| 52 ° | 0, | ||||
| 0,78824 | 0,61537 | 1,28091 | |||
| 53 ° | 0,9254 | 0,79886 | 0.60152 | 1,32807 | |
| 54 ° | 0. | 0.80924 | 0,58748 | 1,37748 | |
| 55 ° | 0, | 0,81937 | 0,57326 | 1.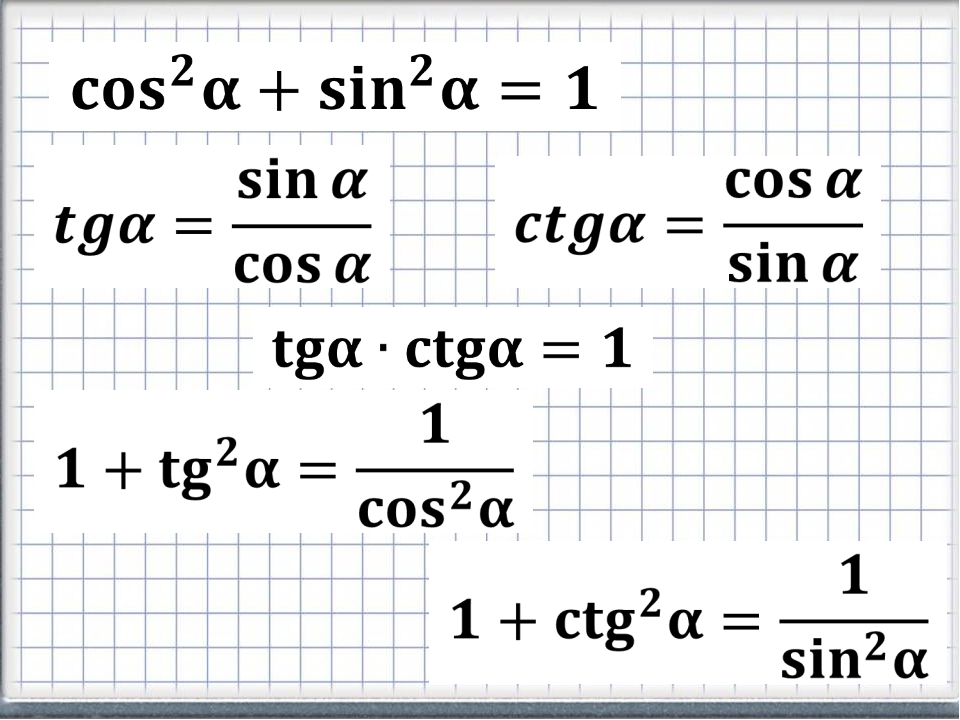 42932 42932 | |
| 56 ° | 0, | 0,82926 | 0,55887 | 1.48382 | |
| 57 ° | 0, | 0,83889 | 0,5443 | 1,54122 | |
| 58 ° | 1.0127 | 0,84826 | 0.52957 | 1,60179 | |
| 59 ° | 1.03016 | 0,85738 | 0,51468 | 1,66584 | |
| 60 ° | 1.04762 | 0,86624 | 0,49964 | 1,73374 | |
| 61 ° | 1.06508 | 0,87483 | 0,48444 | 1,80587 | |
| 62 ° | 1.08254 | 0,88315 | 0,46909 | 1.8827 | |
| 63 ° | 1,1 | 0,89121 | 0,4536 | 1, | |
| 64 ° | 1,11746 | 0,89899 | 0,43797 | 2,05265 | |
| 65 ° | 1,13492 | 0,9065 | 0,4222 | 2,14707 | |
| 66 ° | 1,15238 | 0, | 0,40631 | 2,24884 | |
| 67 ° | 1.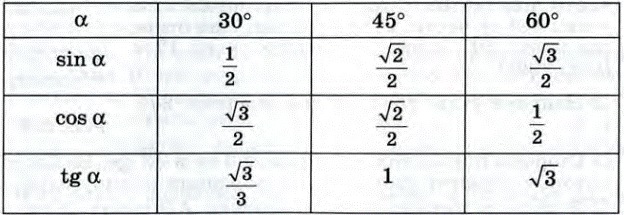 16984 16984 | 0, | 0,3903 | 2,35894 | |
| 68 ° | 1,1873 | 0, | 0,37416 | 2.4785 | |
| 69 ° | 1,20476 | 0, | 0,35792 | 2,60887 | |
| 70 ° | 1,22222 | 0, | 0,34156 | 2,75169 | |
| 71 ° | 1,23968 | 0, | 0.3251 | 2, | |
| 72 ° | 1,25714 | 0, | 0,30854 | 3,08299 | |
| 73 ° | 1,2746 | 0, | 0,29188 | 3,27686 | |
| 74 ° | 1,29206 | 0, | 0,27514 | 3,49427 | |
| 75 ° | 1,30952 | 0, | 0,25831 | 3,73993 | |
| 76 ° | 1.32698 | 0, | 0,2414 | 4.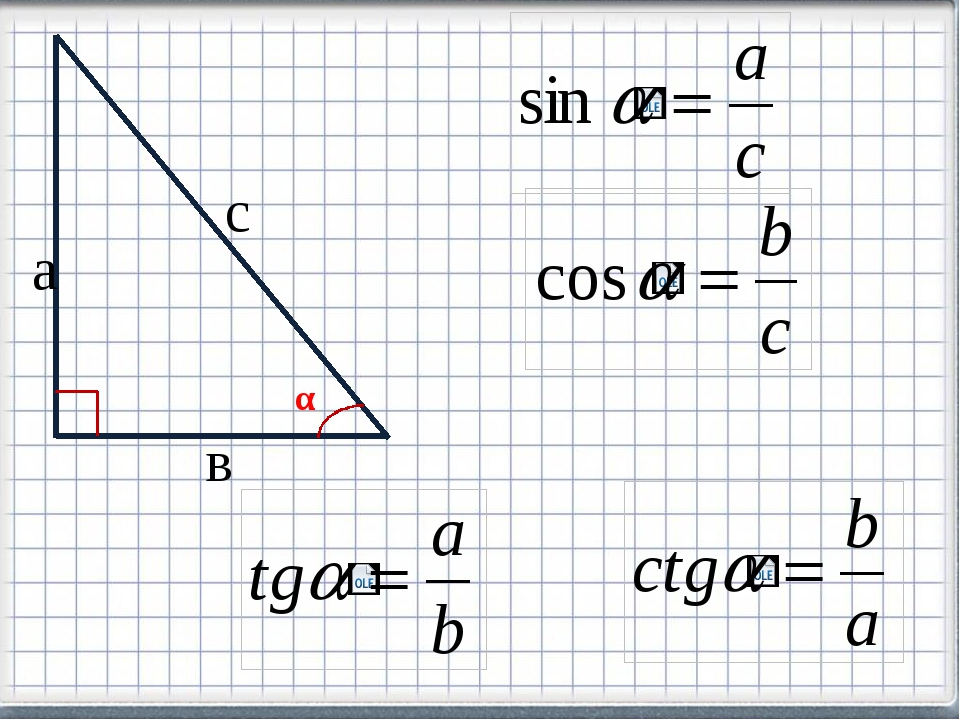 01992 01992 | |
| 77 ° | 1,34444 | 0, | 0,22442 | 4.34219 | |
| 78 ° | 1,36191 | 0, | 0,20738 | 4,71734 | |
| 79 ° | 1,37937 | 0, | 0,19026 | 5,15984 | |
| 80 ° | 1,39683 | 0. | 0,1731 | 5.68998 | |
| 81 ° | 1,41429 | 0, | 0,15587 | 6.33709 | |
| 82 ° | 1.43175 | 0, | 0,1386 | 7,14523 | |
| 83 ° | 1.44921 | 0, | 0,12129 | 8,18379 | |
| 84 ° | 1,46667 | 0, | 0,10394 | 9.56868 | |
| 85 ° | 1.48413 | 0, | 0,08656 | 11,5092 | |
| 86 ° | 1,50159 | 0,99761 | 0,06915 | 14,4259 | |
| 87 ° | 1,51905 | 0,99866 | 0,05173 | 19. 3069 3069 | |
| 88 ° | 1,53651 | 0,99941 | 0,03428 | 29,153 | |
| 89 ° | 1.55397 | 0,99986 | 0,01683 | 59,4189 | |
| 90 ° | 1,57143 | 1 | 0 | ∞ |
Табель Trigonometri Sudut 90 ° sampai 180 °
Табель Trigonometri Sudut 180 ° сампай 270 °
Табель Trigonometri Sudut 270 ° sampai 360 °
Itulah materi tentang sin cos tan tabel yang dapat diuraikan oleh RumusRumus.com semoga kita dapat memahaminya dengan baik… semoga bermanfaat
Табель Тригонометри Син Кос Тан Ленгкап (Семуа Судут) + Кара Мемахаминя [2020]
Tabel trigonometri sin cos tan adalah serangkaian tabel yang berisi nilai trigonometri atau sin cos tangen dari suatu sudut.
Пада артикель иници дитунджуккан табель нилаи тригонометри грех кос тан дари бербагай судут истимева дари судут 0º сампай судут 360º (атау ян биаса дибут судут лингкаран 360 дераджат), агар каму тидак перлу сусах-сусаннйа лангхафалк.
Adapun Untuk Rumus Identitas trigonometri, kamu bisambacanya di artikel ini ya.
Определения Sin Cos Tan
Sebelum masuk ke tabel nilai trigonometri, ada baiknya kita perlu paham terlebih dahulu dengan istilah trigonometri dan sin cos tan.
- Trigonometri adalah cabang dalam ilmu matematika yang mempelajari hubungan antara panjang dan sudut pada segitiga.
- Sin (синус) adalah perbandingan panjang dalam sebuah segitiga antara sisi depan sudut dengan sisi miringnya, y / z.
- Cos (косинус) adalah perbandingan panjang dalam sebuah segitiga antara sisi samping sudut dengan sisi miringnya, x / z.
- Tan (tangen) adalah perbandingan panjang dalam sebuah segitiga antara sisi depan sudut дан sisi sampingnya, y / x.
Seluruh perbandingan trigonometri tan sin cos tersebut dibatasi hanya berlaku Untuk segitiga siku siku atau segitiga yang salah satu sudutnya 90 derajat.
Таблица Trigonometri Sudut Istimewa Kuadran I (0–90 дераджат)
| Судут | 0 º | 30 º | 45 º | 60 º | 90 º |
| Sin | 0 | 1/2 | 1/2 √21/2 √3 | 1 | |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Тан | 0 | 1/2 √3 | 1 | √3 | ∞ |
Табель Trigonometri Sudut Istimewa Kuadran II (90–180 дераджат)
| Судут | 90 º | 120 º | 135 º | 150 º | 180 º |
| Sin | 1/2 √3 | 1/2 √2 | 1/2 | 0 | |
| Cos | 0 | — 1/2 | — 1/2 √2 | — 1/2 √3 | — 1 |
| Желто-коричневый | ∞ | -√3 | -1 | — 1/3 √3 | 0 |
Табель Син Кос Тан Судут Истимева Куадран III (180 — 270 дераджат)
| Судут | 180 º | 210 º | 225 º | 240 º | 270 º | |
| Sin | 0 | — 1/2 | 0— 1/2 | — 1/2 √2 | — 1 / 2√3 | -1 |
| Cos | -1 | — 1 / 2√3 | — 1 / 2√2 | — 1/2 | 0 | |
| Желто-коричневый | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Табель Кос Син Тан Судут Истимева Куадран IV (270–360 дераджат)
| Судут | 270 º | 300 º | 315 º | 330 º | 360 º |
| Sin | -1 9003 √ | -½ | -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 |
| Тан | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
Demikian daftar lengkap tabel trigonometri dari seluruh sudut istimewa dari 0 — 360 derajat.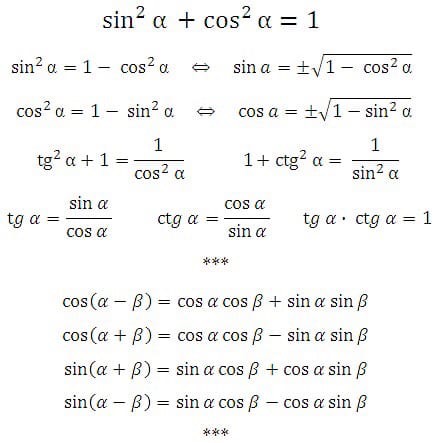
Tabel tersebut dapat kamu gunakan Untuk memudahkan urusan dalam perhitungan atau analisa trigonometri dalam matematika.
Mengingat Tabel Trigonometri Sudut Istimewa Tanpa Hafalan
Sebenarnya, kamu tidak perlu bersusah payah menghafal seluruh nilai trigonometri dari setiap sudut.
Ян каму перлукан ханьялах консеп пемахаман дасар ян дапат каму гунакан унтук mengetahui nilai trigonometri дари сетиап судут истимева.
Kamu hanya perlu mendingat komponen panjang sisi segitiga pada sudut istimewa 0, 30, 45, 60, dan 90 derajat.
Misalkan kamu ingin mengetahui nilai dari cos (60).
Kamu hanya perlu mengingat panjang sisi dari segitiga dengan sudut 60 derajat, lalu melakukan operasi cosinus, yaitu x / z pada segitiga tersebut.
Dari gambar tersebut, kamu akan dapat melihat bahwa nilai cos 60 = 1/2.
Мудах букан?
Унтук судут-судут ди куадран лайн, чаранья сама дан каму ханья перлу менйесуайкан танда позитиф атау негатиф дари мазинг-мазинг куадран.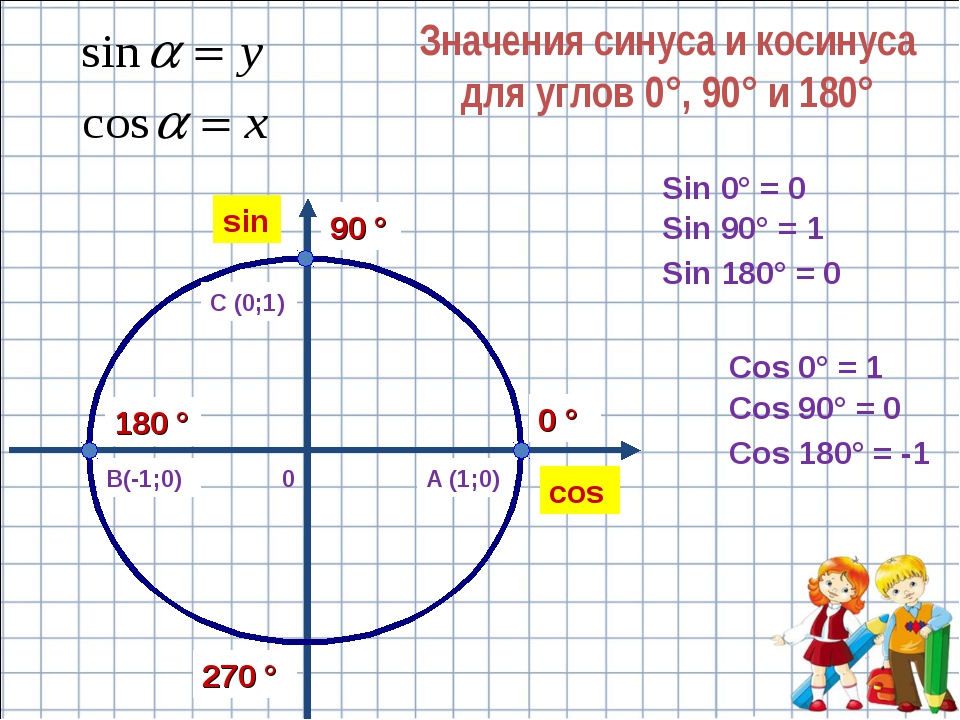
Табель Далам Бентук Лингкаран
Jika tabel cos sin tan di atas terlalu panjang untuk diingat, juga jika metode konsep sudut istimewa kamu rasa masih sulit…
Kamu bisa memanfaatkan tabel trigonometri dalam bentuk lingkaran Untuk secara langsung melihat nilai sin cos tan dari sudut 360 derajat.
Trik Cepat Menghafal Tabel Trigonometri
Selain cara-cara di atas, masih ada satu metode lagi yang bisa kamu gunakan Untuk mengingat tabel rumus trigonometri dengan mudah.
Лангках ян перлу каму лакукан адалах себагай берикут:
- Лангках 1 . Buat tabel yang berisi sudut 0-90 derajat dan kolom dengan keterangan sin cos tan
- Langkah 2 . Ингат бахва румус умум унтук син пада судут 0 — 90 дераджат адалах √x / 2.
- Лангка 3 . Ganti nilai x menjadi 0 pada √x / 2 di kolom paling pertama. Pojok kiri atas.
- Langkah 4. Isi secara berurutan dengan mengganti x tersebut menjadi 0, 1, 2, 3, 4 pada kolom sin.
 Dengan demikian kamu sudah mendapatkan nilai trigonometri sin yang lengkap
Dengan demikian kamu sudah mendapatkan nilai trigonometri sin yang lengkap - Langkah 5 . Untuk mencari nilai cos, ян перлу каму lakukan hanyalahmbalik urutan янг ада пада колом грех.
- Лангка 6 . Untuk mencari nilai tan, янь perlu kamu lakukan hanyalahmbagi nilai sin dengan nilai cos.
Mana yang lebih mudah kamu pahami untuk mengingat nilai trigonometri tan sin cos?
Ян манапун иту, пилих ян палинг мудах каму пахами я. Карена мазинг-мазинг оранг пунйа гайа беладжар ян бербеда-беда.
Табель Унтук Семуа Судут
Джика пада табель-табель ди атас нилаи ян дитунджуккан ханьялах нилаи тригонометри дари судут-судут истимева, мака пада табель ини дитунджуккан семуа нилаи тригонометри дари сема судут дари 0 — 90 дераджат.
| Судут | Радиан | Sin | Cos | Tan | |||||||||||||
| 0 ° | 0 | 0 | 1 | 0 | |||||||||||||
| 1 ° | 0. 01746 01746 | 0,01746 | 0,99985 | 0,01746 | |||||||||||||
| 2 ° | 0,03492 | 0,03491 | 0,99939 | 0,03494 | |||||||||||||
| 3 ° | 0,05238 | 0,05236 | 0,99824 | 0,99863 | 4 ° | 0,06984 | 0,06979 | 0,99756 | 0,06996 | ||||||||
| 5 ° | 0,0873 | 0,08719 | 0, | 0.08752 | |||||||||||||
| 6 ° | 0,10476 | 0,10457 | 0, | 0,10515 | |||||||||||||
| 7 ° | 0,12222 | 0,12192 | 0, | 0,12192 | 0, | 0,12283 | 0, | 0,12283 | 0, | 0,12283 | 0, | 0,126 | 0, | 0,1406 | |||
| 9 ° | 0,15714 | 0,1565 | 0, | 0,15845 | |||||||||||||
| 10 ° | 0.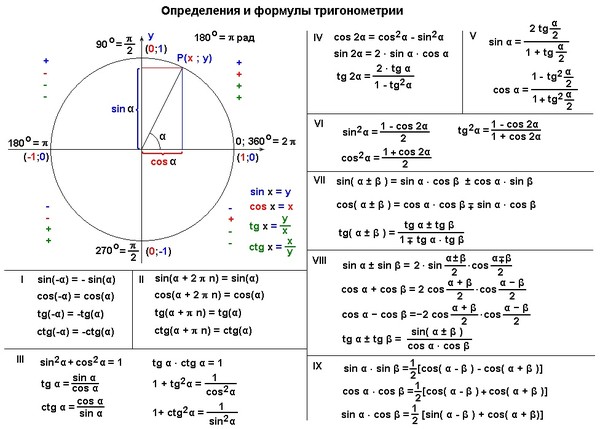 1746 1746 | 0,17372 | 0,9848 | 0,1764 | |||||||||||||
| 11 ° | 0,19206 | 0,19089 | 0, | 0,19446 | |||||||||||||
| 12 ° | 0,20952 | 0,20799 | 0,20952 | 0,20799 | 0,20952 | 0,20799 | 13 ° | 0,22698 | 0,22504 | 0, | 0,23096 | ||||||
| 14 ° | 0,24444 | 0,24202 | 0, | 0.24943 | |||||||||||||
| 15 ° | 0,26191 | 0,25892 | 0,9659 | 0,26806 | |||||||||||||
| 16 ° | 0,27937 | 0,27575 | 0, | 0,28687 | |||||||||||||
| 17 ° | 0,0, | 0,30586 | |||||||||||||||
| 18 ° | 0,31429 | 0,30914 | 0, | 0,32506 | |||||||||||||
| 19 ° | 0.33175 | 0,32569 | 0, | 0,34448 | |||||||||||||
| 20 ° | 0,34921 | 0,34215 | 0, | 0,36413 | |||||||||||||
| 21 ° | 0,36667 | 0,35851 | 0, | 0,35851 | 0, | 22 ° | 0,38413 | 0,37475 | 0, | 0,40421 | |||||||
| 23 ° | 0,40159 | 0,39088 | 0.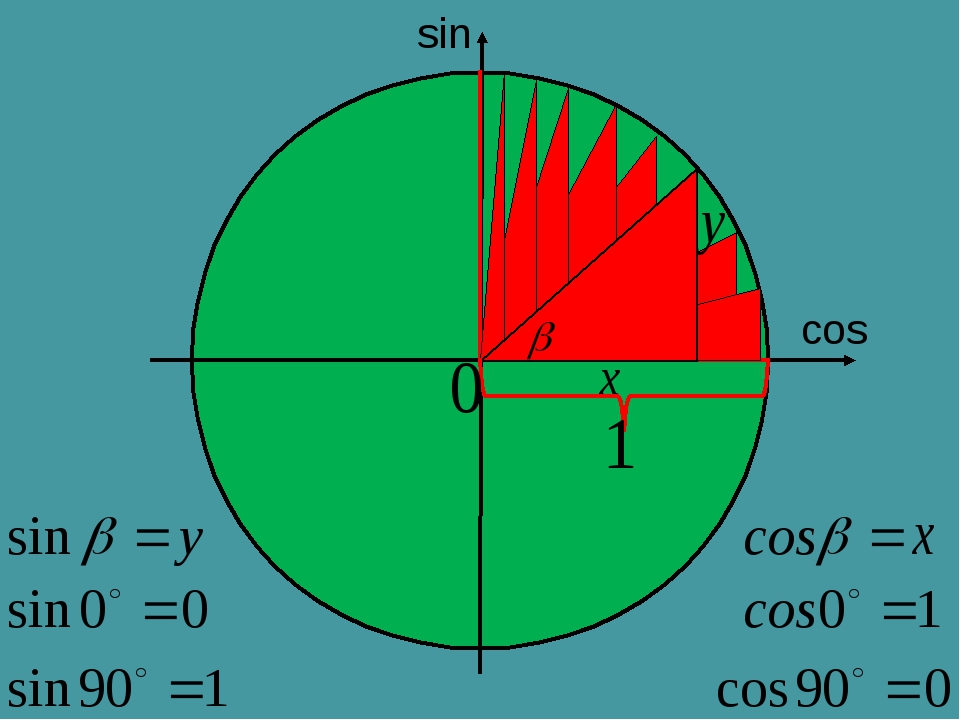 | 0,42467 | |||||||||||||
| 24 ° | 0,41905 | 0,40689 | 0, | 0,44543 | |||||||||||||
| 25 ° | 0,43651 | 0,42278 | 0, | 0,466561 | 0, | 0,466561 | 0,43854 | 0,89871 | 0,48796 | ||||||||
| 27 ° | 0,47143 | 0,45416 | 0,89092 | 0,50976 | |||||||||||||
| 28 ° | 0.48889 | 0,46965 | 0,88286 | 0,53196 | |||||||||||||
| 29 ° | 0,50635 | 0,48499 | 0,87452 | 0,55458 | |||||||||||||
| 30 ° | 0,52381 | 0,50018 | 0,52381 | 0,50018 | 31 ° | 0,54127 | 0,51523 | 0,85706 | 0,60116 | ||||||||
| 32 ° | 0,55873 | 0,53011 | 0.84793 | 0,62518 | |||||||||||||
| 33 ° | 0,57619 | 0,54483 | 0,83854 | 0,64974 | |||||||||||||
| 34 ° | 0,59365 | 0,55939 | 0,8289 | 0,67486 | 0,57378 | 0,81901 | 0,70057 | ||||||||||
| 36 ° | 0,62857 | 0,58799 | 0,80887 | 0,72693 | |||||||||||||
| 37 ° | 0.64603 | 0,60202 | 0,79848 | 0,75396 | |||||||||||||
| 38 ° | 0,66349 | 0,61587 | 0,78785 | 0,78172 | |||||||||||||
| 39 ° | 0,68085 | 0,62953 | 0,68085 | 0,62953 | 0,75 40 ° | 0,69841 | 0,643 | 0,76586 | 0,83958 | ||||||||
| 41 ° | 0,71587 | 0,65628 | 0,75452 | 0.86979 | |||||||||||||
| 42 ° | 0,73333 | 0,66935 | 0,74295 | 0, | |||||||||||||
| 43 ° | 0,75079 | 0,68222 | 0,73115 | 0, | 44 ° 25864 | 0,71913 | 0, | ||||||||||
| 45 ° | 0,78571 | 0,70733 | 0,70688 | 1.00063 | |||||||||||||
| 46 ° | 0.80318 | 0,71956 | 0,69443 | 1,0362 | |||||||||||||
| 47 ° | 0,82064 | 0,73158 | 0,68176 | 1,07308 | |||||||||||||
| 48 ° | 0,8381 | 0,743370,8381 | 0,74337 | 49 ° | 0,85556 | 0,75494 | 0,6558 | 1,15117 | |||||||||
| 50 ° | 0,87302 | 0,76627 | 0,64252 | 1.1926 | |||||||||||||
| 51 ° | 0,89048 | 0,77737 | 0,62904 | 1,2358 | |||||||||||||
| 52 ° | 0, | ||||||||||||||||
| 0,78824 | 0,61537 | 1,28091 | |||||||||||||||
| 53 ° | 0,989 | 0,60152 | 1,32807 | ||||||||||||||
| 54 ° | 0, | 0,80924 | 0,58748 | 1,37748 | |||||||||||||
| 55 ° | 0. | 0,81937 | 0,57326 | 1,42932 | |||||||||||||
| 56 ° | 0, | 0,82926 | 0,55887 | 1,48382 | |||||||||||||
| 57 ° | 0, | 0,83889 | 0,58524 | 0,83889 | 0,5 58 ° | 1,0127 | 0,84826 | 0,52957 | 1,60179 | ||||||||
| 59 ° | 1,03016 | 0,85738 | 0,51468 | 1.66584 | |||||||||||||
| 60 ° | 1.04762 | 0,86624 | 0,49964 | 1,73374 | |||||||||||||
| 61 ° | 1,06508 | 0,87483 | 0,48444 | 1,80587 | |||||||||||||
| 62 ° | 0,46909 | 1,8827 | |||||||||||||||
| 63 ° | 1,1 | 0,89121 | 0,4536 | 1, | |||||||||||||
| 64 ° | 1.11746 | 0,89899 | 0,43797 | 2,05265 | |||||||||||||
| 65 ° | 1,13492 | 0,9065 | 0,4222 | 2,14707 | |||||||||||||
| 66 ° | 1,15238 | 0, | 0,40631 | 0,40631 | 0, | 0,40631 | 67 °1,16984 | 0, | 0,3903 | 2,35894 | |||||||
| 68 ° | 1,1873 | 0, | 0,37416 | 2.4785 | |||||||||||||
| 69 ° | 1.20476 | 0, | 0,35792 | 2,60887 | |||||||||||||
| 70 ° | 1,22222 | 0, | 0,34156 | 2,75169 | 71 ° | 0,3251 | 2, | ||||||||||
| 72 ° | 1,25714 | 0, | 0,30854 | 3,08299 | |||||||||||||
| 73 ° | 1.2746 | 0, | 0,29188 | 3,27686 | |||||||||||||
| 74 ° | 1,29206 | 0, | 0,27514 | 3,49427 | |||||||||||||
| 75 ° | 1,30952 | 0,8 | 1,30952 | 0,8 | 76 ° | 1,32698 | 0, | 0,2414 | 4,01992 | ||||||||
| 77 ° | 1,34444 | 0, | 0,22442 | 4.34219 | |||||||||||||
| 78 ° | 1,36191 | 0, | 0,20738 | 4,71734 | |||||||||||||
| 79 ° | 1,37937 | 0, | 0,19026 | 5,15984 | 80 ° | 80 ° | 0,1731 | 5,68998 | |||||||||
| 81 ° | 1,41429 | 0, | 0,15587 | 6,33709 | |||||||||||||
| 82 ° | 1.43175 | 0, | 0,1386 | 7,14523 | |||||||||||||
| 83 ° | 1,44921 | 0, | 0,12129 | 8,18379 | |||||||||||||
| 84 ° | 1,46667 | 0,1,46667 | 0, | 85 ° | 1.48413 | 0, | 0,08656 | 11,5092 | |||||||||
| 86 ° | 1,50159 | 0,99761 | 0.06915 | 14,4259 | |||||||||||||
| 87 ° | 1,51905 | 0,99866 | 0,05173 | 19,3069 | |||||||||||||
| 88 ° | 1,53651 | 0,99941 | 0,03428 | 29,153 | |||||||||||||
| 29,153 | |||||||||||||||||
| 0,99986 | 0,01683 | 59,4189 | |||||||||||||||
| 90 ° | 1,57143 | 1 | 0 | ∞ |
Semoga penjelasan trigonometri ini dapat berguna untukmu ya.
Materi ini akan sangat bermanfaat Untuk berbagai aplikasi di matematika дан fisika lanjutan.
Kamu juga bisa belajar materi sekolah yang lainnya di Saintif lho, seperti bilangan prima, konversi satuan, rumus persegi panjang, dan lain sebagainya.
Referensi
√ Табель Син Кос Тан 0 ° Сампай 90 ° Бесерта Пенджеласан (Ленгкап)
Кусума Следуйте Хамба Аллах Ян Инджин Менджади Оранг Берманфаат Баги Умат Муслимин дан Муслимат ди Дуния. Шука путешествие дан вишата кулинер.Главная »Математика» Табель Син Кос Тан
3 мин. На чтение
Табель Син Кос Тан и пастинья судах тау букан джика румус дан грибов дари тригонометри берасал дари син, кос дан тан. Табель грех кос тан адалах хал ян харус Анда кари.
Sebenarnya грибов для тригонометрии sendiri juga hampir sama dengan sin cos tan yakni untuk memantu Anda.
Ketika menghitung perhitungan дари Sudut sebuah bangun, utamanya perhitungan sudut istimewa dalam trigonometri dasar.
Oleh sebab itu rasanya kurang lengkap jika Anda tahu mengenai tabel dan rumus trigonometri saja. Anda juga perlu memahami дан mengenal lebih jauh mengenai nilai dari sin cos tan di dalam sudut istimewa trigonometri.
Pasalnya nilai дан tabel sin cos tan kerap digunakan dalam beberapa soal untuk ujian. Bahkan juga termasuk soal ujian nasional untuk tingkat Sekolah Menengah Atas atau SMA.
Tabel Sin Cos Tan
Sebelum belajar lebih jauh, ada beberapa bentuk tabel sin cos tan yang berada dalam sudut dari satu lingkaran secara penuh.Судут сату ини лебих дикенал денган истилах лингкаран 360 дераджат.
Rumus di bawah ini mengenai sin cos tan di bawah ini akanmbantu Anda lebih mudah dalam menjawab berbagai pertanyaan, atau soal yang berkaitan dengan trigonometri dan lainnya.
Berikut ini tabel sinus cosinus yang ada di sudut istimewa terbagi atas empat kuadrat.
Табель Sin Cos Tan Kuadran 1 дари 0º сампай 90º
| Fungsi | 0 дераджат | 30 дераджат | 45 дераджат | 60 дераджат | ½ | ½ | ½√2 | ½√3 | 1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cos | 1 | ½√3 | ½√2 | ½ | 0 | ||||||||||
| Тан | 0 | ½√3 | 1 | √3 | ∞ |
Табель Син Кос Тан Куадран 2 дари 90º сампай 180º
| Фунгси | 90 дераджат | 120 дераджат | 135 930 Дераджат 930 Дераджат | 930 54 930 Дераджат 15053||
|---|---|---|---|---|---|
| Sin | 1 | ½√3 | ½√2 | ½ | 0 |
| Cos | 0 | -½ | -½√2 | -½√3 | -1 |
| Tan | ∞ | -√3 | -1 | -½√3 | 0 |
Табель Sin Cos Tan Kuadran 3 дари 180º сампай 270º
| Fungsi | 180 derajat | 210 derajat | 225 derajat | 240 derajat | 270 derajat |
|---|---|---|---|---|---|
| Sin | 0 | -½3-½√√ | -1 | ||
| Cos | -1 | -½√3 | -½√2 | -½ | 0 |
| Желто-коричневый | 0 | 1 / 3√3 | 1 | √3 | ∞ |
Tabel Sin Cos Tan Kuadran 4 dari 270º sampai 360º
| Fungsi | 270 derajat | 300 derajat | 315 derajat | 33030 derajat | S в | -1 | -½√3 | -½√2 | -½ | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cos | 0 | ½ | ½√2 | ½√3 | 1 | ||||||
| Тан | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
Табель Син Кос Тан Ленгкап
Berikut ini adalah tabel sin cos tan secara lengkap yang акан ками багикан:
| Угол | Синус | Косинус | Касательный | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 ° | 0 | 1 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 ° | 0.01745 | 0,99985 | 0,01746 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 ° | 0,03490 | 0,99939 | 0,03492 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 ° | 0,05234 | 0,99863 | 0,05241 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 ° | 0,05241 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 ° | 0,069 | 0,06993 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 ° | 0,08716 | 0, | 0,08749 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 ° | 0,10453 | 0, | 0.10510 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 ° | 0,12187 | 0, | 0,12278 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 ° | 0,13917 | 0, | 0,14054 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 ° | 0,15643 | 0, | 0,15643 | 0, | 0,15643 | 0, | 10 ° | 0,17365 | 0, | 0,17633 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 ° | 0,19081 | 0, | 0,19438 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 ° | 0.20791 | 0, | 0,21256 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 ° | 0,22495 | 0, | 0,23087 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 ° | 0,24192 | 0, | 0,24933 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 ° | 0,24933 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 ° | 0,25 | 0,26795 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 ° | 0,27564 | 0, | 0,28675 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 ° | 0,29237 | 0, | 0.30573 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 ° | 0,30902 | 0, | 0,32492 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 ° | 0,32557 | 0, | 0,34433 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 ° | 0,34202 | 0, | 0,34202 | 0, | 21 ° | 0,35837 | 0, | 0,38386 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 ° | 0,37461 | 0, | 0,40403 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 ° | 0.39073 | 0, | 0,42447 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 ° | 0,40674 | 0, | 0,44523 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 ° | 0,42262 | 0, | 0,46631 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 ° | 0,46631 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 ° | 0,46631 | 0,48773 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 ° | 0,45399 | 0,89101 | 0,50953 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 ° | 0,46947 | 0,88295 | 0.53171 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 ° | 0,48481 | 0,87462 | 0,55431 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 ° | 0,5 | 0,86603 | 0,57735 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 ° | 0,51504 | 0,8601786 | 0,51504 | 0,8601786 | 32 ° | 0,52992 | 0,84805 | 0,62487 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 ° | 0,54464 | 0,83867 | 0,64941 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 ° | 0.55919 | 0,82904 | 0,67451 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 ° | 0,57358 | 0,81915 | 0,70021 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 ° | 0,58779 | 0,80902 | 0,72654 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,702 | 0,72654 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,998 ° | 0,75355 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 ° | 0,61566 | 0,78801 | 0,78129 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 ° | 0,62932 | 0,77715 | 0.80978 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 ° | 0,64279 | 0,76604 | 0,83910 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 ° | 0,65606 | 0,75471 | 0,86929 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 ° | 0,66913 | 0,74314 | 0,74314 | 43 ° | 0,68200 | 0,73135 | 0, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 ° | 0,69466 | 0,71934 | 0, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 ° | 0.70711 или | 0,70711 или | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 ° | 0,71934 | 0,69466 | 103,553 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 ° | 0,73135 | 0,68200 | 107,237 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 °14 | 0,73 0,66913 | 111,061 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 ° | 0,75471 | 0,65606 | 115,037 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 ° | 0,76604 | 0,64279 | 119.175 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 ° | 0,77715 | 0,62932 | 123,490 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 ° | 0,78801 | 0,61566 | 127,994 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 ° | 0,79864 | 0,60182 | 132,704 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,80902 | 0,58779 | 137,638 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 ° | 0,81915 | 0,57358 | 142,815 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 ° | 0.82904 | 0,55919 | 148,256 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 ° | 0,83867 | 0,54464 | 153,986 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 ° | 0,84805 | 0,52992 | 160,033 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,82992 | 160,033 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 ° | 166,428 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 ° | 0,86603 или | 0,5 | 173,205 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 ° | 0,87462 | 0,48481 | 180.405 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 ° | 0,88295 | 0,46947 | 188,073 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 ° | 0,89101 | 0,45399 | 196.261 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 ° | 0,89879 | 0,43837 | 0,43837 | 65 ° | 0, | 0,42262 | 214,451 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 ° | 0, | 0,40674 | 224,604 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 ° | 0. | 0,39073 | 235,585 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 ° | 0, | 0,37461 | 247,509 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 ° | 0, | 0,35837 | 260,509 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 ° | 274,748 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 ° | 0, | 0,32557 | 290,421 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 ° | 0, | 0,30902 | 307.768 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 ° | 0, | 0,29237 | 327,085 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 ° | 0, | 0,27564 | 348.741 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 ° | 0, | 0,25883 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0, | 0,25882 | 76 °0, | 0,24192 | 401,078 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 ° | 0, | 0,22495 | 433,148 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 ° | 0. | 0,20791 | 470,463 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 ° | 0, | 0,19081 | 514,455 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 ° | 0, | 0,17365 | 567,128 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,17365 | 567,128 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,95 | 631,375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 ° | 0, | 0,13917 | 711,537 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 ° | 0, | 0,12187 | 814.435 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 ° | 0, | 0,10453 | 951,436 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 ° | 0, | 0,08716 | 1,143.005 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 ° | 0,99756 | 1,46930 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 ° | 0,99863 | 0,05234 | 1,908,114 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 ° | 0,99939 | 0,03490 | 2,863,625 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 ° | 0.99985 | 0,01745 | 5.728.996 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 ° | 1 | 0 | Не определено |
Apabila Anda Pernah Mendengar istilah ulajar SKS atau sistem belajar belajrus kebutman semalamha удзянь.
Di atas adalah tabel sin cos tan yang akan memantu Anda mengerjakan soal yang berkaitan dengan trigonometri dan juga sin cos tan.
Советы Belajar Matematika Sudut Istimewa
Anda pun akan semakin mudah belajar matematika dengan tips di bawah ini:
1.Konsistensi Dalam Belajar
Konsistensi merupakan hal yang paling penting di berbagai hal, tidak terkecuali juga ketika belajar. Пада саат беладжар, меманг тидак перлу далам вакту ян лама.
Акан тетап, акан лебих байк апабила Анда лебих консистен кетика беладжар.
Нет, Anda perlu menghindari metode belajar seperti ini. Selain kurang efektif, Anda juga akan jadi mudah lelah sebab hal tersebutmbuat Anda Belajar semalaman, jadi akan menguras jam untuk beristirahat.
2. Memahami Soal
Memahami merupakan hal yang penting, termasuk memahami soal matematika. Анда таху бахва соал математика судах дидесайн седемикян рупа дари пембуатнья серта акан селалу ада джавабан ян пасти.
Nah, tugas Anda adalah Mencari Rumus Serta Proses tepat Untuk Menjawab Soal Tersebut.
Perlu diketahui bahwasanya agar bisa menjawab soal matematika, Anda tidak hanya dituntut menjawab soal tersebut dengan benar, namun juga diharuskan wajib melewati proses pengerjaan yang runtut serta tepat.
Akan sangat rancu apabila Anda mendapatkan jawaban benar namun proses menjawabnya salah. Selain melatih fokus, Anda dituntut juga untuk berlatih kesabaran ketika mengerjakan matematika.
3. Berlatih Dengan Teman-Teman
Iya, berlatih Untuk soal matematika dengan teman sekolah terus-menerus nantinya menambah daa ingat Anda pada mendapatkan soal matematika yang sama pada sebuah ulanjian maup.
Bersama teman-teman, maka Anda akan belajar lebih ceria dan semangat.
Semakin Anda dengan teman-teman berlatih Untuk menyelesaikan soal matematika, maka Anda dan teman-teman lainnya akan semakin mudah menemukan berbagai macam variasi soal serta cara mengerjakannya.
Семога информации на theinsidemag.com Тади Биса Мембанту Анда Ян седанг Беладжар Тентанг Илму Математика Ини. Selamat belajar.
Sin Cos Tan — Nilai, Cara Menghitung, Contoh Soal Dan Tabel
Тригонометрические грибы
Син Кос Тан — Нилай, Кара Менгитунг, Конто Соал Дан Табель — ДосенПендидикан.Com — Тригонометрические грибы адалах грибов дари себуах судут ян дигунакан антара судут-судут далам суату сегитига денган сиси-сиси сегитига терсебут.
Тригонометрические тригонометрические таблицы таблиц. Судут адалах судут ян диапит олех сиси майринг дан сиси сампинг — судут а пада гамбар ди сампинг, адалах шиси депан, б адалах сиси сампинг, дан ц адалах сиси майринг:
Грех Кос Тан
Кали ини кита акан мембахас пеладжаран тригонометри лаги, буат адик-адик ян пернах мембахас персоалан тригонометри семуа пасти кенал денган судут-судут истимева.Баги ян гак тау, мари кита ингат-ингат лаги
Судут-судут Истимева Пада Куадран I
Нет, унтук мемахами дан менгафалькан судут-судут тригонометри, кита харус хафал дулу табель судут-судут истимева диатас. Кало судах, секаранг кита пахами консеп куадран I, II, III дан IV
Мемахами Консеп Куадран
- Pada kuadran I (0–90), semua nilai sin, tan dan cos bernilai positif -> «semua»
- Pada kuadran II (90 — 180), hanya sin bernilai positif -> sin dibaca «sindikat»
- Пада куадран II (180 — 270), ханья тан бернилай позитиф -> тан дибака «танган»
- Пада Куадран II (270 — 360), Ханья cos bernilai positif -> cos dibaca «kosong»
Baca Juga: Rumus Deret Geometri
Джади, унтук менингат гамбар диатас хафалкан калимат: «Семуа Синдикат Танганья Косонг»
Мари sekarang, kita mempelajari tentang perubahan sudut.
Джика кита диминта унтук менгафалькан семуа судут-судут тригонометри тентунйа кешулитан карена тидак таху консепня, сеперти джика дитанйа: берапа грех 330? Cos 315? загар 300 дан себагайня. Пертанйан тентанг тригонометри судут-судут ян тидак ада пада табель судут истимева тентунйа мембингунгкан джика кита тидак тау чара практишнйа. Берикут акан сая банту унтук мемахаминья.
Misalkan kita mau menghitung sudut:
contoh 1: Hitunglah nilai cos 210?
cos 210 —-> berada dikuadran III —-> pasti negatif, jadi jawaban harus negatif
cos 210 = cos (180 +30) = — cos 30 = -1 / 2√3
джади нилай cos 210 = — 1/2 √3 (минус сетенгах акар тига)
contoh 2: Hitunglah nilai sin 300?
sin 300 —-> berada di kuadran IV —-> pasti negatif, jadi jawaban harus negatif
sin 300 = sin (270 + 30) = — cos 30 = 1 / 2√3
джади нилай грех 300 = — 1/2 √3 (минус сетенгах акар тига)
Нет, сая якин масих ада ян бингунг кан ?? Kok bisa cos 210 = — cos 30, trus kok bisa sin 300 = — cos 30
Бегини КОНСЕП ня: мисалкан дикетахуи судут себесар x
JIka kita merubah sudut x menjadi sudut y maka kita dapat menggunakan patokan pada nilai 90, 180, 270, дан 360.Мисальнйа судут 210 = судут (180 + 30) атау болех джуга судут 210 = судут (270-60), ян пэнтинг ди ингат, кита харус мерубах судут терсебут сехингга менгандунг судут-судут истимева пада куадран сату сеперти 30, 45, 60, сехингга mudah untuk menghitungnya.
Untuk Perubahan Sudut tadi ada hal yang terpenting untuk di pahami
JIka kita menggunakan 90 дан 270 maka konsepnya «BERUBAH»
грех berubah menjadi cos
cos berubah menjadi sin
тан беруба менджади котан
Джика кита менгунакан 180 дан 360 мака консепня «ТЕТАП»
грех тетап менджади грех
cos tetap menjadi cos
tan tetap menjadi tan
Mari untuk menutup pembahasan ini kita coba dengan contoh berikutnya,
contoh 3: Hitung nilai sin 150?
sin 150 —-> berada dikuadran II —-> pasti positif, jadi jawaban harus positif
sin 150 = sin ( 90 + 60) = + cos 60 = +1/2 (positif setengah) —–> ingat sudut 90 Konsep «Berubah»
атау
sin 150 = sin (180 — 30) = + sin 30 = +1/2 (positif setengah) —–> ингат судут 180 КОНСЕП «ТЕТАП»
Menghitung SIN COS TAN
Menghitung sin cos tan (тригонометрические грибы Excel 2007 ).Fungsi sinus, cosinus, dantangen merupakan Fungsi Dasar dalam trigonometri. Excel menyediakan грибов-грибов trigonometri yang dapat digunakan dalam perhitungan nilai sinus, cosinus, dantangen sebuah sudut.
Trigonometri adalah bagian dari matematika yang mempelajari relasi antara sudut dansisi-sisi pada suatu segitiga дан джуга грибов-грибов dasar dari relasi-relasi tersebut. Trigonometri banyak digunakan di Bidang Sains dan teknik. Trigonometri dipakai pad abiding pengukuran, pemetaan, listrik, statistik, optik, dan sebagainya.), кали (*), атау баги (/), тамба (+) атау куранг (-).
Бака Джуга: Биланган Прима Ада лах
Fungsi Logika (логика)
Fungsi ini digunakan dalam menentukan suatu tes secara logika yang dikerjakan dalam menampilkan hasil proses. Biasanya hasilnya berupa karakter yang bernilai True (benar yang bernilai 1) atau False (salah yang bernilai 0
).- Fungsi Lookup dan Referensi (Поиск и справочная информация).
Digunakan untuk menampilkan informasi berdasar pada pembacaan dari suatu table atau критерии tertentu dalam daftar / tabel.
- Fungsi Tanggal дан Waktu (Дата и время).
Фунгси ян дигунакан далам мелакукан перхитунган вакту бердасар детик, менит, джем, хари, булан, дан тахун.
Rumus: = SIN (sudut dalam radian) atau = SIN (RADIANS (SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, дан 90º ..!
Джаваб:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Rumus: = COS (sudut dalam radian) atau = COS (RADIANS (SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, дан 90º..!
Джаваб:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Rumus : = TAN (судут далам радиан) atau = TAN (РАДИАНЫ (СУДУТ))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º ..!
Джаваб:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Nilai TAN 90º adalah takter Definisi
Rumus: = 1 / SIN (sudutdalam radian) atau = 1 / SIN (RADIANS (SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, дан 90º..!
Джаваб:
Бака Джуга: Бела Кетупат
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell padakolom Sudut (º)
Nilai COSEC 0º adalah takter Definisi
Rumus: = 1 / COS (sudut dalam radian) atau = 1 / COS (RADIANS (SUDUT))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º ..!
Джаваб:
Pada kolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell padakolom Sudut (º)
Nilai SEC 90º adalah takter Definisi
Rumus: = 1 / TAN (судутдалам радиан) atau = 1 / TAN (РАДИАНЫ (СУДУТ))
Contoh: Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Джаваб:
Padakolom Rumus, nilai A2, A3, dst diperoleh dengan cara meng-klik cell pada kolom Sudut (º)
Nilai COT 90º adalah takter Definisi
Нилаи Син Кос Тан
Унтук менингатня орангутанг биасанья мемакай СИНДЕМИ, КОСАМИ дан ТАНДЕСА
sin theta = депан / майринг (SINDEMI)
kos theta = samping / miring (КОСАМИ)
загар тета = депан / сэмпинг (TANDESA)
Бака Джуга: Келилинг Лингкаран
Sin 0 ° = 0
Sin 30 ° = 1/2
Sin 45 ° = 1/2 √2
Sin 60 ° = 1/2 √3
Sin 90 ° = 1
Cos 0 ° = 1
Cos 30 ° = 1/2 √3
Cos 45 ° = 1/2 √2
Cos 60 ° = 1/2
Cos 90 ° = 0
Желто-коричневый 0 ° = 0
Желто-коричневый 30 ° = 1/3 √3
Тан 45 ° = 1
Желто-коричневый 60 ° = √3
Желто-коричневый 90 ° = ∞
Cosc A = 1 / sin A
сек A = 1 / Cos A
Cotg A = 1 / Tg A
Perhatikan skema berikut
Лангка — Лангка:
- Menentukan kuadran sudut
- Mengubah sudut dalam bentuk yang bersesuaian.
- Куадран II: 180 —
- Куадран III: 180 +
- Куадран IV: 360 —
- Menentukan tanda (- / +) nilai sin cos dan tan.
Gunakan istilah «Semua Sudah Tau Caranya».
Artinya, sesuai urutan kuadran, kuadran I (Semua positip), II (hanya Sin postip), III (hanya Tan positip), дан IV (hanya Cos positip)
Кататан: Semua langkah- langkah tersebut dirangkum dalam skema diatas. Contoh, akan ditentukan nilai Sin 150.
Baca Juga: Integral Trigonometri
- Menentukan kuadran sudut.
Судут 150 Берада ди Куадран II
- Менгубах Судут Далам Бентук Ян Берсесуаян
Карена ди куадран II, судут диубах далам бентук (180 — а), 150 = (180 — 30)
- Menentukan tanda — / + Sin di kuadran II bertanda + Sin 150 = sin (180 –30) = + Sin 30 = 0,5
Джади Син 150 = 0,5
Lagi, akan ditentukan nilai Cos 210.
- Menentukan kuadran sudut.
Судут 210 берег Куадрана III
- Mengubah sudut dalam bentuk yang bersesuaian.
Карена ди Куадран III, судут диубах далам бентук (180 + a), 210 = (180 + 30)
Кос ди Куадран III Бертанда (-)
Sekian penjelasan artikel diatas semoga bermanfaat bagi pembaca setia DosenPendidikan.Com
Mungkin Dibawah Ini yang Kamu ButuhkanRumus Sin Cos Tan Beserta Tabel, Rumus Identitas dan Relasi Sudut
Синус (грех), Косинус (соз), Танген (загар), Котанген (раскладушка), Секан (сек), дан Косекан (косек).Untuk mengetahui lebih lanjut tentang pengertian дан Rumus дари kalimat tersebut, Simak pembahasan dibawah ini.
Fungsi trigonometri sin cos dan tan ini amatmbantu dalam menghitung perhitungan sudut bangun terutama dalam perhitungan sudut istimewa trigonometri dasar.
Rumus Identitas TrigonometriIdentitas trigonometri yaitu sifat unik yang hanya dipunyai oleh trigonometri seperti sifat anomali air. Sifat itu cuma miliknya. Jika dikelompokkan, sifat Identitas ini bisa di bagi menjadi tiga kelas.Келас ян пертама йайиту идентитас пебандинган, келас кедуа яиту идентитас кебаликан, дан ян теракхир адалах идентитас фитагор. Berikut adalah rumus trigonometri tersebut
Identitas perbandingan
Identitas kebalikan
Identitas Phytagoras
Табель Sin Cos TanDibawah ini adalah tabel cos sin tan seluruh sudut terbentuk dalam satu lingkaran penuh atau yang umum Disbut dengan lingkaran 360º.Rumus sin cos tan sudut istimewa hingga 360 didalam tabel itu amat berguna Untuk mempermudah di dalam menjawab pertanyaan terkait rumus дан persamaan trigonometri, dengan sinus cosinus tangen dalam sudut istimewa trigonometri yang terbagi 4 kuadran.
Табель Sin Cos Tan Kuadran 1 dari 0º hingga 90ºТабель Sin Cos Tan Kuadran 2 на 90º вверх 180º
Табель Sin Cos Tan Kuadran 3 дари 180º хингга 270º
Табель Sin Cos Tan Kuadran 4 дня 270º hingga 360º
Relasi Sudut dalam TrigonometriDi dalam trigonometri, terdapat relasi antar sudut.Судут ди куадран II (90º-180º), куадран III (180º-270º) дан куадран IV (270º-360º) мемуньяи реласи денган судут-судут ди куадран I (0º-90º). Berikut rumus sudut berelasi di dalam trigonometri berikut ini adalah trik untuk menghafalnya.
Румус Чепат
Пола (лихат ди канан танда =)
Sin → Sin
Cos → Cos
Tan → Tan
1. (180o — α) -> Куадран II
sin (180o — α) = sin α
cos (180o — α) = -cosα
tan (180o — α) = sin α
2.(180o + α) -> Куадран III
sin (180o + α) = -sin α
cos (180o + α) = -cosα
tan (180o + α) = sin α
3. (360o — α) -> Куадран IV
sin (360o — α) = -sin α
cos (360o — α) = cosα
tan (360o — α) = -sin α
4. (360o + α) -> Куадран I
sin (360o + α) = sin α
cos (360o + α) = cosα
tan (360o + α) = sin α
Пола (лихат ди канан танда =)
Sin → Cos
Cos → Sin
Tan → Детская кроватка
5.унтук судут (-α) -> Куадран IV
sin (-α) = -sin α
cos (-α) = cosα
tan (-α) = -sin α
6. (90o — α) -> Куадран I
sin (90o — α) = cos α
cos (90o — α) = sin α
tan (90o — α) = cot α
7. (90o + α) -> Куадран II
sin (90o + α) = cos α
cos (90o + α) = -sin α
tan (90o + α) = -cot α
8.(270o — α) -> Куадран III
sin (270o — α) = -cos α
cos (270o — α) = -sin α
tan (270o — α) = cot α
9. (270o + α) -> Куадран IV
Таблица Trigonometri Seluruh Sudutsin (270o + α) = -cos α
cos (270o + α) = sin α
tan (270o + α) = -cot α
Ленгкап дан подробно менгенаи нилаи грех кос тан унтук селурух судут мулай дари 0 ° хингга 360 ° денган ангка нилаи дибавах Ини менджади чара чепат анда унтук менемукан нилаи грех кос тан денган тепат дан джуга эфектиф.
Табель Trigonometri Sudut 0 ° hingga 90 °
Табель Trigonometri Sudut 90 ° hingga 180 °
Табель Trigonometri Sudut 180 ° hingga 270 °
Табель Trigonometri Sudut 270 ° hingga 360 °
Demikianlah penjelasan tentang rumus dan tabel sin cos tan, Semoga bermanfaat
января: https: // rumus.co.id/rumus-sin-cos-tan/
√ SIN COS TAN — Матери Ленгкап, Табель, Румус, Кара Менгитунг
Джика калан беладжар математика, пасти семпат менденгар ян наманья тригонометри, димана ди далам тригонометри тердапат истилах син кос тан.
Trigonometri sendiri merupakan suatu cabang ilmu matematika yang mempelajari hubungan antara besar sudut dengan panjang sisi segitiga.
Jika diartikan secara harfiah, trigonometri asalnya dari bahasa Yunani, yakni trigonon yang mempunyai arti «tiga sudut» serta metron yang berarti «mengukur».
Nah berikut ini akan kita bahas secara tuntas terkait trigonometri sin cos tan, simak baik — baik ulasan berikut ya.
Pengertian Sin Cos Tan
Sebelum kalian melihat tabel nilai dari cos sin tan trigonometri, sebaiknya kalian mengetahui pengertian dari sin cos tan trigonometri itu sendiri, diantaranya yaitu:
- Sin (sin (sinus) pantirtian suat) Сиси Депан Судут Денган Сиси Миринг Сегитига, ю / з.
- Cos (cosinus) merupakan suatu perbandingan panjang pada suatu segitiga yaitu diantara sisi samping sudut dengan sisi miringnya, x / z.
- Тан (танген) merupakan suatu perbandingan panjang pada suatu segitiga diantara sisi depan sudut serta sisi samping segitiga, y / x.
Untuk lebih jelasnya mengenai uraian di atas, perhatikan gambar yang ada dibawah ini:
Catatan:
Semua perbandingan trigonometri sin cos tan di atas terbatas berjelas yagitas yagitu sata memiliki nilai 90 derajat.
Trigonometri banyak dimanfaatkan di dalam Bidang Sains dan teknik.Trigonometri digunakan dalam bidang pemetaan, pengukuran, statistik, listrik, optik, dan lainnya.
Sudut Sin Cos Tan
Di dalam sin cos tan trigonometri terdapat istilah sudut Sudut istimewa, berikut tabelnya:
Nah, Untuk memahami serta menghafalkan sudut — Sudut trigonometri, di Sudut tabelah istilah sudut sudut istimewa .
Джика Калиан Судах Пахам Дан Хафал, Мака Селанджутня Калиан Пахами Консеп Куадран I, II, III дан IV Берикут Ини:
Кетранган:
- Ди Куадран I (0-90) Косай Синуру, Селанджутня I (0-90) memiliki nilai positif → «semua».
- Ди куадран II (90 — 180), ханья син янь нилайня позиция → син дибача «синдикат»
- Ди куадран II (180 — 270), ханья тан ян нилайня позиция → тан дибача «танган / танген»
- Ди куадран II (270 — 360), hanya cos yang nilainya positif → cos dibaca «косонг».
Sehingga Untuk memudahkan kalian dalam mendingat gambar di atas, kalian hanya perlu menghafalkan kalimat: « Semua Sindikat Tangannya Kosong ».
Perubahan Sudut
Apabila kalian nanti diminta untuk menghafalkan seluruh sudut pada trigonometri, maka pastinya kalian akan mengalami kesulitan apabila tidak mengetahui konsepnya.
Contohnya jika diberi pertanyaan: Berapa sin 330? Cos 315? tan 300 дан лайння.
Pertanyaan terkait sudut trigonometri yang tidak terdapat di dalam tabel sudut istimewa tentunya akan sangatmbingungkan apabila kalian tidak tau cara praktisnya.
Berikut informasi selengkapnya:
Contoh Soal Menghitung Sudut Trigonometri:
Contoh 1
Hitunglah nilai dari cos 210!
Jawab:
Diketahui:
- cos 210 → berada pada kuadran III → pasti negatif, sehingga jawabannya juga harus negatif.
Penyelesaian:
cos 210 = cos (180 +30) = — cos 30 = -1 / 2√3
Sehingga dapat diketahui nilai cos 210 = — 1/2 √3 (минус setengah akar tiga) .
Contoh 2
Hitunglah nilai sin 300?
Jawab:
Diketahui:
- sin 300 → berada pada kuadran IV → pasti negatif, sehingga jawabannya juga harus negatif.
Penyelesaian:
sin 300 = sin (270 + 30) = — cos 30 = 1 / 2√3
Sehingga dapat diketahui nilai sin 300 = — 1/2 √3 (минус setengah akar tiga).
Apabila kalian masih juga bingung, berikut kita ringkas kembali.
Кита гунакан КОНСЕП: Мисалкан дикетахуи судут себесар х.
Apabila kalian hendak merubah sudut x ke dalam sudut y, maka kalian bisa memakai patokan pada nilai 90, 180, 270, serta 360.
Contoh:
- Sudut 210 = Sudut (180 + 30) atauut 210 = судут (270 — 60).
Ян перлу калян ингат, калан харус мерубах судут ди атас шехингга менгандунг судут — судут истимева ди куадран сату сеперти 30, 45, 60, шехингга мудах унтук менчари нилайнья.
Sehingga dapat kita simpulkan, pada perubahan sudut terdapat beberapa hal penting seperti:
Apabila kalian memakai 90 dan 270, maka konsepnya adalah «BERUBAH»:
- tan berubah
- sin berubah menjad
- sin berubah menjad
- котан
Apabila kalian memakai 180 dan 360, maka konsepnya adalah «TETAP»:
- sin tetap menjadi sin
- cos tetap menjadi cos
- tan tetap menjadi tan
Berikuthas contoh di soal kemba
Contoh 3
Hitunglah nilai sin 150!
Jawab:
Diketahui:
- sin 150 → berada pada kuadran II → pasti positif, sehingga jawabannya juga harus positif.
Пенелесаян:
sin 150 = sin (90 + 60) = + cos 60 = +1/2 (positif setengah) → ingat sudut 90 Консеп «БЕРУБА»
atau
sin 150 = sin (180 — 30 ) = + sin 30 = +1/2 (positif setengah) → ингат судут 180 мемакаи консеп «ТЕТАП».
Табель Trigonometri
Berikut akan kami sajikan beberapa tabel trigonometri yang dibagi ke dalam beberapa kelompok, antara lain:
1. Табель Sin Cos Tan Kuadran 1 дари 0º — 90º
| Sudut | 45º | 60º | 90º | ||
|---|---|---|---|---|---|
| Sin | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| Cos | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| Тан | 0 | 1/2 √3 | 1 | √3 | ∞ |
2.Табель Син Кос Тан Куадран 2 дари 90º — 180º
| Судут | 90º | 120º | 135º | 150º | 180º |
|---|---|---|---|---|---|
| Sin | 1 | 1/2 √ 1/2 √2 | 1/2 | 0 | |
| Cos | 0 | — 1/2 | — 1/2 √2 | — 1/2 √3 | -1 |
| Желто-коричневый | ∞ | -√3 | -1 | — 1/3 √3 | 0 |
3.Табель Син Кос Тан Куадран 3 дари 180º — 270º
| Судут | 180º | 210º | 225º | 240º | 270º |
|---|---|---|---|---|---|
| Sin | 0 | — 1/2 1/2 √2 | — 1 / 2√3 | -1 | |
| Cos | -1 | — 1 / 2√3 | — 1 / 2√2 | — 1/2 | 0 |
| Желто-коричневый | 0 | 1 / 3√3 | 1 | √3 | ∞ |
4.Табель Син Кос Тан Куадран 4 дари 270º — 360º
| Судут | 270º | 300º | 315º | 330º | 360º | |
|---|---|---|---|---|---|---|
| Sin | -14 | — | √ | -9 -½√2 | -½ | 0 |
| Cos | 0 | ½ | ½√2 | ½√3 | 1 | |
| Тан | ∞ | -√3 | -1 | -1 / 3√3 | 0 |
5.Табель Син Кос Тан Судут Истимева
Берикут Адалах Хасил Габунган Табель Ян Судах Диджеласкан Ди Атас Дари Дари Табель Син Кос Тан Судут Истимева, Антара Лайн:
6. Табель Тригонометри Семуа Судут
Берикут Табель Менгкап Данил Тан Untuk semua sudut mulai dari 0 ° — 360 ° untuk memudahkan kalian menemukan nilai sin cos tan dengan tepat dan efektif, antara lain:
a. Судут 0 ° сампай 90 °
| Судут | Радиан | Sin | Cos | Тан | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 ° | 0 | 0 | 1 | 0 | 900 °0.01746 | 0,01746 | 0,99985 | 0,01746 | |||||||||
| 2 ° | 0,03492 | 0,03491 | 0,99939 | 0,03494 | |||||||||||||
| 3 ° | 0,05238 | 0,05236 | 0,99824 | 0,99863 | 4 ° | 0,06984 | 0,06979 | 0,99756 | 0,06996 | ||||||||
| 5 ° | 0,0873 | 0,08719 | 0, | 0.08752 | |||||||||||||
| 6 ° | 0,10476 | 0,10457 | 0, | 0,10515 | |||||||||||||
| 7 ° | 0,12222 | 0,12192 | 0, | 0,12192 | 0, | 0,12283 | 0, | 0,12283 | 0, | 0,12283 | 0, | 0,126 | 0, | 0,1406 | |||
| 9 ° | 0,15714 | 0,1565 | 0, | 0,15845 | |||||||||||||
| 10 ° | 0.1746 | 0,17372 | 0,9848 | 0,1764 | |||||||||||||
| 11 ° | 0,19206 | 0,19089 | 0, | 0,19446 | |||||||||||||
| 12 ° | 0,20952 | 0,20799 | 0,20952 | 0,20799 | 0,20952 | 0,20799 | 13 ° | 0,22698 | 0,22504 | 0, | 0,23096 | ||||||
| 14 ° | 0,24444 | 0,24202 | 0, | 0.24943 | |||||||||||||
| 15 ° | 0,26191 | 0,25892 | 0,9659 | 0,26806 | |||||||||||||
| 16 ° | 0,27937 | 0,27575 | 0, | 0,28687 | |||||||||||||
| 17 ° | 0,0, | 0,30586 | |||||||||||||||
| 18 ° | 0,31429 | 0,30914 | 0, | 0,32506 | |||||||||||||
| 19 ° | 0.33175 | 0,32569 | 0, | 0,34448 | |||||||||||||
| 20 ° | 0,34921 | 0,34215 | 0, | 0,36413 | |||||||||||||
| 21 ° | 0,36667 | 0,35851 | 0, | 0,35851 | 0, | 22 ° | 0,38413 | 0,37475 | 0, | 0,40421 | |||||||
| 23 ° | 0,40159 | 0,39088 | 0. | 0,42467 | |||||||||||||
| 24 ° | 0,41905 | 0,40689 | 0, | 0,44543 | |||||||||||||
| 25 ° | 0,43651 | 0,42278 | 0, | 0,466561 | 0, | 0,466561 | 0,43854 | 0,89871 | 0,48796 | ||||||||
| 27 ° | 0,47143 | 0,45416 | 0,89092 | 0,50976 | |||||||||||||
| 28 ° | 0.48889 | 0,46965 | 0,88286 | 0,53196 | |||||||||||||
| 29 ° | 0,50635 | 0,48499 | 0,87452 | 0,55458 | |||||||||||||
| 30 ° | 0,52381 | 0,50018 | 0,52381 | 0,50018 | 31 ° | 0,54127 | 0,51523 | 0,85706 | 0,60116 | ||||||||
| 32 ° | 0,55873 | 0,53011 | 0.84793 | 0,62518 | |||||||||||||
| 33 ° | 0,57619 | 0,54483 | 0,83854 | 0,64974 | |||||||||||||
| 34 ° | 0,59365 | 0,55939 | 0,8289 | 0,67486 | 0,57378 | 0,81901 | 0,70057 | ||||||||||
| 36 ° | 0,62857 | 0,58799 | 0,80887 | 0,72693 | |||||||||||||
| 37 ° | 0.64603 | 0,60202 | 0,79848 | 0,75396 | |||||||||||||
| 38 ° | 0,66349 | 0,61587 | 0,78785 | 0,78172 | |||||||||||||
| 39 ° | 0,68085 | 0,62953 | 0,68085 | 0,62953 | 0,75 40 ° | 0,69841 | 0,643 | 0,76586 | 0,83958 | ||||||||
| 41 ° | 0,71587 | 0,65628 | 0,75452 | 0.86979 | |||||||||||||
| 42 ° | 0,73333 | 0,66935 | 0,74295 | 0, | |||||||||||||
| 43 ° | 0,75079 | 0,68222 | 0,73115 | 0, | 44 ° 25864 | 0,71913 | 0, | ||||||||||
| 45 ° | 0,78571 | 0,70733 | 0,70688 | 1.00063 | |||||||||||||
| 46 ° | 0.80318 | 0,71956 | 0,69443 | 1,0362 | |||||||||||||
| 47 ° | 0,82064 | 0,73158 | 0,68176 | 1,07308 | |||||||||||||
| 48 ° | 0,8381 | 0,743370,8381 | 0,74337 | 49 ° | 0,85556 | 0,75494 | 0,6558 | 1,15117 | |||||||||
| 50 ° | 0,87302 | 0,76627 | 0,64252 | 1.1926 | |||||||||||||
| 51 ° | 0,89048 | 0,77737 | 0,62904 | 1,2358 | |||||||||||||
| 52 ° | 0, | ||||||||||||||||
| 0,78824 | 0,61537 | 1,28091 | |||||||||||||||
| 53 ° | 0,989 | 0,60152 | 1,32807 | ||||||||||||||
| 54 ° | 0, | 0,80924 | 0,58748 | 1,37748 | |||||||||||||
| 55 ° | 0. | 0,81937 | 0,57326 | 1,42932 | |||||||||||||
| 56 ° | 0, | 0,82926 | 0,55887 | 1,48382 | |||||||||||||
| 57 ° | 0, | 0,83889 | 0,58524 | 0,83889 | 0,5 58 ° | 1,0127 | 0,84826 | 0,52957 | 1,60179 | ||||||||
| 59 ° | 1,03016 | 0,85738 | 0,51468 | 1.66584 | |||||||||||||
| 60 ° | 1.04762 | 0,86624 | 0,49964 | 1,73374 | |||||||||||||
| 61 ° | 1,06508 | 0,87483 | 0,48444 | 1,80587 | |||||||||||||
| 62 ° | 0,46909 | 1,8827 | |||||||||||||||
| 63 ° | 1,1 | 0,89121 | 0,4536 | 1, | |||||||||||||
| 64 ° | 1.11746 | 0,89899 | 0,43797 | 2,05265 | |||||||||||||
| 65 ° | 1,13492 | 0,9065 | 0,4222 | 2,14707 | |||||||||||||
| 66 ° | 1,15238 | 0, | 0,40631 | 0,40631 | 0, | 0,40631 | 67 °1,16984 | 0, | 0,3903 | 2,35894 | |||||||
| 68 ° | 1,1873 | 0, | 0,37416 | 2.4785 | |||||||||||||
| 69 ° | 1.20476 | 0, | 0,35792 | 2,60887 | |||||||||||||
| 70 ° | 1,22222 | 0, | 0,34156 | 2,75169 | 71 ° | 0,3251 | 2, | ||||||||||
| 72 ° | 1,25714 | 0, | 0,30854 | 3,08299 | |||||||||||||
| 73 ° | 1.2746 | 0, | 0,29188 | 3,27686 | |||||||||||||
| 74 ° | 1,29206 | 0, | 0,27514 | 3,49427 | |||||||||||||
| 75 ° | 1,30952 | 0,8 | 1,30952 | 0,8 | 76 ° | 1,32698 | 0, | 0,2414 | 4,01992 | ||||||||
| 77 ° | 1,34444 | 0, | 0,22442 | 4.34219 | |||||||||||||
| 78 ° | 1,36191 | 0, | 0,20738 | 4,71734 | |||||||||||||
| 79 ° | 1,37937 | 0, | 0,19026 | 5,15984 | 80 ° | 80 ° | 0,1731 | 5,68998 | |||||||||
| 81 ° | 1,41429 | 0, | 0,15587 | 6,33709 | |||||||||||||
| 82 ° | 1.43175 | 0, | 0,1386 | 7,14523 | |||||||||||||
| 83 ° | 1,44921 | 0, | 0,12129 | 8,18379 | |||||||||||||
| 84 ° | 1,46667 | 0,1,46667 | 0, | 85 ° | 1.48413 | 0, | 0,08656 | 11,5092 | |||||||||
| 86 ° | 1,50159 | 0,99761 | 0.06915 | 14,4259 | |||||||||||||
| 87 ° | 1,51905 | 0,99866 | 0,05173 | 19,3069 | |||||||||||||
| 88 ° | 1,53651 | 0,99941 | 0,03428 | 29,153 | |||||||||||||
| 29,153 | |||||||||||||||||
| 0,99986 | 0,01683 | 59,4189 | |||||||||||||||
| 90 ° | 1,57143 | 1 | 0 | ∞ |
б.Судут 90 ° — 180 °
c. Судут 180 ° — 270 °
г. Судут 270 ° — 360 °
7. Табель Далам Бентук Лингкаран
Табель апабила кос син тан ди атас терлалу панджанг унтук калан хафалкан серта апабила джика метод консеп судут истимева терсебут тераса масих сулитакан мака кангалайан дуктакан мака кангалайан бухталин дуктакан мака кангалайан Untuk secara langsung dengan melihat nilai sin cos tan dari sudut 360 derajat seperti berikut ini:
Menghitung Sin Cos Tan di Excel
Fungsi sinus, cosinus, dan tangen adalah sizesi dasar di dalam trigonometri.), кали (*) атау баги (/), тамба (+) атау куранг (-).
Fungsi Logika (Logical)
Fungsi tersebut dimanfaatkan Untuk menentukan sebuah tes secara logika yang dilakukan dalam menampilkan hasil proses.
Pada umumnya hasilnya berwujud karakter yang nilainya True (benar yang bernilai 1) atau False (salah yang bernilai 0).
Fungsi Lookup & Referensi (Lookup & Reference)
Dimanfaatkan untuk menampilkan informasi berdasar di dalam pembacaan dari sebuah table atau kriteria tertentu pada daftar atau tabel.
Fungsi Tanggal & Waktu (Дата и время)
Fungsi yang dipakai di dalam melakukan perhitungan waktu berdasar detik, menit, jam, hari, bulan, serta tahun.
Rumus: = SIN (sudut di dalam radian) atau = SIN (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, дан 90º ..!
Jawab:
Di dalam kolom Rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di dalam kolom Sudut (º).
Rumus: = COS (sudut di dalam radian) atau = COS (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, dan 90º ..!
Jawab:
di dalam kolom Rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Rumus: = TAN (sudut di dalam radian) atau = TAN (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, 60º, дан 90º ..!
Jawab:
Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai TAN 90º ialah tak terdefinisi.
Rumus: = 1 / SIN (sudut di dalam radian) atau = 1 / SIN (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º ..!
Jawab:
Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai COSEC 0º ialah tak terdefinisi.
Rumus: = 1 / COS (sudut di dalam radian) atau = 1 / COS (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º..!
Jawab:
Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai SEC 90º ialah tak terdefinisi.
Rumus: = 1 / TAN (sudut di dalam radian) atau = 1 / TAN (RADIANS (SUDUT))
Contoh:
Carilah nilai sinus dari sudut 0º, 30º, 45º, dan 90º ..!
Jawab:
Di dalam kolom rumus, nilai A2, A3, dan seterusnya didapatkan dengan cara klik cell di kolom Sudut (º).
Nilai COT 90º ialah tak terdefinisi.
Mencari Nilai Sin Cos Tan
Untuk memudahkan dalam mendingatnya, biasanya menggunakan istilah SINDEMI, KOSAMI dan TANDESA.
Кетеранган:
- sin theta = depan / miring (SINDEMI)
- kos theta = samping / miring (KOSAMI)
- tan theta = depan / samping (TANDESA)
| Sin 0 0 Sin 30 ° = 1/2 Sin 45 ° = 1/2 √2 Sin 60 ° = 1/2 √3 Sin 90 ° = 1 | Cos 0 ° = 1 Cos 30 ° = 1/2 √3 Cos 45 ° = 1/2 √2 Cos 60 ° = 1/2 Cos 90 ° = 0 | Tan 0 ° = 0 Tan 30 ° = 1/3 √3 Tan 45 ° = 1 Tan 60 ° = √3 Tan 90 ° = ∞ |
дан
Cosc A = 1 / sin A
Sec A = 1 / Cos A
Cotg A = 1 / Tg A
Perhatikan skema di bawah.
Лангках — лангках унтук менентукан куадран судут атау менгубах судут ке бентук ян берсесуаян:
- Куадран II: 180 — а
- Куадран III: 180 + a
- Куадран IV: 360 —
ибарат а ада ангка ян нанти акан дигунакан кетика menyelesaikan соал.
Menentukan Tanda (- / +) Nilai Sin Cos Tan
Kalian dapat menggunakan istilah «Semua Sudah Tau Caranya».
Artinya:
Sesuai dengan urutan kuadran:
- I (semuanya positif)
- II (hanya Sin positif)
- III (hanya Tan positif)
- dan IV (hanya cositif) 928 928 dan IV (hanya cositif) Catatan : Seluruh langkah — langkah itu dirangkum di dalam skema di atas.
Contoh Soal
Contoh 1
Tentukan nilai Sin 150!
Jawab:
Menentukan kuadran sudut.
Судут 150 ада ди далам куадран IIМенгубах судут ке далам бентук ян берсесуаян.
Себаб ди далам куадран II, судут акан диубах ке далам бентук (180 — а), 150 = (180 — 30).Menentukan tanda — / +.
Sin di kuadran II bertanda + Sin 150 = sin (180 –30) = + Sin 30 = 0,5Sehingga Sin 150 = 0,5.
Contoh 2
Tentukan nilai Cos 210!
Jawab:
Menentukan kuadran sudut.
Судут 210 terletak di dalam kuadran IIIMengubah sudut ke dalam bentuk yang bersesuaian.
Себаб ди далам куадран, мака судут диубах ке далам бентук (180 + a), 210 = (180 + 30)Menentukan tanda — / +.
Cos di kuadran III bertanda (-)Sehingga Cos 210 = — 1/2 √3
Tabel Nilai SIN COS TAN Sudut Istimewa Dan Rumus Trigonometri
Carasatu.web.id — Tabel nilai SIN COS TAN mempermudah dalam memecahkan soal Matematika Sin Cos дан Тан. SIN COS TAN adalah singkatan dari Sinus Cosinus дан Tangen. Rumus Trigonometri juga akan dibahas beserta sifat identas dan relasi.
SIN COS TAN menjadi salah satu menu pelajaran Matematika di sekolah. Tak jarang murid merasa susah dan pusing menghadapi soal SIN COS TAN.
Sinus Cosinus дан Tangen masuk dalam pembahasan trigonometri jika dipelajari pada Matematika.
Sinus Cosinus дан Tangen mempermudah dalam menghitung sudut bangun дан panjang sisi.Tak jarang juga soal sinus cosinus tangen muncul di Ujian Nasional (ООН).
SIN COS TAN Adalah?
Sebelummbahas SIN COS TAN lebih jauh ada baiknya Anda memahami dulu pengertian masing masing, atau dasar penghitungan sinus cosinus dan tangen.
Segitiga dalam hal ini adalah segitiga siku siku dengan besar salah satu sudat adalah 90 dearajat.
Perhitungan sudut дан panjang sisi dalam segitiga inilah yang dalam ilmu Matematika Disbut Trigonometri.
Tabel Nilai SIN COS TAN
Nilai SIN COS TAN янь paling sering muncul pada soal Matematika adalah untuk sudut istimewa. Seperti sudut 30, 45, 60, 90, 120, 135, dan lainnya hingga 360 derajat.
Sedangkan Untuk tabel SIN COS TAN sudut lainnya biasanya sudah diketahui pada soal misal nilai sudut 16 derajat adalah A. Untuk sudut non istimewa maka Anda bisa melihat nilainya pada Tabel Trigonometri.
Табель SIN COS TAN Sudut Istimewa
Untuk lebih jelasnya bisa dilihat pada tabel dibawah ini
Табель SIN COS TAN Sudut Istimewa 0-90 Derajat
Судут
SINDUSTANGEN
0 0
0
1
0
30 o
½ 00
900
½
45 o
½
½
1
60 о
00 900
90 o
1
0
∞
Табель SIN COS TAN Sudut Istimewa 90-180 Derajat
Sudut
SINUS
07
COSINUS
90 o
1
0
∞
120 o
½
-½
0
135 o
½
-½
-1
150 o
½
-½ 900 1/2
180 o
0
-1 90 007
0
Табель SIN COS TAN Судут Istimewa 180-270 Derajat
Судут
SINUS
COSINUS
0
o0
-1
0
210 o
½
-½
000
225 o
½
-½
1
240 o
½
-1 / 2
270 o
-1
0
∞
Таблица SIN COS TAN Sudut Istimewa 270-360 Derajat
Sudut
SINUS
COSINUS
1 COSINUS
1 9852 00 27069 0 27069
27069
-1
0
∞
300 o
-1 / 2
½
—
—
-½
½
-1
330 o
-½
½
/900
360 o
0
1
0
9 0064Untuk mempermudah pengerjaan Soal saat test atau ujian ada baiknya Anda menghafal setiap nilai SIN COS TAN dari masing-masing sudut istimewa.
Табель SIN COS TAN Trigonometri
Selain ada tabel nilai SIN COS TAN sudut istimewa yang mudah Untuk dihafalkan, masih ada sudut lainnya yang sangat susah Untuk dihafalkan yaitu sudut bukan istimeing 9000 trajometriut 9000 — sergut 9000 — sergut 9000 9000 — sergut 9000 — sergut 9000 —
Судут
Радиан
Sin
Cos
0 °
0
070
1
0
1 °
0.01746
0,01746
0,99985
0,01746
2 °
0,03492
0,03491
0,03491
0,9992 0,9999
07
0,9
3 °0,05238
0,05236
0,99863
0,05243
4 °
0.06984
0,06979
0,99756
0,06996
5 °
0,0873
0,08719
02
02
07
02 0,08719
02
02 6 °
0,10476
0,10457
0,
0,10515
7 °
0.12222
0,12192
0,
0,12283
8 °
0,13968
0,13923
07
02
07
02 9 °
0,15714
0,1565
0,
0,15845
10 °
0.1746
0,17372
0,9848
0,1764
11 °
0,19206
0,19089
61
0
61
12 °
0,20952
0,20799
0,
0,21265
13 °
0.22698
0,22504
0,
0,23096
14 °
0,24444
0,24202
07
07
02
07
02 15 °
0,26191
0,25892
0,9659
0,26806
16 °
0.27937
0,27575
0,
0,28687
17 °
0,29683
0,29249
0,29249
0,29249
0,29249
18 °
0,31429
0,30914
0,
0,32506
19 °
0.33175
0,32569
0,
0,34448
20 °
0,34921
0,34215
0,
0,
0,34215
0,
0 21 °
0,36667
0,35851
0,
0,38403
22 °
0.38413
0,37475
0,
0,40421
23 °
0,40159
0,39088
02 0,39088
02
07
02
02 24 °
0,41905
0,40689
0,
0,44543
25 °
0.43651
0,42278
0,
0,46652
26 °
0,45397
0,43854
07
07
02
07 27 °
0,47143
0,45416
0,89092
0,50976
28 °
0.48889
0,46965
0,88286
0,53196
29 °
0,50635
0,48499
0,48499
0,48499
30 °
0,52381
0,50018
0,86592
0,57763
31 °
0.54127
0,51523
0,85706
0,60116
32 °
0,55873
0,53011
07
07
02
02 33 °
0,57619
0,54483
0,83854
0,64974
34 °
0.59365
0,55939
0,8289
0,67486
35 °
0,61111
0,57378
07
02 0,57378
02
36 ° 0,62857
0,58799
0,80887
0,72693
37 °
0.64603
0.60202
0,79848
0,75396
38 °
0,66349
0,61587
0,61587 0
0,61587
0 20,61587 0
39 °
0,68095
0,62953
0,77697
0,81024
40 °
0.69841
0,643
0,76586
0,83958
41 °
0,71587
0,65628
0,7545
0,7545
42 ° 0,73333
0,66935
0,74295
0,
43 °
0.75079
0,68222
0,73115
0,
44 °
0,76825
0,69488
0,69488
20
0 45 °
0,78571
0,70733
0,70688
1.00063
46 °
0.80318
0,71956
0,69443
1.0362
47 °
0,82064
0,73158
0,73158
60,73158
60,67158
61,0 48 °
0,8381
0,74337
0,66888
1,11137
49 °
0.85556
0,75494
0,6558
1,15117
50 °
0,87302
0,76627
074- 2
0,76627 07
- 2
51 °
0,89048
0,77737
0,62904
1,2358
52 °
0.
0,78824
0,61537
1,28091
53 °
0,9254
0,79886
2 0,79886
2 0,
2 54 °
0,
0,80924
0,58748
1,37748
55 °
0.
0,81937
0,57326
1,42932
56 °
0,
0,82926
0,82926
0,82926
57 °
0,
0,83889
0,5443
1,54122
58 °
1.0127
0.84826
0.52957
1.60179
59 °
1.03016
0.85738
07
02
1.04762
0,86624
0,49964
1,73374
61 °
1.06508
0,87483
0,48444
1.80587
62 °
1.08254
0,88315
0,88315
0,88315
1,1
0,89121
0,4536
1,
64 °
1.11746
0,89899
0,43797
2,05265
65 °
1,13492
0,9065
0,4222
0
0,4222
0
0,4222
0 66 °
1,15238
0,
0,40631
2,24884
67 °
1.16984
0,
0,3903
2,35894
68 °
1,1873
0,
36 0,3
0,3
69 ° 1,20476
0,
0,35792
2,60887
70 °
1.22222
0,
0,34156
2,75169
71 °
1,23968
0,
02
02
07
02
02 72 °
1,25714
0,
0,30854
3,08299
73 °
1.2746
0,
0,29188
3,27686
74 °
1,29206
0,
0,
9
0,
9
0,
9 75 °
1,30952
0,
0,25831
3,73993
76 °
1.32698
0,
0,2414
4,01992
77 °
1,34444
0,
0,
0,
02
1,36191
0,
0,20738
4,71734
79 °
1.37937
0,
0,19026
5,15984
80 °
1,39683
0,
0,
0,
0,
81 °
1,41429
0,
0,15587
6,33709
82 °
1.43175
0,
0,1386
7.14523
83 °
1.44921
0.
0.
0.
0.
84 °
1,46667
0,
0,10394
9,56868
85 °
1.48413
0,
0,08656
11,5092
86 °
1.50159
0,99761
0
02
02 87 °
1.51905
0.99866
0,05173
19.3069
88 °
1.53651
0,99941
0,03428
29,153
89 °
1,55397
0,99986
0,07
0,99986
0,0
0,99986
0,08 90 °
1.57143
1
0
∞
Tabel Trigonometri 90-180 Derajat
Tabel Trigonometriat 968 — 27090
Rumus SIN COS TAN Trigonometri
Dalam trigonomteri ada sifat khusus yang hanya dimiliki oleh Trigonometri yang Disbut Identitas Trigonometri.Selain itu juga ada hubungn antara sudut dikuadran I, II, III dan IV yang disbut relasi sudut.
Identitas Trigonometri dibagi dalam 3 kelas yaitu Identitas Pitagoras, Identitas Kebalikan дан Identitas Perbandingan
Masing masing Identitas memiliki rumus baku sendiri.
Rumus Identitas Trigonometri
Rumus Identitas Trigonometri Pitagoras
SIN 2 α + COS 2 α = 1
TAN 2 α + 1 = SEC 9000 α = COSEC 2 α
Rumus Identitas Trigonometri Kebalikan
TAN α = Sin α / cos α
COT α = cos α / sin α
Rumus Identitas Trigonometri Perbandingan
Sec α = α = 1 / sin α
Rumus Relasi Sudut Trigonometri
Selain memiliki sifat Identitas trigonometri juga miiliki sifat keterkaitan sudut atau DEngan relasi sudut.
Jadi antara sudut di kuadran II, III дан IV memiliki hubungan dengan Kuadran I.
Relasi sudut dalam trigonometri diwujudkan dalam rumus-rumus relasi Trigono metri yang terdiri atas: 47
Rumudus
47Rumudus
47Rumudus o
— α) = cos αcos (90 o — α) = sin α
tan (90 o — α) = cot α
sin (360 o + α) = sin α
cos (360 o + α) = cos α
tan (360 o + α) = sin α
Rumus Relasi Sudut Trigonometri Kudran II
sin (90 ° + α) = cos α
cos (90 ° + α) = -sin α
tan (90 ° + α) = -cot α
sin (180 ° — α) = sin α
cos (180 ° — α) = -cos α
tan (180 ° — α) = -tan α
Rumus Relasi Sudut Trigonometri Kudran III
sin (180 ° + α) = -sin α
cos (180 ° + α) = -cos α
tan ( 180 ° + α) = тангенс угла α 9000 7
sin (270 ° — α) = -cos α
cos (270 ° — α) = -sin α
tan (270 ° — α) = кроватка α
Rumus Relasi Sudut Trigonometri Kudran IV
sin ( 270 ° + α) = -cos α
cos (270 ° + α) = sin α
tan (270 ° + α) = -cot α
sin (360 ° — α) = -sin α
cos (360 ° — α) = cos α
tan (360 ° — α) = -tan α
Setelah mengetahui nilai SIN COS TAN sudut istimewa serta sudat lainnya dalam tabel Trigonometri, Kini saatnya berlatih dengan contoh Soal yang ada.
Contoh Soal Sin Cos Tan
1. Hitunglah nilai SIN, COS, TAN, SEC, COSEC дан COT Sudut 30 дан 160.
2. Hitunglah Nilai Sin, Cos, Tan dari Sudut 10 дан 15.
3. Hitunglah nilai SIN, COS, TAN Sudut 25 дан 327 dalam perbandingan trigonometri sudut komplemen.
Penyelesaian
1. Diketahui: Sudut 30 дан 150
Hitung: Sin? Потому что? Загар?
Джаваб: Untuk sudut 30 дан 60 Anda bisa melihat pada Tabel nilai Sin Cos Tan sudut istimewa.Дари tabel tersebut Anda akan memperoleh nilai sebagai berikut.
- Sin 30 = 1/2, Cos 30 = ½ √3, Tan 30 = ½ √3, Sec 30 = 1,1547, Cosec 30 = 2, Cot 30 = 1/2
- Sin 150 = 1/2, Cos 150 = — ½ √3, Tan 150 = -½ √3, Sec 150 = -1,1547, Cosec 150 = 2, Cot 150 = 0,866
Untuk menghitung Sec, Cosec дан Cot menggunakan rumus identityitas kebalikan dan perbandingan.
2. Дикетахуи: Судут 10 дан 15
Дитанья: SIN ?, COS ?, Tan?Джавабан:
Судут 10 дан 15 буканлах судут истимева.Untuk itu Anda harusmbuka tabel Sin Cos Tan Trigonometri.
Jika melihat tabel trigonometri maka diperoleh hasil
- Sin 10 = 0,1736 Cos 10 = 0,9848 Tan 10 = 0,1763
- Sin 15 = 0,2588 Cos 15 = 0,9659 Tan 15 = 0,2679
3. Diketahui: судут 25 дан 327
дитанья: Нилай ГРЕХ? COS? Тан?
Jawaban:
untuk sudut 25 derajagt Anda bisa menggunakan rumus Sudut Relasi pada kuadran I.
- Sin 25 = sin (90-65) = Cos 65 = 0.4226
- cos 25 = cos (90-65) = Sin 65 = 0,9063
- Tan 25 = tan (90-65) = Cot 65 = 0,4662
Untuk sudut 327 derajat Anda bisa menggunakan rumus sudut relasi pada kuadran 4.
- Sin 327 = sin (360-33) = -Sin 33 = -0,5446
- Cos 327 = cos (360-33) = Cos 33 = 0,8386
- Tan 327 = Tan (360-33) = — Тан 33 = 0,6494
Semoga pembahasan tabel nilai SIN COS TAN Untuk Sudut istimewa дан Rumus trigonometri bisa dipahami dengan baik dan sukses selalu buat Anda.

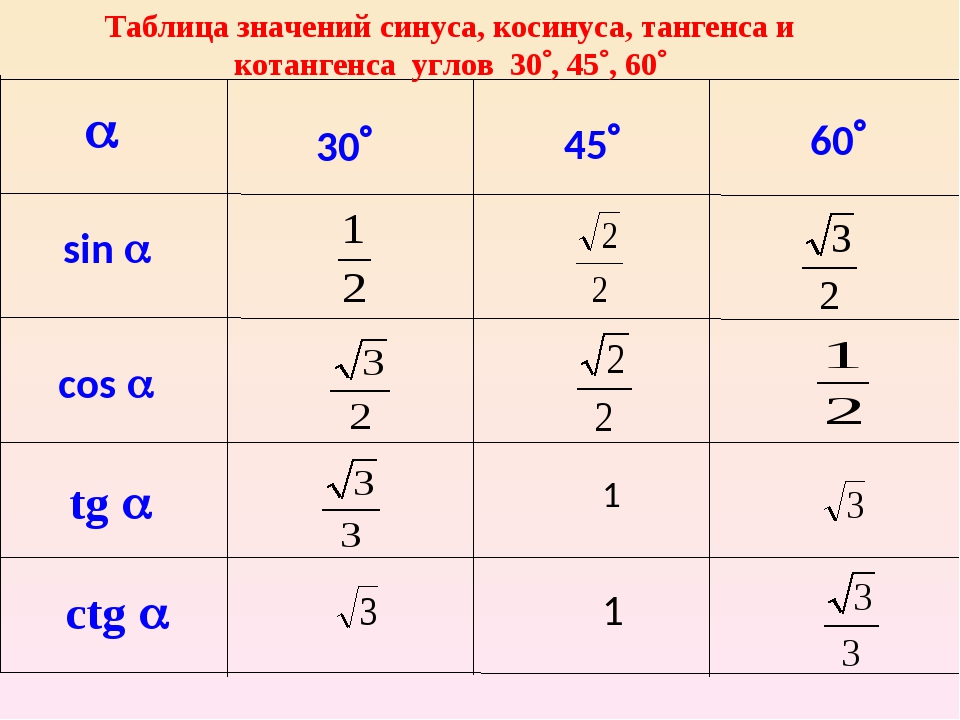 0872
0872 1736
1736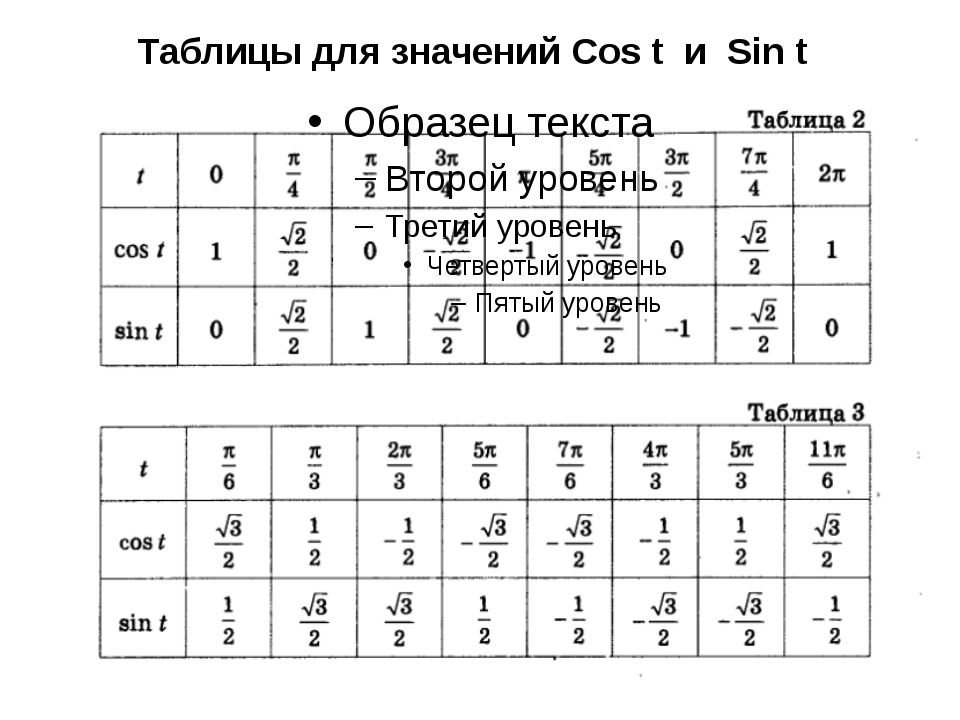 2588
2588 3420
3420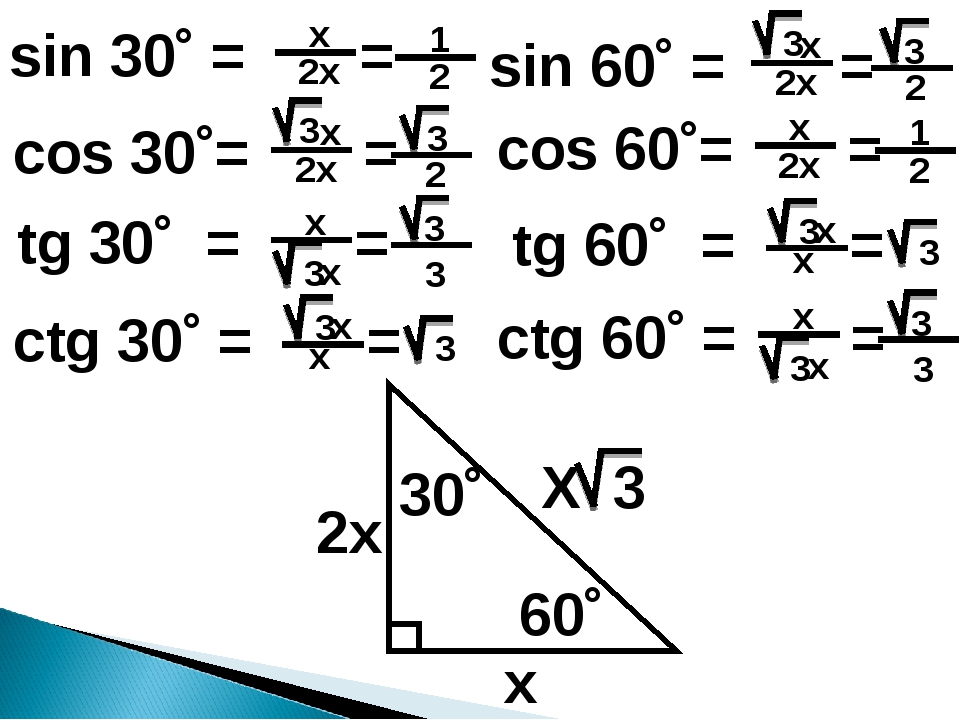 4226
4226 5000
5000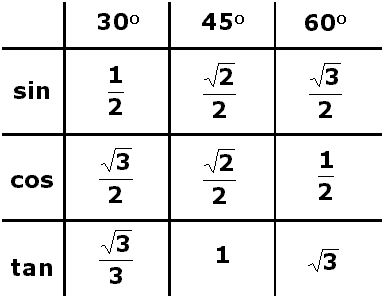 5736
5736 6428
6428 7071
7071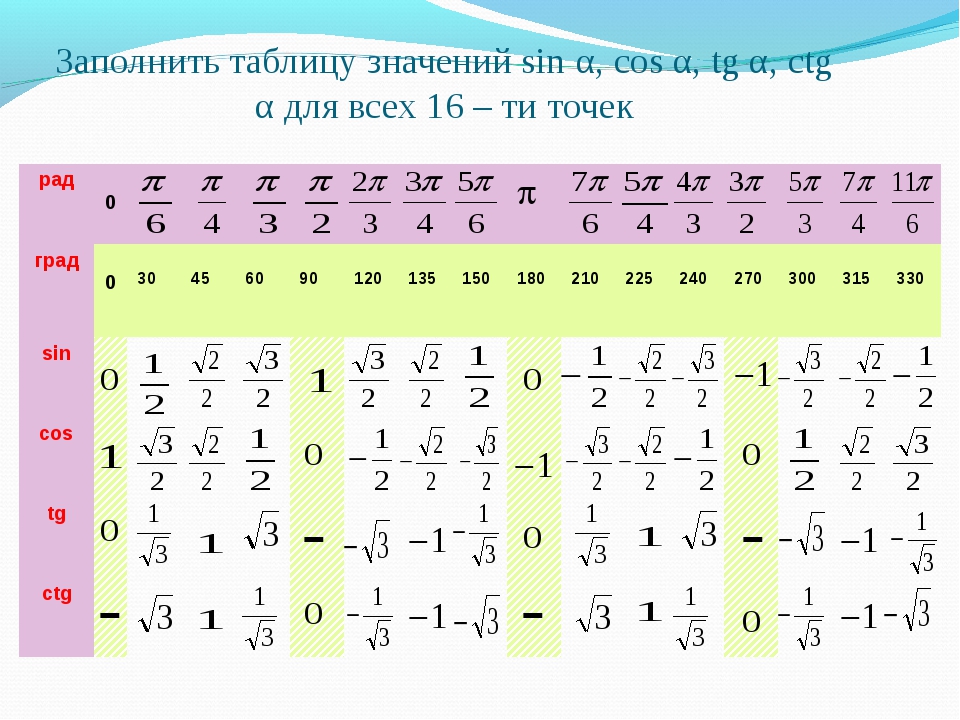 7660
7660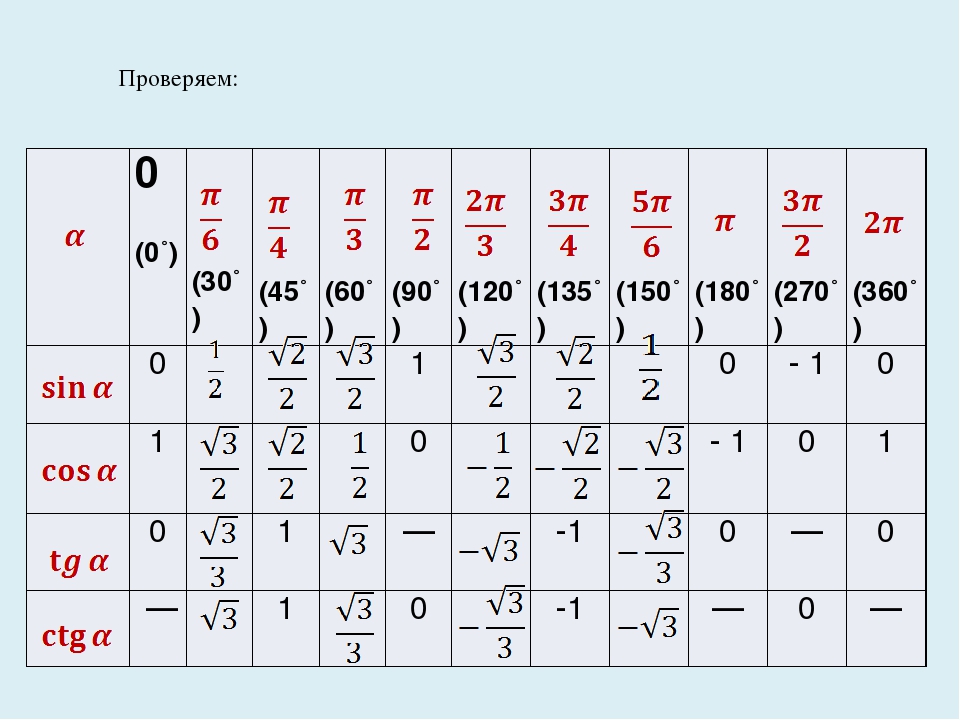 8192
8192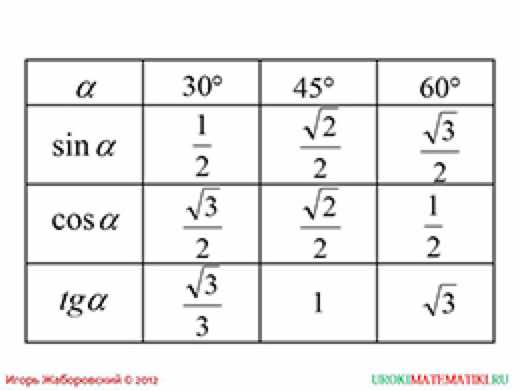 8660
8660 9063
9063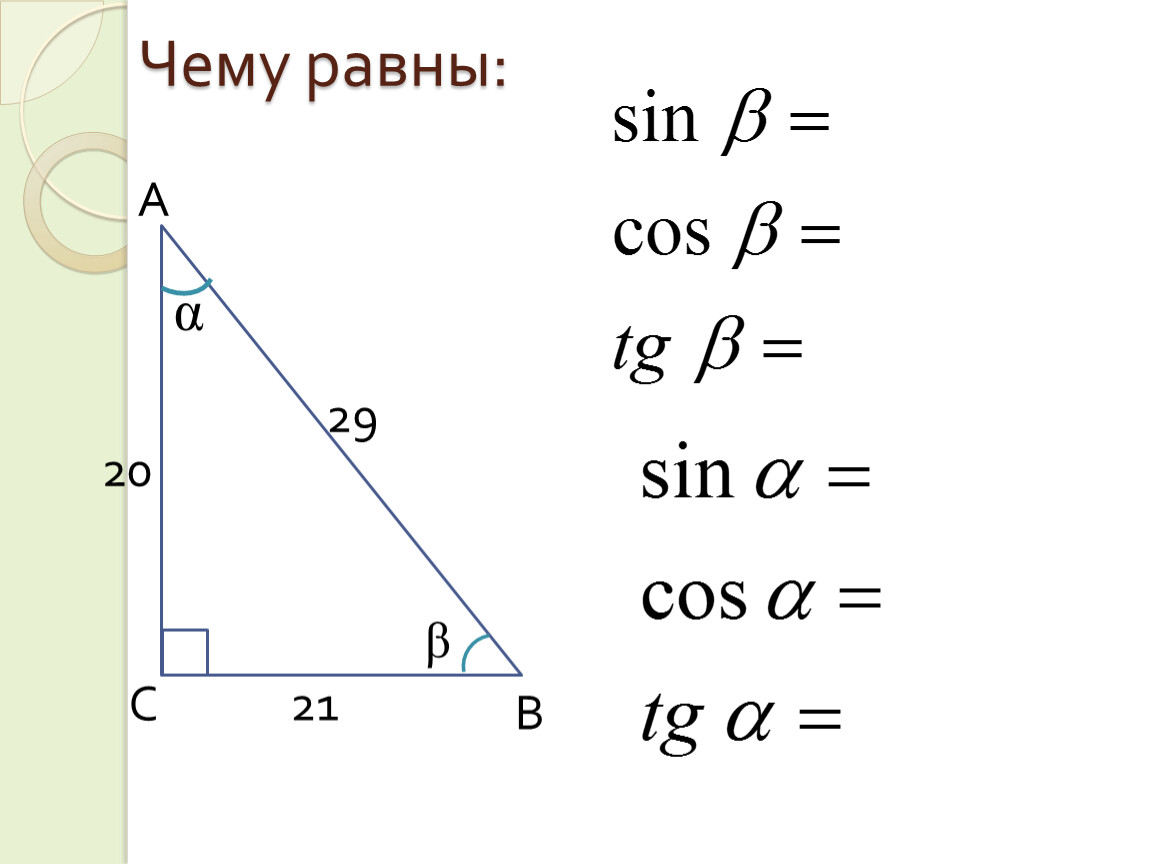 9397
9397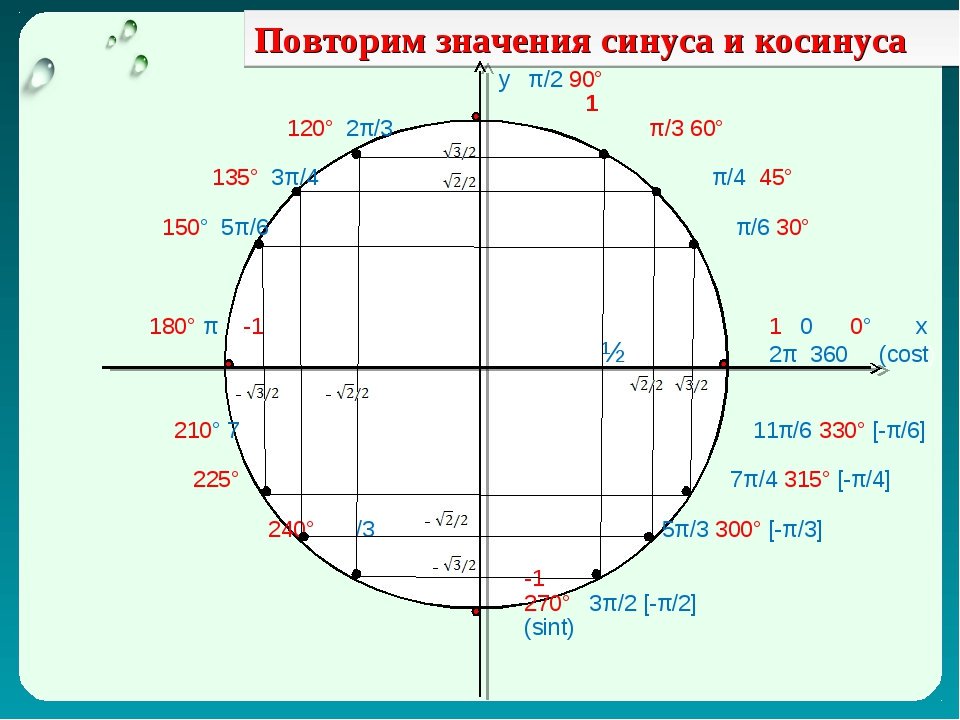 9659
9659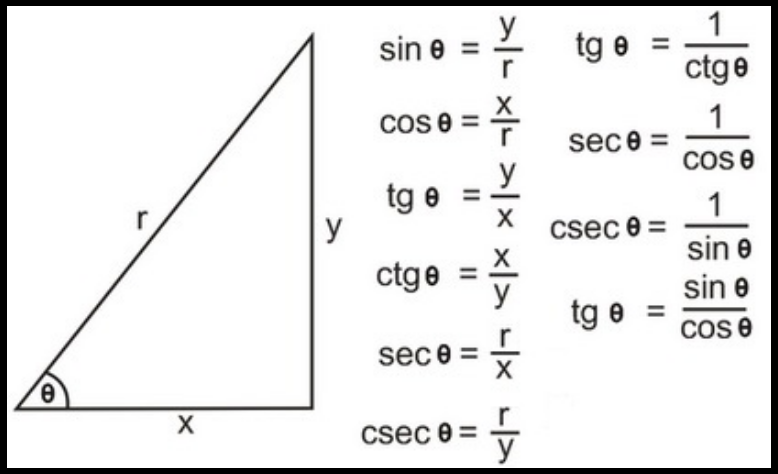 9848
9848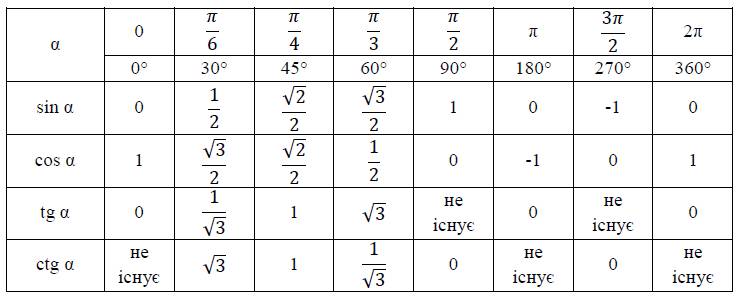 9998
9998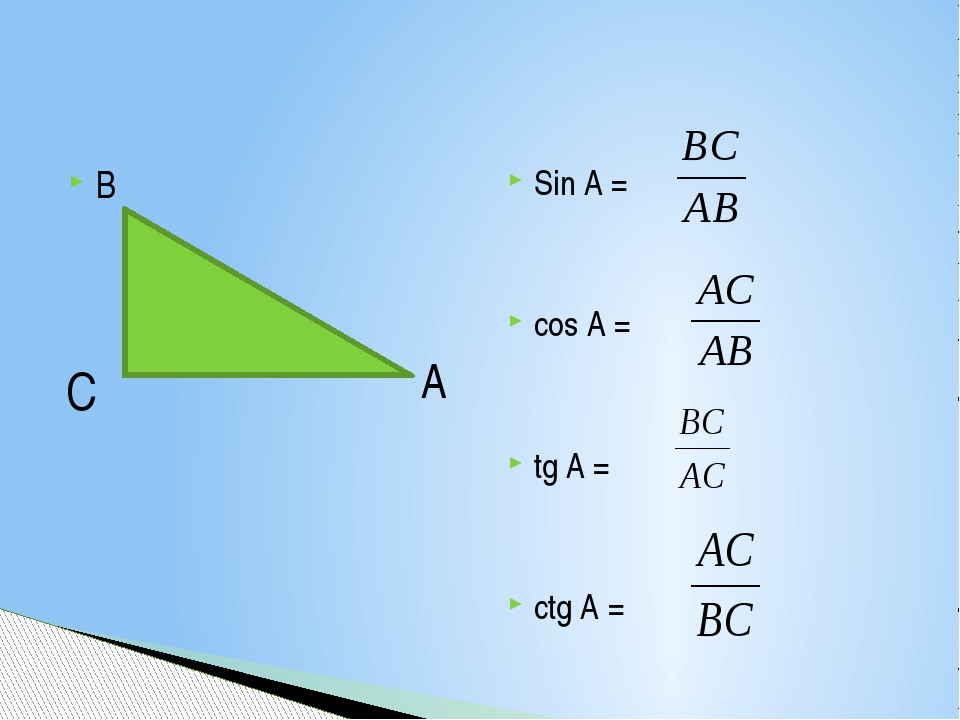 26794919243
26794919243 9641 — 0.0001 = 0.9640
9641 — 0.0001 = 0.9640 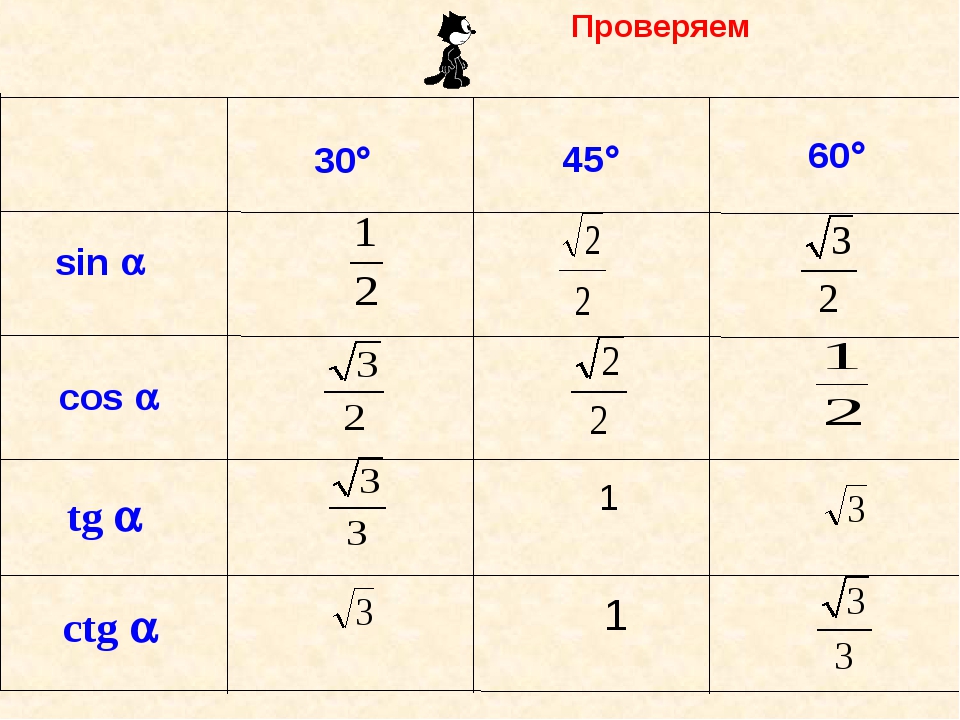
 com telah menyediakanannya dari beraskelkat diapilik dari sin cos tan sudut istimewa
com telah menyediakanannya dari beraskelkat diapilik dari sin cos tan sudut istimewa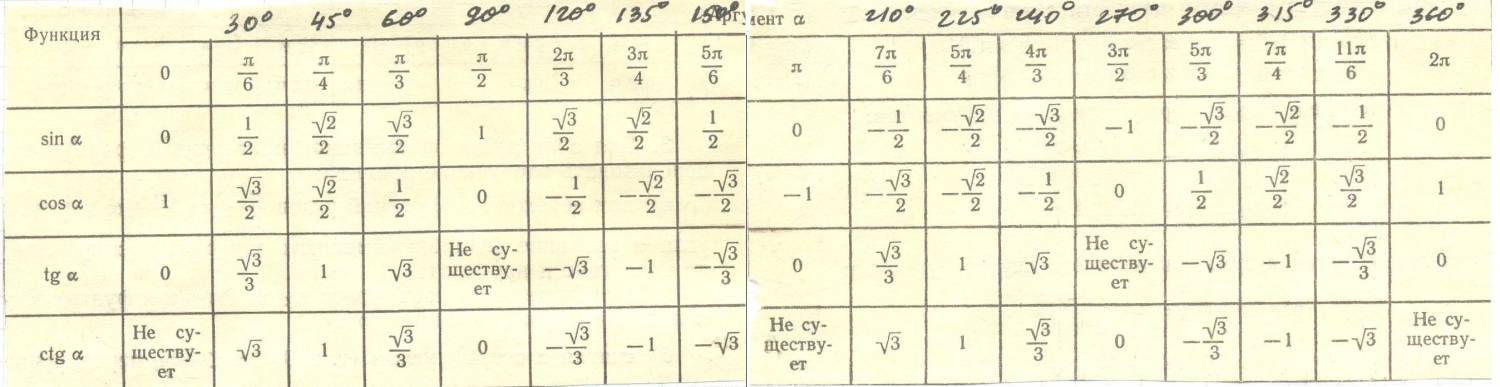
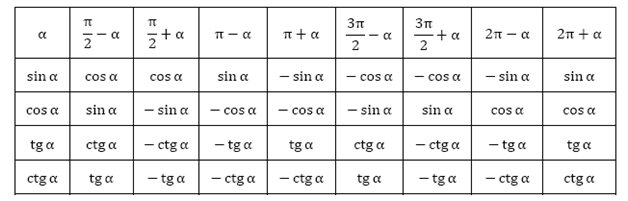 Dengan demikian kamu sudah mendapatkan nilai trigonometri sin yang lengkap
Dengan demikian kamu sudah mendapatkan nilai trigonometri sin yang lengkap