тригонометрия — Мысленная оценка тангенса угла (от $0$ до $90$ градусов)
спросил
Изменено 9 лет, 8 месяцев назад
Просмотрено 7к раз
$\begingroup$
Кто-нибудь знает, как вычислить тангенс угла в уме? Точность не имеет решающего значения, но в пределах $5%$ процентов, вероятно, будет хорошо, 10% может быть приемлемым.
Я довольно хорошо умею вычислять синусы и косинусы, но считаю деление на произвольные значения слишком сложным для этой задачи. Умножение нескольких значений обычно допустимо, а сложение и вычитание — нормально.
Углы у меня в градусах, и я предпочитаю не мысленно преобразовывать их в радианы, хотя при необходимости могу. Кроме того, все интересующие меня углы находятся в диапазоне [0, 90 градусов].
Меня также интересует оценка арктангенса при тех же условиях, с точностью до 5 градусов было бы хорошо.
Предыстория
Я работаю над определением пути солнца по небу. Я могу довольно легко оценить склонение, но теперь я хочу оценить количество дневного света в любой день и на заданной широте. Я свел это к арккосинусу произведения двух касательных, но решение двух касательных теперь является моей камнем преткновения. Я также хочу вычислить высоту солнца для любого времени суток, дня года и широты, которая у меня сводится к арктангенсу.
- тригонометрия
- оценка
- ментальная арифметика
$\endgroup$
10
$\begingroup$
Если вы хотите остаться в пределах 10%, следующая кусочно-линейная функция удовлетворяет $$.9\tan\theta \le y \le 1.1\tan\theta$$ для $0\le\theta\le60$ градусов:
$$y={\theta\over60}\text{для}0\le\theta\le20$$ $$y={2\theta-15\over75}\text{ для }20\le\theta\le45$$ $$y={\theta-20\over25}\text{для}45\le\theta\le60$$
Может помочь переписать их как
$$y={5\theta\over300}\text{ для }0\le\theta\le20$$ $$y={8\theta-60\over300}\text{ для }20\le\theta\le45$$ $$y={4\theta-80\over100}\text{ for }45\le\theta\le60$$
, так что вам действительно не нужно делить ни на что, кроме $3$.
Аппроксимации линейного сегмента лежат на выше $\tan\theta$ от $\theta\ приблизительно25$ до $\theta=45$ и на ниже в другом месте, поэтому вам следует округлить в меньшую сторону на и в большую сторону на соответственно при выполнении ментальная арифметика. Очевидно, что это возможно расширить для углов, превышающих $60$ градусов, но неясно, можно ли (и насколько далеко) сделать это с формулами, которые используют только «простые» умножения и деления.
Слово объяснения : То, что я пытался сделать здесь, это серьезно отнестись к запросу ОП о оценках, которые вы можете вычислить в своей голове. Способность к арифметике в уме, конечно, у разных людей разная, поэтому я использовал себя в качестве меры. Что касается происхождения формул, моей отправной точкой было наблюдение, что коэффициент преобразования между градусами и радианами, $180/\pi$, приблизительно равен $60$, поэтому оценка $\tan\theta\приблизительно\theta/60$ должна быть в порядке некоторое время.
\circ = 1/5$$ 9\circ$
$$\tan a = 1/\tan(90°−a)$$
Вы также можете рекурсивно повторить этот процесс, чтобы получить все более и более точное приближение:
$$a_i=a_{i-1}\pm b_{i-1}$$
$$\tag 4 \tan b_i=b_i=x — a_i$$
Где $a_0$ и $b_0$ выбираются из таблицы, а $x$ — начальное значение угла
При оценке $(4)$ вам необходимо преобразовать в радианы. Это просто умножение на $7/400$ Так что вам нужно аппроксимировать $x-a_i$ такой дробью, что у нее $7$ в знаменателе и/или делители $400$ в числителе.
Найдите в Google документ «Fast_Approximation_of_Elementary_Functions.pdf» для получения дополнительной информации об этом трюке. Прямая ссылка запрещена по какой-то странной причине.
П.С. Рисунок для использования вместо запоминания хеш-таблицы и для быстрого подбора $a_0$ $b_0$:
П.П.С. Чтобы запомнить $(2)$, рассмотрим произведение двух комплексных чисел
$$z=(D1,N1)(D2,N2)$$
поэтому $(2)$ становится:
$$\frac {\Im z}{\Re z}$$
чтобы получить $(3)$ просто поменяйте знаки
$\endgroup$
9{\ circ} — \ frac {180} {3x + 1} \ quad \ mathrm {for} \ quad x > 1 $ $
где $\theta$ измеряется в градусах.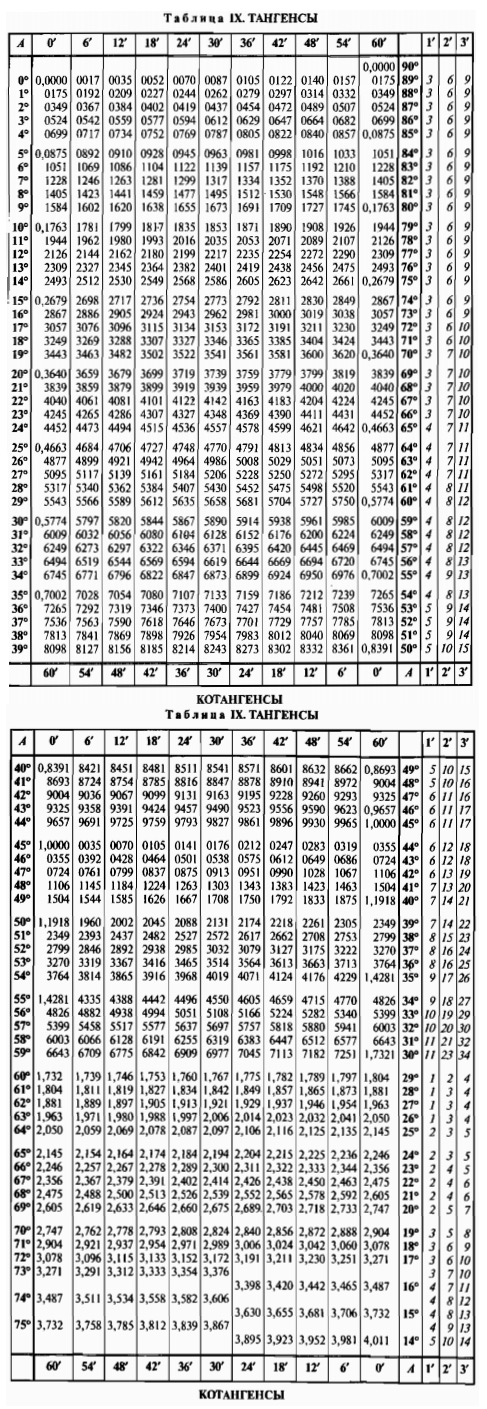
$\endgroup$
$\begingroup$
Возможно, это не лучший вариант для расчетов в уме, но для $x$ в градусах $$ \tan\left(\frac{\pi x}{180}\right)\приблизительно\frac{x(990-4x)}{(90-x)(630+4x)}\tag{1} $$ скидка не более $0,6\%$ за $0\le x\le90$.
Вот график относительной ошибки: $\displaystyle\left.\frac{x(990-4x)}{(90-x)(630+4x)}\middle/\tan\left(\frac{ \pi x}{180}\right)-1\right.$ :
$\hspace{2cm}$
Уравнение $(1)$ выглядит немного устрашающе, но по крайней мере $x$ выражено в градусах, и относительная ошибка довольно мала. На самом деле единственная константа, которую нужно помнить для $(1)$, это $\frac{990}{4}$; то есть, $$ P (x) = x \ left (\ frac {990} {4} -x \ right) \ подразумевает \ tan \ left (\ frac {\ pi x} {180} \ right) \ приблизительно \ frac {P (x )}{P(90-x)}\тег{2} $$
$\endgroup$2
$\begingroup$
Имеем $\tan(x) = \frac{1}{\cot(x)}$, поэтому разобьем $[0,\frac{\pi}{2}]$ на 4 инверсии длины $\frac {\pi}{8}$, а затем используйте
\begin{align} f_1(x) &= x & f_2(x) &= -0,19+1,5x \\ f_3 (x) &= \ frac {1} {f_2 (\ frac {\ pi} {2}-x)} & f_4 (x) & = \ frac {1} {f_1 (\ frac {\ pi} {2 }-Икс)} \end{align}
Функции $f_1$ и $f_4$ имеют относительную погрешность $6\%$, тогда как $f_2$ и $f_3$ около $4\%$, см.
\circ$), я думаю, что можно без чрезвычайного количества механического запоминания сделать очень грубые оценки. Для большей точности или, по крайней мере, перекрестной ссылки, можно было бы составить аналогичный треугольник, оценить соотношение сторон напрямую и выполнить однократное деление. 92\свыше 90-х}$$
дает относительную ошибку менее $6\%$ во всем диапазоне $[0,{\pi\over2}[\ $. См. следующий рисунок:
$\endgroup$
Калькулятор касательной | Calculators.vip
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету.
.
Поделитесь расчетом:
Найдите значение
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A=ARC COS(A)A=ARC TAN(X)A=ARC CTN(X)
Исходные данные
Градусы
Радиан
0 Рассчитать3
0175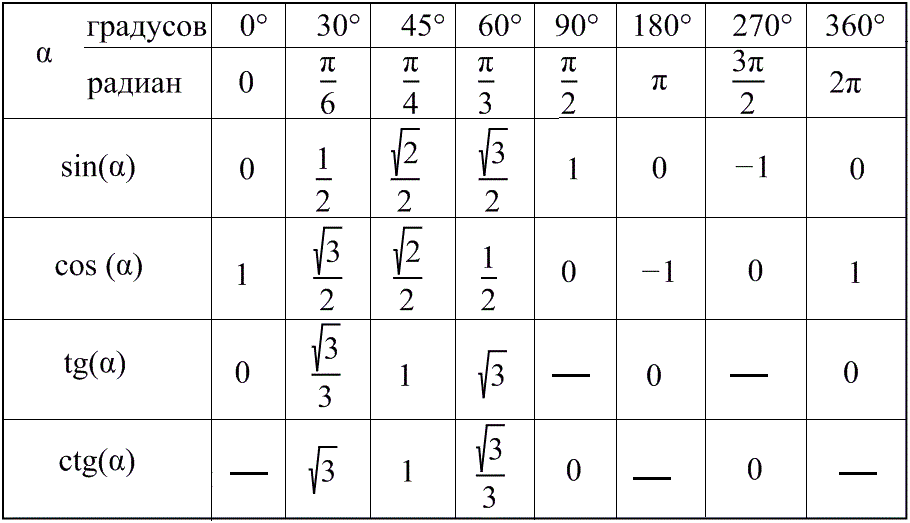
4245
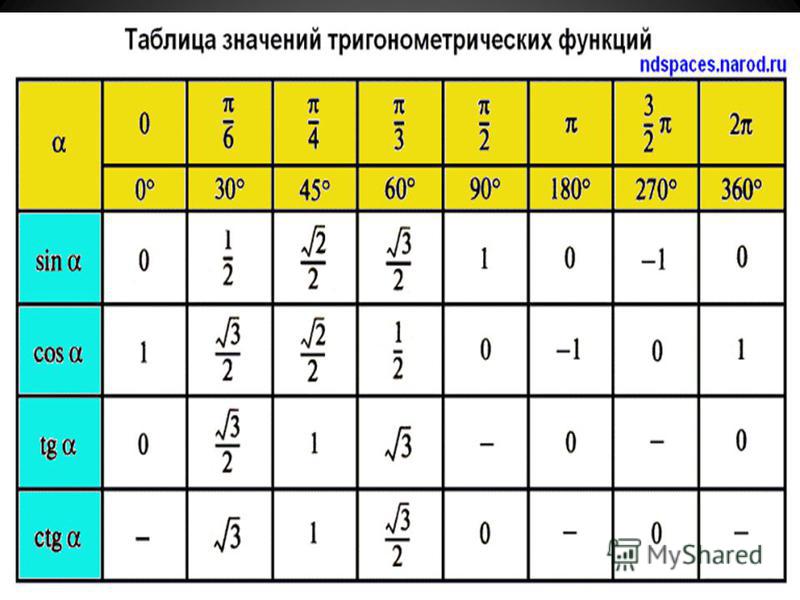9657