Таблица логики: Онлайн-калькулятор по информатике

Построение таблиц истинности для логических выражений

Похожие презентации:

Основы логики. Таблица истинности. Равносильные логические выражения

Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2)

Построение таблиц истинности сложных высказываний

Логика высказываний

Логические основы ЭВМ. Алгоритмы логики. Построение таблиц истинности

Логика высказываний. Таблицы истинности

Логическое высказывание. Виды сложных высказываний

Построение таблиц истинности. 8 класс

Логическая модель. Логика высказываний. Основы логики высказываний

Формулы алгебры высказываний

Тема урока:
«Построение таблиц истинности для
логических выражений»
Цель: Формирование навыков применения технологии
построения таблиц истинности для составных логических
выражений.

2. Построение таблицы истинности

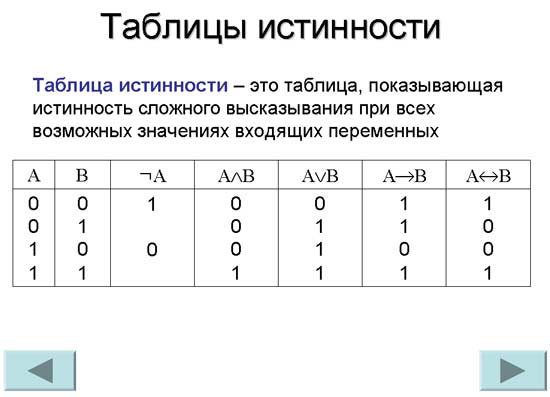
Таблица истинности – это таблица, показывающая
истинность сложного высказывания при всех возможных
значениях входящих переменных.
Последовательность действий:
1. Определить количество строк в таблице:
• количество строк = 2n+1,
где n – количество
логических переменных, 1 – строка заголовков
2. Определить количество столбцов в таблице:
• количество столбцов = количеству логических
переменных + количество логических операций
3. Расставить приоритеты действий:
• приоритеты: ( ), ¬, &, V, импликация, эквиваленция;
4. Заполнить столбцы входных переменных наборами
значений.
5. Заполнить таблицу истинности, выполняя логические
операции в соответствии с приоритетами действий.

3. В составных высказываниях логические операции выполняются в следующем порядке:

1.
2.
3.
4.
5.
6.
В составных высказываниях логические
операции выполняются в следующем
порядке:
Действия в скобках
Отрицание (не)
Конъюнкция (и)
Дизъюнкция (или)
Импликация
Эквиваленция

4. Заполнение таблицы истинности

22+1=5
¬( A&B)
A
B
A&B
¬( A&B)
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
2+2=4
Наборы входных переменных, во избежание ошибок,
рекомендуют вводить следующим образом:
1) разделить столбец значений первой переменной
пополам и заполнить верхнюю часть колонки нулями, а
нижнюю — единицами;
2) разделить столбец значений второй переменной на
четыре части и заполнить четверти чередующимися
группами нулей и единиц, начиная с группы нулей;
3) продолжать деление столбцов значений последующих
переменных на 8, 16 и т. д. частей и заполнение их
группами нулей или единиц до тех пор, пока группа нулей
(единиц) не будет состоять из одного символа.

6. например:

Построить таблицу истинности для выражения:
F=(A
А
В
0
0
0
А
В
B)&(A
B)
А
В
А
В
0
1
1
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
F

7. РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, у которых
таблицы истинности совпадают,
называют равносильными.

8. Доказать, что логические выражения: А & В и А В, равносильны

Доказать, что логические выражения:
А & В и А В, равносильны
Таблица истинности для А&В
Таблица истинности для А v В
А
В
А
В
А & В
А
В
А
В
А
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
1
1
0
Таблицы истинности совпадают, следовательно, логические
выражения равносильны.
В
Построим таблицу истинности для логического выражения A v А & В.
В нём две переменные, две операции, причём сначала выполняется
конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре
столбца:
Наборы входных переменных — это целые числа от 0 до 3
представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со
столбцом А. В таком случае говорят, что логическое выражение A v А& В
равносильно логической переменной А.
Таблица Для 3 переменных
(А В С)
А
В
С
С
В С
А В С (А В С)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
1
0
1
1
1
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
Свойства логических операций
Законы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B

English     Русский Правила

iMath Wiki — Алгебра логики.

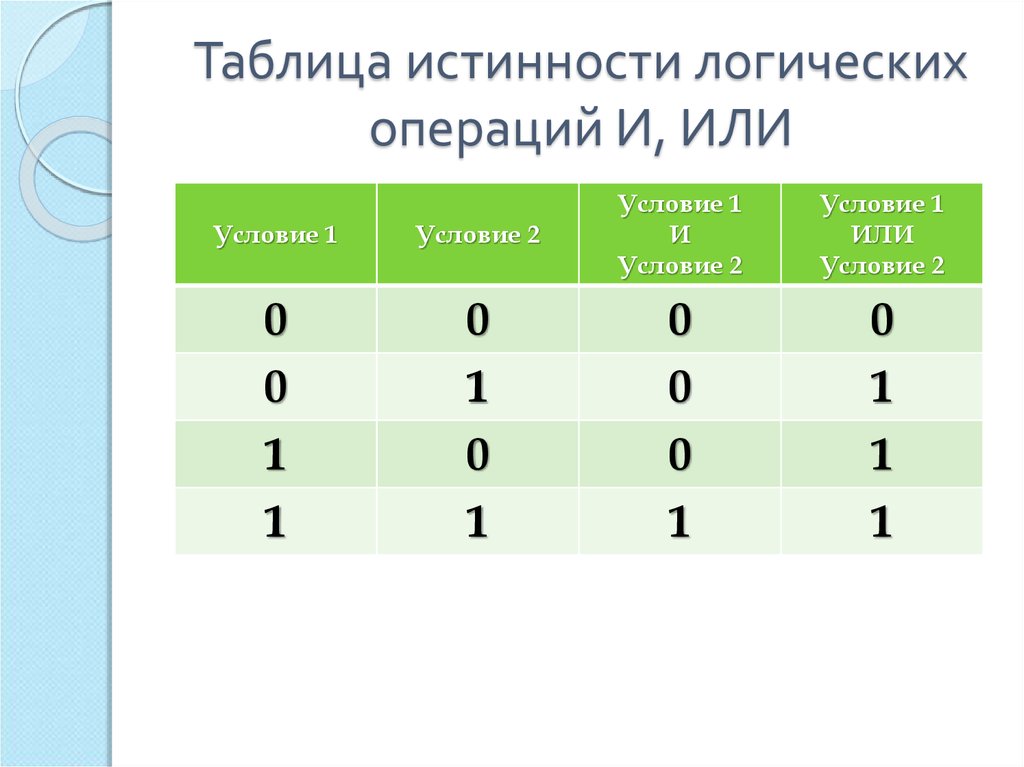Основные логические операции и их таблицы истинности. Основные законы алгебры логики.

Мы выяснили, как информация представляется в памяти вычислительных устройств и установили алгоритмы проведения операций над этими представлениями.

Теперь, давайте попробуем разобраться, как именно реализуются операции над двоичными представлениями. Для этого, для начала, нам придется разобраться с алгеброй логики.

Алгебра логики является частью дискретной математики – раздела математики, изучающего свойства структур конечного характера.

Сама алгебра логики изучает свойства функций, у которых значения как аргументов, так и самих функций ограничены двумя значениями, например, \(\{0,1\}\).

Отцом алгебры логики считается английский математик Джордж Буль (1815-1864), поэтому алгебру логики иногда называют булевой алгеброй.

Долгое время алгебра логики была известна лишь узкому кругу специалистов, и только в 1938 году американский математик Клод Шеннон (1916-2001), стоявший у истоков современной информатики, показал, что алгебра логики применима для описания самых разных процессов, в том числе релейных и транзисторных схем. n\] Не имеет решений в целых ненулевых числах \(a,\,b,\,c\)

Как известно, сформулированная Пьером Ферма в 1637 году, была окончательно доказана только в 1994.

Введем не совсем формальное, но достаточное для наших целей определение

Высказывание

это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.

Это определение было предложено Аристотелем.

Проблема языковых образований в рамках алгебры логики в том, что они могут иметь весьма своеобразную структуру. Например, фраза “это высказывание является ложным” не может считаться высказыванием, поскольку бессмысленно говорить о его истинности или ложности. Причиной парадокса является структура фразы: она ссылается сама на себя. Подобные парадоксы могут быть устранены введением следующего определения:

Элементарное высказывание

это такое высказывание, никакая часть которого не является высказыванием.

Следует заметить, что высказыванием в строгом смысле является только утверждение о конкретных объектах.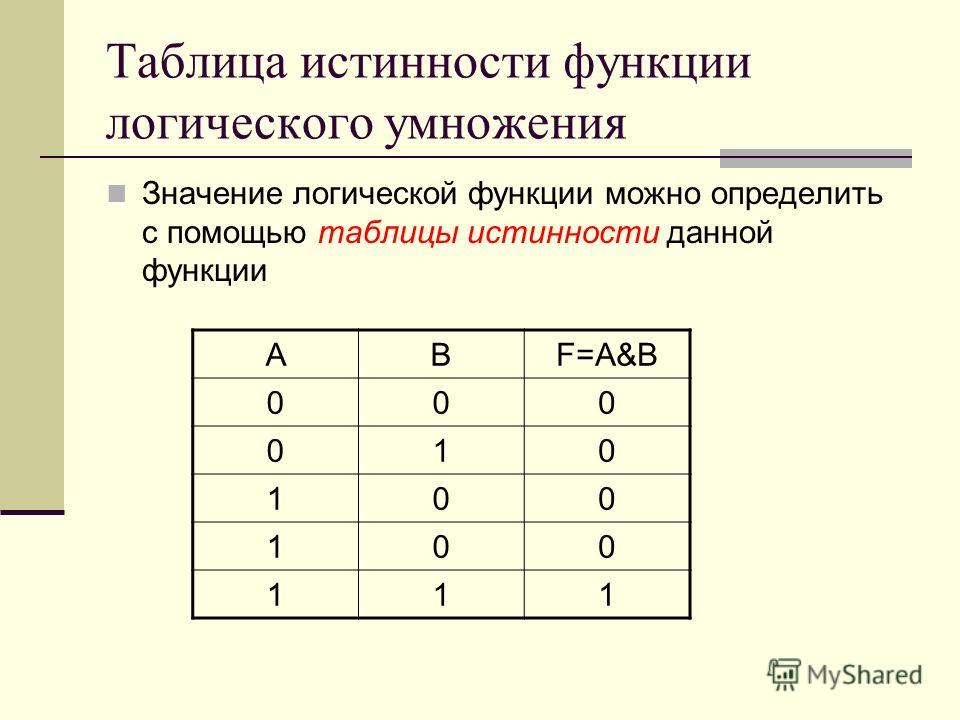 Если речь идет о неких переменных, например, “x – рациональное число”, то мы говорим о неких функциях, имеющих значение “истина” или “ложь”. Такие функции называются предикатами.

Так же следует заметить, что алгебра логики отвлекается от смыслового содержания высказываний, и занимается скорее связями между высказываниями. Если мы договоримся считать за аксиому, что “солнце светит ночью”, то есть, договоримся что это высказывание истинно, то в рамках нашей аксиоматики сможем делать какие-то обоснованные выводы. Эти выводы, конечно, не будут иметь много общего с действительностью.

Примерами таких отвлеченных, на первый взгляд, систем, может служить, например, геометрия Лобачевского, которая имеет не слишком много общего с нашим псевдоевклидовым пространством. ¹

Различные языковые связки, такие, как “не”, “если …, то …”, “или”, “и”, и т.п. позволяют строить из элементарных высказываний более сложные.

В алгебре логики существуют соответствующие подобным связкам операции.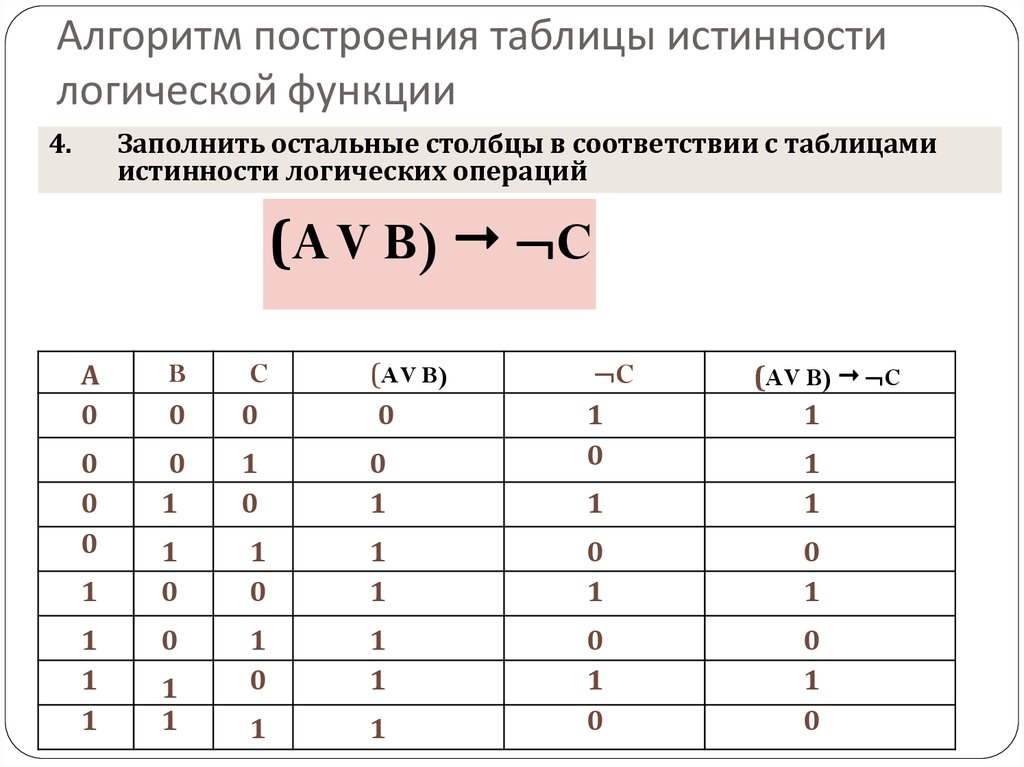

Введем некоторые из них.

Конъюнкция, или логическое умножение

логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Конъюнкция обозначается различными способами, в частности, амперсандом \(a \,\&\,b\), точкой \(a \cdot b\), или “крышкой” \(a \wedge b\), и соответствует языковой связке “и”. Мы будем в основном использовать амперсанд.

Поскольку оба исходных высказывания имеют по два возможных значения, и конъюнкция имеет два возможных значения, мы можем записать это определение в виде таблицы истинности:

0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция, или логическое сложение

логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из исходных высказываний истинно.

Дизъюнкция соответствует союзу “или”, и обозначается плюсом \(a+b\), или “галочкой” \(a\vee b\). Мы будем использовать в основном второй вариант.

Таблица истинности дизъюнкции, по определению:

0	0	0
0	1	1
1	0	1
1	1	1

Строгая дизъюнкция, или сложение по модулю 2

логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда только одно из исходных высказываний истинно.

Строгая дизъюнкция соответствует связке “либо …, либо …”, и обозначается плюсом в кружочке \(a\oplus b\), или треугольником \(a\vartriangle b\). Будем в основном пользоваться первым обозначением.

Таблица истинности, по определению:

0	0	0
0	1	1
1	0	1
1	1	0

Импликация

логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда первое из исходных высказываний (условие) истинно, а второе (следствие) – ложно.

Импликация соответствует связке “если …, то …”, и обозначается стрелкой \(a \rightarrow b\), или \(a \Rightarrow b\)

Таблица истинности, по определению:

0	0	1
0	1	1
1	0	0
1	1	1

Импликация, на первый взгляд, имеет не очевидное определение: как вдруг из ложных условий получается истинное следствие. Однако, в математике это никакая не новость. Например, возьмем очевидно ложное утверждение “один равен двум”:

\[1 = 2\] \[2 = 1\]

Складывая эти равенства, получим очевидно истинный результат:

\[3=3.\]

С другой стороны, из заведомо истинных посылок формально нельзя вывести ложный результат (конечно, человеческий фактор никто не отменял, но человеческий фактор выходит за пределы рассмотрения формальной логики).

Эквивалентность

логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Эквивалентность соответствует связке “тогда и только тогда, когда”, и обозначается \(a \Leftrightarrow b\), или \(a \equiv b\), или \(a \sim b\), или \(a \leftrightarrow b\). Будем в основном пользоваться первыми двумя обозначениями.

Таблица истинности, по определению:

0	0	1
0	1	0
1	0	0
1	1	1

Инверсия, или отрицание

логическая операция, ставящая в соответствие элементарному высказыванию новое высказывание, являющееся истинным тогда и только тогда, исходное ложно.

Инверсия соответствует связке “не”, и обозначается \(\neg a\), или \(\;\overline{a}\;\), или \(!a\). Будем в основном пользоваться первыми двумя обозначениями.

Таблица истинности, по определению:

0	1
1	0

В заключение, таблица истинности основных логических операций:

0	0	1	0	0	0	1	1
0	1	1	0	1	1	1	0
1	0	0	0	1	1	0	0
1	1	0	1	1	0	1	1

Введем некоторые определения, аналогичные алгебре действительных чисел, для алгебры логики.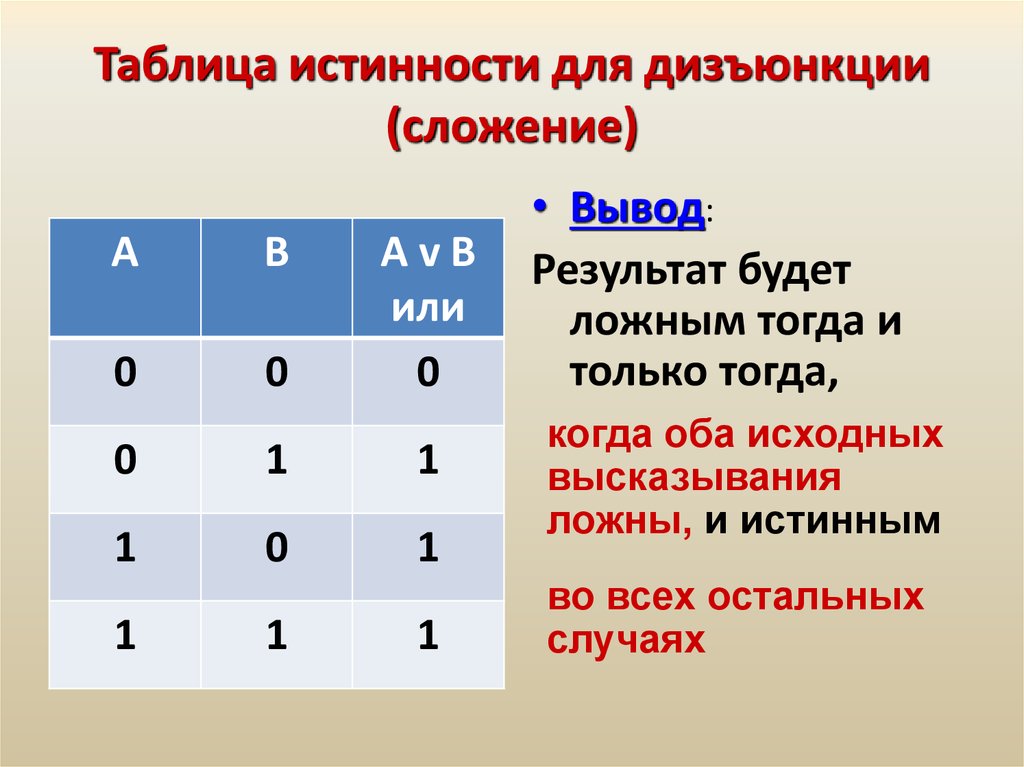

Логическая переменная

Переменная, значением которой может быть любое высказывание. Обозначать будем маленькими латинскими буквами.

Логическая формула

любая переменная, а так же любая из констант “0” (“ложь”) и “1” (“истина”)

Любая комбинация логических формул, составленная с помощью логических операций.

Эквивалентные формулы

такие формулы, которые зависят от одного и того же набора переменных, и при одинаковых значениях этих переменных, формулы так же имеют одинаковые значения. Обозначать будем знаком равенства.

Существуют следующие “законы” алгебры логики, определяющие некий набор эквивалентных формул:

Законы коммутативности

\[x \,\&\,y = y \,\&\,x\] \[x \vee y = y\vee x\]

Законы ассоциативности

\[ (x \,\&\,y) \,\&\,z = x \,\&\,(y \,\&\,z)\] \[ (x \vee y) \vee z = x \vee(y \vee z)\]

Законы поглощения

\[x\vee 0 = x\] \[x\,\&\,1 = x\]

Законы дистрибутивности

\[ x\,\&\,(y\vee z) = (x\,\&\,y) \vee(x\,\&\,z)\] \[ x\vee(y\,\&\,z) = (x \vee y) \,\&\,(x\vee z)\]

Закон противоречия

\[ x \,\&\,\;\overline{x}\; = 0\]

Закон исключения третьего

\[ x \vee\;\overline{x}\; = 1\]

Закон равносильности

\[ x \,\&\,x = x\] \[ x \vee x = x \]

Закон двойного отрицания

\[\;\overline{\;\overline{x}\;}\; = x \]

Законы де Моргана

\[ \;\overline{x\,\&\,y}\; = \;\overline{x}\; \vee\;\overline{y}\; \] \[ \;\overline{x\vee y}\; = \;\overline{x}\; \,\&\,\;\overline{y}\; \]

Законы поглощения

\[ x\vee(x\,\&\,y) = x\] \[ x\,\&\,(x\vee y) = x\]

Все перечисленные законы элементарно доказываются составлением таблиц истинности.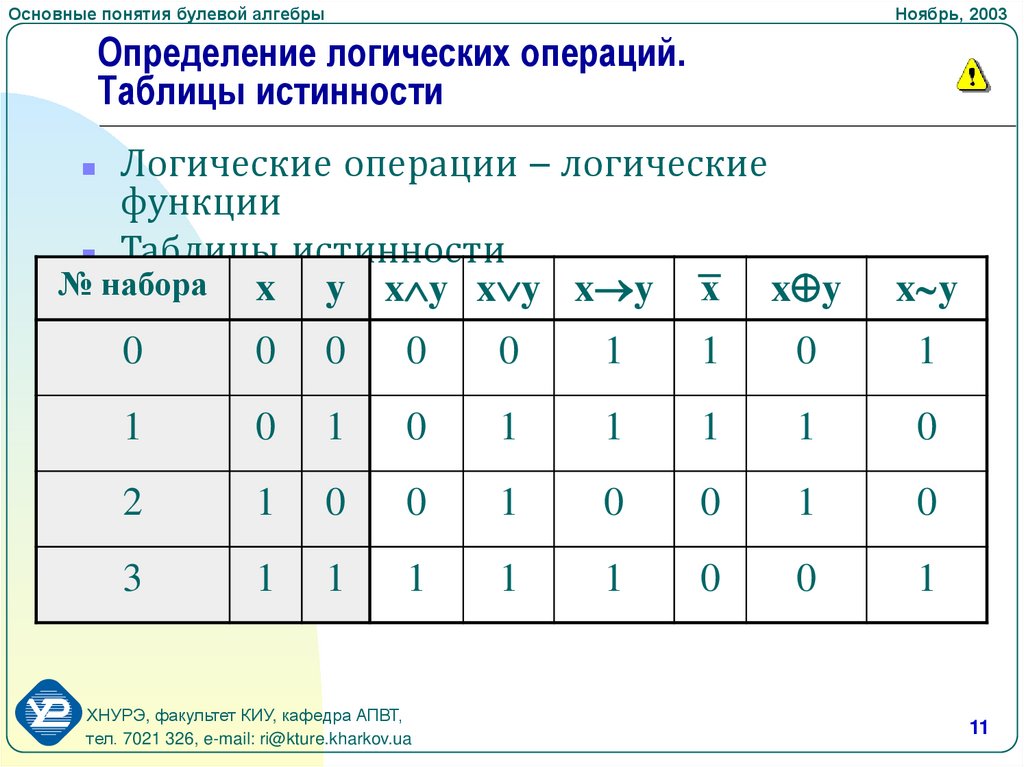

Например, первый закон де Моргана:

0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	0	1	1
1	1	1	0	0	0	0

3 и 6 столбец одинаковы, следовательно, соответствующие формулы эквивалентны.

Введем еще одно определение

Тавтология

логическая формула, которая всегда истинна.

Например, тавтологией является формула, выражающая закон исключения третьего.

Оказывается, алгебра логики хорошо подходит для решения логических задач. Решение логических задач, конечно, умеренно бессмысленное времяпрепровождение (исключая случаи, когда на их примере рассматриваются более сложные вопросы), однако это хороший способ поработать с алгеброй логики и осмыслить основные концепции.

Итак, формальный способ решения логических задач:

1. Из условий задачи выделяются простые высказывания и обозначаются как логические переменные.
2. Условия задачи записываются в виде логических формул
3. Составляется единое логическое выражение, соответствующее условию задачи. По условию задачи оно является истинным.
4. Полученное выражение упрощается, либо составляется таблица истинности для него (либо и то, и другое)
5. Выбирается решение задачи (случаи, когда условие истинно)
6. Решение формулируется в исходных терминах задачи.

Пример: (источник)

На весеннем фестивале, четыре садовника показывали выращенные ими розы.

Всего розы были четырех цветов и у каждого садовника было по две розы.

Известно, что

• У первого была желтая роза
• У второго не было красной розы
• У третьего была синяя роза, но не было зеленой
• У одного из садовников с зеленой розой не было красной
• Ни у одного из садовников с желтой розой не было зеленой
• Ни у кого нет роз двух одинаковых цветов

Введем переменные, в которых название переменной соответствует цвету, а индекс – садовнику (номеру).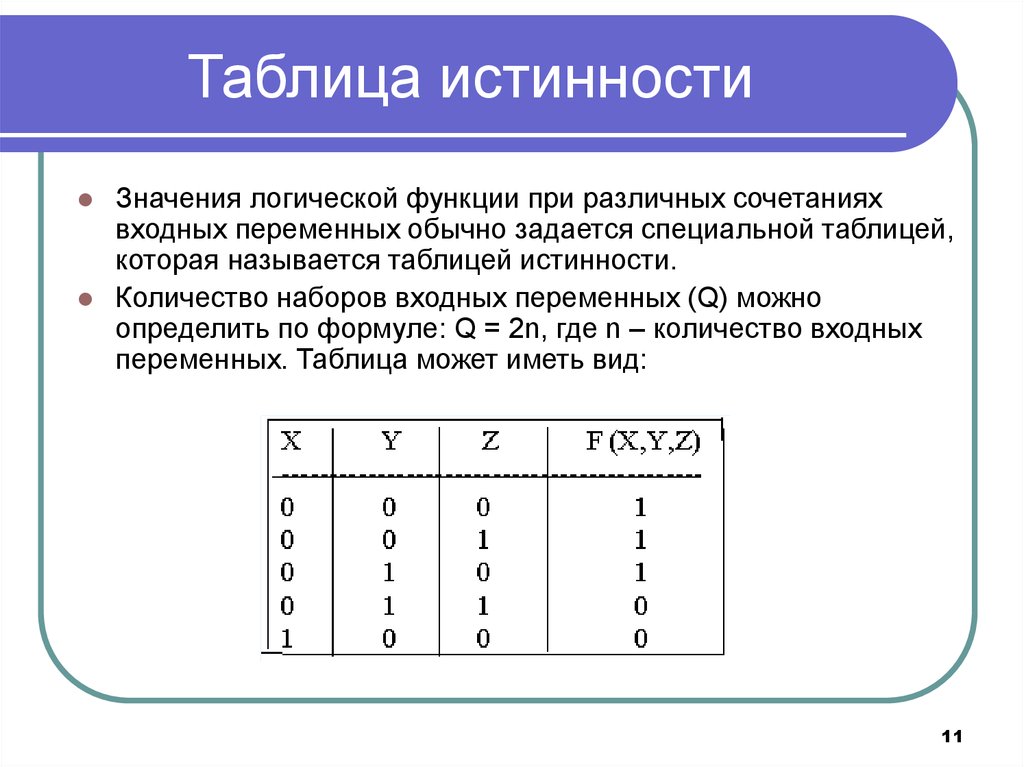 Это автоматически учитывает условие “Ни у кого нет роз двух одинаковых цветов”. Тогда условия задачи запишутся в виде:

• \(y_1\)
• \(\;\overline{r_2}\;\)
• \(b_3 \,\&\,\;\overline{g_3}\;\)
• \((g_1\rightarrow\;\overline{r_1}\;) \oplus(g_2\rightarrow\;\overline{r_2}\;)\oplus(g_3\rightarrow\;\overline{r_3}\;)\oplus(g_4\rightarrow\;\overline{r_4}\;)\)
• \((y_1\rightarrow\;\overline{g_1}\;) \,\&\,(y_2\rightarrow\;\overline{g_2}\;)\,\&\,(y_3\rightarrow\;\overline{g_3}\;)\,\&\,(y_4\rightarrow\;\overline{g_4}\;)\)

Дополнительно, у каждого садовника по условиям задачи по две розы: Поэтому, если у садовника есть розы двух цветов, то роз двух других цветов у него нет. Учтем подразумеваемые импликации постфактум.

Далее для простоты записи, амперсанды опускаются (если между переменными нет ничего – значит там амперсанд). В случае отсутствия скобок, сначала применяется конъюнкция, потом все остальное.

Рассматривая последнее условие:

\((y_1\rightarrow\;\overline{g_1}\;) (y_2\rightarrow\;\overline{g_2}\;)(y_3\rightarrow\;\overline{g_3}\;)(y_4\rightarrow\;\overline{g_4}\;)\)

Первая импликация истинна, только если \(\;\overline{g_1}\;\) истинно. Предпоследняя импликация истинна всегда, \(\;\overline{g_3}\;\). Можем переписать в виде:

\(y_1 \;\overline{g_1}\; (y_2\rightarrow\;\overline{g_2}\;) (y_4\rightarrow\;\overline{g_4}\;)\)

Рассмотрим предпоследнее условие

\[ (g_1 \rightarrow\;\overline{r_1}\;) \oplus(g_2 \rightarrow\;\overline{r_2}\;) \oplus(g_3 \rightarrow\;\overline{r_3}\;) \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]

Первая импликация всегда истинна, поскольку \(\;\overline{g_1}\;\), вторая всегда истинна, поскольку \(\;\overline{r_2}\;\), третья всегда истинна, поскольку \(\;\overline{g_3}\;\). Получаем:

\[ 1 \oplus 1 \oplus 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]

\[ 1 \oplus(g_4 \rightarrow\;\overline{r_4}\;) \]

Легко показать, что \(1 \oplus x = \;\overline{x}\;\). Тогда условие принимает вид

\[ \;\overline{g_4 \rightarrow\;\overline{r_4}\;}\; \]

Импликацию можно представить в виде \(x \rightarrow y = \;\overline{x}\; \vee y\)

Применяя закон де Моргана,

\[ r_4 g_4 \]

Записывая все условия вместе:

\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) (\;\overline{y_4}\; \vee\;\overline{g_4}\;) b_3 \;\overline{g_3}\; g_4 r_4 \]

Учитывая \(g_4 (\;\overline{y_4}\; \vee\;\overline{g_4}\;) = g_4 \;\overline{y_4}\;\),

\[ y_1 \;\overline{g_1}\; \;\overline{r_2}\; (\;\overline{y_2}\; \vee\;\overline{g_2}\;) b_3 \;\overline{g_3}\; \;\overline{y_4}\; g_4 r_4 \]

Известно, что зеленые розы должны быть у двух садовников:

\[ \;\overline{g_1}\; \;\overline{g_2}\; g_3 g_4 \vee\;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \vee\;\overline{g_1}\; g_2 g_3 \;\overline{g_4}\; \vee g_1 \;\overline{g_2}\; \;\overline{g_3}\; g_4 \vee g_1 \;\overline{g_2}\; g_3 \;\overline{g_4}\; \vee g_1 g_2 \;\overline{g_3}\; \;\overline{g_4}\; \]

А так как \(\;\overline{g_3}\;\) и \(\;\overline{g_1}\;\)

\[ \;\overline{g_1}\; g_2 \;\overline{g_3}\; g_4 \]

Получаем \(g_2\), тогда \(g_2 (\;\overline{y_2}\; \vee\;\overline{g_2}\;) = g_2 \;\overline{y_2}\;\)

Аналогично для желтых:

\[ y_1 \;\overline{y_2}\; y_3 \;\overline{y_4}\; \]

Получаем \(y_3\).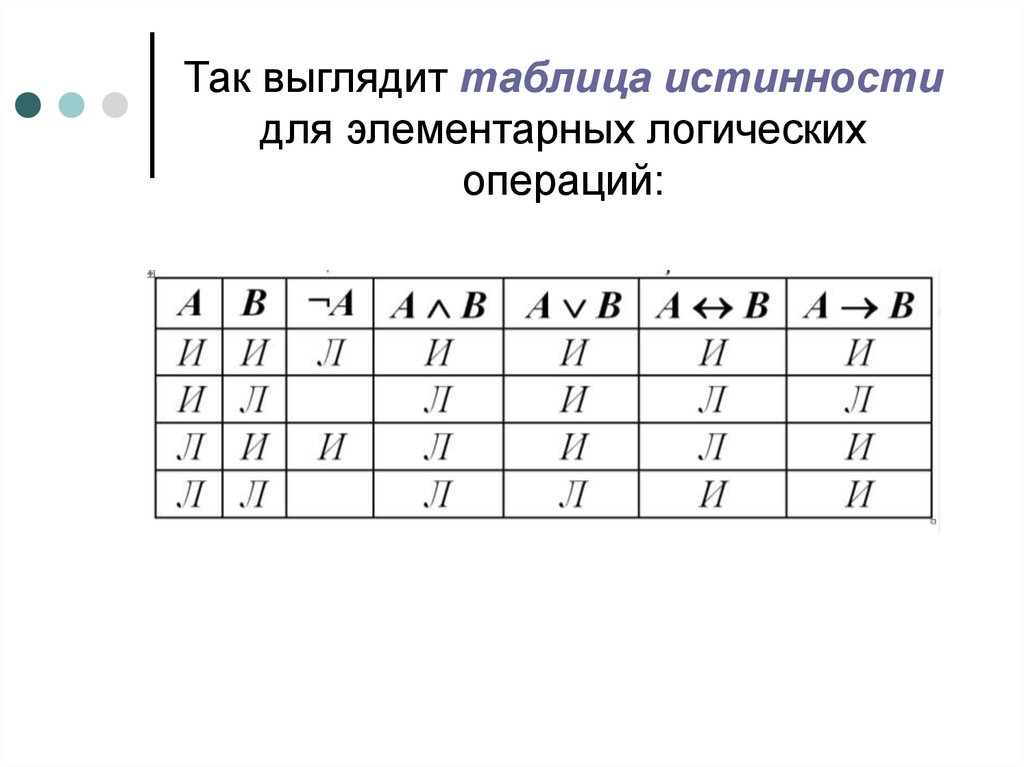 Поскольку \(y_3 b_3\), можно утверждать \(\;\overline{r_3}\; \;\overline{g_3}\;\)

Для красных тогда:

\[ r_1 \;\overline{r_2}\; \;\overline{r_3}\; r_4 \]

Получаем \(r_1\). Поскольку \(r_1 y_1\), можем утверждать \(\;\overline{b_1}\; \;\overline{g_1}\;\)

Для синих:

\[ \;\overline{b_1}\; b_2 b_3 \;\overline{b_4}\; \]

Получаем \(b_2\).

Итого

\[ y_1 r_1 g_2 b_2 b_3 y_3 g_4 r_4 \]

---

1. Вообще сейчас считается, что у пространства, в котором мы находимся, времеподобная метрика Миньковского.↩︎

Булева логика и таблицы истинности

Последнее изменение: 09 августа 2021 г.

И используется, чтобы найти, где несколько условий верны

ИЛИ используется, чтобы найти, где хотя бы одно из нескольких условий верно

Если говорить более подробно, булева логика — это способ представления того, как обрабатываются биты в компьютере. Давайте больше изучим эти условные операторы (например, операторы if-else, where или case-when) с таблицами истинности, чтобы понять, как именно работает логическая логика.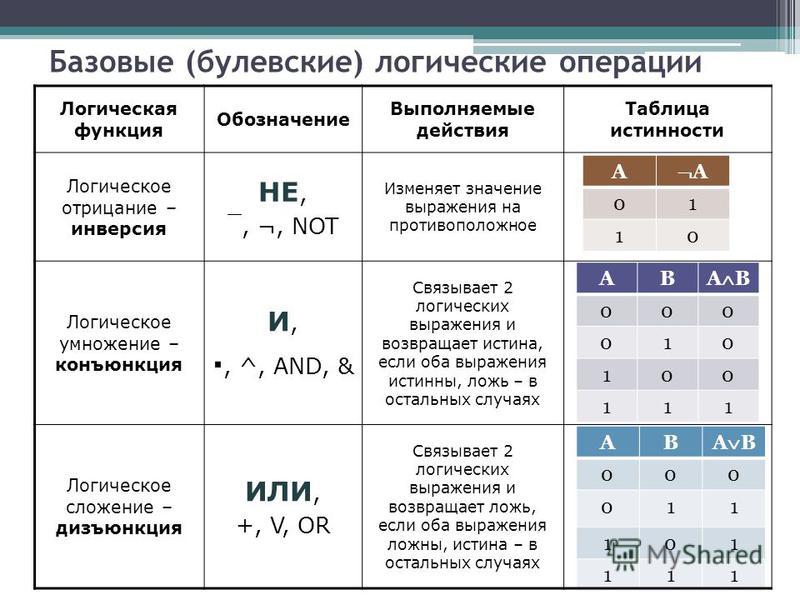

Таблицы истинности

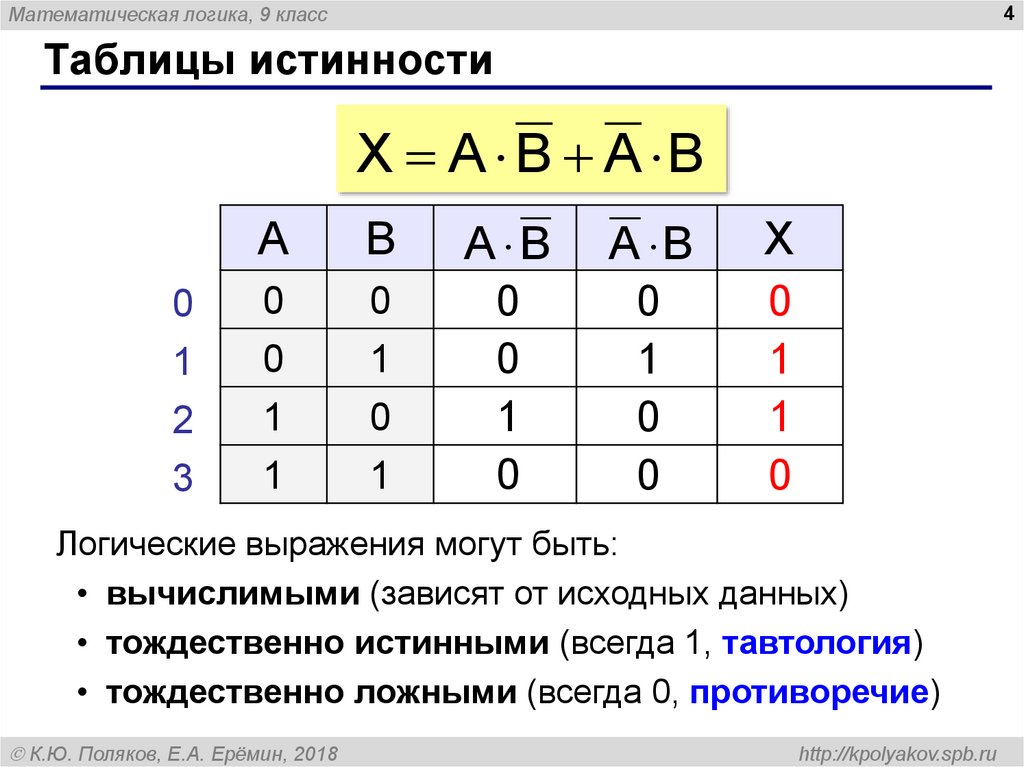
Например, давайте посмотрим на следующее условное выражение:

Если: А и В

Затем: С

Возвращает значение C, если значения A и B верны. Мы можем представить это с помощью так называемой таблицы истинности. Таблица истинности — это способ представления всех возможных входных данных и соответствующих им выходных данных. Таблица истинности для этого оператора AND выглядит так:

.

А	Б	С
1	1	1
1	0	0
0	1	0
0	0	0

В таблице истинности 1 соответствует истине, а 0 представляет ложь. Глядя на эту таблицу, становится очевидным, что единственный случай, когда С истинно, — это когда истинны и А, и В.

Существует также оператор ИЛИ. Оператор ИЛИ верен, когда верно A OR B:

Если: А или В

Затем: С

Таблица истинности:

А	Б	С
1	1	1
1	0	1
0	1	1
0	0	0

Эта таблица истинности может немного отличаться от ожидаемой. Это связано с тем, что оператор ИЛИ является ложным только тогда, когда оба входных значения (A и B) имеют значение False.

Создание таблицы правды 93 или 8 ряд.

Далее нам нужно решить, сколько столбцов использовать. В этом случае у нас будет один столбец для каждого входа, один для вывода и один для значений A и B. Таблица истинности будет выглядеть так:

А	Б	С	А или В	Д
1	1	1	1	1
1	1	0	1	0
1	0	1	1	1
1	0	0	1	0
0	1	1	1	1
0	1	0	1	0
0	0	1	0	0
0	0	0	0	0

Как и ожидалось, когда таблица заполнена, единственный верный результат — это когда верны все 3 входа.

Логика короткого замыкания

Из-за того, как работает логика И и ИЛИ , языки программирования могут использовать так называемую «логику короткого замыкания». Это когда оцениваются не все входные данные, потому что компьютер может угадать ответ по первому проверенному вводу. Чтобы увидеть, как это работает, снова взгляните на таблицу истинности AND:

.

А	Б	С
1	1	1
1	0	0
0	1	0
0	0	0

Обратите внимание, что, когда A имеет значение False ( 0 ), C также всегда имеет значение False. Это связано с тем, что C истинно только тогда, когда оба входа истинны, поэтому одно ложное значение C ложно.

Если компьютер использует условие И и первое входное значение ложно, то второе входное значение B никогда не будет проверяться. ИЛИ будет оцениваться как истина без проверки второго ввода, когда первый ввод верен. Эта способность компьютера аннулировать более поздние шаги логической логики может сэкономить много ненужной вычислительной мощности для вашего запроса.

Примеры в SQL

Пример условия WHERE :

ВЫБЕРИТЕ * ИЗ [таблицы]
КУДА
[столбец A]=5 И [столбец B]=22;
 

Пример оператора CASE-WHEN

КЕЙС
КОГДА [столбец A]=21 ИЛИ [столбец B]=7 ТО [Действие]
КОНЕЦ
 

Резюме

• Булева логика И/ИЛИ может быть визуализирована с помощью таблицы истинности
  • Таблицы истинности две по количеству входных строк в них
  • 1 — верно
  • 0 — ложь
• Логика короткого замыкания
  • Если первый ввод гарантирует конкретный результат, то второй вывод не будет прочитан
  • И — первый ввод false приведет к короткому замыканию на false
  • ИЛИ — первый ввод true приведет к короткому замыканию на true

Написано: Мэтью Лейн
Отзыв: Мэтт Дэвид

Оставьте отзыв о нашем Документе Google Далее – Условная логика

• Дом
• Веб-книги
• Авторы
• Миссия
• Пожертвовать
• Slack-сообщество

Наши веб-книги

• Обмен данными
• Управление облачными данными
• Как спроектировать панель мониторинга
• Как учить людей SQL
• Изучите SQL
• Избегайте искажения данных
• Оптимизация SQL
• Основы анализа

Логические таблицы — символьная логика

Переключить боковую панель оглавления

Логическая таблица — это, по сути, двумерный массив, созданный классом операторов.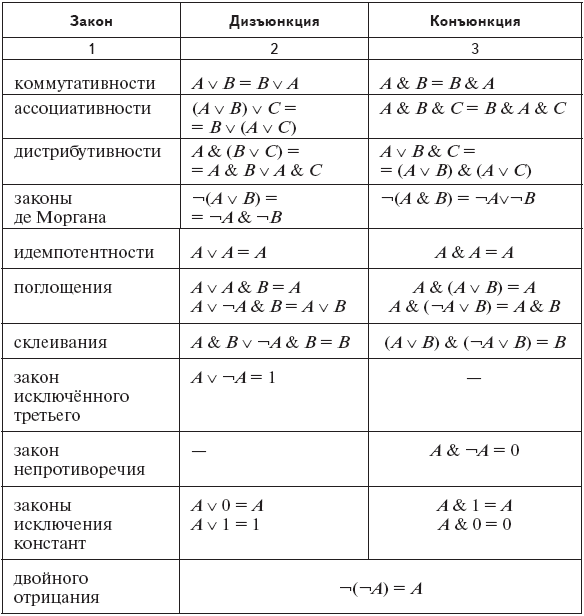 и хранится в таблице частных глобальных переменных вместе со списком, содержащим имена переменных, которые будут использоваться, по порядку.

Порядок, в котором указана таблица, по существу сводится к подсчету в двоичный. Например, с переменными \(A\), \(B\) и \(C\) таблица истинности выглядит так:

 Значение A B C
Ложь Ложь Ложь?
Ложь Ложь Верно?
Ложь Верно Ложь?
Ложь Верно Верно?
Верно Ложно Ложно?
Верно Ложно Верно?
Верно Верно Ложно?
Правда Правда Правда?
 90 значение
0 0 0 0
0 0 1 1
0 1 0 2
0 1 1 3
1 0 0 4
1 0 1 5
1 1 0 6
1 1 1 7
 

Учитывая, что можно создать таблицу, соответствующую любому диапазону допустимых значения для данного оператора, легко найти значение оператора для произвольных значений его переменных.

АВТОРОВ:

• Уильям Штейн (2006 г.): начальная версия

• Крис Горецки (2006 г.): начальная версия

• Пол Шурек (03 августа 2013 г.): обновлено форматирование строки документации

ПРИМЕРЫ:

Создать таблицу истинности булевой формулы:

 шалфей: импортируйте sage. logic.propcalc как propcalc
мудрец: s = propcalc.formula("a&b|~(c|a)")
мудрец: s.truetable()
а б в значение
Ложно Ложно Ложно Верно
Ложно Ложно Верно Ложно
Неверно Верно Ложно Верно
Неверно Верно Верно Ложно
Верно Ложно Ложно Ложно
Верно Ложно Верно Ложно
Верно Верно Ложно Верно
Правда Правда Правда Правда
 

Получить летекс-код для таблицы истинности:

 шалфей: латекс (s.truetable (5,11))
\\\begin{tabular}{llll}c & b & a & value \\\hline True & False & True & False \\True & True & False & True \\True & True & True & True\end{tabular }
 

Использование бессмысленных числовых входных данных не является ошибкой:

 мудрец: s = propcalc.formula("a&b|~(c|a)")
мудрец: s.truetable(5, 9)
а б в значение
Верно Ложно Верно Ложно
Верно Верно Ложно Верно
Правда Правда Правда Правда
мудрец: s.truetable(9, 5)
а б в значение
 

Если указан один аргумент, truetable по умолчанию до конца:

 мудрец: s.truetable(-1)
а б в значение
Ложно Ложно Ложно Верно
Ложно Ложно Верно Ложно
Неверно Верно Ложно Верно
Неверно Верно Верно Ложно
Верно Ложно Ложно Ложно
Верно Ложно Верно Ложно
Верно Верно Ложно Верно
Правда Правда Правда Правда
 

Если второй аргумент отрицательный, truetable по умолчанию до конца:

 мудрец: s.
No related posts.