Решение №2481 В параллелограмме ABCD тангенс угла А равен 1,5.
В параллелограмме ABCD тангенс угла А равен 1,5. На продолжениях сторон АВ и ВС параллелограмма за точку В выбраны точки N и М соответственно, причём BC = CN и АВ = AM.
а) Докажите, что DN = DM.
б) Найдите MN, если АС = √13.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
а) Доказать: BN = BM.
Рассмотрим ΔMAD и ΔDCN. В них по условию и как стороны параллелограмма AM = AB = DC, AD = CB = CN. Трапеции MADC (AM = DC) и ADCN (AD = CN) равнобедренные. Углы при верхних основаниях равны (как и при нижних), т.е. в трапеции MADC при основании AD ∠AMD = ∠ADC, в трапеции ADCN при основании DC ∠ADC = ∠DCN, отсюда ∠AMD = ∠DCN. {2} – 2·\sqrt{13}\cdot \sqrt{13}\cdot \frac{5}{13}
{2} – 2·\sqrt{13}\cdot \sqrt{13}\cdot \frac{5}{13}
MN2 = 13 + 13 – 2·\frac{13\cdot 5}{13}
MN2 = 26 – 10
MN2 = 16
MN = √16 = 4
Ответ: б) 4.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.5 / 5. Количество оценок: 17
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:10.11.2021
- Рубрика записи16. Планиметрическая задача
- Автор записи:Andrei Maniakin
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | sin(theta)^2+cos(theta)^2 | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.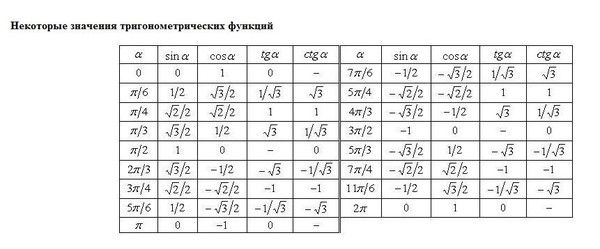 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.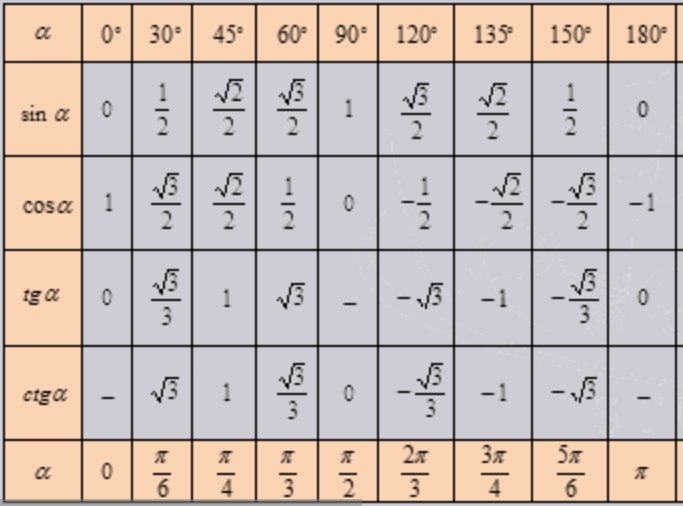 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Обратный тангенс (обратный тангенс) — Формула, График
Обратный тангенс является одной из обратных тригонометрических функций и записывается как тангенс -1 х и читается как «тангенс инверсный х». Он также известен как арктан (x). У нас есть 6 обратных тригонометрических функций, которые соответствуют шести тригонометрическим функциям. Функция обратного загара является одной из них.
Он также известен как арктан (x). У нас есть 6 обратных тригонометрических функций, которые соответствуют шести тригонометрическим функциям. Функция обратного загара является одной из них.
Здесь мы подробно изучим функцию обратного тангенса (arctan), а также ее свойства, график, домен и диапазон. Кроме того, мы изучим формулы, производную и интеграл тангенса, обратный x, а также несколько решенных примеров.
| 1. | Что такое обратный загар? |
| 2. | Формула обратного загара |
| 3. | Домен, диапазон и график обратного загара |
| 4. | шагов, чтобы найти инверсию загара x |
| 5. | Свойства обратного загара |
| 6. | Производное обратного загара |
| 7. | Интеграл обратного загара |
| 8. | Часто задаваемые вопросы по Inverse Tan |
Что такое обратный загар?
Обратный тангенс является обратной функцией тангенса и одной из обратных тригонометрических функций. Она также известна как функция арктангенса, которая произносится как «арктангенс». Математически это записывается как «атан х» (или) «тан -1 x» или «arctan x». Мы читаем «tan -1 x» как «tan inverse x». Если две функции f и f -1 являются обратными друг другу, то когда f(x ) = y , имеем x = f -1 (y).Таким образом, tan x = y ⇒ x = tan -1 (y) , т. е. когда «tan» перемещается с одной стороны на другую
Она также известна как функция арктангенса, которая произносится как «арктангенс». Математически это записывается как «атан х» (или) «тан -1 x» или «arctan x». Мы читаем «tan -1 x» как «tan inverse x». Если две функции f и f -1 являются обратными друг другу, то когда f(x ) = y , имеем x = f -1 (y).Таким образом, tan x = y ⇒ x = tan -1 (y) , т. е. когда «tan» перемещается с одной стороны на другую
Примеры обратного тангенса
- tan 0 = 0 ⇒ 0 = tan -1 (0)
- тангенс π/4 = 1 ⇒ π/4 = тангенс -1 (1)
- тангенс π/6 = 1/√3 ⇒ π/6 = тангенс -1 (1/√3)
Формула обратного загара
В прямоугольном треугольнике тангенс угла (θ) равен отношению противолежащего катета к прилежащему. т. е. tan θ = (противоположная сторона) / (прилегающая сторона). Затем, согласно определению обратного загара, формула обратного загара имеет вид θ = tan -1 [(противоположная сторона) / (прилегающая сторона)] .
Таким образом, формула обратного тангенса используется для нахождения угла в прямоугольном треугольнике, когда даны противолежащая сторона и прилежащая сторона.
Домен, диапазон и график обратного загара
В этом разделе давайте посмотрим, как мы можем найти домен и диапазон функции обратного тангенса. Кроме того, мы увидим процесс его построения.
Область и диапазон обратного тангенса
Мы знаем, что тангенс функция является функцией от R — {x : x = (2n + 1) (π/2), где n ∈ Z} до R. (Это потому, что функция тангенса НЕ определена для нечетных чисел, кратных π/2). Но функция тангенса НЕ является взаимно однозначной в своей области, поэтому обратная ей функция не существует в этой области. Чтобы функция тангенса была взаимно однозначной, ее область определения можно ограничить одним из интервалов (-3π/2, -π/2), (-π/2, π/2), (π/2, 3π/ 2) и т. д. По отношению к каждому из этих интервалов мы получаем ветвь обратного тангенса. Но область определения функции тангенса обычно ограничивается (-π/2, π/2), чтобы сделать ее взаимно однозначной. т. е. tan x : (-π/2, π/2) → R.
т. е. tan x : (-π/2, π/2) → R.
Домен и диапазон функции тангенса являются соответственно диапазоном и доменом обратного тангенса. т. е. arctan x (или) tan -1 x : R → (-π/2, π/2). Следовательно,
- домен tan, обратный x, равен R.
- диапазон обратного тангенса х равен (-π/2, π/2).
График функции обратного загара
График функции обратного загара с диапазоном, который должен быть главной ветвью (-π/2, π/2), можно построить с помощью следующей таблицы. Здесь мы выбрали случайные значения для x в области тангенса, обратного x, который равен R.
| х | г = тангенс -1 х |
|---|---|
| -2 | тангенс -1 (-2) = -тангенс -1 (2) ≈ -1,107 |
| -1 | тангенс -1 (-1) = -тангенс -1 (1) = -π/4 ≈ -0,78 |
| 0 | тан -1 (0) = 0 |
| 1 | тангенс -1 (1) = π/4 ≈ 0,78 |
| 2 | рыжевато-коричневый -1 (2) ≈ 1,107 |
Нанеся эти точки на график, получим график обратного тангенса.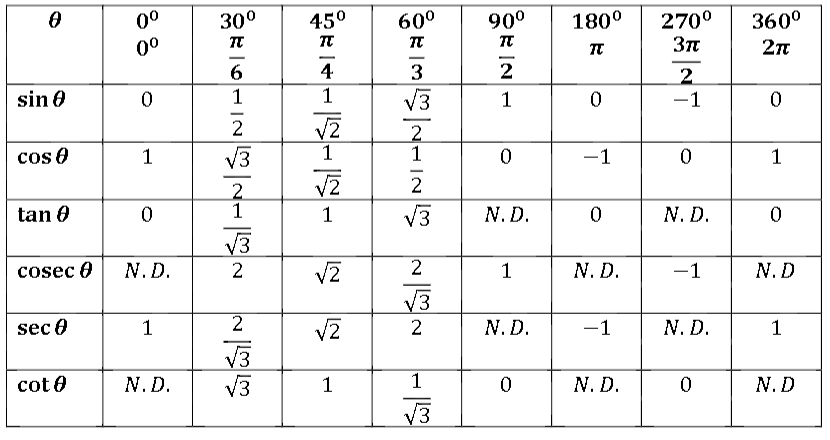
шагов, чтобы найти инверсию загара x
Вот шаги, чтобы найти тангенс, обратный x.
- Поскольку диапазон тангенса, обратного х, равен (-π/2, π/2), ответ должен лежать в этом интервале.
- Предположим, что y = tan -1 х. Тогда по определению обратного загара тангенс у = х.
- Значение y в интервале (-π/2, π/2), которое удовлетворяет уравнению tan y = x, является ответом.
Вот несколько примеров, с помощью которых мы можем понять, как найти тангенс, обратный x.
Примеры нахождения тангенса, обратного х
Обратите внимание, что тангенс -1 х всегда должен давать некоторый угол, лежащий в интервале (-π/2, π/2).
- тангенс -1 (1) = π/4 как тангенс π/4 = 1
- тангенс -1 (-1) = -π/4 как тангенс (-π/4) = -1
- тангенс -1 (-√3) = -π/3 как тангенс (-π/3) = -√3
Вы можете найти обратный загар любого значения, используя этот Калькулятор обратного загара. Вы можете попробовать использовать этот калькулятор.
Вы можете попробовать использовать этот калькулятор.
Свойства обратного загара
Вот некоторые свойства/формулы обратного загара. Они очень полезны при решении задач или доказательстве тождеств в тригонометрии.
- тангенс (тангенс -1 х) = х, для всех действительных чисел х.
- tan -1 (tan x) = x, только когда x ∈ R — {x : x = (2n + 1) (π/2), где n ∈ Z}.
т. е. tan -1 (tan x) = x, только если x НЕ является нечетным кратным π/2. В противном случае tan -1 (tan x) не определен. - tan -1 (-x) = -tan -1 x, для всех x ∈ R.
- tan -1 (1/x) = cot -1 x, когда x > 0.
- tan -1 x + cot -1 x = π/2, когда x ∈ R.
- tan -1 x + tan -1 y = tan -1 [(x + y)/(1 — xy)], когда xy < 1.
tan -1 x — tan -1 y = tan -1 [(x — y)/(1 + xy)], когда xy > -1.
- У нас есть 3 формулы для 2tan -1 х.
2tan -1 x = sin -1 (2x / (1+x 2 )), когда |x| ≤ 1
2tan -1 х = cos -1 ((1-x 2 ) / (1+x 2 )), когда x ≥ 0
2tan -1 x = tan -1 (2x / (1-x 2 )), когда -1 < x < 1
Производное обратного загара
Найдем производную от y = tan -1 x. По определению обратного тангенса y = тангенс -1 x можно записать как тангенс y = x. Мы дифференцируем это с обеих сторон по x, используя цепное правило. Тогда мы получим
сек 2 y (dy/dx) = 1
dy/dx = 1/сек 2 y … (1)
Теперь у нас есть sec 2 y — tan 2 г. = 1 ⇒ sec 2 y = 1 + tan 2 y = 1 + x 2
Подставив это в (1),
dy/dx = 1 / (1 + x 2 900 04 )
Таким образом, обратная производная тангенса (или) обратная производная тангенса х равна 1 / (1 + x 2 ) .
Интеграл обратного загара
Найдем ∫ tan -1 x dx с помощью интегрирования по частям. Для этого мы запишем приведенный выше интеграл как
∫ tan -1 x · 1 dx
Используя LIATE, u = tan -1 x и v’ = 1 dx.
Тогда du = 1/(1 + x 2 ) dx и v = x.
Используя интегрирование по частям,
∫ u dv = uv — ∫ v du
∫ tan -1 x · 1 dx = tan -1 x (x) — ∫ x/(1 + x 90 003 2 ) + С
∫ загар -1 x dx = x tan -1 x — ∫ x/(1 + x 2 ) + C
Вычислим интеграл в правой части, используя метод u-подстановки. Для этого предположим, что 1 + x 2 = u. Тогда 2x dx = du (или) x dx = du/2.
∫ tan -1 x dx = x tan -1 x — ∫(1/u) (1/2) du + C
= x tan -1 x — (1/2) ln |у| + C
= x tan -1 x — (1/2) ln |1 + x 2 | + C
Следовательно, ∫ tan -1 x dx = x tan -1 x — (1/2) ln |1 + x 2 | + C.
Важные замечания по обратному тангенсу:
- 2, п/2).
- Обратный загар НЕ совпадает с (tan x) -1 как (tan x) -1 = 1/(tan x) = cot x.
- tan(tan -1 x) всегда x.
- желтовато-коричневый -1 (тангенс х) равен х, только если х НЕ является нечетным кратным π/2.
Если x является нечетным кратным π/2, то tan -1 (tan x) НЕ определен.
☛ Похожие темы:
- sin cos tan
- Тригонометрическая таблица
- Калькулятор обратного загара
- Формула арктангенса
Часто задаваемые вопросы об обратном загаре
Что такое Tan, обратный x?
Обратный тангенс x – это обратная функция тангенса. т. е. если y = tan x, то x = tan -1 (y). Здесь тангенс -1 является обратной функцией тангенса.
Как решить арктангенс x?
Чтобы найти арктангенс любого числа, просто посмотрите, какая функция угла тангенса дает это число. Например, тангенс -1 (1/√3) = π/6, поскольку тангенс π/6 = 1/√3. Но убедитесь, что угол лежит в интервале (-π/2, π/2).
Например, тангенс -1 (1/√3) = π/6, поскольку тангенс π/6 = 1/√3. Но убедитесь, что угол лежит в интервале (-π/2, π/2).
Что такое обратный загар 1?
Мы знаем, что тангенс π/4 = 1. Тогда по определению обратного тангенса тангенс -1 (1) = π/4. т. е. значение обратного загара 1 равно π/4.
Является ли противоположность Tan Cot?
Нет, обратная сторона загара не является детской кроваткой. На самом деле, функция, обратная тангенсу тангенса -1 (или) арктангенса. Но обратите внимание, что (tan x) -1 = 1/(tan x) = cot x, но это не обратная функция tan.
Как написать обратный загар?
Обратный тангенс x записывается одним из следующих способов:
- арктанг (х)
- атан (х)
- рыжевато-коричневый -1 x
Почему мы используем арктанент?
Функция арктангенса используется для нахождения углов в прямоугольном треугольнике, когда известны его противоположная сторона и прилежащая сторона.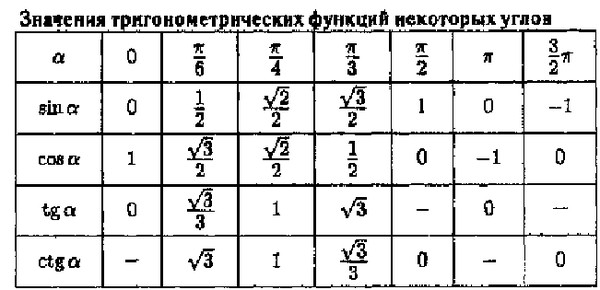 т. е. угол = тангенс -1 (противоположная сторона/прилегающая сторона).
т. е. угол = тангенс -1 (противоположная сторона/прилегающая сторона).
Что такое производная Tan, обратная x?
Производная tan -1 x is 1 / (1 + x 2 ). Математически это записывается как d/dx(tan -1 х) = 1 / (1 + х 2 ) (или) (тангенс -1 х)’ = 1 / (1 + х 2 ).
Что такое интеграл обратного загара?
Интеграл tan -1 x is x tan -1 x — (1/2) ln |1 + x 2 | + C. Математически это записывается как ∫ tan -1 x dx = x tan -1 x — (1/2) ln |1 + x 2 | + C.
Определен ли обратный тангенс для всех действительных чисел?
Область определения функции обратного тангенса представляет собой набор всех действительных чисел и, следовательно, она определена для всех действительных чисел.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.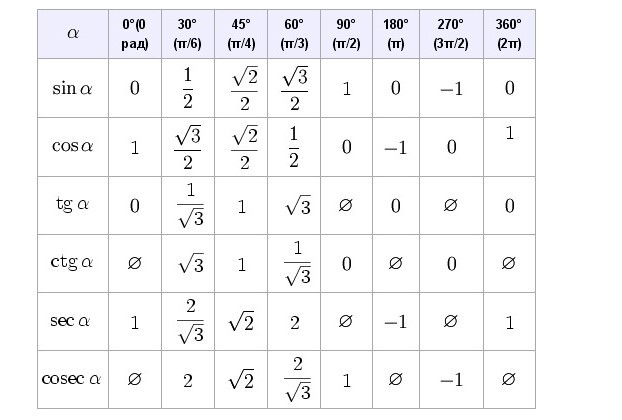 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 пи)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 пи)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.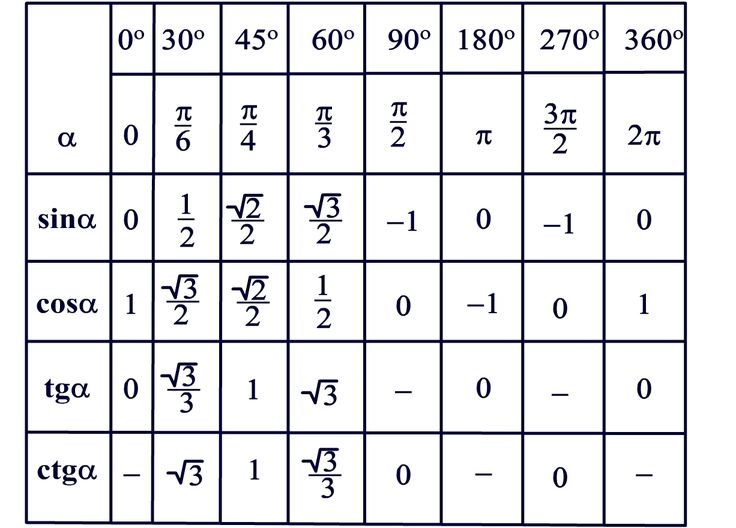 |

