Почему Грех,Кос,Тан
Гаурари ДассГаурари Дасс
Старший инженер данных в EMBL-EBI
Опубликовано 7 мая 2015 г.
+ Подписаться
Три функции, но одна и та же идея.
Прямоугольный треугольник
Синус, косинус и тангенс основаны на прямоугольном треугольнике. Противоположный» противоположен углу θ
Синус, косинус и тангенс
Синус , Косинус и Тангенс — три основные функции в тригонометрии.
Их часто сокращают до sin , cos и tan .
Чтобы вычислить их:
Разделите длину одной стороны на другую сторону
… но какие стороны?
Для треугольника с углом θ они вычисляются следующим образом:
На картинке:
Пример: чему равен синус 35°?
Используя этот треугольник (длины только до одного десятичного знака):
Как запомнить? Думай «Сохкахтоа» ! Это работает так:
Вы можете прочитать больше о sohcahtoa … пожалуйста, запомните это, это может помочь на экзамене!
Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, поэтому синус, косинус и тангенс также меняются между положительными и отрицательными значениями.
На хороших калькуляторах есть sin, cos и tan, чтобы вам было проще. Просто вставьте угол и нажмите кнопку.
Но вам все равно нужно помнить, что они означают!
Примеры
Пример: чему равны синус, косинус и тангенс угла 30°?
Классический 30-градусный треугольник имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону √3:
Теперь, когда мы знаем длины, мы можем вычислить функции:
(достаньте калькулятор и проверьте их!)
Пример: каковы синус, косинус и тангенс угла 45°?
Классический треугольник с углом 45° имеет две стороны, равные 1, и гипотенузу, равную √2:
Почему?
Почему важны эти функции?
- Потому что они позволяют нам вычислять углы, когда мы знаем стороны
- И они позволяют нам вычислять стороны, когда мы знаем углы
Пример: Используйте функцию синуса
, чтобы найти «d»Мы знаем:
- Кабель образует угол 39°
- Кабель имеет длину 30 метров .

И мы хотим знать «d» (расстояние вниз).
Глубина «d» равна 18,88 м
Упражнение
Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию для всех углов от 0° до 360°, а затем изобразить результат на графике. Это поможет вам понять эти относительно простые функции.
Вы также можете увидеть Графики синуса, косинуса и тангенса.
Менее распространенные функции
Для полноты картины есть еще 3 функции, где мы делим одну сторону на другую, но они не так часто используются.
Они равны 1 разделить на cos , 1 разделить на sin и 1 разделить на tan :
Ссылка:
https://www.mathsis-cosine.com tangent.html
Sohcahtoa: синус, косинус, тангенс
Sohca… что? Просто простой способ запомнить как работают синус, косинус и тангенс:
Итак. | S ine = O pposite / H ypotenuse |
…ках… | C осин = A djacent / H ypotenuse |
…тоа | T угол = O точка / A точка |
Прямоугольный треугольник
Хорошо, давайте посмотрим, что это такое.
Во-первых, имена Противоположный, Смежный и Гипотенуза происходят от прямоугольного треугольника:
- «Противоположный» противоположен углу θ
- «Смежный» примыкает (рядом) к углу θ
- «Гипотенуза» длинная
Смежный всегда рядом с углом
(и против против угла)
Синус, косинус и тангенс
И Синус , Косинус и Тангенс
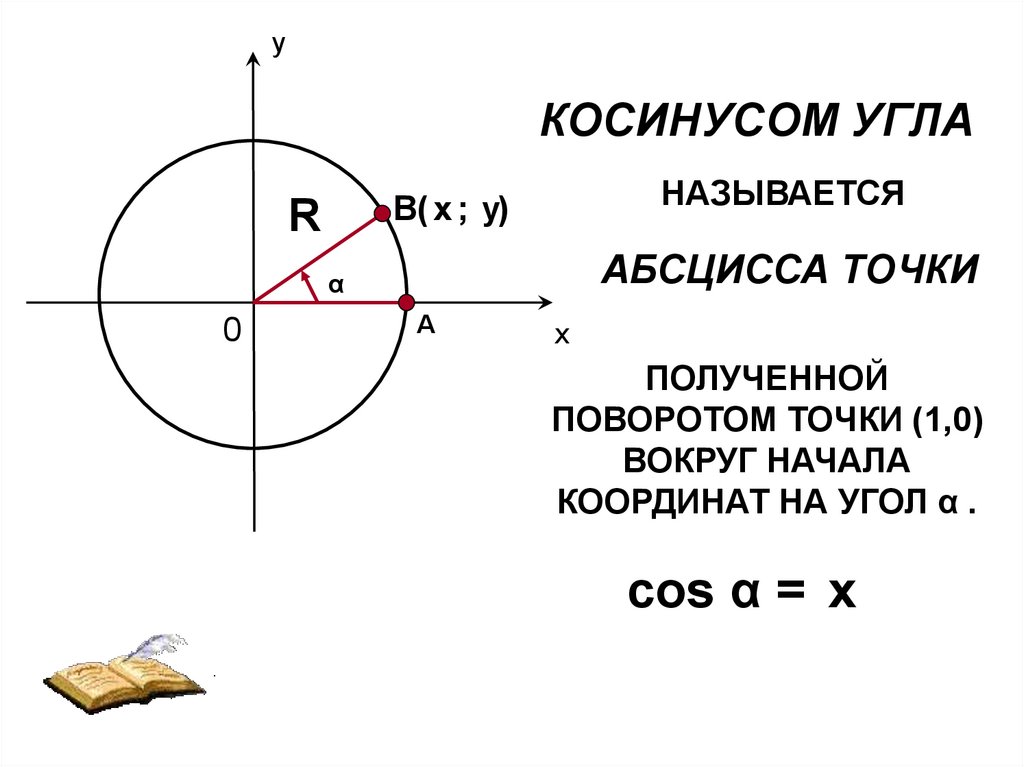
Их часто сокращают до sin , cos и tan .
Вычисление просто одна сторона прямоугольного треугольника делится на другую сторону … нам просто нужно знать, какие стороны, и вот где «sohcahtoa» помогает.
Для треугольника с углом θ функции вычисляются следующим образом:
Функция синуса: | так… | с дюйм( θ ) = o pposite / h ypotenuse |
Функция косинуса: | …ка… | c os( θ ) = a djacent / h ypotenuse |
Касательная функция: | … до | t an( θ ) = o точка / a djacent |
Пример: чему равны синус, косинус и тангенс угла 30°?
Классический треугольник 30° имеет гипотенузу (длинная сторона) длиной 2 , противолежащую сторону длиной 1 и прилежащую сторону √3 , например:
Теперь мы знаем длины, мы можем вычислить функции:
Синус | так. |

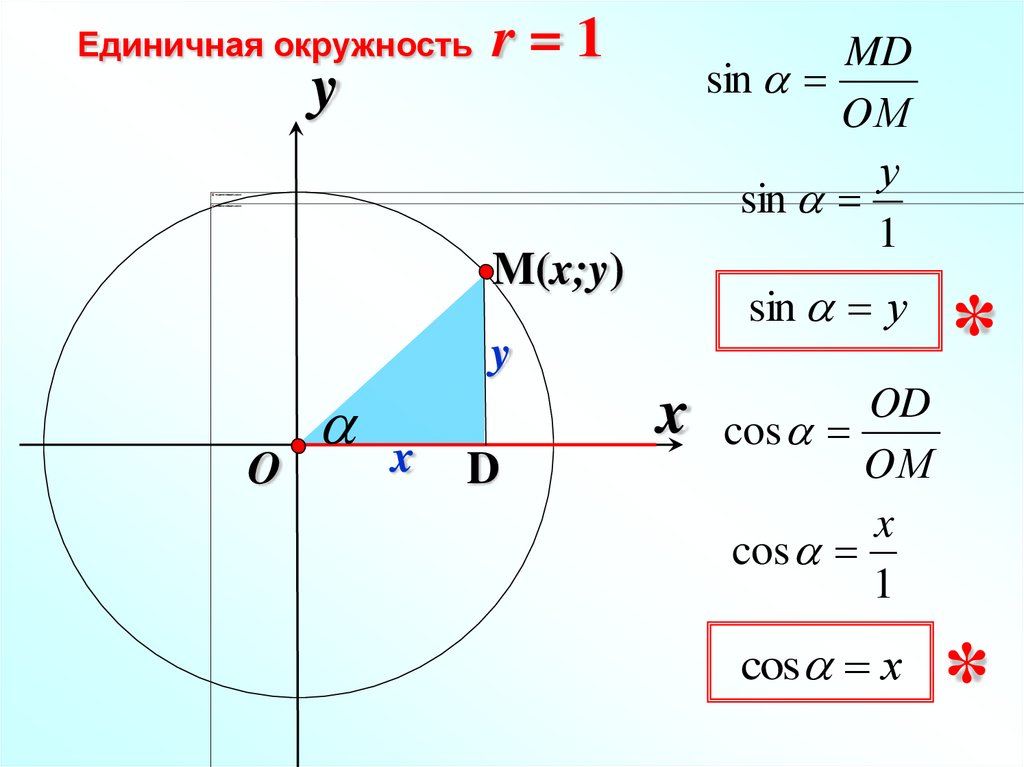
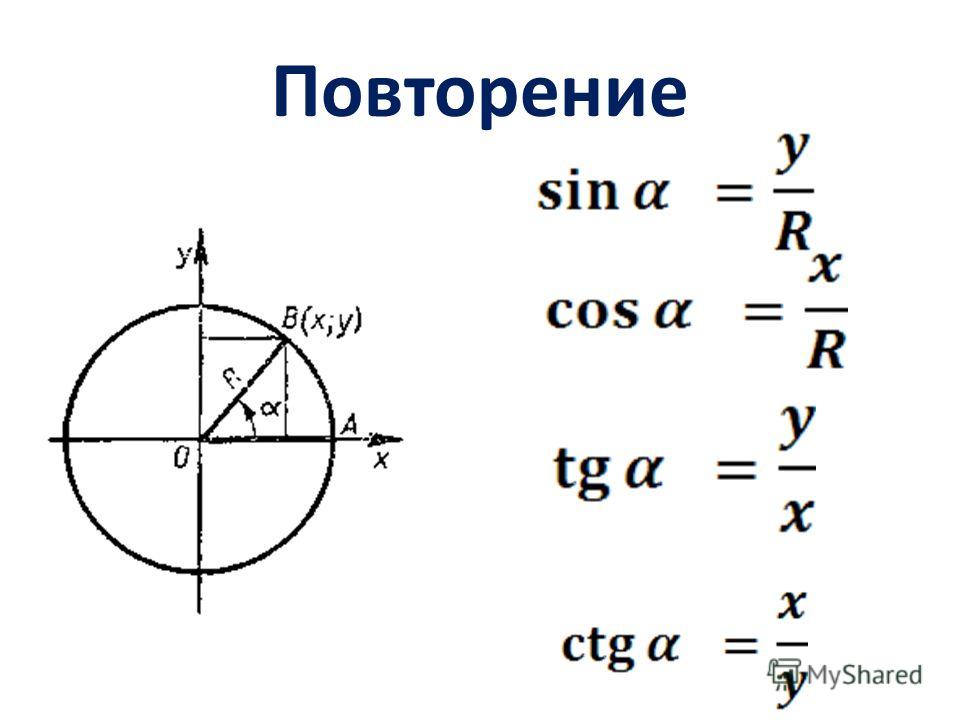 ..
..