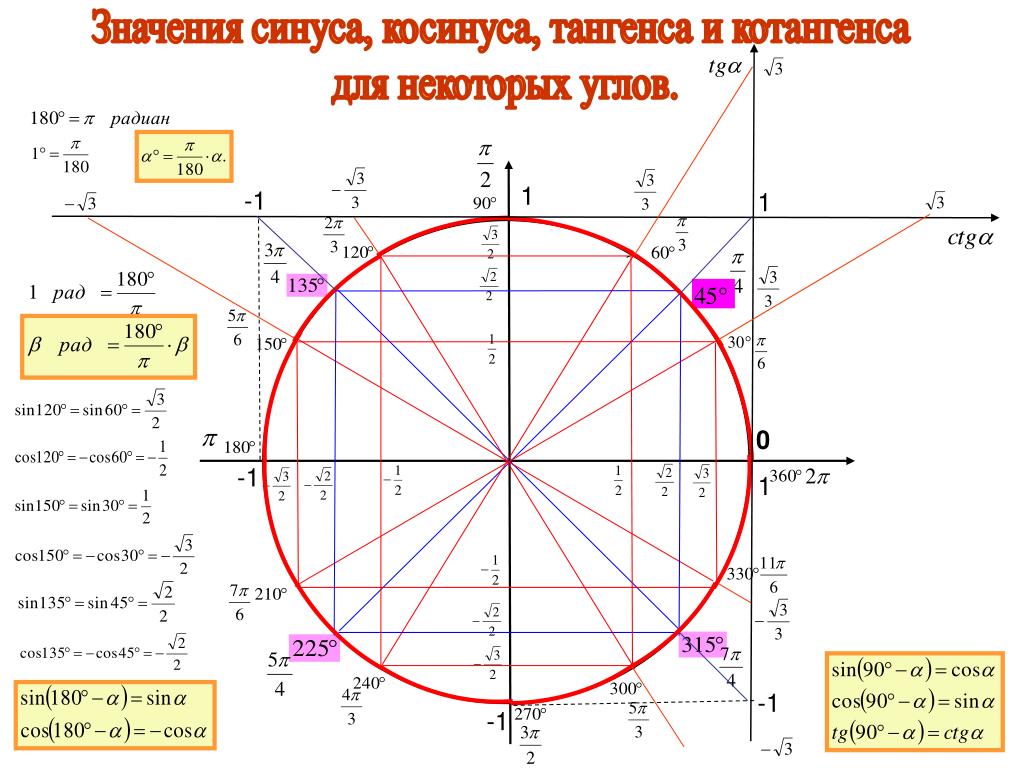
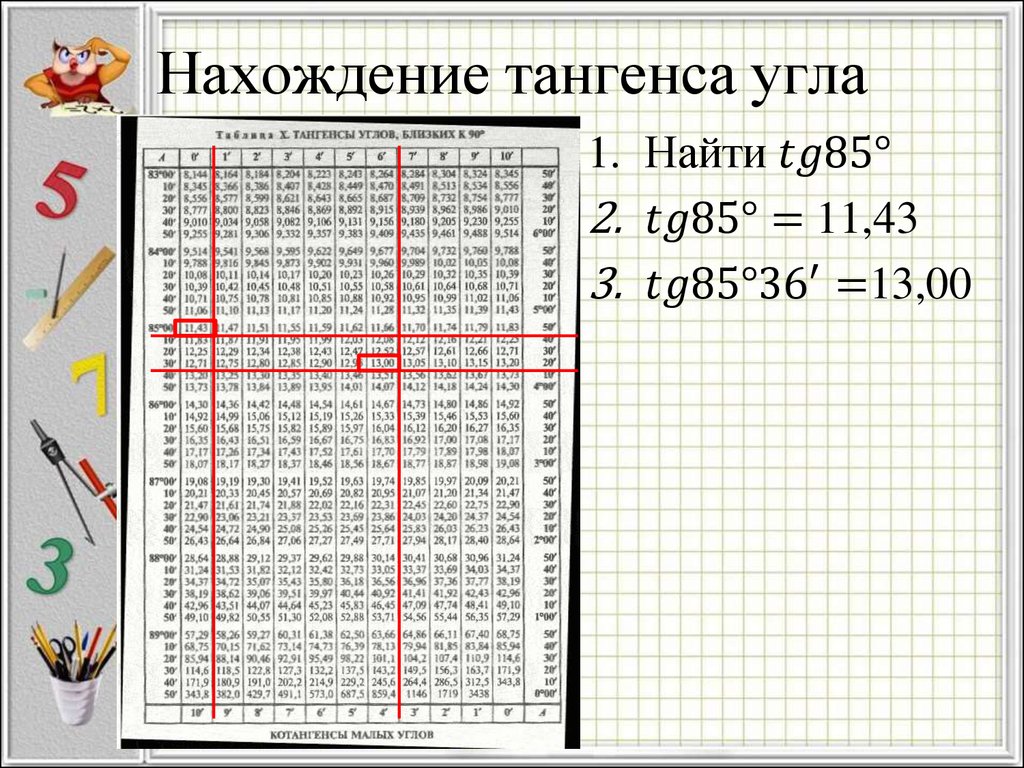
2 tg 0
2 tg 0Вы искали 2 tg 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 тангенс 0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 tg 0».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 tg 0,2 тангенс 0,4 тангенс,4 тангенс 0,5 tg 2,tg 0 2,tg 0 5,tg 0 75,tg 0 равен,tg 0 чему равен,tg 1 2 в градусах,tg 1 4,tg 1 в градусах,tg 1 в пи,tg 15 градусов равен,tg 18,tg 2 0,tg 2 3,tg 2 5,tg 20 градусов,tg 25,tg 3 2,tg 3 4,tg 36,tg 360,tg 4 1,tg 5 2,tg 70,tg a 1,tg a 180,tg значения,tg равен 0,tg таблица,tg10,значение тангенса таблица,значения tg,значения тангенса,значения тангенса таблица,значения тангенсов,значения тангенсов таблица,как перевести тангенс в градусы,перевести тангенс в градусы,таблица tg,таблица значение тангенс,таблица значений тангенса,таблица значений тангенсов,таблица значения тангенса,таблица значения тангенсов,таблица котангенса и тангенса,таблица тангенс котангенс,таблица тангенс угла,таблица тангенс углов,таблица тангенса,таблица тангенса и котангенса,таблица тангенса углов,таблица тангенсов,таблица тангенсов значений,таблица тангенсов и котангенсов,таблица тангенсов и котангенсов с пи,таблица тангенсов котангенсов,таблица тангенсов с минутами,таблица тангенсов углов,таблица тангенсов углов от 0 до 90,таблица тангенсы,таблица тангенсы углов,таблица углов тангенс,таблица углов тангенса,таблица углов тангенсов,таблицы тангенсов,таблиця тангенсів,табличные значения тангенса,тангенс 0,тангенс 0 2,тангенс 0 25,тангенс 0 4,тангенс 0 5,тангенс 0 5 равен,тангенс 0 6,тангенс 0 75,тангенс 0 градусов,тангенс 1 4,тангенс 1 в градусах,тангенс 1 градуса,тангенс 1 равен в градусах,тангенс 10,тангенс 10 градусов равен,тангенс 12,тангенс 12 градусов,тангенс 13,тангенс 14 градусов,тангенс 15,тангенс 15 градусов равен,тангенс 18,тангенс 180,тангенс 180 градусов,тангенс 2 0,тангенс 2 3,тангенс 2 5,тангенс 2 градусов,тангенс 2 корень из 2,тангенс 2 п,тангенс 20,тангенс 20 градусов,тангенс 22,тангенс 225,тангенс 25,тангенс 25 градусов,тангенс 25 градусов равен,тангенс 27,тангенс 3,тангенс 3 2,тангенс 3 4,тангенс 3 градусов,тангенс 3 какого угла равен,тангенс 3 равен,тангенс 30 градусов равен таблица,тангенс 35,тангенс 35 градусов равен,тангенс 36,тангенс 36 градусов,тангенс 360,тангенс 4,тангенс 4 1,тангенс 4 3,тангенс 4 3 в градусах,тангенс 4 равен,тангенс 40,тангенс 40 градусов,тангенс 40 градусов равен,тангенс 5,тангенс 5 2,тангенс 5 градусов,тангенс 50,тангенс 55,тангенс 6,тангенс 65,тангенс 7,тангенс 75,тангенс 75 градусов,тангенс 8,тангенс 80,тангенс 90 градусов равен таблица,тангенс x 0 x,тангенс в градусах,тангенс значение таблица,тангенс и котангенс таблица,тангенс икс равен 0,тангенс какого угла равен 4,тангенс корень из 2,тангенс корень из 2 на 2,тангенс котангенс таблица,тангенс п,тангенс п 5,тангенс равен 0 5,тангенс равен 0 чему равен угол,тангенс равен 1 2,тангенс равен 1 чему равен угол,тангенс равен 3,тангенс равен 4,тангенс равен 4 чему равен угол,тангенс таблица,тангенс таблица значений,тангенс таблица углов,тангенс угла 7,тангенс угла таблица,тангенс углов таблица,тангенс х равен 0,тангенсы,тангенсы и котангенсы таблица,тангенсы таблица,тангенсы углов от 0 до 90,тангенсы углов таблица.
Решить задачу 2 tg 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
I вариант. 1. Закончи предложение. Квадрат любой стороны треугольника равен … 2. Заполни пропуски. В треугольнике KHT . 3. В треугольнике CDO известны стороны CD и CO. Величину, какого угла необходимо знать, чтобы найти длину стороны DO? 4. Дан треугольник DEF. Выберите верное равенство: 5. В треугольнике CKE найдите сторону CE, если CK = 6, KE = 8, K = 60°? | II вариант. 1. Выберите верное утверждение: 3. В треугольнике АВС известны: длина стороны ВС и величина угла С. Чтобы вычислить сторону АВ, нужно знать: 4. Выберите верное равенство: 5. В треугольнике KHN найдите сторону KN, если KH = , HN = 5, H = 45°. | III вариант. 1. Закончи предложение. Квадрат любой стороны треугольника равен … в) сумме квадратов двух других его сторон; . 3. В треугольнике CDO известны стороны CD и CO. Величину, какого угла необходимо знать, чтобы найти длину стороны DO? 4. Дан треугольник DEF. Выберите верное равенство: 5. В треугольнике CKE найдите сторону CE, если CK = 6, KE = 8, K = 60°? | IV вариант. 1. Выберите верное утверждение: 2. Заполни пропуски. В треугольнике ESR 3. В треугольнике АВС известны: длина стороны ВС и величина угла С. Чтобы вычислить сторону АВ, нужно знать: 4. Выберите верное равенство: 5. В треугольнике KHN найдите сторону KN, если KH = , HN = 5, H = 45°. |
Тангенс угла – формулы и примеры
Тангенс угла можно определить с помощью прямоугольного треугольника. Тангенс равен длине стороны, противолежащей углу, деленной на длину прилежащей стороны. Хотя тангенс определяется углами прямоугольного треугольника, функцию тангенса можно использовать для любого угла.
Здесь мы узнаем больше о тангенсе угла. Мы узнаем о значениях тангенса важных углов и решим некоторые практические задачи.
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение тангенса угла на примерах.
См. примеры
примеры
Содержание
ТРИГОНОМЕТРИЯ
Актуально для …
Изучение тангенса угла на примерах.
См. примеры
Определение тангенса угла
Синус и косинус — не единственные часто используемые тригонометрические функции. Тангенс угла — еще одна очень важная тригонометрическая функция. Тангенс определяется в терминах единичной окружности.
На приведенной ниже диаграмме касательной является длина вертикальной линии ED, которая касается от точки касания E до точки D, где касательная пересекает луч AD, образованный углом.
Касательные относительно синуса и косинуса
Треугольники ABC и ADE на приведенном выше рисунке подобны, поэтому пропорции их сторон равны. Это означает, что у нас есть:
$latex \frac{ED}{AE}=\frac{CB}{AC}$
Глядя на диаграмму, мы видим, что у нас есть $latex EA=\tan(A)$ . Мы используем единичный круг, поэтому имеем $latex AE=1$. Кроме того, у нас также есть отношения $latex CB=\sin(A)$ и $latex AC=\cos(A)$. Используя это, мы находим фундаментальное тождество:
Кроме того, у нас также есть отношения $latex CB=\sin(A)$ и $latex AC=\cos(A)$. Используя это, мы находим фундаментальное тождество:
| $latex \tan(A)=\frac{\sin(A)}{\cos(A)}$ |
Касательные и прямоугольные треугольники можно найти через стороны прямоугольного треугольника, мы можем сделать то же самое и с касательными. Мы собираемся использовать прямоугольный треугольник ABC с прямым углом C.
Мы можем использовать отношения, которые мы уже видели. Сначала у нас есть $latex \tan(A)=\frac{\sin(A)}{\cos(A)}$. Мы также используем отношения $latex \sin(A)=\frac{a}{c}$ и $latex \cos(A)=\frac{b}{c}$. Используя это, мы можем разделить $latex \frac{a}{c}$ на $latex \frac{b}{c}$.
Сокращая c в числителе и знаменателе, заключаем, что $latex \tan(A) = \frac{a}{b}$. Это означает, что касательная равна противолежащей стороне, деленной на прилежащую сторону:
Касательные для обычных специальных углов
Тангенс наиболее распространенных углов находится с использованием пропорций сторон специальных треугольников и того факта, что тангенс равен синусу над косинусом.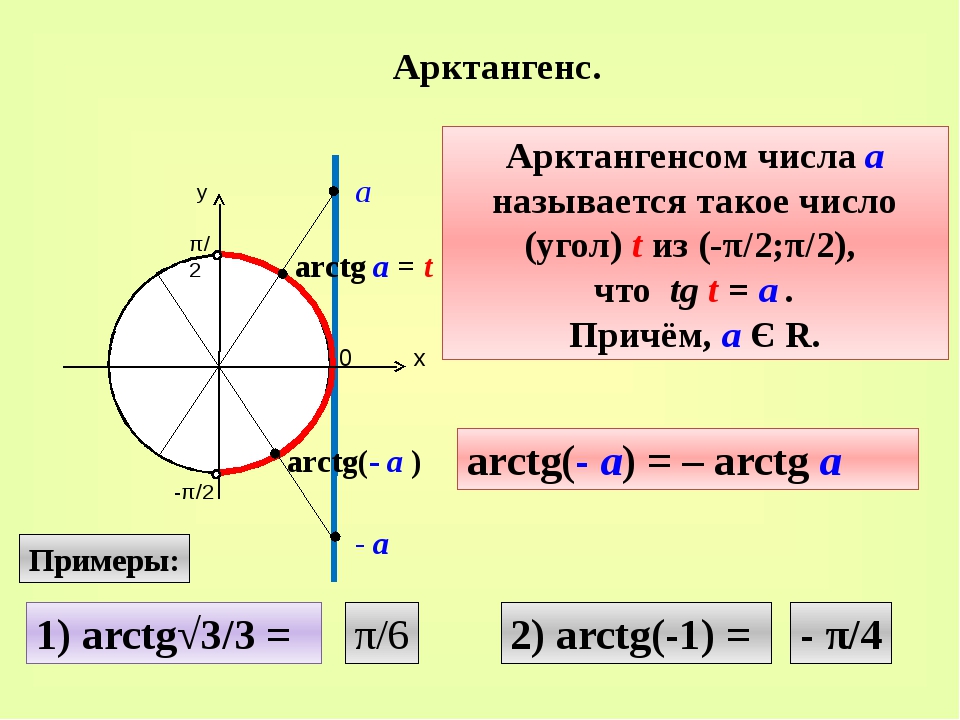 Например, мы будем использовать прямоугольный равнобедренный треугольник с углами 45°-45°-9.{\circ})=\frac{\sqrt{3}}{2}$.
Например, мы будем использовать прямоугольный равнобедренный треугольник с углами 45°-45°-9.{\circ})=\frac{\sqrt{3}}{2}$.
| градусов | Радианы | SINE | $ $ | $$ $ | 0 | Не определено |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac {1}{2}$ | $латекс\sqrt{3}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{\sqrt{2}} {2}$ | 1 |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{1}{2}$ | $latex \frac{\sqrt{ 3}}{2}$ | $latex \frac{\sqrt{3}}{3}$ |
| 0° | 0 | 0 | 1 | 0 |
Tangent of угол – Примеры с ответами
Следующие примеры решаются с использованием того, что мы узнали о тангенсах углов.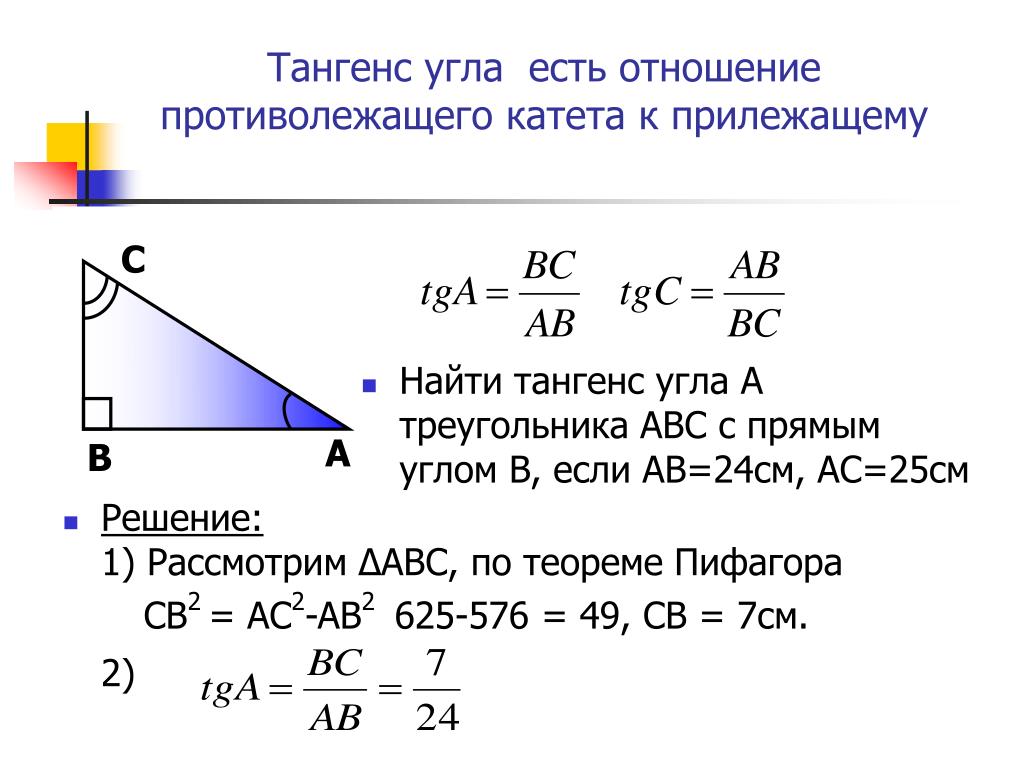 Все примеры относятся к прямоугольному треугольнику, показанному выше.
Все примеры относятся к прямоугольному треугольнику, показанному выше.
В треугольнике у нас есть $латекс \tan(A) = 1,2$ и $латекс b = 5$, чему равно a ?
Решение
Мы используем треугольник выше в качестве ориентира. Следовательно, имеем соотношение $latex \tan(A) = \frac{b}{a}$. Используя значения, указанные в этой формуле, и решив для c, имеем:
$latex \tan(A)=\frac{b}{a}$
$latex 1.2=\frac{5}{a}$
$latex a=\frac{ 5}{1.2}$
$латекс a=4,17$
Длина a равна 4,17.
ПРИМЕР 2Определите значение b , если $латекс a=11$ и $латекс \tan(B)=0,78$.
Решение
Используя приведенный выше треугольник в качестве эталона, мы можем получить отношение $latex \tan (B) = \frac{b}{a}$. Подставляем значения, данные в эту формулу и при решении c, имеем:
$латекс \tan(B)=\frac{b}{a}$
$латекс 0,78=\frac{b}{11}$
$латекс b=0,78(11 )$
$латекс b=8,58$
Длина b равна 8,58.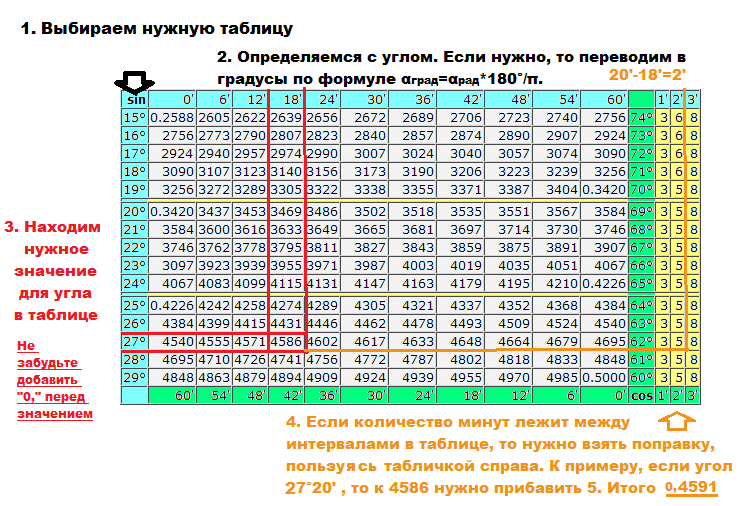
Определите меру угла A, если мы имеем $латекс a = 12$ и $латекс b = 8$.
Решение
Составим выражение $latex \tan(A)=\frac{a}{b}$. Следовательно, используя заданные значения, мы имеем:
$latex \tan(A)=\frac{a}{b}$ 9{-1}}=56,3$°
Угол А равен 56,3°.
→ Калькулятор тангенса (градусы и радианы)
Тангенс угла – Практические задачи
Используйте приведенную выше формулу тангенса для решения следующих практических задач. Определите длину стороны или меру угла с заданной информацией.
Если у нас есть $latex b = 5,7$ и $latex tan(A) = 1,8$, каково значение a?
Выберите ответ
$латекс a=9.23$
$латекс a=10,26$
$латекс a=11,23$
$latex a=12,24$
Если у нас есть $latex b=15$ и $latex tan(B)=1,9$, каково значение a?
Выберите ответ
$латекс a=8.2$
$латекс a=12,6$
$latex a=17,5$
Если у нас есть $latex b=12$ и $latex a=18$, каково значение A?
Выберите ответ
$латекс A=45,6$°
$латекс A=49,1$°
$латекс A=56,3$°
$latex A=59.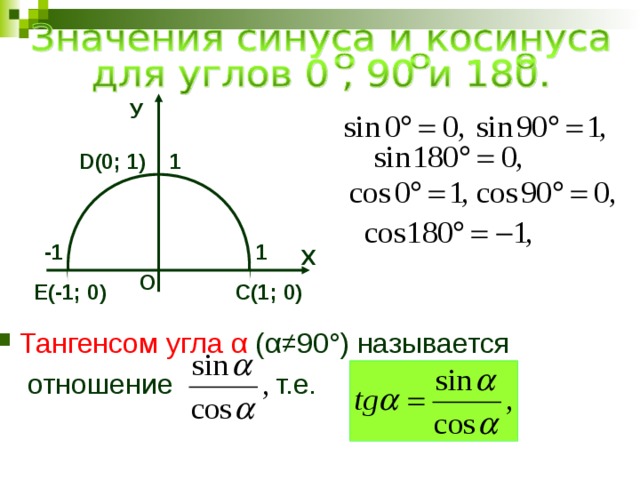 7$°
7$°
См. также
Хотите узнать больше о тангенсе угла? Взгляните на эти страницы:
- Калькулятор тангенса (градусы и радианы)
- График тангенса с примерами
- Арктангенс – формулы, графики и примеры
- Единичная окружность – формулы и диаграммы
, Trigculus Notes 4
Диаграмма поведения синуса
Начнем с того, что вспомним нашу диаграмму поведения синуса из прошлого раза.
Диаграмма поведения косинуса
Теперь мы продолжим нашу работу, разработав диаграмму поведения для
функция косинуса. Поскольку косинус определяется как смежный катет, разделенный
по гипотенузе, теперь мы будем внимательно следить за горизонтальным катетом
каждого из нескольких прямоугольных треугольников при повороте углов от 0 до 360.
Мы видим, что при нуле градусов прямоугольный треугольник будет сжат по вертикали,
а горизонтальный катет будет полной длины или 1.
При работе со вторым и третьим квадрантами у нас будет горизонтальная длина ноги слева от оси Y, и поэтому будет считаться быть отрицательным. Итак, когда мы двигаемся от 90 до 180 градусов, мы можем «видеть» горизонтальная ветвь, идущая от нулевой длины к длине -1, поэтому косинус обезжиривает снова (это было и в первом) во втором квадранте.
В третьем квадранте он движется от -1 обратно к нулю и поэтому увеличение. В четвертом квадранте мы переходим от 0 к 1 и, следовательно, продолжаем увеличиваться.
Диаграмма поведения касательной
Теперь нам нужна диаграмма поведения касательной
функция. Опять же, мы возвращаемся к нашим корням геометрии и помним значение тангенс . Вы помните, что касательная — это линия, которая
пересекает окружность только в 1 точке, называемой точкой касания. В нашем
единичный круг подумайте о линии, касательной к единичному кругу в точке (1,0).
Если гипотенуза вытянута за пределы прямоугольного треугольника до пересечения
эта касательная, вертикальная длина, отрезанная этой вытянутой гипотенузой
использование точки (1,0) в качестве конечной точки является касательной. (см. ниже)
Опять же, мы возвращаемся к нашим корням геометрии и помним значение тангенс . Вы помните, что касательная — это линия, которая
пересекает окружность только в 1 точке, называемой точкой касания. В нашем
единичный круг подумайте о линии, касательной к единичному кругу в точке (1,0).
Если гипотенуза вытянута за пределы прямоугольного треугольника до пересечения
эта касательная, вертикальная длина, отрезанная этой вытянутой гипотенузой
использование точки (1,0) в качестве конечной точки является касательной. (см. ниже)
При нуле градусов длина этой касательной будет равна нулю.
Следовательно, тангенс(0)=0. По мере увеличения нашего угла в первом квадранте тангенс будет увеличиваться
очень быстро. Когда мы приблизимся к 90 градусам, эта длина станет невероятно
большой. При 90 градусах мы должны сказать, что тангенс не определен (und), потому что
когда вы делите противоположную ногу на соседнюю ногу, вы не можете разделить на
нуль.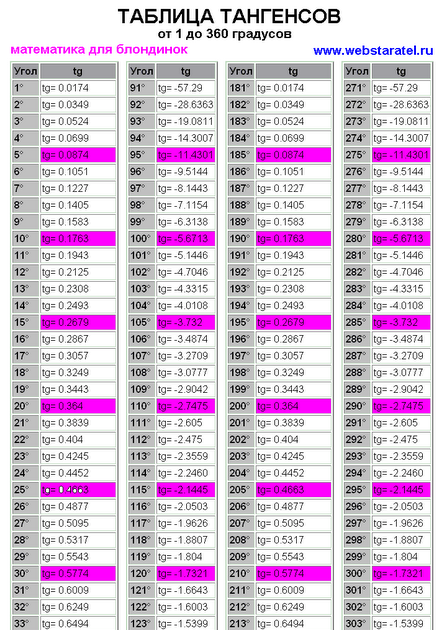


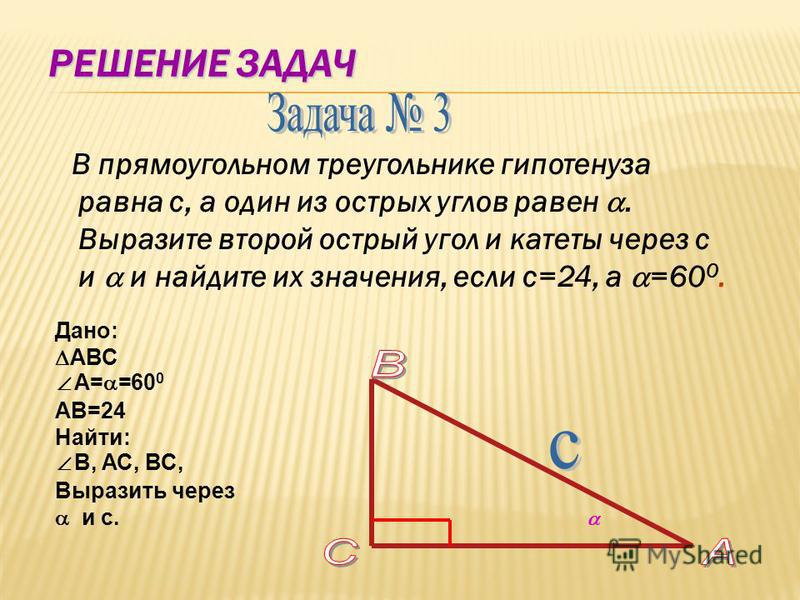 Заполни пропуски. В треугольнике ESR
Заполни пропуски. В треугольнике ESR