Тригонометрия | Математические формулы | Indigomath Математика
Синус и косинус Найти Известно, что: a = Вычислить ‘a’Тангенс Найти Известно, что: a = Вычислить ‘a’Котангенс Найти Известно, что: a = Вычислить ‘a’Произведение тангенса и котангенса Найти Известно, что: a = Вычислить ‘a’Тангенс и косинус Найти Известно, что: a = Вычислить ‘a’Котангенс и синус Найти Известно, что: a = Вычислить ‘a’Синус суммы углов Найти Известно, что: ab = Вычислить ‘a’Синус разницы углов НайтиТангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)
Обновлено 21 февраля 2023 Просмотров: 19 623 Автор: Дмитрий ПетровЖивущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.
Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.
Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.
Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.
Тангенс угла
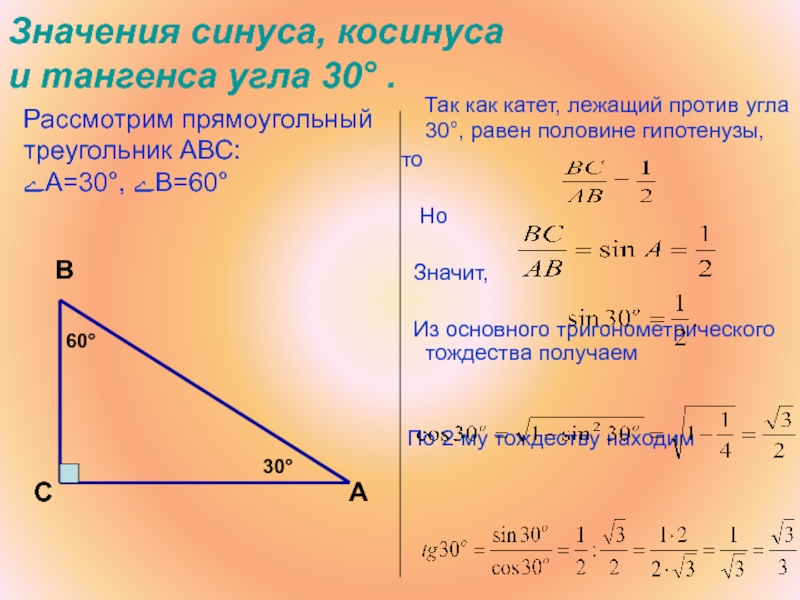
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой.
Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Приняты обозначения:
Вместо «тангенс угла альфа» пишут: tgα.
На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Как найти тангенс угла (формулы)
Первое свойство тангенса вытекает из его определения как отношения катетов.
Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому
Так как тангенс – это отношение катетов, то
Получается, что
Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.
В частности,
Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.
Как найти тангенс по клеточкам
Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.
Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:
Из формулы тангенсов, записывающей кратко второе определение
и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.
Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:
Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Математика, математика и статистика — Комплект академических навыков
Синус, косинус и тангенс
ContentsToggle Главное меню 1 Синус1.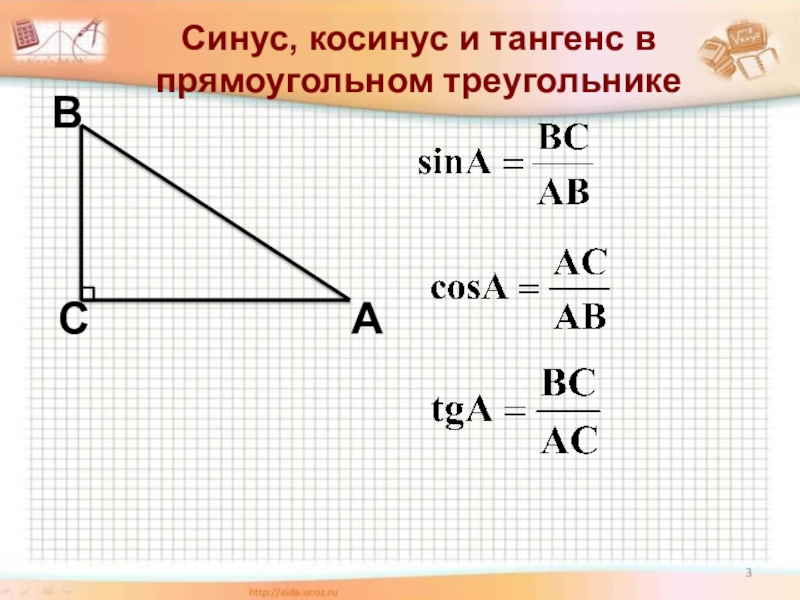
1 Определение 2 Косинус2.1 Определение 3 Тангенс3.1 Определение 4 Общие коэффициенты запуска 5 Производные 6 Инверсия 7 Видеопримеры 8 Рабочая тетрадь 9 См. также 10 Внешние ресурсы
Синус
Определение
Синус является нечетной периодической функцией с периодом $2\pi$. Функция синуса имеет область определения всех действительных чисел, а ее диапазон равен $-1\leq\sin x \leq 1$.
|центр
Косинус
Определение
Косинус является четной функциональной функцией и периодической с периодом $2\pi$. Функция косинуса имеет область определения всех действительных чисел, и ее диапазон составляет $-1\leq \cos x \leq 1$.
|центр
Касательная
Определение
Функция тангенса повторяется в интервалах $\pi$ и имеет асимптоты для каждого кратного $\dfrac{n\pi}{2}$ для нечетных $n$. Функция тангенса имеет все действительные числа, кроме нечетных, кратных $9.
{\circ}$ или $\pi/2$ в своей области определения, а его диапазон содержит все действительные числа.
|центр
Тангенс определяется как \[\tan x = \dfrac{\sin x}{\cos x}.\]
Общие тригонометрические отношения
Вот таблица общих углов и значений их соответствующих тригонометрических отношений .
$\sin x$ | $\;\;0\;\;$ | $\;\,\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | $\;\;1\;\;$ |
$\cos x$ | $\;\;1\;\;$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\;\,\dfrac{1}{2}$ | $\;\;0\;\;$ |
$\tan x$ | $\;\;0\;\;$ | $\dfrac{1}{\sqrt{3}}$ | $\;\;1\;\;$ | $\sqrt{3}$ | $\;\infty\;$ |
Производные
Триггерные функции могут быть дифференцированы и интегрированы.
$\sin x$ | 9{-1}$.
w3.org/1999/xhtml»> Тригонометрия синуса, косинуса и тангенса
H> дает два десятичных знака
#INCLUDE 
6 ;DB6a на контакте 12
#define LCD_DB7 PortB.7 ;DB7 на контакте 13
#define LCD_NO_RW 1 ;заземлить линию RW на LCD
;----- Переменные
dim ii как целое число
dim outStr, valStr как строка
;----- Программа
dir PortB out ;все выходы на LCD
для ii = от -720 до 720; аргументы от -720 до 720
клс
напечатать "sin(" ;напечатать метку
print ii ;и аргумент
print ")=" ;и закрывающая скобка
найти 1,0
printTrig(sin(ii)) ;вывести значение синуса
ждать 500 мс ;пауза для просмотра
cls ;сделать то же самое для косинуса
напечатать "потому что("
печатать II
распечатать ")="
найти 1,0
printTrig(cos(ii))
ждать 500 мс ;пауза для просмотра
cls ;сделайте то же самое для касательной
напечатать "загар("
печатать II
распечатать ")="
найти 1,0
printTrig(загар(ii))
ждать 500 мс ;пауза для просмотра
следующий я
sub printTrig (в значении как целое число)
;печатать прилично отформатированные результаты триггера
outStr = "" ; предположим положительное значение (без знака)
если значение < 0, то ;обрабатывать отрицательные значения
outStr = "-" ;перед знаком минус
значение = -1 * значение; но работайте с положительными значениями
конец, если
valStr = строка (значение)
длина = длина (valStr)
выберите длину корпуса
Дело 1:
outStr = outStr + "0.