Урок по геометрии в 8 классе по теме «Теорема Фалеса» | План-конспект урока по геометрии (8 класс) на тему:
Урок геометрии в 8 классе.
Тема: «Теорема Фалеса»
Дата проведения: 20.10.2014 г.
Учитель: Ярославцева Мария Николаевна.
Место проведения: МКОУ «Сухоплотавская ООШ», Тульская область, Воловский район, д. Сухие Плоты.
Цели:
Образовательные:
— рассмотреть теорему Фалеса и её доказательство;
— закрепить теорему Фалеса в процессе решения задач;
— совершенствовать навыки решения задач на применение знаний по теме «Трапеция»
Воспитательные:
— формирование способностей анализировать свои действия, умения внимательно слушать
Развивающие:
Развитие логического мышления, воображения, памяти, кругозора, умения рассуждать и аргументировать.
Оборудование: доска, циркуль, линейка, треугольник, компьютер, проектор, экран, презентация.
Ход урока.
- Сообщение темы и целей урока.
Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.
Тема сегодняшнего урока «Теорема Фалеса». Вы не только познакомитесь с этой теоремой, её доказательством, но также увидите, где можно ее применить.
Предлагаю выполнить такое задание: разделить отрезок на две, четыре, три части с помощью циркуля. (Учащиеся выходят к доске и показывают)
Перед вами стоит проблема деления отрезка на три равные части, а ученые столкнулись с проблемой деления отрезка на равные части много веков назад. И, конечно, они нашли выход из положения.
И чтобы нам сегодня справиться с возникшей задачей, докажем одну из важнейших теорем геометрии, которая называется Теорема Фалеса. Кем же был Фалес, что в его честь даже названа теорема в геометрии?
Кем же был Фалес, что в его честь даже названа теорема в геометрии?
Фалес Милетский – древнегреческий философ из г. Милета (Малая Азия – территория современной Турции). Сведения о его жизни до сих пор носят противоречивый характер, но считается, что:
— именно он привез геометрию из Египта и познакомил с нею греков; его последователи и ученики основали Милетскую школу;
— именно его греки уже в древности называли «отцом философии»;
— именно он «открыл» для греков созвездие Малой Медведицы как путеводный инструмент;
— именно он ввёл календарь по египетскому образцу, в котором год состоял из 365 дней.
— одна из легенд гласит, что будучи в Египте, Фалес поразил фараона Амасиса тем, что сумел точно измерить высоту пирамиды. Как вы думаете, как он это сделал? Дождался пока длина тени от палки станет равной самой палке, значит и тень от пирамиды равна будет самой пирамиде;
— он предсказал солнечное затмение в мае 585 года до н.э.
Но одна из важнейших заслуг Фалеса в том, что ученый первый стал доказывать геометрические теоремы:
- круг делится диаметром пополам;
- в равнобедренном треугольнике углы при основании равны;
- при пересечении двух прямых образуемые ими вертикальные углы равны;
- два треугольника равны, если два угла и сторона одного из них равны двум углам и соответствующей стороне другого.

Вот такой был Фалес Милетский, в честь которого названа теорема в геометрии и эту теорему мы сегодня и рассмотрим.
- Изучение нового материала.
Помощь в доказательстве Теоремы Фалеса нам окажет задача № 384, которую мы сейчас решим. (презентация)
Задача. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Доказательство.
- Проведем DC║АВ.
- Рассмотрим Δ AMN и ΔNDC.
- AM = MВ (по условию), МВ = DC (как противоположные стороны параллелограмма BMDC), поэтому AM = DC.
- Угол 1 равен углу 2, угол 3 равен углу 4 (как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и MD)
Из 1) и 2) Δ AMN = ΔNDC, значит AN = NC, что и требовалось доказать.
Какой вывод из этой задачи мы можем сделать?
Если в треугольнике через середину одной стороны провести прямую, параллельную одной из двух других сторон, то эта прямая пройдет через середину третьей стороны.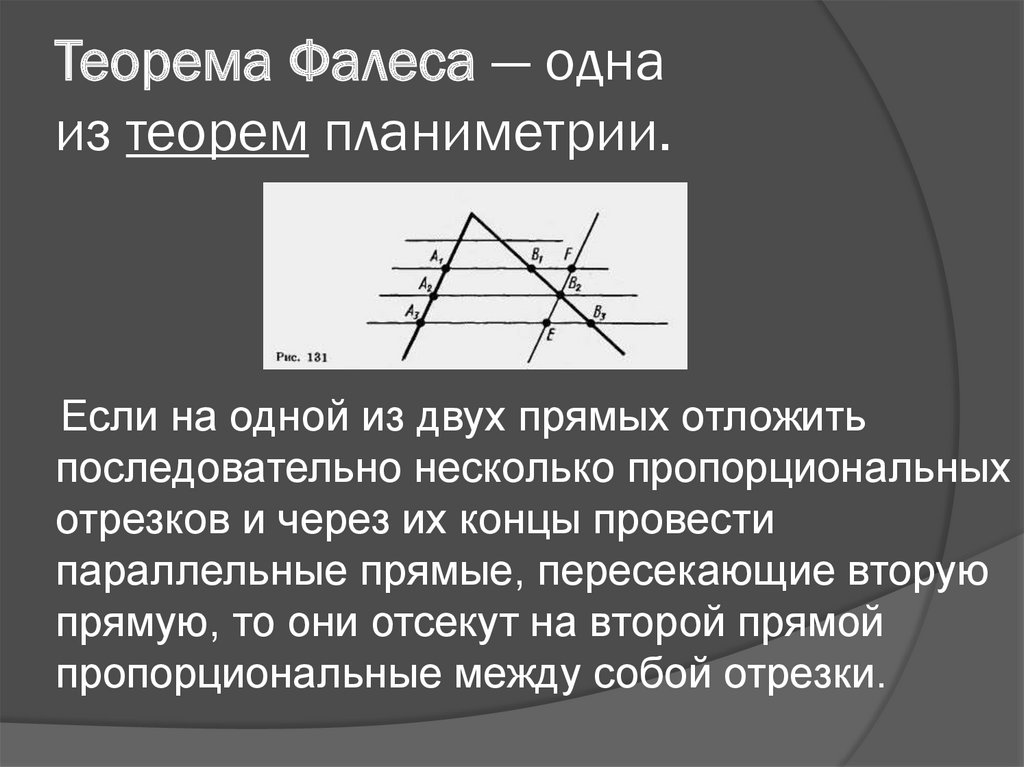
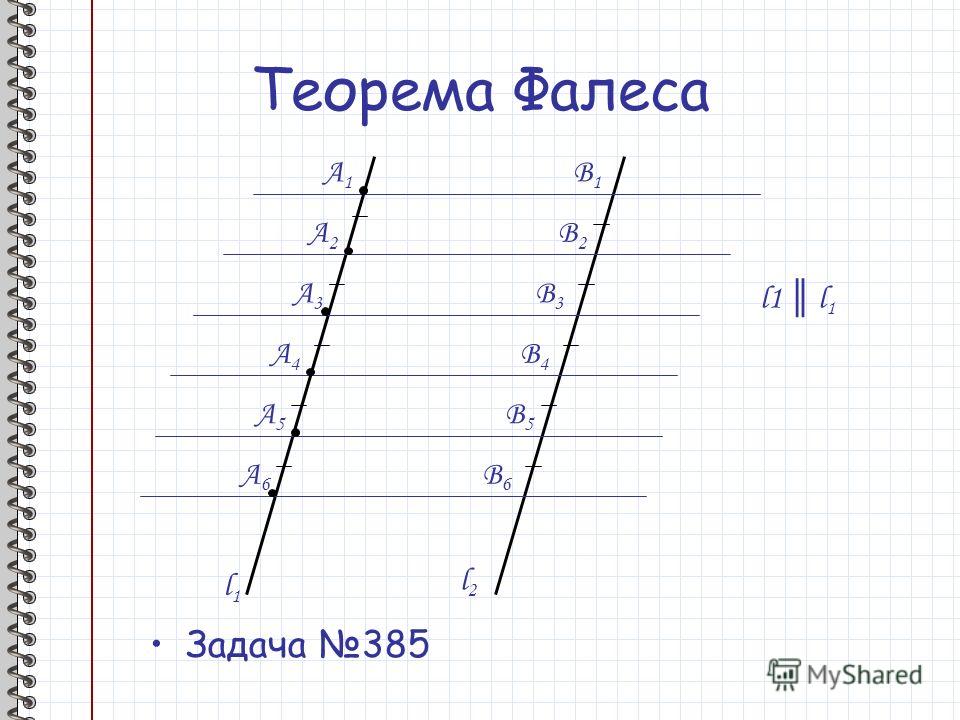
Теорема Фалеса: «Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки».
Доказательство:
Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, … и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, …. Требуется доказать, что отрезки В1В2, В2В3, В3В4, … равны друг другу. Докажем , например, что В1В2 = В2В3.
- Пусть l1║l2. Тогда А1А2 = В1В2, А2А3 = В2В3, как противоположные стороны параллелограммов А1 В1В2 А2 и А2В2В3А3. Т.к. А1А2 = А2А3, то и В1В2 = В2В3.
- Если l1 и l2 не параллельны, то через точку В1 проведем прямую l║ l1. Она пересечет прямые А2В2 и А3В3 в некоторых точках C и D. Так как А1А2 = А2А3, то по ранее доказанному В1С = СD. Отсюда получаем В1В2 = В2В3.
Теорема доказана.
- Закрепление пройденного материала.

Решение задач на готовых чертежах.
- Практическая работа.
Разделить отрезок на 5 равных частей.
- Итоги урока.
— С какой теоремой вы сегодня познакомились?
— На сколько частей вы теперь можете разделить данный отрезок?
Собрать из кусочков Теорему Фалеса.
- Домашнее задание.
Решить задачу № 391
Выучить доказательство теоремы Фалеса
(см. запись в тетради или задачи № 384, 385)
Выполнить практическую работу:
Разделить отрезок на 11 равных частей.
Геометрия 8 Мерзляк Контрольная 3 с ответами (2 варианта)
Администратор
Контрольная работа № 3 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема: Теорема Фалеса. Подобие треугольников. Дидактические материалы. Цитаты из пособия использованы в учебных целях. Геометрия 8 Мерзляк Контрольная 3. Ответы адресованы родителям.
Геометрия 8 Мерзляк Контрольная 3. Ответы адресованы родителям.
Контрольная работа № 3 по геометрии
8 класс УМК Мерзляк и др.
КР-3. Вариант 1 (транскрипт заданий)
- На рисунке 124 АВ || CD, МА = 12 см, АС = 4 см, BD = б см. Найдите отрезок МВ.
- Треугольники АВС и А1В1С1 подобны, причём сторонам АВ и ВС соответствуют стороны А1В1 и В1С1. Найдите неизвестные стороны этих треугольников, если АВ = 8 см, ВС = 10 см, А1В1 = 4 см, А1С1 = 6 см.
- Отрезок АК — биссектриса треугольника АВС, АВ = 12 см, ВК = 8 см, СК = 18 см. Найдите сторону АС.
- На стороне ВС треугольника АВС отметили точку М так, что ВМ : МС = 2 : 9. Через точку М провели прямую, которая параллельна стороне АС треугольника и пересекает сторону АВ в точке К. Найдите сторону АС, если МК = 18 см.
- В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, ВС : AD = 3 : 5, BD = 24 см.
 Найдите отрезки ВО и OD.
Найдите отрезки ВО и OD. - Через точку М, находящуюся на расстоянии 15 см от центра окружности радиусом 17 см, проведена хорда, которая делится точкой М на отрезки, длины которых относятся как 1 : 4. Найдите длину этой хорды.
КР-3. Вариант 2 (транскрипт заданий)
- На рисунке 125 MN || КР, NP = 20 см, РО = 8 см, МК = 15 см. Найдите отрезок КО.
- Треугольники АВС и А1В1С1 подобны, причём сторонам АВ и ВС соответствуют стороны А1В1 и В1С1 . Найдите неизвестные стороны этих треугольников, если ВС = 5 см, АВ = б см, В1С1 = 15 см, А1С1 = 21 см.
- Отрезок CD — биссектриса треугольника АВС, АС -= 12 см, ВС = 18 см, AD = 10 см. Найдите отрезок BD.
- На стороне АВ треугольника АВС отметили точку Е так, что АЕ : BE = 3 : 4. Через точку Е провели прямую, которая параллельна стороне АС треугольника и пересекает сторону ВС в точке F.
 Найдите отрезок ЕF, если АС = 28 см.
Найдите отрезок ЕF, если АС = 28 см. - В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, ВО : OD = 2:3, АС = 25 см. Найдите отрезки АО и ОС.
- Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см. Найдите расстояние от точки Р до центра окружности, если её радиус равен 6 см.
ОТВЕТЫ на контрольную работу
ОТВЕТЫ НА ВАРИАНТ 1.
№ 1. МВ = 18 см.
№ 2. АС = 12 см; В1С1 = 5 см.
№ 3. АС = 27 см.
№ 4. АС = 22 см.
№ 5. ВО = 9 см; OD = 15 см.
№ 6. АВ = 20 см.
ОТВЕТЫ НА ВАРИАНТ 2.
№ 1. КО = 6 см.
№ 3. BD = 15 см.
№ 4. EF = 16 см
№ 5. СО = 10 см; АО = 15 см.
№ 6. ОР = 4 см.
Вы смотрели: Контрольная работа № 3 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Теорема Фалеса. Подобие треугольников. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др. / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 3 + ответы.
Вернуться к списку контрольных работ по геометрии 8 класс (Мерзляк)
ОтветыТеорема Фалеса — Geeksforgeeks
Напишите статью
Глава 1: Реальные числа
Глава 2: Полиномии
Глава 3: Пара линейных уравнений в двух переменных
Глава 4: квадратичные уравнения
Глава 5: АРИФТМЕТИЧЕСКИЕ ПРОГРАММЫ.
Глава 7: Координатная геометрия
Глава 8: Введение в тригонометрию
Глава 9: Некоторые приложения тригонометрии
Глава 10: Окружности
Глава 11: Построения
Глава 12: Площади, относящиеся к окружностям
Глава 13: Площади и объемы поверхности
Глава 14: Статистика
Глава 15: Вероятность
Решения NCERT Глава 1: Реальные числа
4 9 : Многочлен Решения NCERT Глава 3. Пара линейных уравнений с двумя переменными
Пара линейных уравнений с двумя переменными
Решения NCERT Глава 4. Квадратные уравнения
Решения NCERT Глава 5. Арифметические прогрессии
Решения NCERT Глава 6: Треугольники
Решения NCERT Глава 7: Геометрия координат
Решения NCERT Глава 8: Введение в тригонометрию
Решения NCERT Глава 9: Некоторые приложения тригонометрии Глава 11: Конструкции
Решения NCERT Глава 12: Области, относящиеся к кругам
NCERT Глава 13: Площади и объемы поверхности
NCERT Глава 15: Вероятность
Решения RD Sharma Глава 1: Вещественные числа
Решения RD Sharma Глава 2: Многочлены
Решения RD Sharma Глава 3: Пара линейных уравнений с двумя переменными
Решения RD Sharma Глава 4: Треугольники
RD Sharma Solutions Глава 5 : Тригонометрические отношения
Решения RD Sharma Глава 6: Тригонометрические тождества
RD Solutions Sharma Глава 7: Статистика
RD Solutions Sharma Глава 8: Квадратные уравнения
https://www. geeksforgeeks.org/class-10-rd-sharma-solutions-chapter-8-quadratic-equations-exercise-8-7-set-2/
geeksforgeeks.org/class-10-rd-sharma-solutions-chapter-8-quadratic-equations-exercise-8-7-set-2/
RD Sharma Solutions Глава 10: Круги
Решения RD Sharma Глава 11: Построения
Решения RD Sharma Глава 12: Некоторые приложения тригонометрии
Решения RD Sharma Глава 13: Вероятность
Решения RD Sharma Глава 14: Координатная геометрия
Решения RD Sharma, относящиеся к Круги
RD Sharma Solutions Глава 16: Площади поверхности и объемы
Улучшить статью
Сохранить статью
- Последнее обновление: 19 янв, 2021
Улучшить статью
Сохранить статью
Утверждение теоремы: Теорема Фалеса или основная теорема пропорциональности утверждает, что если провести прямую, параллельную одной стороне треугольника, пересекающую две другие стороны в различных точках, то две другие стороны делятся в том же отношении.
Доказательство основной теоремы о пропорциональностиПредположим, что у нас есть треугольник ABC, если мы проведем прямую LM, параллельную стороне BC, тогда теорема утверждает, что B к M на линии AC и соедините вершину C на линии AB.
Затем опустите перпендикуляр MX на линию AB и перпендикуляр LY на линию AC. На приведенной ниже диаграмме показана конструкция того же самого.
Поскольку площадь треугольника =
Площадь ALM=
Площадь LBM=
Площадь ALM=
Площадь LMC=
Отношение площадей ALM и LBM:
—(1) :
—-(2)
Согласно свойству треугольников, треугольники на одном основании и между одинаковыми параллельными прямыми имеют равные площади.
Следовательно, LBM и LMC имеют равные площади.—-(3)
Из уравнений (1), (2) и (3) можно сделать вывод:
Таким образом, основная теорема о пропорциональности доказана.
Решенные примеры по основной теореме пропорциональностиПример 1. В ∆ABC стороны AB и AC пересекаются прямой в точках D и E соответственно, параллельной стороне BC. Докажите, что AD/AB = AE/AC.
Решение:
Дано: DE || ДО Н.
Э. Итак, AD/DB = AE/EC
или Поменяв местами отношения как => DB/AD = EC/AE
Теперь добавьте 1 с обеих сторон => (дБ/AD) + 1 = (EC/AE) + 1
(DB + AD)/AD = (EC + AE)/AE
AB/AD = AC / AE
Если еще раз поменять местами отношения, то получим => AD/AB = AE/AC
Следовательно, доказано.
Пример 2. В треугольнике ABC, где DE — прямая, проведенная из середины треугольника AB и заканчивающаяся серединой треугольника AC в точке E. AD/DB = AE/EC и ∠ADE = ∠ACB. Затем докажите, что треугольник ABC равнобедренный.
Решение:
Дано: AD/DB = AE/EC
По обращению основной теоремы о пропорциональности получаем => DE || BC
Согласно вопросу => ∠ADE = ∠ACB
Следовательно, ∠ABC = ∠ACB
Сторона, противоположная равным углам, также равна AB = AC
Следовательно, треугольник ABC равнобедренный.
Статьи по теме
Что нового
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта.
Основная теорема о пропорциональности Класс 10 Math Notes
Теорема 1:
Если провести прямую, параллельную одной стороне треугольника, чтобы пересечь две другие стороны в разных точках, то две другие стороны делятся в том же отношении.
Дано: треугольник ABC, в котором прямая, параллельная стороне BC, пересекает две другие стороны AB и AC в точках D и E соответственно.
Доказать:
Конструкция: Соедините BE и CD и начертите DM ⊥ AC и EN ⊥ AB.
Доказательство: площадь Δ ADE
(Взяв AD за основу)
Итак, [Площадь Δ ADE обозначается как ar (ADE)].
Аналогично,
[Δ BDE и DEC находятся на одном основании DE и между одними и теми же параллелями BC и DE.]
Следовательно, из (i), (ii) и (iii) имеем:
.
Следствие: Из приведенного выше уравнения мы имеем
.
Прибавляя 1 к обеим сторонам, получаем
.
Теорема 2:
(Обратное из теоремы BPT) Если прямая делит любые две стороны треугольника в одинаковом отношении, докажите, что она параллельна третьей стороне.
Дано: В ΔABC DE — прямая такая, что .
Доказать: DE || ДО Н.Э.
Конструкция: Если DE не параллелен BC, нарисуйте DF, пересекающий AC в точке F.
Доказательство. Пусть в ∆ABC DF || БК
[∴ Линия, проведенная параллельно одной стороне Δ, делит две другие стороны в том же отношении.]
Но . …(ii) [дано]
Из (i) и (ii) мы получаем
.
⇒ ФК = ЭК.
Возможно только при совпадении E и F
Следовательно, ДЭ || ДО Н.Э.
НЕКОТОРЫЕ ВАЖНЫЕ РЕЗУЛЬТАТЫ И ТЕОРЕМЫ:
(i) Внутренняя биссектриса угла треугольника делит противолежащую сторону внутри в отношении сторон, содержащих этот угол.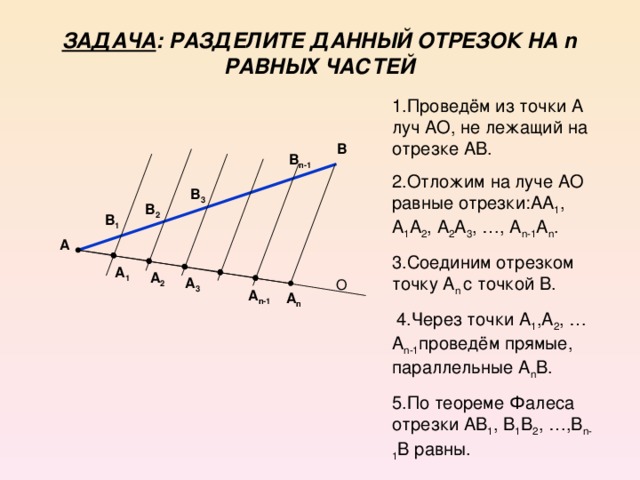
(ii) В треугольнике ABC, если D — точка на BC такая, что D делит BC в отношении AB : AC, то AD — биссектриса ∠A.
(iii) Внешняя биссектриса угла треугольника делит противоположные стороны внешне в отношении сторон, содержащих этот угол.
(iv) Линия, проведенная из середины одной стороны треугольника параллельно другой стороне, делит третью сторону пополам.
(v) Прямая, соединяющая середины двух сторон треугольника, параллельна третьей стороне.
(vi) Диагонали трапеции пропорционально делят друг друга.
(vii) Если диагонали четырехугольника делят друг друга пропорционально, то это трапеция.
(viii) Любая линия, параллельная параллельным сторонам трапеции, пропорционально делит непараллельные стороны.
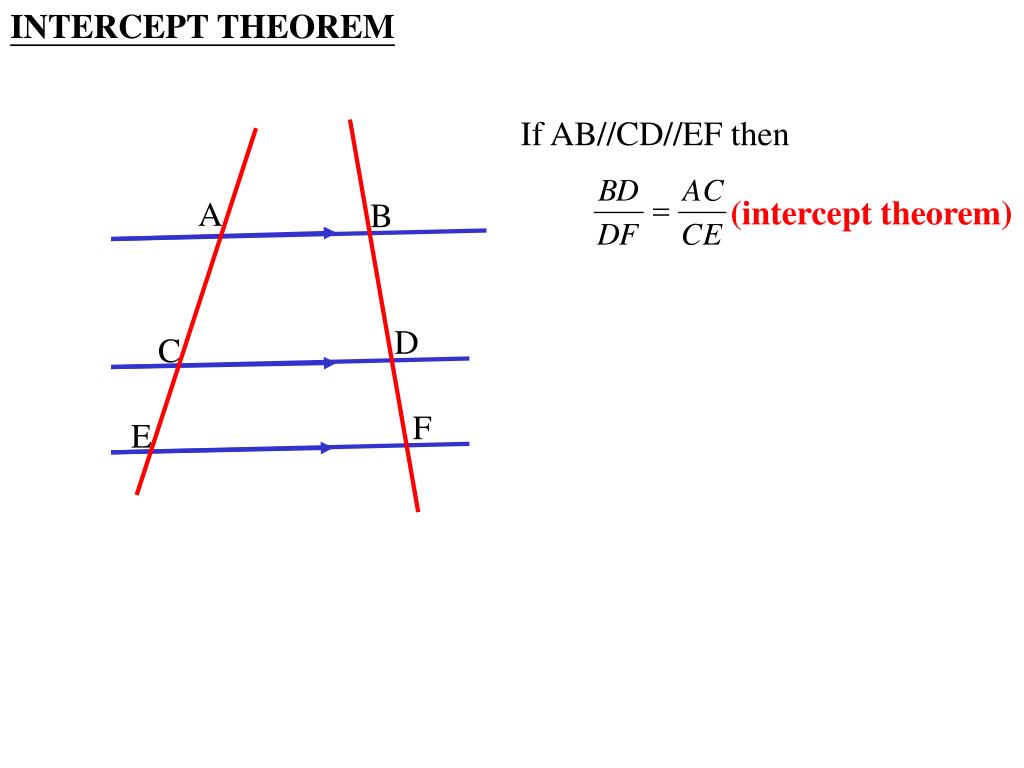
(ix) Если три или более параллельных прямых пересекаются двумя секущими, то пересечения ими на секущей пропорциональны.
Если каким-либо учащимся необходимо пройти онлайн-тест, чтобы проверить свои концепции или понимание, они могут посетить вопрос по базовой теории пропорциональности .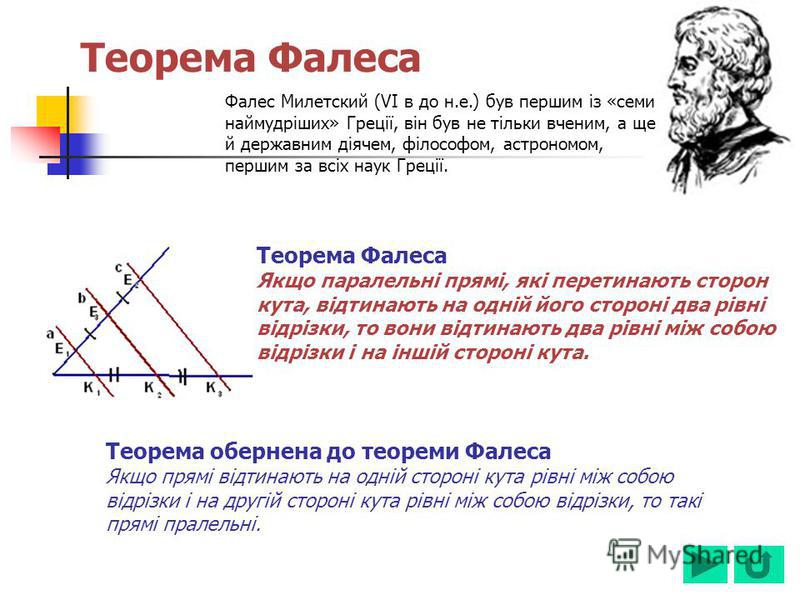
Вопрос 1. В ΔABC точки D и E на сторонах AB и AC соответственно такие, что DE || ДО Н.Э. Если AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 и CE = 5x – 3, найдите значение x.
Решение: В ΔABC у нас есть
DE||БК.
∴ . [По основной теореме пропорциональности]
⇒ 20x 2 – 15x – 12x + 9 = 24x 2 – 21x – 8x + 7
⇒ 20x 2 – 27x + 9 = 24x 2 – 29x + 7
⇒ 4×2 – 2x – 2 = 0
⇒ 2х2 – х – 1 = 0
⇒ (2х + 1) (х – 1) = 0
⇒ х = 1 или х = –1/2
Итак, искомое значение x равно 1.
[x = — 1/2 пренебрегается, так как длина не может быть отрицательной].
Вопрос 2. D и E — точки на сторонах AB и AC ΔABC соответственно, такие что AB = 12 см, AD = 8 см, AE = 12 см и AC = 18 см, покажите, что DE || ДО Н.Э.
Решение: У нас есть,
AB = 12 см, AC = 18 м, AD = 8 см и AE = 12 см.
∴ ВД = АВ — АД = (12 – 8) см = 4 см.
CE = AC – AE = (18 12) см = 6 см.
.
Таким образом, DE делит стороны AB и AC треугольника ΔABC в одинаковом отношении. Следовательно, по обратной теореме о пропорциональности имеем DE||BC.
Вопрос 3. В трапеции ABCD AB||DC и DC = 2AB. EF, проведенный параллельно AB, пересекает AD в F и BC в E так, что. Диагональ DB пересекает EF в точке G. Докажите, что 7FE = 10AB.
Решение: В ΔDFG и ΔDAB,
∠1 = ∠2 [Соответствующее ∠s ∴ AB || ФГ]
∠FDG = ∠ADB [Общий]
∴ ΔDFG ~ ΔDAB [По правилу подобия АА]
Из (i) и (ii) мы получаем
FG/AB = 4/7 т.е. FG = 4/7 AB ……(iii)
В ΔBEG и ΔBCD имеем
∠BEG = ∠BCD [Соответствующий угол ∴EG||CD]
∠GBE = ∠DBC [Общий]
∴ ΔBEG ~ ΔBCD [По правилу подобия АА]
Значит доказано.
Вопрос 4. В ΔABC, если AD — биссектриса ∠A, докажите, что .
В ΔABC, если AD — биссектриса ∠A, докажите, что .
Решение: В ΔABC AD является биссектрисой ∠A.
∴ AB/AC = BD/DC….(i) [По теореме о внутренней биссектрисе]
Из розыгрыша A AL⊥BC
.
[Из (i)] Следовательно Доказано.
Вопрос 5. ∠BAC = 90o, AD — его биссектриса. ЕСЛИ DE⊥ AC, докажите, что DE × (AB + AB) = AB × AC.
Решение: Дано, что AD является биссектрисой ∠A треугольника ΔABC.
В CDE и CBA Δ у нас есть
∠DCE = ∠BCA [Общий]
∠DEC = ∠BAC. [Каждый равен 90o]
Значит по АА-критерию подобия
Δ CDE ~ Δ CBA
⇒ DE × (AB + AC) = AB × AC.
Вопрос 6. На данном рисунке PA, QB и RC перпендикулярны AC. Докажи это.
Решение: В ΔPAC у нас есть BQ||AP
В ΔACR у нас есть BQ||CR
Отсюда доказано
Вопрос 7.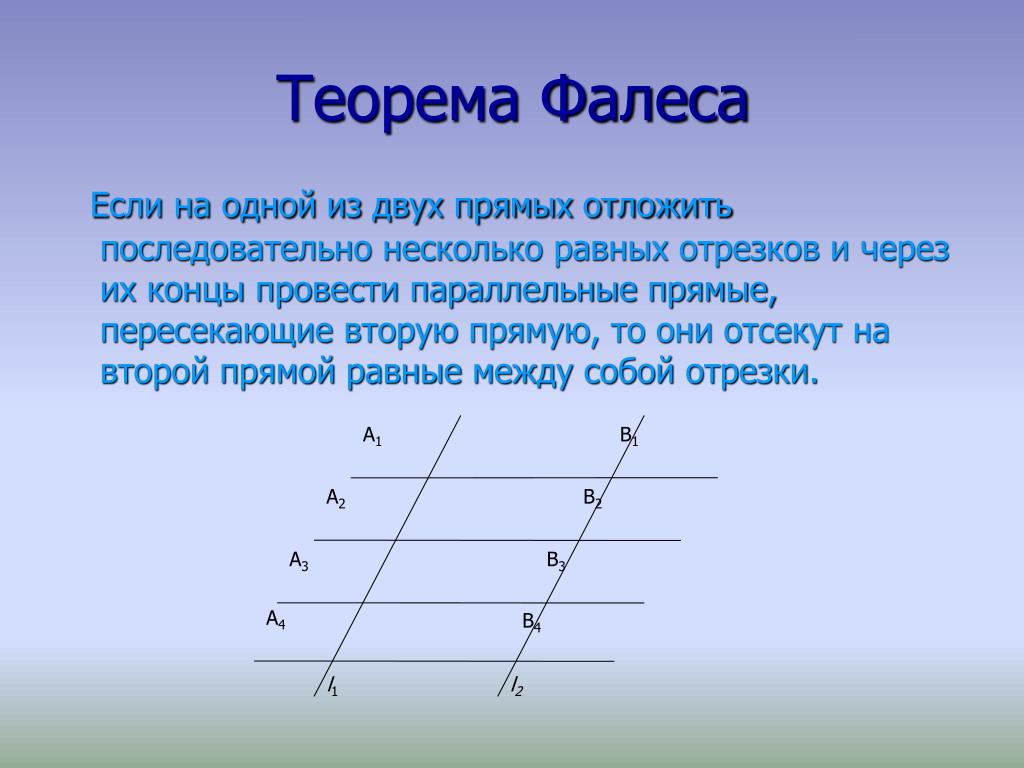 На данном рисунке AB||CD. Найдите значение х.
На данном рисунке AB||CD. Найдите значение х.
Решение: Так как диагонали трапеции делят друг друга пропорционально.
∴
⇒
⇒ 12х – 76 = х 2 – 4х – 3х + 12
⇒ х 2 – 19х + 88 = 0
⇒ х 2 – 11х – 8х + 88 = 0
⇒ (х – 8) (х – 11) = 0
⇒ х = 8 или х = 11.
КРИТЕРИИ ПОДОБИЯ ДВУХ ТРЕУГОЛЬНИКОВ
Два треугольника называются подобными, если (i) их соответствующие углы равны и (ii) их соответствующие стороны находятся в одном и том же отношении (или пропорциональны).
Таким образом, два треугольника ABC и A’B’C’ подобны, если
(и) и
(ii) .
В этом разделе мы будем использовать теоремы, обсуждавшиеся в предыдущих разделах, чтобы вывести некоторые критерии подобных треугольников, которые, в свою очередь, подразумевают, что любое из двух вышеупомянутых условий может быть использовано для определения подобия двух треугольников.



 Найдите отрезки ВО и OD.
Найдите отрезки ВО и OD. Найдите отрезок ЕF, если АС = 28 см.
Найдите отрезок ЕF, если АС = 28 см. Затем опустите перпендикуляр MX на линию AB и перпендикуляр LY на линию AC. На приведенной ниже диаграмме показана конструкция того же самого.
Затем опустите перпендикуляр MX на линию AB и перпендикуляр LY на линию AC. На приведенной ниже диаграмме показана конструкция того же самого.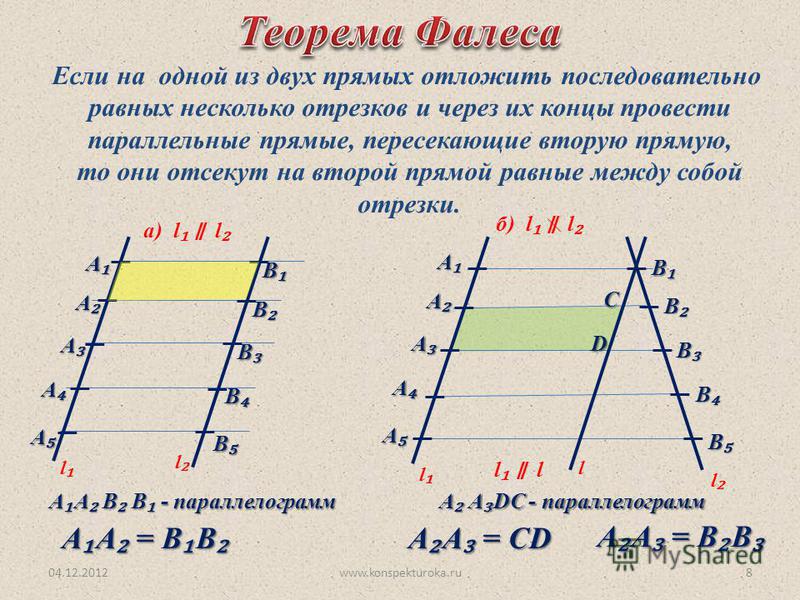 Э. Итак, AD/DB = AE/EC
Э. Итак, AD/DB = AE/EC