Теорема косинусов. Следствия из теоремы косинусов
- Кудрявцев Сергей Владимирович, учитель математики
Разделы: Математика
Цель урока:
- Повторить ранее изученный теоретический материал, изучить теорему косинусов и её следствия, учить делать теоретические обобщения.
- Развивать логику мышления при решении специально подобранных задач.
- Воспитывать потребность в доказательстве высказанной гипотезы.
Тип урока: урок ознакомления с новым материалом.
Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска.
I. Сообщение темы, цели и задач урока. Мотивация учебной деятельности.II. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний
Мотивация учебной деятельности.II. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний(Фронтальная работа с классом)
|
|
III.
Изучение нового материала.Учащимся предлагается задача на готовом чертеже. Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.
Первый способ решения задачи. (Устно)
Дано: ABC, AC = b, AB = c. A __________________ Найти: BC = a = ? |
Проведём CH – высоту. 1) Прямоугольный ACH: AH = bcosA, CH = или CH = bsinA BH = AB – AH. CB2 = a2 = CH2 + BH2 a = . |
Рис. 4 |
Второй способ решения задачи. Координатный метод.
| 1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату.
Решение записывают все учащиеся. |
|
2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). 3. Найдём квадрат стороны BC:
|
Рис. 5 |
Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними.
Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните.
Если С = 90°, то cosC = 0 и 2abcosC = 0, тогда c2 = a2 + b
Вывод: Теорема Пифагора является частным случаем теоремы косинусов.
Рассмотрим следствия из теоремы косинусов.
| 1 следствие. | ||
| Дано:
ABC AC = b, AB = c, AH = bc __________________ Найти: a |
Решение:
Возможны 2 случая: а) A – острый, то cosA > 0, б) A – тупой, то cosA < 0, а) Если A – острый, тогда по теореме косинусов a2 = b2 + c2 – 2bccosA |
Рис. 6 |
В прямоугольном ACH: bc = bcosA. Так как A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой. Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания. (т.к. cosA < 0, то a2 = b2 + c2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой. |
||
| 2 следствие. | ||
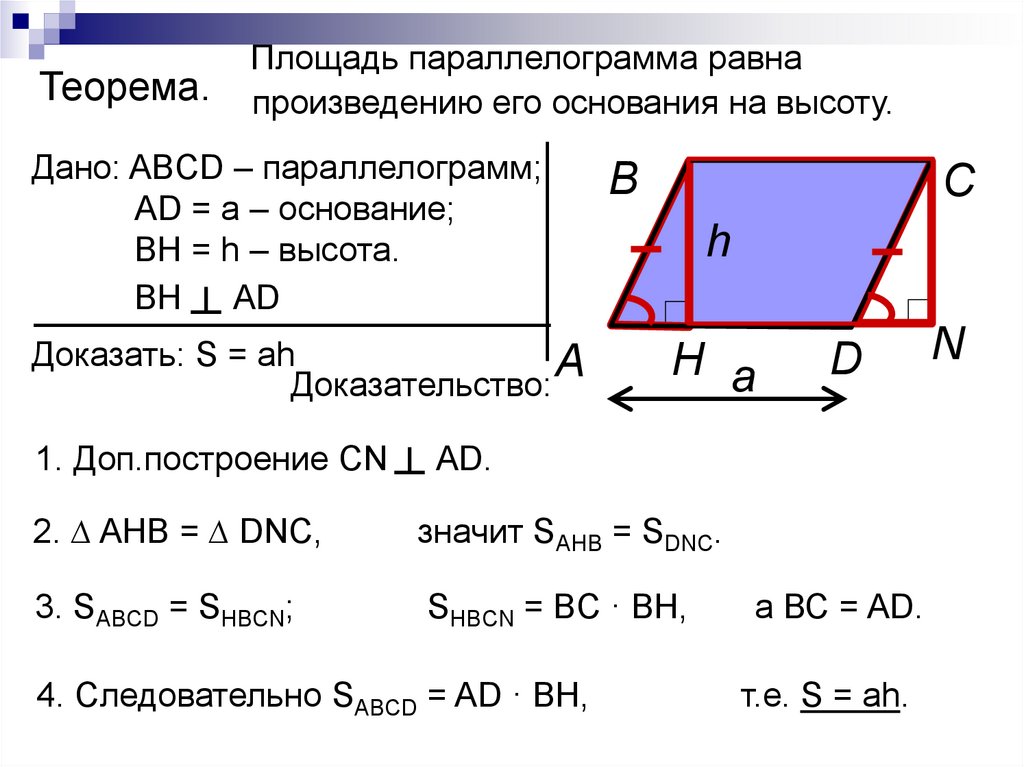
Дано: ABCD – параллелограмм, AB = CD =a, BC = AD = b. __________________ Найти: d12 + d22 . |
Решение: ABC: d12 = a2 + b2 – 2abcosB. ABD: d22 = a2 + b2 – 2abcosA = a2 + b2 – 2abcos(180° — B) = a2 + b2 + 2abcosB. d12 + d22 = a2 + b2 – 2abcosB + a2 + b2 + 2abcosB = a2 + b2 + a2 + b2. d12 + d22 = 2 a2 + 2 b2. |
Рис. 7 |
Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. |
||
| 3 следствие. | ||
Дано: ABC, AB = c, AC = b, BC = a. __________________ Найти: ma |
Решение: Достроим ABC до параллелограмма ABA1C. AA12 + BC2 = 2b2 + 2c2 . BC = a, 2m (2ma)2 + a2 = 2b2 + 2c2 4ma2 = 2(b2 + c2) – a2 ma2 = ma = mb = mc = |
Рис. 8 |
Вывод: В любом треугольнике со сторонами a, b и c длины медиан ma, mb, mc вычисляются по формулам: ma = , mb = , mc = . |
||
IV. Первичное осмысление и закрепление связей и отношений в объектах изучения
.Задача: В треугольнике две стороны равны 20 см и 21 см, а синус угла между ними равен 0,6. Найти третью сторону. Сколько решений имеет задача?
Найти третью сторону. Сколько решений имеет задача?
Дано: sin = 0,6 , AB = 20 см, AC = 21 см. __________________ Найти: BC. |
Решение: sin = 0,6 может быть острым или тупым. |
|
1 случай: – острый BC2 = AB2 + AC2 – 2ABACcos. Так как – острый, то cos>0. Тогда cos = = = = 0.8 BC = = = 13(см). |
Рис. 9 |
|
2 случай: – тупой. BC2 = AB2 + AC2 – 2ABACcos Так как – тупой, то cos<0 cos = -= — = -0. BC = = (см). Ответ: 1) BC = 13 см. 2) BC = см. |
Рис. 10 |
п. 98 №1025(б, в, г).
VI. Подведение итогов урока.
Теорема Косинусов — формула, доказательство, следствия
Главная » геометрия
Обновлено
Чтобы найти строну или угол треугольника применяют Теорему Косинусов.
Эта теорема обобщает теорему Пифагора. Доказать Теорему
Косинусов достаточно просто через треугольник, который
разделяют высотой на два прямоугольных треугольника.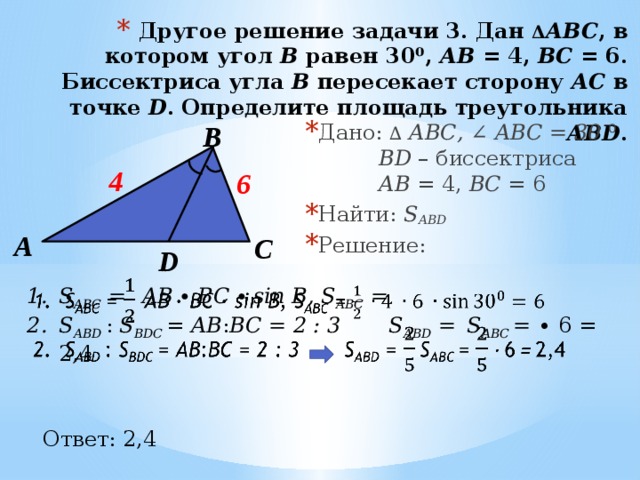
Мы рассмотрим доказательство, формулировку,
следствия из Теоремы Косинусов.
Наряду с одной из известных теорем геометрии — теоремой Пифагора,
существует теорема косинусов. Теорема косинусов похожа по теорему
Пифагора, но отличается. Теорему косинусов, можно применить к абсолютно
любым треугольникам. А теорема Пифагора применяется исключительно
для прямоугольных треугольников.
Теорема косинусов — это теорема геометрии, обобщающая
теорему Пифагора, применяющаяся при нахождении углов
и сторон в любых треугольниках.
Содержание
- Формулировка теоремы косинусов
- Доказательство теоремы косинусов
- Следствия из теоремы косинусов
- Значение теоремы косинусов
Формулировка теоремы косинусов
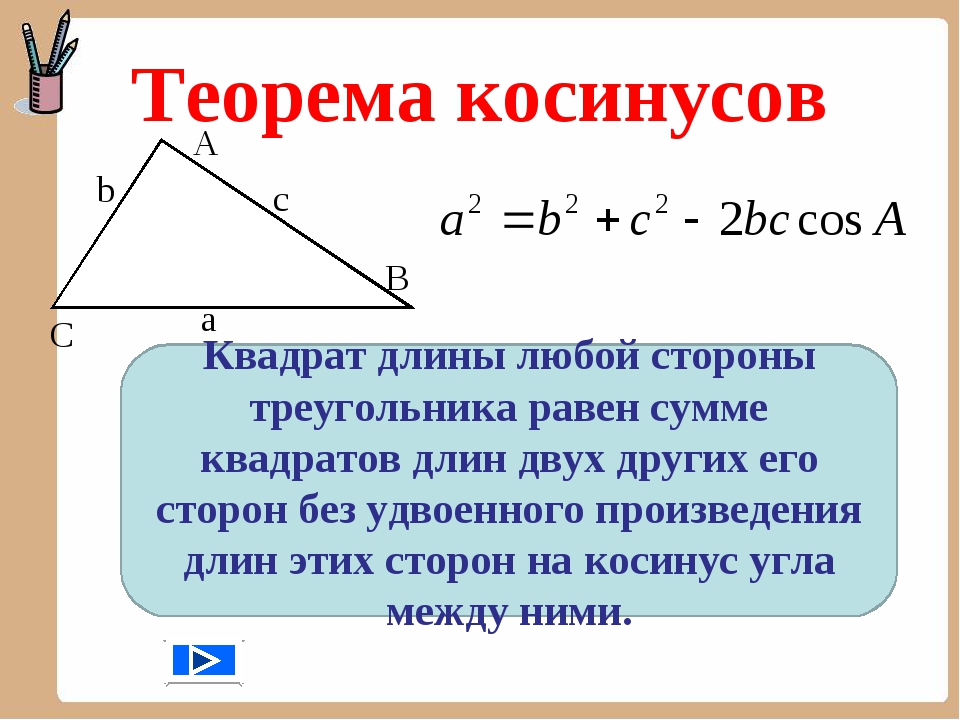
Формулировка у теоремы косинусов такая: в треугольнике квадрат любой из сторон
равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними. 2 — 2ab * cos ∠C \);
2 — 2ab * cos ∠C \);
следовательно теорема косинусов преобразуется в теорему Пифагора.
любого из углов треугольника.
Если b2 + c2 — a2 = 0, ∠A будет прямым.
Если b2 + c2 — a2 < 0, ∠A будет тупым.
Значение теоремы косинусов
Где применяется теорема косинусов?
Теорема косинусов применяется в тригонометрии, в частности
при нахождение сторон и углов в любых треугольниках. Например, зная
формулировку теоремы косинусов, косинус одно из угла треугольника,
и две стороны можно найти неизвестную сторону треугольника.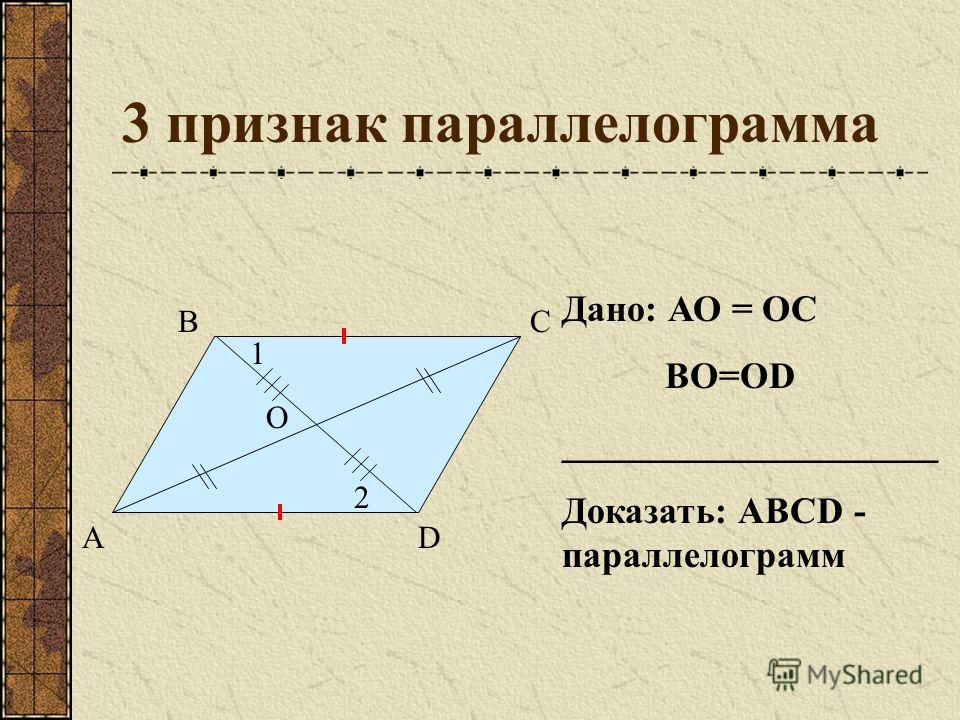
Виды теорем косинусов.
В зависимости от свойств треугольника, длины его сторон, градусной меры
его углов — теорема косинусов немного видоизменяется. Например, в
прямоугольных треугольниках теорема косинусов преобразуется в теорему Пифагора.
косоугольных треугольников
косоугольных треугольниковНаклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» мог бы с таким же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников. Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.
Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.
Решение косоугольных треугольников
Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.Закон косинусов
Это просто сформулированное уравнение: С.Это похоже на теорему Пифагора, за исключением последнего члена, и если C — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), так что закон косинусов на самом деле является обобщением закона косинусов. Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, поскольку вы можете переставлять буквы по своему усмотрению. The other two versions are then a 2 = b 2 + c 2 2 bc cos A, and b 2 = c 2 + a 2 2 ca cos B.
The other two versions are then a 2 = b 2 + c 2 2 bc cos A, and b 2 = c 2 + a 2 2 ca cos B.
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если вы знаете один угол и две смежные стороны, то вы можете определить противоположную сторону. Например, если угол C = 60°, сторона a = 5, а сторона b = 8, то по закону косинусов c 2 = 25 + 64 80 cos 60°. Поскольку косинус угла 60° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7.
Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a = 5, b = 6 и c = 7, то закон косинусов говорит: , с помощью калькулятора, C = 1,3734 радиана = 78,69°.
Примечание: Если треугольник тупоугольный, то cos C отрицателен. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда по закону косинусов 100 = 25 + 36 60 cos C, so cos C = — 49/60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите C = 2,2556 радиана = 129,237°.
Закон синусов
Закон синусов также представляет собой просто сформулированное уравнение| син А а | = | син Б б | = | син С с |
Обратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них. Например, если угол A = 30°, угол B = 45°, а сторона a = 16, то по закону синусов (sin 30°)/16 = (sin 45°)/ b. Решение для b дает b = 16(sin 45°)/(sin 30°) = 22,6274.
Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы почти можете определить угол, противолежащий другой из них. Например, если сторона a = 25, сторона b = 15, а угол A = 40°, то по закону синусов (sin 40°)/25 = (sin В )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0,38567. Теперь арксинус 0,38567 = 22,686°. Предупреждение: у вас может не быть правильного ответа. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
557. В треугольнике ABC, a = 700 футов, B = 73° 48′, и C = 37° 21′. Если M является средней точкой BC найти длины AM, и углы BAM и MAC.
561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B — точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол A = 73° 40′, а C = 52° 38′. Найти АБ.
Угол A = 73° 40′, а C = 52° 38′. Найти АБ.
570. P и Q две недоступные точки. Чтобы найти расстояние между ними, берется точка A в произведенном QP и измеряется линия AB длиной 1200 футов, образующая угол PAB = 26° 35′. Угол ABP = 48° 12′ и ABQ = 106° 42′. Как долго PQ ?
579. Стороны параллелограмма равны AB = 209.16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, угол ABC = 110° 48′ 12″, а BAC = 27° 19′ 36″. Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.
590. Стороны четырехугольника по порядку равны 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
Найдите остальные три угла.
593. A и B — это две точки на противоположных сторонах водоема, и замеры должны производиться по линии AB в точках на одну четверть, половину и три четверти расстояния от A по B. На берегу линия AC измерена длина 1200 футов, а углы BAC = 63° 19′ и ACB = 78° 43′. Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, в соответствующих точках на АВ ?
608. На одной стороне линии потока PA = 586,3 фута, PB = 751,6 фута являются мерами, угол APB равен 167° 36′. Q — точка на противоположной стороне потока. Угол PAQ = 63° 18′ и PBQ = 49° 24′. Найдите ПК.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, откладывается линия AB длиной 763,4 фута так, что AB пересекает PQ внешне [то есть два отрезка линии AB и PQ не пересекаются]. Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Советы
553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C до AB. Это означает, что вы опускаете перпендикуляр из точки C на эту линию и определяете ее длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и строку BC , чтобы найти его.
557. Та же подсказка, что и для 553.
561. Окружности касаются друг друга, поэтому линия, проведенная из одного центра в другой, равна сумме радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
579. Вы знаете стороны треугольников ABC, и ADC, , поэтому можете определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другим включенным углом является его дополнение 180° 70° 12′ 38″. Пусть P будет точкой пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной. Используйте закон косинусов для двух треугольников с вершинами P и две вершины параллелограмма.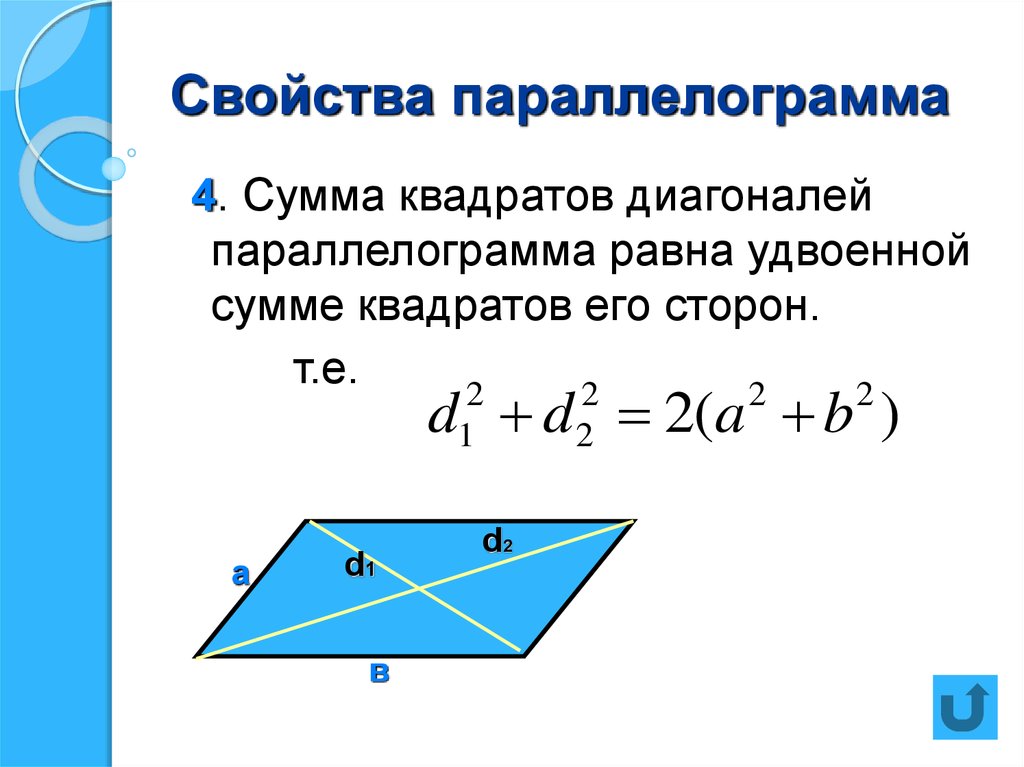
590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, и можете найти его углы.
593. Сначала определите расстояние AB по закону синусов. Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , чтобы можно было определить нужный угол по закону косинусов.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник AQB.
612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Затем используйте закон косинусов для треугольника ПАК.
Ответы
553. 345,43 фута.
557. 490,83 фута.
561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106° 18′ 46″, 73° 41′ 14″, 452,92.
580. 255,93, 372,11, 369,22.
586. 231,94, 328,93.
590,125° 6′ 12″, 70° 57′ 54″, 110° 42′ 42″.
593. 23° 27′, 47° 58, 66° 34′.
608. 854,6 фута.
612. 920,76 футов.
Оглавление. | Вернемся к тригонометрическим функциям. | К тригонометрическим тождествам.
© 1996, 1997.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс 01610
Электронная почта: [email protected]
Краткий триггерный курс Дэйва находится по адресу http://aleph0.clarku.edu/~djoyce/java/trig.
Формулы суммы и разности Птолемея
Формулы суммы и разности Птолемея Когда Птолемей создал свою таблицу хорд функций, обсуждавшуюся в разделе о вычислении тригонометрических функций, ему понадобились способы вычисления тригонометрических функций для сумм и разностей углов. Его основной триггерной функцией была хорда угла, в то время как мы используем синусы и косинусы. Преобразовав его формулы в синусы и косинусы, мы получим следующие четыре важных тождества.
Его основной триггерной функцией была хорда угла, в то время как мы используем синусы и косинусы. Преобразовав его формулы в синусы и косинусы, мы получим следующие четыре важных тождества.Вы можете использовать эти идентификаторы, не зная, почему они верны. Если вам интересно, почему, продолжайте читать, в противном случае перейдите к следующей странице.
Теорема Птолемея
Чтобы доказать свои формулы суммы и разности, Птолемей сначала доказал то, что мы сейчас называем теоремой Птолемея.
Мы не будем здесь доказывать теорему Птолемея. |
Формула суммы синусов
Мы будем следовать доказательству Птолемея, но немного изменим его, чтобы оно работало с современными синусами. Пусть O будет центром круга радиуса 1, а одна из прямых, AC , будет диаметром круга. Мы интерпретируем каждую из линий AC, BD, AB, CD, AD и BC в терминах синусов и косинусов углов. Мы уже знаем AC = 2.
Пусть α будет ∠ БАК . Напомним, что синус угла равен половине хорды удвоенного угла. Предложение Евклида III.20 гласит, что угол в центре круга в два раза больше угла на окружности, поэтому ∠ BOC равно 2 α . Таким образом, синус α составляет половину хорды ∠ BOC , так что это равно BC / 2, и поэтому BC = 2 sin α . Лет β быть &угол; канадских долларов . Это половина ∠ ХПК , так что sin β равно CD /2, а CD = 2 sin β . Тогда α + β равно ∠ BAD , поэтому BD = 2 sin ( α + β ). Нам еще предстоит интерпретировать AB и AD . Отрезок AB в два раза больше синуса ∠ АСВ . Треугольник ABC является прямоугольным по теореме Тале (предложение Евклида III.31: угол в полуокружности прямой). Следовательно, sin ∠ ACB cos α . Следовательно, AB = 2 cos α . Аналогично, AD = 2 cos β . Теперь мы можем написать теорему Птолемея через синусы и косинусы. Это говорит  После деления на 4 получаем формулу сложения синусов. |
Другие формулы сумм и разностей
Вы можете непосредственно показать, что формула суммы для косинусов и две формулы разности верны, приняв один из отрезков прямой в теореме Птолемея за диаметр круга, интерпретируя другие как хорды центральных углов, то есть удвоенные синусы углов на окружности и с помощью теоремы Таля для преобразования синусов в косинусы.Например, примем AD за диаметр, α за ∠ BAD и β должны быть ∠ CAD , то можно напрямую показать формулу разности для синусов.
В качестве альтернативы вы можете показать остальные три формулы, начиная с формулы суммы синусов, которую мы уже доказали. Если вы замените β на − β , вы получите формулу разности. Если вы замените определенные углы их дополнениями, то вы можете получить формулы суммы и разности для косинусов.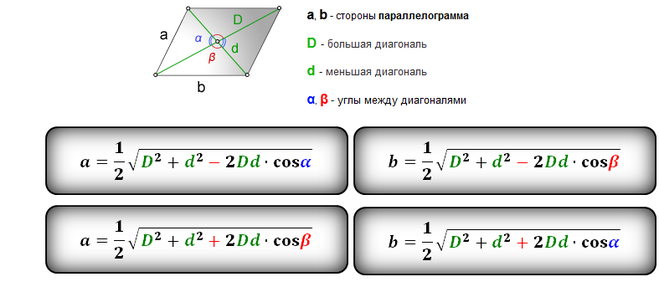

 Что вы можете сказать об углах 1 и 2. Односторонние, 1 +2 = 180° . Если 2 = , тогда 1 = 180° —
Что вы можете сказать об углах 1 и 2. Односторонние, 1 +2 = 180° . Если 2 = , тогда 1 = 180° —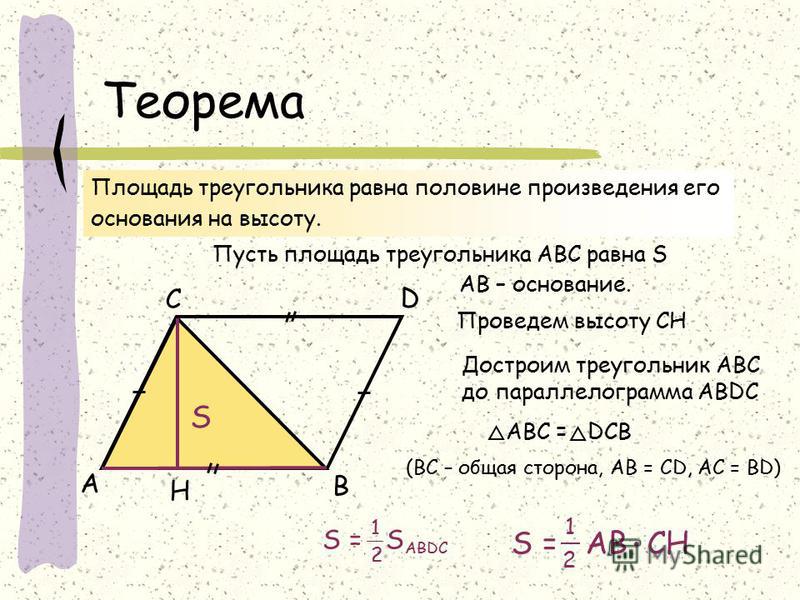



 Доказательство зависит от свойств подобных треугольников и теоремы Пифагора. Вместо этого мы воспользуемся теоремой Птолемея для вывода формул суммы и разности.
Доказательство зависит от свойств подобных треугольников и теоремы Пифагора. Вместо этого мы воспользуемся теоремой Птолемея для вывода формул суммы и разности.