1.12. Интегральная теорема Лапласа
Если вероятность появления
случайного события в каждом испытании
постоянна, то вероятность – того, что в
испытаниях событие наступит не менее и не более раз (от до раз включительно), приближённо равна:
, где – функция Лапласа,
а аргументы рассчитываются по формулам .
Как и в локальной теореме, количество испытаний должно быть достаточно большими вероятность не слишком мала, и на практике следует ориентироваться на выполнение того же неравенства , в противном случае приближение к точному результату (полученному по Бернулли) будет плохим.
Задача 77
Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) от 60 до 80 раз, б) не менее 65 раз
 Вероятность попадания в цель при каждом выстреле составляет
, следовательно, вероятность промаха: .
Вероятность попадания в цель при каждом выстреле составляет
, следовательно, вероятность промаха: .
Оценим эффективность применения интегральной теоремы Лапласа:
, значит, теорема Лапласа даст хорошее
приближение.
а) Найдём вероятность – того, что при 100 выстрелах мишень будет поражена от до раз. Используем интегральную теорему Лапласа:
, где – функция Лапласа.
Сначала вычислим значения аргументов:
Обращаю внимание, что произведение не
обязано извлекаться из-под корня нацело (как любят «подгонять» числа авторы задач) – без тени сомнения извлекаем корень
приближённо и округляем результат; я привык оставлять 4 знака после запятой.
А вот полученные значения обычно
округляют до 2 знаков – эта традиция идёт из таблицы значений функции (см. Приложение Таблицы), где аргументы
представлены именно в таком виде.
Таким образом:
Как вычислить значения функции ?
Ручные вычисления и микрокалькулятор здесь не помогут, поскольку этот интеграл не берётся. Но вот в Экселе соответствующий функционал есть
– используйте Пункт 5 Калькулятора.
Кроме того, ОБЯЗАТЕЛЬНО найдите значение в таблице!
И, учитывая нечётность функции Лапласа , получаем, распишу подробно:
– вероятность того, что при 100
выстрелах мишень будет поражена от 60 до 80 раз.
Результат чаще всего округляют до 4 знаков после запятой
б) Найдём вероятность того, что при 100 выстрелах мишень будет поражена не менее 65 раз. Это означает, что , а .
Вычислим значения аргументов:
Таким образом, по интегральной теореме Лапласа и таблице значений функции Лапласа (лучше использовать такую формулировку!), получаем:
– вероятность того, что при 100
выстрелах мишень будет поражена не менее 65 раз.
Примечание: начиная с , можно считать, что , или, если записать строже: .
Ответ: а) , б)
И ради исследовательского интереса я вычислил более точные значения с помощью формулы Бернулли («протянув» в Экселе формулу БИНОМРАСП):
– как видите, расхождение получилось существенным, это обусловлено небольшим значением . А ещё, надо признать, рассматриваемый метод устарел, ибо экселевские
расчёты отняли у меня буквально минуту. Но мы отнесёмся к этому с пониманием, таки Пьер-Симон маркиз де Сад Лаплас жил в 18-19 веках J
Следующая задача для самостоятельного решения:
Задача 78
В здании имеется 2500 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что вечером будет
включено:
а) половина ламп,
б) не менее 1250 и не более 1275 ламп,
в) не более 1000 ламп
Примерный образец чистового оформления решения в конце книги.
Следует отметить, что рассматриваемые задачи очень часто встречаются в «обезличенном» виде, примерно таком:
Производится некоторый опыт, в котором случайное событие может появиться с вероятностью 0,5. Опыт повторяется в неизменных условиях 2500 раз. Определить вероятность того, что в 2500 опытах событие произойдет от 1250 до 1275 раз.
1.13. Относительная частота события и статистическая вероятность
1.11. Локальная теорема Лапласа
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Интегральная теорема Муавра — Лапласа. Теория вероятностей
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Предположим, что производится
испытаний, в каждом из которых вероятность
появления события
постоянна и равна
.
Интегральная теорема Муавра — Лапласа
Если вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях от до раз, приближенно равна определенному интегралу:
где
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл
не выражается через элементарные функции. Таблицы для интеграла
можно найти на сайте по ссылке Функция Лапласа — таблица значений. В
таблице даны значения функции
для положительных значений
и для
; для
пользуются той же таблицей (функция
нечетна, то есть
).
В
таблице даны значения функции
для положительных значений
и для
; для
пользуются той же таблицей (функция
нечетна, то есть
).
В таблице приведены значения интеграла лишь до так как при можно принять . Функцию называют функцией Лапласа.
Для того, чтобы можно было пользоваться таблицей функции Лапласа, преобразуем формулу:
Интегральная формула Муавра — Лапласа
Таким образом, вероятность того, что событие появится в независимых испытаниях от до раз:
где
На основе интегральной теоремы Лапласа можно вывести формулу вероятности отклонения относительной частоты от постоянной вероятности, которая используется для решения достаточно большого круга задач.
Условие применимости интегральной формулы Муавра-Лапласа
Чем
больше
, тем точнее интегральная
формула Муавра-Лапласа.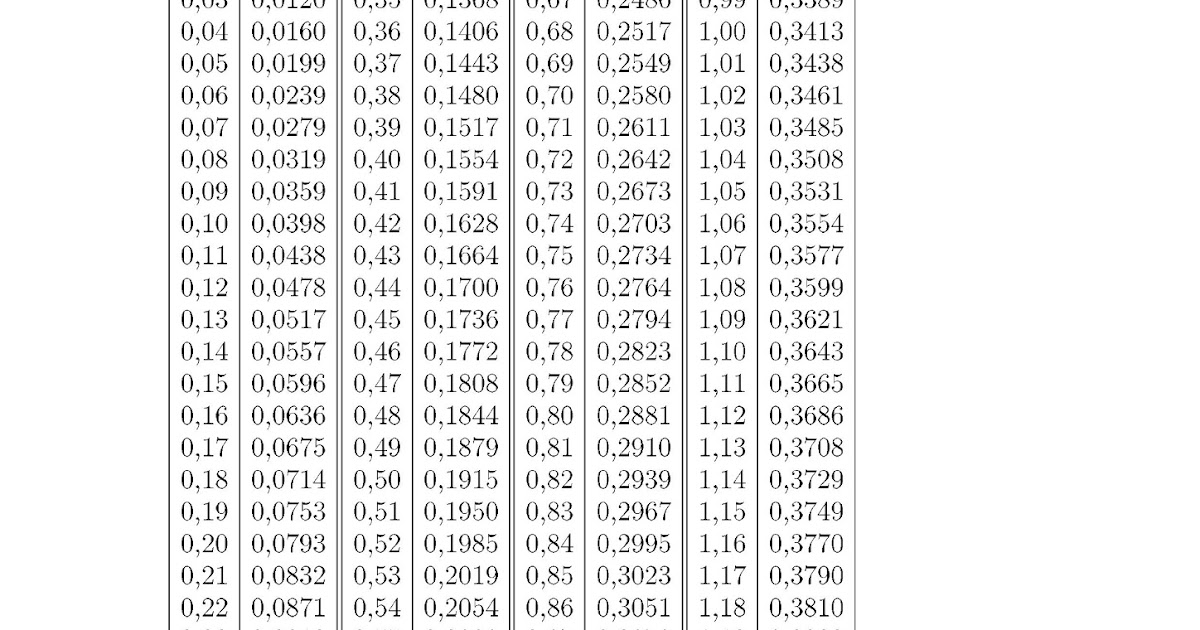 Приближенные значения вероятности, даваемые
интегральной формулой, на практике используются как точные при
порядка двух и более десятков, то есть при
условии
.
Приближенные значения вероятности, даваемые
интегральной формулой, на практике используются как точные при
порядка двух и более десятков, то есть при
условии
.
Смежные темы решебника:
- Формула Бернулли
- Локальная теорема Муавра-Лапласа
- Следствия интегральной теоремы Муавра-Лапласа
- Формула Пуассона
Примеры решения задач
Пример 1
При автоматической прессовке карболитовых болванок 2/3 общего числа из них не имеют зазубрин. Найдите вероятность того, что из 450 взятых наудачу болванок количество болванок без зазубрин заключено между 280 и 320.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Если количество независимых испытаний достаточно большое, то для упрощения вычислений применяют интегральную и локальную теоремы Лапласа, которые дают близкий к формуле Бернулли результат при большом количестве испытаний.
Воспользуемся интегральной теоремой Лапласа.
Вероятность того, что событие появится в независимых испытаниях от до раз:
В нашем случае
Искомая вероятность:
Ответ: p=0.9544
Пример 2
В жилом доме имеется 600 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет заключено между 280 и 320.
Решение
Воспользуемся интегральной теоремой Лапласа.
Вероятность того, что событие появится в независимых испытаниях от до раз:
где:
В нашем случае
По таблице функции Лапласа:
Искомая вероятность:
Ответ:
Пример 3
Производятся
испытания по схеме Бернулли с вероятностью успеха в одном испытании
.
Найти вероятность того, что в испытаниях число успехов будет не меньше и не больше .
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Воспользуемся интегральной теоремой Лапласа.
Вероятность того, что событие появится в независимых испытаниях от до раз:
По таблице функции Лапласа:
Искомая вероятность:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Игральная
кость бросается 12000 раз. Найти вероятность того, что число выпадений одного
очка будет от 1900 до 2150 раз?
Найти вероятность того, что число выпадений одного
очка будет от 1900 до 2150 раз?
Задача 2
Вероятность рождения мальчика примем равной 0,5. Найти вероятность того, что среди 200 новорожденных детей будет от 90 до 110 мальчиков.
Задача 3
100 пациентов принимают экспериментальный препарат, причем улучшение состояния в течение для отмечают 80%. Найдите вероятность того, что в течение дня улучшение почувствуют от 75 до 85 пациентов.
Задача 4
Вероятность выхода из строя за время одного конденсатора равна 0,2. Найдите вероятность того, что за время из 100 независимо работающих конденсаторов выйдут из строя от 14 до 26 конденсаторов.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 5
Вероятность реализации одной акции некоторой компании равна 0,8. Брокерская контора предлагает 100 акций этой компании. Какова вероятность того, что будет продано не менее 85 акций?
Задача 6
Вероятность, что безработный найдет работу, обратившись в службу занятости, равна 0,3. Чему равна вероятность того, что из 320, обратившихся за месяц, работу получат от 100 до 200?
Задача 7
Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из 800 посеянных семян взойдет не менее 700.
Задача 8
Всхожесть семян кукурузы 95%. На опытном участке посеяно 200 семян. Какова вероятность, что взойдет не менее 185? Сколько надо посадить чтобы взошло не менее 200 с вероятностью 97%?
Задача 9
Монету подбрасывают 100 раз. Найти вероятность того, что число выпавших гербов окажется меньше 42.
Задача 10
Было
посажено 500 деревьев. Найти вероятность того, что число прижившихся деревьев
больше 390, если вероятность того, что отдельное дерево приживется, равна 0,8.
Сколько деревьев надо посадить, чтобы 400 прижилось с вероятностью 95%?
Найти вероятность того, что число прижившихся деревьев
больше 390, если вероятность того, что отдельное дерево приживется, равна 0,8.
Сколько деревьев надо посадить, чтобы 400 прижилось с вероятностью 95%?
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 11
Найти вероятность того, что среди 10000 случайных цифр цифра 7 появится не более 968 раз.
Задача 12
На базе хранится 760 ед. продукции. Вероятность того, что она не испортится, равна 0.65. Найти вероятность того, что количество испорченных изделий будет меньше 282.
Задача 13
Производится
некоторый опыт, в котором случайное событие A может появиться с
вероятностью 0,6. Опыт повторяют в неизменных условиях 1000 раз.
Определить вероятность того, что в 1000 опытах событие произойдет не менее чем 580 раз.
Задача 14
Найти вероятность того, что в партии из 100 изделий число изделий высшего сорта заключено между 80 и 90, если вероятность того, что изделие высшего сорта, равна 0,8.
Задача 15
Вероятность того, что изделие предприятия имеет брак, равна p=0,02. Найти вероятность, что из 1000 изделий бракованных будет от 20 до 40 включительно.
Задача 16
Стоматологическая клиника распространяет рекламные листки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет находиться в границах от 35 до 45.
Задача 17
Вероятность
того, что деталь не проверялась в ОТК, равна 0,2. Найти вероятность того, что
среди 400 случайно отобранных деталей окажется от 70 до 100 деталей, не
проверенных в ОТК.
Задача 18
Применение вакцины от гриппа обещает защиту от болезни с вероятностью 0,9. Какова вероятность, что из 200 студентов института не заболеют гриппом от 170 до 190 человек?
Задача 19
На сборы приглашено 120 спортсменов. Вероятность для каждого спортсмена выполнить норматив 0,7. Определить вероятность того, что выполнят норматив не менее 80 спортсменов.
Задача 20
Каждый из 100 компьютеров в интернет-кафе занят клиентами в среднем в течение 80% рабочего времени. Какова вероятность, что в некоторый момент клиентами будет занято от 70 до 90 компьютеров.
Задача 21
Посетитель магазина совершает покупку с вероятностью 0,8. Какова вероятность, что из 400 посетителей сделают покупки от 300 до 350 человек?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
теория вероятности, примеры, таблица значений для вычисления определителей
Содержание:
-
Локальная и интегральная теоремы Муавра-Лапласа
- Локальная теорема Лапласа
- Интегральная предельная теорема Муавра-Лапласа
- Таблица значений для вычисления определителей
- Пример решения задачи
Содержание
-
Локальная и интегральная теоремы Муавра-Лапласа
- Локальная теорема Лапласа
- Интегральная предельная теорема Муавра-Лапласа
- Таблица значений для вычисления определителей
- Пример решения задачи
Локальная и интегральная теоремы Муавра-Лапласа
В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно. Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.
Упростить решение задачи или доказательство выражения можно с помощью локальной и интегральной теорем Лапласа. Данные закономерности позволяют получить результат испытаний, приближенный к итогам вычислений по формуле Бернулли, и характеризуются меньшими расчетами.
Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.
Локальная теорема Лапласа
В том случае, когда вероятность p возникновения явления A характеризуется постоянством, и \(p\ne 0\) и \(p\ne 1\), то вероятность \(P_n ( k )\) того, что событие A возникнет k раз в n экспериментах, равна приближенно (увеличивая n, получаем более точный результат испытаний и меньше погрешность) значению функции \(y=\frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \frac { 1 } { \sqrt { 2\pi } } \cdot e^ { — { x^2 } / 2 } =\frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \varphi ( x )\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).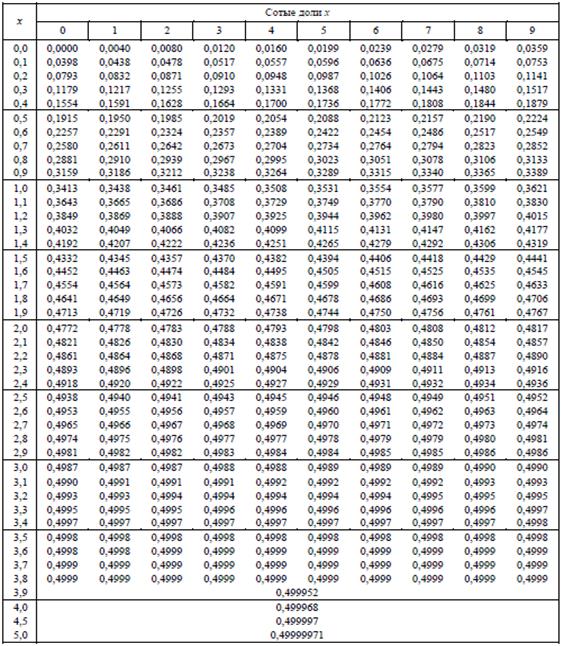 Если нет возможности написать самому, закажите тут.
Если нет возможности написать самому, закажите тут.
В данном случае\( x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Из выражения можно сделать вывод:
\(label { eq2 } P_n ( k )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \varphi ( x )\)
где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Следует отметить, что функция \(\varphi ( x )=\varphi ( { -x } )\) является четной.
Свойства представленной функции:
- функция является четной;
- если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.
Интегральная предельная теорема Муавра-Лапласа
Вероятность P, что возникнет событие A, для каждого эксперимента по порядку обладает стабильным значением, и \(p\ne 0\) и \(p\ne 1\), тогда вероятность \(P_n ( { k_1 ,k_2 } )\) того, что явление A наступит от \(k_ { 1 }\) до \(k_ { 2 }\) раз в n опытах, равна \(P_n ( { k_1 ,k_2 } )\approx \frac { 1 } { \sqrt { 2\cdot \pi } } \int\limits_ { x_1 } ^ { x_2 } { e^ { — { z^2 } / 2 } dz } =\Phi ( { x_2 } )-\Phi ( { x_1 } )\)
В смысле данной формулировки,\( x_1 =\frac { k_1 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\) , \(x_2 =\frac { k_2 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Следует отметить, что \(\Phi ( x )=\frac { 1 } { \sqrt { 2\cdot \pi } } \int { e^ { — { z^2 } / 2 } dz }\) можно определить с помощью специальных табличных схем.
\(\Phi ( { -x } )=-\Phi ( x )\) является нечетной функцией.
Рассматриваемая функция обладает следующими основными свойствами:
- функция является нечетной;
- если аргумент больше, чем 5, то значение функции составляет 0,5.
Таблица значений для вычисления определителей
В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:
Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ruТаблица значений интегральной функции Лапласа имеет следующий вид:
Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ruПрименительно к вероятностям распределения Пуассона сформирована таблица:
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st. ru
ru
Пример решения задачи
Задача № 1
Требуется определить, какова вероятность возникновения события А в течение 80 раз во время проведения 400 опытов. Следует учитывать вероятность появления данного события в каждом эксперименте составляет\( р = 0,2.\)
Решение:
В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8
Таким образом:
\(P_ { 400 } ( { 80 } )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \varphi ( x )\,,\,\)
где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
В таком случае:
\(\begin{array} { l } x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } } =\frac { 80-400\cdot 0,2 } { \sqrt { 400\cdot 0,2\cdot 0,8 } } =\frac { 80-80 } { \sqrt { 400\cdot 0,16 } } =0 \\ \varphi ( 0 )=0,3989\,,\,P_ { 400 } ( { 80 } )\approx \frac { 0,3989 } { 20\cdot 0,4 } =\frac { 0,3989 } { 8 } =0,0498 \\ \end{array}\)
Ответ: вероятность равна 0,0498
Задача № 2
По условиям задания, в процессе контроля качества выявляют 10% брака от произведенных изделий. Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.
Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.
Решение:
В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:
\(n=625, \ p=0,9, \ q=0,1, \ k_1 =550,\ k_2 =575\)
Тогда:
\(n\cdot p=625\cdot 0,9=562,5\)
Исходя из полученного выражения, определим:
\(\begin{array} { l } P_ { 625 } (550,575)\approx \Phi ( { \frac { 575-562,5 } { \sqrt { 625\cdot 0,9\cdot 0,1 } } } )- \Phi ( { \frac { 550-562,5 } { \sqrt { 626\cdot 0,9\cdot 0,1 } } } )\approx \Phi (1,67)- \Phi (-1,67)=2 \Phi (1,67)=0,9052 \\ \end{array}\)
Ответ: вероятность составит 0,9052
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Локальная теорема Лапласа.Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn(k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции ,где Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Pn(k1, k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу: — интегральная функция Лапласа. Дискретная случайная величина: определение, закон распределения, функция распределения. Случайнойназывают величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной (прерывной)называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случайной величиныназывают соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
сумма вероятностей второй строки таблицы, равна единице: p1+p2+ …+pn=1. многоугольником распределения Функцией распределения случайной величины X называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x. F(x) = P(X < x). Функция F(x) называется также интегральной функцией распределения или интегральным законом распределения. Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки x. Числовые характеристики: Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на соответствующие вероятности : Математическое ожидание называют также средним значением случайной величины Х Дисперсией D(X) случайной величины Х называют средний квадрат отклонения случайной величины от ее центра распределения: . Для того, чтобы рассматривать отклонение в тех же единицах, что и значения случайной величины, вводится еще одна характеристика – среднее квадратическое отклонение s(Х), которое определяется как .
Биноминальное распределение. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q=1—р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Биномиальное распределение — дискретное распределение вероятностей случайной величины ξ, принимающей целочисленные значения с вероятностями где — параметр биномиального распределения, иногда называемый «вероятностью положительного исхода»; одно из основных распределений вероятностей, порождаемых конечным множеством независимых случайных экспериментов (испытаний).
Распределение Пауссона. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Произведение nр сохраняет постоянное значение, а именно nр = . Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным. Таким образом, ⇐ Предыдущая1234Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
Теорема 11.1. (Пуассона) Пусть производится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р. Тогда, если число испытаний неограниченно возрастает, а p→0, причём n∙p=a – величина постоянная, то Pn(k) .
По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
Pn(k)= pkqn-k= pk(1 — p)n-k.
Отсюда
Pn(k)= pk(1 — p)n-k= pk(1 — p)n-k.
По условию a=n∙p p= , подставляя, получим:
Pn(k)= =
= … =
= … .
Переходя к пределу при n→∞
= = [ т.к. ].
Замечание 11.2. Теоремой Пуассона удобно пользоваться, когда p→0, причём a=n∙p 10.Существуют специальные таблицы, в которых приведены значения вероятностей для различных параметров a и k.
Формула Бернулли удобна, когда значение n не очень велико. В противном случае используют приближенные формулы из теорем Муавра-Лапласа.
Теорема 11.3. (локальная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0< p <1, то вероятность того, что событие A появится ровно k раз в n независимых испытаниях
Pn(k) , где – малая функция Лапласа, , q=1-p.
Имеются специальные таблицы значений функции . Нужно учитывать, что функция – чётная, т.е. = .
Теорема 11.4.(интегральная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от отлична от 0 и 1, т.е. 0< p <1, то вероятность того, что событие А появится от k1до k2 раз в n независимых испытаниях, определятся выражением:
Pn(k1,k2) , где – функция Лапласа, , , q=1-p.
Функция Лапласа – нечётная, т.е. . Значения находят по таблице.
Пример 11.5. Пусть вероятность события А в каждом отдельном испытании p=0,8. Найти вероятность того, что событие А появится 75 раз в 100 независимых испытаниях.
По локальной теореме Муавра-Лапласа х = = = –1,25. Значение (–1,25)= (1,25)=0,1826 находится по таблице.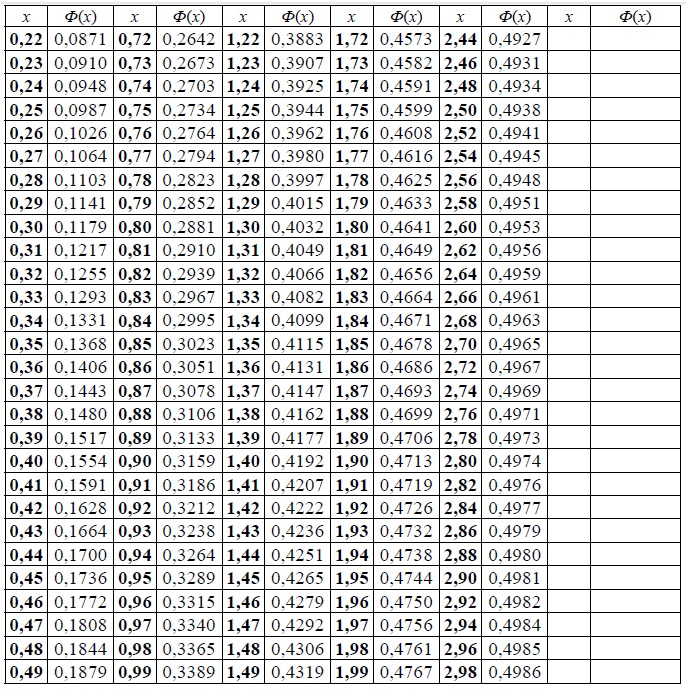
Тогда вероятность
P100(75) *0,1826 0,04565.
Пример 11.6. Вероятность Р(А) появления события А в одном испытании равна 0,8. Найти вероятность того, что событие А появится более 69 раз в 100 независимых испытаниях.
n=100, p=0,8, q=0,2, k1=70, k1=100.
По интегральной теореме Муавра-Лапласа = = = –1,25, = = = 5. По таблице (-2,5)= — (2,5)= -0,4938, (5)=0,5, P100(70,100) (5) — (-2,5)=0,5+0,4938=0,9938
Случайные величины
Определение 12.1. Случайной величиной Хназывается функция Х(ω), отображающая пространство элементарных исходов Ω во множество действительных чисел . Т.о. Х(ω): Ω→ .
Пример 12.2. Дважды подбрасывается монета. Рассмотрим случайную величину Х – число выпадений герба, определённую на пространстве элементарных исходов Ω={(г,г),(г,p),(p,г),(p,p)}. Множество возможных значений случайной величины Х-{0,1,2}. Составим таблицу
Множество возможных значений случайной величины Х-{0,1,2}. Составим таблицу
| ω | (г,г) | (г,p) | (p,г) | (p,p) |
| Х(ω) |
Одной из важнейших характеристик случайной величины является её функция распределения.
Определение 12.3. Функцией распределения случайной величины Хназывается функция F(x)=FX(x) действительной переменной х, определяющая вероятность того, что случайная величина X примет в результате эксперимента значение, меньшее некоторого фиксированного числа х
F(x)=P{X< x}=P{X (-∞; x)}.
Замечание 12.4.Если рассматривать случайную величину Х как случайную точку на оси Ox, то функция распределения F(x) с геометрической точки зрения – это вероятность того, что случайная точка Х в результате реализации эксперимента попадёт левее точки х.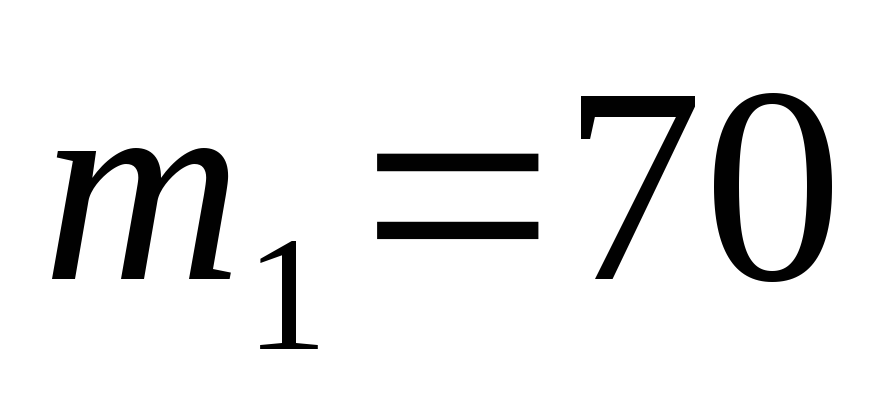
Свойства функции распределения
Свойство 12.5.Функция распределения F(x) – неубывающая функция, т.е.для таких, что выполняется условие F(x) F(x).
Поскольку , то события { }={ }+{ }, по определению функции распределения F( )=F( )+P{ }.
Т.к. P{ } 0, то F( )>F( ).
Свойство 12.6. Для таких, что справедливо равенство P{ }= F( )–F( ).
Замечание 12.7. Если функция распределения F(x) – непрерывная, то свойство 12.6 выполняется и при замене знаков и < на < и .
Свойство 12.8. F(x)=0; F(x)=1.
F(-∞)=P{X<-∞}=P(Ø)=0, F(+∞)=P{X<+∞}=P(Ω)=1.
Свойство 12.9. Функция распределения F(x) непрерывна слева ( F(x)=F( )).
Свойство 12.10. P{X x}=1-F(x).
{X<+∞}={X<x}+{X x}, по свойству вероятности P{X<+∞}=P{X<x}+P{X x};
P(Ω)=1= F(x)+ P{X x}, откуда P{X x}=1- F(x).
Дата добавления: 2016-06-15; просмотров: 2183; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Теорема Муавра-Лапласа — презентация онлайн
1. ТЕОРЕМА МУАВРА-ЛАПЛАСА
ТЕОРЕМА МУАВРАЛАПЛАСАЛокальная и интегральная
Пьер-Симо́н Лаплас (1749- 1827) — выдающийся
французский математик, физик и астроном; один
из создателей теории вероятностей. Был членом
Французского Географического общества.
Абрахам де Муавр (1667- 1754) — английский
математик французского происхождения. Член
Лондонского королевского общества (1697),
Парижской (1754) и Берлинской (1735) академий
наук.
Теорема Муавра — Лапласа — простейшая из
предельных теорем теории вероятностей.
В общем виде теорема доказана Лапласом в книге
«Аналитическая теория вероятностей» (1812).

Один частный случай теоремы был известен
Муавру (1730), в связи с чем она и называется
теоремой Муавра-Лапласа.
Утверждает, что число успехов при многократном
повторении одного и того же случайного
эксперимента с двумя возможными исходами
приблизительно имеет нормальное распределение.
Рассмотрим последовательность из n независимых
опытов, в каждом из которых событие A может
произойти с вероятностью p, либо не произойти с вероятностью q = 1 − p. Обозначим через Pn(m)
вероятность того, что событие A произойдет ровно
m раз из n возможных. Если n будет достаточно
большим, то найти значение Pn(m) по теореме
Бернулли становится нереально из-за огромного
объема вычислений. Локальная теорема Муавра Лапласа позволяет найти приближенное значение
вероятности.
Локальная теорема Муавра — Лапласа. Если
в схеме Бернулли число n велико, а число p
отлично от 0 и 1, тогда:
Pn ( m)
m np
1
, где ( x)
npq
npq
1
e
2
x2
2
Функция φ(x) называется функцией Гаусса.

Теорема Муавра-Лапласа утверждает, что
асимптотическим выражением для биномиального
распределения является нормальная функция.
Для расчетов составлена таблица значений функции φ
(x), необходимо учитывать свойства:
1. φ(−x) = φ(x) — четная, в таблице приведены значения
функции лишь для положительных аргументов;
2. Функция φ(x) — монотонно убывающая. Предел φ(x)
при x→∞ равен нулю.
3. Если х > 5, то можно считать, что φ(х) ≈ 0. Функция
φ(х) уже при х = 5 очень мала: φ(5)=0,0000015.
Поэтому таблица значений не продолжена для х > 5.
Пример. Вероятность покупки при посещении
клиентом магазина составляет р = 0,75. Найти
вероятность, что при 100 посещениях клиент
совершит покупку ровно 80 раз.
Решение. n = 100, m = 80, p = 0,75, q = 0,25.
80 100 0, 75
x
1,16
Находим
,
100 0, 75 0, 25
определяем (1,16) = 0,2036, тогда:
Р100(80) =
0, 2036
0, 047
100 0, 75 0, 25
Задание. Вероятность выпуска бракованного
изделия равна 0,02.
 Какова вероятность того, что
Какова вероятность того, чтосреди 2500 выпущенных изделий окажется 50
бракованных
Варианты ответов:
1) 0,1045;
2) 0,86; 3) 0,0570;
4) 0,0172;
5) 0,3989.
Ответ: пункт 5
Фрагмент таблицы функции (x)
x
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
0
0,242
2179
1942
1714
1497
1295
1109
0940
0790
0656
1
2396
2155
1919
1691
1476
1276
1092
0925
0775
0644
2
2371
2131
1895
1669
1456
1257
1074
0909
0761
0632
3
2347
2107
1872
1647
1435
1238
1057
0893
0748
0620
4
2323
2083
1849
1626
1415
1219
1040
0878
0734
0608
5
2299
2059
1826
1604
1394
1200
1023
0863
0721
0596
6
2275
2036
1804
1582
1374
1182
1006
0848
0707
0584
1
2
7
2251
2012
1781
1561
1354
1163
0989
0833
0694
0573
2
x
e 2
8
2227
1989
1758
1539
1334
1145
0973
0818
0681
0562
9
2203
1965
1736
1518
1315
1127
0957
0804
0669
0551
Интегральная теорема Муавра – Лапласа.
 Если
Есливероятность р наступления события А в каждом
испытании постоянна и отлична от 0 и 1, то
вероятность, что в n независимых испытаниях
(n>>1) событие А состоится число раз,
заключенное в границах от а до b включительно:
Pn (a m b) Ф( x2 ) Ф( x1 )
a np
b np
x1
, x2
.
npq
npq
где функция Ф (х) определяется равенством
Ф( x)
1
2
x
e
t2
2
dt
0
Формула называется интегральной формулой
Муавра— Лапласа.
Получаемые по интегральной и локальной
формулам Муавра — Лапласа вероятности
достаточно точны, если произведение nр
составляет несколько сотен!!!
Свойства функции Ф(х)
Функция Ф(х) нечетная, Ф (- х) = — Ф(х).
Функция Ф(х) монотонно возрастающая.
Предел функции Ф(х) при x→∞ равен 0,5.
Для всех значений х > 5 считают, что Ф (х) ≈ 0,5.
Уже Ф (5) = 0,4999992, при увеличении х
функция Ф (х) возрастает, но не может превосходить 0,5. Поэтому в таблицах функция дана
для значений х < 5.

Оценка отклонения относительной частоты от
постоянной вероятности
Вероятность, что в n независимых испытаниях, в
каждом из которых вероятность появления
события А постоянна и равна р, абсолютная
величина отклонения относительной частоты
появления события А от его постоянной
вероятности не превысит положительного числа ,
приближенно равна:
m
P
p 2Ф
n
n
pq
.
Пример. Вероятность появления события в
каждом из 625 независимых испытаний равна 0,8.
Найти вероятность, что относительная частота
появления события отклонится от его вероятности
по абсолютной величине не более, чем на 0,04.
Решение. По условию задачи: n = 625; p = 0,8;
=0,04. Отсюда q =1– p = 0,2. Требуется найти
вероятность:
m
Р
— 0,8 0, 04 = ?
625
Для решения задачи воспользуемся формулой,
определяющей оценку отклонения относительной
частоты от постоянной вероятности:
m
P
p 2Ф
n
n
pq
.

Ф(х) – интегральная функция Лапласа. Найдем
аргумент функции Лапласа:
n
625
x
0, 04
2,5
pq
0,8 0,2
По табл. функции Лапласа: Ф(2,5) = 0,4938, т.е.
2Ф(х) = 0,9876.
Итак, искомая вероятность:
m
Р
— 0,8 0,04 0,9876.
625
Пример. При установившемся технологическом
режиме завод выпускает в среднем 70% продукции
1-го сорта. Определить вероятность, что из 1000
изделий число первосортных заключено между 652
и 760.
Решение. p = 0,7; q = 1 – p = 0,3; n = 1000;
np = 0,7 × 1000 = 700; npq = 700 × 0,3 = 210
Получение гауссовского распределения вероятностей: новый подход
Прикладная математика Том 11 № 06 (2020 г.), № статьи: 100627, 11 стр.
10.4236/am.2020.116031
Вывод гауссовского распределения вероятностей: новый подход
A. T. Adeniran 1 , O. Faweya 2* , T. O. Ogunlade 3 , K. O. Balogun 4
1 Департамент Statistist of IBADAN of IBADAN of IBADAN of IBADAN of IBADAN of IBADAN of IBADAN of IBADAN of IBADAN.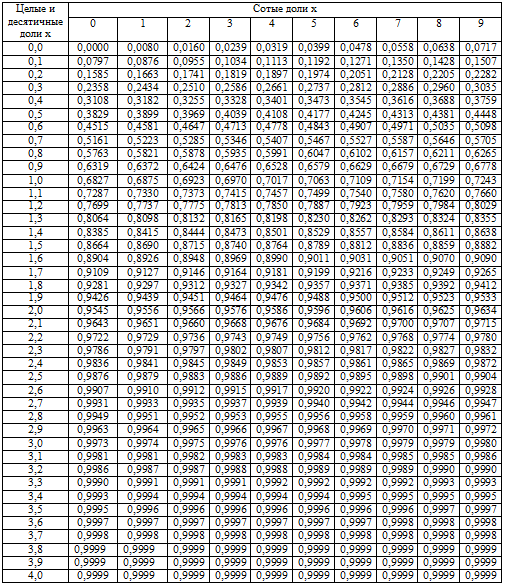 , Ибадан, Нигерия
, Ибадан, Нигерия
2 Кафедра статистики Государственного университета Экити (EKSU), Адо-Экити, Нигерия
3 Факультет математики Государственного университета Экити (EKSU), Адо-Экити, Нигерия
4 Департамент статистики , Федеральная школа статистики, Ибадан, Нигерия.
http://creativecommons.org/licenses/by/4.0/
Получено: 17 марта 2020 г.; Принято: 29 мая 2020 г.; Опубликовано: 1 июня 2020 г.
АННОТАЦИЯ
Знаменитая предельная теорема Лапласа де Муавра доказала функцию плотности вероятности гауссовского распределения из биномиальной функции массы вероятности при заданных условиях. Подход Лапласа де Муавра громоздок, поскольку он сильно зависит от множества лемм и теорем. В этой статье предложен альтернативный и менее строгий метод получения гауссовского распределения на основе базового случайного эксперимента при некоторых предположениях.
Ключевые слова:
Предельная теорема Де Муавра Лапласа, Биномиальная функция вероятности вероятности, Гауссово распределение, Случайный эксперимент распределение имени немецкого математика Карла Фридриха Гаусса в 1809 году.
Определение 1.1 Пусть мю и о be константы с − ∞ < мю < ∞ и о > 0 . Функция
ф ( Икс ; мю , о ) знак равно 1 2 π о 2 е − 1 2 ( Икс − мю о ) 2 ; за − ∞ < Икс < ∞ (1)
называется нормальной функцией плотности вероятности случайной величины X с параметрами мю
а также о
.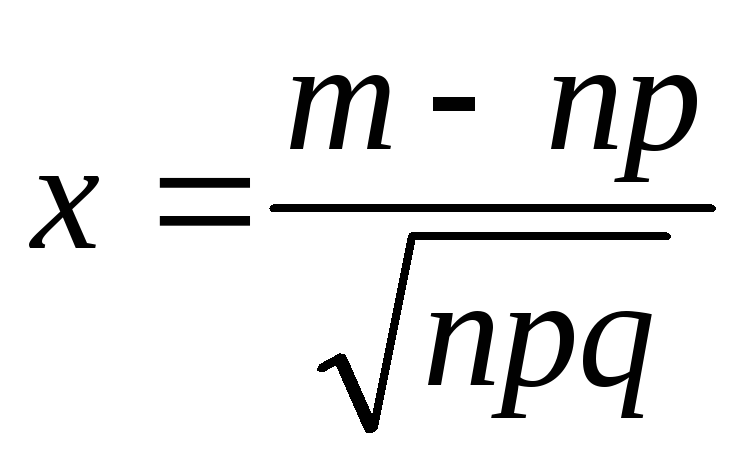
Как в теории, так и в приложениях, без элемента двусмысленности, функция распределения Гаусса является наиболее важным и широко используемым распределением в статистике.
Хорошо известный метод получения этого распределения впервые появился во втором издании «Учения о шансах» Абрахама де Муавра (отсюда и предельная теорема Лапласа де Муавра), опубликованном в 1738 г. ([1] [2] [3] [4 ] [5]). Далее следует математическое утверждение популярной теоремы де Муавра.
Теорема 1.1 (предельная теорема Лапласа де Муавра) При росте n большое ( н → ∞ ), для x в окрестности из NP , для Модные Значения из 66666666666669 666666666666666 ( . п ≠ 0 и п ≠ 1 ), мы можем приблизительно
(
н
Икс
)
п
Икс
д
н
−
Икс
≈
1
2
π
н
п
д
е
−
(
Икс
−
н
п
)
2
2
н
п
д
,
п
+
д
знак равно
1,
п
,
д
>
0. (2)
(2)
В явном виде теорема утверждает, что предположим н е ℤ + , и пусть p и q — вероятности, причем п + д знак равно 1 . Функция
б ( Икс ; н , п ) знак равно ( н Икс ) п Икс ( 1 − п ) н − Икс за Икс знак равно 0 , 1 , 2 , ⋯ , н (3)
, называемая биномиальной функцией вероятности, сходится к функции плотности вероятности нормального распределения как н
→
∞
со средним значением np и стандартным отклонением н
п
(
1
−
п
)
.
Хотя Де Муавр доказал результат для п знак равно 1 2 ([6] [7]). [8] распространил и обобщил доказательство на все значения p (вероятность успеха в любом испытании), такие, что p не слишком мало и не слишком велико. Результат Феллера был изложен в [9]. [10] [11] [12] [13] использовали свойство единственности метода производящей функции момента для доказательства той же теоремы.
В этой статье мы пытаемся найти ответ на вопрос: существует ли какая-либо альтернативная процедура для вывода гауссовской функции плотности вероятности, помимо подхода с использованием предельной теоремы Лапласа де Муавра, который в значительной степени опирается на многие леммы и теоремы (приближенная формула Стирлинга, разложение в ряды Маклорена и др.), о чем свидетельствуют работы [8] и [9] ?
2. Существующая методика
В этом разделе представлено краткое доказательство существующей предельной теоремы Лапласа де Муавра. Прежде всего, изучите с доказательством важнейшую лемму предельной теоремы Лапласа де Муавра, принцип аппроксимации Стирлинга.
Лемма 2.1 (принцип приближения Стирлинга) Дано целое н ; н > 0 , the factorial of a large number n can be replaced with the approximation
н ! ≈ 2 π н ( н е ) н
Proof 2.1 This lemma can be derived using the integral definition of the factorial ,
н ! знак равно Г ( н + 1 ) знак равно ∫ 0 ∞ Икс н е − Икс д Икс (4)
Обратите внимание, что производная от логарифма подынтегральной функции может быть записана как
д д Икс п ( Икс н е − Икс ) знак равно д д Икс ( н п Икс − Икс ) знак равно н Икс − 1 (5)
Подынтегральная функция имеет резкий пик с вкладом, важным лишь вблизи Икс
знак равно
н
. Поэтому пусть Икс
знак равно
н
+
дельта
куда дельта
≤
н
, и напишите
Поэтому пусть Икс
знак равно
н
+
дельта
куда дельта
≤
н
, и напишите
п ( Икс н е − Икс ) знак равно н п ( н + дельта ) − ( н + дельта ) знак равно н п [ н ( 1 + дельта н ) ] − ( н + дельта ) знак равно н [ п ( н ) + п ( 1 + дельта н ) ] − ( н + дельта ) (6)
Напомним, что серия Маклорена ф
(
Икс
)
знак равно
п
(
1
+
Икс
)
знак равно
Икс
−
1
2
Икс
2
+
0
(
н
)
. Следовательно,
Следовательно,
ln(xne−x)=n[ln(n)+δn−12(δ2n2)+⋯]−(n+δ)=ln(nn)−n−δ22n+⋯ (7)
Взяв экспоненту с обеих сторон предыдущего уравнения (7), мы получим
Икс н е − Икс ≈ е п ( н н ) − н − дельта 2 2 н знак равно е п ( н н ) е − н е − дельта 2 2 н знак равно ( н е ) н е − дельта 2 2 н (8)
Подстановка (8) в интегральное выражение для н ! , то есть (4) дает
н ! ≈ ∫ 0 ∞ ( н е ) н е − дельта 2 2 н д дельта знак равно ( н е ) н ∫ − ∞ ∞ е − дельта 2 2 н д дельта (9)
Из (9) пусть я знак равно ∫ 0 ∞ е − дельта 2 2 н г дельта и учитывая дельта а также κ как фиктивная переменная такая, что
я 2 знак равно ∫ 0 ∞ е − дельта 2 2 α г дельта × ∫ 0 ∞ е − κ 2 2 н г κ знак равно ∫ 0 ∞ ∫ 0 ∞ е − 1 2 н ( дельта 2 + κ 2 ) г дельта г κ (10)
Трансформация я 2 от алгебры к полярным координатам дает дельта знак равно р потому что ( θ ) , κ знак равно р грех ( θ ) что подразумевает дельта 2 + κ 2 знак равно р 2 с якобианом (J) преобразования как
Дж знак равно | ∂ дельта ∂ р ∂ дельта ∂ θ ∂ κ ∂ р ∂ κ ∂ θ | знак равно | потому что ( θ ) − р грех ( θ ) грех ( θ ) р потому что ( θ ) | знак равно р (11)
Следовательно,
я 2 знак равно ∫ 0 2 π ∫ 0 ∞ е − р 2 2 н | Дж | г р г θ знак равно ∫ 0 2 π ∫ 0 ∞ е − р 2 2 н р г р г θ знак равно − н ∫ 0 2 π [ е − ты ] 0 ∞ г θ знак равно н ∫ 0 2 π г θ знак равно 2 π н (12)
Следовательно, я
знак равно
я
знак равно
2
π
н
. Замена I в (9) дает
Замена I в (9) дает
н ! ≈ 2 π н ( н е ) н ⊡ (13)
Теперь мы начнем с доказательства теоремы (1.1) с использованием популярной существующей техники.
Доказательство 2.2 с использованием Результат из LEMMA (2,1), Уравнение (3) CAN BE . ф ( Икс ; н , п ) ≈ 2 π н ( н е ) н 2 π Икс ( Икс е ) Икс 2 π ( н − Икс ) ( н − Икс е ) н − Икс п Икс ( 1 − п ) н − Икс знак равно 1 2 π н н + 1 2 Икс Икс + 1 2 ( н − Икс ) н − Икс + 1 2 п Икс ( 1 − п ) н − Икс (14)
Умножение числителя и знаменателя уравнения (14) на н ≡ н 1 2 чтобы получить
ф ( Икс ; н , п ) ≈ 1 2 π н н н + 1 2 + 1 2 + Икс − Икс Икс Икс + 1 2 ( н − Икс ) н − Икс + 1 2 п Икс ( 1 − п ) н − Икс знак равно 1 2 π н ( Икс н ) − Икс − 1 2 ( н − Икс н ) − н + Икс − 1 2 п Икс ( 1 − п ) н − Икс (15)
Так как x находится в окрестности np, замените переменные Икс
знак равно
н
п
+
ε
, куда ε
измеряет расстояние от среднего значения np бинома и измеренной величины x. Перепишем (15) в терминах ε
и далее упростить следующим образом
Перепишем (15) в терминах ε
и далее упростить следующим образом
ф ( Икс ; н , п ) ≈ 1 2 π н ( н п + ε н ) − Икс − 1 2 ( н − н п − ε н ) − н + Икс − 1 2 п Икс ( 1 − п ) н − Икс ≈ 1 2 π н [ п ( 1 + ε н п ) ] − Икс − 1 2 [ ( 1 − п ) ( 1 − ε н ( 1 − п ) ) ] − н + Икс − 1 2 п Икс ( 1 − п ) н − Икс ≈ 1 2 π н ( 1 + ε н п ) − Икс − 1 2 ( 1 − ε н ( 1 − п ) ) − н + Икс − 1 2 п − 1 2 ( 1 − п ) − 1 2
чтобы получить
ф ( Икс ; н , п ) ≈ 1 2 π н п ( 1 − п ) ( 1 + ε н п ) − Икс − 1 2 ( 1 − ε н ( 1 − п ) ) − н + Икс − 1 2 (16)
Обратите внимание, что Икс
знак равно
опыт
(
п
Икс
)
. Следовательно, переписав (16) в экспоненциальной форме, получим
Следовательно, переписав (16) в экспоненциальной форме, получим
ф ( Икс ; н , п ) ≈ 1 2 π н п ( 1 − п ) опыт [ п { ( 1 + ε н п ) − Икс − 1 2 ( 1 − ε н ( 1 − п ) ) − н + Икс − 1 2 } ] ≈ 1 2 π н п ( 1 − п ) опыт [ ( − Икс − 1 2 ) п ( 1 + ε н п ) + ( − н + Икс − 1 2 ) п ( 1 − ε н ( 1 − п ) ) ]
ф ( Икс ; н , п ) ≈ 1 2 π н п ( 1 − п ) опыт [ ( − н п − ε − 1 2 ) п ( 1 + ε н п ) + ( − н ( 1 − п ) + ε − 1 2 ) п ( 1 − ε н ( 1 − п ) ) ] (17)
Допустим ф
(
Икс
)
знак равно
п
(
1
+
Икс
)
, используя ряд Маклорена ф
(
Икс
)
знак равно
Икс
−
1
2
Икс
2
+
0
(
н
)
и аналогично ф
(
Икс
)
знак равно
п
(
1
−
Икс
)
знак равно
−
Икс
−
1
2
Икс
2
+
0
(
н
)
. Чтобы, п
(
1
+
ε
н
п
)
≈
ε
н
п
−
1
2
(
ε
н
п
)
2
а также п
(
1
−
ε
н
(
1
−
п
)
)
≈
−
ε
н
(
1
−
п
)
−
1
2
(
ε
н
(
1
−
п
)
)
2
. В результате
Чтобы, п
(
1
+
ε
н
п
)
≈
ε
н
п
−
1
2
(
ε
н
п
)
2
а также п
(
1
−
ε
н
(
1
−
п
)
)
≈
−
ε
н
(
1
−
п
)
−
1
2
(
ε
н
(
1
−
п
)
)
2
. В результате
ф ( Икс ; н , п ) ≈ 1 2 π н п ( 1 − п ) опыт [ − ε + ε 2 2 н п − ε 2 н п + ε + ε 2 2 н ( 1 − п ) − ε 2 н ( 1 − п ) ] знак равно 1 2 π н п ( 1 − п ) опыт [ − 1 2 ( ε 2 н п ( 1 − п ) ) ] (18)
Напомним, что Икс
знак равно
н
п
+
ε
что подразумевает, что ε
2
знак равно
(
Икс
−
н
п
)
2
. Из биномиального распределения н
п
знак равно
мю
, а также н
п
(
1
−
п
)
знак равно
о
2
что подразумевает, что н
п
(
1
−
п
)
знак равно
о
. Соответствующая замена их в уравнении (18) дает
Из биномиального распределения н
п
знак равно
мю
, а также н
п
(
1
−
п
)
знак равно
о
2
что подразумевает, что н
п
(
1
−
п
)
знак равно
о
. Соответствующая замена их в уравнении (18) дает
ф ( Икс ; н , п ) ≈ 1 2 π о 2 опыт [ − 1 2 ( Икс − мю ) 2 о 2 ] знак равно 1 о 2 π е − 1 2 ( Икс − мю о ) 2 ; за − ∞ < Икс < ∞ (19)
Теорема подтверждена.
Мы рекомендуем читателям, интересующимся подробным доказательством теоремы, обратиться к исследованию, изложенному в [9].
3. Предлагаемая методика
Предположим, проводится случайный эксперимент по метанию иглы или любого другого предмета, связанного с дротиком, в начало декартовой плоскости с целью попасть в центр (см. рис. 1).
Из-за непоследовательности или несовершенства человеческой природы разные результаты метания порождают случайные ошибки. Чтобы сделать вывод возможным и менее строгим, мы делаем следующие предположения:
1) Ошибки не зависят от ориентации системы координат.
2) Ошибки в перпендикулярных направлениях независимы. Это означает, что слишком высокое значение не влияет на вероятность отклонения вправо.
Рис. 1. Возможные результаты эксперимента с дротиком.
3) Небольшие ошибки более вероятны, чем большие. То есть броски с большей вероятностью попадут в область P, чем в область Q или R, поскольку область P находится ближе к цели (источнику).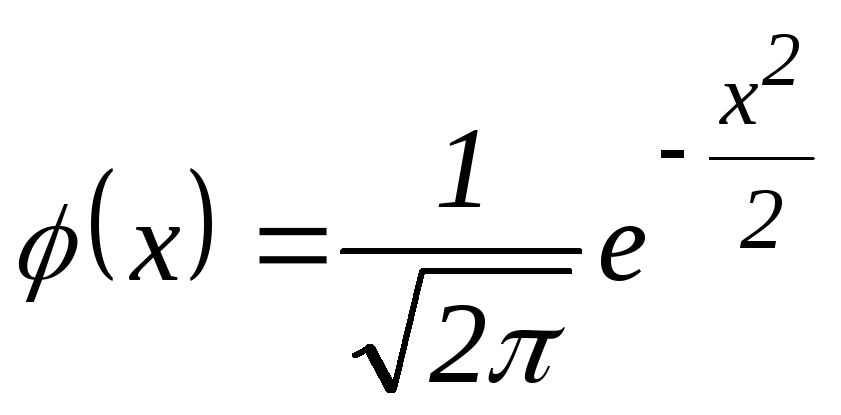 Точно так же, по той же причине, область Q более вероятна, чем область R. Кроме того, существует более высокая вероятность или тенденция попадания в область V, чем в S или T, поскольку V имеет более широкую или большую площадь поверхности, а расстояния от начала координат равны. примерно так же.
Точно так же, по той же причине, область Q более вероятна, чем область R. Кроме того, существует более высокая вероятность или тенденция попадания в область V, чем в S или T, поскольку V имеет более широкую или большую площадь поверхности, а расстояния от начала координат равны. примерно так же.
Из рисунка 2 пусть вероятность попадания иглы в вертикальную полосу от x до Икс
+
Δ
Икс
обозначаться как п
(
Икс
)
Δ
Икс
. Аналогично, вероятность попадания иглы в горизонтальную полосу от y до у
+
Δ
у
быть п
(
у
)
Δ
у
. Очевидно, функция не может быть постоянной из-за стохастического характера эксперимента. В данном исследовании наш интерес состоит в том, чтобы узнать и получить вид и характеристики функции п
(
Икс
)
. Из второго предположения вероятность попадания иглы в заштрихованную область ABCD (см. рис. 2) равна 9.0006
рис. 2) равна 9.0006
п ( Икс ) Δ Икс ⋅ п ( у ) Δ у
Обратите внимание, что любые регионы r единиц от начала координат с площадью Δ Икс Δ у имеет ту же вероятность, которая является следствием предположения о том, что ошибки не зависят от ориентации. Можно сказать, что
п ( Икс ) Δ Икс ⋅ п ( у ) Δ у знак равно п ( Икс ) п ( у ) Δ Икс Δ у знак равно грамм ( р ) Δ Икс Δ у (20)
где
грамм ( р ) знак равно п ( Икс ) п ( у ) (21)
из основного правила исчисления, дифференцируя (используя правило произведения) обе части уравнения (21) по отношению к θ дает
0 знак равно п ( Икс ) д д θ п ( у ) + п ( у ) д д θ п ( Икс ) (22)
Здесь, грамм
′
(
р
)
знак равно
0
поскольку грамм
(
. )
не зависит от ориентации. Преобразовав в полярные координаты, Икс
знак равно
р
потому что
θ
а также у
знак равно
р
грех
θ
, мы можем переписать производные в уравнении (22) как
)
не зависит от ориентации. Преобразовав в полярные координаты, Икс
знак равно
р
потому что
θ
а также у
знак равно
р
грех
θ
, мы можем переписать производные в уравнении (22) как
Рисунок 2. Типичный пример эксперимента.
0 знак равно п ( Икс ) д д θ п ( у знак равно р грех θ ) + п ( у ) д д θ п ( Икс знак равно р потому что θ ) (23)
Используя цепное правило дифференцирования, (23) становится
0 знак равно п ( Икс ) п ′ ( у ) р потому что θ − п ( у ) п ′ ( Икс ) р грех θ (24)
Переписать уравнение (24) еще раз, заменив р потому что θ с х и р потому что θ с y дает
0 знак равно п ( Икс ) п ′ ( у ) Икс − п ( у ) п ′ ( Икс ) у (25)
Приведенное выше дифференциальное уравнение можно представить в такой форме, чтобы его можно было решить с помощью метода разделения переменных, как
п ′ ( Икс ) п ( Икс ) Икс знак равно п ′ ( у ) п ( у ) у (26)
Это дифференциальное уравнение может быть верным только для любых x и y, x и y независимы
тогда и только тогда, когда отношение п
′
(
Икс
)
п
(
Икс
)
Икс
знак равно
п
′
(
у
)
п
(
у
)
у
определяемая формулой (26), является константой. То есть если
То есть если
п ′ ( Икс ) п ( Икс ) Икс знак равно п ′ ( у ) п ( у ) у знак равно с . (27)
Учитывать п ′ ( Икс ) п ( Икс ) Икс знак равно с в (27) и переставить так, чтобы
п ′ ( Икс ) п ( Икс ) знак равно с Икс . (28)
Интегрирование уравнения (28) дает
п
п
(
Икс
)
знак равно
с
Икс
2
2
+
к
1
так
что
п
(
Икс
)
знак равно
к
е
с
Икс
2
2
;
куда
к
знак равно
е
к
1
. (29)
(29)
По третьему предположению c должно быть отрицательным, поэтому мы записываем функцию вероятности (29)
п ( Икс ) знак равно к е − с 2 Икс 2 ; куда с е ℝ + (30)
При горизонтальном смещении цели от начала координат до произвольной точки мю которые теперь отмечают новый центр/цель, то функция вероятности в (30) становится равной
п ( Икс ) знак равно к е − с 2 ( Икс − мю ) 2 (31)
Дифференцируя (31) и приравнивая производную к нулю, получаем
п ′ ( Икс ) знак равно − с к ( Икс − мю ) е − с ( Икс − мю ) 2 2 знак равно 0 (32)
с е
−
с
(
Икс
−
мю
)
2
2
≠
0
подразумевает Икс
знак равно
мю
. Следовательно, уравнение (31) имеет максимальное значение при Икс
знак равно
мю
и точка перегиба в Икс
знак равно
мю
±
1
к
. Очевидно, (31) дало
Следовательно, уравнение (31) имеет максимальное значение при Икс
знак равно
мю
и точка перегиба в Икс
знак равно
мю
±
1
к
. Очевидно, (31) дало
используем базовую форму распределения Гаусса с константами k и c и областью значений X как − ∞ к ∞ . Следовательно, чтобы уравнение (31) можно было рассматривать как правильную функцию плотности вероятности, общая площадь под кривой должна быть равна 1. То есть
∫ − ∞ ∞ к е − с 2 ( Икс − мю ) 2 д Икс знак равно 1 (33)
Для симметричной функции ф
(
Икс
)
,
∫
−
∞
∞
ф
(
Икс
)
д
Икс
знак равно
2
∫
0
∞
ф
(
Икс
)
д
Икс
. Применение этого свойства к уравнению (33) дает
Применение этого свойства к уравнению (33) дает
∫ 0 ∞ е − с 2 ( Икс − мю ) 2 д Икс знак равно 1 2 к . (34)
Возведение обеих сторон (34) в квадрат, чтобы получить
∫ 0 ∞ е − с 2 ( Икс − мю ) 2 д Икс ⋅ ∫ 0 ∞ е − с 2 ( у − мю ) 2 д у знак равно 1 2 к × 1 2 к (35)
Это возможно, поскольку x и y являются просто фиктивными переменными. Напомним, что x и y также независимы, поэтому мы можем записать произведение (35) в LHS как двойной интеграл, чтобы получить
Напомним, что x и y также независимы, поэтому мы можем записать произведение (35) в LHS как двойной интеграл, чтобы получить
∫ 0 ∞ ∫ 0 ∞ е − с 2 [ ( Икс − мю ) 2 + ( у − мю ) 2 ] д Икс д у знак равно 1 4 к 2 . (36)
Ввод Икс − мю знак равно г ⇒ д Икс знак равно д г а также у − мю знак равно ж ⇒ д у знак равно д ж в предыдущем уравнении (36) дает
∫
0
∞
∫
0
∞
е
−
с
2
[
г
2
+
ж
2
]
д
г
д
ж
знак равно
1
4
к
2
.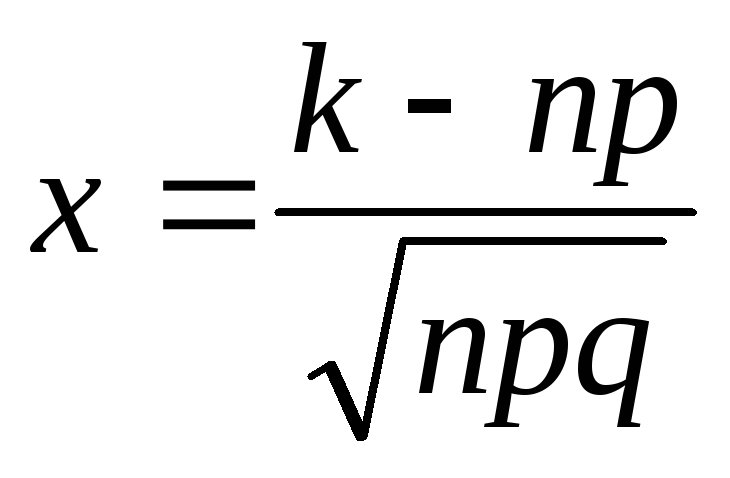 (37)
(37)
Двойной интеграл (37) можно вычислить с использованием полярных координат как г знак равно р потому что θ а также у знак равно р грех θ с якобианом (J) преобразования как
Дж знак равно | ∂ ( г , ж ) ∂ ( р , θ ) | знак равно | г г г р г г г θ г ж г р г ж г θ | знак равно | потому что θ − р грех θ грех θ р потому что θ | знак равно р , (38)
и
г
2
+
ж
2
знак равно
(
р
потому что
θ
)
2
+
(
р
грех
θ
)
2
знак равно
р
2
. (39)
(39)
Итак, уравнение (37) теперь становится
∫ 0 π 2 ∫ 0 ∞ е − с р 2 2 | Дж | д р д θ знак равно ∫ 0 π 2 ∫ 0 ∞ е − с р 2 2 р д р д θ знак равно 1 4 к 2 . (40)
Вычисление двойного интеграла ∫ 0 π 2 ∫ 0 ∞ е − с р 2 2 р д р д θ в уравнении (40), сначала пуская ты знак равно с р 2 2 , и решение для k в полученном уравнении дает
к знак равно с 2 π (41)
Подставляя (41) в (31), плотность вероятности п ( Икс ) , становится
п ( Икс ) знак равно с 2 π е − с 2 ( Икс − мю ) 2 (42)
Опять же, интегрирование функции вероятности по ее области определения дает 1. Следовательно, из (42)
Следовательно, из (42)
∫ − ∞ ∞ п ( Икс ) г Икс знак равно ∫ − ∞ ∞ с 2 π е − с 2 ( Икс − мю ) 2 г Икс знак равно 2 ∫ 0 ∞ с 2 π е − с 2 ( Икс − мю ) 2 г Икс знак равно 1 (43)
Дальнейшее упрощение предыдущего уравнения (43) дает
∫ 0 ∞ е − с 2 ( Икс − мю ) 2 знак равно π 2 с (44)
Одной из важных целей математической теории статистики является получение среднего значения и дисперсии любой изучаемой функции вероятности. Значение, мю
, определяется как значение интеграла ∫
−
∞
∞
Икс
п
(
Икс
)
д
Икс
. Дисперсия, о
2
, является значением интеграла ∫
−
∞
∞
(
Икс
−
мю
)
2
п
(
Икс
)
д
Икс
. Поэтому, используя уравнение (42),
Значение, мю
, определяется как значение интеграла ∫
−
∞
∞
Икс
п
(
Икс
)
д
Икс
. Дисперсия, о
2
, является значением интеграла ∫
−
∞
∞
(
Икс
−
мю
)
2
п
(
Икс
)
д
Икс
. Поэтому, используя уравнение (42),
о 2 знак равно ∫ − ∞ ∞ ( Икс − мю ) 2 с 2 π е − с 2 ( Икс − мю ) 2 г Икс знак равно 2 ∫ 0 ∞ ( Икс − мю ) 2 с 2 π е − с 2 ( Икс − мю ) 2 г Икс (45)
или эквивалентно
о 2 знак равно 2 с π ∫ 0 ∞ ( Икс − мю ) [ ( Икс − мю ) е − с 2 ( Икс − мю ) 2 ] д Икс (46)
рассмотреть уравнение (46) и с помощью интегрирования по частям ( ∫ ты г в знак равно ты в − ∫ в г ты ) с ты знак равно Икс − мю ⇒ г ты знак равно г Икс а также г в знак равно ( Икс − мю ) е − с 2 ( Икс − мю ) 2 г Икс ⇒ в знак равно − 1 с е − с 2 ( Икс − мю ) 2 , у нас
о 2 знак равно 2 с π [ − Икс − мю с е − с 2 ( Икс − мю ) 2 − ∫ 0 ∞ − 1 с е − с 2 ( Икс − мю ) 2 г Икс ] знак равно 2 с π [ − 1 с лим н → ∞ ( Икс − мю ) е − с 2 ( Икс − мю ) 2 | 0 н + 1 с ∫ 0 ∞ е − с 2 ( Икс − мю ) 2 г Икс ] знак равно 2 с π [ − 1 с лим н → ∞ ( н − мю ) е − с 2 ( н − мю ) 2 + 1 с ∫ 0 ∞ е − с 2 ( Икс − мю ) 2 г Икс ] знак равно 2 с π [ 0 + 1 с ∫ 0 ∞ е − с 2 ( Икс − мю ) 2 г Икс ] знак равно 1 с 2 с π ∫ 0 ∞ е − с 2 ( Икс − мю ) 2 г Икс
подставив (44) в предыдущее уравнение выше, получим
о 2 знак равно 1 с × 2 с π × π 2 с ⇒ с знак равно 1 о 2 (47)
Подставляя (47) в (42), полученная функция плотности вероятности имеет вид
п
(
Икс
)
знак равно
1
2
π
о
2
е
−
1
2
о
2
(
Икс
−
мю
)
2
знак равно
1
о
2
π
е
−
1
2
(
Икс
−
мю
о
)
2
,
−
∞ <
Икс
<
∞
. (48)
(48)
Основываясь на трех вышеупомянутых основных допущениях, мы легко вывели уравнение (48), широко известное во всем мире как функция нормального или гауссовского распределения со средним мю и стандартное отклонение о .
Для проверки того, что уравнение (19) является правильной функцией плотности вероятности с параметрами мю а также о состоит в том, чтобы показать, что интеграл
я знак равно ∫ − ∞ ∞ 1 о 2 π опыт [ − 1 2 ( Икс − мю о ) 2 ] д Икс
равно 1.
Изменить переменные интегрирования, разрешив г
знак равно
Икс
−
мю
о
, из чего следует, что г
Икс
знак равно
о
г
г
. Затем
Затем
я знак равно ∫ − ∞ ∞ 1 о 2 π е − г 2 2 о г г знак равно 2 2 π ∫ 0 ∞ е − г 2 2 г г знак равно 2 π ∫ 0 ∞ е − г 2 2 г г
так что
я 2 знак равно [ 2 π ∫ 0 ∞ е − Икс 2 2 г Икс ] [ 2 π ∫ 0 ∞ е − у 2 2 г у ] знак равно 2 π ∫ 0 ∞ ∫ 0 ∞ е − Икс 2 + у 2 2 г Икс г у
Здесь Икс
,
у
являются фиктивными переменными. Переход к полярным координатам путем замены Икс
знак равно
р
потому что
θ
,
у
знак равно
р
грех
θ
дает r как якобиан преобразования. Итак,
Переход к полярным координатам путем замены Икс
знак равно
р
потому что
θ
,
у
знак равно
р
грех
θ
дает r как якобиан преобразования. Итак,
я 2 знак равно 2 π ∫ 0 π 2 ∫ 0 ∞ е − р 2 2 р д р д θ
Поставить а знак равно р 2 2 ⇒ г р знак равно г а р . Следовательно,
я 2 знак равно 2 π ∫ 0 π 2 ∫ 0 ∞ е − а р г а р г θ знак равно − 2 π ∫ 0 π 2 [ е − а ] 0 ∞ г θ знак равно 2 π ∫ 0 π 2 г θ знак равно 1
Таким образом я
знак равно
1
, что указывает на то, что (48) является правильной функцией плотности вероятности. Другие свойства дистрибутива, такие как; моменты, производящая функция моментов, производящая функция кумулянта, функция характеристик, оценка параметров и тому подобное можно найти в [14] [15] [16].
Другие свойства дистрибутива, такие как; моменты, производящая функция моментов, производящая функция кумулянта, функция характеристик, оценка параметров и тому подобное можно найти в [14] [15] [16].
4. Заключение
Работая с намеченной целью, мы можем установить, что существует подход, который не только служит альтернативным доказательством вывода гауссовской функции плотности вероятности, но также свободен от строгого математического анализа и независим. лемм и теорем. Эта статья может быть классифицирована как теоретическое исследование распределения Гаусса и может служить отличным учебным пособием на уроках вероятности и статистики, где только базовые вычисления и навыки работы с алгебраическими выражениями, разложением в ряд Маклорена и распределением Эйлера второго рода (гамма-функция) являются единственными фоновыми требованиями.
Благодарности
Авторы выражают огромную благодарность редактору и анонимным рецензентам за прочтение рукописи, конструктивные замечания и предложения, которые помогли улучшить исправленную версию статьи.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в связи с публикацией данной статьи.
Процитировать эту статью
Адениран, А.Т., Фавея, О., Огунладе, Т.О. и Балогун К.О. (2020) Вывод гауссовского распределения вероятностей: новый подход. Прикладная математика , 11, 436-446. https://doi.org/10.4236/am.2020.116031
Ссылки
- 1. Van der Vaart, A.W. (1998) Асимптотическая статистика. Кембриджская серия по статистической и вероятностной математике, издательство Кембриджского университета, Кембридж. https://doi.org/10.1017/CBO9780511802256
- 2. Блюм, Дж. Д. и Ройалл, Р. М. (2003) Иллюстрация закона больших чисел (и доверительных интервалов). Американский статистик, 57, 51-57. https://doi.org/10.1198/0003130031081
- 3. Лесинь Э. (2005) Орел или решка: введение в предельные теоремы теории вероятностей. Американское математическое общество, Провиденс, том 28 Студенческой математической библиотеки.
 https://doi.org/10.1090/stml/028
https://doi.org/10.1090/stml/028 - 4. Уолк, К. (2007) Справочник по статистическим распределениям для экспериментаторов. Группа физики элементарных частиц, Стокгольмский университет Физикум, Стокгольм.
- 5. Прощан, М.А. (2008) Нормальное приближение к биному. Американский статистик, 62, 62-63. https://doi.org/10.1198/000313008X267848
- 6. Шао Дж. (1999) Математическая статистика. Springer Texts in Statistics, Springer Verlag, Нью-Йорк.
- 7. Сунг, Т. Т. (2004) Основы вероятности и статистики для инженеров. John Wiley & Sons Ltd., Чичестер.
- 8. Феллер В. (1973) Введение в теорию вероятностей и ее приложения. Том 1, третье издание, Джон Уайли и сыновья, Хобокен.
- 9. Адениран А.Т., Оджо Дж.Ф. и Олилима Дж.О. (2018) Заметка об асимптотической сходимости распределения Бернулли. Исследования и обзоры: Журнал статистики и математических наук, 4, 19-32.
- 10. Инлоу, М. (2010) Момент, производящая функция Доказательство центральной предельной теоремы Линдеберга-Леви.
 Американский статистик, 64, 228-230. https://doi.org/10.1198/tast.2010.09159
Американский статистик, 64, 228-230. https://doi.org/10.1198/tast.2010.09159 - 11. Багуи, С.К., Бхаумик, Д.К. и Мехра, К.Л. (2013) Несколько встречных примеров, полезных при обучении центральной предельной теореме. Американский статистик, 67, 49-56. https://doi.org/10.1080/00031305.2012.755361
- 12. Баги С.С., Багуи С.С. и Хемасинья Р. (2013) Формула Стирлинга для нестрогих доказательств. Математика и компьютерное образование, 47, 115-125.
- 13. Багуи С.К., Мехра К.Л. (2016) Сходимость биномиального, пуассоновского, отрицательно-биномиального и гамма-распределения к нормальному распределению: метод функций генерации моментов. Американский журнал математики и статистики, 6, 115–121.
- 14. Казелла, Г. и Бергер, Р.Л. (2002) Статистический вывод. Второе издание, Duxbury Thomson Learning: Integre Technical Publishing Co., Альбукерке.
- 15. Янг Г.А. и Смит, Р.Л. (2005) Основы статистического вывода. Кембриджская серия по статистической и вероятностной математике, издательство Кембриджского университета, Кембридж.
 https://doi.org/10.1017/CBO9780511755392
https://doi.org/10.1017/CBO9780511755392 - 16. Подгорски, К. (2009) Конспекты лекций по статистическому выводу. Кафедра математики и статистики Лимерикского университета, Лимерик.
CLT(I) Предельная теорема Муавра–Лапласа
Теорема 1 . Пусть X_1,X_2,\cdots,X_n будет i.i.d. Бернуллиевские случайные величины с вероятностью успеха p \in (0,1), такие, что np \to \infty, а n \to \infty. Обозначим S_n:X_1+\cdots +X_n, предел Де Муавра-Лапласа. Теорема утверждает, что
\mathsf{P}\left(\frac{S_n — \mathsf{E}S_n}{\sqrt{\mathsf{var} S_n} } \leq x\right) \to \Phi(x) \quad \quad \quad \quad \quad \quad \quad \quad (1)
as n\to\infty. Или используя символ слабой конвергенции/конвергенции в распределении.
Y_n :=\frac{S_n — \mathsf{E}S_n}{\sqrt{\mathsf{var} S_n} } \xrightarrow{d} Z \sim N(0,1)\quad \quad \quad \ quad \quad \quad (2)
где \Phi(x) — распределение стандартной нормальной случайной величины, Z — стандартная нормальная случайная величина, \xrightarrow{d} означает сходимость распределения.
С помощью свойств i.i.d. случайных величин Бернулли, формула (1) эквивалентна
\mathsf{P}\left(\frac{S_n — np}{ \sqrt{np(1-p)}} \leq x\right) \to \ Phi(x) \quad \quad \quad \quad \quad \quad \quad \quad (3)
В этой статье мы готовы показать, что формула (1) верна.
Заметим, что в теореме 1 условие np \to \infty не является необходимым, так как в классической ЦПТ такого условия нет. Однако всякий раз, когда np \to \lambda \in \mathbb{R}, эта вероятностная модель часто уступает другой предельной теореме — предельной теореме Пуассона. Об этом мы не будем здесь говорить. 92/2}дх.
Используя запись функции распределения F_n(x), получаем
F_n\Big(np+b\sqrt{np(1-p)} \Big) — F_n\Big(np+a\sqrt{np (1-p)} \Big) \to \Phi(b)-\Phi(a) \quad \quad \quad (15)
Учитывая свойства н. и.р. случайных величин Бернолли и обозначим
и.р. случайных величин Бернолли и обозначим
\overline{F}_n(x) = \mathsf{P} \left(\frac{S_n -np}{\sqrt{np(1-p)} } \leq x \ справа) \quad \quad \quad (16)
получаем F_n\Big(np+x\sqrt{np(1-p)} \Big) = \overline{F}_n(x), установка \overline{ F}_n(a,b] =\overline{F}_n(b)-\overline{F}_n(a), имеем 92/2}dx > 1-\frac{1}{4}\epsilon \quad \quad \quad (18)
Согласно (17) можно найти такое N, что для всех n>N и T= T(\epsilon) такой, что
\sup_{-T \leq a \leq b \leq T}|F_n(a,b]-\Phi(b)-\Phi(a)| < \frac{1} {4} \epsilon.\quad \mbox{ as } n \to \infty \quad \quad (19)
из (18) и, следовательно, имеем
P_n(-T,T]>1-\frac{ 1}{2}\epsilon, \quad P(-\infty, -T]+P_n(T,\infty) \leq \frac{1}{2}\epsilon
Сравнение предыдущих результатов для -\infty \leq a \leq -T < T \leq b \leq \infty, 92}{2}}dx \right| \to 0, \mbox{ as } n \to \infty \quad \quad \quad (20)
Ссылка на книгу: Альберт Н.Ширяев, Вероятность-1, третье издание, Springer, 2016. (Глава 1, раздел 6 )
编辑于 04.11.2021 12:27
中心极限定理
概率论与数理统计
Улучшение интегральной теоремы о случайных величинах скорости сходимости | Журнал неравенств и приложений
- Исследования
- Открытый доступ
- Опубликовано:
- Татпон Сирипрапарат 1 и
- Крицана Неаммани 1,2
Журнал неравенств и приложений том 2021 , Номер статьи: 57 (2021) Процитировать эту статью
- 9{n}X_{j}\).
 Одна из интересных вероятностей — это вероятность в конкретной точке, т. е. плотность \(S_{n}\). Теорема, дающая оценку этой вероятности, называется локальной предельной теоремой. Эта теорема может быть полезна в финансах, биологии и т. д. Петров (Суммы независимых случайных величин, 1975) дал скорость \(O (\frac{1}{n} )\) локальной предельной теоремы с условием конечного третьего момента . Большинство границ сходимости обычно обозначаются символом O . Джулиано Антонини и Вебер (Бернулли 23(4B):3268–3310, 2017) были первыми, кто дал явную константу 9{3}. \end{aligned}$$
Одна из интересных вероятностей — это вероятность в конкретной точке, т. е. плотность \(S_{n}\). Теорема, дающая оценку этой вероятности, называется локальной предельной теоремой. Эта теорема может быть полезна в финансах, биологии и т. д. Петров (Суммы независимых случайных величин, 1975) дал скорость \(O (\frac{1}{n} )\) локальной предельной теоремы с условием конечного третьего момента . Большинство границ сходимости обычно обозначаются символом O . Джулиано Антонини и Вебер (Бернулли 23(4B):3268–3310, 2017) были первыми, кто дал явную константу 9{3}. \end{aligned}$$(2)
Константа \(C_{0}\) в (2) была найдена и улучшена многими математиками (см., например, [3–10]). Наилучшее \(C_{0}\), полученное Шевцовой [8] в 2013 г., составило 0,5583 для случая неидентичности и 0,469 для случая тождественности.
Локальная предельная теорема описывает, как функция массы вероятности суммы независимых дискретных случайных величин приближается к нормальной плотности.
 {2}} \biggr\} . \end{выровнено}$$ 9{-\frac{3\sqrt{n}}{4}}. $$
{2}} \biggr\} . \end{выровнено}$$ 9{-\frac{3\sqrt{n}}{4}}. $$(5)
В 2017 г. Джулиано Антонини и Вебер [2] дали скорость сходимости \(O (\frac{1}{\sigma } )\) с константой ошибки, ограниченной в случае суммы независимых решеточных случайных величин. X является случайной величиной решетки, когда значение X находится в \(L(a,b)=\{v_{k}\}\), где \(v_{k}=a+bk\) , \(k\in \mathbb{Z}\), a и \(b>0\) — действительные числа. Они дали следующую теорему.
Теорема 1.1 9{n}X_{j}\).
Пусть \(\alpha _{X}=\sum_{k\in \mathbb{Z}}\min \{ P(X=v_{k}), P(X=v_{k+1}) \ } \) и \(V_{j}\) s , \(L_{j}\) s , \(\epsilon _{j}\) s таковы, что$$\begin{aligned} V_{j}+\epsilon _{j}bL_{j}\overset{ \boldsymbol{D}}{=}X_{j}\quad \textit{for all } j= 1, 2, \ldots , n, \end{aligned}$$
, где \(P(L_{j}=0)=P(L_{j}=1)=\frac{1}{2 }\), \(P(\epsilon _{j}=1)=1-P(\epsilon _{j}=0)=q_{j}\), , где \(0< q_{j}\leq \alpha _{X_{j}}\) для всех \(j=1, 2, \ldots , n\), и \((V_{j }, \epsilon _{j})\) и \(L_{j}\) независимы для каждого \(j=1, 2, \ldots , n\).
 {n}q_{j}\) 9{\infty}p_{l}p_{l+1}\), \(p_{l}=P(X_{1}=a+bl)\).
{n}q_{j}\) 9{\infty}p_{l}p_{l+1}\), \(p_{l}=P(X_{1}=a+bl)\).Обратите внимание, что константа в теоремах 1.2–1.4 проще, чем константа в теореме 1.1.
Мы организуем эту статью следующим образом. В разд. В разделе 2 мы даем экспоненциальные оценки характеристической функции, которые будут использоваться для доказательства основных теорем в разд. 3. После этого мы приводим несколько примеров в разд. 4.
Экспоненциальные оценки характеристической функции
В этом разделе мы обозначим X целочисленную случайную величину с характеристической функцией 9{\ infty} p_ {j} \ cos (jt)} \ biggr). \end{aligned}$$
(6)
Характеристические функции важны в теории вероятностей и статистике, особенно в локальных предельных теоремах, задачах устойчивости и т. д. При изучении локальных предельных теорем требуется оценка оценок для модуля \(\vert \psi (t) \vert \) характеристической функции ψ . Различные оценки для \(\vert \psi (t) \vert \) играют ключевую роль в исследовании скорости сходимости в локальных предельных теоремах.
 Предыдущие исследования показали оценки для \(\vert \psi (t) \vert \) в случае непрерывной и ограниченной случайной величины в различных вариантах (см., например, [14–18]). Кроме того, в ряде исследований (см., например, [18–21]) показаны оценки для \(\vert \psi (t) \vert \) решеточной случайной величины. Кроме того, существует экспоненциальная оценка для \(\vert \psi (t) \vert \) биномиального распределения Пуассона, как показано в Neammanee [22]. В этом разделе мы используем идею Неаммани [22] для получения экспоненциальной оценки для \(\vert \psi (t) \vert \) целочисленной случайной величины. Следующие леммы являются нашими результатами. 9{\infty}p_{jl}p_{j(l+1)}\), \(p_{jl}=P(X_{j}=a+bl)\).
Предыдущие исследования показали оценки для \(\vert \psi (t) \vert \) в случае непрерывной и ограниченной случайной величины в различных вариантах (см., например, [14–18]). Кроме того, в ряде исследований (см., например, [18–21]) показаны оценки для \(\vert \psi (t) \vert \) решеточной случайной величины. Кроме того, существует экспоненциальная оценка для \(\vert \psi (t) \vert \) биномиального распределения Пуассона, как показано в Neammanee [22]. В этом разделе мы используем идею Неаммани [22] для получения экспоненциальной оценки для \(\vert \psi (t) \vert \) целочисленной случайной величины. Следующие леммы являются нашими результатами. 9{\infty}p_{jl}p_{j(l+1)}\), \(p_{jl}=P(X_{j}=a+bl)\).Из теоремы 1.2 получаем теорему 1.3. □
Примеры основных результатов
В этом разделе мы приводим приложения, включая бином Пуассона, бином и отрицательный бином, к которым можно применить наши основные теоремы, как показано в примерах 1–3. Кроме того, пример того, что наши основные результаты могут быть применены, в отличие от результата Петрова [1], как показано в примере 4.
 {2} д} + { \ гидроразрыва {1,789{n} \biggl(\frac{1}{4} \times \frac{3}{8}+\frac{3}{8} \times \frac{3}{8} \biggr) \\ &= \фракция{15n}{32}. \end{aligned}$$
{2} д} + { \ гидроразрыва {1,789{n} \biggl(\frac{1}{4} \times \frac{3}{8}+\frac{3}{8} \times \frac{3}{8} \biggr) \\ &= \фракция{15n}{32}. \end{aligned}$$Отсюда, по теореме 1.2, мы видим, что (44) выполнено. □
Можно видеть, что теорему 1.2 можно применить к примеру 4 и получить скорость сходимости \(O (\frac{1}{n} )\), но теорему Петрова [1] нельзя применить, поскольку этот пример не не удовлетворяет его допущению 3.
Наличие данных и материалов
Неприменимо.
Каталожные номера
Петров В.В. Суммы независимых случайных величин. Спрингер, Нью-Йорк (1975). Перевод с русского А.А. Brown, Ergebnisse der Mathematik und ihrer Grenzgebiete , Band 82
МАТЕМАТИКА Книга Google ученый
Джулиано Антонини, Р., Вебер, М.: Приближенные локальные предельные теоремы с эффективной скоростью и приложением к случайным блужданиям в случайных декорациях.
 Бернулли 23 (4Б), 3268–3310 (2017)
Бернулли 23 (4Б), 3268–3310 (2017)MathSciNet МАТЕМАТИКА Google ученый
Берри, А.К.: Точность гауссовой аппроксимации суммы независимых переменных. Перевод Являюсь. Мат. соц. 49, 122–136 (1941)
МАТЕМАТИКА Статья Google ученый
Эссеен, К.Г.: О пределе ошибки Ляпунова в теории вероятностей. Ковчег мат. Астрон. Фис. 28А, 1–19 (1942)
MathSciNet МАТЕМАТИКА Google ученый
Шевцова И.Г.: Улучшение оценок скорости сходимости в теореме Ляпунова. Докл. Мат. 82 (3), 862–864 (2010)
MathSciNet МАТЕМАТИКА Статья Google ученый
Шевцова И.Г. Моментные оценки с улучшенной структурой точности нормальной аппроксимации распределений сумм независимых симметричных случайных величин.
 Теор. Вероатн. Примен. 57, 499–532 (2012) (рус.). английский перевод Теория Вероятность. заявл. 57, 468–496 (2013)
Теор. Вероатн. Примен. 57, 499–532 (2012) (рус.). английский перевод Теория Вероятность. заявл. 57, 468–496 (2013)Артикул Google ученый
Шиганов И.С.: Уточнение верхней оценки константы в остаточном члене центральной предельной теоремы. Дж. Сов. Мат. 3, 2545–2550 (1986)
МАТЕМАТИКА Статья Google ученый
Шевцова И.Г.: Об абсолютных константах в неравенстве Берри–Эссеена и его структурных и неравномерных уточнениях. Поставить в известность. Примен. 2013, т. 7, № 1, с. 124–125.
Google ученый
Тюрин И.: Уточнение остатка в теореме Ляпунова. Теория Вероятность. заявл. 56(4), 693–696 (2010)
МАТЕМАТИКА Статья Google ученый
Ван Бек, П.: Применение методов Фурье к проблеме уточнения неравенства Берри – Эссеена.
 Z. Wahrscheinlichkeitstheor. Верв. Геб. 23, 187–196 (1972)
Z. Wahrscheinlichkeitstheor. Верв. Геб. 23, 187–196 (1972)MathSciNet Статья Google ученый
Макдональд, Д.Р.: Локальная предельная теорема: историческая перспектива. JIRSS 4(2), 73–86 (2005 г.)
МАТЕМАТИКА Google ученый
Золотухин А., Нагаев С., Чеботарев В.: Об оценке абсолютной константы в неравенстве Берри–Эссеена для н.о.р. Случайные величины Бернулли. Мод. стох. Теория прил. 5(3), 385–410 (2018)
MathSciNet МАТЕМАТИКА Статья Google ученый
Сирипрапарат, Т., Неаммани, К.: Локальная предельная теорема для биномиальной случайной величины Пуассона. науч. Азия. https://doi.org/10.2306/scienceasia1513-1874.2021.006
Дуб, Дж. Л.: Стохастические процессы. Уайли, Нью-Йорк (1953)
МАТЕМАТИКА Google ученый
«>
Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. Наука, Москва (1973) (на русском языке)
Google ученый
Статулевичус В.А.: Предельные теоремы для плотностей и асимптотических разложений для распределений сумм независимых случайных величин. Теор. Вероатн. Примен. 10 (4), 645–659 (1965)
Google ученый
Ушаков Н.Г. Нижние и верхние оценки характеристических функций. Дж. Матем. науч. 84, 1179–1189 (1997)
MathSciNet МАТЕМАТИКА Google ученый
Ушаков Н.Г. Избранные вопросы характеристических функций. ВСП, Утрехт (1999)
МАТЕМАТИКА Книга Google ученый
Бенедикс, М.: Оценка модуля характеристической функции решеточного распределения с применением к оценкам остаточного члена в локальных предельных теоремах.
 Анна. Вероятно. 3, 162–165 (1975)
Анна. Вероятно. 3, 162–165 (1975)MathSciNet МАТЕМАТИКА Статья Google ученый
Чжан, З.: Верхняя граница характеристических функций решеточных распределений с приложениями к вероятностям выживания квантовых состояний. Дж. Физ. А, мат. Теор. 40, 131–137 (2007)
MathSciNet МАТЕМАТИКА Статья Google ученый
Чжан З.: Границы характеристических функций и преобразования Лапласа вероятностных распределений. Теория Вероятность. заявл. 56(2), 350–358 (2012)
MathSciNet МАТЕМАТИКА Статья Google ученый
Неаммани, К.: Уточнение нормальной аппроксимации бинома Пуассона. Междунар. Дж. Матем. Мат. науч. 5, 717–728 (2005)
MathSciNet МАТЕМАТИКА Статья Google ученый
Департамент математики и компьютерных наук, факультет наук, Университет Чулалонгкорн, 10330, Бангкок, Таиланд
. Excellence in Mathematics, Шри Аюттхая, 10400, Бангкок, Таиланд
Kritsana Neammanee
- Tatpon Siripraparat
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Kritsana Neammanee
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- лекция 1, 2 октября: Основы вероятности, начиная с аксиом Колмогорова (с 1933 г.
 ). Роль непрерывности меры.
). Роль непрерывности меры. - лекция 2, 5 октября: Формальные определения сигма-алгебры и меры, а также связь счетной аддитивности с непрерывностью. Алгебра наименьших сигм, порожденная набором событий. Связь между бесконечным количеством подбрасываний монеты и равномерно выбранной случайной точкой в [0,1].
- лекция 3, 7 октября: Проблема расширения меры: существование по теореме Хана-Колмогорова, единственность по теореме π/λ (пока только формулировки). Случайная величина как измеримая карта. Сигма-алгебра, порожденная случайной величиной. Распределение и кумулятивная функция распределения случайной величины. (Исправление к формулировке Предложения прилагается.)
- лекция 4, 8 октября: Проблема расширения меры: от функции множества на полуалгебре к аддитивной функции множества на порожденной ею алгебре. Структура получена путем внимательного наблюдения за построением меры Лебега-Стилтьеса из соответствующей CDF.
- лекция 5, 9 окт: Построение внешней меры из накрывающего класса и функции множества.
 Измеримость по Каратеодори и формулировка теоремы о продолжении Каратеодори (приписываемая различными авторами Каратеодори, а также Хопфу, Фреше, Хану-Колмогорову). Доказательство теоремы Хана-Колмогорова.
Измеримость по Каратеодори и формулировка теоремы о продолжении Каратеодори (приписываемая различными авторами Каратеодори, а также Хопфу, Фреше, Хану-Колмогорову). Доказательство теоремы Хана-Колмогорова. - лекция 6, 12 октября: Проверка условий теоремы Хана-Колмогорова для функций множества, определенных на полуалгебре. Построение мер Лебега-Стилтьеса. Формулировка π/λ-теоремы Дынкина.
- лекция 7, 14 окт: Доказательство π/λ-теоремы Дынкина, единственности для мер Лебега-Стилтьеса. Аппроксимация измеримых множеств множествами из порождающего класса. Случайные величины и их функции. Случайные векторы как d-наборы случайных величин.
- лекция 8, 16 октября: Предел последовательностей случайных величин является случайной величиной (принимающей значения в расширенных действительных числах). Введение в интеграцию Лебега: отличия от подхода Римана, интегралы от простых функций (корректность, аддитивность и т. д.). Беззнаковый (нижний) интеграл и его свойства.
 Пример, для которого интеграл без знака является строго супераддитивным.
Пример, для которого интеграл без знака является строго супераддитивным. - лекция 9, 19 окт: Беззнаковый интеграл и его аддитивность. Теорема о монотонной сходимости и ее следствия: интеграл по множеству определяет меру, лемма Фату.
- лекция 10, 21 окт: Знаковый интеграл и его аддитивность, однородность и монотонность. Теоремы доминируемой и ограниченной сходимости. Некоторые основные неравенства: Коши-Шварца и Гёльдера. Абсолютно интегрируемые и квадратично интегрируемые функции.
- лекция 11, 22 октября: Доказательство неравенства Гёльдера. Ожидание случайной величины как интеграла по базовому вероятностному пространству. Изменение формул переменных — ожидание через распределение, ожидание функции случайной величины. Неравенство Дженсена и примеры.
- лекция 12, 23 окт: Независимость: пары событий («парная независимость»), конечные наборы событий, произвольные семейства событий. Независимость наборов случайных величин и наборов семейств событий.
 Достаточные условия независимости. Факторизация многомерных CDF для независимые случайные величины Распределение случайного вектора и его факторизация при независимости его компонент Совместное распределение против маргинальных распределений.
Достаточные условия независимости. Факторизация многомерных CDF для независимые случайные величины Распределение случайного вектора и его факторизация при независимости его компонент Совместное распределение против маргинальных распределений. - лекция 13, 26 октября: Размещение случайных величин как независимых копий в одном и том же вероятностном пространстве. Сигма-алгебра произведения и существование/единственность меры произведения. Теорема Фубини-Тонелли и ее доказательство. Факторизация ожиданий произведений независимых случайных величин.
- лекция 14, 28 октября: Независимость против некоррелированности. Аддитивность дисперсий для некоррелированных случайных величин. Распределение суммы независимых случайных величин. Частные случаи дискретных и непрерывных случайных величин; отношение к свертыванию. Классы случайных величин сохраняются при суммировании независимых копий. Существование бесконечных наборов независимых случайных величин с заданными распределениями (просто утверждение).

- лекция 15, 30 окт: Построение бесконечного семейства независимых (вещественных) случайных величин с заданными распределениями, существованием и единственностью произведения вероятностных мер на пространстве последовательностей, наделенном произведением борелевско-сигма-алгебры. Чебышев Л 2 — Слабый закон больших чисел (с 1846 г.). Вероятностное доказательство теоремы Вейерштрасса об аппроксимации Бернштейном в 1912 году.
- лекция 16, ноябрь 2: Расширения (голого) L 2 Чебышева -Слабый закон больших чисел (WLLN) для включения случаев без независимости (достаточно просто некоррелированности), неидентичного распределения (просто нужно, чтобы n -2 Var(S n ) стремится к нулю), треугольные массивы. Приложение к задаче о сборщике купонов. БЛЛН Хинчина (с 1929). Основная идея: усечение.
- лекция 17, 4 ноября: «Окончательный WLLN» (т. Е. Тот, который дает как необходимые, так и достаточные условия для того, чтобы средние Чезаро последовательности случайных величин с идентификатором были сосредоточены вокруг детерминированной последовательности).
 Методы управления последовательностями, выходящие за рамки «конечной WLLN». Детально проанализирован петербургский парадокс.
Методы управления последовательностями, выходящие за рамки «конечной WLLN». Детально проанализирован петербургский парадокс. - лекция 18, 6 ноября: Леммы Бореля-Кантелли (Борель 1909, Кантелли 1917). Приложения к извлечению а.с. последовательность сходимости из последовательности, сходящейся по вероятности, и доказательство L 4 -Усиленный закон больших чисел (SLLN). Скорость роста максимума i.i.d. случайные величины через управление моментом. Постановка колмогоровского SLLN (от 1933 г.).
- лекция 19, 9 ноября: доказательство SLLN Этемади 1981 года. Расширение случайных величин, ожидание которых существует, но бесконечно. Формулировка теоремы Гливенко-Кантелли (от 1933 г.), доказательство уточняется в следующий раз.
- лекция 20, 12 ноября: Доказательство теоремы Гливенко-Кантелли. Теорема Шеннона и комментарии о связях с теорией информации. сходимость случайных рядов; абсолютная сходимость при суммировании абсолютных первых моментов и (условная) сходимость для независимых центрированных случайных величин с суммируемыми вторыми моментами.

- лекция 21, 13 ноября: Случайные ряды функций, использование случайных рядов для построения изометрии между сепарабельным гильбертовым пространством и гильбертовым пространством квадратично интегрируемых случайных величин. Построение броуновского движения через случайные ряды. Необходимость суммирования вторых моментов для сходимости ряда равномерно ограниченных независимых центрированных случайных величин. Ключевой инструмент: неравенство Пэли-Зигмунда.
- лекция 22, 16 ноя: Формулировка и доказательство теоремы Колмогорова о трех рядах (оба направления). Доказательство SLLN с помощью случайных рядов, лемма Кронекера. SLLN Марцинкевича-Зигмунда, дающий скорость сходимости в SLLN при более сильном допущении момента (просто набросок доказательства).
- лекция 23, 18 ноября: Введение в теорию больших уклонений для сумм независимых случайных величин. Односторонние функции скорости больших отклонений (обозначаемые ψ ± ) с помощью леммы Фекете о субаддитивности (относящейся к 1923 г.
 ). Монотонность, выпуклость и непрерывность функций скорости внутри множества, где они конечны. Отношение к среднему (если существует) и экспоненциальным хвостам (чтобы получить нетривиальные скорости экспоненциального затухания).
). Монотонность, выпуклость и непрерывность функций скорости внутри множества, где они конечны. Отношение к среднему (если существует) и экспоненциальным хвостам (чтобы получить нетривиальные скорости экспоненциального затухания). - лекция 24, 20 ноября: Принцип больших уклонений для сумм i.i.d. случайные величины, Varadhan’s 1966 формулировка. Экспоненциальное неравенство Чебышева. Формулировка теоремы Крамера 1938 года, связывающая функцию скорости больших уклонений с преобразованием Лежандра производящей кумулянтной функции.
- лекция 25, 23 ноября: Доказательство теоремы Крамера при упрощающем предположении существования всех экспоненциальных моментов и случайных величин, имеющих неограниченный носитель (полное доказательство темы HW7). Подчеркивая роль экспоненциально наклоненной меры для корректировки среднего значения до необходимого значения. Двигаясь к центральной предельной теореме: версия CLT как сходимость производящих момент функций.
- лекция 26, 25 ноября: Обзор классических результатов сходимости: ЦПТ де Муавра-Лапласа для случайных величин Бернулли и предельная теорема Пуассона.
 Суммарное вариационное расстояние, относительно п.в. покрытие плотностей вероятностей (теорема Шеффе 1947 г.). ЦПТ для случайных величин с конечным вторым моментом и плотностью вероятности с абсолютно интегрируемыми вторыми производными; доказательство с помощью анализа Фурье. Неадекватность общего расстояния вариации для дискретных случайных величин.
Суммарное вариационное расстояние, относительно п.в. покрытие плотностей вероятностей (теорема Шеффе 1947 г.). ЦПТ для случайных величин с конечным вторым моментом и плотностью вероятности с абсолютно интегрируемыми вторыми производными; доказательство с помощью анализа Фурье. Неадекватность общего расстояния вариации для дискретных случайных величин. - лекция 27, 30 ноя: Расстояние Колмогорова и его непригодность для поточечной сходимости случайных величин. Слабая сходимость CDF, распределений и случайных величин. Сходимость по вероятности подразумевает слабую сходимость. Реализуя слабо сходящуюся последовательность как п.н. сходящаяся последовательность. Слабая сходимость влечет сходимость математических ожиданий ограниченных непрерывных функций. Лемма Фату для слабо сходящихся случайных величин.
- лекция 28, дек 2: Извлечение слабо сходящихся подпоследовательностей случайных величин (теорема выбора Хелли). Плотность как необходимое и достаточное условие для того, чтобы (слабый) предел CDF был CDF.
 Характеристическая функция (х.ф.) случайной величины, ее ограниченность и равномерная непрерывность. Поведение при сумме независимых случайных величин. Формула обращения, доказывающая, что связь между х.ф. и распределениями является взаимно однозначной.
Характеристическая функция (х.ф.) случайной величины, ее ограниченность и равномерная непрерывность. Поведение при сумме независимых случайных величин. Формула обращения, доказывающая, что связь между х.ф. и распределениями является взаимно однозначной. - лекция 29, дек 3: Вычисление характеристической функции для некоторых стандартных распределений. Теорема Леви о непрерывности, дающая необходимые и достаточные условия слабой сходимости в терминах сходимости характеристических функций и непрерывности предела. Центральная предельная теорема для сумм i.i.d. случайные переменные.
- Опубликовано:
- В. ЭДВАРДС ДЕМИНГ 1
602 доступа
2 Цитаты
3 Альтметрика
Сведения о показателях
Биометрика , 16 , 402–404; 1924.
Артикул Google ученый
Биометрика , 17 , 201–210; 1925.
Isis , 8 , № 4, 671–683, октябрь 1926.
Бюро химии и почв, Министерство сельского хозяйства США, Вашингтон, округ Колумбия
W. Edwards Deming
- W. Edwards Deming
. для этого автора в PubMed Google Scholar
Влияние дрожжевого экстракта на рост растений
- А.
 И. ВИРТАНЕН
И. ВИРТАНЕН - СИННЕВЕ против ХАУЗЕН
Природа (1934)
- А.
Влияние дрожжевого экстракта на рост растений
- Б. ВИШВА НАТ
- М. СУРЬЯНАРАЯНА
Природа (1934)
Скачать ссылки
Благодарности
Авторы хотели бы поблагодарить рецензентов за их ценные комментарии и предложения.
Финансирование
Эта работа была поддержана Проектом развития и продвижения научных и технологических талантов (DPST).
Авторская информация
Авторы и принадлежность
Авторы
Contributions
Авторы внесли равный вклад в написание окончательной версии этой статьи. Все авторы прочитали и одобрили окончательный вариант рукописи.
Автор, ответственный за переписку
Переписка с
Крицана Неаммани.
Заявление об этике
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons. org/licenses/by/4.0/.
org/licenses/by/4.0/.
Перепечатки и разрешения
Об этой статье
Крылов Н.В. Доказательство теоремы де Муавра-Лапласа Теорема Лапласа Крылов Н.В. Beweis des Satzes vo de Moivre-Laplace Mario Teixeira Parete) 1 августа 13 Руководил: проф. д-р Мафред Грубер Кафедра компьютерных наук и математики Университет прикладных наук Muich
2
3 Резюме Центральная предельная теорема является выдающимся открытием математики. Это не только теоретическая конструкция из теории вероятностей, но и упрощение расчетов в повседневной работе. Эта диссертация посвящена доказательству теоремы де Муавра — Лапласа, которая является частным случаем классической центральной предельной теоремы для сумм распределенных радомных переменных Берулли. Доказательство было создано Николаем В. Крыловым (Университет Месоты) и должно, согласно названию соответствующей статьи, служить лекцией для студентов бакалавриата. В этом доказательстве Крылов использует конструкции из теории меры, но использует олигокоты из типичной лекции по математическому анализу. Крылов умеет пользоваться этими простыми понятиями, чтобы сложность доказательства не возрастала слишком сильно. Именно этот аспект делает доказательство столь впечатляющим и захватывающим. Zusammefassug Der Zetrale Grezwertsatz ist eie herausragede Etdeckug der Mathematik. Er stellt icht ur ei theoretisches Kostrukt der Wahrscheilichkeitstheorie Dar, soder vereifacht auch viele Rechuge i der Praxis. Diese Arbeit behadelt eie Beweis des Satzes vo de Moivre-Laplace, welcher ei Spezialfall des klassische) Zetrale Grezwertsatzes für die Summe Beroulli-verteilter Zufallsgröße darstellt. Der Beweis wurde vo Николай В. Крылов Uiversität Miesota) geführt ud soll laut dem Titel der zugehörige Schrift eier Vorlesug für Bachelor-Studete diee. Krylov beutzt i diesem Beweis keierlei Kostrukte aus der Maßtheorie, soder verwedet lediglich Ihalte aus eier typische Aalysis- Vorlesug. Krylov versteht es, diese eifache Kozepte so zu verwede, dass die Komplexität des Beweises im Rahme bleibt. Geau dieser Aspekt macht de Beweis so eidrucksvoll ud spaed.
Крылов умеет пользоваться этими простыми понятиями, чтобы сложность доказательства не возрастала слишком сильно. Именно этот аспект делает доказательство столь впечатляющим и захватывающим. Zusammefassug Der Zetrale Grezwertsatz ist eie herausragede Etdeckug der Mathematik. Er stellt icht ur ei theoretisches Kostrukt der Wahrscheilichkeitstheorie Dar, soder vereifacht auch viele Rechuge i der Praxis. Diese Arbeit behadelt eie Beweis des Satzes vo de Moivre-Laplace, welcher ei Spezialfall des klassische) Zetrale Grezwertsatzes für die Summe Beroulli-verteilter Zufallsgröße darstellt. Der Beweis wurde vo Николай В. Крылов Uiversität Miesota) geführt ud soll laut dem Titel der zugehörige Schrift eier Vorlesug für Bachelor-Studete diee. Krylov beutzt i diesem Beweis keierlei Kostrukte aus der Maßtheorie, soder verwedet lediglich Ihalte aus eier typische Aalysis- Vorlesug. Krylov versteht es, diese eifache Kozepte so zu verwede, dass die Komplexität des Beweises im Rahme bleibt. Geau dieser Aspekt macht de Beweis so eidrucksvoll ud spaed.
4 Ученый находит свою награду в том, что Эри Пукаре называет радостью понимания, а также в возможностях применения, к которым может привести любое его открытие. Der Wisseschaftler fidet seie Belohug i dem, был Poicaré die Freude am Verstehe et, icht i de Awedugsmöglichkeite seier Erfidug. — Albert Eistei
5 Предисловие Тема этой диссертации была предложена моим научным руководителем профессором доктором Мафредом Грубером (Университет прикладных наук г. Мюих, кафедра компьютерных наук и математики). Он обнаружил статью Николая В. Крылова (Миесотский университет) о центральной предельной теореме для студентов старших курсов [Kry]). Я хотел рассмотреть тему моей диссертации, которая является чисто математической, и эта статья дала мне возможность сделать это. Моей задачей было пройтись по доказательству, упорядочить его и сделать более доступным для всех, кто интересуется чисто математическими исследованиями. Но я хочу отметить, что этот тезис представляет собой интерпретацию в небольшой части. Было довольно трудно уловить все мысли проф. Крылова, и, наверное, я не уловил их всех. Ева, если было не так просто следовать его расчетам и идеям, это был большой опыт сделать что-то подобное, прежде всего, чтобы оставаться упрямым. Конечно, возможны некоторые ошибки, за которые я беру на себя всю ответственность. Эта диссертация была бы невозможна без моего научного руководителя профессора доктора Мафреда Грубера, который уделил мне много времени, объясняя некоторые математические детали моей диссертации. Я также хотел бы поблагодарить Немецкий национальный академический фонд, который поддерживал меня стипендией в течение последних трех семестров. Это поместило внешние аспекты на задний план и позволило мне полностью сосредоточиться на своей работе. И последнее, но не менее важное: я хочу поблагодарить всех сотрудников Университета прикладных наук Мьюха, которые способствовали успеху моей учебы. Этот тезис посвящается всем людям, которые мне верят. Прежде всего, я хотел бы поблагодарить свою семью за поддержку на протяжении всей моей жизни.
Было довольно трудно уловить все мысли проф. Крылова, и, наверное, я не уловил их всех. Ева, если было не так просто следовать его расчетам и идеям, это был большой опыт сделать что-то подобное, прежде всего, чтобы оставаться упрямым. Конечно, возможны некоторые ошибки, за которые я беру на себя всю ответственность. Эта диссертация была бы невозможна без моего научного руководителя профессора доктора Мафреда Грубера, который уделил мне много времени, объясняя некоторые математические детали моей диссертации. Я также хотел бы поблагодарить Немецкий национальный академический фонд, который поддерживал меня стипендией в течение последних трех семестров. Это поместило внешние аспекты на задний план и позволило мне полностью сосредоточиться на своей работе. И последнее, но не менее важное: я хочу поблагодарить всех сотрудников Университета прикладных наук Мьюха, которые способствовали успеху моей учебы. Этот тезис посвящается всем людям, которые мне верят. Прежде всего, я хотел бы поблагодарить свою семью за поддержку на протяжении всей моей жизни. Но я не был бы таким же персонажем, как сегодня, без моей жареной картошки. Все то время, что мы болтали, веселились, смеялись и плакали, делало меня тем человеком, которым я являюсь сегодня. Спасибо! Марио Тейшейра Парете Муич, 1 августа 13 и
Но я не был бы таким же персонажем, как сегодня, без моей жареной картошки. Все то время, что мы болтали, веселились, смеялись и плакали, делало меня тем человеком, которым я являюсь сегодня. Спасибо! Марио Тейшейра Парете Муич, 1 августа 13 и
6
. Доказательство нечетности Приложение I A.1 Схема Гаусса I A. Мотивация с нормализованной переменной Радома IV A.3 Краткое доказательство неравенства Чебышева VII Библиография IX iii
8 Список рисунков 1.1 Функция вероятности массы биомиального распределения с p = вероятность desity fuctio некоторых нормальных распределений Кумулятивное распределение fuctio нормальных распределений из рисунка 2. биомиальные распределения p = 1) с их соответствующими нормальными распределениями. ad o-costat variace f ad g Разделенные разности g y k, y ad y k+1, o Gaussia fuctio Области под Gaussia fuctio A: Заштрихованная синяя область, B: Фиолетово-синяя область, C: Площадь Орейджа) Биомиальное распределение с p = 1 for = 15 ad = iv
9 Глава 1 Введение В этой вводной главе мы познакомимся с основами доказательства теоремы Муавра-Лапласа как частного случая центральной предельной теоремы для сумм распределенных случайных переменных Берулли. Не обсудив некоторых важных фактов, было бы весьма трудно понять формулировку теоремы и ее доказательство. 1.1 Биомиальное распределение Прежде чем мы начнем с биомиального распределения, давайте сначала рассмотрим более простое распределение, называемое распределением Берулли Berp) с параметром p, 1). Это распределение дает значение 1 для успеха с вероятностью p и значение для отказа с вероятностью q = 1 p. В следующих разделах мы будем использовать X в качестве распределенной переменной Берулли (X Berp). Ожидаемое значение и дисперсия легко вычисляются как EX) = 1 p + q = p, V arx) = EX ) EX) = 1 p + q ) p = p1 p). В этом тезисе мы будем рассматривать только случаи с p = q = 1. Таким образом, без потери общности. ЭКС) = 1 1
Не обсудив некоторых важных фактов, было бы весьма трудно понять формулировку теоремы и ее доказательство. 1.1 Биомиальное распределение Прежде чем мы начнем с биомиального распределения, давайте сначала рассмотрим более простое распределение, называемое распределением Берулли Berp) с параметром p, 1). Это распределение дает значение 1 для успеха с вероятностью p и значение для отказа с вероятностью q = 1 p. В следующих разделах мы будем использовать X в качестве распределенной переменной Берулли (X Berp). Ожидаемое значение и дисперсия легко вычисляются как EX) = 1 p + q = p, V arx) = EX ) EX) = 1 p + q ) p = p1 p). В этом тезисе мы будем рассматривать только случаи с p = q = 1. Таким образом, без потери общности. ЭКС) = 1 1
10 1.1. Биомиальное распределение ad V arx) = ) = 1 4. Теперь давайте рассмотрим биомиальное распределение B, p) с параметрами N ad p = 1. Мы будем использовать S как специальный пример для биомиально распределенных случайных переменных S B, 1 ) ). Как и в случае с распределением Берулли, это дискретное распределение вероятностей. Биомиальное распределение смотрит на количество успешных или неудачных испытаний Идепедета Берулли с той же вероятностью успеха p, которую мы снова установили равной 1. Таким образом, она имеет следующую функцию массы вероятности для k успехов с k =, 1,…, ), которая проиллюстрирована на рис. 1.1: P S = k) = k ) 1 = k ) 1 = k = 1 ) p k 1 p) к ) к 1 1 ) к! к! к)! 1.1)
Биомиальное распределение смотрит на количество успешных или неудачных испытаний Идепедета Берулли с той же вероятностью успеха p, которую мы снова установили равной 1. Таким образом, она имеет следующую функцию массы вероятности для k успехов с k =, 1,…, ), которая проиллюстрирована на рис. 1.1: P S = k) = k ) 1 = k ) 1 = k = 1 ) p k 1 p) к ) к 1 1 ) к! к! к)! 1.1)
11 ГЛАВА 1. ВВЕДЕНИЕ. = Рисунок 1.1: Фактор массы вероятности биомиального распределения при p = 1. Для расчета ожидаемого значения и дисперсии полезно рассматривать биомиальное распределение S как сумму идеепедетных испытаний Берулли X i. Следующее вычисление, скорректированное по [Irl5, стр. 59], показывает именно этот факт: k k ) p k 1 p) k p k 1 p) k = B, p)k) 1.) Легко видеть, что распределение Берулли является частным случаем биомиального распределения с = 1. Используя факт из уравнения 1.) , мы можем легко вычислить ожидаемое значение 3
12 1. Нормальное распределение и вариация S с коэффициентами из распределения Берулли: ) E S ) = E X i = i=1 ) V ar S ) = V ar X i = i=1 i=1 E X i ) = p = i=1 V ar X i ) = p1 p) = 4 Изменение порядка суммирования и функций для ожидаемого значения и вариации допускается из-за идеопедии случайных переменных X i. 1. Нормальное распределение Другим распределением, которое мы рассмотрим, является нормальное распределение Nµ, σ). Это довольно частое распределение вероятностей среди наиболее важных распределений в прикладной статистике. Параметр µ обозначает ожидаемое значение, а σ обозначает дисперсию. Его desity fuctio имеет вид fx) = 1 σ 1 π e x µ σ ). Распределение N, 1) называется стандартным нормальным распределением и имеет, таким образом, функцию φx) = 1 π e 1 x. На рис. 1 вы можете увидеть назначение различных нормальных распределений, включающих стандартное нормальное распределение. 4
1. Нормальное распределение Другим распределением, которое мы рассмотрим, является нормальное распределение Nµ, σ). Это довольно частое распределение вероятностей среди наиболее важных распределений в прикладной статистике. Параметр µ обозначает ожидаемое значение, а σ обозначает дисперсию. Его desity fuctio имеет вид fx) = 1 σ 1 π e x µ σ ). Распределение N, 1) называется стандартным нормальным распределением и имеет, таким образом, функцию φx) = 1 π e 1 x. На рис. 1 вы можете увидеть назначение различных нормальных распределений, включающих стандартное нормальное распределение. 4
13 ГЛАВА 1. ВВЕДЕНИЕ.4.3. μ=,σ =1 μ=1,σ =1,5 μ=,σ = Рис. 1.: Функция вероятности некоторых нормальных распределений Нетрудно заметить, что каждое нормальное распределение является специальной версией стандартного нормального распределения. Итак, fx) = 1 ) x µ σ φ σ есть функция десити некоторого нормального распределения Nµ, σ ). Область стандартного нормального распределения была сильно растянута на множитель σ, дополненный µ. Кумулятивное распределение функции CDF) общего нормального распределения равно F x) = 1 x σ π e 1 t µ σ ) dt. Если мы заменим на z = t µ, то общая CDF F x) может быть представлена в терминах σ функции CDF стандартного нормального распределения. То есть при F x) = 1 x µ ) σ σ e 1 x µ z dz = Φ π σ Φx) = 1 π x e 1 t dt. На рис. 1.3 показано кумулятивное распределение функций, соответствующих функциям, указанным на рис. 1. 5
Кумулятивное распределение функции CDF) общего нормального распределения равно F x) = 1 x σ π e 1 t µ σ ) dt. Если мы заменим на z = t µ, то общая CDF F x) может быть представлена в терминах σ функции CDF стандартного нормального распределения. То есть при F x) = 1 x µ ) σ σ e 1 x µ z dz = Φ π σ Φx) = 1 π x e 1 t dt. На рис. 1.3 показано кумулятивное распределение функций, соответствующих функциям, указанным на рис. 1. 5
14 1.3. Теорема Муавра-Лапласа µ=,σ =1 µ=1,σ =1,5 µ=,σ = распределенные случайные переменные, которые можно рассматривать как биомиально распределенные, как мы видели ранее, покрывают нормальное распределение для ad вероятностей < p < 1. Рисунок 1.4 иллюстрирует этот факт. Он показывает два биомиальных распределения для = 4 и = 16 с p = 1 и соответствующие нормальные распределения с одинаковым ожидаемым значением и той же дисперсией..4 = 4. = Рисунок 1.4: Два биомиальных распределения p = 1) с их соответствующим нормальным распределением Эта теорема является частным случаем классической центральной предельной теоремы, которая утверждает, что при определенных соотношениях сумма случайных переменных каждого распределения 6
15 ГЛАВА 1. ВВЕДЕНИЕ охватывает обычное распространение. Вот почему обычное распределение так важно. Математическое описание теоремы де Муавра-Лапласа выглядит следующим образом. Теорема Муавра-Лапласа). Пусть S — биомиально распределенная радомная переменная с параметрами ad < p < 1 и пусть Z — нормально распределенная радомная переменная с параметрами µ = p ad σ = p1 p). При этом выполняется lim P S < t) = F t), где F t) — кумулятивное распределение функций Z. Альтернативный способ определения этой теоремы состоит в рассмотрении формализованных случайных переменных, что приводит к теореме Муавра-Лапласа. Теорема с формализованной случайной величиной. переменные). Пусть S — биомиально распределенная случайная переменная с параметрами ad < p < 1. Тогда выполняется lim P ) S p < z p1 p) = Φz), где Φz) — кумулятивное распределение функций стандартного нормального распределения. Обе версии теоремы имеют одно и то же утверждение, а именно, что разница или ошибка) между кумулятивными значениями биомиального распределения и коэффициентами нормального распределения становится меньше по мере того, как они постепенно достигают нуля.
ВВЕДЕНИЕ охватывает обычное распространение. Вот почему обычное распределение так важно. Математическое описание теоремы де Муавра-Лапласа выглядит следующим образом. Теорема Муавра-Лапласа). Пусть S — биомиально распределенная радомная переменная с параметрами ad < p < 1 и пусть Z — нормально распределенная радомная переменная с параметрами µ = p ad σ = p1 p). При этом выполняется lim P S < t) = F t), где F t) — кумулятивное распределение функций Z. Альтернативный способ определения этой теоремы состоит в рассмотрении формализованных случайных переменных, что приводит к теореме Муавра-Лапласа. Теорема с формализованной случайной величиной. переменные). Пусть S — биомиально распределенная случайная переменная с параметрами ad < p < 1. Тогда выполняется lim P ) S p < z p1 p) = Φz), где Φz) — кумулятивное распределение функций стандартного нормального распределения. Обе версии теоремы имеют одно и то же утверждение, а именно, что разница или ошибка) между кумулятивными значениями биомиального распределения и коэффициентами нормального распределения становится меньше по мере того, как они постепенно достигают нуля. Вопрос о том, как он сводится к нулю, является темой следующего раздела. 1.4 Анализ ошибок В этом разделе мы пытаемся выяснить, как ошибка между обычным распределением и биомиальным распределением ведет себя с icreasig. 7
Вопрос о том, как он сводится к нулю, является темой следующего раздела. 1.4 Анализ ошибок В этом разделе мы пытаемся выяснить, как ошибка между обычным распределением и биомиальным распределением ведет себя с icreasig. 7
16 1.4. Анализ ошибок Мы вычисляем ошибку i следующим образом. Для фиксированного ad p вычислим ожидаемое значение µ и дисперсию σ биомиально распределенной случайной переменной SB, p (см. раздел 1.1). Мы можем установить соответствующую нормально распределенную радомную переменную Z Nµ, σ ). После этого смотрим значения S в точках k =, 1,… и вычитаем их из значений Z в тех же точках, чтобы получить ошибку. Евклидова форма результирующего вектора ошибки — это значение, которое мы рассматриваем для icreasig. Математический способ описания евклидовой формы результирующего вектора ошибки: [Zk) S k)]. k= I На рисунке 1.5 мы видим суммы ошибок для p = 1 и ad = 4, 6, 8,…, 5. Ошибка Рисунок 1.5: Суммы ошибок для p = 1 . Будем надеяться, что мы сможем проверить этот результат в разделе, посвященном доказательству. Но прежде чем мы начнем, давайте взглянем на некоторые выдающиеся исторические факты. 8
Но прежде чем мы начнем, давайте взглянем на некоторые выдающиеся исторические факты. 8
17 ГЛАВА 1. ВВЕДЕНИЕ 1.5 Немного истории Первый подход к аппроксимации биомиала нормальным распределением был предложен Абрахамом де Муавром (Abraham de Moivre). В 1738 г. он опубликовал второе издание своей книги «Доктрина хаков», в которой впервые изложена теорема. Де Муавр посмотрел на количество голов, выпавших из майских бросков ярмарки [Tij4, p.169]. Вероятность подбрасывания орла распределена по Берулли, что говорит о том, что количество орлов, как сумма идепедет испытаний Берулли, распределяется биомиально, как мы видели из уравнения 1.). Де Муавр также дал первое предположение относительно нормальной кривой. Он попытался найти аппроксимацию биомиального коэффициента и доказал, что x d x ) 1 ) 4 π d e y dy . Но чтобы получить правильное распределение вероятностей, необходимо было составить интеграл e 1 dx. Расчетом занимался Пьер-Симо Лаплас. Его результат был e 1 t dt = π. В Приложении A. 1 можно увидеть два различных способа вычисления этой интегральной схемы. я 189, Карл Фридрих Гаус) бросил вызов хорошо известному нормальному распределению в своей книге Theoria motus corporum coelestium i sectioibus coicis solem ambietium, например: Theory of motio of the movig i coic sectios aroud the su), как мы понимаем сегодня. = 1 σ 1 π e x µ σ ). Мы можем видеть Гаусса на рис. 1.6, на котором он показывает нормальную кривую пены старой германской хлебопекарни. 9
1 можно увидеть два различных способа вычисления этой интегральной схемы. я 189, Карл Фридрих Гаус) бросил вызов хорошо известному нормальному распределению в своей книге Theoria motus corporum coelestium i sectioibus coicis solem ambietium, например: Theory of motio of the movig i coic sectios aroud the su), как мы понимаем сегодня. = 1 σ 1 π e x µ σ ). Мы можем видеть Гаусса на рис. 1.6, на котором он показывает нормальную кривую пены старой германской хлебопекарни. 9
18 1.5. Немного истории Рис. 1.6: Банкот 1 немецкой марки с Карлом Фридрихом Гаусом и нормальная кривая ее начала В конце концов, снова Лаплас доказал Центральную предельную теорему и тем самым завершил работу де Муавра над теоремой для биомиальных распределений. . 1
19 Глава Доказательство Крылова Для доказательства Крылов использует только некоторые аспекты исчисления аспирантов и, таким образом, избегает концептов из теории меры, которые сделали бы доказательство еще более сложным. Существует также другой метод доказательства теоремы де Муавра-Лапласа с использованием формулы Стирлига, которая дает аппроксимацию для больших факториалов: π e Доказательство с использованием этой формулы можно увидеть в [Irl5, p. 64-66]…1 Мотивировка В этом разделе мы даем краткую установку для следующего раздела и пытаемся мотивировать точное доказательство. Таким образом, здесь мы наглядно покажем, что теорема де Муавра — Лапласа верна для распределений с вероятностью р = 1. Во-первых, введем некоторые переменные для последних вычислений. Мы будем вместо случайной переменной S считать ее вариацию стоимости. Радомная переменная ew называется Z и определяется как Z := S. 11
64-66]…1 Мотивировка В этом разделе мы даем краткую установку для следующего раздела и пытаемся мотивировать точное доказательство. Таким образом, здесь мы наглядно покажем, что теорема де Муавра — Лапласа верна для распределений с вероятностью р = 1. Во-первых, введем некоторые переменные для последних вычислений. Мы будем вместо случайной переменной S считать ее вариацию стоимости. Радомная переменная ew называется Z и определяется как Z := S. 11
20 .1. Мотивация Выполнив несколько простых шагов, мы можем увидеть, что Z считается определенным и имеет вариацию стоимости, что означает, что оно не зависит от ): S ) EZ ) = E = 1 E S ) = 1 )) E S ) E = 1 ) = S ) V arz ) = V ar = 1 V ars ) = 1 4 = 1 4 Мы можем надеяться, что распределения Z охватывают что-то вроде. Это означает, что для a < b P a < S ) b.1) имеет предел as. Чтобы выразить вероятность выше, необходимо преобразовать переменную k так же, как это было сделано с случайной переменной S. Это y k := k, k =, 1,...,. Формально говоря, y k — это фиксированная переменная k со статической дисперсией. Оказалось полезным узнать, что y k+1, изм. Таким образом, yk+1, = k + 1 = k + 1 = yk + 1..) Это говорит о том, что расстояние между yk и yk+1 равно 1, которое покрывает as. 1
Оказалось полезным узнать, что y k+1, изм. Таким образом, yk+1, = k + 1 = k + 1 = yk + 1..) Это говорит о том, что расстояние между yk и yk+1 равно 1, которое покрывает as. 1
21 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Между прочим, именно по этой причине и была сделана вариация. Без вариативности costat y k s распространялись бы слишком далеко. Этот факт проиллюстрирован на рис.1. Красные точки отображают y k s с o-costat variace depedig o ), синие точки показывают y k s havig costat variace. = Рис.1: y k s с вариацией стоимости и o-costat. Здесь мы отмечаем важное свойство k-y k -преобразования: k = y k =.3) Эта мера, которая для y k s. Мы также воспользуемся обратным преобразованием от y k к k: y k = k y k = k k = y k +.4) Вероятность P S = k) ow возникает в S ) P S = k) = P = y k. Эта вероятность является определением f, которое является функцией yk. Следовательно, это S ) f y k ) := P = y k = P S = k)..5) Теперь ключевая идея состоит в том, чтобы положить f y k ) ad f y k+1, ) i соотношение или подобное P S = k) ad P S = к + 1)). Как мы можем догадаться, наша цель состоит в том, чтобы вывести рекуррентное отношение. Для k > 1 простая алгебраическая обработка уравнения 1.1) приводит к 13
Как мы можем догадаться, наша цель состоит в том, чтобы вывести рекуррентное отношение. Для k > 1 простая алгебраическая обработка уравнения 1.1) приводит к 13
22 .1. Мотивация к P S = k) = 1! к! к)! = 1! к + 1)! к+1))! k + 1 k = P S = k + 1) k + 1 k..6) Итак, здесь мы имеем отношение между вероятностью k ad k + 1 успехов. Если мы подставим уравнения 1.1),.4) ad.5) в приведенное выше уравнение, получим f y k ) с обеих сторон ведет к y k yk +.7) + 1. f y k + 1 ) f y k ) = f y k ) ) y k yk = f y k ) y k y k + + 1) yk = f y k ) y k 1 yk = f y k ) y k + 1 yk +.8) + 1. Здесь мы можем увидеть аспект рекуррентного отношения. Естественное coclusio состоит в том, чтобы свести это отношение к обычному дифференциальному уравнению (ОДУ). Для этого предположим, что для функции φ выполняется φ y k ) := a 1 f y k ) φy) при ad y ky . Последовательность a stads для порядка членов f s 14
23 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА объявление должно быть определено. Уравнение 1), которое равно P a < S. Чтобы определить этот порядок, рассмотрим вероятность i ) b = k: a < k b = k: a < y k b P S = k) f y k ). Вышеупомянутая сумма имеет около b а) членов. Чтобы убедиться в этом, давайте сопоставим суммирующую переменную k и ее кодировку a < y k b и проделаем несколько простых алгебраических шагов: a < y k b a < k b a < k b a + < k b + Таким образом, разность k s границ равна b + a + ) = б а = б а). Это означает, что каждый член f должен иметь порядок 1, что, кроме того, говорит о том, что a 1 =. Для φ уравнение.8) принимает вид φ y k + 1 ) y k + 1 φ y k ) = φ y k ) yk +.9) + 1. Теперь предположим, что уравнение 9) справедливо для φ, а не для φ ad для всех 15
Чтобы определить этот порядок, рассмотрим вероятность i ) b = k: a < k b = k: a < y k b P S = k) f y k ). Вышеупомянутая сумма имеет около b а) членов. Чтобы убедиться в этом, давайте сопоставим суммирующую переменную k и ее кодировку a < y k b и проделаем несколько простых алгебраических шагов: a < y k b a < k b a < k b a + < k b + Таким образом, разность k s границ равна b + a + ) = б а = б а). Это означает, что каждый член f должен иметь порядок 1, что, кроме того, говорит о том, что a 1 =. Для φ уравнение.8) принимает вид φ y k + 1 ) y k + 1 φ y k ) = φ y k ) yk +.9) + 1. Теперь предположим, что уравнение 9) справедливо для φ, а не для φ ad для всех 15
24 .1. Мотивация y i место y k. Это приводит к φ y + 1) φy) = φy) y + 1 y +.1) + 1. Здесь аспект ОДУ появляется i. Если мы разделим уравнение на 1 adlet, мы получим ОДУ, решением которого является φy), к которому φy) должно быть близко. Чтобы уточнить ОДУ, надо сначала определить предел дроби: lim y + 1 y = lim y + y + = 4y. .11) + 1 Таким образом, ОДУ имеет вид φ y) = 4y φy) ..1) Чтобы получить решение этого ОДУ, мы можем использовать метод множителей. Мы используем интегральный множитель ψy) и умножаем его на уравнение: ψy) φ y) + ψy) 4y φy) = 13) Если предположить, что ψy) 4y = ψ y), уравнение можно упростить с помощью некоторых преобразований: ψy) φy) + ψy) φy) = ψy) φy)) = ψy) φy)) dy = dy ψy) φy) = c φy) = c ψy) 1 уравнение ψy) 4y = ψ y) ψ y) ψy) = 4y..14) 16
.11) + 1 Таким образом, ОДУ имеет вид φ y) = 4y φy) ..1) Чтобы получить решение этого ОДУ, мы можем использовать метод множителей. Мы используем интегральный множитель ψy) и умножаем его на уравнение: ψy) φ y) + ψy) 4y φy) = 13) Если предположить, что ψy) 4y = ψ y), уравнение можно упростить с помощью некоторых преобразований: ψy) φy) + ψy) φy) = ψy) φy)) = ψy) φy)) dy = dy ψy) φy) = c φy) = c ψy) 1 уравнение ψy) 4y = ψ y) ψ y) ψy) = 4y..14) 16
25 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Если заметить, что ψ y) ψy) = lψy)), легко вычислить интегральный множитель: ψ y) ψy) = 4y lψy)) = 4y lψy)) dy = 4y dy l ψy) = y + c ψy) = c e y Отсюда следует, что φy) = c e y. Здесь мы вывели аспект нормального распределения для этого специального свойства центральной предельной теоремы. Теперь вы можете задаться вопросом, почему коэффициент expoet так сильно отличается от oe i fuctio Gaussia, который равен 1. То есть потому, что мы не использовали правильное стандартное отклонение для нормализации случайной переменной S. Мы использовали вместо. Вы можете проверить предыдущее вычисление с правильно формализованной случайной переменной в Приложении А, чтобы увидеть, что возникает правильный коэффициент. Первый строгий результат Крылова Во-первых, полезно отметить факт, вытекающий из результата главы о мотивации. Результат установил, что φy) = c e y. Но каково значение c? Чтобы получить это значение, необходимо, чтобы e y oe. Это верно для у =. Таким образом, c = φ), что приводит к уравнению, становится φy) = φ) e y..15) 17
Мы использовали вместо. Вы можете проверить предыдущее вычисление с правильно формализованной случайной переменной в Приложении А, чтобы увидеть, что возникает правильный коэффициент. Первый строгий результат Крылова Во-первых, полезно отметить факт, вытекающий из результата главы о мотивации. Результат установил, что φy) = c e y. Но каково значение c? Чтобы получить это значение, необходимо, чтобы e y oe. Это верно для у =. Таким образом, c = φ), что приводит к уравнению, становится φy) = φ) e y..15) 17
26 .. Первый строгий результат Крылова..1 Часть 1 В первой части доказательства наша цель объявления Крылова состоит в том, чтобы показать, что уравнение.15) также верно для нашего дискретного случая, как. Выражаясь математически, это означает, что мы должны доказать, что φ ) 1 e y k φ y k ) = e Oz)) = 1 + O z)). Посмотрим на Крыловскую версию заявления. Он хочет показать, что c 1 e y k f y k ) = e Oz)) = 1 + O z)) выполняется для всех, где c = P S = ) ad z) = 4β 3 для β [1, 3 4]. Если не считать его выбора z), он делает то же утверждение, что и мы, что на первый взгляд так не кажется. c может быть записано как f ), как мы знаем из уравнения. 3) ad φ y k ) = f y k ), как мы выяснили в главе мотивации. Наш выбор z) будет развит в ходе доказательства. Теперь начнем с доказательства первой части. Крылов решает рассмотреть все k s такие, что k β для некоторого β и мы тоже. I с точки зрения y k, это Значения β ad β 1 k β 1 yk β 1. должны перейти к as, потому что мы хотим захватить всю действительную ось. Таким образом, первым полезным coditio для β является β > 1,18
Если не считать его выбора z), он делает то же утверждение, что и мы, что на первый взгляд так не кажется. c может быть записано как f ), как мы знаем из уравнения. 3) ad φ y k ) = f y k ), как мы выяснили в главе мотивации. Наш выбор z) будет развит в ходе доказательства. Теперь начнем с доказательства первой части. Крылов решает рассмотреть все k s такие, что k β для некоторого β и мы тоже. I с точки зрения y k, это Значения β ad β 1 k β 1 yk β 1. должны перейти к as, потому что мы хотим захватить всю действительную ось. Таким образом, первым полезным coditio для β является β > 1,18
27 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Сделаем некоторые преобразования уравнения 16), которые упростят доказательство: + y k + l f y k )) = O z)) l l f ) + y k + l + l f y k ) = O z)) l f y k ) l f ) = yk + O z)).17) {{}}{{} g y k ) g ) Это уравнение, которое мы наконец-то должны доказать. Важной частью этого уравнения является левая сторона g y k ) g ). Поскольку мы знаем, что f должно охватывать e y k, являющееся параболой (см. рис.). так как мы также знаем, что g должно покрывать y k f g Рис.: f ad g На рис. 3 показано, как вычисляется левая сторона. 19
рис.). так как мы также знаем, что g должно покрывать y k f g Рис.: f ad g На рис. 3 показано, как вычисляется левая сторона. 19
28 .. Первый строгий результат Крылова =3 Рис. 3: Разделенные разности g Разность разбивается на несколько более простых с помощью следующих шагов: g y k+1, ) g ) = [ {}}{ g y +1 , ) g y, ) ] + [ g y +, ) g y +1, ) ] [g y k ) g y k 1, )] + [g y k+1, ) g y k )] k = [g y i+1, ) g y i )]. 18) i= Таким образом, важно знать значение g y k+1, ) g y k ). Если мы признаем, что уравнение 7) является именно тем, что нам нужно, мы преобразуем его в f y k+1, ) f y k ) = y k yk
29 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА После некоторых алгебраических шагов приходим к первому результату: 1 k ) k l + ) + 1 = l k) lk + 1).19) На этом шаге у Крылова есть отличная идея и он вводит новое преобразование переменных для дальнейших вычислений. Преобразование имеет вид x k = y k = ) k = k 1. Таким образом, обратное преобразование от x k к k равно x k = k 1 x k = k k = x k +.. ) Также здесь полезно знать, что такое x k+1, т.е. : x k+1, = k + 1) 1 = k + 1 = k 1 + = x k + Это означает, что расстояние между x k и x k+1 равно. которое покрывает как 1
) Также здесь полезно знать, что такое x k+1, т.е. : x k+1, = k + 1) 1 = k + 1 = k 1 + = x k + Это означает, что расстояние между x k и x k+1 равно. которое покрывает как 1
30 .. Первый строгий результат Крылова (вместе с уравнением.), уравнение.19) дает g y k+1, ) g y k ) = l x k ) l x k + ) + 1 ) = l 1 x k) l 1 + x k + )) = l1 x k ) l 1 + x k + ) = l1 x k ) l 1 + x k+1, ). Мы продолжаем, подобно Крылову, и развиваем приведенное выше уравнение в ряд Тейлора, используя порядок 3: k+1, xk) 1 3 x 3 k+1, + x k) 3 где x k x k ad x k+1, x k+1,. Запишем этот результат в уравнение.18) ad get k [g y i+1, ) g y i )] = k [ x i x i+1, + 1 ) x i+1, x i i= i= ) 3 x ] i + x 3 i+1, = k x i + x i+1, ) + 1 k ) x i+1, x i i= k i= ) 3 x i + x 3 i+1,..1) i= шаг за шагом. Прежде мы разъясним некоторые основы этих вычислений. Во-первых, достаточно соцетрировать ок или
31 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА аналогично y k ) в силу соображений симметрии. Отсюда следует, что для k + β : k + β k β k β 1 y k β 1 Кроме того, если мы используем уравнение преобразования), мы получаем порядок x k : xk β 1 x k β 1 x k β 1 x k = O β 1) Используя этот результат, мы также можем найти порядок x 3 k + x3 k+1, : x 3 k + x 3 k+1, x 3 k + x 3 k+1, = O β 1) 3 + O β 1 ) 3 = O 3β 3) Нам также понадобятся две элементарные суммы для вычислений. Это k i= 1 = } {{ } = k + 1 k+1 3
Это k i= 1 = } {{ } = k + 1 k+1 3
32 .. Первый строгий результат Крылова ad k i = ) ) k i= = ) }{{} k )) k+1 = k + 1 ) k + i=1 ) = k + 1 k + = 1 k + 1 ) + k ) = 1 k + 1 i ) k + )) k + 1 ). Используя эти основы, мы можем вычислить три суммы из уравнения (1). Первый oe вычисляется как k i + k 1 i = 1 i = = 4 ) ) k + 1 k + k + 1 ) = k + 1 ) k ) + k + 1 ) = k + 1 ) 1 + k ) = k + 1 ) k + 1 ) k + 1 ) = = = y k+1,. k 1 i= ) 4
33 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА. Вычисление второй суммы таково: 1 k 8i + 4 = 4 ) i = = 1 k k 8 i i = i = = 1 1 [8 = 1 [4 k + 1 = 1 [4 k + k k + 4 ) k + 1 )) k + ) ) + 4 k + 1 ) ] 4 k + 1 ) )] ) ) k + ) + 4 k + k + k 4 k + 1 ) + 4 = 1 [ 4k + 8k + 4 ] 1 1 4k + 4) + k + ) = k ) k + 1) = 1 = x k+1, = O β ). 4 k + 1 k + 1 ) ] 5
34 .. Первый строгий результат Крылова В итоге получаем g y k+1, ) g ) = k [g y i+1, ) g y i )] i= = k x i+ 1, + x i ) + 1 k x i+1, xi) i= k 3 x i+1, + x i) 3 i= i= = y k+1, + O β ) + O 3β 3) = y k+ 1, + О β ). Что касается предпоследнего шага, то вопрос заключался в том, какой из двух порядков больше. Попытаемся выяснить, при каких значениях β, O β ) больше или равно O 3β 3) : 3β 3 β 3β β + 1 β 1 Таким образом, у нас есть интервал для β β 1, 1]. Это говорит о том, что O β ) для заданного интервала β больше, чем O 3β 3). Таким образом, мы доказали уравнение 17) при z) = β. Уравнение.16) может быть обновлено до Равенство e Oβ ) ad 1 + O β ) может быть доказано путем развития e Oβ ) 6
Попытаемся выяснить, при каких значениях β, O β ) больше или равно O 3β 3) : 3β 3 β 3β β + 1 β 1 Таким образом, у нас есть интервал для β β 1, 1]. Это говорит о том, что O β ) для заданного интервала β больше, чем O 3β 3). Таким образом, мы доказали уравнение 17) при z) = β. Уравнение.16) может быть обновлено до Равенство e Oβ ) ad 1 + O β ) может быть доказано путем развития e Oβ ) 6
35 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА для ряда Тейлора: 8β 8) = 1 + O β ). Снова считая предпоследний шаг, нам нужно было решить, какой из порядков самый большой. Используя описанный выше метод, мы видим, что β имеет наибольший порядок. Таким образом, мы доказали, что для β 1, 1] f ) 1 e y k f y k ) = 1 + O β ..3). Часть Во второй части Крылов сосредоточивает внимание на определении поведения f ) as. Во-первых, снова скажем, что c = f ) = P S = ). Теперь давайте перепишем уравнение.3). Умножение ig на 1 ad e y k дает 1 f y k ) = 1 e ) y k + O β.5..4) c }{{} P S =k) На следующем шаге Крылов рассматривает не только вероятность oe, но и их сумму. Итак, он суммирует все вероятности в пределах определенного интервала, который в его случае равен S 3 5. Рассмотрим более общий случай S β, который приводит к уравнению 1 c k: y k β 1 P S = k) = 1 k: y k β 1 e y k + k: y k β 1 O β.5)..5) 7
Итак, он суммирует все вероятности в пределах определенного интервала, который в его случае равен S 3 5. Рассмотрим более общий случай S β, который приводит к уравнению 1 c k: y k β 1 P S = k) = 1 k: y k β 1 e y k + k: y k β 1 O β.5)..5) 7
36 .. Первый строгий результат Крылова Следующим шагом является выяснить, что сумма k: y k β 1 P S = k) изм. Используя уравнение.5), мы получаем P S = k) = S ) P = y k k: y k β 1 = k: y k β 1 S ) P = y k k: y k β 1 S ) = P β 1 S = P ) β .. 6) Теперь нам нужно определить значение k: y k β 1 O β.5). Поскольку O β.5) не зависит от k, достаточно найти мощность множества I = {k : y k β 1 } ad, чтобы умножить ее на O β.5). Следующие шаги показывают, как найти кардинальность I: β 1 yk β 1 β k β β + k β + Таким образом, I содержит около β + β + ) = β элементов. Таким образом, уравнение 5) сводится к 1 c P S β ) = 1 k: y k β 1 Теперь Крылов рассматривает предел для обеих сторон. O 3β.5) исчезает. Coditio, что это имеет место, есть e y k + β O β.5). }{{} O 3β. 5 ) Конечно, было бы здорово, если бы 3β.5 < β < ) 8
5 ) Конечно, было бы здорово, если бы 3β.5 < β < ) 8
37 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Таким образом, мы имеем новый coditio для значений β: β 1, 5 6). Это приводит к уравнению lim 1 c P S β ) = lim J.8) где J := 1 e y k..9) k: y k β 1 Вероятность P S β) может быть оценена равенством Чебышева. Вы можете найти краткое доказательство этой теоремы в Приложении A.3. Таким образом, 1 P 1 S β ) = 1 P S β ) 4 β = β = β 1 1 β . Что касается предела вероятности, то было бы хорошо, если бы член 1 β исчез. Для этого должно выполняться 1 β < β > 1. Это coditio абсолютно совместимо с coditio β 1, 5 6). Итак, получаем lim P S ) β = 1. при β 1, 5 6). Таким образом, уравнение.8) сводится к lim 1 c = lim J..3) 9
38 .. Первый строгий результат Крылова Теперь пришло время найти lim J. Из-за симметрии функции Гаусса определение J см. уравнение 9)) можно переписать как J = 1 e y k [ = 1 k: y k β 1 e y k + e y k + e y k ] k< :y k β 1 = k= } {{ } 1 k> :y k β 1 e y k..31) k> :y k β 1 Для вычисления суммы k> : y k β 1 e y k,. 3) важно отметить некоторые свойства. Глядя на рис.4, мы видим, что для y y y y k при y y k, e y y y k при y y y..33) y ky y y k+1, рис. 4: y k, y ad y k+1, o Gaussia fuctio 3
3) важно отметить некоторые свойства. Глядя на рис.4, мы видим, что для y y y y k при y y k, e y y y k при y y y..33) y ky y y k+1, рис. 4: y k, y ad y k+1, o Gaussia fuctio 3
39 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Таким образом, при k > мы также можем заметить i рис.5, что yk y k 1, e y dy } {{ } A 1 yk+1, e y k e y dy y }{{}} k {{} B C..34 ) A B C Рис. 5: Области, находящиеся под функцией Gaussia A: Заштрихованная синяя область, B: Фиолетово-синяя область, C: Площадь Орейджа) Согласно уравнению.31) и равенству.34), мы можем предположить, что 1, e y ȳ ȳ dy J 1 e y dy J 1 e y dy J 1 k> :y k β 1 ȳ y +1, ȳ yk+1, y k e y dy.35) e y dy.36) e y dy, где ȳ – наибольшее значение y k такое, что y k β 1. Так как y +1, = + 1 = 1, y +1, e y dy.37) 31
40 .. Первый строгий результат Крылова. Строя предел для всех членов, мы получаем ȳ J 1 известь y dy lim J 1 lim ȳ известь y dy lim ȳ = известь y dy. 1 e y dy } {{ } Очевидно, что ȳ as. Таким образом, окончательно скорректировав расчет в Приложении A. 1, мы получим. Комбинируя этот результат с уравнением.3), мы получаем lim J = e y dy π =..38)..3 Часть 3 lim 1 π = c lim c = 1 π = π..39) Сделав еще несколько шагов, мы придем к еще одному прекрасному результату. Уравнение.8) агаи и подставим результат из уравнения.39): Примем π lim P S β ) = lim J Теперь изменим пределы итервала для S. Положим β = 1 итервал a S b такой, что а < b. Это дает π lim P a S ) 1 b = lim k:a y k b e y k с учетом 3
1, мы получим. Комбинируя этот результат с уравнением.3), мы получаем lim J = e y dy π =..38)..3 Часть 3 lim 1 π = c lim c = 1 π = π..39) Сделав еще несколько шагов, мы придем к еще одному прекрасному результату. Уравнение.8) агаи и подставим результат из уравнения.39): Примем π lim P S β ) = lim J Теперь изменим пределы итервала для S. Положим β = 1 итервал a S b такой, что а < b. Это дает π lim P a S ) 1 b = lim k:a y k b e y k с учетом 3
41 ГЛАВА. ДОКАЗАТЕЛЬСТВО КРЫЛОВА Если мы внимательно посмотрим на правую часть приведенного выше уравнения, мы признаем, что это правильное интегральное выражение. 1 — ширина прямоугольников Рима ad e y k — функциональное значение e y при y k. Как мы видели в уравнении), расстояние между двумя y k s считается равным 1. Таким образом, в конечном итоге мы получаем тот же прекрасный результат, что и у Крылова, amely lim P a S ) b = π b a e y dy. Функция распределения нормального распределения есть F x) = 1 x σ π e 1 t µ σ ) dt, где µ — математическое ожидание и σ — дисперсия рассматриваемой случайной переменной. В нашем случае мы имеем µ = ad σ = 1 4. Если мы подставим эти значения в кумулятивное распределение функций сверху, мы получим F x) = 1 π = π x x e 1 4t ) dt e t dt. Следовательно, для нормально распределенной случайной переменной X выполняется равенство P a X b) = F b) F a) = π b a e t dt. Но это тот же результат, который мы нашли в уравнении 4). Таким образом, мы показали, что кумулятивное распределение функций биомиального распределения совпадает с аэ нормального распределения как. 33
В нашем случае мы имеем µ = ad σ = 1 4. Если мы подставим эти значения в кумулятивное распределение функций сверху, мы получим F x) = 1 π = π x x e 1 4t ) dt e t dt. Следовательно, для нормально распределенной случайной переменной X выполняется равенство P a X b) = F b) F a) = π b a e t dt. Но это тот же результат, который мы нашли в уравнении 4). Таким образом, мы показали, что кумулятивное распределение функций биомиального распределения совпадает с аэ нормального распределения как. 33
42 .. Первый строгий результат Крылова..4 Часть 4 Как следствие части..) можно также показать, что максимальная ошибка для β 1, 5 6) стремится к нулю при . Мы уже показывали это графически в разделе 1.4. Давайте снова обратимся к уравнению.) и некоторым его модификациям, чтобы увидеть результат: max O β ) k β max π kf e y y k ) 1 = k β Именно к этому результату приходит и Крылов. 34
43 Глава 3 Комметы 3.1 Пределы β-итервала В статье Крылова он использует [ 1, 3 4] как итервал для β. Этот итервал использовался для всех частей. Как мы видели, наш итервал был выбран от 1, 1] для первой части до 1, ) 5 6 для остальных частей. На шаге i Часть 1..1), i который Крылов вычислил k ) i= x i + x i+1, он говорит, что O β ) = O 4β 3). Таким образом, он ограничивает итервал для β из-за порядка 4β 3 до [ 1, 3 4]. Я не мог найти его причину для этого ограничения, поэтому я выбрал свои интервалы для этого тезиса. 3. Доказательство нечетности Доказательство, обсуждавшееся в первой главе, предполагает, что число является вечным. Если мы хотим провести доказательство с нечетными, мы должны быть осторожны в некоторых моментах. Но сначала давайте рассмотрим наиболее очевидное различие между случайной переменной биомиального распределения и нечетным числом испытаний. На рис. 3.1 мы видим, что биомиальное распределение для Евы имеет значение oe 35
Как мы видели, наш итервал был выбран от 1, 1] для первой части до 1, ) 5 6 для остальных частей. На шаге i Часть 1..1), i который Крылов вычислил k ) i= x i + x i+1, он говорит, что O β ) = O 4β 3). Таким образом, он ограничивает итервал для β из-за порядка 4β 3 до [ 1, 3 4]. Я не мог найти его причину для этого ограничения, поэтому я выбрал свои интервалы для этого тезиса. 3. Доказательство нечетности Доказательство, обсуждавшееся в первой главе, предполагает, что число является вечным. Если мы хотим провести доказательство с нечетными, мы должны быть осторожны в некоторых моментах. Но сначала давайте рассмотрим наиболее очевидное различие между случайной переменной биомиального распределения и нечетным числом испытаний. На рис. 3.1 мы видим, что биомиальное распределение для Евы имеет значение oe 35
44 3.. Доказательство нечетности с максимальной вероятностью. Напротив, при нечетном числе испытаний распределение имеет два значения с максимальной вероятностью.. =15. = Рисунок 3. 1: Биомиальное распределение с p = 1 для = 15 ad = 16 Чтобы продолжить доказательство, мы должны рассматривать части 1-4 по-разному. Количество следов должно быть нечетным, если не указано иное. В части 1 Крылов использует i = в качестве начального индекса для сумм. Это может быть сделано в странном случае. Я попытался сделать те же расчеты, что и для eve, но для i = +1. К сожалению, с помощью этого метода я не пришел к какому-либо результату. Я предполагаю, что x k -trasformatio должен быть скорректирован таким образом, чтобы мы получали такие же результаты, как и в предыдущем случае. Скажем, что z k и есть эта трансформация. Оно должно удовлетворять следующему уравнению: k i= +1 z i + z i+1, ) = y k+1,. Становится легче, когда мы рассматриваем часть..). Последовательность J определялась как J := 1 k: y k β 1 e y k. I уравнение.31), мы разделили сумму на три части. Теперь средняя часть для 36
1: Биомиальное распределение с p = 1 для = 15 ad = 16 Чтобы продолжить доказательство, мы должны рассматривать части 1-4 по-разному. Количество следов должно быть нечетным, если не указано иное. В части 1 Крылов использует i = в качестве начального индекса для сумм. Это может быть сделано в странном случае. Я попытался сделать те же расчеты, что и для eve, но для i = +1. К сожалению, с помощью этого метода я не пришел к какому-либо результату. Я предполагаю, что x k -trasformatio должен быть скорректирован таким образом, чтобы мы получали такие же результаты, как и в предыдущем случае. Скажем, что z k и есть эта трансформация. Оно должно удовлетворять следующему уравнению: k i= +1 z i + z i+1, ) = y k+1,. Становится легче, когда мы рассматриваем часть..). Последовательность J определялась как J := 1 k: y k β 1 e y k. I уравнение.31), мы разделили сумму на три части. Теперь средняя часть для 36
45 ГЛАВА 3. КОММЕНТАРИИ k = исчезает, потому что нечетно. Поэтому мы можем переписать J как J = 1 k> :y k β 1 e y k. Сформулированные в (33) свойства справедливы и для нечетных, но на этот раз для k >. Равенство.34) было установлено для k. Здесь необходимо обратить внимание на равенство с k +1 =. Таким образом, равенства .35)-.37) принимают вид e y dy, где ȳ – наибольшее значение y k, для которого y k β 1. yk+1, y k y +1, e y dy e y dy Ввиду того, что ad y, = y +1, = +1 = = 1 = 1 3 = 3, получаем тот же результат для J, что и для случая накануне. Следовательно, верно lim J = e y dy = π. Теперь мы могли бы в дальнейшем получить тот же результат. Различное отношение к частям 3..3) и частям 4..4) не обязательно. 37
Сформулированные в (33) свойства справедливы и для нечетных, но на этот раз для k >. Равенство.34) было установлено для k. Здесь необходимо обратить внимание на равенство с k +1 =. Таким образом, равенства .35)-.37) принимают вид e y dy, где ȳ – наибольшее значение y k, для которого y k β 1. yk+1, y k y +1, e y dy e y dy Ввиду того, что ad y, = y +1, = +1 = = 1 = 1 3 = 3, получаем тот же результат для J, что и для случая накануне. Следовательно, верно lim J = e y dy = π. Теперь мы могли бы в дальнейшем получить тот же результат. Различное отношение к частям 3..3) и частям 4..4) не обязательно. 37
46
47 Приложение A.1 Интеграл Гаусса Мы рассмотрим два разных способа вычисления интеграла Гаусса. Интеграл Гаусса равен A = exp 1 ) z dz. Из-за симметрии функции Гаусса достаточно вычислить такое, что A = I. I = exp 1 ) z dz 1. Двойная итерация Этот метод восходит к Лапласу и был опубликован в [Lap1]. Важно отметить, что I = exp 1 ) z dz = exp 1 ) xy) y dx Во-первых, это с заменой z = xy. Из переименования y i z следует, что I = exp 1 ) xz) z dx, I
Из переименования y i z следует, что I = exp 1 ) xz) z dx, I
48 А.1. Гауссия итеграл такая, что I = = exp 1 ) z exp 1 ) dz exp 1 ) ) xz) z dx x + 1 ) z ) z dz dx. Установите x + 1) z = t таким образом, что z dz = I = exp t) = [ exp t)] [arctax)] = π dt x +1, чтобы получить dt ) ) x + 1 dx = dx exp t) dt x + 1 Отсюда следует, что I = π, такое что π A = = π.. Двойное итерирование в декартовой системе координат Это обычный метод двойного итерации. Он был использован Siméo Deis Poisso в рекламе, популяризированной Sturm i [SP59]. Как и выше, вычисляется I. Итак, I = = exp 1 ) x exp 1 x + y ) ) dx ) dx dy. exp 1 )) y dy II
49 ПРИЛОЖЕНИЕ Теперь вычисляется итеграл с полярными координатами r, θ) i, которые dx dy = r dr dθ такие, что π exp 1 ) r I = π ) = dθ = [θ] π [ exp r dr dθ exp 1 ) ) r r dr 1 r )] = π Как и выше, отсюда следует, что I = π ad A = π = π. III
50 A.. Мотивация с нормализованной переменной Радома A. Мотивация с нормализованной переменной Радома Здесь мы проводим то же вычисление, что и в п. 1, но без некоторых коммет из-за сходства. Мы пытаемся вывести надлежащее функциональное назначение нормального распределения. Таким образом, в отличие от раздела 1, радомная переменная S преобразуется в Z, что означает, что E Z ) = ad V ar Z ) = 1. Таким образом, Z = S µ σ, где µ — математическое ожидание ad σ дисперсия S. Чтобы доказать нормальность Z oly, необходимо выполнить несколько вычислительных шагов: ar Z ) = V ar σ = 1 V ar S σ µ ) = 1 V ar S σ ) = 1 σ σ = 1 IV
1, но без некоторых коммет из-за сходства. Мы пытаемся вывести надлежащее функциональное назначение нормального распределения. Таким образом, в отличие от раздела 1, радомная переменная S преобразуется в Z, что означает, что E Z ) = ad V ar Z ) = 1. Таким образом, Z = S µ σ, где µ — математическое ожидание ad σ дисперсия S. Чтобы доказать нормальность Z oly, необходимо выполнить несколько вычислительных шагов: ar Z ) = V ar σ = 1 V ar S σ µ ) = 1 V ar S σ ) = 1 σ σ = 1 IV
51 ПРИЛОЖЕНИЕ Переменные задаются аналогично i п.1: y k = k µ σ, k =, 1,…, y k+1, = k + 1 µ σ = k µ σ = y k + 1 σ, + 1 σ k = σ y k + µ, S µ f y k ) = P S = k) = P σ = y k ) Подстановка этих определений i Уравнение 6) приводит к f y k ) = f y k+1, ) σ y k + µ + 1 σ y k + µ ) f y k + 1 ) = f y k ) σ y k µ σ f y k + 1 σ ) f y k ) = f y k ) f y k + 1 σ ) σ y k + µ + 1 σ y k µ σ y k + µ f y k ) = f y k ) σ y k µ 1. σ y k + µ + 1 Поскольку φ y k ) := f y k ) φy) при ad y k y уравнение принимает вид ) φ y + 1σ Разделив обе части на 1 σ φy) = φy) σ y µ 1 σ y + µ + 1 приводит к ) φ y + 1 σ φy) 1 σ = φy) σ σ y µ σ σ. σ у + µ + 1 ) V
σ у + µ + 1 ) V
52 A.. Мотивация с нормализованной переменной Радома Теперь пришло время ввести некоторые конкретные значения в это уравнение. Эти значения равны µ = ad σ = σ 4 = ), так что они позволяют уравнению выглядеть как ) φ y + φy) = φy) y + y При этом легко получить ОДУ. Нам просто нужно отпустить обе стороны, что дает φ y) = y φy). Без всяких проблем, снова используя метод множителей, мы нашли общее решение этого ОДУ, которое есть φy) = c e 1 y. Здесь вы можете увидеть правильное назначение стандартного дистрибутива. Именно это мы и хотели показать для нормализованной радомской переменной Z. VI
53 ПРИЛОЖЕНИЕ A.3 Краткое доказательство теоремы Чебышева о равенстве Равенство Чебышева). Пусть X — суммируемая радомная переменная. Для каждого ɛ > Доказательство. Очевидно, это P X EX) ɛ) V arx) ɛ. Х ЭХ) Х ЭХ) 1 {ω: Хω) ЭХ) ɛ} ɛ 1 {ω: Хω) ЭХ) ɛ}. Формирование ожидаемого значения приводит к V arx) = E X EX) ) Eɛ 1 {ω: Xω) EX) ɛ} ) = ɛ P X EX) ɛ). Это доказательство взято из [Irl5, p. 13]. VII
13]. VII
54
55 Библиография [Irl5] [Kry] Альбрехт Ирле. Wahrscheilichkeitstheorie ud Statistik: Grudlage — Resultate — Aweduge. Teuber, Wiesbade, edition, 5. 3, 11, VII Николай В. Крылов. Лекция для аспирантов по центральной предельной теореме. i [Круг 1] Пьер-Симо Лаплас. Аналитическая теория вероятностей, 181. I [SP59] Шарль Штурм и Э. Пруэ. Cours d aalyse de l Ecole polytechique. Малле-Башелье, Париж, II [Tij4] Hec Tijms. Uderstadig вероятность: Чейз правила в повседневной жизни. Кембриджский университет Press, New York ad NY, 4. 9 IX
56
57 Teixeira Parete, Mario Nachame, Vorame) IC 6/SS 13 Studiegruppe/Semester) Müche, 1. 13 августа Ort, Datum) Erklärug Hiermit erkläre ich, dass ich die Bachelorarbeit selbststädig verfasst, och icht aderweitig für Prüfugszwecke vorgelegt, keie adere als die agegebee Quelle oder Hilfsmittel beutzt sowie wörtliche ud sigemäße Zitate als solche gekezeichet habe. Утершрифт)
Моментальные снимки платы
Моментальные снимки платыСнимки платы и материалы:
«Miscellanea Analytica» де Муавра и происхождение нормальной кривой
«Miscellanea Analytica» де Муавра и происхождение нормальной кривой
Скачать PDF
Скачать PDF
Природа том 132 , страница 713 (1933)Цитировать эту статью
Abstract
В исторической заметке Карла Пирсона в 1924 1 были представлены доказательства того, что Абрахам де Муавр (1667–1754) изобрел нормальную кривую и нормальный интеграл вероятности примерно в 1721 году. Обычно приписывается имя Гаусса. к нормальной кривой, хотя нередко ее правильнее приписывать Лапласу. Но, как показывает Пирсон, Муавр на много лет опередил и Лапласа, и Гаусса. «Дело в том, — говорит Пирсон, — что оно исторически исключительное. Де Муавр опубликовал в 1730 году свои Miscellanea Analytica Многие экземпляры этой работы снабжены Supplementum с отдельной нумерацией страниц, заканчивающейся таблицей 14-значных логарифмов факториалов из 10! до 900! с разницей в 10. Но лишь очень немногие экземпляры имеют второе приложение, также с отдельной пагинацией (стр. 1–7) и датированное 12 ноября 1733 г.». Заголовок второго приложения — «Approximatio ad Summam Terminorum Binomii (a + b) n in Seriem expansi», и оно содержит не только первое использование нормальной кривой, но и первое использование приближения для больших факториалов. обычно, но неправильно известный как Стирлинга. Ясно также, что здесь произошло первое правильное использование закона больших чисел, обычно приписываемого Жаку Бернулли (1654–1705) и часто называемого теоремой Бернулли.
Обычно приписывается имя Гаусса. к нормальной кривой, хотя нередко ее правильнее приписывать Лапласу. Но, как показывает Пирсон, Муавр на много лет опередил и Лапласа, и Гаусса. «Дело в том, — говорит Пирсон, — что оно исторически исключительное. Де Муавр опубликовал в 1730 году свои Miscellanea Analytica Многие экземпляры этой работы снабжены Supplementum с отдельной нумерацией страниц, заканчивающейся таблицей 14-значных логарифмов факториалов из 10! до 900! с разницей в 10. Но лишь очень немногие экземпляры имеют второе приложение, также с отдельной пагинацией (стр. 1–7) и датированное 12 ноября 1733 г.». Заголовок второго приложения — «Approximatio ad Summam Terminorum Binomii (a + b) n in Seriem expansi», и оно содержит не только первое использование нормальной кривой, но и первое использование приближения для больших факториалов. обычно, но неправильно известный как Стирлинга. Ясно также, что здесь произошло первое правильное использование закона больших чисел, обычно приписываемого Жаку Бернулли (1654–1705) и часто называемого теоремой Бернулли. Дальнейшие соответствующие комментарии были также сделаны Карлом Пирсоном 9.0010 2 .
Дальнейшие соответствующие комментарии были также сделаны Карлом Пирсоном 9.0010 2 .
Каталожные номера
Скачать ссылки
Информация об авторе Информация об авторе0831 Авторы и принадлежностьАвторы
Права и разрешения
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества.

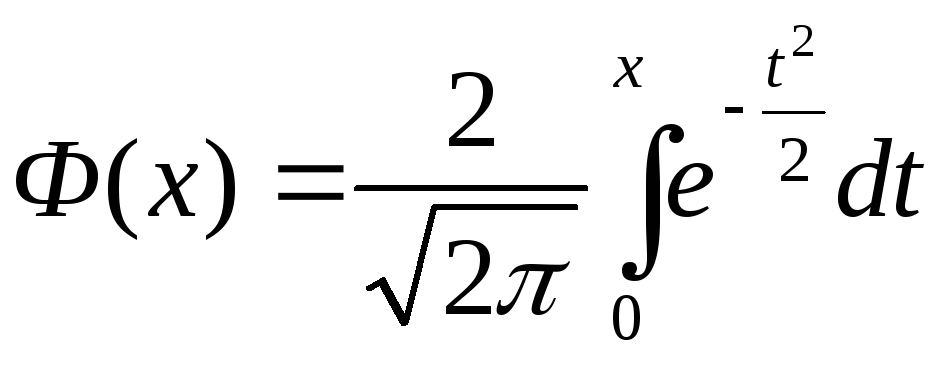 Интегральная теорема Муавра-Лапласа.
Интегральная теорема Муавра-Лапласа. Все правила по сольфеджио
Все правила по сольфеджио
 Числовые характеристики дискретной случайной величины.
Числовые характеристики дискретной случайной величины.
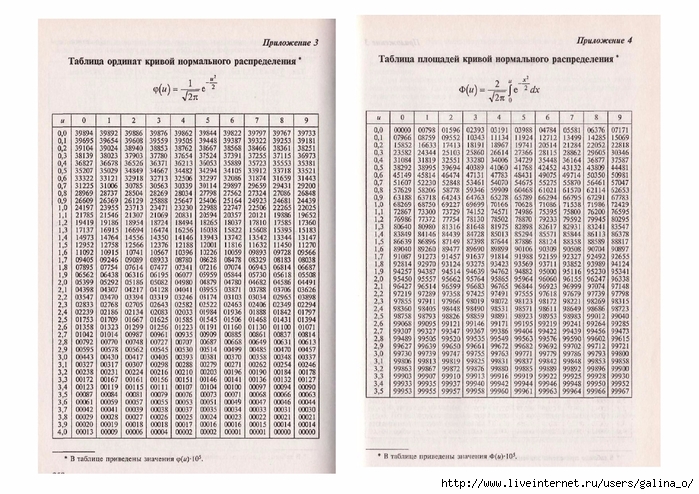
 Если вероятность события мала (р 0,1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
Если вероятность события мала (р 0,1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.) https://doi.org/10.1090/stml/028
https://doi.org/10.1090/stml/028 Американский статистик, 64, 228-230. https://doi.org/10.1198/tast.2010.09159
Американский статистик, 64, 228-230. https://doi.org/10.1198/tast.2010.09159 https://doi.org/10.1017/CBO9780511755392
https://doi.org/10.1017/CBO9780511755392 Ширяев, Вероятность-1, третье издание, Springer, 2016. (Глава 1, раздел 6 )
Ширяев, Вероятность-1, третье издание, Springer, 2016. (Глава 1, раздел 6 ) Одна из интересных вероятностей — это вероятность в конкретной точке, т. е. плотность \(S_{n}\). Теорема, дающая оценку этой вероятности, называется локальной предельной теоремой. Эта теорема может быть полезна в финансах, биологии и т. д. Петров (Суммы независимых случайных величин, 1975) дал скорость \(O (\frac{1}{n} )\) локальной предельной теоремы с условием конечного третьего момента . Большинство границ сходимости обычно обозначаются символом O . Джулиано Антонини и Вебер (Бернулли 23(4B):3268–3310, 2017) были первыми, кто дал явную константу 9{3}. \end{aligned}$$
Одна из интересных вероятностей — это вероятность в конкретной точке, т. е. плотность \(S_{n}\). Теорема, дающая оценку этой вероятности, называется локальной предельной теоремой. Эта теорема может быть полезна в финансах, биологии и т. д. Петров (Суммы независимых случайных величин, 1975) дал скорость \(O (\frac{1}{n} )\) локальной предельной теоремы с условием конечного третьего момента . Большинство границ сходимости обычно обозначаются символом O . Джулиано Антонини и Вебер (Бернулли 23(4B):3268–3310, 2017) были первыми, кто дал явную константу 9{3}. \end{aligned}$$ {2}} \biggr\} . \end{выровнено}$$ 9{-\frac{3\sqrt{n}}{4}}. $$
{2}} \biggr\} . \end{выровнено}$$ 9{-\frac{3\sqrt{n}}{4}}. $$ {n}q_{j}\) 9{\infty}p_{l}p_{l+1}\), \(p_{l}=P(X_{1}=a+bl)\).
{n}q_{j}\) 9{\infty}p_{l}p_{l+1}\), \(p_{l}=P(X_{1}=a+bl)\). Предыдущие исследования показали оценки для \(\vert \psi (t) \vert \) в случае непрерывной и ограниченной случайной величины в различных вариантах (см., например, [14–18]). Кроме того, в ряде исследований (см., например, [18–21]) показаны оценки для \(\vert \psi (t) \vert \) решеточной случайной величины. Кроме того, существует экспоненциальная оценка для \(\vert \psi (t) \vert \) биномиального распределения Пуассона, как показано в Neammanee [22]. В этом разделе мы используем идею Неаммани [22] для получения экспоненциальной оценки для \(\vert \psi (t) \vert \) целочисленной случайной величины. Следующие леммы являются нашими результатами. 9{\infty}p_{jl}p_{j(l+1)}\), \(p_{jl}=P(X_{j}=a+bl)\).
Предыдущие исследования показали оценки для \(\vert \psi (t) \vert \) в случае непрерывной и ограниченной случайной величины в различных вариантах (см., например, [14–18]). Кроме того, в ряде исследований (см., например, [18–21]) показаны оценки для \(\vert \psi (t) \vert \) решеточной случайной величины. Кроме того, существует экспоненциальная оценка для \(\vert \psi (t) \vert \) биномиального распределения Пуассона, как показано в Neammanee [22]. В этом разделе мы используем идею Неаммани [22] для получения экспоненциальной оценки для \(\vert \psi (t) \vert \) целочисленной случайной величины. Следующие леммы являются нашими результатами. 9{\infty}p_{jl}p_{j(l+1)}\), \(p_{jl}=P(X_{j}=a+bl)\). {2} д} + { \ гидроразрыва {1,789{n} \biggl(\frac{1}{4} \times \frac{3}{8}+\frac{3}{8} \times \frac{3}{8} \biggr) \\ &= \фракция{15n}{32}. \end{aligned}$$
{2} д} + { \ гидроразрыва {1,789{n} \biggl(\frac{1}{4} \times \frac{3}{8}+\frac{3}{8} \times \frac{3}{8} \biggr) \\ &= \фракция{15n}{32}. \end{aligned}$$ Бернулли 23 (4Б), 3268–3310 (2017)
Бернулли 23 (4Б), 3268–3310 (2017) Теор. Вероатн. Примен. 57, 499–532 (2012) (рус.). английский перевод Теория Вероятность. заявл. 57, 468–496 (2013)
Теор. Вероатн. Примен. 57, 499–532 (2012) (рус.). английский перевод Теория Вероятность. заявл. 57, 468–496 (2013) Z. Wahrscheinlichkeitstheor. Верв. Геб. 23, 187–196 (1972)
Z. Wahrscheinlichkeitstheor. Верв. Геб. 23, 187–196 (1972) Анна. Вероятно. 3, 162–165 (1975)
Анна. Вероятно. 3, 162–165 (1975)