Урок 33. вероятность события. сложение вероятностей — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Глоссарий по теме
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Равновозможные события — такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.242-261.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege. sdamgia.ru/.
sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Рассмотрим пример:
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
Варианты ответов:
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Определение.
Испытанием называется осуществление определенных действий.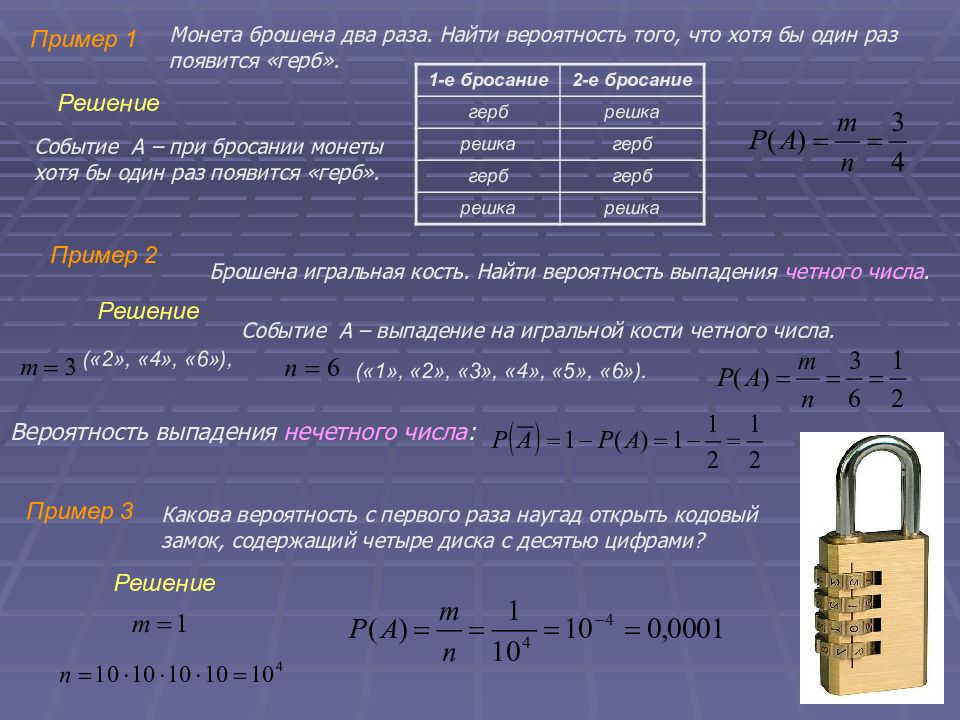
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
- Процесс доставания предмета из коробки является испытанием.
- Результат доставания предмета из корзины является событием.
- Событие «вынутый предмет окажется клубком» является достоверным событием.
- События «вынутый предмет не окажется клубком» или «вынутый предмет окажется красным клубком» являются невозможными событиями.
- Событие «вынутый предмет окажется зеленым клубком» является вероятным событием.
А={вынутый предмет оказался клубком}.
В={вынутый предмет не оказался клубком.
С={вынутый предмет оказался зеленым клубком}.
D ={вынутый предмет оказался красным клубком}.
2. Определим еще несколько важных понятий теории вероятностей
Определение
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω= {w 1, w 2, w 3, w 4, w 5, w6}, где wi— выпадение i очков.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Например:
- A – сдал экзамен по математике;
- Ᾱ – не сдал экзамен по математике.
Определение.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Пример .
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпало два «орла»
— Выпало две «решки»
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Определение.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события.
Статистическая вероятность события рассчитывается опытным путем.
Пример.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий,
 Тогда вероятностью события А называется число
Тогда вероятностью события А называется числоСогласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
2 .Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Например:
- Пусть А — идет дождь, B — идет снег, тогда А + В – «идет снег или дождь»
- При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 — «произошло не больше двух попаданий»
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅D — из урны вынули два белых шара
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅- из урны вынули два шара: белый и не белый
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Решение:
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
Задачи по теории вероятностей. Вероятность появления хотя бы одного события
Задачи по теории вероятностей
Вероятность появления хотя бы одного события
Содержание
- В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: р1 = 0,1; р2 = 0,15; р3 = 0,2. Найти вероятность того, что тока в цепи не будет.

- Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
- Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4: 0,6; 0,7.
- Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку
- Вероятность успешного выполнения упражнения для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди, причем каждый делает по две попытки.
 Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами. - Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
- Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
- Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
- Многократно измеряют некоторую физическую величину. Вероятность того, что при считывании показаний прибора допущена ошибка, равна р. Найти наименьшее число измерений, которое необходимо произвести, чтобы с вероятностью Р > можно было ожидать, что хотя бы один результат измерений окажется неверным.
Содержание
Метки задачи, теория вероятностей.
 Смотреть запись.
Смотреть запись.
Теория вероятностей. Решение задач (ЕГЭ — 2021)
Так стоп! Новое определение.
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента. Ряд несовместных событий образуют полную группу событий. |
Давай разбираться. Возьмем нашу изношенную монетку и бросим её \( 3\) раза.
Возможные варианты:
Так вот, несовместные события – это определенная, заданная последовательность событий. \( 1),\text{ }2),\text{ }3),\text{ }4)\ldots \text{ }8)\) – это несовместные события.
Вероятности несовместных событий складываются. |
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности \( 1\)) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
\( \displaystyle p=\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{8}\)
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно \( 1\) раз, т.е. варианты \( 4),\text{ }6)\) и \( 7)\), то мы должны сложить вероятности этих последовательностей.
Всего вариантов \( 8\), нам подходит \( 3\).
\( \displaystyle p=\frac{{{N}_{б}}}{N}=\frac{3}{8}\)
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
\( \displaystyle p={{p}_{4}}+{{p}_{6}}+{{p}_{7}}=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\)
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Есть отличное правило, помогающее не запутаться, когда умножать, а когда складывать:
Описав, что должно произойти, используя союзы «И» или «ИЛИ», вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения. |
Возвратимся к примеру, когда мы подбросили монетку \( 3\) раза, и хотим узнать вероятность увидеть орла \( 1\) раз.
Что должно произойти?
Должны выпасть:
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
Вот и получается:
\( \displaystyle \left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)+\left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)+\left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\)
Давай рассмотрим несколько примеров.
готовимся к собеседованию и разрешаем «парадоксы» / Блог компании Образовательные проекты JetBrains / Хабр
Каждый год я участвую примерно в сотне собеседований в образовательных проектах JetBrains: собеседую абитуриентов в Computer Science Center и корпоративную магистратуру ИТМО (кстати, набор на программу идёт прямо сейчас).
 Все собеседования устроены по одному шаблону: мы просим на месте порешать задачи и задаём базовые вопросы по дисциплинам, которые студенты изучали в университетах. Большинство вопросов, которые мы задаём, довольно простые — нужно дать определение некоторого понятия, сформулировать свойство или теорему. К сожалению, у значительной доли студентов все эти определения выветриваются сразу после экзаменов в университетах. Казалось бы, что тут удивительного? В современном мире любое определение можно за пару секунд нагуглить, если это нужно. Но невозможность восстановить базовое определение свидетельствует о непонимании сути предмета.
Все собеседования устроены по одному шаблону: мы просим на месте порешать задачи и задаём базовые вопросы по дисциплинам, которые студенты изучали в университетах. Большинство вопросов, которые мы задаём, довольно простые — нужно дать определение некоторого понятия, сформулировать свойство или теорему. К сожалению, у значительной доли студентов все эти определения выветриваются сразу после экзаменов в университетах. Казалось бы, что тут удивительного? В современном мире любое определение можно за пару секунд нагуглить, если это нужно. Но невозможность восстановить базовое определение свидетельствует о непонимании сути предмета.Если непонимание алгебры или математического анализа может мало влиять на вашу жизнь, то непонимание теории вероятностей делает из вас лёгкую мишень для обмана и манипулирования. Суждения о вероятностях различных событий настолько глубоко вошли в нашу повседневную жизнь, что умение правильно рассуждать и отличать правду от невежества или манипуляции является необходимым. В этом небольшом обзоре мы поговорим о базовых понятиях теории вероятностей, научимся правильно формулировать утверждения про простые случайные процессы и разберём несколько парадоксов. Часть материала позаимствована из брошюры А. Шеня «Вероятность: примеры и задачи», которую я очень рекомендую для самостоятельного изучения.
В этом небольшом обзоре мы поговорим о базовых понятиях теории вероятностей, научимся правильно формулировать утверждения про простые случайные процессы и разберём несколько парадоксов. Часть материала позаимствована из брошюры А. Шеня «Вероятность: примеры и задачи», которую я очень рекомендую для самостоятельного изучения.
Перед тем, как говорить об определениях, нам нужно договориться о том, откуда же в нашем мире берётся случайность. Например, почему мы считаем, что подбрасывание монеты — это случайный процесс? С точки зрения классической физики, описывающей процессы в макромире, всё детерминировано, поэтому по параметрам подброса монеты можно однозначно определить, какой стороной она упадёт. Однако на практике оказывается, что измерить и учесть все силы, которые действуют на монетку фактически, невозможно, и поэтому результат этого эксперимента принято считать случайным. Важно понимать, что этот вопрос не является вопросом теории вероятностей. Теория вероятностей работает с моделями — для неё монетка, у которой орёл и решка выпадают одинаково часто, и монетка, у которой орлов в два раза больше, чем решек, — это просто две разные модели. Вопрос о том, какая из моделей больше соответствует наблюдаемой действительности — это вопрос нашего опыта (опыт показывает, что частота орла и решки примерно одинаковая). Таким образом, первым делом мы должны договориться о модели.
Вопрос о том, какая из моделей больше соответствует наблюдаемой действительности — это вопрос нашего опыта (опыт показывает, что частота орла и решки примерно одинаковая). Таким образом, первым делом мы должны договориться о модели.
Определения
Для определения модели, которая позволит нам говорить о вероятностях, нужно описать вероятностное пространство.
Вероятностное пространство в самом простом конечном случае состоит из множества элементарных исходов и набора неотрицательных чисел , таких что их сумма равна . Довольно часто все исходы считаются равновероятными, т.е. . В более сложном бесконечном случае нужно отдельно выделять множество интересующих нас событий и задавать вероятности событий при помощи функции, называемой вероятностной мерой. Событием называется множество, состоящее из элементарных событий, т.е. любое подмножество . Вероятность события , обозначается , — это сумма всех таких , что . В частности, вероятность пустого события равна нулю, а события равна 1. В случае, когда все исходы считаются равновероятными, вероятность события просто равна отношению количества исходов, содержащихся в событии, к общему количеству элементарных исходов, т.е. .
В случае, когда все исходы считаются равновероятными, вероятность события просто равна отношению количества исходов, содержащихся в событии, к общему количеству элементарных исходов, т.е. .
Вероятность любого события заключена между 0 и 1. Если вероятность события нулевая, то такое событие называется невозможным, если же вероятность события равна единице, то такое событие называется достоверным.
Важно, что без определения вероятностного пространства нельзя (в математическом смысле) говорить о вероятности чего-либо.
Замечание
На основе определения вероятностного пространства легко провести разделение между теорией вероятностей и статистикой: теория вероятностей предсказывает частоты на основе знания вероятностного пространства, а статистика решает обратную задачу — на основе наблюдаемых частот определяет параметры неизвестного вероятностного пространства.
Пример: подбрасывание монетки
Будем считать, что монетка
 е. она одинаково часто выпадает орлом и решкой, а на ребро никогда не встаёт. Тогда множество элементарных исходов состоит из двух элементов, . Так как мы договорились, что монетка «правильная», то разумно считать, что . Теперь давайте перечислим все возможные события и их вероятности.
е. она одинаково часто выпадает орлом и решкой, а на ребро никогда не встаёт. Тогда множество элементарных исходов состоит из двух элементов, . Так как мы договорились, что монетка «правильная», то разумно считать, что . Теперь давайте перечислим все возможные события и их вероятности.- Не выпадет ни орёл, ни решка. Это соответствует событию , .
- Выпадет орёл, , .
- Выпадет решка, , .
- Выпадет орёл или решка, , .
Пример: подбрасывание игрального кубика
Как и в случае с монеткой мы будем предполагать, что игральный кубик выпадает всеми гранями одинаково часто. Тогда множество элементарных исходов состоит из шести элементов, , все их вероятности равны . Количество различных событий в этом эксперименте равно (это количество всех подмножеств множества из 6 элементов). Удивительным образом вопрос «сколько существует различных событий в эксперименте с подбрасывание игрального кубика?», по моим наблюдения, ставит в тупик 9 из 10 абитуриентов.

Давайте рассмотрим некоторые примеры событий.
- Выпадет 1, , .
- Выпадет число большее трёх, , .
- Выпадет число кратное трём, , .
Пример: два подбрасывания монетки
В тех же предположениях о «симметричености» монеты мы определим множество элементарных исходов как множество упорядоченных пар Симметриченость монетки позволяет нам заключить, что все элементарные исходы равновероятны, т.е. .
Примеры событий.
- В первом броске выпадет решка, , .
- Выпадет хотя бы одна решка, , .
- Монетка дважды выпадет одной стороной, , .
Пример: выбираем случайное число из календаря 2020 года
Множество элементарных исходов . Как выбрать вероятности? Это зависит от того, как устроен эксперимент. Например, мы можем вырвать случайный лист отрывного календаря и посмотреть число на нем. Наиболее точной моделью, описывающей этот эксперимент, было бы вероятностное пространство с исходами, где одинаковые числа разных месяцев различаются.
 И тогда вероятность того, что выпадет число 1, была бы суммой вероятностей элементарных исходов, соответствующих первым числам разных месяцев, т.е. . Но мы можем для удобства рассмотреть более простое множество элементарных исходов с 31 исходом, но с разными вероятностями: , , .
И тогда вероятность того, что выпадет число 1, была бы суммой вероятностей элементарных исходов, соответствующих первым числам разных месяцев, т.е. . Но мы можем для удобства рассмотреть более простое множество элементарных исходов с 31 исходом, но с разными вероятностями: , , .Пример события: «выпавшее число месяца делится на 10». Это соответствует событию
.
Замечание
Как только мы определили вероятностное пространство (т.е. определились с множеством и вероятностями, которые мы приписываем элементарным исходам), то вопрос о вероятности некоторого события становится чисто арифметическим. Другими словами, как только мы выбрали некоторую математическую модель, которая с нашей точки зрения описывает физический процесс, то вероятности всех событий однозначно определены.
Задачи для самопроверки
В каждой задаче следует сначала описать вероятностное пространство, а уже только потом производить вычисления.
- Бросаем два игральных кубика: красный и синий.
 Определите вероятность того, что цифры на красном и синем кубиках совпадут.
Определите вероятность того, что цифры на красном и синем кубиках совпадут. - В этом же эксперименте с кубиками нужно найти наиболее вероятную сумму цифр на кубиках.
- Наудачу выбирается одно число от 1 до 20. Считая все числа равновозможными, определите вероятность того, что выбранное число:
- чётно;
- делится на 3;
- делится и на 2, и на 3;
- не делится ни на 2, ни на 3;
- имеет сумму цифр 9;
- имеет сумму цифр, делящуюся на 3.
Пример вероятностного пространства, не соответствующего физическому миру
Рассмотрим следующий эксперимент: подбрасываем две монетки и смотрим на то, какими сторонами они выпали. Можно было бы сказать, что в данной задаче всего три исхода: две решки, два орла и орёл и решка. Если предполагать, что все исходы равновозможны, то получается, что вероятность выпадения двух орлов равна 1/3. Математика не запрещает нам рассматривать такое вероятностное пространство, но экспериментальная проверка подсказывает, что в физическом мире ответ скорее ближе к 1/4.
 Поэтому не стоит по умолчанию предполагать все исходы равновозможными, иначе мы получим 1/2 в ответ на вопрос о вероятности встречи динозавра.
Поэтому не стоит по умолчанию предполагать все исходы равновозможными, иначе мы получим 1/2 в ответ на вопрос о вероятности встречи динозавра.Формула суммы вероятностей
Будем называть два события несовместными, если их пересечение равно пустому множеству. Т.е., нет исходов, которые соответствовали бы обоим событиям. Пример: события «на игральном кубике выпало чётное число» и «на игральном кубике выпала единица или тройка» несовместны.
Несовместные события обладают следующим свойством. Пусть и — два несовместных события. Вероятность того, что произойдёт хотя бы одно из них, равна сумме вероятностей и , другими словами , событие также называют суммой событий и и обозначают . Это свойство не выполняется для произвольных событий. Например, события «на игральном кубике выпало чётное число» и «на игральном кубике выпало число больше четырёх» не несовместны и сумма их вероятностей (5/6) больше вероятности их суммы (4/6).
Рассмотрим следующую задачу. В мешке лежат шарики трёх цветов: белые, жёлтые и чёрные. Причём известно, что белых от общего числа, а жёлтых — . Какова вероятность того, что случайно вытащенный шар будет светлым? Аккуратный подсчёт показывает, что если в мешке шаров, то рассматриваемому событию соответствует шаров, т.е. от общего числа шаров. События «вытащен белый шар» и «вытащен жёлтый шар» несовместны, поэтому вероятность, что шар будет светлым равна сумме вероятностей этих событий.
Причём известно, что белых от общего числа, а жёлтых — . Какова вероятность того, что случайно вытащенный шар будет светлым? Аккуратный подсчёт показывает, что если в мешке шаров, то рассматриваемому событию соответствует шаров, т.е. от общего числа шаров. События «вытащен белый шар» и «вытащен жёлтый шар» несовместны, поэтому вероятность, что шар будет светлым равна сумме вероятностей этих событий.
События называются противоположными, если всегда происходит ровно одно из них. Из этого определения можно заключить, что во-первых, эти события несовместны, а во-вторых, их суммарная вероятность равна 1. Событие, противоположное событию , выражается, как (если все элементарные исходы имеют положительную вероятность, то это единственное такое событие).
Задача для самопроверки
Наудачу выбирается число от 1 до 100. Рассмотрим следующие события:
- число чётно;
- число нечётно;
- число делится на 4;
- число имеет остаток 2 при делении на 4;
- число имеет остаток 1 при делении на 4.

Какие из этих событий несовместны? (укажите все пары)
Формула включений и исключений
Как определить вероятность суммы двух событий, которые не являются несовместными? Рассмотрим следующий пример. Среди учеников школы процентов знают французский язык и знают немецкий. Доля тех, кто владеет обоими языками всего . Какова доля учеников, знающих хотя бы один из этих двух языков? Если нарисовать диаграмму, если мы сложим доли знающих французский и знающих немецкий, то мы дважды посчитаем тех, кто знает оба языка. Поэтому ответ: .
Этот же вопрос можно сформулировать и на языке теории вероятностей: с какой вероятностью случайно выбранный школьник знает хотя бы один из двух языков? Аналогичное рассуждение приводит нас к следующей формуле: где — это пересечение событий и , т.е. это событие состоящее из тех элементарных исходов, которые входят одновременно и в , и в (такое событие также называют произведением событий и и обозначают ).

Задача для самопроверки
Известно, что ученики класса, имеющие двойки по алгебре, составляют 25%, а ученики, имеющие двойки по геометрии, составляют 15%. Сколько учеников имеют двойки и по алгебре, и по геометрии, если ученики, не имеющие двоек ни по одному из предметов, составляют 70%?
Условная вероятность
Снова рассмотрим задачу про учеников и иностранные языки. Какая доля среди школьников знающих немецкий знает и французский? Ответ легко вычислить, посмотрев на картинку. Нужно вычислить отношение количества школьников знающих оба языка к количеству школьников знающих немецкий, т.е. . Переходя к языку теории вероятностей можно задаться следующим вопросом: какова вероятность, что случайно выбранный школьник знает французский при условии, что он знает немецкий? Пусть события и соответствуют тому, что случайно выбранный школьник знает французский и немецкий соответственно. Тогда искомая вероятность называется условной вероятностью наступления при условии и обозначается .
 По аналогии получаем следующую формулу для условной вероятности: Какова вероятность, что случайно выбранный школьник знает немецкий при условии, что он знает французский?
По аналогии получаем следующую формулу для условной вероятности: Какова вероятность, что случайно выбранный школьник знает немецкий при условии, что он знает французский?Из формулы условной вероятности можно получить формулу для вероятности произведения двух событий.
Словами: чтобы найти вероятность того, что произойдут оба события и , надо умножить вероятность события на условную вероятность события при известном .Задача для самопроверки
В классе 50% мальчиков; среди мальчиков 60% любит мороженое. Какова доля мальчиков, любящих мороженое, среди учеников класса? Как это переформулировать на языке теории вероятностей?
Независимость
Рассмотрим эксперимент с бросанием двух игральных кубиков: красного и синего. В этом эксперименте имеются 36 исходов, которые мы считаем равновозможными. Вероятность того, что на красном кубике выпадет тройка, равна (6 исходов из 36), вероятность того, что на синем кубике выпадет тройка, тоже равна . Какова вероятность того, что на синем кубике выпадет тройка при условии, что на красном выпала тройка? По формуле условной вероятности нужно посчитать отношение вероятности выпадения тройки на обоих кубиках к вероятности выпадения тройки на красном.
 Получаем . Заметим, что наличие информации о том, что на красном кубике выпала тройка, никак не влияет на вероятность выпадения тройки на синем. Такие события будем называть независимыми. Будем говорить, что события и независимы, если (В этом определении предполагаются, что обе вероятности событий и строго больше нуля.)
Получаем . Заметим, что наличие информации о том, что на красном кубике выпала тройка, никак не влияет на вероятность выпадения тройки на синем. Такие события будем называть независимыми. Будем говорить, что события и независимы, если (В этом определении предполагаются, что обе вероятности событий и строго больше нуля.)Альтернативное определение можно получить, если воспользоваться определением условной вероятности: два события называются независимыми, если вероятность их произведения равна произведению их вероятностей.
Задачи для самопроверки
- Являются ли события «знать немецкий» и «знать французский» независимыми?
- Бросаем один игральный кубик. Являются ли независимыми события:
- «выпало чётное» и «выпало нечётное»,
- «выпало чётное» и «выпало 2»,
- «выпало чётное» и «выпало кратное трём».
Следующий шаг — это разговор про формулу Байеса, которая выводится из определения условной вероятности.
 Перепишем определение:
Перепишем определение:И подставив это в определение получаем формулу Байеса
которая позволяет менять местами событие и условие под знаком вероятности. Думаю, что про применение формулы Баейса нужно писать отдельный пост, например, такой.
На этом мы закончим с определениями и перед тем, как перейти к парадоксам, давайте обсудим, а в каких случаях мы можем говорить о вероятности.
Когда мы можем говорить о вероятности?
Предлагаю рассмотреть несколько вопросов, которые проиллюстрируют важность формулировок.
Какова вероятность того, что гуляя по улице вы встретите динозавра?
Я думаю, что всем ясно, что это не 1/2. Но всё же, как правильно ответить на этот вопрос? Проблема этого вопроса в том, что он сформулирован некорректно — из него нельзя однозначным образом определить вероятностное пространство, а следовательно и о вероятности говорить нельзя. Можно предложить какую-нибудь другую формулировку вопроса, в которой это будет очевидно. Например, начиная с завтрашнего дня на каждой улице города каждую минуту с вероятностью 0.00001 материализуется динозавр и существует в течение часа, никуда не уходя. В данной формулировке понятен случайный процесс и можно оценить вероятность встречи, если определить, как устроена прогулка, сколько длится и сколько улиц она затрагивает.
Например, начиная с завтрашнего дня на каждой улице города каждую минуту с вероятностью 0.00001 материализуется динозавр и существует в течение часа, никуда не уходя. В данной формулировке понятен случайный процесс и можно оценить вероятность встречи, если определить, как устроена прогулка, сколько длится и сколько улиц она затрагивает.
Вы подбросили монетку и не подглядывая накрыли её рукой. Какова вероятность того, что монетка повёрнута орлом вверх?
Очень хочется сказать, что в данном случае уж точно вероятность — 1/2. Однако, строго говоря, никакого случайного процесса уже нет. Монетка уже упала какой-то стороной. От того, что вы чего-то не знаете, не значит, что это что-то случайное. Например, если вы не знаете решение уравнения — это не значит, что его решением с одинаковой вероятностью может быть любое число. Поэтому в данном случае описать вероятностное пространство не получится. Можно переформулировать вопрос, например, так: «Какова вероятность, что вы угадаете сторону монетки, если наугад равновероятно выберите орёл или решку?». В такой формулировке уже ясно, что является случайным процессом (выбор орла или решки), как определить вероятностное пространство и получить ответ 1/2. При этом, в такой формулировке уже совершенно неважно, была монетка «честной» или нет.
В такой формулировке уже ясно, что является случайным процессом (выбор орла или решки), как определить вероятностное пространство и получить ответ 1/2. При этом, в такой формулировке уже совершенно неважно, была монетка «честной» или нет.
Замечание. Нашу уверенность в чём-то тоже можно описывать в терминах теории вероятностей — это делается в рамках Байесовской интерпретации теории вероятностей. Эта интерпретации позволяет использовать аппарат теории вероятностей для оценки нашей уверенности в истинности каких-то утверждений (не обязательно случайных) основываясь на информации, которая нам известна. Однако стоит заметить, что в этом случае понятие вероятности становится субъективным — у одного и того же события с точки зрения разных наблюдателей может быть разная вероятность. Например, в покере вы можете считать вероятность выпадения пиковой дамы положительной (так как вы не видите её на столе и в своей руке), а ваш противник, у которого в руке уже есть пиковая дама, будет оценивать вероятность её выпадения как нулевую. При этом можно придумать и такой вариант, в котором обе оценки окажутся отличными от «реальной», объктивной, вероятности. В этом нет противоречия, т.к. в это три различные величины (игроки обладают разной информацией, а объективная вероятность в данном случае соответствует полной информации).
При этом можно придумать и такой вариант, в котором обе оценки окажутся отличными от «реальной», объктивной, вероятности. В этом нет противоречия, т.к. в это три различные величины (игроки обладают разной информацией, а объективная вероятность в данном случае соответствует полной информации).
Вы проснулись утром. Какова вероятность того, что сегодня воскресенье?
Думаю, что вы уже поняли, что ответ 1/7 — неправильный, а точнее, вопрос некорректный. Не понятно, что является случайный процессом. Для того, чтобы получить 1/7 нужно уточнить вопрос, например, так: вы засыпаете в воскресенье вечером и случайным образом просыпаетесь в любое утро на следующей неделе, какова вероятность, что вы проснётесь в воскресенье? Но даже с этим уточнением, если спросить вас о дне недели уже после того, как вы проснулись (после того, как случайный выбор был сделан), то такой вопрос останется некорректным — иначе придётся предполагать, что вы находитесь в суперпозиции всех дней недели до тех пор, пока не посмотрите на календарь.
Я написал на доске некоторое (конкретное) число и утверждаю, что дважды успешно проверил его на простоту вероятностным алгоритмом, который ошибается с вероятность менее 1%. С какой вероятностью это число простое?
Хотелось бы сказать, что это число простое с вероятностью более 99.99%. Однако, с математической точки зрения число может быть либо простым, либо нет. Поэтому так говорить некорректно. После того, как алгоритм завершил работу, ничего случайного в этой постановке задачи уже нет, следовательно нет и вероятности. Правильно было бы сказать, что вы уверены на 99.99%, что это число простое, но и это вы можете заявить только в том случае, если доверяете мне на 100% 🙂
Парадоксы
В этом разделе мы попробуем разобрать несколько известных «парадоксов» теории вероятностей и понять, что в них либо нет противоречий, либо вопросы поставлены некорректно.
Парадокс Монти-Холла
Этот очень известный парадокс. Об него было сломано много копий, в том числе даже именитые математики давали неправильный ответ.

Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Как подсказывает Википедия, для того, чтобы задача была определена корректно, нам требуется уточнить, что участнику игры заранее известны следующие правила:
- автомобиль равновероятно размещён за любой из трёх дверей;
- ведущий знает, где находится автомобиль;
- ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор;
- если у ведущего есть выбор, какую из двух дверей открыть, он выбирает любую из них с одинаковой вероятностью.

Если вы не знакомы с этим парадоксом, то я предлагаю вам несколько минут подумать о том, каким будет правильный ответ.
Для того, чтобы ответить на заданный вопрос, давайте разберёмся, что тут является случайным процессом. По уточнению видно, что случайный процесс упоминается только в пунктах 1 и 4: «автомобиль равновероятно размещён за любой из трёх дверей» и «если у ведущего есть выбор, какую из двух дверей открыть, он выбирает любую из них с одинаковой вероятностью». Вопрос, на который мы должны научиться отвечать, звучит так: «Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор». Т.е. нас спрашивают о том, какая из двух стратегий даёт большую вероятность выигрыша. Замечу, что условие номер 4 никак не влияет на факт выигрыша игрока, поэтому нет смысла включать его в вероятностное пространство. Поэтому предлагается выбрать вероятностное пространство с множеством элементарных исходов , соответствующим номеру двери, за которым находится автомобиль, и вероятностями .
 Теперь рассмотрим две стратегии игрока: «оставить выбранную дверь», обозначим , и «сменить дверь», обозначим .
Теперь рассмотрим две стратегии игрока: «оставить выбранную дверь», обозначим , и «сменить дверь», обозначим .Мы не знаем, как игрок делает выбор первой двери, но нам и не нужно это знать. Достаточно проверить, как работает стратегия при всех выборах первой двери. Обозначим через дверь, которую игрок выбрал изначально, а через — дверь, за которой спрятан автомобиль. Тогда для любого событие «игрок выиграл при использовании стратегии » соответствует тому, что он угалад правильную дверь с первой попытки. Говоря формально, нас интересует событие , т.е. , и его вероятность . Событие «игрок выиграл при использовании стратегии » соответствует противоположному событию , т.е. , и его вероятность . Осталось ещё раз отметить, что, если этот анализ верен для любого выбора , поэтому верен и при любой стратегии выбора первой двери. Кроме того, заметим, что мы никак не использовали условие 4.
Как видите, никаких неоднозначностей тут нет, парадоксом эта задача называется только потому, что ответ может не соответствовать интуиции. Но так в математике случается довольно часто.
Но так в математике случается довольно часто.
Парадокс мальчика и девочки
Цитирую Википедию.
Впервые задача была сформулирована в 1959 году, когда Мартин Гарднер опубликовал один из самых ранних вариантов этого парадокса в журнале Scientific American под названием «The Two Children Problem», где привёл следующую формулировку:
- У мистера Джонса двое детей. Старший ребёнок — девочка. Какова вероятность того, что оба ребёнка — девочки?
- У мистера Смита двое детей. Хотя бы один ребёнок — мальчик. Какова вероятность того, что оба ребёнка — мальчики?
Сам Гарднер изначально давал ответ и соответственно, но впоследствии понял, что ситуация во втором случае неоднозначна. Ответом на второй вопрос может быть и в зависимости от того, как было выяснено, что один из детей — мальчик.
Вероятностное пространоство задано и все вероятности равны . В первом случае нам известно, что выполнено событие .
 Поэтому при условии вероятность двух девочек равна 1/2.
Поэтому при условии вероятность двух девочек равна 1/2.Во втором случае всё сложнее, т.к. не понятно, как мы узнали, что у мистера Смита один из детей мальчик. Можно предположить два варианта:
- Выбирается случайный человек с двумя детьми и его спрашивают, есть ли среди его детей мальчик. Тогда вероятность двух мальчиков получится 1/3, т.к. это соответствует вероятности ММ при условии события .
- Выбирается случайный человек с двумя детьми, выбирается случайный его ребёнок (старший или младший) и спрашивается его пол. Этот эксперимент соответствует другому вероятностному пространству, в котором нужно ещё учесть выбор того ребёнка, про которого спрашивают. В нём будет 8 элементарных исходов, и нам подойдут четыре из них (ММ и спросили про старшего, ММ и спросили про младшего, МД и спросили про старшего, ДМ и спросили про младшего). Нам подходят два исхода, поэтому ответом будет 1/2.
Парадокс Спящей Красавицы
Обсуждение этого парадокса мотивировано вот этим постом на хабре, который вызвал широкое обсуждение, но описание этого парадокса есть и в википедии.

Испытуемой («Спящей Красавице») делается укол снотворного. Бросается симметричная монетка. В случае выпадения орла её будят, и эксперимент на этом заканчивается. В случае выпадения решки её будят, делают второй укол (после чего она забывает о побудке) и будят на следующий день, не бросая монеты (в таком случае эксперимент идёт два дня подряд). Вся эта процедура Красавице известна, однако у неё нет информации, в какой день её разбудили.Представьте себя на месте Спящей Красавицы. Вас разбудили. Какова вероятность того, что монетка упала решкой?
Предлагается рассмотреть два альтернативных решения с разными результатами.
Решение 1
У вас нет никакой информации о результате выпадения монеты и предыдущих побудках. Поскольку известно, что монетка честная, можно предположить, что вероятность выпадения решки равна .
Решение 2
Проведём эксперимент 1000 раз. Спящую Красавицу будят в среднем 500 раз с орлом и 1000 раз с решкой (т.
 к. при выпадении решки Спящую Красавицу спрашивают 2 раза). Поэтому вероятность выпадения решки равна .
к. при выпадении решки Спящую Красавицу спрашивают 2 раза). Поэтому вероятность выпадения решки равна .Кажется, что оба решения могут претендовать на звание правильного. Однако, при попытке определить вероятностное пространство нас ожидают серьёзные трудности. Что же является случайным процессом? Дело в том, что когда Спящая Красавица просыпается, никакого случайного процесса уже нет. Выбор уже сделан. Ей не известен результат этого выбора, но ничего случайного уже нет. Это возвращает нас к примеру с динозавром. Если вы не знаете, есть ли за углом динозавр, то это не значит, что он там есть с вероятностью 1/2. Поэтому «Решение 1» отвечает не на вопрос про вероятность, а на вопрос про степень уверенности Спящей Красавицы. А «Решение 2» предлагает рассмотреть совершенно другой эксперимент, в котором задаётся в общем-то совершенно другой вопрос, на который предлагается ответить внешнему наблюдателю до начала эксперимента.
Для того, чтобы придать этому вопросу математический смысл и получить желаемый ответ 2/3, придётся воспользоваться каким-нибудь философским приёмом, вроде «подселения душ». Например, так: вы заходите в аппарат переселения душ, после этого подбрасывается монетка для Спящей Красавицы, которая создаёт две параллельные вселенные: одну, где монетка выпала орлом, и другую, где выпала решкой. Суммарно в пространстве-времени этих двух альтернативных вселенных есть три различных пробуждения Спящей Красавицы. Аппарат по переселению душ с вероятностью 1/3 подселяет вашу душу в тело Спящей Красавицы незадолго до одного из этих пробуждений. Какова вероятность, что вы проснетесь в параллельной вселенной, где выпала решка?
Например, так: вы заходите в аппарат переселения душ, после этого подбрасывается монетка для Спящей Красавицы, которая создаёт две параллельные вселенные: одну, где монетка выпала орлом, и другую, где выпала решкой. Суммарно в пространстве-времени этих двух альтернативных вселенных есть три различных пробуждения Спящей Красавицы. Аппарат по переселению душ с вероятностью 1/3 подселяет вашу душу в тело Спящей Красавицы незадолго до одного из этих пробуждений. Какова вероятность, что вы проснетесь в параллельной вселенной, где выпала решка?
Как видите, для придания математического смысла этому вопросу, придётся хорошенько пофантазировать, но этим занимаются не математики, а философы (подробнее в этом посте). Утверждать, что «оба решения правильные», некорректно с математической точки зрения.
Задача для самопроверки
Объясните, почему в задаче о детях моряка, с которой начинается этот пост, вопрос поставлен некорректно (т.е. ни 1/2, ни 1/3 не являются правильным ответом).

Бесконечный случай
Когда мы переходим к бесконечному случаю, т.е. рассматриваем эксперименты с бесконечным числом элементарных исходов, то всё становится значительно сложнее. Я не буду вдаваться в детали и даже не буду определять вероятностное пространство для бесконечного случая, т.к. это требует более сложной математики. Однако, для иллюстрации отмечу, что в бесконечном случае могут быть такие (плохие) множества элементарных исходов, которые не имеют вероятности (неизмеримые множества). При этом для всех хороших (измеримых) событий вероятность определена однозначно. Поэтому и те «парадоксы», которые возникают в бесконечном случае, тоже возникают из-за неоднозначности выбора вероятностного пространства. Хорошим наглядным примером служит парадокс Бертрана, показывающий, как казалось бы эквивалентные (на самом деле нет) вероятностные пространства приводят к разным результатам.
Вместо заключения
Даже если вы не собираетесь никуда поступать или проходить собеседования на технические позиции в IT-компании, то вы всё равно можете захотеть освежить знания по математике, которые могут пригодиться в программировании.
 Могу посоветовать онлайн-курс СS центра по теории вероятностей, который читает А.И. Храбров.
Могу посоветовать онлайн-курс СS центра по теории вероятностей, который читает А.И. Храбров.БОНУС
Приглашаю всех послушать лекция Александра Шеня «Генераторы «случайных чисел»: теория и практика» в это воскресенье 26 апреля в 14:00 в Computer Science клубе. Лекция будет читаться в zoom-е, для участия нужно записаться на курс или подписаться на рассылку.Вероятность
независимых событий: правило «хотя бы одно» — видео и стенограмма урока
«По крайней мере одно правило»
Иногда при вычислении независимых событий важно, чтобы событие произошло хотя бы один раз. Это называется правилом «По крайней мере один» . Чтобы рассчитать вероятность того, что событие произойдет хотя бы один раз, это будет дополнение к событию, которое никогда не произойдет. Это означает, что вероятность того, что событие никогда не произойдет, и вероятность того, что событие произойдет хотя бы один раз, будет равна единице или 100% -ному шансу.
Например, вероятность выиграть главный приз в местном розыгрыше составляет 1 из 30. Тим и его жена Джейн купили билеты. Какова вероятность того, что хотя бы один из них выиграет главный приз? Сначала нам нужно определить вероятность того, что Тим и Джейн не выиграют главный приз. Поскольку вероятность того, что один человек выиграет приз, составляет 1 из 30, вероятность того, что один человек не выиграет главный приз, составляет 29/30, или 0,96.
Тим и его жена Джейн купили билеты. Какова вероятность того, что хотя бы один из них выиграет главный приз? Сначала нам нужно определить вероятность того, что Тим и Джейн не выиграют главный приз. Поскольку вероятность того, что один человек выиграет приз, составляет 1 из 30, вероятность того, что один человек не выиграет главный приз, составляет 29/30, или 0,96.
Помните, что для расчета вероятности нескольких независимых событий — в данном случае, когда оба они не выиграют главный приз — мы находим вероятность того, что каждое событие произойдет отдельно, и умножаем их вместе.2 = 0,935.
Таким образом, вероятность того, что ни Тим, ни Джейн не выиграют главный приз, составляет 0,935. Чтобы вычислить вероятность того, что хотя бы один из них выиграет главный приз, нам нужно найти дополнение к этому числу. Вероятность не выигрыша плюс вероятность хотя бы одного выигрыша равняется целому. Таким образом, вычитая 1–0,935, мы видим, что вероятность того, что Тим или Джейн выиграют главный приз, составляет 0,065, или 6,5%.
Когда диктор подходит к микрофону, чтобы назвать выигрышный билет, Тиму и Джейн не нравятся их шансы.Диктор подходит к микрофону и выкрикивает имя Джейн. Джейн так взволнована и прыгает от радости, что ей удалось превзойти все шансы на получение главного приза.
Пример
Давайте посмотрим на другой пример. Тим и Джейн планируют потратить свой главный приз на четырехдневную лыжную прогулку. Они хотят быть уверены, что снег будет хотя бы один день, пока они в пути. На горнолыжном курорте, который они забронировали, есть вероятность 65%, что снег будет идти каждый день. Какова вероятность того, что во время их четырехдневной лыжной поездки хотя бы один день пойдет снег?
Первый шаг для расчета вероятности выпадения снега хотя бы в один день — это определить вероятность того, что снегопад не будет во время их четырехдневной поездки.4, что составляет 0,015. Вероятность того, что за их четырехдневную поездку вообще не будет снега, составляет 0,015.
Чтобы рассчитать вероятность того, что по крайней мере один день будет снег, нам нужно вычислить дополнение этого события. Для этого вычтем 1 — 0,015, что равно 0,985. Тим и Джейн знают, что вероятность выпадения снега хотя бы в один день во время их лыжной поездки составляет 0,985 или 98,5%. Когда Тим и Джейн прибывают на горнолыжный курорт, начинает падать снег. Это самое красивое зрелище, которое они когда-либо видели.
Для этого вычтем 1 — 0,015, что равно 0,985. Тим и Джейн знают, что вероятность выпадения снега хотя бы в один день во время их лыжной поездки составляет 0,985 или 98,5%. Когда Тим и Джейн прибывают на горнолыжный курорт, начинает падать снег. Это самое красивое зрелище, которое они когда-либо видели.
Сводка урока
Итак, для анализа, независимых событий — это события, которые не влияют на результат последующих событий. В независимом событии каждая ситуация отличается от предыдущих событий. Иногда при вычислении независимых событий важно, чтобы событие произошло хотя бы один раз. Это называется правилом «По крайней мере один» . Чтобы рассчитать вероятность того, что событие произойдет хотя бы один раз, она будет дополнением к вероятности того, что событие никогда не произойдет.При расчете этой суммы вы можете использовать экспоненты, чтобы умножить количество произошедших событий.
Результат обучения
После просмотра этого урока вы должны быть в состоянии интерпретировать процесс дополнительных событий, чтобы узнать вероятность того, что что-то произойдет хотя бы один раз.
Вероятность | Безграничная алгебра
Основы теории вероятностей
Вероятность — это раздел математики, который имеет дело с вероятностью наступления определенных результатов.Есть пять основных правил, или аксиом, которые нужно понимать, изучая основы вероятности.
Цели обучения
Объясните самые основные и самые важные правила определения вероятности события
Основные выводы
Ключевые моменты
- Вероятность — это число, которое может быть присвоено исходам и событиям. Он всегда больше или равен нулю и меньше или равен единице.
- Сумма вероятностей всех исходов должна равняться [латекс] 1 [/ латекс].
- Если два события не имеют общих исходов, вероятность того, что то или иное произойдет, является суммой их индивидуальных вероятностей.
- Вероятность того, что событие не произойдет, равна [latex] 1 [/ latex] минус вероятность того, что событие действительно произойдет.
- Два события [latex] A [/ latex] и [latex] B [/ latex] независимы, если знание того, что одно происходит, не меняет вероятность того, что другое произойдет.

Ключевые термины
- событие : подмножество выборочного пространства.
- пробел : набор всех результатов эксперимента.
- эксперимент : то, что делается, что дает измеримые результаты, называемые результатами.
- результат : один из отдельных результатов, которые могут быть получены в эксперименте.
В качестве дискретной вероятности мы предполагаем хорошо определенный эксперимент , такой как подбрасывание монеты или бросание кости. Каждый индивидуальный результат, который мог произойти, называется исходом .Набор всех результатов называется выборкой пространством , а любое подмножество выборочного пространства называется событием .
Например, рассмотрим эксперимент по подбрасыванию монеты два раза. Есть четыре индивидуальных результата, а именно [латекс] HH, HT, TH, TT. [/ Latex] Таким образом, пробелом является [latex] \ {HH, HT, TH, TT \}. [/ Latex] Событие «в выпадет хотя бы одна решка »будет набором [латекс] \ {HH, HT, TH \}. [/ latex] Если бы монета была обычной монетой, мы бы присвоили вероятность [latex] 1/4 [/ latex] к каждому исходу.
[/ Latex] Событие «в выпадет хотя бы одна решка »будет набором [латекс] \ {HH, HT, TH \}. [/ latex] Если бы монета была обычной монетой, мы бы присвоили вероятность [latex] 1/4 [/ latex] к каждому исходу.
В теории вероятностей вероятность [латекс] P [/ латекс] некоторого события [латекс] E [/ латекс], обозначаемого [латекс] P (E) [/ латекс], обычно определяется таким образом, что [латекс ] P [/ latex] удовлетворяет ряду аксиом или правил. Ниже перечислены самые основные и самые важные правила.
Правила вероятности
- Вероятность — это число. Он всегда больше или равен нулю и меньше или равен единице . Это можно записать как [латекс] 0 \ leq P (A) \ leq 1 [/ latex].Невозможное событие или событие, которое никогда не произойдет, имеет вероятность [latex] 0 [/ latex]. Событие, которое происходит всегда, имеет вероятность [latex] 1 [/ latex]. Событие с вероятностью [латекс] 0,5 [/ латекс] произойдет в половине случаев.
- Сумма вероятностей всех возможностей должна равняться [латекс] 1 [/ латекс]. В каждом испытании должен быть какой-то результат, и сумма всех вероятностей составляет 100%, или в данном случае [латекс] 1 [/ латекс]. Это можно записать как [latex] P (S) = 1 [/ latex], где [latex] S [/ latex] представляет все пространство сэмплов.
- Если два события не имеют общих исходов, вероятность того, что одно или другое произойдет, является суммой их индивидуальных вероятностей . Если одно событие происходит в [latex] 30 \% [/ latex] испытаний, другое событие происходит в [latex] 20 \% [/ latex] испытаний, и эти два события не могут происходить вместе (если они не пересекаются) , то вероятность того, что то или иное произойдет, составляет [латекс] 30 \% + 20 \% = 50 \% [/ латекс]. Иногда это называют правилом сложения, и его можно упростить следующим образом: [латекс] P (A \ \ text {или} \ B) = P (A) + P (B) [/ latex].Слово «или» в математике означает то же самое, что и союз, в котором используется следующий символ: [латекс] \ чашка [/ латекс]. Таким образом, когда [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, мы имеем [latex] P (A \ cup B) = P (A) + P (B) [/ latex].
- Вероятность того, что событие не произойдет, равна [латекс] 1 [/ latex] минус вероятность того, что событие действительно произойдет . Если событие происходит в [латексе] 60 \% [/ latex] всех испытаний, оно не может произойти в другом [латексе] 40 \% [/ latex], потому что [латекс] 100 \% — 60 \% = 40 \%[/латекс].c [/ latex] является дополнением к [latex] A [/ latex].
- Два события [латекс] A [/ латекс] и [латекс] B [/ латекс] являются независимыми, если знание того, что одно происходит, не изменяет вероятность того, что другое произойдет . Это часто называют правилом умножения. Если [латекс] A [/ latex] и [latex] B [/ latex] независимы, то [latex] P (A \ \ text {and} \ B) = P (A) P (B) [/ latex] . Слово «и» в математике означает то же самое, что и пересечение, в котором используется следующий символ: [latex] \ cap [/ latex].Следовательно, когда A и B независимы, мы имеем [latex] P (A \ cap B) = P (A) P (B). [/ Latex]
Расширение примера
Продолжая описанный выше пример подбрасывания двух монет, присвойте вероятность [latex] 1/4 [/ latex] каждому из результатов [latex] 4 [/ latex]. Мы рассматриваем каждое из пяти правил выше в контексте этого примера.
1. Обратите внимание, что каждая вероятность составляет [латекс] 1/4 [/ латекс], что находится между [латексом] 0 [/ латексом] и [латексом] 1 [/ латексом].
2. Обратите внимание, что сумма всех вероятностей равна [latex] 1 [/ latex], поскольку [latex] \ frac {1} {4} + \ frac {1} {4} + \ frac {1} {4 } + \ frac {1} {4} = 1 [/ латекс].
3. Предположим, что [latex] A [/ latex] — это событие, когда происходит ровно одна голова, а [latex] B [/ latex] — это событие, когда происходит ровно два хвоста. Тогда [latex] A = \ {HT, TH \} [/ latex] и [latex] B = \ {TT \} [/ latex] не пересекаются. Кроме того, [латекс] P (A \ cup B) = \ frac {3} {4} = \ frac {2} {4} + \ frac {1} {4} = P (A) + P (B). [/ латекс]
4. Вероятность того, что выпадет голова, составляет [латекс] 1/4 [/ латекс], что равно [латексу] 1-3 / 4 [/ латекс]. Итак, если [latex] A = \ {HT, TH, HH \} [/ latex] — это событие, при котором возникает голова, мы имеем [latex] P (A ^ c) = \ frac {1} {4} = 1 — \ frac {3} {4} = 1-P (A).[/ латекс]
5. Если [latex] A [/ latex] — это событие, когда первый флип — это решка, а [latex] B [/ latex] — это событие, когда второй флип является хедом, то [latex] A [/ latex ] и [latex] B [/ latex] независимы. У нас есть [латекс] A = \ {HT, HH \} [/ latex] и [latex] B = \ {TH, HH \} [/ latex] и [латекс] A \ cap B = \ {HH \}. [/ latex] Обратите внимание, что [латекс] P (A \ cap B) = \ frac {1} {4} = \ frac {1} {2} \ cdot \ frac {1} {2} = P (A) P (B). [/ Латекс]
Кубик: Игральные кости часто используются при изучении правил вероятности.
Союзы и пересечения
Объединение и пересечение — два ключевых понятия в теории множеств и вероятности.
Цели обучения
Приведите примеры пересечения и объединения двух или более множеств
Основные выводы
Ключевые моменты
- Объединение двух или более наборов — это набор, который содержит все элементы двух или более наборов. Союз обозначается символом [латекс] \ чашка [/ латекс].
- Общее правило сложения вероятностей для объединения двух событий гласит, что [латекс] P (A \ cup B) = P (A) + P (B) -P (A \ cap B) [/ latex], где [latex ] A \ cap B [/ latex] — это пересечение двух наборов.
- Правило сложения может быть сокращено, если наборы не пересекаются: [латекс] P (A \ cup B) = P (A) + P (B) [/ latex]. Это может быть даже расширено на большее количество множеств, если все они не пересекаются: [латекс] P (A \ cup B \ cup C) = P (A) + P (B) + P (C) [/ latex].
- Пересечение двух или более наборов — это набор элементов, общих для каждого набора. Символ [латекс] \ крышка [/ латекс] используется для обозначения пересечения.
- Когда события независимы, мы можем использовать правило умножения для независимых событий, которое гласит, что [latex] P (A \ cap B) = P (A) P (B) [/ latex].
Ключевые термины
- независимый : Не зависит от чего-либо еще.
- непересекающиеся : не имеющие общих членов; имеющий пересечение, равное пустому множеству.
Введение
Вероятность использует математические идеи множеств, как мы видели в определении как выборочного пространства эксперимента, так и в определении события. Чтобы выполнить базовые вычисления вероятности, нам необходимо рассмотреть идеи теории множеств, относящиеся к операциям объединения, пересечения и дополнения множеств.
Союз
Объединение двух или более наборов — это набор, который содержит все элементы каждого из наборов; элемент входит в объединение, если он принадлежит хотя бы к одному из множеств. Символ объединения — [latex] \ cup [/ latex] и связан со словом «или», потому что [latex] A \ cup B [/ latex] — это набор всех элементов, которые находятся в [latex] A [/ latex] или [latex] B [/ latex] (или оба.) Чтобы найти объединение двух наборов, перечислите элементы, которые находятся в одном (или обоих) наборах. В терминах диаграммы Венна объединение наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано как два полностью заштрихованных взаимосвязанных круга.
Объединение двух наборов: Закрашенная диаграмма Венна показывает объединение набора [латекс] A [/ латекс] (круг слева) с набором [латекс] B [/ латекс] (круг справа). Сокращенно это можно записать как [латекс] A \ чашка B [/ латекс].
В символах, поскольку объединение [latex] A [/ latex] и [latex] B [/ latex] содержит все точки, которые находятся в [latex] A [/ latex] или [latex] B [/ latex] или оба, определение союза:
[латекс] \ Displaystyle A \ чашка B = \ {x: x \ in A \ text {или} \ x \ in B \} [/ латекс]
Например, если [латекс] A = \ {1, 3, 5, 7 \} [/ латекс] и [латекс] B = \ {1, 2, 4, 6 \} [/ латекс], то [латекс ] A \ cup B = \ {1, 2, 3, 4, 5, 6, 7 \} [/ латекс].Обратите внимание, что элемент [latex] 1 [/ latex] не указан дважды в объединении, хотя он присутствует в обоих наборах [latex] A [/ latex] и [latex] B [/ latex]. Это приводит нас к общему правилу сложения для объединения двух событий:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) — P (A \ cap B) [/ латекс]
Где [латекс] P (A \ cap B) [/ latex] — пересечение двух наборов. Мы должны вычесть это, чтобы избежать двойного счета включения элемента.
Если наборы [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, то событие [latex] A \ cap B [/ latex] не имеет результатов и является пустым набором, обозначенным как [latex] \ emptyset [/ latex], вероятность которого равна нулю.Таким образом, приведенное выше правило может быть сокращено только для непересекающихся множеств:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) [/ латекс]
Это может быть даже расширено на большее количество наборов, если все они не пересекаются:
[латекс] \ Displaystyle P (A \ чашка B \ чашка C) = P (A) + P (B) + P (C) [/ латекс]
Перекресток
Пересечение двух или более наборов — это набор элементов, общих для каждого из наборов. Элемент находится в пересечении, если он принадлежит всем множествам. Символ пересечения — [латекс] \ cap [/ latex] и связан со словом «и», потому что [latex] A \ cap B [/ latex] — это набор элементов, которые находятся в [латексе] A [ / latex] и [latex] B [/ latex] одновременно.Чтобы найти пересечение двух (или более) наборов, включите только те элементы, которые перечислены в обоих (или во всех) наборах. В терминах диаграммы Венна пересечение двух наборов [латекс] A [/ латекс] и [латекс] B [/ латекс] может быть показано в заштрихованной области в середине двух взаимосвязанных кругов.
Пересечение двух наборов: Набор [латекс] A [/ latex] — круг слева, набор [латекс] B [/ latex] — круг справа, а пересечение [латекса] A [/ латекс] и [латекс] B [/ латекс] или [латекс] A \ cap B [/ latex] — это заштрихованная часть в середине.
В математической записи пересечение [латекса] A [/ latex] и [latex] B [/ latex] записывается как [latex] A \ cap B = \ {x: x \ in A \ \ text {и} \ x \ in B \} [/ латекс]. Например, если [латекс] A = \ {1, 3, 5, 7 \} [/ латекс] и [латекс] B = \ {1, 2, 4, 6 \} [/ латекс], то [латекс] A \ cap B = \ {1 \} [/ latex], потому что [latex] 1 [/ latex] — единственный элемент, который присутствует в обоих наборах [latex] A [/ latex] и [latex] B [/ latex].
Когда события независимы, то есть результат одного события не влияет на результат другого события, мы можем использовать правило умножения для независимых событий, которое гласит:
[латекс] \ Displaystyle P (A \ cap B) = P (A) P (B) [/ латекс]
Например, предположим, что мы дважды подбрасывали монету, и мы хотим узнать вероятность того, что выпадет две орла.Поскольку первый бросок не влияет на второй, события независимы. Скажем, это событие, когда первый бросок — орел, а [латекс] B [/ latex] — это событие, когда второй бросок — это орел, тогда [латекс] P (A \ cap B) = \ frac {1} {2 } \ cdot \ frac {1} {2} = \ frac {1} {4} [/ latex].
Условная вероятность
Условная вероятность события — это вероятность того, что событие произойдет, при условии, что произошло другое событие.
Цели обучения
Объясните значение теоремы Байеса для манипулирования условными вероятностями
Основные выводы
Ключевые моменты
- Условная вероятность [latex] P (B \ vert A) [/ latex] события [latex] B [/ latex], учитывая событие [latex] A [/ latex], определяется следующим образом: [latex] P (B | A) = \ frac {P (A \ cap B)} {P (A)} [/ latex], когда [latex] P (A)> 0 [/ latex].
- Если знание того, что событие [latex] A [/ latex] происходит, не изменяет вероятность того, что событие [latex] B [/ latex] происходит, то [latex] A [/ latex] и [latex] B [/ latex] являются независимыми событиями, и, следовательно, [latex] P (B | A) = P (B) [/ latex].
- Математически теорема Байеса дает соотношение между вероятностями [латекс] A [/ латекс] и [латекс] B [/ латекс], [латекс] P (A) [/ латекс] и [латекс] P (B) [/ latex], и условные вероятности [latex] A [/ latex] для [latex] B [/ latex] и [latex] B [/ latex] для [latex] A [/ latex], [latex] P (A | B) [/ латекс] и [латекс] P (B | A) [/ латекс].В наиболее распространенной форме это: [латекс] P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ latex].
Ключевые термины
- условная вероятность : вероятность того, что событие произойдет с учетом ограничительного допущения, что произошло другое событие или что имело место сочетание других событий
- независимый : не зависимый; не случайный или зависящий от чего-то еще; бесплатно.
Вероятность [латекса] B [/ латекса] с учетом того, что [латекс] A [/ латекс] имел место
Наша оценка вероятности события может измениться, если мы знаем, что произошло какое-то другое событие.Например, вероятность того, что свернутый кубик показывает [латекс] 2 [/ латекс], составляет [латекс] 1/6 [/ латекс] без какой-либо другой информации, но если кто-то посмотрит на кубик и скажет вам, что это четный число, теперь вероятность [latex] 1/3 [/ latex], что это [latex] 2 [/ latex]. Обозначение [латекс] P (B | A) [/ latex] указывает условную вероятность, то есть указывает вероятность одного события при условии, что мы знаем, что другое событие произошло. Бар «|» можно читать как «данный», так что [латекс] P (B | A) [/ latex] читается как «вероятность [латекса] B [/ latex] с учетом того, что [latex] A [/ latex] произошел ».
Условная вероятность [latex] \ displaystyle P (B | A) [/ latex] события [latex] B [/ latex], учитывая событие [latex] A [/ latex], определяется следующим образом:
[латекс] \ Displaystyle P (B | A) = \ frac {P (A \ cap B)} {P (A)} [/ латекс]
Когда [латекс] P (A)> 0 [/ латекс]. Обязательно запомните различные роли [латекса] B [/ латекса] и [латекса] A [/ латекса] в этой формуле. Набор после бара — это тот, который, как мы предполагаем, произошел, и его вероятность входит в знаменатель формулы.
Пример
Предположим, что монета подбрасывается 3 раза, что дает пробел:
[латекс] S = \ {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT \} [/ латекс]
Каждый индивидуальный исход имеет вероятность [латекс] 1/8 [/ латекс].Предположим, что [latex] B [/ latex] — это событие, при котором выпадает хотя бы одна голова, а [latex] A [/ latex] — это событие, когда все монеты [latex] 3 [/ latex] одинаковы. Тогда вероятность [latex] B [/ latex] для [latex] A [/ latex] равна [latex] 1/2 [/ latex], поскольку [latex] A \ cap B = \ {HHH \} [/ latex ] с вероятностью [латекс] 1/8 [/ латекс] и [латекс] A = \ {HHH, TTT \} [/ latex] с вероятностью [латекс] 2/8 [/ латекс] и [латекс] \ frac {1/8} {2/8} = \ frac {1} {2}. [/ latex]
Независимость
Условная вероятность [латекс] P (B | A) [/ latex] не всегда равна безусловной вероятности [latex] P (B) [/ latex].Причина этого в том, что возникновение события [latex] A [/ latex] может предоставить дополнительную информацию, которая может изменить вероятность возникновения события [latex] B [/ latex]. Если знание о том, что происходит событие [latex] A [/ latex], не изменяет вероятность того, что событие [latex] B [/ latex] происходит, то [latex] A [/ latex] и [latex] B [/ latex] являются независимые события, и, таким образом, [латекс] P (B | A) = P (B) [/ latex].
Теорема Байеса
В теории вероятностей и статистике теорема Байеса (альтернативно закон Байеса или правило Байеса) является важным результатом при математическом манипулировании условными вероятностями.Его можно вывести из основных аксиом вероятности.
Математически теорема Байеса дает соотношение между вероятностями [латекс] A [/ латекс] и [латекс] B [/ латекс], [латекс] P (A) [/ латекс] и [латекс] P (B) [/ latex] и условные вероятности [latex] A [/ latex] для [latex] B [/ latex] и [latex] B [/ latex] для [latex] A [/ latex]. В наиболее распространенной форме это:
[латекс] \ Displaystyle P (A | B) = \ frac {P (B | A) P (A)} {P (B)} [/ латекс]
Это может быть легче запомнить в этой альтернативной симметричной форме:
[латекс] \ Displaystyle \ frac {P (A | B)} {P (B | A)} = \ frac {P (A)} {P (B)} [/ латекс]
Пример:
Предположим, кто-то сказал вам, что приятно поговорил с кем-то в поезде.Ничего не зная об этом разговоре, вероятность того, что они говорили с женщиной, составляет [латекс] 50 \% [/ латекс]. Теперь предположим, что они также сказали вам, что у этого человека были длинные волосы. Теперь более вероятно, что они разговаривали с женщиной, поскольку женщины в этом городе чаще имеют длинные волосы, чем мужчины. Теорема Байеса может использоваться для расчета вероятности того, что это женщина.
Чтобы увидеть, как это делается, пусть [latex] W [/ latex] представляет событие, в котором беседа велась с женщиной, а [latex] L [/ latex] обозначает событие, когда беседа велась с длинным волосатый человек.Можно предположить, что для этого примера женщины составляют половину населения. Итак, не зная ничего другого, вероятность того, что [latex] W [/ latex] встречается, равна [latex] P (W) = 0,5 [/ latex].
Предположим, также известно, что [латекс] 75% [/ латекс] женщин в этом городе имеют длинные волосы, которые мы обозначаем как [латекс] P (L | W) = 0,75 [/ латекс]. Аналогично предположим, что известно, что [латекс] 25 \% [/ латекс] мужчин в этом городе имеют длинные волосы, или [латекс] P (L | M) = 0,25 [/ латекс], где [латекс] M [/ латекс] является дополнительным элементом [латекс] W [/ латекс], т.е.е., событие, при котором беседа велась с мужчиной (при условии, что каждый человек является мужчиной или женщиной).
Наша цель — вычислить вероятность того, что разговор велся с женщиной, учитывая тот факт, что у человека были длинные волосы, или, в наших обозначениях, [латекс] P (W | L) [/ латекс]. Используя формулу теоремы Байеса, имеем:
[латекс] \ displaystyle \ begin {align} P (W | L) & = \ frac {P (L | W) P (W)} {P (L)} \\ & = \ frac {P (L | W) P (W)} {P (L | W) P (W) + P (L | M) P (M)} \\ & = \ frac {0.c [/ latex] или [latex] \ bar {A} [/ latex].
Ключевые термины
- взаимоисключающие : описание нескольких событий или состояний, при которых возникновение одного подразумевает ненаступление всех остальных
- исчерпывающий : включая все возможные элементы
Что такое дополнительные события?
В теории вероятностей дополнением к любому событию [latex] A [/ latex] является событие [latex] [\ text {not} \ A] [/ latex], т.е.е. событие, при котором [латекс] A [/ латекс] не встречается. Событие [latex] A [/ latex] и его дополнение [latex] [\ text {not} \ A] [/ latex] являются взаимоисключающими и исчерпывающими, что означает, что если одно происходит, то другое не происходит, и что обе группы охватить все возможности. c [/ latex] или [latex] \ bar {A} [/ latex] .
Простые примеры
Типичным примером, используемым для демонстрации дополнительных событий, является подбрасывание монеты. Допустим, монета подбрасывается и предполагается, что она не может упасть на край. Он может приземлиться либо на голову, либо на хвост. Других возможностей нет (исчерпывающие), и оба события не могут происходить одновременно (взаимоисключающие). Поскольку эти два события дополняют друг друга, мы знаем, что [latex] P (\ text {Head}) + P (\ text {tails}) = 1 [/ latex].
Подбрасывание монеты: Часто в спортивных играх, например в теннисе, подбрасывание монеты используется для определения того, кто подаст первым, поскольку орел и решка дополняют друг друга.
Еще один простой пример дополнительных событий — вытаскивание мяча из мешка. Допустим, в пакете три пластиковых мяча. Один синий и два красных. Предполагая, что каждый мяч имеет равные шансы вытащить из мешка, мы знаем, что [latex] P (\ text {blue}) = \ frac {1} {3} [/ latex] и [latex] P (\ текст {красный}) = \ frac {2} {3} [/ latex]. Поскольку мы можем выбрать только синий или красный (исчерпывающий), и мы не можем выбрать оба одновременно (взаимоисключающие), выбор синего и красного являются дополнительными событиями, а [latex] P (\ text {blue}) + P ( \ text {red}) = 1 [/ latex].
Наконец, давайте рассмотрим не пример дополнительных событий. Если бы вас попросили выбрать любое число, вы могли бы подумать, что это число может быть простым или составным. Ясно, что число не может быть одновременно простым и составным, так что это учитывает взаимоисключающее свойство. Однако быть простым или составным не являются исчерпывающими, потому что число 1 в математике обозначается как «уникальное». ”
Правило сложения
Правило сложения утверждает, что вероятность двух событий — это сумма вероятностей того, что одно из них произойдет, минус вероятность того, что оба события произойдут.
Цели обучения
Рассчитайте вероятность события с помощью правила сложения
Основные выводы
Ключевые моменты
- Правило сложения: [латекс] P (A \ cup B) = P (A) + P (B) -P (A \ cap B). [/ Latex]
- Последний член учитывался дважды, один раз в [латексе] P (A) [/ latex] и один раз в [латексе] P (B) [/ latex], поэтому его необходимо вычесть один раз, чтобы он не удваивался. -считано.
- Если [латекс] A [/ latex] и [latex] B [/ latex] не пересекаются, то [latex] P (A \ cap B) = 0 [/ latex], поэтому формула становится [латекс] P (A \ чашка B) = P (A) + P (B).[/ латекс]
Ключевые термины
- вероятность : относительная вероятность того, что событие произойдет.
Закон о добавлении
Закон сложения вероятностей (иногда называемый правилом сложения или правилом сумм), гласит, что вероятность того, что [латекс] A [/ латекс] или [латекс] B [/ латекс] возникнет, является суммой вероятностей того, что [latex] A [/ latex] произойдет, и что [latex] B [/ latex] произойдет, за вычетом вероятности того, что произойдет и [latex] A [/ latex], и [latex] B [/ latex].Правило сложения резюмируется формулой:
[латекс] \ Displaystyle P (A \ чашка B) = P (A) + P (B) -P (A \ cap B) [/ латекс]
Рассмотрим следующий пример. При вытягивании одной карты из колоды игральных карт [latex] 52 [/ latex], какова вероятность получить черву или лицевую карту (король, дама или валет)? Пусть [latex] H [/ latex] обозначает рисование сердца, а [latex] F [/ latex] обозначает рисование лицевой карты. Так как есть [латексные] 13 [/ латексные] червы и в общей сложности [латексные] 12 [/ латексные] лицевые карты ([латекс] 3 [/ латекс] каждой масти: пики, червы, бубны и трефы), но только [latex] 3 [/ latex] лицевых карты червей, получаем:
[латекс] \ Displaystyle P (H) = \ frac {13} {52} [/ латекс]
[латекс] \ Displaystyle P (F) = \ frac {12} {52} [/ латекс]
[латекс] \ displaystyle P (F \ cap H) = \ frac {3} {52} [/ latex]
Используя правило сложения, получаем:
[латекс] \ displaystyle \ begin {align} P (H \ cup F) & = P (H) + P (F) -P (H \ cap F) \\ & = \ frac {13} {52} + \ frac {12} {52} — \ frac {3} {52} \ end {align} [/ latex]
Причина вычитания последнего члена состоит в том, что в противном случае мы будем считать среднюю часть дважды (поскольку [латекс] H [/ латекс] и [латекс] F [/ латекс] перекрываются).
Правило сложения для непересекающихся событий
Предположим, что [latex] A [/ latex] и [latex] B [/ latex] не пересекаются, их пересечение пусто. Тогда вероятность их пересечения равна нулю. В условных обозначениях: [латекс] P (A \ cap B) = 0 [/ латекс]. Затем закон сложения упрощается до:
[латекс] P (A \ cup B) = P (A) + P (B) \ qquad \ text {when} \ qquad A \ cap B = \ emptyset [/ latex]
Символ [latex] \ emptyset [/ latex] представляет собой пустой набор, который указывает, что в этом случае [latex] A [/ latex] и [latex] B [/ latex] не имеют общих элементов (они имеют не перекрываются).
Пример:
Предположим, что карта взята из колоды из 52 игральных карт: какова вероятность получить короля или королеву? Пусть [latex] A [/ latex] представляет событие, когда выпадает король, а [latex] B [/ latex] представляет событие, когда вытаскивается ферзь. Эти два события не пересекаются, поскольку нет королей, которые также были бы королевами. Таким образом:
[латекс] \ displaystyle \ begin {align} P (A \ cup B) & = P (A) + P (B) \\ & = \ frac {4} {52} + \ frac {4} {52} \\ & = \ frac {8} {52} \\ & = \ frac {2} {13} \ end {align} [/ latex]
Правило умножения
Правило умножения утверждает, что вероятность того, что [latex] A [/ latex] и [latex] B [/ latex] встречаются, равна вероятности того, что [latex] B [/ latex] встречается, умноженная на условную вероятность того, что [latex] ] A [/ latex] встречается при условии, что встречается [latex] B [/ latex].
Цели обучения
Примените правило умножения для вычисления вероятности того, что [latex] A [/ latex] и [latex] B [/ latex] встречаются
Основные выводы
Ключевые моменты
- Правило умножения можно записать как: [latex] P (A \ cap B) = P (B) \ cdot P (A | B) [/ latex].
- Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.
Ключевые термины
- пробел : набор всех возможных исходов игры, эксперимента или другой ситуации.
Правило умножения
В теории вероятностей правило умножения гласит, что вероятность того, что [латекс] A [/ латекс] и [латекс] B [/ латекс] встречается, равна вероятности того, что [латекс] A [/ латекс] встречается, умноженная на условную вероятность что [latex] B [/ latex] встречается, учитывая, что мы знаем, что [latex] A [/ latex] уже произошло. Это правило можно записать:
[латекс] \ Displaystyle P (A \ cap B) = P (B) \ cdot P (A | B) [/ латекс]
Переключая роли [latex] A [/ latex] и [latex] B [/ latex], мы также можем записать правило как:
[латекс] \ Displaystyle P (A \ cap B) = P (A) \ cdot P (B | A) [/ латекс]
Мы получаем общее правило умножения, умножая обе части определения условной вероятности на знаменатель.То есть в уравнении [латекс] \ displaystyle P (A | B) = \ frac {P (A \ cap B)} {P (B)} [/ latex], если мы умножим обе стороны на [латекс] P (B) [/ latex], получаем Правило умножения.
Правило полезно, когда мы знаем оба [латекс] P (B) [/ latex] и [латекс] P (A | B) [/ latex], или оба [латекс] P (A) [/ latex] и [ латекс] П (В | А). [/ латекс]
Пример
Предположим, что мы вытягиваем две карты из колоды карт, и пусть [latex] A [/ latex] будет событием, когда первая карта является тузом, а [latex] B [/ latex] будет событием, что вторая карта туз, то:
[латекс] \ Displaystyle P (A) = \ frac {4} {52} [/ латекс]
А:
[латекс] \ displaystyle P \ left ({B} | {A} \ right) = \ frac {3} {51} [/ latex]
Знаменатель во втором уравнении [латекс] 51 [/ латекс], поскольку мы знаем, что карта уже разыграна.Таким образом, осталось всего [латекс] 51 [/ латекс]. Мы также знаем, что первой картой был туз, поэтому:
[латекс] \ displaystyle \ begin {align} P (A \ cap B) & = P (A) \ cdot P (B | A) \\ & = \ frac {4} {52} \ cdot \ frac {3 } {51} \\ & = 0,0045 \ end {align} [/ latex]
Независимое событие
Обратите внимание, что когда [latex] A [/ latex] и [latex] B [/ latex] независимы, мы имеем, что [latex] P (B | A) = P (B) [/ latex], поэтому формула становится [латекс] P (A \ cap B) = P (A) P (B) [/ latex], с которым мы столкнулись в предыдущем разделе.В качестве примера рассмотрим эксперимент по бросанию игральной кости и подбрасыванию монеты. Вероятность того, что мы получим [латекс] 2 [/ latex] на кубике и решки на монете, равна [latex] \ frac {1} {6} \ cdot \ frac {1} {2} = \ frac {1 } {12} [/ latex], поскольку два события независимы.
Независимость
Сказать, что два события независимы, означает, что возникновение одного не влияет на вероятность другого.
Цели обучения
Объяснить понятие независимости применительно к теории вероятностей
Основные выводы
Ключевые моменты
- Два события являются независимыми, если верно следующее: [latex] P (A | B) = P (A) [/ latex], [latex] P (B | A) = P (B) [/ latex], и [латекс] P (A \ \ text {and} \ B) = P (A) \ cdot P (B) [/ latex].
- Если любое из этих условий верно, то все они верны.
- Если события [latex] A [/ latex] и [latex] B [/ latex] независимы, то вероятность возникновения [latex] A [/ latex] не влияет на вероятность [latex] B [/ latex] происходящие и наоборот.
Ключевые термины
- независимость : Возникновение одного события не влияет на вероятность наступления другого.
- теория вероятностей : математическое исследование вероятности (вероятность возникновения случайных событий с целью прогнозирования поведения определенных систем).
Независимые мероприятия
В теории вероятностей утверждение, что два события независимы, означает, что возникновение одного не влияет на вероятность того, что другое произойдет. Другими словами, если события [латекс] A [/ латекс] и [латекс] B [/ латекс] независимы, то вероятность возникновения [латекса] A [/ латекса] не влияет на вероятность [латекса] B [ / латекс] и наоборот. Концепция независимости распространяется на коллекции, состоящие из более чем двух событий.
Два события являются независимыми, если выполняется одно из следующих условий:
- [латекс] \ Displaystyle P (A | B) = P (A) [/ латекс]
- [латекс] \ Displaystyle P (B | A) = P (B) [/ латекс]
- [латекс] \ Displaystyle P (A \ \ text {и} \ B) = P (A) \ cdot P (B) [/ латекс]
Чтобы показать, что два события независимы, вы должны показать только одно из перечисленных выше условий.Если хотя бы одно из этих условий верно, то все они верны.
Переводя символы в слова, первые два перечисленных выше математических утверждения говорят, что вероятность события с условием такая же, как вероятность события без условия. Для независимых событий условие не меняет вероятность события. Третье утверждение гласит, что вероятность возникновения обоих независимых событий [латекс] A [/ latex] и [латекс] B [/ latex] такая же, как вероятность возникновения [latex] A [/ latex], умноженная на вероятность [латекс] Б [/ латекс] встречающийся.
В качестве примера представьте, что вы последовательно выбираете две карты из полной колоды игральных карт. Эти два выбора не являются независимыми. Результат первого выбора изменяет оставшуюся колоду и влияет на вероятность второго выбора. Это называется выбором «без замены», потому что первая карта не была заменена в колоду до того, как будет выбрана вторая карта.
Однако предположим, что вы выбрали две карты «с заменой», вернув первую карту в колоду и перетасовав колоду перед тем, как выбрать вторую карту.Поскольку колода карт является полной для обоих вариантов выбора, первый выбор не влияет на вероятность второго выбора. При выборе карт с заменой выбор не зависит.
независимых событий: выбор двух карт из колоды, сначала выбирая одну, затем заменяя ее в колоде перед выбором второй, является примером независимых событий.
Рассмотрим роль справедливого кубика, которая представляет собой еще один пример независимых событий. Если человек, играющий роль двоих, умирает, результат первого броска не меняет вероятность результата второго броска.
Пример
Два друга играют в бильярд и решают подбросить монету, чтобы определить, кто будет играть первым в каждом раунде. В первых двух раундах монета выпадает орлом. Они решают сыграть в третий раунд и снова подбрасывают монету. Какова вероятность того, что монета снова упадет орлом?
Во-первых, обратите внимание, что каждое подбрасывание монеты — независимое событие. Сторона, на которую приземляется монета, не зависит от того, что произошло ранее.
Для любого подбрасывания монеты существует [latex] {\ frac {1} {2}} [/ latex] шанс, что монета упадет орлом.Таким образом, вероятность того, что монета упадет орлом во время третьего раунда, равна [latex] {\ frac {1} {2}} [/ latex].
Пример
При подбрасывании монеты, какова вероятность получить решки [латекс] 5 [/ латекс] раз подряд?
Напомним, что каждый бросок монеты независим, и вероятность выпадения решки составляет [латекс] {\ frac {1} {2}} [/ latex] для любого подбрасывания. Также напомним, что для любых двух независимых событий A и B справедливо следующее утверждение:
[латекс] \ Displaystyle P (A \ \ text {и} \ B) = P (A) \ CDOT P (B) [/ латекс]
Наконец, концепция независимости распространяется на коллекции более чем [latex] 2 [/ latex] событий.
Следовательно, вероятность получить хвосты [латекс] 4 [/ латекс] раза подряд составляет:
[латекс] \ displaystyle {\ frac {1} {2}} \ cdot {\ frac {1} {2}} \ cdot {\ frac {1} {2}} \ cdot {\ frac {1} {2 }} = {\ frac {1} {16}} [/ latex]
Экспериментальные вероятности
Вероятность эксперимента — это отношение количества исходов, при которых происходит событие, к общему количеству испытаний в эксперименте.
Цели обучения
Рассчитать эмпирическую вероятность события на основе данной информации
Основные выводы
Ключевые моменты
- В общем смысле экспериментальная (или эмпирическая) вероятность оценивает вероятности на основе опыта и наблюдений.
- В простых случаях, когда результат испытания только определяет, произошло ли указанное событие, может быть целесообразным моделирование с использованием биномиального распределения; тогда эмпирическая оценка является оценкой максимального правдоподобия.
- Если испытание дает больше информации, эмпирическая вероятность может быть улучшена путем принятия дополнительных предположений в форме статистической модели. Если такая модель подобрана, ее можно использовать для получения оценки вероятности указанного события.
Ключевые термины
- биномиальное распределение : Дискретное распределение вероятностей количества успехов в последовательности [латекс] n [/ латекс] независимых экспериментов да / нет, каждый из которых дает успех с вероятностью [латекс] p [/ латекс].
- экспериментальная вероятность : Вероятность того, что произойдет определенный результат, определяемая экспериментально.
- дискретный : отдельный; отчетливый; физическое лицо; прерывистый.
Экспериментальная (или эмпирическая) вероятность относится к данным, взятым из ряда испытаний. Это вероятность, рассчитанная на основе опыта, а не теории. Если наблюдается выборка испытаний [латекс] x [/ латекс], которая приводит к событию [латекс] e [/ латекс], происходящему [латекс] n [/ латекс] раз, вероятность события [латекс] e [ / латекс] рассчитывается как соотношение [латекс] n [/ латекс] к [латекс] x [/ латекс].
[латекс] \ displaystyle \ text {экспериментальная вероятность события} = \ frac {\ text {количество случаев события}} {\ text {общее количество испытаний}} [/ latex]
Экспериментальная вероятность контрастирует с теоретической вероятностью, чего мы и ожидали.Например, если мы подбросим монету [латекс] 10 [/ латекс] раз, мы можем ожидать, что она упадет на голову [латекс] 5 [/ латекс] раз, или в половине случаев. Мы знаем, что на практике это вряд ли произойдет. Если мы проводим большее количество испытаний, часто случается, что экспериментальная вероятность становится ближе к теоретической. По этой причине обычно ценятся большие размеры выборки (или большее количество испытаний).
С точки зрения статистики, эмпирическая вероятность — это оценка вероятности.В простых случаях, когда результат испытания только определяет, произошло ли указанное событие, может быть целесообразным моделирование с использованием биномиального распределения. Биномиальное распределение — это дискретное распределение вероятностей количества успехов в последовательности [латексных] n [/ латексных] независимых экспериментов да / нет. В таких случаях наиболее вероятной оценкой является эмпирическая вероятность.
Если испытание дает больше информации, эмпирическую вероятность можно улучшить, приняв дополнительные допущения в форме статистической модели: если такая модель подобрана, ее можно использовать для оценки вероятности указанного события.Например, можно легко присвоить вероятность каждому возможному значению во многих дискретных случаях: при броске кубика каждое из шести значений от [латекс] 1 [/ латекс] до [латекс] 6 [/ латекс] имеет вероятность [ латекс] \ frac {1} {6} [/ латекс].
Преимущества
Преимущество оценки вероятностей с использованием эмпирических вероятностей состоит в том, что эта процедура включает несколько предположений. Например, рассмотрим оценку вероятности среди популяции мужчин, удовлетворяющих двум условиям:
- Они более шести футов в высоту.
- Они предпочитают клубничное варенье малиновому.
Прямая оценка может быть получена путем подсчета числа мужчин, которые удовлетворяют обоим условиям, чтобы дать эмпирическую вероятность комбинированного состояния.
Альтернативная оценка может быть получена умножением доли мужчин ростом более шести футов на долю мужчин, которые предпочитают клубничное варенье малиновому джему, но эта оценка основана на предположении, что эти два условия статистически независимы.
Недостатки
Недостаток использования эмпирических вероятностей заключается в том, что без теории, которая их «осмысляет», легко сделать неверные выводы. Если бросить шестигранный кубик сто раз, вполне возможно, что больше [латекса] \ frac {1} {6} [/ latex] валков упадет на [латекс] 4 [/ latex]. Интуитивно мы знаем, что вероятность выпадения любого номера должна быть равна вероятности выпадения следующего. Эксперименты, особенно с меньшим размером выборки, могут подсказать обратное.
Этот недостаток становится особенно проблематичным при оценке вероятностей, которые либо очень близки к нулю, либо очень близки к единице. Например, вероятность выпадения числа от [latex] 1 [/ latex] до [latex] 1000 [/ latex] равна [latex] \ frac {1} {1000} [/ latex]. Если берется [latex] 1000 [/ latex] розыгрышей и первое число выпадает [latex] 5 [/ latex], остается [latex] 999 [/ latex] розыгрышей, чтобы нарисовать [латекс] 5 [/ latex] снова и, таким образом, имеем экспериментальные данные, которые показывают вдвое большую ожидаемую вероятность вытягивания [латекса] 5 [/ латекса].
В этих случаях потребуются очень большие размеры выборки, чтобы оценить такие вероятности с хорошим стандартом относительной точности. Здесь могут помочь статистические модели, в зависимости от контекста.
Например, рассмотрите возможность оценки вероятности того, что самая низкая из максимальных дневных температур на участке в феврале за любой год будет ниже нуля градусов Цельсия. Запись таких температур в прошлые годы может быть использована для оценки этой вероятности. Альтернативой, основанной на модели, будет выбор семейства распределений вероятностей и подгонка его к набору данных, содержащему значения прошлых лет.Подобранное распределение предоставит альтернативную оценку желаемой вероятности. Этот альтернативный метод может обеспечить оценку вероятности, даже если все значения в записи больше нуля.
Основные понятия вероятности
Основные понятия
Автор (ы)
Дэвид М. ЛейнПредварительные требования
Вступление к вероятностиЦели обучения
- Вычислить вероятность в ситуации, когда есть равновероятные результаты
- Применить концепции к картам и играм в кости
- Вычислить вероятность двух независимых событий, оба произошедших
- Вычислить вероятность наступления любого из двух независимых событий
- Решать задачи, связанные с условными вероятностями
- Вычислите вероятность того, что в комнате из N человек не менее двух день рождения
- Опишите ошибку игрока
Вероятность единичного события
Если вы бросите шестигранный кубик, есть шесть возможных результаты, и каждый из этих исходов в равной степени вероятен.Шесть с такой же вероятностью выпадет, как тройка, и точно так же для другого четыре стороны кости. Какова же тогда вероятность того, что один подойдет? Поскольку существует шесть возможных исходов, вероятность составляет 1/6. Какова вероятность того, что один или шесть появиться? Два результата, которые нас беспокоят (один или приближающаяся шестерка) называются благоприятными результаты. Учитывая, что все исходы одинаково вероятны, мы можем вычислите вероятность одного или шести по формуле:
В этом случае есть два благоприятных исхода и шесть возможных результаты.Таким образом, вероятность выпадения единицы или шестерки равна 1/3. Не обманывайтесь, когда мы используем термин «благоприятный», Кстати. Вы должны понимать это в смысле «благоприятный к рассматриваемому событию «. Это событие может не быть благоприятным для вашего благополучия. Вы можете сделать ставку на тройку, Например.
Приведенная выше формула применима ко многим азартным играм. Например, какова вероятность того, что случайно выпавшая карта из колоды игральных карт будет туз? Поскольку в колоде четыре туза, есть четыре благоприятных исхода; поскольку в колоде есть 52 карты, есть 52 возможных исхода.Вероятность поэтому 4/52 = 1/13. Как насчет вероятности того, что карта будет клуб? Так как треф 13, вероятность 13/52 = 1/4.
Допустим, у вас есть сумка с 20 вишнями: 14 сладких и 6 кис. Если вы выберете вишню наугад, какова вероятность что будет сладко? Есть 20 возможных вишен, которые могут быть выбранным, поэтому количество возможных исходов равно 20.Из этих 20 возможных исходов, 14 благоприятных (сладких), поэтому вероятность что вишня будет сладкой — 14/20 = 7/10. Есть один потенциал Однако этот пример усложняется. Следует предположить, что вероятность собрать любую из вишен такая же, как вероятность выбора любого другого. Это было бы неправдой, если бы (представим) черешня меньше кислой единицы.(Вишня легче подойдет, когда вы взяли образец из сумки.) Давайте помнить, что когда мы оцениваем вероятности с точки зрения соотношения благоприятных во всех возможных случаях мы в значительной степени полагаемся на предположение о равных вероятность для всех исходов.
Вот более сложный пример. Вы бросаете 2 кубика. Какова вероятность того, что сумма двух кубиков будет равна 6? Чтобы решить эту проблему, перечислите все возможные исходы.Есть 36 из них, так как каждая игральная кость может выпасть одним из шести способов. 36 возможности показаны ниже.
| Умереть 1 | Умереть 2 | Общее | Умереть 1 | Умереть 2 | Общее | Умереть 1 | Умереть 2 | Общее | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 1 | 4 | 5 | 1 | 6 | ||
| 1 | 2 | 3 | 3 | 2 | 5 | 5 | 2 | 7 | ||
| 1 | 3 | 4 | 3 | 3 | 6 | 5 | 3 | 8 | ||
| 1 | 4 | 5 | 3 | 4 | 7 | 5 | 4 | 9 | ||
| 1 | 5 | 6 | 3 | 5 | 8 | 5 | 5 | 10 | ||
| 1 | 6 | 7 | 3 | 6 | 9 | 5 | 6 | 11 | ||
| 2 | 1 | 3 | 4 | 1 | 5 | 6 | 1 | 7 | ||
| 2 | 2 | 4 | 4 | 2 | 6 | 6 | 2 | 8 | ||
| 2 | 3 | 5 | 4 | 3 | 7 | 6 | 3 | 9 | ||
| 2 | 4 | 6 | 4 | 4 | 8 | 6 | 4 | 10 | ||
| 2 | 5 | 7 | 4 | 5 | 9 | 6 | 5 | 11 | ||
| 2 | 6 | 8 | 4 | 6 | 10 | 6 | 6 | 12 |
Как видите, 5 из 36 вариантов в сумме составляют 6.Следовательно,
вероятность 5/36.
Если вы знаете вероятность наступления события, легко вычислить вероятность того, что событие не происходить. Если P (A) — вероятность события A, то 1 — P (A) равно вероятность того, что событие не произойдет. В последнем примере вероятность того, что сумма будет равна 6, составляет 5/36. Следовательно, вероятность что сумма не 6, это 1 — 5/36 = 31/36.
Вероятность двух (или более) независимых событий
События A и B независимы события, если вероятность возникновения События B равна то же самое независимо от того, происходит ли событие А. Возьмем простой пример. Честная монета подбрасывается два раза. Вероятность того, что голова выпадает при втором броске 1/2 независимо от того, или не поднялась голова при первом же подбрасывании.Два события (1) первый бросок — это голова и (2) второй бросок — это голова. Так эти события независимы. Рассмотрим два события (1) «Это завтра будет дождь в Хьюстоне » и (2) «Завтра пойдет дождь в Галвестоне» (город недалеко от Хьюстон). Эти события не являются независимыми, потому что это более Вероятно, что в Галвестоне пойдет дождь в дни, когда идет дождь в Хьюстоне чем по дням это не так.
Вероятность A и B
Когда два события независимы, вероятность того и другого является продуктом вероятностей отдельные события. Более формально, если события A и B независимы, тогда вероятность появления как A, так и B равна:
P (A и B) = P (A) x P (B)
где P (A и B) — вероятность событий A и B оба происходят, P (A) — вероятность наступления события A, и P (B) — вероятность наступления события B.
Если подбросить монету дважды, какова вероятность что оба раза это поднимет голову? Событие А заключается в том, что монета выпадает орел при первом броске, и Событие B заключается в том, что монета выпадает на второй бросок. Поскольку и P (A), и P (B) равны 1/2, вероятность того, что оба события произойдут, равна
.1/2 х 1/2 = 1/4.
Возьмем другой пример. Если вы подбросите монетку и бросьте шестигранный кубик, какова вероятность того, что монета выпадает орел и выпадает 1? Поскольку два события независимы, вероятность — это просто вероятность голова (что в 1/2 раза больше вероятности выпадения кубика) вверх 1 (что составляет 1/6).Следовательно, вероятность обоих событий происходит 1/2 x 1/6 = 1/12.
Последний пример: вы берете карту из колоды карты, положите ее обратно и возьмите еще одну карту. Какова вероятность что первая карта — сердце, а вторая — черная? С в колоде 52 карты и 13 из них червы, вероятность Что первая карта — это сердце, 13/52 = 1/4. Поскольку есть 26 черных карт в колоде, вероятность того, что вторая карта черный — 26/52 = 1/2.Вероятность наступления обоих событий поэтому 1/4 x 1/2 = 1/8.
См. Раздел об условных вероятностях на на этой странице, чтобы узнать, как вычислить P (A и Б) когда А и В не независимы.
Вероятность A или B
Если события A и B независимы, вероятность что происходит событие A или событие B:
P (A или B) = P (A) + P (B) — P (A и B)
В этом обсуждении, когда мы говорим «встречается A или B» мы включаем три возможности:
- А встречается, а В не встречается
- B встречается, а A не встречается
- Встречаются как A, так и B
Это слово «или» технически называется инклюзивным или потому, что он включает случай, когда встречаются как A, так и B.Если бы мы включили только первые два случая, тогда мы будем использовать эксклюзивный или же.
(Необязательно) Мы можем вывести закон для P (A-or-B) из нашего закона о P (A-and-B). Мероприятие «А-или-Б» может произойти любым из следующих способов:
- А-а-Б бывает
- А-а-не-Б бывает
- не-А-а-Б бывает.
Простое событие A может произойти, если A-и-B случается или случается А-а-не-Б.Точно так же простое событие B происходит, если случаются либо A-and-B, либо нет-A-and-B. P (A) + P (B), следовательно, P (A-and-B) + P (A-and-not-B) + P (A-and-B) + P (не-A-and-B), тогда как P (A-or-B) — это P (A-and-B) + P (A-and-not-B) + P (не-A-and-B). Мы можем уравнять эти две суммы, вычитая одно вхождение P (A-and-B) с первого. Следовательно, P (A-or-B) = P (A) + P (B) — P (A-и-B).
Теперь несколько примеров.Если подбросить монету два раза, какова вероятность, что вы получите голову первым флип или голова на втором флипе (или и то, и другое)? Разрешение событию А быть голова при первом подбрасывании и Событие B — голова при втором подбрасывании, тогда P (A) = 1/2, P (B) = 1/2 и P (A и B) = 1/4. Следовательно,
P (A или B) = 1/2 + 1/2 — 1/4 = 3/4.
Если вы бросите шестигранный кубик, а затем подбросите монету, какова вероятность, что вы получите либо 6 на кубике или голова на подбрасывании монеты (или и то, и другое)? Используя формулу,
P (6 или голова) = P (6) + P (голова) — P (6 и голова)
=
(1/6) + (1/2) — (1/6) (1/2)
=
7/12
Альтернативный подход к вычислению этого значения состоит в том, чтобы начать с вычисления вероятности не получить 6 или голова.Затем вычтите это значение из 1, чтобы вычислить вероятность получить 6 или голову. Хотя это сложный метод, он имеет то преимущество, что он применим к проблемам с более двух событий. Вот расчет в данном случае. Вероятность не получить 6 или голову можно изменить. как вероятность
(не получает 6) И (не получает голову).
Это следует потому, что если вы не получили 6 и вы не получили голову, значит, вы не получили 6 или голову.В вероятность не получить шестерку составляет 1 — 1/6 = 5/6. Вероятность не получить голову 1 — 1/2 = 1/2. Вероятность не получить шестерку и не получить голову — 5/6 x 1/2 = 5/12. Этот следовательно, вероятность не получить 6 или голову. В поэтому вероятность получить шестерку или голову (еще раз) 1 — 5/12 = 7/12.
Если вы бросите кубик три раза, какова вероятность что один или несколько ваших бросков принесут вам 1? Это, какова вероятность получить 1 при первом броске ИЛИ 1 при втором броске ИЛИ 1 при третьем броске? Самый простой способ чтобы подойти к этой проблеме, нужно вычислить вероятность
НЕ получает 1 за первый бросок
И не получает 1 за второй бросок
И не получает 1 за третий бросок.
Ответ будет 1 минус эта вероятность. В вероятность не получить 1 при любом из трех бросков — 5/6 х 5/6 х 5/6 = 125/216. Следовательно, вероятность получения 1 хотя бы на один из бросков составляет 1 — 125/216 = 91/216.
Условные вероятности
Часто требуется вычислить вероятность события, учитывая, что произошло другое событие.Например, какова вероятность, что две случайные карты вытянуты из колода игральных карт будет как тузами? Может показаться, что вы можете использовать формулу вероятности двух независимых события и просто умножьте 4/52 x 4/52 = 1/169. Это было бы неправильно, однако, потому что эти два события не являются независимыми. Если первая вытянутая карта — туз, тогда вероятность того, что вторая карта тоже туз будет ниже, потому что будет только в колоде осталось три туза.
Если первой выбранной картой является туз, вероятность то, что вторая выбранная карта также является тузом, называется условным вероятность выпадения туза. В этом случае «условие» в том, что первая карта — туз. Символически мы пишем это как:
P (туз при второй розыгрыше | туз при первой розыгрыше)
Вертикальная черта «|» читается как «данный», поэтому приведенное выше выражение является сокращением от: «Вероятность того, что при втором розыгрыше выдается туз, если был вытянут туз по первому розыгрышу.»Какова эта вероятность? Поскольку после при первом розыгрыше разыгрывается туз, из них 3 туза Всего осталось 51 карта. Это означает, что вероятность того, что один из этих тузов выпадет 3/51 = 1/17.
Если события A и B не являются независимыми, то P (A и B) = P (A) x P (B | A).
Применяя это к проблеме двух тузов, вероятность выпадения двух тузов из колоды 4/52 x 3/51 = 1/221.
Еще один пример: если вы берете две карты из колоды, какова вероятность того, что вы получите бубновый туз а черная карта? Есть два способа выполнить это условие: (1) Сначала вы можете получить бубновый туз, а затем черную карту. или (2) вы можете сначала получить черную карту, а затем бубновый туз. Рассчитаем случай A. Вероятность того, что первая карта окажется Бубновый туз равен 1/52.Вероятность того, что вторая карта черный, учитывая, что первая карта — бубновый туз — 26/51 потому что 26 из оставшейся 51 карты черные. Вероятность поэтому 1/52 x 26/51 = 1/102. Теперь для случая 2: вероятность что первая карта черная — 26/52 = 1/2. Вероятность того, что вторая карта — бубновый туз, учитывая, что первая карта черный — 1/51. Таким образом, вероятность случая 2 равна 1/2 x 1/51 = 1/102, как вероятность случая 1.Напомним, что вероятность A или B равна P (A) + P (B) — P (A и B). В этом проблема, P (A и B) = 0, поскольку карта не может быть бубновым тузом. и быть черной картой. Следовательно, вероятность случая 1 или случая 2 равно 1/102 + 1/102 = 2/102 = 1/51. Итак, 1/51 — это вероятность того, что при розыгрыше вы получите бубновый туз и черную карту две карты из колоды.
Проблема дня рождения
Если в комнате 25 человек, какой вероятность того, что хотя бы двое из них имеют один и тот же день рождения.Если вы сначала подумали, что это 25/365 = 0,068, вы будете удивлен, узнав, что это намного выше, чем это. Эта проблема требует применение разделов на P (A и B) и условных вероятность.
К этой проблеме лучше всего подойти, спросив, что такое вероятность того, что у двух людей нет одного дня рождения. Один раз мы знаем эту вероятность, мы можем просто вычесть ее от 1 до найти вероятность того, что у двух человек один день рождения.
Если мы выберем двух человек наугад, какой вероятность, что у них не будет одного дня рождения? Из 365 дней на которых у второго человека мог быть день рождения, их 364 отличаются от дня рождения первого человека. Следовательно вероятность 364/365. Определим P2 как вероятность того, что второй нарисованный человек не разделяет день рождения с этим человеком нарисованный ранее.Таким образом, P2 равен 364/365. Теперь определим P3 как вероятность того, что нарисованное третье лицо не разделяет день рождения с кем-либо нарисованным ранее, учитывая, что нет предыдущих совпадений по дням рождения. Таким образом, P3 является условным вероятность. Если нет совпадений с предыдущими днями рождения, то два из 365 дней были «израсходованы», в результате чего осталось 363 несоответствующие дни. Следовательно, P3 = 363/365. Аналогичным образом, P4 = 362/365, P5 = 361/365 и так далее до P25 = 341/365.
Чтобы не было совпадений, второй человек не должен совпадать ни с одним предыдущим человеком и третье лицо не должно совпадать с каким-либо предыдущим лицом, и четвертое лицо не должно совпадать с каким-либо предыдущим и т. д. P (A и B) = P (A) P (B), все, что нам нужно сделать, это умножить P2, P3, P4 … P25 вместе. Результат 0,431. Следовательно, вероятность хотя бы одного совпадения 0.569.
Заблуждение игрока
Честная монета подбрасывается пять раз и выпадает. головы каждый раз. Какова вероятность, что это произойдет головы на шестом броске? Правильный ответ, конечно, 1/2. Но многие люди считают, что хвост более вероятен. бросив пять голов. Их ошибочные рассуждение может звучать примерно так: «В конечном итоге число орла и решки будут одинаковыми, поэтому у хвостов есть наверстать упущенное.»Выявлены недостатки этой логики. в моделировании в этой главе.
Пожалуйста, ответьте на вопросы:
Биология 301
В заключительных лекциях этого класса мы изложим основы теории вероятностей и подчеркнем важность вероятностного моделирования в биологии.До сих пор мы изучили только детерминированных моделей, в которых будущие состояния полностью определяются текущим состоянием системы.
Однако в реальном мире случайность играет важную роль в динамике популяции. Молния может поразить человека. Пожар может уничтожить население. Отдельные особи могут не воспроизвести или произвести прекрасный урожай потомства. Новые полезные мутации могут случайно произойти у людей, не оставляющих детей. Могут случиться засуха и голод, или дожди и избыток.
Вероятностные модели включают случайные события и исходы и могут приводить к результатам, которые отличаются от чисто детерминированных моделей.
В этой лекции мы начнем с некоторых основных определений и правил теории вероятностей.
Для получения дополнительной информации прочтите «Теорию вероятностей» Джо Романо, из которой я взял несколько из следующих определений.
Какая вероятность?- Интерпретация частоты: «Вероятности понимаются как математически удобные приближения к долгосрочным относительным частотам».
- Субъективная интерпретация: «Утверждение о вероятности выражает мнение некоторого человека о том, насколько определенно должно произойти событие.»
Правило разницы: Если A является подмножеством B, то вероятность появления B, но не A, равна P (B) — P (A) = P (B A c ).
Правило включения-исключения: Вероятность появления A или B (или обоих) равна P (A U B) = P (A) + P (B) — P (AB).
Пример: если вероятность иметь зеленые глаза составляет 10%, вероятность иметь каштановые волосы составляет 75%, а вероятность того, что они будут зеленоглазым шатеном, составляет 9%, какова вероятность
- у вас нет зеленых глаз? [найти P (A c )]
- с зелеными глазами, но не с каштановыми волосами? [найти P (A) — P (AB)]
- с зелеными глазами и / или каштановыми волосами? [найти P (A U B)]
Условная вероятность: Вероятность того, что A произойдет при условии, что B произошло, = P (A | B).Другими словами, среди тех случаев, когда произошло событие B, P (A | B) — это доля случаев, в которых произошло событие A.
Правило умножения: Вероятность появления A и B равна вероятности B, умноженной на вероятность того, что A произойдет, при условии, что B имеет: P (AB) = P (B) P (A | B).Следовательно, условная вероятность равна P (A | B) = P (AB) / P (B).
Точно так же вероятность того, что произойдет A и что B произойдет, при условии, что A имеет: P (A) P (B | A) = P (AB), поэтому P (B | A) = P (AB) / P (A).
Пример: какова вероятность того, что у вас будут каштановые волосы, если у вас зеленые глаза? [найти P (B | A)]
Какова вероятность того, что у вас будут зеленые глаза, если у вас каштановые волосы? [найти P (A | B)]
Правило Байеса:
P (B | A) = P (B) P (A | B) / P (A) Эта формула связывает условную вероятность B для данного A с условной вероятностью A для данного B.Пример: Считается, что способность ощущать вкус фенилтиокарбамида (PTC) определяется одним доминантным геном с неполной пенетрантностью.Среди североамериканских белых вероятность попробовать PTC составляет 70% [P (дегустатор) = 0,7]. Если каждый, кто пробует PTC, является носителем [P (носитель | дегустатор) = 1], и если 80% населения несет ген [P (носитель) = 0,8], какова пенетрантность гена? То есть, какова вероятность попробовать PTC, если вы — перевозчик, P (дегустатор | перевозчик)?
Формула среднего: Предположим, что набор A можно полностью разделить на n взаимоисключающих подмножеств. Тогда общая вероятность A равна средней вероятности A в подмножествах, взвешенных по вероятности этих подмножеств: P (A) = P (A | B 1 ) P (B 1 ) + P (A | B 2 ) P (B 2 ) +… + P (A | B n ) P (B n )Пример: Какова общая вероятность смерти от малярии в регионе, где шанс умереть от малярии составляет 15% для лиц, не являющихся носителями аллеля серповидноклеточных клеток, и 1% для носителей? Предположим, что частота несущих равна 0,25.
P (умирает) =? = P (умирающий | не-носитель) P (не-носитель) + P (умирающий | носитель) P (носитель) = 0,15 * 0,75 + 0,01 * 0,25 Таким образом, общая вероятность смерти от малярия составляет 11,5%, что значительно ниже, чем если бы аллель серповидных клеток отсутствовал в популяции.Независимость: Если вероятность A не зависит от того, встречается ли B, то мы говорим, что A и B независимы.
ТОЛЬКО для независимых мероприятий,
- P (A | B) = P (A)
- P (AB) = P (A) P (B)
Пример: В США частота группы крови O составляет около 0,45, а частота Rh + составляет около 0,86. Какая часть населения имела бы группу крови O +, если бы это были независимые гены?
Если два объекта извлекаются из пула случайным образом с заменой , то они независимы, поскольку первое наблюдение не влияет на второе.
Пример: если в популяции N самцов, и конкретная самка выбирает себе партнера случайным образом из числа самцов, какова вероятность того, что, если она спаривается дважды за сезон, она будет спариваться с конкретным самцом оба раза?
Вернуться на домашнюю страницу биологии 301.
Определение сложной вероятности
Что такое сложная вероятность?
Сложная вероятность — это математический термин, относящийся к вероятности двух независимых событий.Сложная вероятность равна вероятности первого события, умноженной на вероятность второго события. Сложные вероятности используются страховыми андеррайтерами для оценки рисков и распределения премий по различным страховым продуктам.
Понимание сложной вероятности
Самый простой пример сложной вероятности — это дважды подбросить монету. Если вероятность выпадения орла составляет 50 процентов, то шансы выпадения орла дважды подряд будут (0,50 X.50) или 0,25 (25 процентов). Сложная вероятность объединяет как минимум два простых события, также называемых сложным событием. Вероятность того, что на монете выпадет орел, когда вы подбросите только одну монету, очень проста.
Что касается страхования, страховщики могут пожелать узнать, например, доживут ли оба члена супружеской пары до 75 лет, учитывая их независимые вероятности. Или страховщик может захотеть узнать вероятность того, что два крупных урагана обрушатся на данный географический регион в течение определенного периода времени.Результаты их математических расчетов определят, сколько будет взиматься плата за страхование людей или имущества.
Ключевые выводы
- Сложная вероятность — это произведение вероятностей наступления двух независимых событий, известных как сложные события.
- Формула для вычисления сложных вероятностей различается в зависимости от типа сложного события, независимо от того, являются ли они взаимоисключающими или взаимоисключающими.
Составные события и сложная вероятность
Есть два типа составных событий: взаимоисключающие составные события и взаимно включающие составные события.Взаимоисключающее сложное событие — это когда два события не могут происходить одновременно. Если два события, A и B, являются взаимоисключающими, то вероятность того, что произойдет либо A, либо B, является суммой их вероятностей. Между тем, взаимно включающие сложные события — это ситуации, когда одно событие не может происходить с другим. Если два события (A и B) включаются, то вероятность того, что произойдет либо A, либо B, является суммой их вероятностей за вычетом вероятности возникновения обоих событий.
Составные формулы вероятности
Существуют разные формулы для расчета двух типов составных событий: скажем, A и B — два события, затем для взаимоисключающих событий: P (A или B) = P (A) + P (B). Для взаимно включающих событий P (A или B) = P (A) + P (B) — P (A и B).
Используя метод организованного списка, вы должны составить список всех возможных результатов, которые могут произойти. Например, если вы подбрасываете монету и бросаете кубик, какова вероятность выпадения решки и четного числа? Во-первых, нам нужно начать с перечисления всех возможных результатов, которые мы могли бы получить. (h2 означает переворачивание головы и выпадение 1.)
| h2 | Т1 |
| h3 | Т2 |
| h4 | Т3 |
| h5 | Т4 |
| H5 | Т5 |
| H6 | Т6 |
Другой метод — это модель площади.Чтобы проиллюстрировать это, снова рассмотрим подбрасывание монеты и бросок кубика. Какова сложная вероятность выпадения решки и четного числа?
Начните с создания таблицы с результатами одного события, перечисленными вверху, и результатами второго события, перечисленными сбоку. Заполните ячейки таблицы соответствующими результатами для каждого события. Заштрихуйте ячейки, соответствующие вероятности.
Изображение Джули Банг © Investopedia 2020В этом примере двенадцать ячеек, три заштрихованы.Таким образом, вероятность: P = 3/12 = 1/4 = 25 процентов.
Вероятность: независимые события
Жизнь полна случайных событий!
Чтобы он был умным и успешным человеком, нужно его «чувствовать».
Подбрасывание монеты, бросание кубиков и розыгрыш лотереи — все это примеры случайных событий.
Может быть:
Зависимые события , где то, что происходит зависит от того, что произошло раньше, например, если брать карты из колоды, каждый раз получается меньше карт (подробнее см. В разделе «Условная вероятность»), илиНезависимые события , о которых мы узнаем здесь.
Независимые мероприятия
независимых событий — это , на которые не влияют предыдущие события.
Это важная идея!
Монета не «знает», что раньше выпадала орел.
И каждое подбрасывание монеты — совершенно изолированная вещь.
Пример: вы подбрасываете монету, и она трижды выпадает «орел» … каков шанс, что
при следующем подбрасывании также будет «орлом»?Шанс просто ½ (или 0.5) просто как ЛЮБОЙ бросок монеты.
То, что он делал в прошлом, не повлияет на текущий бросок!
Некоторые люди думают, что «это уже поздно для хвоста», но на самом деле следующий бросок монеты полностью не зависит от предыдущих подбрасываний.
Сказать «Хвостик должен» или «еще раз, моя удача изменится» называется Заблуждение игрока
Конечно, ваша удача может измениться , потому что каждый бросок монеты имеет равные шансы.
Вероятность независимых событий
«Вероятность» (или «Шанс») — , насколько вероятно , что что-то должно произойти.
Итак, как рассчитать вероятность?
Вероятность наступления события = Количество способов, которыми это может случиться Общее количество исходов
Пример: какова вероятность получить «голову» при подбрасывании монеты?
Количество способов, которыми это может произойти: 1 (Голова)
Общее количество исходов: 2 (Голова и хвост)
Значит, вероятность = 1 2 = 0.5
Пример: какова вероятность получить «4» или «6» при броске кубика?
Количество способов, которыми это может произойти: 2 («4» и «6»)
Общее количество исходов: 6 («1», «2», «3», «4», «5» и «6»)
Значит, вероятность = 2 6 знак равно 1 3 = 0,333 …
Способы отображения вероятности
Вероятность изменяется от 0 (невозможно) до 1 (точно):
Часто отображается в виде десятичной дроби или дроби .
Пример: вероятность получить «голову» при подбрасывании монеты:
- В десятичном формате: 0,5
- В виде дроби: 1/2
- В процентах: 50%
- Или иногда так: 1-в-2
Два или более событий
Мы можем рассчитать шансы двух или более независимых событий, умножив на шансов.
Пример: вероятность появления 3 голов в ряду
Для каждого подбрасывания монеты вероятность выпадения головы равна 0,5:
.Итак, шанс выпадения 3 решек подряд равен 0,125
.Таким образом, каждый бросок монеты с вероятностью ½ выпадет орлом, но лотов орла подряд маловероятны.
Пример: Почему маловероятно выпадение, скажем, 7 орлов подряд, когда
каждый бросок монеты имеет ½ шанс выпадения орла?Потому что мы задаем два разных вопроса:
Вопрос 1: Какова вероятность выпадения 7 орлов подряд?
Ответ: 1 2 × 1 2 × 1 2 × 1 2 × 1 2 × 1 2 × 1 2 = 0.0078125 (менее 1%)
Вопрос 2: Когда у нас только что выпало 6 орлов подряд, какова вероятность того, что при следующем подбрасывании также является решкой?
Ответ: ½, поскольку предыдущих подбрасываний не влияют на следующий подбрасывание
Вы можете поиграть с Quincunx, чтобы увидеть, как многие независимые эффекты могут иметь узор.
Обозначение
Мы используем «P» для обозначения «Вероятность»,
Итак, для независимых событий:
P (A и B) = P (A) × P (B)
Вероятность A и B равна вероятности A, умноженной на вероятность B
Пример: ваш босс (чтобы быть справедливым) случайным образом назначает всем дополнительные 2 часа работы по вечерам в выходные с 4 до полуночи.
Каковы шансы, что у вас будет суббота между 4 и 6?
День: в выходные два дня, поэтому P (суббота) = 0,5
Время: вы хотите 2 часа «от 4 до 6», из 8 часов из 4 до полуночи):
P («от 4 до 6») = 2/8 = 0,25
А:
| P (суббота и «от 4 до 6») | = P (суббота) × P («от 4 до 6») |
| = 0.5 × 0,25 | |
| = 0,125 |
Или с вероятностью 12,5%
(Примечание: мы ТАКЖЕ могли бы решить, что вам нужно 2 часа из всех возможных 16 часов, что составляет 2/16 = 0,125. Оба метода здесь работают.)
Другой пример
Пример: вероятность задержки рейса составляет 0,2 (= 20%), каковы шансы отсутствия задержек на рейсе туда и обратно
Вероятность того, что рейс не будет задержан, составляет 1 — 0.2 = 0,8 , так что это все возможные результаты:
| 0,8 × 0,8 = | 0,64 шанс без задержек | |
| 0,2 × 0,8 = | 0,16 вероятность задержки первого рейса | |
| 0,8 × 0,2 = | 0,16 вероятность задержки обратного рейса | |
| 0,2 × 0,2 = | 0.04 Вероятность задержки обоих рейсов |
Если сложить все возможности, мы получим:
0,64 + 0,16 + 0,16 + 0,04 = 1,0
Все они добавляют к 1.0, что является хорошим способом проверки наших расчетов.
Результат: 0,64 , или 64% шанс отсутствия задержек
Еще один пример
Представьте, что есть две группы:
- Член каждой группы выбирается случайным образом в круг победителей,
- , затем , один из них случайным образом выбирается для получения большого денежного приза:
Каковы ваши шансы выиграть большой приз?
- есть 1/5 шанс попасть в круг победителей
- и 1/2 шанса выиграть большой приз
Итак, у вас есть шанс 1/5, за которым следует 1/2… что дает шанс 1/10 в целом:
1 5 × 1 2 = 1 5 × 2 = 1 10
Или мы можем вычислить с использованием десятичных знаков (1/5 — 0,2, а 1/2 — 0,5):
0,2 x 0,5 = 0,1
Итак, ваш шанс выиграть большие деньги составляет 0,1 (что равно 1/10).
совпадение!
На самом деле, многие «совпадения» вполне вероятны.
Пример: вы находитесь в комнате с 30 людьми и обнаруживаете, что Зак и Анна празднуют свой день рождения в один и тот же день.
Вы скажете:
- «Ого, как странно!», Или
- «Это кажется разумным, ведь здесь так много людей»
На самом деле существует вероятность 70%, что произойдет … так что это , скорее всего, .
Почему так высок шанс?
Потому что вы сравниваете всех со всеми (а не только одного со многими).
А при 30 человек то есть 435 сравнений
(Прочтите общие дни рождения, чтобы узнать больше.)
Пример: Snap!
Вы когда-нибудь говорили что-то точно в в то же время, что и кто-то другой ?
Ого, как здорово!
Но вы, вероятно, делились опытом (фильм, путешествие, что угодно), и поэтому ваши мысли были схожими.
И есть очень много способов что-то сказать…
… так это похоже на карточную игру «Снап!» (также называется Slap или Slapjack) …
… если вы скажете достаточно слов вместе, они в конечном итоге совпадут.
Так что, может быть, не так уж и здорово, просто случай на работе.
Можете ли вы вспомнить другие случаи, когда «совпадение» было просто вероятным?
Заключение
- Вероятность: (Количество способов, которыми это может произойти) / (Общее количество исходов)
- Зависимые события (например, удаление шариков из мешка) зависят от предыдущих событий
- Независимые события (например, подбрасывание монеты) не затронуты предыдущими событиями
- Мы можем вычислить вероятность двух или более независимых событий, умножив на .
- Не все совпадения действительно маловероятны (если подумать).
Основные правила вероятности »Биостатистика» Колледж общественного здравоохранения и медицинских профессий »Университет Флориды
CO-6: Примените основные концепции вероятности, случайной вариации и обычно используемых статистических распределений вероятностей.
LO 6.4: Связать вероятность события с вероятностью его возникновения.
LO 6.5: Примените подход относительной частоты для оценки вероятности события.
LO 6.6: Примените основные логические и вероятностные правила, чтобы найти эмпирическую вероятность события.
В предыдущем разделе мы ввели вероятность как способ количественно оценить неопределенность , возникающую в результате проведения экспериментов с использованием случайной выборки из интересующей совокупности.
Мы увидели, что вероятность события (например, случай, когда случайно выбранный человек имеет группу крови O) может быть оценена как по относительной частоте , , с которой происходит событие в длинной серии испытаний .Таким образом, мы собирали данные у большого количества людей, чтобы оценить вероятность того, что у кого-то группа крови O.
В этом разделе мы установим базовые методы и принципы для нахождения вероятностей событий.
Мы также рассмотрим некоторые из основных правил вероятности , которые можно использовать для вычисления вероятностей .
Введение
Мы начнем с классического вероятностного примера подбрасывания честной монеты три раза.
Так как орел и решка одинаково вероятны для каждого броска в этом сценарии, каждая из возможностей, которые могут возникнуть в результате трех бросков, также будут одинаково вероятными, так что мы можем перечислить все возможные значения и использовать этот список для расчета вероятностей.
Поскольку наш курс сосредоточен на данных и статистике (а не на теоретической вероятности), в большинстве наших будущих задач мы будем использовать обобщенный набор данных, обычно таблицу частот или двустороннюю таблицу, для вычисления вероятностей.
ПРИМЕР: Трижды подбросьте честную монету
Перечислим все возможные исходы (или возможные результаты):
{HHH, THH, HTH, HHT, HTT, THT, TTH, TTT}
Теперь определим следующие события:
Событие A: «Нет H»
Событие B: «Получение ровно одного H»
Событие C: «Получение хотя бы одного H»
Обратите внимание, что каждое событие на самом деле является заявлением о результате эксперимента.На практике каждое событие соответствует некоторой совокупности (подмножеству) возможных результатов.
Событие A: «Нет H» → TTT
Событие B: «Получение ровно одного H» → HTT, THT, TTH
Событие C: «Получение хотя бы одного H» → HTT, THT, TTH, THH, HTH, HHT, HHH
Вот визуальное представление событий A, B и C.
Из этого визуального представления событий легко увидеть, что событие B полностью включено в событие C в том смысле, что каждый результат в событии B также является результатом события C.Также обратите внимание, что событие A отличается от событий B и C в том смысле, что они не имеют общего результата или не перекрываются. На данный момент это только заслуживающие внимания наблюдения, но, как вы обнаружите позже, они очень важные.
Что, если бы мы добавили новое событие:
Событие D: «Получение T с первого броска» → THH, THT, TTH, TTT
Как бы это выглядело, если бы мы добавили событие D к диаграмме выше? (Ссылка на ответ)
Помните, поскольку H и T равновероятны при каждой подбрасывании, и поскольку существует 8 возможных исходов, вероятность каждого исхода равна 1/8.
Посмотрите, сможете ли вы ответить на следующие вопросы, используя диаграммы и / или список результатов для каждого события, а также то, что вы узнали о вероятности.
Если вы смогли правильно ответить на эти вопросы, у вас, вероятно, есть хороший инстинкт вычисления вероятности! Читайте дальше, чтобы узнать, как мы применим эти знания.
Если нет, мы постараемся помочь вам развить этот навык в этом разделе.
Комментарий:
- Обратите внимание, что в событии C «Получение хотя бы одной головы» отсутствует только один возможный результат: «НЕТ голов» = TTT.Мы обратимся к этому еще раз, когда будем говорить о правилах вероятности, в частности о правиле дополнения. На этом этапе мы просто хотим, чтобы вы подумали о том, что эти два события являются «противоположностями» в этом сценарии.
ОЧЕНЬ важно понимать, что то, что мы можем перечислить возможные результаты, не означает, что каждый результат одинаково вероятен.
Это (забавное) сообщение из ролика Daily Show, который мы представили на предыдущей странице. Но давайте еще раз подумаем об этом.В этом ролике Уолтер утверждает, что, поскольку есть два возможных исхода, вероятность равна 0,5. Два возможных результата:
.- Мир будет разрушен из-за использования большого адронного коллайдера
- Мир НЕ будет разрушен из-за использования большого адронного коллайдера
Надеюсь, ясно, что эти два исхода не одинаково вероятны !!
Давайте рассмотрим более распространенный пример.
ПРИМЕР: Врожденные пороки
Предположим, мы случайным образом выбираем троих детей и интересуемся вероятностью того, что ни у одного из детей нет врожденных дефектов.
Мы используем обозначение D для обозначения ребенка, рожденного с врожденным дефектом, и N для обозначения ребенка, рожденного без врожденного дефекта. Мы можем перечислить возможные результаты так же, как и при подбрасывании монеты, это:
{DDD, NDD, DND, DDN, DNN, NDN, NND, NNN}
Являются ли события DDD (все трое детей рождаются с врожденными дефектами) и NNN (ни один из детей не родился с врожденными дефектами) равновероятны?
Для вас должно быть разумным, что P (NNN) намного больше, чем P (DDD) .
Это потому, что P (N) и P (D) не являются одинаково вероятными событиями.
Редко (конечно, не 50%) случайно выбранный ребенок рождается с врожденным дефектом.
Правила вероятности
Теперь мы переходим к изучению некоторых основных правил вероятности.
К счастью, эти правила очень интуитивно понятны, и если они применяются систематически, они позволят нам решать более сложные проблемы; в частности, те проблемы, для решения которых наша интуиция может быть неадекватной.
Начиная с , большинство вероятностей, которые вас попросят найти, можно вычислить как , используя как
и
- правила, которые мы будем изучать,
мы даем следующие советы в качестве принципа.
ПРИНЦИП:
Если вы можете рассчитать вероятность, используя логику и подсчет, вам НЕ НУЖНО правило вероятности (хотя всегда можно применить правильное правило)
Правило вероятности 1
Наше первое правило просто напоминает нам об основном свойстве вероятности, которое мы уже узнали.
Вероятность события, которая информирует нас о вероятности его возникновения, может варьироваться от 0 (указывает, что событие никогда не произойдет) до 1 (указывает, что событие обязательно).
Правило вероятности первое:
- Для любого события A, 0 ≤ P (A) ≤ 1.
ПРИМЕЧАНИЕ: Одно из практических применений этого правила состоит в том, что его можно использовать для идентификации любого вычисления вероятности, которое оказывается больше 1 (или меньше 0), как неправильное.
Прежде чем перейти к другим правилам, давайте сначала рассмотрим пример, который предоставит контекст для иллюстрации следующих нескольких правил.
ПРИМЕР: Группа крови
Как обсуждалось ранее, вся кровь человека может быть типизирована как O, A, B или AB.
Кроме того, частота встречаемости этих групп крови зависит от этнических и расовых групп.
По данным Центра крови Стэнфордского университета (bloodcenter.stanford.edu), это вероятности групп крови человека в Соединенных Штатах (вероятность для группы A была намеренно опущена):
Мотивирующий вопрос для правила 2: Человек в Соединенных Штатах выбирается случайным образом.Какова вероятность того, что у человека группа крови А?
Ответ: Наша интуиция подсказывает нам, что, поскольку четыре группы крови O, A, B и AB исчерпывают все возможности, их вероятности вместе должны составлять 1, что является вероятностью «определенного» события (у человека есть одна из этих 4 групп крови наверняка).
Поскольку суммы вероятностей O, B и AB вместе составляют 0,44 + 0,1 + 0,04 = 0,58 , вероятность типа A должна равняться оставшимся 0.42 (1 — 0,58 = 0,42):
Правило 2 вероятности
Этот пример иллюстрирует наше второе правило, которое говорит нам, что вероятность всех возможных результатов вместе должна быть 1.
Правило вероятности два:
Сумма вероятностей всех возможных исходов равна 1 .
Это хорошее место для сравнения и сопоставления того, что мы делаем здесь, с тем, что мы узнали в разделе Исследовательский анализ данных (EDA).
- Обратите внимание, что в этой задаче мы по существу сосредоточены на одной категориальной переменной: группе крови.
- Мы суммировали эту переменную выше, как мы суммировали отдельные категориальные переменные в разделе EDA, перечислив, какие значения принимает переменная и как часто она их принимает.
- В EDA мы использовали проценты, а здесь мы используем вероятности, но они передают одну и ту же информацию.
- В разделе EDA мы узнали, что круговая диаграмма обеспечивает соответствующее отображение, когда задействована единственная категориальная переменная, и аналогичным образом мы можем использовать ее здесь (используя проценты вместо вероятностей):
Хотя то, что мы делаем здесь, действительно похоже на то, что мы делали в разделе EDA, есть тонкое, но важное различие между основными ситуациями.
- В EDA мы суммировали данные, полученные из выборки лиц, для которых были зарегистрированы значения интересующей переменной.
- Здесь, когда мы представляем вероятность каждой группы крови, мы имеем в виду все населения человек в Соединенных Штатах, для которых мы предполагаем, что знаем общую частоту значений, принимаемых интересующей переменной.
Правило 3 вероятности
Что касается вероятности и ее приложений, нас часто интересует вероятность того, что определенное событие произойдет , а не .
Здесь важно понимать, что «событие A не происходит» — это отдельное событие , которое состоит из всех возможных результатов, которых нет в A, и называется « дополнительным событием A .”
Обозначение: мы будем писать «не А» , чтобы обозначить событие, при котором А не происходит , а не . Вот визуальное представление того, как событие А и дополнительное к нему событие «не А» вместе представляют все возможные результаты.
Комментарий:
- Такое визуальное отображение называется «диаграммой Венна». Диаграмма Венна — это простой способ визуализировать события и отношения между ними с помощью прямоугольников и кругов.
Правило 3 касается взаимосвязи между вероятностью события и вероятностью его дополнительного события.
Учитывая, что событие А и событие «не А» вместе составляют все возможные исходы, и поскольку правило 2 говорит нам, что сумма вероятностей всех возможных исходов равна 1, следующее правило должно быть довольно интуитивным:
Правило вероятности третье (Правило дополнения):
- P (не A) = 1 — P (A)
- , то есть вероятность того, что событие не произойдет, равна 1 минус вероятность того, что оно действительно произойдет.
ПРИМЕР: Группа крови
Вернуться к примеру группы крови:
Дополнительная информация:
- Человек с типом A может сдать кровь человеку с типом A или AB .
- Человек с типом B может сдать кровь человеку с типом B или AB .
- Человек с типом AB может сдавать кровь только человеку с типом AB .
- Человек с кровью типа O может сдавать кровь кому угодно.
Какова вероятность того, что случайно выбранный человек не сможет сдать кровь всем? Другими словами, какова вероятность того, что случайно выбранный человек не имеет группы крови O? Нам нужно найти P (не O).Используя правило дополнения, P (не O) = 1 — P (O) = 1 — 0,44 = 0,56. Другими словами, 56% населения США не имеют группы крови O:
.Очевидно, что мы также могли бы найти P (не O) напрямую, сложив вероятности B, AB и A.
Комментарий:
- Обратите внимание, что правило дополнения P (not A) = 1 — P (A) может быть переформулировано как P (A) = 1 — P (not A).
- P (не A) = 1 — P (A)
- можно переформулировать как P (A) = 1 — P (не A).
- Эта, казалось бы, тривиальная алгебраическая манипуляция имеет важное применение и фактически отражает силу правила дополнения.
- В некоторых случаях, когда найти P (A) напрямую очень сложно, может быть намного проще найти P (не A), а затем просто вычесть его из 1, чтобы получить желаемое P (A).
- Мы скоро вернемся к этому комментарию и предоставим дополнительные примеры.
Комментарии:
- Правило дополнения может быть полезно, когда легче вычислить вероятность дополнения события, чем самого события.
- Обратите внимание, мы снова использовали фразу «хотя бы один».
- Теперь мы увидели, что дополнение «по крайней мере один…» равно «нет…» или «нет…». (как мы упоминали ранее, говоря о том, что события являются «противоположностями»).
- В приведенном выше упражнении мы видим, что
- P (НЕТ из этих двух побочных эффектов) = 1 — P (по крайней мере, один из этих двух побочных эффектов)
- Это обычное применение правила дополнения, которое часто можно узнать по фразе «хотя бы один» в задаче.
Вероятности, включающие несколько событий
Нам часто будет интересно найти вероятности, включающие несколько событий, например
- P (A или B) = P (происходит событие A, или событие B, или оба события)
- P (A и B) = P (происходит как событие A, так и событие B)
Общая проблема с терминологией связана с тем, как мы обычно думаем о «или» в повседневной жизни. Например, когда родитель говорит своему ребенку в магазине игрушек: «Ты хочешь игрушку А или игрушку Б?», Это означает, что ребенок получит только одну игрушку, и ему придется выбирать между ними.Получение обеих игрушек обычно не вариант.
В отличие от:
С вероятностью «ИЛИ» означает либо одно, либо другое, либо и то, и другое.
и поэтому P (A или B) = P (происходит событие A, или событие B, или ОБА)
Сказав это, следует отметить, что в некоторых случаях просто невозможно, чтобы оба события произошли одновременно.
Правило вероятности четыре
Различие между событиями, которые могут произойти вместе, и теми, которые не могут произойти, является важным.
Несвязанный: Два события, которые не могут произойти одновременно, называются несвязанными или взаимоисключающими. (Мы будем использовать непересекающиеся.)
Из рисунка должно быть ясно, что
- в первом случае, когда события НЕ не пересекаются, P (A и B) ≠ 0
- во втором случае, когда события НЕ пересекаются, P (A и B) = 0.
Вот два примера:
ПРИМЕР:
Рассмотрим следующие два события:
A — случайно выбранный человек имеет группу крови A, и
B — случайно выбранный человек имеет группу крови B.
В редких случаях у человека может быть более одного типа крови, протекающей по его или ее венам, но для наших целей мы будем предполагать, что у каждого человека может быть только одна группа крови. Следовательно, события A и B не могут происходить вместе.
- События A и B — DISJOINT
С другой стороны…
ПРИМЕР:
Рассмотрим следующие два события:
A — случайно выбранный человек имеет группу крови A
B — случайно выбранный человек — женщина.
В этом случае возможно, события A и B произойдут вместе.
- События A и B НЕ РАЗЪЕДИНЕННЫЕ.
Диаграммы Венна предполагают, что другой способ думать о непересекающихся и не пересекающихся событиях состоит в том, что непересекающиеся события не перекрывают . У них нет общих возможных результатов, и поэтому они не могут произойти вместе.
С другой стороны, неразделимые события перекрываются в том смысле, что они разделяют некоторые из возможных результатов и, следовательно, могут происходить одновременно.
Теперь мы начнем с простого правила нахождения P (A или B) для непересекающихся событий.
Правило вероятности четвертое (правило сложения для непересекающихся событий):
- Если A и B — непересекающиеся события, то P (A или B) = P (A) + P (B).
Комментарий:
- При работе с вероятностями слово «или» всегда будет ассоциироваться с операцией сложения; отсюда и название этого правила — «Правило сложения».
ПРИМЕР: Группа крови
Вспомните пример группы крови:
Дополнительная информация
- Человек с типом A может сдать кровь человеку с типом A или AB .
- Человек с типом B может сдать кровь человеку с типом B или AB .
- Человек с типом AB может сдать кровь человеку с типом AB
- Человек с кровью типа O может сдавать кровь кому угодно.
Какова вероятность того, что случайно выбранный человек станет потенциальным донором для человека с группой крови A?
Из предоставленной информации мы знаем, что быть потенциальным донором для человека с группой крови A означает иметь группу крови A или O.
Следовательно, нам нужно найти P (A или O). Поскольку события A и O не пересекаются, мы можем использовать правило сложения для непересекающихся событий, чтобы получить:
- P (A или O) = P (A) + P (O) = 0,42 + 0,44 = 0,86.
Легко понять, почему добавление вероятности действительно имеет смысл.
Если 42% населения имеет группу крови A, а 44% населения имеет группу крови O,
- , то 42% + 44% = 86% населения имеют группу крови A или O и, следовательно, являются потенциальными донорами человека с группой крови A.
Это рассуждение о том, почему правило сложения имеет смысл, можно визуализировать с помощью круговой диаграммы ниже:
Комментарий:
- Правило сложения для непересекающихся событий естественным образом может быть расширено на более чем два непересекающихся события. Возьмем, к примеру, три. Если A, B и C — три непересекающихся события
, то P (A или B или C) = P (A) + P (B) + P (C). Правило одинаково для любого количества непересекающихся событий.
Теперь мы закончили с первой версией правила сложения (правило четыре), которое ограничено версией непересекающихся событий.Прежде чем рассматривать вторую версию, мы должны сначала обсудить P (A и B).
Поиск P (A и B) с использованием логики
Перейдем к вычислению
- P (A и B) = P (происходит как событие A, так и событие B)
Позже мы обсудим правила вычисления P (A и B).
Во-первых, мы хотим проиллюстрировать, что правило не требуется, если вы можете определить ответ с помощью логики и подсчета.
Особый случай:
Есть один особый случай, для которого мы знаем, что равно P (A и B), не применяя никаких правил.
Итак, если события A и B не пересекаются , то (по определению) P (A и B) = 0. Но что, если события не пересекаются?
Напомним, что у правила 4, правила сложения, есть две версии. Один ограничен непересекающимися событиями, которые мы уже рассмотрели, и мы рассмотрим более общую версию позже в этом модуле. То же самое будет верно для вероятностей с участием AND
Однако , за исключением особых случаев, мы будем полагаться на ЛОГИКУ, чтобы найти P (A и B) в этом курсе.
Прежде чем рассматривать какие-либо формальные правила, давайте рассмотрим пример, в котором события не пересекаются.
ПРИМЕР: Периодонтальный статус и пол
Рассмотрим следующую таблицу, касающуюся пародонтального статуса людей и их пола. Пародонтальный статус относится к заболеванию десен, при котором люди классифицируются как здоровые, страдающие гингивитом или заболеванием пародонта.
Мы уже видели этот тип таблиц раньше, когда обсуждали анализ данных в случае C → C.Для этого вопроса мы будем использовать эти данные как нашу «совокупность» и рассмотрим случайный выбор одного человека.
Нам нравится задавать вероятностные вопросы, аналогичные предыдущему примеру (с использованием двусторонней таблицы, основанной на данных), поскольку это позволяет вам устанавливать связи между этими темами и помогает сохранить в памяти некоторые из того, что вы узнали о данных.
Помните, наша основная цель в этом курсе — анализировать реальные данные!
Правило 5 вероятности
Теперь мы готовы перейти к расширенной версии правила сложения.
В этом разделе мы узнаем, как найти P (A или B), когда A и B не обязательно не пересекаются.
- Мы назовем эту расширенную версию «Общим дополнительным правилом » и обозначим ее как «Правило вероятности № 5 ».
Мы начнем с формулировки правила и приведем пример, аналогичный типам задач, которые мы обычно задаем в этом курсе. Затем мы представим еще один пример, в котором у нас нет необработанных данных из образца для работы.
Правило 5 вероятности:
- Общее правило сложения: P (A или B) = P (A) + P (B) — P (A и B).
ПРИМЕЧАНИЕ. Для поиска P (A и B) лучше всего использовать логику , а не другую формулу.
ОЧЕНЬ распространенная ошибка — неправильное применение правила умножения для независимых событий, описанных на следующей странице. Это будет правильно, только если A и B независимы (см. Определения ниже), что редко бывает в данных, представленных в двусторонних таблицах.
Как мы видели в предыдущих примерах, когда два события не пересекаются, между ними есть некоторое перекрытие.
- Если мы просто сложим две вероятности вместе, мы получим неправильный ответ, потому что мы дважды посчитали некоторую «вероятность»!
- Таким образом, мы должны вычесть эту «дополнительную» вероятность, чтобы прийти к правильному ответу. Диаграмма Венна и двусторонние таблицы помогают визуализировать эту идею.
Это правило является более общим, поскольку оно работает для любой пары событий (даже для непересекающихся событий).Мы советуем по-прежнему пытаться ответить на вопрос, используя логику и подсчет, когда это возможно, в противном случае мы должны быть очень осторожны, чтобы выбрать правильное правило для проблемы.
ПРИНЦИП:
Если вы можете рассчитать вероятность, используя логику и подсчет, вам НЕ НУЖНО правило вероятности (хотя всегда можно применить правильное правило)
Обратите внимание, что если A и B не пересекаются, то P (A и B) = 0 и правило 5 сводится к правилу 4 для этого особого случая.
Вернемся к последнему примеру:
ПРИМЕР: Периодонтальный статус и пол
Рассмотрите возможность случайного выбора одного человека из представленных в следующей таблице относительно пародонтального статуса людей и их пола. Пародонтальный статус относится к заболеванию десен, при котором люди классифицируются как здоровые, страдающие гингивитом или заболеванием пародонта.
Давайте посмотрим, что мы узнали на данный момент. Мы можем рассчитать любую вероятность в этом сценарии, если сможем определить, сколько людей удовлетворяют событию или комбинации событий.
- P (Мужской) = 3009/8027 = 0,3749
- P (Женский) = 5018/8027 = 0,6251
- P (Здоровый) = 3750/8027 = 0,4672
- P (не здоровый) = P (гингивит или перио) = (2419 + 1858) / 8027 = 4277/8027 = 0,5328
Мы также можем вычислить это, используя правило дополнения: 1 — P (здоровый)
Ранее мы также обнаружили, что
- P (Мужчина И Здоровый) = 1143/8027 = 0,1424
Вспомните правило 5, P (A или B) = P (A) + P (B) — P (A и B).Теперь мы используем это правило для расчета P (мужчина ИЛИ здоровый)
.- P (мужчина или здоровый) = P (мужчина) + P (здоровый) — P (мужчина и здоровый) = 0,3749 + 0,4672 — 0,1424 = 0,6997 или около 70%
Ранее мы решили этот вопрос, просто посчитав, сколько человек являются мужчинами, здоровыми или и тем, и другим. На рисунке ниже показаны значения, которые нам нужно объединить. Нам нужно сосчитать
- Все мужчины
- Все здоровые
- НО, дважды не считать никого !!
Используя этот логический подход, мы найдем
- P (мужчина или здоровый) = (1143 + 929 + 937 + 2607) / 8027 = 5616/8027 = 0.6996
У нас есть небольшая разница в наших ответах в последнем десятичном разряде из-за округления, которое произошло, когда мы вычислили P (мужской), P (здоровый) и P (мужской и здоровый), а затем применили правило 5.
Ясно, что ответ практически тот же, около 70%. Если бы мы перенесли наши ответы на большее количество знаков после запятой или использовали исходные дроби, мы могли бы полностью устранить это небольшое расхождение.
Давайте рассмотрим последний пример, чтобы проиллюстрировать правило вероятности 5, когда это правило необходимо — i.е. когда у нас нет фактических данных.
ПРИМЕР: Важная доставка!
Очень важно, чтобы определенный документ был доставлен по назначению в течение одного дня. Чтобы максимизировать шансы своевременной доставки, две копии документа отправляются с использованием двух служб, службы A и службы B. Известно, что вероятность своевременной доставки составляет:
- 0,90 для услуги A ( P (A) = 0,90 )
- 0,80 для услуги B ( P (B) = 0,80 )
- 0,75 для обоих сервисов вовремя ( P (A и B) = 0.75 )
(Обратите внимание, что A и B не являются или не пересекаются . Они могут произойти вместе с вероятностью 0,75.)
Диаграммы Венна ниже иллюстрируют вероятности P (A), P (B) и P (A и B) [не в масштабе]:
В контексте этой проблемы очевиден интересующий вопрос:
- Какова вероятность своевременной доставки документа с использованием этой стратегии (отправки через обе службы)?
Документ будет доставлен в пункт назначения вовремя, если он будет доставлен вовремя службой A, службой B или обеими службами.Другими словами, когда происходит событие A, или событие B, или то и другое одновременно. так….
P (своевременная доставка с использованием этой стратегии) = P (A или B) , что представлено заштрихованной областью на диаграмме ниже:
Теперь мы можем
- использовать три диаграммы Венна, представляющие P (A), P (B) и P (A и B)
- , чтобы увидеть, что мы можем найти P (A или B) , добавив P (A) (представлен левым кружком) и P (B) (представлен правым кружком),
- затем вычитает P (A и B) (представленное перекрытием), , так как мы включили его дважды, один раз как часть P (A) и один раз как часть P (B).
Это показано на следующем изображении:
Если мы применим это к нашему примеру, мы обнаружим, что:
- P (A или B) = P (своевременная доставка с использованием этой стратегии) = 0,90 + 0,80 — 0,75 = 0,95.
Таким образом, наша стратегия использования двух служб доставки увеличивает вероятность своевременной доставки до 0,95.
Хотя диаграммы Венна отлично подходят для визуализации общего правила сложения, в подобных случаях гораздо проще отображать информацию и работать с двусторонней таблицей вероятностей, так же как мы исследовали взаимосвязь между двумя категориальными переменными в Раздел исследовательского анализа данных.
Мы просто покажем вам таблицу, а не то, как мы ее составили, поскольку вас не попросят сделать это за нас. Вы должны увидеть, что некоторая логика и простое сложение / вычитание — это все, что мы использовали для заполнения таблицы ниже.
При использовании двусторонней таблицы мы должны не забывать смотреть на всю строку или столбец, чтобы найти общие вероятности, включающие только A или только B.
- P (A) = 0,90 означает, что в 90% случаев, когда используется услуга A, она доставляет документ вовремя.Чтобы найти это, мы смотрим на полную вероятность строки, содержащей A. При нахождении P (A) мы не знаем, произойдет B или нет.
- P (B) = 0,80 означает, что в 80% случаев, когда используется услуга B, она доставляет документ вовремя. Чтобы найти это, мы смотрим на полную вероятность столбца, содержащего B. При нахождении P (B) мы не знаем, произойдет A или нет.
Комментарий
- Когда мы использовали двусторонние таблицы в разделе исследовательского анализа данных (EDA), нам нужно было записать значения двух категориальных переменных для конкретной выборки человек.
- Напротив, информация в двусторонней таблице вероятностей предназначена для всей генеральной совокупности , и значения довольно абстрактны.
- Если бы мы рассмотрели что-то вроде примера доставки в разделе EDA, мы бы записали фактическое количество своевременных (и несвоевременных) доставок для образцов документов, отправленных по почте с помощью службы A или B.
- В этом разделе долгосрочные вероятности представлены как известные .
- Предположительно, указанные вероятности в этом примере доставки были основаны на относительных частотах, записанных во многих повторениях.
Правило округления для вероятности:
Следуйте приведенным ниже общим рекомендациям в этом курсе. В случае сомнений укажите больше десятичных знаков. Если укажем, дайте именно то, что требуется
- Как правило, для промежуточных шагов следует приводить вероятности как минимум к 4 десятичным знакам.
- Мы часто округляем окончательный ответ до двух или трех десятичных знаков.
- Для чрезвычайно малых вероятностей важно иметь 1 или две значащие цифры (ненулевые цифры), например 0.000001 или 0,000034 и т. Д.
Многие компьютерные пакеты могут отображать очень маленькие значения с использованием научных обозначений, таких как
.- 58 × 10 -5 или 1,58 E -5 для представления 0,0000158
Подведем итоги
Итак, в нашем исследовании вероятности вы познакомились с иногда нелогичной природой вероятности и фундаментальными принципами, лежащими в основе вероятности, такими как относительная частота .
Мы также предоставили вам несколько инструментов, которые помогут вам определить вероятности событий, а именно правила вероятности .
Вы, наверное, заметили, что раздел вероятностей значительно отличался от двух предыдущих разделов; он имеет гораздо больший технический / математический компонент, поэтому результаты, как правило, носят скорее «правильный или неправильный» характер.
В разделе «Исследовательский анализ данных», по большей части, компьютер заботился о технических аспектах вещей, и наши задачи заключались в том, чтобы указать ему, чтобы он действовал правильно, а затем интерпретировать результаты.
Вероятно, мы выполняем работу от начала до конца, от выбора правильного инструмента (правила) для использования, до его правильного использования и до интерпретации результатов.
Вот краткое изложение правил, которые мы уже представили.
1. Правило вероятности № 1 гласит:
- Для любого события A, 0 ≤ P (A) ≤ 1
2. Правило вероятности № 2 гласит:
- Сумма вероятностей всех возможных исходов 1
3.Правило дополнения (# 3) гласит, что
или при перестановке
Последнее представление правила дополнения особенно полезно, когда нам нужно найти вероятности событий типа «по крайней мере одно из…»
4. Общее правило сложения (# 5) гласит, что для любых двух событий
- P (A или B) = P (A) + P (B) — P (A и B),
где под P (A или B) мы подразумеваем P (встречается A, встречается B или и то, и другое).
В особом случае непересекающихся событий , событий, которые не могут происходить вместе, общее правило сложения может быть сокращено до правила сложения для непересекающихся событий (# 4), которое равно
- P (A или B) = P (A) + P (B).

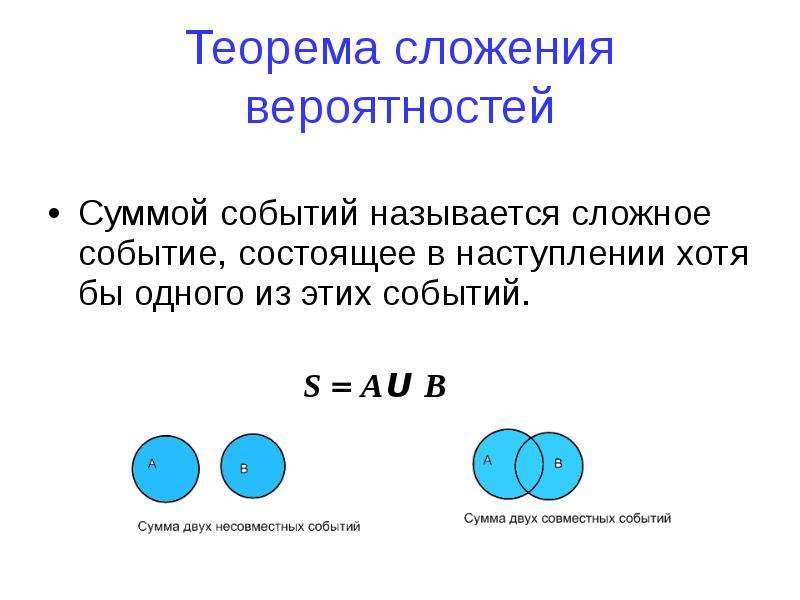
 Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами. Определите вероятность того, что цифры на красном и синем кубиках совпадут.
Определите вероятность того, что цифры на красном и синем кубиках совпадут.

